Технологии программирования (Возникновение теории кодирования)

Содержание:

ВВЕДЕНИЕ

Целью написания курсовой работы является изучение основных методов кодирования данных в информационных системах и определение связи с такими научными дисциплинами, как теория кодирования и теория информации.

Предметом является совокупность процессов преобразования данных в иную форму, предназначенную для хранения в памяти компьютера, а так же, передачи и защиты от несанкционированного доступа.

При написании курсовой были использованы различные учебники по теории информации, кибернетике, алгоритмам, сжатию информации и прочим, связанным с технологиями программирования, дисциплинам.

Помимо учебников были изучены переводы статей, написанных авторами исследуемых теорий.

1. Сущность кодирования данных в информационных системах.

1.1 Возникновение теории кодирования

Теория кодирования и теория информации возникли в начале XX века.

Теория информации это раздел прикладной математики, радиотехники (теория обработки сигналов) и информатики, относящийся к измерению количества информации, её свойств и устанавливающий предельные соотношения для систем передачи данных. Как и любая математическая теория, она оперирует математическими моделями, а не реальными физическими объектами (источниками и каналами связи). Использует, главным образом, математический аппарат теории вероятностей и математической статистики. [2]

Суть теории кодирования заключается в решении задачи выбора (отыскания) кода, оптимального по тому или иному критерию.[4]

Начало развитию этих теорий как научных дисциплин положило появление в 1948 г. Статей Клода Шеннона, которые заложили фундамент для дальнейших исследований в этой области.

Само понятие теории информации появилось задолго до публикации этой статьи. Множество авторов своими работами создавали базу для новой теории. К примеру, в 1924 году в журнале компании «Bell System» была публикация Найквиста, которая содержала в себе некоторые положения, послужившие основой для данной статьи.[12]

При публикации Шеннон не думал, что она станет важным открытием. Математик в значительной мере опирался на опыт предшественников. Выделяя это, он в самом начале статьи пишет: «Некоторые основные положения этой теории имеются в важных работах Найквиста и Хартли. В настоящей статье мы расширим теорию с тем, чтобы включить некоторое число новых факторов, в частности, влияние шума в канале»[5]

1.2 Модель передачи данных

По мнению Шеннона, теория информации — раздел математической теории связи. Теория информации определяет основные границы возможностей систем передачи информации, задает первичные принципы их разработки и практического применения. Задачи теории информации представляются с помощью структурной схемы, стандартной системы передачи или хранения информации. [9] Схема системы связи изображена на рисунке 1 в приложении.

Источником в схеме является любой объект, формирующий сообщения, передающиеся во времени и пространстве. Все подлежащие передаче сообщения, независимо от их изначальной физической природы, преобразовываются в форму электрических сигналов, которые являются - выходом источника.

Кодер источника представляет эти электрические сигналы в наиболее компактном виде.

Кодер канала обрабатывает полученную информацию для предохранения сообщений от помех при передаче по каналу связи или возможных искажений при хранении данных.

Модулятор перерабатывает информацию, созданную кодером канала, в сигналы, согласованные с физической природой канала связи или средой накопителя информации.

Среда распространения информации (канал связи) делает процесс прочтения информации более проблематичным за счёт внесения в передаваемое сообщение случайных шумов, искажающих его.

Блоки, на стороне приёмника действуют в обратном порядке по той же схеме, в итоге предоставляя получателю исходную информацию в удобном для понимания формате.

Сложность трансляции информации не зависит от его сути, так передавать сообщения, не имеющие смысловой нагрузки одинаково сложно, как и осмысленные.

Информацию можно выразить и как свойство объектов, и как результат их взаимодействия. Факт объективного существования информации независимо от нашего сознания для некоторых исследователей послужил поводом построения весьма неординарной точки зрения, что информация является третьей (наряду с материей и энергией) субстанцией материального мира. Но для информации пока не сформулировано фундаментальных законов сохранения и перехода в эквивалентное количество материи и/или энергии. На данный момент принято считать, что информация существует независимо от того, воспринимается она или нет, но проявляется только при взаимодействии.

1.3 Понятие кодирования информации

Другой вариант изображения «модели системы передачи сигналов» показан на рисунке 2.

Начальным звеном в приведенной модели является источник информации.

Рассмотрим дискретные источники без памяти, в которых выходом является последовательность символов некоторого фиксированного алфавита.

Множество всех различных символов, порождаемых некоторым источником, называется алфавитом источника, количество символов в этом множестве – размер алфавита источника.

Например, текст на русском языке порождается источником с алфавитом из 33 русских букв, пробела и знаков препинания.

Кодирование дискретного источника заключается в сопоставлении символов алфавита А источника символам некоторого другого алфавита В.

Обычно символу исходного алфавита А ставится в соответствие не один, а группа символов алфавита В, которая называется кодовым словом.

Кодовый алфавит – множество различных символов, используемых для записи кодовых слов.

Кодом называется совокупность всех кодовых слов, применяемых для представления порождаемых источником символов. Например, азбука Морзе является известным кодом из символов телеграфного алфавита, в котором буквам русского языка соответствуют кодовые слова (последовательности) из «точек» и «тире».

Далее будем рассматривать двоичное кодирование, т.е. размер кодового алфавита равен 2.

Конечную последовательность битов (нулей или единиц) назовем кодовым словом, а количество битов в этой последовательности – длиной кодового слова.

Например код ASCII (американский стандартный код для обмена информацией) каждому символу ставит в однозначное соответствие кодовое слово длиной 8 бит. Пример таблицы ASCII можно посмотреть на рисунке 3.

Кодирование  — это процесс преобразования данных из формы, удобной для непосредственного использования, в форму, удобную для передачи, хранения, автоматической переработки и сохранения от несанкционированного доступа. [4] К основным проблемам теории кодирования относят вопросы взаимной однозначности кодирования и сложности реализации канала связи при заданных условиях  

В связи с развитием информационных технологий кодирование является центральным вопросом при решении самых разных задач программирования, таких как:

• представление данных произвольной структуры (числа, текст, графика) в памяти компьютера;
• обеспечение помехоустойчивости при передаче данных по каналам связи;
• сжатие информации в базах данных.

Дадим строгое определение кодирования.

Пусть даны алфавит источника A = {a1,a2,…an}, кодовый алфавит B = {b1,b2,…,bn}.

Обозначим через A* множество всевозможных последовательностей в алфавите А. Множество всех сообщений в алфавите А обозначим S. Тогда отображение F: S→B*, которое преобразует множество сообщений S в кодовые слова в алфавите В, называется кодированием. Обратное отображение F-1 (если оно существует) называется декодированием.

Задача кодирования сообщения ставится следующим образом:

требуется при заданных алфавитах А и В и множестве сообщений S найти такое кодирование F, которое обладает определенными свойствами и оптимально в некотором смысле.

Свойства, которые требуются от кодирования, могут быть различными. Некоторые из них:

• существование декодирования;
• помехоустойчивость или исправление ошибок при кодировании;
• заданная трудоемкость (время, объем памяти).

Известны два класса методов кодирования дискретного источника информации: равномерное и неравномерное кодирование.

Под равномерным кодированием понимается использование кодов со словами постоянной длины. Для того чтобы декодирование равномерного кода было возможным, разным символам алфавита источника должны соответствовать разные кодовые слова. При этом длина кодового слова должна быть не меньше log_nm символов, где m – размер исходного алфавита, n – размер кодового алфавита.

Пример.

Для кодирования источника, порождающего 26 букв латинского алфавита, равномерным двоичным кодом требуется построить кодовые слова длиной не меньше log_nm=5 бит.

При неравномерном кодировании источника используются кодовые слова разной длины. Причем кодовые слова обычно строятся так, что часто встречающиеся символы кодируются более короткими кодовыми словами, а редко встречающиеся символы – более длинными кодовыми словами. За счет этого и достигается «сжатие» данных.

Под сжатием данных понимается компактное представление данных, достигаемое за счет избыточности информации, содержащейся в сообщениях.

Большое значение для практического использования имеет неискажающее сжатие, позволяющее полностью восстановить исходное сообщение.

При неискажающем сжатии происходит кодирование сообщения перед началом передачи или хранения, а после окончания процесса сообщение однозначно декодируется. Это соответствует модели канала без шума (помех).

Методы сжатия данных можно разделить на две группы:

• статические методы;
• адаптивные методы.

Статические методы сжатия данных предназначены для кодирования конкретных источников информации с известной статистической структурой, порождающих определенное множество сообщений.

Эти методы базируются на знании статистической структуры исходных данных.

К наиболее известным статическим методам сжатия относятся коды Хаффмана, Шеннона - Фано, Гилберта-Мура, арифметический код и другие методы, которые используют известные сведения о вероятностях порождения источником различных символов или их сочетаний.

Если статистика источника информации неизвестна или изменяется с течением времени, то для кодирования сообщений такого источника применяются адаптивные методы сжатия.

В адаптивных методах при кодировании очередного символа текста используются сведения о ранее закодированной части сообщения для оценки вероятности появления очередного символа.

В процессе кодирования адаптивные методы «настраиваются» на статистическую структуру кодируемых сообщений, т.е. коды символов меняются в зависимости от накопленной статистики данных.

Это позволяет адаптивным методам эффективно и быстро кодировать сообщение за один просмотр.

В данной главе мы рассмотрели понятия двух основополагающих теорий – теории информации и теории кодирования. Был определён ключевой момент в истории, положивший фундамент в развитии рассматриваемого направления информатики. Так же была описана основная модель системы передачи данных от отправителя до получающей стороны. И в итоге было выведено понятие кодирования информации: на каком этапе передачи данных оно происходит, какие решает задачи, на какие методы условно делится.

Описанное выше раскрывает сущность кодирования данных, его основные вопросы и процессы. В связи с этим глава и имеет соответствующее название.

Если формулировать основные причины, по которым кодирование информации необходимо и актуально в наше время, на мой взгляд, это будут передача информации по каналам связи и защита её от несанкционированного доступа. Примеры основных методов кодирования данных будут представлены в следующей главе.

2. Основные методы кодирования данных

2.1 Кодирование целых чисел

Рассмотрим семейство методов кодирования, не учитывающих вероятности появления символов источника. Поскольку все символы алфавита источника можно пронумеровать, то будем считать, что алфавит источника состоит из целых чисел.

Каждому целому числу из определенного диапазона ставится в соответствие свое кодовое слово. Поэтому эту группу методов также называют представлением целых чисел (representation of integers).

Основная идея кодирования целых чисел: отдельно кодировать порядок значения элемента («экспоненту» ) и отдельно – значащие цифры значения («мантиссу» i).

Значащие цифры мантиссы начинаются со старшей ненулевой цифры, порядок числа определяется позицией старшей ненулевой цифры в двоичной записи числа.

Как и при десятичной записи, порядок равен числу цифр в записи числа без предшествующих незначащих нулей.

Пример:

Двоичное число 000001101
Порядок равен 4, мантисса – 1101

Рассмотрим две группы методов кодирования целых чисел. Условно их можно обозначить так:

• Fixed + Variable (фиксированная длина порядка + переменная длина мантиссы)
• Variable + Variable (переменная длина порядка + переменная длина мантиссы)

В кодах класса Fixed + Variable под запись значения порядка числа отводится фиксированное количество бит, а значение порядка числа определяет, сколько бит потребуется под запись мантиссы.

Для кодирования целого числа необходимо произвести с числом две операции:

• определение порядка числа
• выделение бит мантиссы

Можно также хранить в памяти заранее построенную таблицу кодовых слов и по ней получать код числа.

2.1.1 Код класса Fixed + Variable

Пусть R = 15 – количество бит исходного числа.

Отведем E = 4 бита под порядок, т.к. R ≤ 2⁴.

При записи мантиссы можно сэкономить 1 бит: не писать первую единицу, т.к. это всегда будет только единица.

Таким образом, количество бит мантиссы меньше на один бит, чем значение порядка числа.

Таблица 1

Коды чисел класса Fixed + Variable

Число	Двоичное представление	Кодовое слово	Длина кодового слова
0 1	000000000000000 000000000000001	0000 0001	4
2 3	000000000000010 000000000000011	0010 0 0010 1	5
4 5 6 7	000000000000100 000000000000101 000000000000110 000000000000111	0011 00 0011 01 0011 10 0011 11	6
8 9 10 … 15	000000000001000 000000000001001 000000000001010 … 000000000001111	0100 000 0100 001 0100 010 … 0100 111	7
16 17 …	000000000010000 000000000010001 …	0101 0000 0101 0001 …	8

2.1.2 Код класса Variable + Variable

В качестве кода числа берется двоичная последовательность, построенная следующим образом: несколько нулей (количество нулей равно значению порядка числа), затем мантисса переменной длины.

Таблица 2

Коды чисел класса Variable + Variable

Число	Двоичное представление	Кодовое слово	Длина кодового слова
0 1	00000000000 00000000001	00 01	1 2
2 3	00000000010 00000000011	00 10 00 11	4
4 5 6 7	00000000100 00000000101 00000000110 00000000111	000 100 000 101 000 110 000 111	6
8 9 10	00000001000 00000001001 00000001010	0100 000 0100 001 0100 010	8

Если в рассмотренном выше коде исключить кодовое слово для нуля, то можно уменьшить длины кодовых слов на 1 бит, убрав первый нуль во всех кодовых словах. Таким образом строится гамма-код Элиаса (γ-код Элиаса).

Таблица 3

γ-код Элиаса

Число	Кодовое слово	Длина кодового слова
1	1	1
2 3	0 10 0 11	3
4 5 6 7	00 100 00 101 00 110 00 111	5
8 9 10	000 1000 000 1001 00 1010	7

Другим примером кода класса Variable + Variable является омега-код Элиаса (ω-код Элиаса).

В нем первое значение (кодовое слово для единицы) задается отдельно. Другие кодовые слова состоят из последовательности групп длиной L₁ L₂ …L_m , начинающихся с единицы.

Конец всей последовательности задается нулевым битом.

Длина первой группы составляет 2 бита, длина каждой следующей группы равна двоичному значению битов предыдущей группы плюс 1.

Значение битов последней группы является итоговым значением всей последовательности групп, т.е. первые m-1 групп служат лишь для указания длины последней группы, которая содержит собственно мантиссу числа.

Таблица 4

ω-код Элиаса

Число	Кодовое слово	Длина кодового слова
1 2 3	0 10 0 11 0	1 3 3
4 5 6 7	10 100 0 10 101 0 10 110 0 10 111 0	6 6 6 6
8 9 .. 15	11 1000 0 11 1001 0 .. 11 1111 0	7 7 .. 7
16 17 .. 31	10 100 10000 0 10 100 10001 0 .. 10 100 11111 0	11 11 .. 11
32	10 101 100000 0	12

В омега-коде Элиаса (P. Elias):

При кодировании формируется сначала последняя группа, затем предпоследняя и т.д., пока процесс не будет завершен.

При декодировании, наоборот, сначала считывается первая группа, по значению ее битов определяется длина следующей группы, или итоговое значение числа, если следующая группа – 0.

• Рассмотренные типы кодов могут быть эффективны в следующих случаях:
• Вероятности чисел убывают с ростом значений элементов и их распределение близко к такому: P(x) ≥ P(x+1), при любом x, т.е. маленькие числа встречаются чаще, чем большие.
• Диапазон значений входных элементов не ограничен или неизвестен.
  Например, при кодировании 32-битовых чисел реально большинство чисел маленькие, но могут быть и большие.
• При использовании в составе других схем кодирования, например, кодировании длин серий.

2.2 Кодирование длин серий

Метод кодирования длин серий (RLE), предложенный П. Элиасом (P.Elias), при построении использует коды целых чисел. Входной поток для кодирования рассматривается как последовательность из нулей и единиц.

Идея кодирования заключается в том, чтобы кодировать последовательности одинаковых элементов (например, нулей) как целые числа, указывающие количество элементов в этой последовательности.

Последовательность одинаковых элементов называется серией, количество элементов в ней – длиной серии.

2.2.1 Пример кодирования длин серий

Входную последовательность (31 бит) можно разбить на серии, а затем закодировать их длины.

000000 1 00000 1 0000000 1 1 00000000 1

Длины серий нулей: 6 5 7 0 8

Используем, например, γ-код Элиаса.

Поскольку в γ-коде Элиаса нет кодового слова для нуля,то будем кодировать длину серии +1: 65708 ⇒ 76819

7 6 8 1 9 ⇒ 00111 00110 0001000 1 0001001

Длина полученной кодовой последовательности 25 бит.

Метод длин серий актуален для кодирования данных, в которых есть длинные последовательности одинаковых бит. В нашем примере, если P(0)>>P(1).

2.3 Код Хафмана

Код Хаффмана (англ. Huffman's algorithm) — алгоритм оптимального префиксного кодирования алфавита. Разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. [7]

Кодирование Хаффмана широко применяется при сжатии данных, в том числе при сжатии фото- и видеоизображений (JPEG, MPEG), в популярных архиваторах (PKZIP, LZH и др.), в протоколах передачи данных HTTP (Deflate), MNP5 и MNP7 и других. [3]

В 2013 году была предложена модификация алгоритма Хаффмана, позволяющая кодировать символы дробным количеством бит — ANS. На базе данной модификации реализованы алгоритмы сжатия Zstandard (Zstd, Facebook, 2015—2016) и LZFSE[fr] (Apple, OS X 10.11, iOS 9, 2016).

2.3.1 Определение

Пусть A={a₁,a₂,…,a_n} — алфавит из n различных символов, W={w₁,w₂,…,w_n} — соответствующий ему набор положительных целых весов. Тогда набор бинарных кодов C={c₁,c₂,…,c_n}, где c_i является кодом для символа a_i, такой, что:

c_i не является префиксом для c_j, при i≠j,

cумма ∑_i∈[1,n]w_i⋅|c_i| минимальна (|c_i| — длина кода c_i),

называется кодом Хаффмана.[7]

2.3.2 Алгоритм построения бинарного кода Хаффмана

Построение кода Хаффмана сводится к построению соответствующего бинарного дерева по следующему алгоритму:

1. Составим список кодируемых символов, при этом будем рассматривать один символ как дерево, состоящее из одного элемента c весом, равным частоте появления символа в строке.
2. Из списка выберем два узла с наименьшим весом.
3. Сформируем новый узел с весом, равным сумме весов выбранных узлов, и присоединим к нему два выбранных узла в качестве детей.
4. Добавим к списку только что сформированный узел вместо двух объединенных узлов.
5. Если в списке больше одного узла, то повторим пункты со второго по пятый.

2.3.3 Время работы

Если сортировать элементы после каждого суммирования или использовать приоритетную очередь, то алгоритм будет работать за время O(N log N).Такую асимптотику можно улучшить до O(N), используя обычные массивы.

2.3.4 Пример выполнения алгоритма

Закодируем слово abracadabra. Тогда алфавит будет A={a,b,r,c,d} а набор весов (частота появления символов алфавита в кодируемом слове) W={5,2,2,1,1}. Графическое представление можно посмотреть в приложении на рисунке 4.

В дереве Хаффмана будет 5 узлов:

Таблица 5

Построение дерева Хафмана. Шаг 1

Узел	a	b	r	с	d
Вес	5	2	2	1	1

По алгоритму возьмем два символа с наименьшей частотой - это c и d. Сформируем из них новый узел cd весом 2 и добавим его к списку узлов:

Таблица 6

Построение дерева Хафмана. Шаг 2

Узел	a	b	r	cd
Вес	5	2	2	2

Затем опять объединим в один узел два минимальных по весу узла - r и cd:

Таблица 7

Построение дерева Хафмана. Шаг 3

Узел	a	rcd	b
Вес	5	4	2

Еще раз повторим эту же операцию, но для узлов rcd и b:

Таблица 8

Построение дерева Хафмана. Шаг 4

Узел	brcd	a
Вес	6	5

На последнем шаге объединим два узла – brcd и a:

Таблица 9

Построение дерева Хафмана. Шаг 5

Узел	abrcd
Вес	11

Остался один узел, значит, мы пришли к корню дерева Хаффмана (смотри рисунок). Теперь для каждого символа выберем кодовое слово (бинарная последовательность, обозначающая путь по дереву к этому символу от корня):

Таблица 10

Построение дерева Хафмана. Шаг 6

Символ	a	b	r	с	d
Код	0	11	101	1000	1001

Таким образом, закодированное слово «abracadabra» будет выглядеть как «01110101000010010111010». Длина закодированного слова – 23 бита. Стоит заметить, что если бы мы использовали алгоритм кодирования с одинаковой длиной всех кодовых слов, то закодированное слово заняло бы 33 бита, что существенно больше.

2.3.5 Корректность алгоритма Хаффмана

Чтобы доказать корректность алгоритма Хаффмана, покажем, что в задаче о построении оптимального префиксного кода проявляются свойства жадного выбора и оптимальной подструктуры. Ниже показано соблюдение свойства жадного выбора.

Пусть C — алфавит, каждый символ c∈C которого встречается с частотой f[c]. Пусть x и y - два символа алфавита C с самыми низкими частотами. Тогда для алфавита C существует оптимальный префиксный код, кодовые слова символов x и y в котором имеют одинаковую максимальную длину и отличаются лишь последним битом.

Доказательство:

Возьмем дерево T, представляющее произвольный оптимальный префиксный код для алфавита C. Преобразуем его в дерево, представляющее другой оптимальный префиксный код, в котором символы x и y - листья с общим родительским узлом, находящиеся на максимальной глубине.

Пусть символы a и b имеют общий родительский узел и находятся на максимальной глубине дерева T. Предположим, что f[a]⩽f[b] и f[x]⩽f[y]. Так как f[x] и f[y] — две наименьшие частоты, а f[a] и f[b] - две произвольные частоты, то выполняются отношения f[x]⩽f[a] и f[y]⩽f[b]. Пусть дерево T′ - дерево, полученное из T путем перестановки листьев a и x, а дерево T″ - дерево полученное из T′ перестановкой листьев b и y. Разность стоимостей деревьев T и T′ равна:

B(T)−B(T′)=∑_c∈Cf(c)d_T(c)−∑_c∈Cf(c)d_T′(c)=(f[a]−f[x])(d_T(a)−d_T(x)),

что больше либо равно 0, так как величины f[a]−f[x] и d_T(a)−d_T(x) неотрицательны. Величина f[a]−f[x] неотрицательна, потому что x - лист с минимальной частотой, а величина d_T(a)−d_T(x) является неотрицательной, так как лист a находится на максимальной глубине в дереве T. Точно так же перестановка листьев y и b не будет приводить к увеличению стоимости. Таким образом, разность B(T′)−B(T′′) тоже будет неотрицательной.

Таким образом, выполняется неравенство B(T′′)⩽B(T). С другой стороны, T - оптимальное дерево, поэтому должно выполняться неравенство B(T)⩽B(T′′). Отсюда следует, что B(T)=B(T′′). Значит, T″ - дерево, представляющее оптимальный префиксный код, в котором символы x и y имеют одинаковую максимальную длину, что и требовалось доказать.

Пусть дан алфавит C, в котором для каждого символа c∈C определены частоты f[c]. Пусть x и y — два символа из алфавита C с минимальными частотами. Пусть C′ — алфавит, полученный из алфавита C путем удаления символов x и y и добавления нового символа z, так что C′=C∖{x,y}∪z. По определению частоты f в алфавите C′ совпадают с частотами в алфавите C, за исключением частоты f[z]=f[x]+f[y]. Пусть T′ — произвольное дерево, представляющее оптимальный префиксный код для алфавита C′ Тогда дерево T, полученное из дерева T′ путем замены листа z внутренним узлом с дочерними элементами x и y, представляет оптимальный префиксный код для алфавита C.

Для доказательства, сначала покажем, что стоимость B(T) дерева T может быть выражена через стоимость B(T′) дерева T′. Для каждого символа c∈C∖{x,y} верно d_T(C)=d_T′, значит, f[c]d_T(c)=f[c]d_T′(c). Так как d_T(x)=d_T(y)=d_T′(z)+1, то f[x]d_T(x)+f[y]d_T(y)=(f[x]+f[y])(d_T′(z)+1)=f[z]d_T′(z)+(f[x]+f[y])

из чего следует, что B(T)=B(T′)+f[x]+f[y] или B(T′)=B(T)−f[x]−f[y]

Докажем лемму от противного. Предположим, что дерево T не представляет оптимальный префиксный код для алфавита C. Тогда существует дерево T″ такое, что B(T′′)<B(T). Согласно лемме (1), элементы x и y можно считать дочерними элементами одного узла. Пусть дерево T‴ получено из дерева T″ заменой элементов x и y листом z с частотой f[z]=f[x]+f[y]. Тогда

B(T′′′)=B(T′′)−f[x]−f[y]<B(T)−f[x]−f[y]=B(T′),

что противоречит предположению о том, что дерево T′ представляет оптимальный префиксный код для алфавита C′. Значит, наше предположение о том, что дерево T не представляет оптимальный префиксный код для алфавита C, неверно, что и доказывает лемму.

Из вышесказанного следует, что алгоритм Хаффмана дает оптимальный префиксный код.

2.4 Алгоритм Шеннона – Фано

Кодирование Шеннона-Фано является одним из самых первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон (Shannon) и Фано (Fano).

Главная идея этого метода - заменить часто встречающиеся символы более короткими кодами, а редко встречающиеся последовательности более длинными кодами. Таким образом, алгоритм основывается на кодах переменной длины. Для того, чтобы декомпрессор впоследствии смог раскодировать сжатую последовательность, коды Шеннона-Фано должны обладать уникальностью, то есть, не смотря на их переменную длину, каждый код уникально определяет один закодированный символ и не является префиксом любого другого кода.

2.4.1 Построение алгоритма

Рассмотрим алгоритм вычисления кодов Шеннона-Фано (для наглядности возьмём в качестве примера последовательность 'aa bbb cccc ddddd'). Для вычисления кодов, необходимо создать таблицу уникальных символов сообщения c(i) и их вероятностей p(c(i)), и отсортировать её в порядке невозрастания вероятности символов. [6]

Таблица 11

Метод Шеннона-Фано. Шаг 1
Символы сообщения c(i) и их вероятностей p(c(i))

c(i)	p(c(i))
d	5 / 17
c	4 / 17
space	3 / 17
b	3 / 17
a	2 / 17

Далее, таблица символов делится на две группы таким образом, чтобы каждая из групп имела приблизительно одинаковую частоту по сумме символов. Первой группе устанавливается начало кода в '0', второй в '1'. Для вычисления следующих бит кодов символов, данная процедура повторяется рекурсивно для каждой группы, в которой больше одного символа.

Таким образом, для нашего случая получаем следующие коды символов:

Таблица 12

Метод Шеннона-Фано. Шаг 2
Деление на группы

Символ	Код
d	00
c	01
space	10
b	110
a	111

Используя полученную таблицу кодов, кодируем входной поток - заменяем каждый символ соответствующим кодом. Естественно для раскодирования полученной последовательности, данную таблицу необходимо сохранять вместе со сжатым потоком, что является одним из недостатков данного метода. В сжатом виде, наша последовательность принимает вид:

111111101101101101001010101100000000000

Полученная длина 39 бит. Учитывая, что оригинал имел длину равную 136 бит, коэффициент сжатия ~28% - не так уж и плохо.

Глядя на полученную последовательность, возникает вопрос: "А как же теперь это разжать?".

Для раскодирования мы не можем, заменять каждые 8 бит входного потока, кодом переменной длины, как в случае кодирования. Необходимо заменить код переменной длины символом длиной 8 бит.

В данном случае, лучше всего будет использовать бинарное дерево, листьями которого будут являться символы (аналог дерева Хаффмана).

2.5 Сравнение алгоритмов Хафмана и Шеннона – Фано

Данный метод сжатия имеет большое сходство с кодированием Хаффмана, которое появилось на несколько лет позже.

Для работы оба алгоритма должны иметь таблицу частот элементов алфавита.

Итак, алгоритм Хаффмана работает следующим образом:

1. На вход приходят упорядоченные по невозрастанию частот данные.
2. Выбираются две наименьших по частоте буквы алфавита, и создается родитель (сумма двух частот этих «листков»).
3. Потомки удаляются и вместо них записывается родитель, «ветви» родителя нумеруются: левой ветви ставится в соответствие «1», правой «0».
4. Шаг два повторяется до тех пор, пока не будет найден главный родитель — «корень».

Алгоритм Шеннона-Фано работает следующим образом:

1. На вход приходят упорядоченные по невозрастанию частот данные.
2. Находится середина, которая делит алфавит примерно на две части. Эти части (суммы частот алфавита) примерно равны. Для левой части присваивается «1», для правой «0», таким образом мы получим листья дерева
3. Шаг 2 повторяется до тех пор, пока мы не получим единственный элемент последовательности, т.е. листок

Таким образом, видно, что алгоритм Хаффмана как бы движется от листьев к корню, а алгоритм Шеннона-Фано, используя деление, движется от корня к листьям.

Кодирование Шеннона-Фано является достаточно старым методом сжатия, и на сегодняшний день оно не представляет особого практического интереса. В большинстве случаев, длина сжатой последовательности, по данному методу, равна длине сжатой последовательности с использованием кодирования Хаффмана. Но на некоторых последовательностях всё же формируются не оптимальные коды Шеннона-Фано, поэтому сжатие методом Хаффмана принято считать более эффективным.

Для примера, рассмотрим последовательность с таким содержанием символов: 'a' - 14, 'b' - 7, 'c' - 5, 'd' - 5, 'e' - 4. Метод Хаффмана сжимает её до 77 бит, а вот Шеннона-Фано до 79 бит.

Таблица 13

Сравнение Кода Хаффмана и Кода Шеннона-Фано

Символ	Код Хаффмана	Код Шеннона-Фано
a	0	00
b	111	01
c	101	10
d	110	110
e	100	111

Иногда, из-за нестрогого определения способа деления символов на группы, возникают некоторые отличия в степени сжатия.

Способ деления на группы в данном случае:

1. вероятность первой группы (p1) и второй (p2) равна нулю;
2. p1 <= p2 ?
   1. да: добавить в первую группу символ с начала таблицы;
   2. нет: добавить во вторую группу символ с конца таблицы;
3. если все символы разделены на группы, то завершить алгоритм, иначе перейти к шагу 2.

2.6 Алгоритмы Зива-Лемпеля

К словарным методам сжатия относятся алгоритмы Зива-Лемпеля, основанные на использовании словаря. Они были разработаны Якобом Зивом и Авраамом Лемпелом и опубликованы в 1977 и 1978 годах под названиями LZ77 и LZ78. [6]

2.6.1. Алгоритм LZ77

Основная идея LZ77 состоит в том, что повторные вхождения некоторой подстроки сообщения заменяются ссылкой на ее первое вхождение.

Алгоритм использует скользящее окно, разделенное на две части: словарь и буфер. Скользящее окно по мере построения кода передвигается вдоль сообщения. Словарь включает уже просмотренную подстроку сообщения фиксированной длины. Буфер включает текущую еще не закодированную подстроку сообщения. Алгоритм пытается найти в словаре фрагмент наибольшей длины, совпадающий с начальной подстрокой буфера, и кодирует, заменяет найденную подстроку буфера с помощью ссылки на место этой подстроки в словаре. [8]

Обозначим длину словаря через W, и длину буфера через M. Для эффективности кодирования размер словаря должен быть существенно больше размера буфера.

Алгоритм LZ77 выдает коды, состоящие из трех элементов:

1. смещение в словаре относительно его начала подстроки, совпадающей с началом содержимого буфера;
2. длина подстроки;
3. первый символ буфера, следующий за подстрокой.

Пример

Пусть длина словаря W=5, длина буфера M=3. Закодируем с помощью алгоритма LZ77 сообщение a = abbdcabdcaabdaa .

Процесс кодирования представим в виде следующей таблицы:

Таблица 14

Кодирование алгоритмом LZ77

Шаг	Словарь	Буфер	Код
1	-----	abb	(1,0,”a”)
2	----a	bbd	(1,0,”b”)
3	---ab	bdc	(1,1,”d”)
4	-abbd	cab	(1,0,”c”)
5	abbdc	abd	(5,2,”d”)
6	dcabd	caa	(4,2,”a”)
7	bdcaa	bda	(5,2,”a”)
8	aabda	a	(0,0,”a”)

В начале работы словарь пуст, а буфер содержит начальную подстроку сообщения abb. На первом шаге строится код (1,0,”a”). Так как символы буфера не встречаются в словаре, смещение равно 1 (отсчет ведется с самой правой позиции в словаре, она имеет номер 1, хотя это не принципиально), длина подстроки совпадения равна 0 – это значение второго элемента кода, третий элемент равен “a” – это код очередной буквы после найденной подстроки буфера (например, ASCII-код). После выполнения первого шага скользящее окно смещается вправо на 1 позицию.

На шаге 5 максимальное совпадение начальной подстроки буфера cо словарем равно ab, поэтому смещение равно 5 (это номер самой левой подстроки словаря), длина подстроки равна 2, и следующий после найденной подстроки в буфере – символ d. После выполнения шага 5 скользящее окно смещается вправо на 3 позиции.

На шаге 8, так как символ a последний в сообщении, словарь не используется.

Длину кода можно оценить следующим образом. Длина подстроки не может быть больше длины буфера M, а смещение не может быть больше размера словаря W.

Следовательно, для двоичного кода длины подстроки достаточно
|log2 M| битов, а для двоичного кода смещения достаточно |log2 W| битов.

При использовании ASCII-кода общая длина кода будет равна

N × (|log 2 W| + |log 2 M| + 8 ), где N – число шагов. Сжатие алгоритмом LZ77 достигается за счет шагов, аналогичных шагу 5. Различные модификации алгоритма позволяют увеличить степень сжатия.

К недостаткам алгоритма LZ77 следует отнести следующие:

1. невозможность кодирования подстрок, находящихся друг от друга на расстоянии, большем длины словаря;
2. длина подстроки, которую можно закодировать, ограничена размером буфера.

Известны оценки избыточности кодирования LZ77 для источников с конечным числом состояний, приведем одну из них, принадлежащую Х.Морита и К.Кобояши:

R(f₇₇,X)=O|((loglogW)/logW)| при W → ∞

(здесь X – произвольный Марковский источник и W – длина скользящего окна).

2.6.2. Алгоритм LZ78

Алгоритм LZ78 был разработан в 1978 году. Алгоритм не использует скользящее окно, он хранит словарь из уже просмотренных фраз. В начале работы словарь содержит только одну пустую строку (строку длины 0). Алгоритм считывает символы сообщения до тех пор, пока накапливаемая строка входит целиком в одну из строк словаря. После этого алгоритм строит код, состоящий из индекса (номера) строки в словаре, которая совпадает с кодируемой подстрокой сообщения, и следующего символа сообщения. Затем в словарь добавляется закодированная подстрока сообщения плюс следующий символ.

Размер получаемого кода определяется размером словаря, так как каждый код содержит номер строки в словаре.

Пример LZ78

Закодируем с помощью алгоритма LZ78 сообщение
a = abbdcabdcaabdaa . Процесс кодирования представим в виде следующей таблицы:

Таблица 15

Кодирование алгоритмом LZ78

Номер строки в словаре	Словарь	Код	Текущая строка сообщения	Строка Str
0	- (пустая строка)	(0, “a”)	abbdcabdcaabdaa	пустая строка
1	a	(0, “b”)	bbdcabdcaabdaa	пустая строка
2	b	(2, “d”)	bdcabdcaabdaa	b
3	bd	(0, “c”)	dcabdcaabdaa	пустая строка
4	c	(1, “b”)	abdcaabdaa	a
5	ab	(0, “d”)	dcaabdaa	пустая строка
6	d	(4, “a”)	caabdaa	c
7	ca	(5, “d”)	abdaa	ab
8	abd	(1, “a”)	aa	a

Здесь Str – накапливаемая подстрока, которая целиком соответствует какой-либо фразе из словаря (притом максимальная).

На первом шаге построен код (0, “a”), так как словарь содержит только пустую строку, имеющую номер 0 в словаре, первый элемент в коде равен 0 (пустая строка является подстрокой любой другой строки). В словарь добавляется строка, получающаяся конкатенацией пустой строки и следующего после найденной подстроки символа сообщения. Это строка a, она записывается в словарь с номером 1.

На втором шаге так же, как и на первом, максимальная строка словаря, совпадающая с началом текущей строки сообщения, является пустой. Поэтому формируется код (0, “b”). В словарь под номером 2 добавляется строка b.

На третьем шаге начальная подстрока сообщения длины 1 встречается в словаре под номером 2. Поэтому создается код (2, “d”), в котором первый элемент равен номеру найденной строки в словаре, а второй элемент является кодом следующей буквы. К найденной строке b из словаря приписывается буква d, и строка bd добавляется в словарь.

• рассматриваемом примере наибольший вклад в сжатие сообщения дает шаг 7, поскольку строка совпадения имеет длину 2.

Кодируемое сообщение имеет длину 15. Для сообщения длины 15 словарь может содержать 16 строк, включая пустую строку. Поэтому для записи номера строки в словаре требуется 4 бита. Для записи второго элемента в коде требуется 2 бита, так как алфавит сообщения содержит 4 символа. Для кодирования сообщения потребовалось 8 шагов. Поэтому общая длина кода равна 48 битам.

Алгоритм LZ78 так же, как LZ77, является асимптотически оптимальным для марковских источников с конечным числом состояний.

Известна оценка избыточности для LZ77, полученная С.Савари:

R_n(f₇₈,X) ≤0|(1/log_n)| при n → ∞

где X – произвольный марковский источник и n – длина кодируемого сообщения. Алгоритм LZ78 нашел свое практическое применение только после реализации LZW, предложенной Велчем (Welch) в 1984 г. Некоторые изменения коснулись устройства словаря и формирования кодов. Рассмотрим эти изменения.

В начале производится инициализация словаря всеми возможными односимвольными строками (обычно 256 символами расширенного ASCII-кода). В процессе работы словарь разрастается до своего максимального объема Vmax строк (слов). Обычно объем словаря достигает нескольких десятков тысяч слов. Алгоритм работает практически аналогично алгоритму LZ78: символы сообщения считываются до тех пор, пока накапливаемая подстрока входит целиком в одну из фраз словаря Str. Так как словарь первоначально не пустой, такое слово всегда найдется. Как только эта строка перестанет соответствовать хотя бы одной фразе словаря, генерируется код - индекс строки в словаре, которая до последнего введенного символа содержала входную строку (длина кода равна |logV_max|), а словарь пополняется новым словом: Str + символ S, нарушивший совпадение. И далее алгоритм продолжает свою работу по указанной схеме, начиная с символа S. Таким образом, пропала необходимость передавать один символ в чистом виде (в результате того, что словарь изначально не пустой).

Рассмотрим работу алгоритма на строке колокол:

Таблица 16

Кодирование алгоритмом LZ77. Пример

Str	Код	StrS – в словарь	Индекс в словаре
		ASCII	0...255
к	#к	ко	256
о	#о	ол	257
л	#л	ло	258
о	#о	ок	259
ко	256	кол	260
л	#л

Str – накапливаемая подстрока, которая целиком соответствует какой-либо фразе из словаря (притом максимальная). Как только появляется символ S, нарушающий совпадение, генерируется Код – индекс слова в словаре.

StrS – строка Str + символ S, на котором и нарушается совпадение накапливаемой подстроки. Словарь пополняется этим новым словом, которому присваивается соответствующий индекс.

Теперь сравним размер исходной строки и закодированной. Для представления кода (а это индекс в словаре) требуется 9 бит, получаем размер закодированной строки = 6*9 = 54 бита. Тогда как размер исходной строки – 8*7 = 56 бит. Как видим, даже на такой короткой последовательности символов достигается сжатие, которое по мере увеличения размера последовательности будет увеличиваться.

Отметим основные проблемы, которые приходится решать при реализации алгоритма LZW.

Чтобы алгоритмы сжатия были эффективными, важна не только степень сжатия информации, но и скорость работы кодера и декодера, поэтому главная проблема – устройство словаря.

Реализация алгоритма построения словаря и поиска в словаре сами по себе достаточно сложные и медленные процедуры. Бинарные деревья позволяют на несколько порядков ускорить работу архиватора, поэтому они часто используются в реализациях для представления словаря.

Еще одна серьезная проблема алгоритмов семейства LZ78 - переполнение словаря: если словарь полностью заполнен, прекращается его обновление и процесс сжатия может быть заметно ухудшен. Отсюда следует вывод - словарь нужно иногда обновлять, но когда и как значительно? Этому вопросу посвящено множество публикаций. Самый простой способ - как только словарь заполнился, его полностью обновляют. Недостаток очевиден - кодирование начинается на пустом месте, как бы сначала, и пока словарь не накопится, сжатие будет незначительным. Поэтому словарь можно обновлять не сразу после его заполнения, а только после того, как степень сжатия начала падать. Еще более сложными являются эвристические методы обновления словарей в зависимости от частоты использования тех или иных слов.

2.7 Преобразование Барроуза-Уилера

Преобразование Барроуза-Уилера применяется в алгоритмах сжатия для предварительной обработки данных, для того чтобы с помощью перестановки элементов придать исходным данным со сложными зависимостями такие структурные свойства, которые легче смоделировать и учесть при кодировании.[]

Метод преобразования был опубликован в 1994 году в работе Д.Уилера и М.Барроуза и получил сокращенное название BWT. Преобразование Барроуза-Уилера применяется обычно вместе с методами кодирования, специально для него предназначенными (кодирование длин серий, сжатие с помощью «стопки книг» и др.).

Преобразование BWT - это способ перестановки символов в блоке данных. В нем можно выделить четыре этапа:

1. выделяется блок из входного потока;
2. формируется матрица всех перестановок, полученных в результате циклического сдвига блока;
3. все перестановки сортируются в соответствии с лексикографическим порядком символов каждой перестановки;
4. на выход подается последний столбец матрицы и номер строки, соответствующей исходному блоку

2.7.1 Пример преобразования Барроуза-Уилера

Обычно принято иллюстрировать преобразование на примере блока данных, состоящего из слова «абракадабра». Сформируем матрицу циклических перестановок слова «абракадабра», где первой строкой будет исходное слово, второй строкой – слово, сдвинутое на один символ влево, и т.д. Получим следующую матрицу:

Абракадабра
бракадабраа
ракадабрааб
акадабраабр
кадабраабра
адабраабрак
дабраабрака
абраабракад
браабракада
раабракадаб
аабракадабр

Пометим в этой матрице исходную строку и отсортируем все строки в лексикографическом порядке. Получим следующую матрицу циклических перестановок, отсортированных в соответствии с лексикографическим порядком:

Аабракадабр
абраабракад
абракадабра - исходная строка
адабраабрак
акадабраабр
браабракада
бракадабраа
дабраабрака
кадабраабра
раабракадаб
ракадабрааб

Результатом преобразования Барроуза-Уилера является последний столбец полученной матрицы: «рдакраааабб».

Покажем, что преобразование BWT является обратимым, т.е. по последнему столбцу отсортированной матрицы и номеру исходной строки однозначно можно восстановить саму исходную строку.

Рассмотрим процесс восстановления отсортированной лексикографически исходной матрицы. Для этого отсортируем все символы последнего столбца.

0 а
1 а
2 а
3 а
4 а
5 б
6 б
7 д
8 к
9 р
10 р

Так как строки матрицы были отсортированы по лексикографическому порядку, отсортировав последний столбец, мы получили первый столбец отсортированной матрицы. Таким образом, мы имеем два столбца матрицы: первый - аааааббдкрр и последний – рдакраааабб:

0 а р
1 а д
2 а а
3 а к
4 а р
5 б а
6 б а
7 д а
8 к а
9 р б
10 р б

Строки матрицы были получены в результате циклического сдвига исходной строки. Поэтому символы последнего и первого столбца образуют друг с другом пары. Отсортировав эти пары лексикографически, мы получим первые два столбца матрицы:

0 аа р
1 аб д
2 аб а
3 ад к
4 ак р
5 бр а
6 бр а
7 да а
8 ка а
9 ра б
10 ра б

Сортируя тройки символов последнего, первого и второго столбцов, восстановим третий столбец, и т.д.

Таблица 17

Декодирование слова «абракадабра»

№ строки	Шаг 3	Шаг 4	Шаг 9	Отсортированная исходная строка
0	ааб р	аабр…р	аабракада…р	аабракадабр
1	абр…д	абра…д	абраабрак…д	абраабракад
2	абр…а	абра…а	абракадаб…а	абракадабра
3	ада…к	адаб…к	адабраабр…к	адабраабрак
4	ака…р	акад…р	акадабраа…р	акадабраабр
5	бра…а	браа…а	браабрака…а	браабракада
6	бра…а	брак…а	бракадабр…а	бракадабраа
7	даб…а	дабр…а	дабраабра…а	дабраабрака
8	кад…а	када…а	кадабрааб…а	кадабраабра
9	раа…б	рааб…б	раабракад…б	раабракадаб
10	рак…б	рака…б	ракадабра…б	ракадабрааб

Восстановив все столбцы матрицы, по номеру исходной строки в матрице найдем саму строку. Таким образом, для восстановления всей матрицы достаточно помнить лишь ее последний столбец.

Рассмотрим вектор обратного преобразования, позволяющий эффективно находить исходную строку, не восстанавливая матрицу. Заметим, что в процессе выявления очередного столбца матрицы мы делали одни и те же действия: получали новую строку, сливая символ из последнего столбца старой строки с известными символами первых столбцов этой же строки. Новая строка после сортировки перемещалась в другую позицию в матрице.

Чтобы получить вектор обратного преобразования, следует определить порядок получения символов первого столбца из символов последнего, т.е. отсортировать матрицу по номерам новых строк.

Таблица 18

Сортировка таблицы

Номер строки	Последний столбец	Номер новой строки	Перенос последнего столбца в начало
2	а а	0	Аа р
5	б а	1	аб д
6	б а	2	аб а
7	д а	3	ад к
8	к а	4	ак р
9	р б	5	бр а
10	р б	6	бр а
1	а д	7	да а
3	а к	8	ка а
0	а р	9	ра б
4	а р	10	ра б

Вектор обратного преобразования образуют полученные значения номеров строк Т={2,5,6,7,8,9,10,1.3,0,4}. Чтобы получить исходную строку, возьмем элемент вектора, соответствующий номеру исходной строки в матрице циклических перестановок, Т[2]=6.

В качестве первого символа в исходной строке следует взять шестой символ из строки «рдакраааабб» - это символ «а». Для определения второго символа возьмем Т[6]=10, это символ «б», и т.д.

Таблица 19

Соотношение букв и номеров строк

6	10	4	8	3	7	1	5	9	0	2
а	б	р	а	к	а	д	а	б	р	А

Главное свойство преобразования Барроуза-Уилера состоит в том, что оно группирует вместе символы, соответствующие похожим контекстам. Практика показывает, что в результате преобразования обычных текстов более половины всех символов следует за такими же.

Чаще всего вместе с преобразованием BWT используется кодирование с помощью алгоритма сжатия «стопкой книг» (англо-язычное название move to front). Алгоритм легко понять, если представить стопку книг, каждая из которых соответствует определенному символу. По мере востребования из стопки вытаскивается нужная книга и помещается сверху. Через некоторое время те книги, которые используются часто, оказываются ближе к верхушке стопки.

Рассмотрим наш пример слова «рдакраааабб», полученного в результате преобразования Барроуза-Уилера. Символы слова принадлежат алфавиту из пяти символов. Начальный список содержит эти символы в следующем порядке: {а,б,д,к,р}. Символ «р» стоит на пятом месте в списке, поэтому первый код становится равным 4. После перемещения символа «р» на первое место список символов принимает вид {р,а,б,д,к}, и т.д.

Таблица 20

Декодирование шифрования Барроуза-Уилера на примере слова «рдакраааабб»

Символ	Список	Выход
р	{а, б, д,к, р}	4
д	{р, а, б, д,к}	3
а	{д, р, а, б, к}	2
к	{а, д, р, б, к}	4
р	{к, а, д, р, б}	3
а	{р, к, а, д, б}	2
а	{а, р, к, д, б}	0
а	{а, р, к, д, б}	0
а	{а, р, к, д, б}	0
б	{а, р, к, д, б}	4
б	{б, а, р, к, д}	0

В выходной последовательности кодов встречается только четыре различных номера. Применив для их кодирования алгоритм Хаффмана, получим стоимость кодирования, равную двум битам.

Во второй главе были приведены описания основных методов кодирования, с примерами их работы. Это было важно для понимания методов кодирования, самой сути этой фразы, то есть процессов, происходящих во время кодирования информации и того, как так получается, что текст преобразовывается в абсолютно другую форму, сохраняя при этом весь смысл, который можно дешифровать.

Каждый метод использует свои алгоритмы шифрования и математические операции. Каждый имеет качественно и количественно разный объем сжатия, разный вес словарей. В связи с этим один метод может быть более удобен в одном случае, и абсолютно не адаптивен в другом. При работе с данными необходимо знать и учитывать разные способы и выбирать наиболее подходящий для каждой конкретной ситуации, в зависимости как от типа передаваемых данных, так и от количества шума во время передачи сигнала.

ЗАКЛЮЧЕНИЕ

Решение задачи выбора оптимального кода для передачи информации от источника к получателю (приёмнику) является одной из ключевых задач в современном мире. Переоценить качество этого невозможно, ведь при потере части информации или невозможности расшифровать исходные данные, сигнал становится бесполезным. Так же важна и скорость передачи, на которую сильно влияет объем сжатия.

Существует множество разнообразных методов и алгоритмов кодирования данных. Их число и разнообразие растёт в связи с развитием технических средств, изменением физического оборудования передачи данных, внедрением высокоскоростных технологий и других факторов.

В данной курсовой работе были рассмотрены базовые понятия и принципы кодирования информации; основные теоремы кодирования; методы сжатия данных; методы универсального кодирования. Были названы ключевые фамилии, сыгравшие важную роль в развитии науки.

Я считаю, что цель курсовой работы - изучение основных методов кодирования данных в информационных системах и определение связи с такими научными дисциплинами, как теория кодирования и теория информации, была раскрыта в полной мере.

Список литературы

1. Ван Леувен, Ян (1976). «О построении деревьев Хаффмана» (PDF) . ICALP : 382–410 .
2. Кудряшов Б. Д. Теория информации, СПбГУ НИУ ИТМО
3. Левитин А. В. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы. Введение в разработку и анализ — М.: Вильямс, 2006. — С. 392–398. — 576 с. — ISBN 978-5-8459-0987-9
4. Марков А. А. Введение в теорию кодирования. — М.: Наука, 1982. — 192 с.
5. Русский перевод: Шеннон К. Э. Математическая теория связи // Работы по теории информации и кибернетике / Пер. С. Карпова. — М.: ИИЛ, 1963. — 830 с.
6. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ — 2-е изд. — М.: «Вильямс», 2007. — с. 459
7. Хаффман, Д. (1952). «Метод построения кодов минимальной избыточности» (PDF) . Труды IRE . 40 (9): 1098–1101. doi : 10.1109 / JRPROC.1952.273898 .
8. Фурсов В. А. Лекции по теории информации ISBN 5-7883-0458-X
9. Claude E. Shannon, Warren Weaver. The Mathematical Theory of Communication. Univ of Illinois Press, 1963. ISBN 0-252-72548-4
10. Thomas M. Cover, Joy A. Thomas. Elements of information theory New York: Wiley, 1991. ISBN 0-471-06259-6
11. Types of Coding // James Irvine, David Harle Data Communications and Networks. John Wiley & Sons, 2002. pp. 268

Электронный адрес:

1. Archive.org - Nyquist, H. (1924). “Certain factors affecting telegraph speed”. Bell System Technical Journal. 3: 22:324—346 (Дата обращения:

19.05.2019)

Приложение

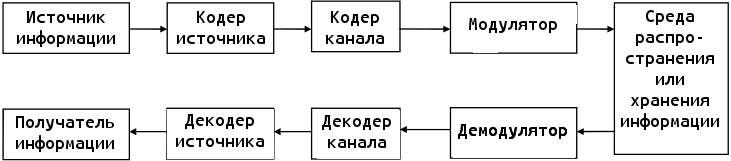
Рис.1 - схема системы связи

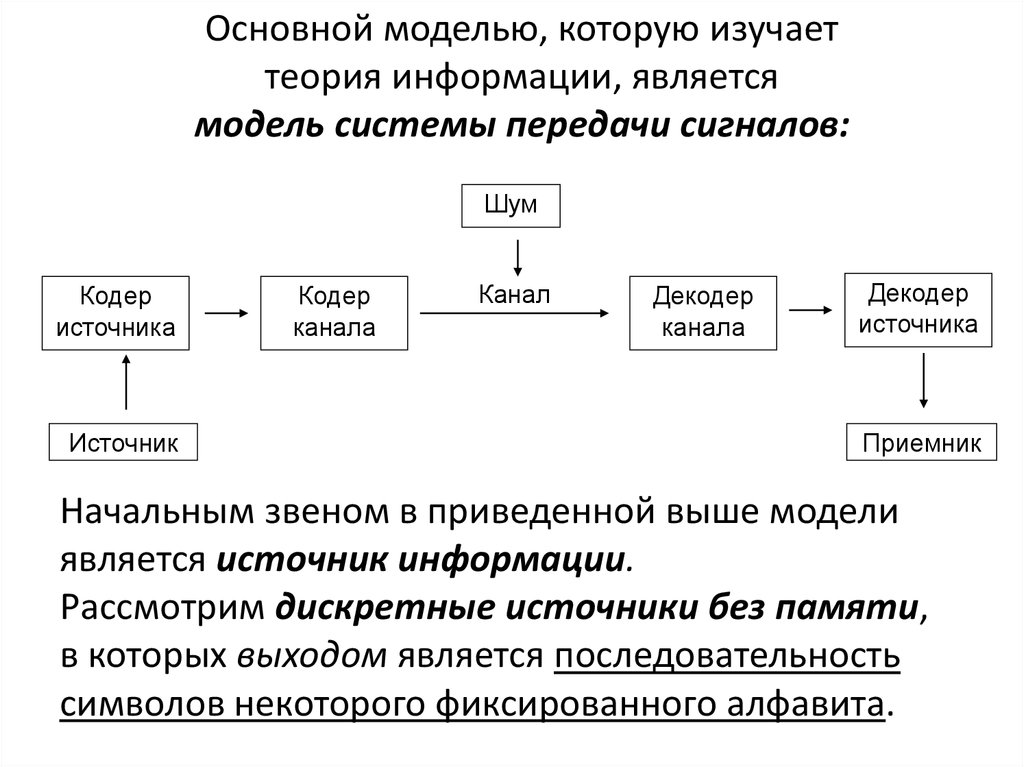
Рис.2 - модель системы передачи сигналов

Рис.3 – кодовая таблица ASCII для русского алфавита

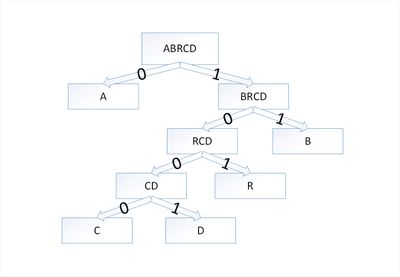
Рис. 4- дерево Хаффмана для слова abracadabra