Оптимизация решений по Парето (Численные методы получения множеств Парето)

Содержание:

Введение

Почти всякая сложная практическая задача принятия решения индивидуального (а тем более группового) является многокритериальной.

Концепция принятия решения в качестве первичного элемента деятельности рассматривает решение как сознательный выбор одного из ряда альтернатив, называемых, в зависимости от их конкретного содержания, стратегиями, планами, вариантами и т.д. Этот выбор производит лицо, принимающее решение и стремящееся к достижению определенных целей. В роли такого лица выступают отдельные люди (группы людей), обладающие правами выбора решения и несущие ответственность за его последствия.

Применение математических методов при принятии решений предполагает построение подходящей математической модели, формализовано представляющей проблемную ситуацию, т.е. ситуацию выбора решений. Для задач принятия решений (задач оптимизации) в условиях определенности, когда случайные и неопределенные факторы отсутствуют, компонентами такой модели являются множество всех (альтернативных) решений, из которых и делается выбор одного наилучшего, или оптимального решения, и описание предпочтений лица, принимающего решение. Для того чтобы была обеспечена возможность выбора, множество должно содержать не менее двух решений.

Методы решения задач математического программирования с одним критерием интенсивно разрабатывались последние 40 лет. Изучение таких методов, однако, отражало самый ранний и простой этап в развитии математического программирования. Жизнь оказалась значительно сложнее. По мере того как мы постепенно вступаем в век информатики, становится ясно, что практически любая серьезная реальная задача характеризуется больше чем одним критерием. Лица, принимающие решения (ЛПР), в значительно большей степени, чем когда бы то ни было, ощущают необходимость оценивать альтернативные решения с точки зрения нескольких критериев.

Результаты исследования задач планирования и управления показывают, что в реальной постановке эти задачи являются многокритериальными. Так, часто встречающееся выражение «достичь максимального эффекта при наименьших затратах» уже означает принятие решения при двух критериях. Оценка деятельности предприятий и планирования как системы принятия решений производится на основе более десятка критериев: выполнение плана производства по объему, по номенклатуре, плана реализации, прибыли по показателям рентабельности, производительности труда и т.д.

Актуальность курсовой работы: исследование сущности оптимальности по Парето.

Цель курсовой работы — исследование сущности оптимальности по Парето, а также того, что можно предпринять, чтобы более эффективно принимать решения.

Для достижения поставленной цели необходимо решить ряд задач:

1) Понятие оптимальности по Парето;

2)Отношение доминирования по Парето. Парето-оптимальность;

3) Изучить аналитические методы построения множества Парето и тд.

Объектом данной курсовой работы является оптимальность решений по Парето, а предметом умение эффективно принимать решения по оптимальности Парето.

Ранее, при исследовании проблемы многокритериальности часто все критерии, кроме одного, выбранного доминирующим, принимались в качестве ограничений. Впервые проблема оптимизации векторного критерия была сформулирована экономистом Парето в 1896 г.

В задачах математического программирования с одним критерием нужно определить значение целевой функция, соответствующее, например, минимальным затратам или максимальной прибыли. Однако, немного подумав, мы практически в любой реальной ситуации обнаружим несколько целей, противоречащих друг другу.

Приведем пример того, насколько широк диапазон проблем, которые могут быть адекватно сформулированы как многокритериальные, и какие характеристики следует использовать в качестве критериев.

1. Оптимальность по Парето

1.1 Отношение доминирования по Парето. Парето-оптимальность

Для облегчения результатов полезно всё время проводить аналогию с однокритериальным (классическим) случаем. Пусть имеется область D и задана функция f – целевая функция (критерий). Задача оптимизации имеет вид:^[1]

min f(X)

X∈D

Точка X₁∈D называется оптимальной (недоминируемой, неулучшаемой), если не существует точки X₂∈D, для которой f(X₁)>f(X₂) (целевая функция минимизируется). Аналогично в МЗО можно исключить из области D точки, которые заведомо не могут оказаться наилучшими.

Очевидно, что в обобщённом смысле определение оптимальности можно трактовать как описание (выделение) в подмножестве D некоторого нового подмножества D₀, т.е. некоторое сужение D до D₀ ⊂D. В зависимости от характера описания, подмножество D₀ может оказаться пустым, состоять из одного элемента, содержать более одного элемента. Описание D₀ можно проводить либо только с помощью критериев Fi, либо использовать дополнительные условия. Здесь мы рассмотрим направление, которое связано с определением оптимальности по Парето.

Как было сказано раньше для всякого решения X∈D набор его оценок по всем критериям, т.е. набор (F₁(X), F₂(X), . . .,Fm(X)), есть векторная оценка решения X. Векторная оценка X содержит полную информацию о ценности (полезности) этого решения ЛПР и сравнение двух решений сравнение их оценок. Пусть в требуется получить значения каждого критерия (минимизировать критерии) Fi(X).

: Пусть имеются решения X₁ и X₂. Говорят, решение X₁ лучше (, эффективнее, доминирует) X₂, если F_i(X₁)<=(X₂) для всех i=1,m, и бы для j - го критерия строгое неравенство (X₁)<F_i(X₂). или

: Решение X₂ называется , если существует X₁, не хуже X₂, т.е. для любой функции Fi, I=1, 2, …, m,

(X₂)≤Fi(X₁) при функции Fi,

(X₂)≥Fi(X₁) при Fi.

В случае при переходе X₂ к X₁ ничего не проиграно ни одному из критериев, но в j - го частного точно будет выигрыш. Говорят, решение X₁ лучше () решения X₂.

Определение: X₁∈D называется эффективной ( по Парето), не существует X₂∈D такой, что (X₂) ≤Fi(X₁), i=1, . . ., m, F(X₂)≠F(X₁), или:

: Если решение доминируемо никаким решением, то называется недоминируемым оптимальным в смысле .^[2]

Очевидно, тогда в множества D нет сохранять решение X₂, вытесняется (или, говорят, “доминируется”) X₁. Ладно, выбросим, X₂ как неконкурентоспособное и к сравнению других по всем . В результате такой отбрасывания заведомо , невыгодных решений D обычно сильно : в нём сохраняются так называемые (иначе “паретовские”) , характерные тем, ни для из них существует доминирующего . Множество таких и называется множеством оптимальных по . Множество точек по Парето между точками , полученных при задачи математического для каждого критерия. В литературе точек оптимальных Парето, как , обозначают буквой P (P⊂D).

.^[3] Множество векторных , соответствующих множеству точек, называют компромиссов (переговорным ) или множеством в области критериев. обозначать Y_P ( ⊆Y_D).

Опр. векторных оценок, множеству неэффективных (доминируемых решений), областью согласия .

В области Y_c противоречия между критериями оптимальности, т.к. точка X∈D может изменена таким , что будет улучшены все критерии.

Если критериев Y_D только из согласия Y_c, существует единственная X_opt∈D, в которой частные критерии между собой в смысле, что движении к точке все F_i(X) i=1, 2, . . ., m, улучшаются. Все критерии достигают в т. X_opt (см. . 1). Такую точку оптимальным решение и этом значения частных критериев в ней минимума.

. 1

Критерии F1 и F2 непротиворечивы

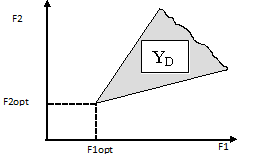
такая ситуация крайне редко. типичным является , когда частные являются противоречивыми и по каждому них достигается в точках. В этом уменьшение одного критерия приводит к других частных (рис. 2).

Рис. 2

F1 и F2 противоречивы на [1; 2]

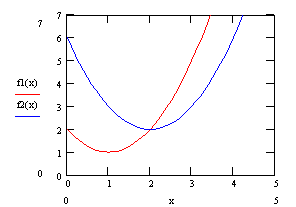
Оптимальность по означает, что дальше улучшать одного критерия, ухудшая при хотя бы из остальных.^[4]

приём выделения решений на задачи с двумя F₁ и F₂ (оба требуется ). Множество D состоит 11 возможных решений. решению соответствуют значения показателей F₁ и F₂. имеются следующие оценки: F(X₁)=(2;4), F(X₂)=(3;5), F(X₃)=(3;3), F(X₄)=(5;2), F(X₅)=(4;3), F(X₆)=(1;3), F(X₇)=(2;3), F(X₈)=(3;2), F(X₉)=(2;2), F(X₁₀)=(3;1), F(X₁₁)=(2;1). Векторные исходов представим координатной плоскости ( оси абсцисс значения критерия F₁, а оси ординат – критерия F₂). Используем оптимальности по для выделения решений. Решение X₁ решением X₂, решение X₂ решений X₃, X₇, X₈, X₉, X₁₀ и X₁₁. Решение X₄ первому критерию решения X₅, а по наоборот, т.е. имеем решения, и т.д. После анализа у нас три решения X₂,X₄, X₅ по Парето.^[5]

критериальное пространство нашей задачи. известно паре соответствует точка плоскости. Занумеруем соответственно номеру (рис 3). Из видно, что точки лежат правой верхней области возможных (Ауд. решить задачу, когда критерия нужно ).

Рис. 3

Множество

Когда из возможных решений эффективные, "переговоры" вестись уже в этого "эффективного" . На рис. 3 три решения X₂, X₄, X₅; них X₄ лучше критерию F₁, а решение X₂ критерию F₂. Дело , выбрать тот , который для предпочтителен и “приемлем” обоим критериям.

. Точка Y₁ выбирается в в том и только в случае, когда другая точка Y₂ Y_D имеет бы по координате значение чем Y₁ (критерии ).

Замечание. Для эффективных точек правило “уголка”. вида^[6] ∟ используется определения компромиссных в критериальном пространстве, критерии максимизируются, а ┐когда критерии .

В случае, когда допустимых исходов непрерывным, их оценки "заполняют" область Y_D плоскости и получается "" вроде изображённой рис. 4. В этом множество Парето- оценок (красная ) представляет собой границы Y_D, говоря, её "-западную" границу". критерии максимизируются – "северо-восточную" области Y_D.

. 4

Пространство оценок и компромиссная кривая ( цвет)

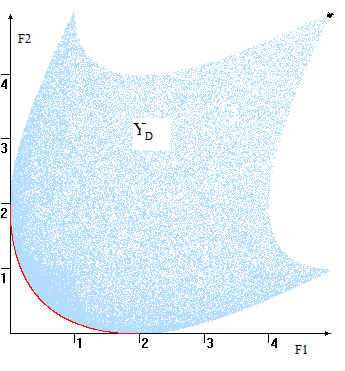
Замечание. В невыпуклой области Парето-оптимальная может иметь "экзотический" вид, , состоять из линий и/или . Для данного (критерии максимизируются) — правый пик.

. Экономисты так оптимальность по . Состояние называется по Парето, выполняется следующее : ничьё благосостояние может быть без ухудшения кого-либо .

Таким образом, оптимально-компромиссным будем понимать из эффективных , являющуюся предпочтительней с зрения ЛПР. векторной оптимизации позволяет однозначно на вопрос, ли оптимальное . Положительный ответ этот вопрос от качественной о важности частных , которая имеется у .

1.2 Аналитические методы множества Парето

кривая:^[7]

Особый для практики — m=2. В случае множество точек представляет одномерное многообразие плоскости и допускает графическое представление.

. ^[8]Множество паретовских в двухмерном пространстве называют компромиссной .

Она может из несвязных и содержать изолированные (см. рис. 5). кривая (КК) монотонно убывает в смысле. Пусть Y₁ и Y₂ точки, принадлежащие . Обозначим их Y₁(y1,y2) и Y₂(y3,y4), если y1<y3, то y2>y4. образом, КК содержит ни , ни вертикальных и её уравнение быть представлено в F₂=u(F₁) и F₁=v(F₂).

Рис. 5

Примеры (компромиссная кривая красным цветом)

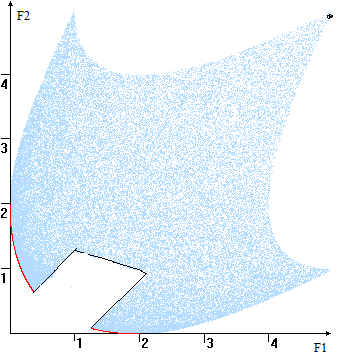
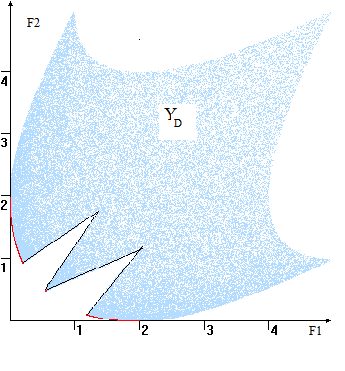
1.3 Примеры компромиссных кривых

подход. Если F₁(X) и F₂(X) дифференцируемы, то попытаться найти место точек поверхностей уровня F₁(X)=b1 и F₂(X)=b2. В точках gradF₁=-λ₂, 0≤ λ< ∞.

Последнее векторное равносильно n скалярным уравнениям которые кривую в пространстве x₁=ϕ₁(λ), ..., x_n=ϕ_n(λ). Если этой кривой, котором λ≥0 принадлежит D, то он и множеству P (P - множество ). Участок КК в случае определяется уравнениями:^[9]

F₁=F₁(ϕ₁(λ), ..., ϕ_n(λ)),

F₂=F₁(ϕ₁(λ), ..., ϕ_n(λ)), λ≥0.

Пример 1. В D={-1≤ x₁ ≤ 1, -1≤ x₂ ≤ 1} заданы два

которые желательно .

1. Находим минимумы F₁ и F₂ . Абсолютные минимумы в точках (0,0) и (-1,1) и принадлежат D.

2. Находим частные

составляем систему :

4x₁=-λ (x₁+1)

x₂=-λ (x₂-1).

Отсюда получаем уравнение кривой в параметров

В данном можно получить этой кривой в прямоугольных координатах. этого решаем уравнения относительно λ. Получим

Приравнивая части и разрешая x₂, получим уравнение кривой P: .

Параметрическое КК будет следующий вид

F₁(λ)=

F₂(λ)=.

КК: F₁ возрастает 0 до 5, а F₂ убывает 2 до 0.

Построим паретовских кривых в D и пространстве критериев (. 6 и 7).^[10]

Рис. 6 Область D и P Рис. 7 Компромиссная

Пример 2. В области D={-0.5 ≤ x₁ ≤ 0.5, 0 ≤ x₂ ≤ 1} два критерия

нужно минимизировать с функциональных ограничений ⎥x₂-x₁-0.375⎥ ≥ 0.125.

а) сначала случай функциональных ограничений

1. минимумы функций^[11] F₁ и F₂. минимумы находятся в X_1opt=(0,0) и X_2opt=(-1,1) и первая точка D, а вторая нет. условный минимум функции F₂: X_2услов=(-0.5, 1); находим F2(-0.5,1)=0.25, F1(-0.5,1)=4.25.

2. Находим частные

составляем систему

2x₁=-λ (x₁+1),

8x₂=-λ (x₂-1).

Отсюда получаем уравнение кривой в параметров

В данном можно получить этой кривой в прямоугольных координатах. этого решаем уравнения относительно λ. Получим:

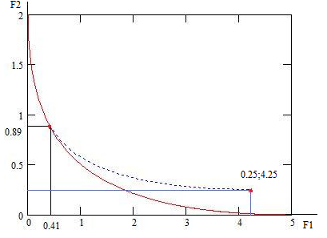
Приравнивая части и разрешая x₂, получим уравнение кривой P: . Найдём пересечения кривой с x₁=-0.5. Xп=(-0.5; 0.2). Это случаю, когда λ от 0 до 1 (0≤ λ≤1).^[12]

уравнение КК иметь следующий (когда точки X_1opt=(0,0) и X_2opt=(-1,1) области D)

F₁(λ)=

F₂(λ)=.

Закономерность : F₁ возрастает от 0 4.25, а F₂ убывает от 2 0.

Построим графики кривых в области D и критериев (рис. 8 и 9).

. 8 Область D и множество P . 9 Компромиссная кривая

Xп

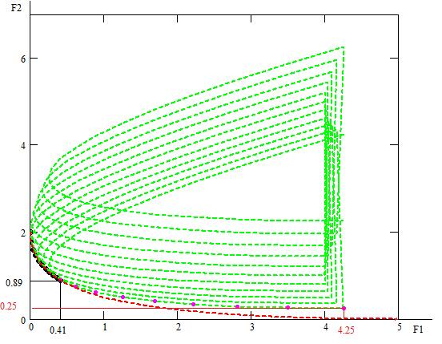
. 10

Пространство оценок и кривая

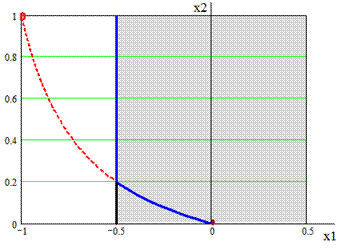
б) введём ограничения. Область D в случае будет вид (рис. 11). условный минимум функции F₁ и F₂ . Они в точках X_1opt=(0,0) и X_2opt=(-0.5, 1). Как из полученных точки минимумов изменились.^[13]

Рис. 11 D Рис. 12 Пространство

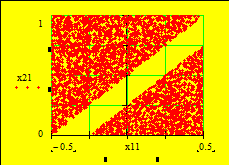
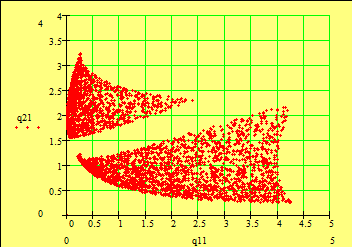
Из рассмотренного видно, что множества P в аналитическом является сложной . Поэтому в настоящее широко используются методы построения оптимальных по (см. раздел " методы получения Парето").

1.4 Способы Парето-оптимального

Выделение множества МЗО часто является удовлетворительным . Это связано с , что при большом исходном вариантов множество оказывается недопустимо для того, ЛПР было в состоянии осуществить самостоятельно. Таким , выделение множества можно рассматривать как предварительный оптимизации, и налицо дальнейшего сокращения множества.

Для одной оптимальной из множества решений в каждой многокритериальной задаче использовать дополнительную о цели операции, т.е. информацию, которая задании векторного осталась неформализованной и неиспользованной.^[14]

Наиболее и последовательным представляется построения бинарного предпочтения, более , чем отношение , позволяющего сузить выбираемых вариантов приемлемых с точки ЛПР размеров. , для этого некоторая дополнительная , которую придётся от ЛПР. может быть о критериях, о самих вариантах и т.п. Задача, перед создателями , заключается в том, с помощью этой обосновать свои по сужению и гарантировать ЛПР того, чтобы один из , представляющих для интерес, не потерян в процессе .

Необходимо отметить, необоснованность сужения Парето является недостатком многих многокритериальной оптимизации.

образом, общая исследования задач решения на математического моделирования МЗО может реализована в рамках из следующих .

Первый подход. заданной многокритериальной оптимизации находится её Парето- решений, а выбор оптимального варианта множества Парето- предоставляется ЛПР.

подход. Как было сказано , производится сужение Парето-оптимальных (в идеале – до элемента) с помощью формализованных процедур, облегчает окончательный для ЛПР. , что такое может быть только при дополнительной информации о или свойствах решения.

Рассмотрим простейшие способы Парето-оптимального , акцентируя при внимание на дополнительной информации. , что задана задача оптимизации.

верхних границ . Дополнительная информация оптимальном исходе ∈D в этом случае вид:^[15]

(1)

Число рассматривается здесь верхняя граница i – му критерию.

, что указание границ по не может "извлечено" из модели задачи решения; набор (C₁, C₂, , C_m) представляет дополнительную информацию, от ЛПР.

. Выбор места :

Предположим, что предстоит выбрать работы из вариантов, представленных в .1. В качестве основных взяты: зарплата З, отпуска Д, время на работу В. смысла задачи , что критерии З и Д максимизировать, а критерий В – . Какой вариант оптимальным?

Таблица 1

Варианты	Критерий
	Зарплата, (руб.)	Длительность отпуска, (дни)	Время поездки, (мин)
1	900	20	60
2	500	30	20
3	700	36	40
4	800	40	50
5	400	60	15
6	600	30	10
7	900	35	60
8	600	24	10
9	650	35	40

. Выделим вначале -оптимальные варианты. доминируемые по варианты {1, 2, 8, 9}, получаем -оптимальное множество {3, 4, 5, 6, 7}. отсутствии информации относительной важности критериев, а также о -либо дополнительных оптимального решения сужение Парето- множества произвести . Тогда формальный заканчивается указанием -оптимального множества и выбор оптимального производится ЛПР этих пяти на основе -то дополнительных .^[16]

Рассмотрим теперь подход, который к сужению Парето- множества на дополнительной информации, от ЛПР.

а) нижних границ . Наложим, например, ограничения на решение:

зарплата — менее 600 рублей;

отпуска — не 30 дней;

время — не более 40 .

Варианты, удовлетворяющие дополнительным ограничения: {3, 6, 9}; них оптимальными Парето являются 3 и 6. Остаётся сделать выбор между 3 и 6.

б) Субоптимизация. Пусть в выделенного (главного, ) критерия выступает зарплата; ограничения отпуска — не 30 дней, время — не более 40 . Отбросим варианты, не удовлетворяют ограничениям; остаются : {2, 3, 5, 6, 9}. Из них зарплату имеет 3. Этот вариант и оптимальным.^[17]

в) Лексикографическая . Упорядочим критерии относительной важности. , следующим образом: (т.е. критерий — зарплата, за ним важности время , наименее важный длительность отпуска). значение по З имеют варианты 1 и 7. сравниваем эти по второму важности критерию В. как время для этих одинакова, переходим к критерию Д; по длительность отпуска является вариант 7, и является здесь .

2. Численные методы множеств Парето

используют следующий . Во множестве D некоторая сетка, , координаты которой с помощью датчика чисел, распределённых равномерному закону. вычисляют значения критерия F в точках сетки, после за конечное сравнений, используя выбора по , строится множество на указанной , являющееся при N приближением множества относительно D (N – число сетки).

В рассмотренных моделях оптимизации выбора наилучшего (оптимального плана) при помощи максимизации скалярной , которая таким отражает степень целей объекта и часто называется функцией.^[18]

Однако такой целевой для реального объекта представляет , как правило, трудную задачу. этого связаны с характером целей , влиянием не экономических, но и факторов, сложностью полезности конечных хозяйственной деятельности и т.п. некая синтезированная цель производственного часто может выражена лишь в форме, но не поддается при помощи выраженной скалярной функции. В связи с оказывается перспективным , что объект перед собой достижения не общей цели, имеет в виду целей, каждой которой отвечает целевая функция. подход позволяет задачу выбора решения как многокритериальной оптимизации множестве Z допустимых интенсивностей технологических .

Пусть f _l ( z ) ( l = 1, ..., L ) целевые , соответствующие системе L производственного объекта, на множестве Z . этом большему f _l отвечает более степень достижения l - цели. Можно , что требуется решение задачи оптимизации.

В данной векторная целевая f ( z ) выступает в виде между различными и позволяет условно некоторую, вообще , некорректную математическую , в которой требуется план, который бы точкой максимума для нескольких различных функций. Для того, чтобы хотя бы частично устранить эту неправильность, используются некоторые примирительные определения решений многокритериальной задачи.

Вообще говоря, оптимум Парето не является единственным. Совокупность всех таких оптимумов образует множество Парето, которое может иметь сложную структуру. Чаще всего представление о множестве Парето дается при помощи графического изображения в пространстве частных целевых функций (критериев).

Проблема описания множества Парето в конкретной задаче многокритериальной оптимизации оказывается обычно очень сложной и решается путем последовательного решения серии вспомогательных однокритериальных задач. При этом используется, в частности, тот факт, что оптимальный план всякой задачи вида является оптимумом Парето. Следовательно, изменяя коэффициенты, можно построить некоторый набор точек множества Парето.^[19]

Заключение

Процедура решения многокритериальной задачи методом последовательных уступок заключается в том, что все частные критерии располагают и нумеруют в порядке их относительной важности; максимизируют первый, наиболее важный критерий; затем назначают величину допустимого снижения значения этого критерия и максимизируют второй по важности частный критерий при условии, что значение первого критерия не должно отличаться от максимального более чем на величину установленного снижения (уступки); снова назначают величину уступки, но уже по второму критерию и находят максимум третьего по важности критерия при условии, чтобы значения первых двух критериев не отличались от ранее найденных максимальных значений больше чем на величины соответствующих уступок; далее подобным, же образом поочередно используются все остальные частные критерии; оптимальной обычно считают любую стратегию, которая получена при решении задачи отыскания условного максимума последнего по важности критерия.

Таким образом, при использовании метода последовательных уступок многокритериальная задача сводится к поочередной максимизации частных критериев и выбору величин уступок. Величины уступок характеризуют отклонение приоритета одних частных критериев перед другими от лексикографического: чем уступки меньше, тем приоритет жестче.

Порядок решения детерминированных многокритериальных задач методом последовательных уступок:

При решении многокритериальной задачи методом последовательных уступок сначала производится качественный анализ относительной важности частных критериев; на основании такого анализа критерии располагаются и нумеруются в порядке убывания важности, так что главным является критерий , менее важен , затем следуют остальные частные критерии . Максимизируется первый по важности критерий и определяется его наибольшее значение.

Затем назначается величина «допустимого» снижения (уступки) критерия и ищется наибольшее значение второго критерия при условии, что значение первого критерия должно быть не меньше, чем .

Снова назначается величина уступки , но уже по второму критерию, которая вместе с первой используется при нахождении условного максимума третьего критерия, и т.д. Наконец, максимизируется последний по важности критерий при условии, что значение каждого критерия из предыдущих должно быть не меньше соответствующей величины; получаемые в итоге стратегии считаются оптимальными.

Список используемых источников

1. Веснин, В.Р. Менеджмент: Учеб.- 4-е изд., перераб. и доп.- М.: ТК Велби, 2016. - 342 с.

2. Герчикова , И.Н. Процесс принятия и реализации управленческих решений/ И.Н. Герчикова //Менеджмент в России и за рубежом, 2016. № 12. - 130 с.

3. Гончаров, В. И. Менеджмент: учебное пособие / В. И. Гончаров. - Минск : Современная школа, 2015.- 255 с.

4. Дробышев, А.В . Методы принятия решений. Методы Дельфи и ЭЛЕКТРА. - Методические указания к лабораторной работе по курсу "Системы поддержки принятий решений". - МГИЭМ. Сост.: И.Е.Сафонова,., К.Ю.Мишин, С.В.Цыганов: М., МГИЭМ, 2015. - 26 с.

5. Евланов, А. Г. Теория и практика принятия решений. -- М.: Экономика, 2015. - 212 с.

6. Коротков, Э. М. Менеджмент : учебник для бакалавров / Э. М. Коротков. Москва :Юрайт, 2016.- 85 с.

7. Кривко, О.Б. Информационные технологии. М.: СОМИНТЭК. 2015. - 179 с.

8. Лафта, Дж. К. Эффективность менеджмента организации. - М.: Русская деловая литература, 2016. - 320 с.

9. Макаров, С.Ф. Менеджер за работой. - М.: ФИНПРЕСС, 2016. - 155 с.

10. Мескон , М. Основы менеджмента: Учебное пособие / М. Мескон, М. Альберт, Ф. Хедоури; М., 2016. - 387 с.

11. Панкрухина , А.П.Теория управления: учебник / [Ю. П. Алексеев и др.]; под общей редакцией: А. Л. Гапоненко, А. П. Панкрухина. - Москва: Издательство РАГС, 2015.- 213 с.

12. Пирожков, В.А. О реализации процессного подхода к управлению в виде системы поддержки принятия решений «Управление деятельностью организации» [Текст] / В.А. Пирожков // Вестник Тамбовского ун-та. Сер.: Гуманитарные науки. - 2015. - Вып. 11. - 489 с.

13. Полушкин, О.А. Стратегический менеджмент: конспект лекций. - М.: ЭКСМО, 2016. - 138 с.

14. Ромащенко, В.Н. Принятие решений: ситуации и советы. - Киев, 2015. - 154 с.

15. Румянцева З.П. Менеджмент организации: учебное пособие. - М.: ИНФРА-М, 2015. - 432 с.

16. Сараев, А. Д., Щербина О. А. Системный анализ и современные информационные технологии //Труды Крымской Академии наук.- Симферополь: СОНАТ, 2016.- 136 с.

17. Терелянский, П.В. Системы поддержки принятия решений. Опыт проектирования : монография / П.В. Терелянский ; ВолгГТУ.- Волгоград, 2015. -127 с.

18. Черняховская Л.Р. Поддержка принятия решений при стратегическом управлении предприятием на основе инженерий знаний / Л. Р. Черняховская и др. Уфа: АН РБ, Гилем, 2016. - 128 с.

1. Веснин, В.Р. Менеджмент: Учеб.- 4-е изд., перераб. и доп.- М.: ТК Велби, 2016. - 342 ↑

2. Герчикова , И.Н. Процесс принятия и реализации управленческих решений/ И.Н. Герчикова //Менеджмент в России и за рубежом, 2016. № 12. - 130 с. ↑

3. Гончаров, В. И. Менеджмент: учебное пособие / В. И. Гончаров. - Минск : Современная школа, 2015.- 255 с. ↑

4. Коротков, Э. М. Менеджмент : учебник для бакалавров / Э. М. Коротков. Москва :Юрайт, 2016.- 85 с. ↑

5. Евланов, А. Г. Теория и практика принятия решений. -- М.: Экономика, 2015. - 212 с. ↑

6. Дробышев, А.В . Методы принятия решений. Методы Дельфи и ЭЛЕКТРА. - Методические указания к лабораторной работе по курсу "Системы поддержки принятий решений". - МГИЭМ. Сост.: И.Е.Сафонова,., К.Ю.Мишин, С.В.Цыганов: М., МГИЭМ, 2015. - 26 с. ↑

7. Кривко, О.Б. Информационные технологии. М.: СОМИНТЭК. 2015. - 179 с. ↑

8. Лафта, Дж. К. Эффективность менеджмента организации. - М.: Русская деловая литература, 2016. - 320 с. ↑

9. Макаров, С.Ф. Менеджер за работой. - М.: ФИНПРЕСС, 2016. - 155 с. ↑

10. Мескон , М. Основы менеджмента: Учебное пособие / М. Мескон, М. Альберт, Ф. Хедоури; М., 2016. - 387 с. ↑

11. Черняховская Л.Р. Поддержка принятия решений при стратегическом управлении предприятием на основе инженерий знаний / Л. Р. Черняховская и др. Уфа: АН РБ, Гилем, 2016. - 128 с. ↑

12. Панкрухина , А.П.Теория управления: учебник / [Ю. П. Алексеев и др.]; под общей редакцией: А. Л. Гапоненко, А. П. Панкрухина. - Москва: Издательство РАГС, 2015.- 213 с. ↑

13. Пирожков, В.А. О реализации процессного подхода к управлению в виде системы поддержки принятия решений «Управление деятельностью организации» [Текст] / В.А. Пирожков // Вестник Тамбовского ун-та. Сер.: Гуманитарные науки. - 2015. - Вып. 11. - 489 с. ↑

14. Полушкин, О.А. Стратегический менеджмент: конспект лекций. - М.: ЭКСМО, 2016. - 138 с. ↑

15. Полушкин, О.А. Стратегический менеджмент: конспект лекций. - М.: ЭКСМО, 2016. - 138 с. ↑

16. Ромащенко, В.Н. Принятие решений: ситуации и советы. - Киев, 2015. - 154 с. ↑

17. Терелянский, П.В. Системы поддержки принятия решений. Опыт проектирования : монография / П.В. Терелянский ; ВолгГТУ.- Волгоград, 2015. -127 с. ↑

18. Румянцева З.П. Менеджмент организации: учебное пособие. - М.: ИНФРА-М, 2015. - 432 с. ↑

19. Сараев, А. Д., Щербина О. А. Системный анализ и современные информационные технологии //Труды Крымской Академии наук.- Симферополь: СОНАТ, 2016.- 136 с. ↑