
Понятие и основные свойства алгоритмов
Содержание:
Введение
Темой данной курсовой работы является: «Основные структуры алгоритмов: сравнительный анализ и примеры их использования».
Актуальность выбранной темы подтверждается тем, что понятие алгоритма является одним из базовых понятий информатики, вычислительной техники и программирования. Умение составлять алгоритмы и программы решения различных практических задач является элементом алгоритмической культуры современного специалиста в области информационных технологий.
Для решения большинства задач, как правило, существует много различных алгоритмов, которые могут отличаться друг от друга по быстродействию, требуемой внутренней и/или внешней памяти, сложности программирования и ряду других критериев. При этом, как правило, не существует алгоритма, который был бы предпочтительнее при любых исходных данных и по всем критериям оценки [12, C.5].
Какой из них выбрать для решения конкретной задачи? Этот вопрос очень важен для любого профессионального программиста. Именно поэтому необходимо уже на ранних этапах обучения студентов «программистских» направлений подготовки уделять как можно больше времени вопросам выбора эффективного алгоритма решения задачи. Начинающий программист должен четко понимать, что один из основных этапов решения любой задачи – анализ и выбор алгоритма ее решения.
Целью данной работы является изучение базовых структур алгоритмов, проведения их сравнительного анализа и изучения их применения на практике.
Объектом изучения данной работы является понятие алгоритма, а предметом его основные структуры и методы применения.
Исходя из поставленной цели в работе решаются следующие задачи:
- Изучения основных структур алгоритмов.
- Рассмотрение методики проведения сравнительного анализа различных структур алгоритмов.
- Анализ применения наиболее известных структур алгоритмов.
Работа состоит из трех глав, введения, заключения, библиографического списка и приложений.
В первой главе рассматривается понятие и основные свойства алгоритмов, способы их описания и основные структуры.
Во второй главе анализируется сложность и эффективность алгоритмов и способы их оптимизации.
В третьей главе изучаются наиболее известные алгоритмы: алгоритм Евклида, алгоритм «перебора делителей», а также алгоритм «решето Эратосфена».
В ходе работы использовались учебники, учебные пособия, статьи из профильных журналов и электронные ресурсы, общий объем использованных ресурсов составил 15 ед.
Глава 1. Основные структуры алгоритмов
1.1 Понятие и основные свойства алгоритмов
В сегодняшнем обществе слово «алгоритм» имеет настолько широкое распространение, что большинству людей понятно интуитивно. Под ним мы понимаем какую-нибудь последовательную цепь шагов для достижения той или иной цели. Однако для теоретической науки понятие «алгоритма» является гораздо более сложным.
Считается, что однозначного определения алгоритма нет, хотя в основном различные источники дают весьма схожие определения.
Итак, в широко распространенных определениях алгоритма (в рамках школьного курса информатики) можно выделить следующие составляющие:
Алгоритм – это конечная последовательность указаний …
–… на языке понятном исполнителю, …
–… задающая процесс решения задач определенного типа …
–… и ведущая к получению результата, однозначно определяемого допустимыми исходными данными [12, C.6].
В последнем пункте определения сообщается о том, что результат выполнения алгоритма напрямую зависит от исходных данных. Т.е. один и тот же алгоритм при различных исходных данных даст различные результаты. С другой стороны, если одному и тому же алгоритму задать повторно несколько раз одни и те же исходные данные, он должен столько же раз выдать один и тот же результат.
Слово «алгоритм» происходит от имени арабского ученого IX века Муххамеда бен Аль–Хорезми («аль–хорезми» –> «алгоритм»), который описал свод правил выполнений арифметических действий в десятичной системе счисления [1, C.8]. Словом «алгоритм» потом и стали обозначать эти правила вычислений. Однако с течением времени определение алгоритма постепенно трансформировалось и в XX веке под ним стали понимать какую-либо заданную последовательность действий, позволяющую прийти к решению поставленной задачи.
Графически эволюция понятия «Алгоритм» представлена на рис. 1.1.
XX век
Последовательность действий для решений различных задач
IX век
Правила арифметических действия
Рис. 1.1 Эволюция значения слова «Алгоритм» [5, C.7]
В первое время определение понятия алгоритма было проблемой математики, однако с течением времени теория алгоритмов стала развиваться за счет влияния открытий не только в математической науке, но и в информатике. На сегодняшний день алгоритм является одним из основных понятий информатики [12, C.4].
Иными словами, следует понимать, что изначально теория алгоритмов появилась в математике и являла собой поиск способов решения задач определенного типа посредством определенного набора указаний.
В таком случае, алгоритм – это описание способа решения задачи, в котором должно предусматриваться разбиение процессов решения на конечную по времени последовательность действий, представленных в виде элементарных операций.
Под элементарной операцией понимается простое действие, которое уже не нуждается в дальнейшей детализации.
Алгоритм может применяться как инструкция для работы, системы управления, автоматического регулятора или другого устройства, выполняющего определённые заданные автоматические действия или операции. Алгоритм может применяться также в качестве схемы решения конкретной задачи [12, C.5].
Алгоритм является основой и базовым ядром для написания программы, которую составляет программист на каком-либо языке программирования с тем, чтобы реализовать автоматический процесс обработки данных на компьютере.
Алгоритм позволяет разбивать весь процесс преобразования информации, направленную на решение определённой задачи, на отдельные, тесно взаимосвязанные между собой этапы. Алгоритм должен точно и аккуратно определять последовательность действий, которые необходимо выполнять на каждом этапе и правильный порядок выполнения этих действий [14].
Решение и постановка задач на персональном ЭВМ представляет собой сложный процесс, состоящий из нескольких последовательных этапов (рис.1.2). Непосредственная разработка алгоритма – это один из этих этапов
Постановка задачи
Построение математической модели
Выбор метода решения задачи на ЭВМ
Разработка алгоритма
Уточнение (подготовка) исходной информации
Программирование
Отладка программы
Решение задачи на ЭВМ и анализ результатов
Рис.1.2 Схема процесса решения задачи на ЭВМ [14]
Постановка задачи – представляет собой детализированное описание и построение самой задачи, описание входящей и выходной информации, формулируется итоговая цель, которой нужно добиться при решении задачи. Постановка задачи зачастую напрямую связана с построением математической модели изучаемого процесса и иногда представляет собой довольно затруднительный этап в решении задачи.
Математическая формулировка – заключается в записи условия задачи с помощью математических обозначений, формул, зависимостей, в определении начальных данных и формы выдачи результатов вычислений [14].
Выбор метода решения задачи на ЭВМ. После построения математической модели нужно определить метод решения задачи на ЭВМ. Выбранный метод является основой построения алгоритма решения задачи.
Разработка алгоритма решения задачи заключается в установлении необходимой последовательности арифметических и логических действий, строгое выполнение которых должно приводить к решению задачи [3, C.11].
Составление программы – заключается в написании программы на выбранном языке программирования.
Отладка программы – этап, необходимый для выявления и устранения ошибок в написанное программе.
Решение задачи на ЭВМ – производится по отлаженной программе для всего множества заданных исходных данных.
1.2 Свойства и способы описания алгоритма
Алгоритм обладает следующими основными свойствами:
– дискретностью;
– определенностью (детерминированностью, точностью);
– массовостью;
– результативностью;
– формальностью [7, C.14].
Графически свойства алгоритма представлены на рис. 1.3.
Детерминированность
Дискретность
Массовость
Алгоритм
Конечность
Формальность
Результативность
Рис.1.3 Свойства алгоритма [7, C.15]
Дискретность – свойство алгоритма, которое должно характеризовать его структуру. Любой алгоритм состоит из отдельных операций (этапов, действий), которые выполняются дискретно (по шагам). Это означает, что алгоритм обладает свойством дискретности.
Детерминированность – свойство алгоритма, указывающее на то, что каждый последовательный шаг алгоритма должен быть строго определен и не может допускать нескольких толкований. Также строго должен быть определен порядок выполнения отдельных последовательных шагов, то есть исполнитель должен точно знать последовательность выполнения операций. Любой алгоритм должен быть представлен таким образом, чтобы он мог быть однозначно (точно) реализован исполнителем. Это свойство алгоритма называют также определенностью, однозначностью или точностью.
Массовость (универсальность) – применимость алгоритма ко всем задачам рассматриваемого типа при любых допустимых множествах исходных данных. Здесь необходимо подчеркнуть, что массовость означает применимость алгоритма ко всем задачам рассматриваемого типа, то есть ко всем задачам, для решения которых он предназначен. Кроме того, здесь важно иметь в виду, что реализация алгоритма возможна при любых, но допустимых множествах исходных данных [8, C.19].
Результативность (конечность) – способность получения конкретного результата для допустимых исходных данных за конечное число шагов. То есть способность завершать процесс за конечное число итераций или создавать информационное окно с сообщением о невозможности дальнейшей обработки данных (например, в связи с тем, что к имеющимся исходным данным этот алгоритм не применим).
Формальность – свойство означающее, что любой исполнитель, выполняющий алгоритм (например, компьютер), действует формально, то есть строго выполняет инструкции, предусмотренные разработчиком алгоритма [8, C.19-20].
Существуют следующие способы описания (представления) алгоритмов:
1. словесное описание;
2. описание алгоритма с помощью математических формул;
3. графическое описание алгоритма в виде блок-схемы;
4. описание алгоритма с помощью псевдокода;
5. комбинированный способ изображения алгоритма с использованием словесного, графического и др. способов [6, C.22].
Словесное описание алгоритма представляет собой описание структуры алгоритма на естественном языке. Например, к приборам бытовой техники, как правило, прилагается инструкция по эксплуатации, т.е. словесное описание алгоритма, в соответствии с которым данный прибор должен использоваться [7, C.16].
Приведем еще один пример: записать алгоритм нахождения наибольшего общего делителя (НОД) двух натуральных чисел (алгоритм Эвклида), который более подробно будет изучен в главе 3 данной курсовой работы.
Алгоритм может быть следующим [8, C.21]:
- задать два числа;
- если числа равны, то взять любое из них в качестве ответа и остановиться, в противном случае продолжить выполнение алгоритма;
- определить большее из чисел;
- заменить большее из чисел разностью большего и меньшего из чисел;
- повторить алгоритм с шага 2.
Описанный алгоритм применим к любым натуральным числам и должен приводить к решению поставленной задачи. Убедимся в этом самостоятельно, определив с помощью этого алгоритма наибольший общий делитель чисел 125 и 75.
Словесный способ не имеет широкого распространения, так как такие описания:
– строго не формализуемы;
– страдают многословностью записей;
– допускают неоднозначность толкования отдельных предписаний [7, C.17].
Графическое описание алгоритма в виде блок-схемы – это описание структуры алгоритма с помощью геометрических фигур с линиями связи.
Блок схема алгоритма – это графическое представление метода решения задачи, в котором используются специальные символы для отображения операций.
На языке блок-схем каждый шаг алгоритма описывается с помощью соответствующей фигуры, а последовательность выполнения шагов определяется линиями-связями. Блок схемы необходимо читать сверху вниз и слева направо [9, C.27].
Блок-схемы полезны и удобны тем, что обеспечивают легкую «читаемость» алгоритма. Однако это применимо не ко всем ситуациям: стоит попытаться нарисовать блок-схему для более-менее сложного алгоритма, как она начнет разрастаться до невероятных размеров и потеряет все свое наглядное преимущество. Поэтому блок-схемы полезны в структурном программировании для описания коротких алгоритмов [13, C.11].
Язык блок-схем прост (хотя существуют его более расширенные варианты):
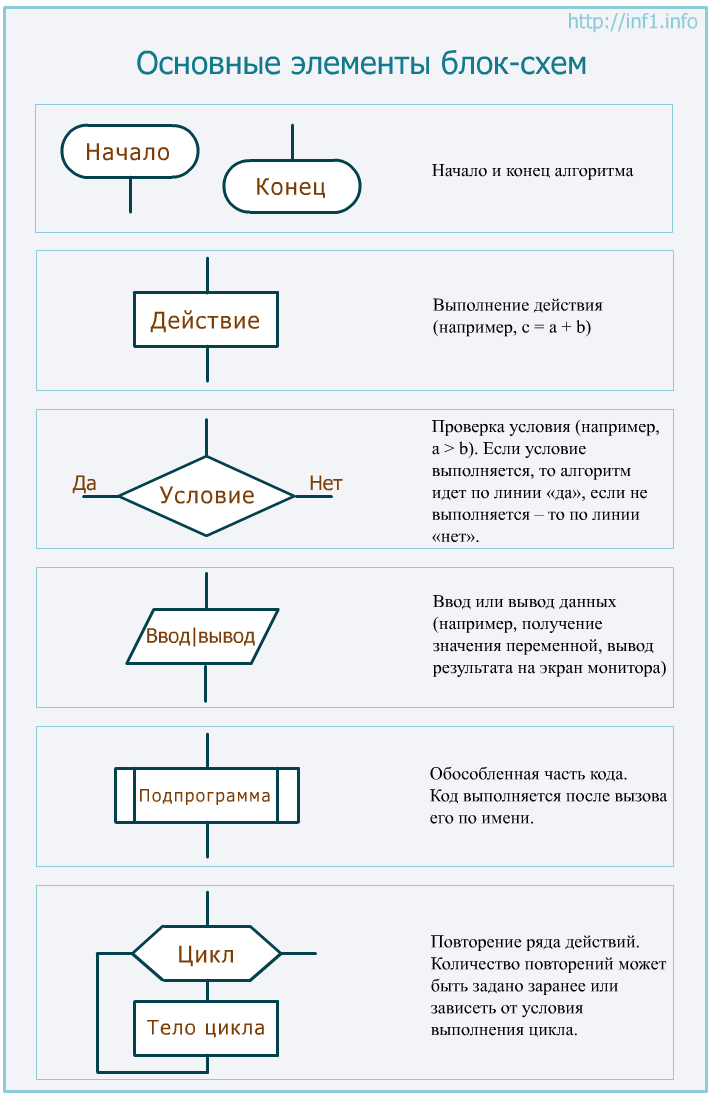
– Прямоугольник – выполнение действия (для примера, c = a + b)
– Ромб – проверка условия (для примера, a > b). Если условие выполняется, то алгоритм идет по линии «да», если не выполняется – то по линии «нет».
– Скругленный прямоугольник – начало и конец алгоритма
– Скошенный прямоугольник – ввод-вывод данных (например, получение значения переменной, вывод результата на экран монитора компьютера). Это не полное описание языка блок-схем [12, C.23].
Основные элементы блок-схем представлены в Приложении 1.
Символы, из которых состоит блок-схема алгоритма, определяются по ГОСТ 19.701-90. Этот ГОСТ соответствует международному стандарту оформления алгоритмов, поэтому блок-схемы алгоритмов, оформленные согласно ГОСТ 19.701-90, в разных странах понимаются однозначно и не имеют двойного толкования [13, C.15].
Псевдокод – описание структуры алгоритма на естественном, но частично формализованном языке. В псевдокоде используются некоторые формальные конструкции и общепринятая математическая символика. Строгих синтаксических правил для записи псевдокода не предусмотрено.
Псевдокод занимает промежуточное место между естественным и формальным языками. С одной стороны, он близок к обычному естественному языку, поэтому алгоритмы могут на нем записываться и читаться как обычный текст. С другой стороны, в псевдокоде используются некоторые формальные конструкции и математическая символика, что приближает запись алгоритма к общепринятой математической записи.
В псевдокоде не приняты строгие синтаксические правила для записи команд, присущие формальным языкам, что облегчает запись алгоритма на стадии его проектирования и дает возможность использовать более широкий набор команд, рассчитанный на абстрактного исполнителя [7, C.22].
Однако в псевдокоде обычно имеются некоторые конструкции, присущие формальным языкам, что облегчает переход от записи на псевдокоде к записи алгоритма на формальном языке. В частности, в псевдокоде, так же, как и в формальных языках, есть служебные слова, смысл которых определен раз и навсегда. Они выделяются в печатном тексте жирным шрифтом, а в рукописном тексте подчеркиваются.
Единого или формального определения псевдокода не существует, поэтому возможны различные псевдокоды, отличающиеся набором служебных слов и основных (базовых) конструкций [7, C.23].
Каждый из перечисленных способов изображения алгоритмов имеет и достоинства и недостатки. Например, словесный способ отличается многословностью и отсутствием наглядности, но дает возможность лучше описать отдельные операции. Графический способ более наглядный, но часто возникает необходимость описать некоторые операции в словесной форме. Поэтому при разработке сложных алгоритмов лучше использовать комбинированный способ.
1.3 Основные структуры алгоритмов
По характеру связей между символами различают алгоритмы линейной, разветвляющейся и циклической структуры.
Линейный алгоритм – это алгоритм, в котором операции выполняются последовательно [14].
Разветвляющийся алгоритм – это алгоритм, в котором последовательность выполнения операций зависит от определенных условий [14].
Если в алгоритме присутствует «действие1» и «действие2» (то есть ветвь 1 и ветвь 2), то это разветвляющийся алгоритм с полной альтернативой. Если же вместо «действия2» предусмотрен переход к выполнению операции «n», которая находится в общей (основной) ветви, то такая форма записи называется неполной альтернативой.
Циклический алгоритм – это алгоритм, в котором многократно выполняются одни и те же действия, например с целью многократного выполнения вычислений по одним и тем же зависимостям при различных значениях входящих в них переменных [14].
Использование циклов существенно сокращает объем алгоритма.
Можно выделить три основных типа циклических алгоритмов:
– цикл с параметром (арифметический цикл или цикл со счетчиком);
– цикл с предусловием;
– цикл с постусловием.
Линейный алгоритм (следование) – состоит из последовательности операций, выполняющихся только один раз в порядке их следования и считается самым простым в информатике. Подразумевая под собой конкретную последовательность выполнения действий, он не позволяет создавать разветвленную систему параметров и отлично служит в тех случаях, где необходимо конкретно и четко описать представленную задачу [12, C.24].
Графически линейный алгоритм представлен на рис.1.4.
Начало
Объявление переменной
Ввод данных
Действия
Вывод данных
Конец
Рис. 1.4 Линейный алгоритм [14]
В математической науке к линейным алгоритмам относят алгоритмы, представленные конкретными формулами. Они являются наиболее простыми для программирования. Нужно отметить, что естественный способ кодировки формул делает программу более легкой для прочтения, но зачастую приводит к излишним вычислениям. Для того, чтобы не допустить повторных вычислений и уменьшить общее количество выполняемых операций совершайте тождественные преобразования выражений. С другой стороны, необходимо понимать, что не всегда нужно выполнять оптимизацию, по той причине, что она является не правилом, а исключением. Этому есть три основания, главное из которых состоит в том, что в некоторых случаях оптимизация ухудшает наглядность программ, вторая – выгоды от оптимизации должны быть существенными.
1.3.2 Разветвляющийся алгоритм
Ветвящимся называется такой вычислительный процесс, в котором выбор направления обработки информации зависит от исходных или промежуточных данных (от результатов проверки выполнения какого-либо логического условия). Он обеспечивает в зависимости от результата проверки условия (да или нет) выбор одного из альтернативных путей работы алгоритма [8, C.32].
Каждый из путей ведет к общему выходу, так что работа алгоритма будет продолжаться независимо от того, какой путь будет выбран. Такой тип алгоритма позволяет реализовать решение более сложных задач.
Графически разветвляющийся алгоритм представлен в Приложении 2.
Циклический алгоритм – вычислительный процесс, содержащий один или несколько повторяющихся циклов. По количеству выполнения циклы делятся на циклы с определенным (заранее заданным) числом повторений и циклы с неопределенным числом повторений [8, C.24].
В цикле с параметром определённая последовательность операций выполняется несколько раз в зависимости от заданной величины, которая называется параметром цикла. Цикл выполняется, пока параметр цикла принимает значения в заданном диапазоне с заданным шагом. Оператор цикла включает имя переменной, конечное значение и шаг.
Выделяют два типа циклов с условием: цикл с предусловием и цикл с постусловием. В циклах с предусловием условие проверяется на входе (до операций, выполняемых в цикле). В циклах с постусловием условие проверяется после выполнения всех операций внутри цикла. В этом случае операторы тела цикла будут реализованы хотя бы один раз или до тех пор, пока не станет возможным условие выхода из цикла [9, C.83].
В циклах с постусловием сначала выполняются все операции, включенные в цикл, и только после этого проверяется заданное условие. В зависимости от результата проверки осуществляется выход из цикла или его повторение. Цикл с условием называют также итерационным циклом.
Внутри алгоритма циклической структуры может быть помещен другой цикл – вложенный цикл, при этом вложенный (внутренний) цикл должен полностью находиться в области внешнего цикла.
Внутри алгоритма циклической структуры может быть помещен другой цикл – вложенный (внутренний) цикл. Вложенный цикл должен полностью находиться в области внешнего цикла. Вложенный цикл может быть один, но может быть и несколько вложенных циклов. Второй вложен в первый, третий – во второй и т.д.
Для организации и внутреннего, и внешнего циклов могут использоваться разные типы алгоритмических структур (цикл с параметром, цикл с предусловием, цикл с постусловием).
В цикле с параметром определенная последовательность операций выполняется несколько раз в зависимости от заданной величины, которая называется параметром цикла. Цикл выполняется, пока параметр цикла принимает значения в заданном диапазоне с заданным шагом. Оператор цикла включает имя переменной, конечное значение и шаг [9, C.83].
Выделяют два типа циклов с условием: цикл с предусловием и цикл с постусловием.
В циклах с предусловием условие проверяется на входе (до операций, выполняемых в цикле). В циклах с постусловием условие проверяется после выполнения всех операций внутри цикла. В этом случае операторы тела цикла будут реализованы хотя бы один раз или до тех пор, пока не станет возможным условие выхода из цикла.
В циклах с постусловием сначала выполняются все операции, включенные в цикл, и только после этого проверяется заданное условие. В зависимости от результата проверки осуществляется выход из цикла или его повторение [8, C.32].
Цикл с условием называют также итерационным циклом.
Внутри алгоритма циклической структуры может быть помещен другой цикл – вложенный цикл, при этом вложенный (внутренний) цикл должен полностью находиться в области внешнего цикла.
Глава 2. Сравнительный анализ структур алгоритмов
2.1 Анализ сложности и эффективности алгоритмов
Существует ряд чрезвычайно важных и значимых практических причин, которые побуждают нас заниматься анализом алгоритмов и их эффективности, в зависимости от сложности и задействованных ресурсов.
Одной из них является необходимость выяснения оценок или границ для занимаемого объема памяти и затраченного времени работы, потребных алгоритму для эффективной обработки входящих данных [9, C.143].
Необходимо избегать написания программы, которая за отведенное для работы машинное время не успеет в нужном объеме обработать входящие данные достаточно большого размера и содержащие в себе множество переменных условий (например, следует признать неудовлетворительной программу и алгоритм обработки уравнений, если из-за нехватки времени и машинных ресурсов она не дает ответа для уравнения, имеющего более трех переменных).
Необходимо заранее (еще в начальной стадии разработки алгоритма) на бумаге и с помощью карандаша верно оценить объем памяти и время, нужные алгоритму, находящемуся в разработке, а затем модернизировать его (или написать новый, более эффективный в использовании) [12, C.49].
Грамотный анализ данных поможет выяснить наиболее временно затратные места в ваших программах (например, те части алгоритма, на выполнение которых расходуется значительная часть отведенного времени), а также подобрать самый подходящий тип алгоритма из широкого доступного класса алгоритмов, которые помогают в решении данной задачи.
В процессе решения прикладных задач выбор подходящего типа алгоритма вызывает некоторого рода трудности. Алгоритм должен удовлетворять следующим противоречащим друг другу требованиям:
1) быть легким для понимания, перевода в программный код и отладки программы;
2) результативно и эффективно использовать доступные вычислительные ресурсы и выполняться по возможности быстро [11].
Если разрабатываемая программа, использующая алгоритм некоторого типа, должна осуществляться только несколько раз, то первое требование является наиболее важным и приоритетным. В таком случае стоимость программы и используемого времени оптимизируется по стоимости написания (а не выполнения) программы. Если решение поставленной задачи требует значительных вычислительных затрат, то стоимость выполнения программы может превысить стоимость написания программы, особенно если программа выполняется несколько раз. В таком случае, перед тем как принимать решение об использовании в программе того или иного алгоритма, необходимо оценить сложность и эффективность этого алгоритма.
Сложность алгоритма – это величина, отражающая порядок величины требуемого ресурса (времени или дополнительной памяти) в зависимости от размерности и сложности задачи [8, C.56].
В таком случае, необходимо ввести временную T(n) и пространственную V(n) переменную сложности алгоритма. При анализе и рассмотрении оценок сложности будет использоваться только временную сложность. Пространственная сложность оценивается таким же образом [8, C.57].
Самым простым способом оценки является экспериментальный, т.е. ввести исходные данные в алгоритм и осуществить полученную программу на нескольких задачах, стараясь оценивать все возможные факторы, анализируя время совершения действий программы. Однако этот конкретный метод имеет ряд недостатков и просчетов. Во-первых, экспериментальное программирование – это дорогостоящий процесс, который затрачивает временные и системные ресурсы. Во-вторых, следует учитывать, что на время выполнения действий программы влияют важные факторы:
1) временная сложность алгоритма программы;
2) качество скомпилированного кода исполняемой программы и наличие в нем ошибок;
3) конкретные машинные инструкции, используемые для выполнения действий программы [8, C.35].
Присутствие второго и третьего факторов не разрешают пользоваться типовыми единицами измерения временной сложности алгоритма (секунды, минуты и т.п.), так как в таком случае можно получить самые разные результаты для одного и того же алгоритма, если использовать в данном случае различных программистов (которые напишут алгоритм каждый по-своему), разные компиляторы, языки программирования и разные вычислительные машины.
Чаще всего временная сложность алгоритма находится в прямой зависимости от числа входящих данных. Обычно говорят, что временная сложность алгоритма имеет порядок T(n) от входных данных размера n. Точно определить величину T(n) на практике представляется довольно трудно. Поэтому прибегают к асимптотическим отношениям с использованием O-символики.
Когда используется обозначение символики O(), имеется в виду не точное время исполнения задачи, а только его верхний предел, причем с точностью до постоянного множителя. Когда говорят, например, что алгоритму требуется время порядка O(n2), имеют в виду, что время исполнения задачи растет не быстрее, чем квадрат количества элементов [11].
На практике время исполнения алгоритма зависит не только от количества входящих данных, но и от их типов и значений, к примеру, время работы некоторых алгоритмов сортировки значительно уменьшается, если первоначальные данные частично упорядочены, тогда как другие методы оказываются не так чувствительны к этому фактору. Чтобы учитывать этот факт, полностью сохраняя при этом возможность анализировать алгоритмы без зависимости от вводных данных, различают: – максимальную сложность, или сложность наиболее неблагоприятного случая, когда алгоритм работает дольше всего; – среднюю сложность – сложность алгоритма в среднем; – минимальную сложность – сложность в наиболее благоприятном случае, когда алгоритм справляется быстрее всего.
2.2 Оптимизация алгоритмов
В настоящее время компьютерные науки не накопили достаточное количество информации для того, чтобы задача минимизации затрат и рабочих ресурсов могла быть представлена с обычной для математики определенностью. Этому мешает сразу несколько факторов.
Во-первых, весьма сложно сформулировать нужный критерий оптимизации, который бы имел одновременно и безусловное практическое значение и однозначно определенный в математическом плане. К примеру, можно поставить задачу минимизации числа выполняемых команд машины Тьюринга – критерий, хорошо определенный математически; но совсем неясно его практическое значение, поскольку маловероятно реально существующая программа на реальном компьютере будет моделировать машину Тьюринга. Возможно поставить задачу минимизации времени выполнения данной программы на реальной машине –понятный с практической точки зрения критерий. Однако нельзя будет решить задачу оптимизации математическими методами, так как затраты времени на выполнение зависит (чаще всего весьма значительно) от архитектуры ЭВМ, а архитектуру современных компьютером невозможно описать маленьким количеством параметров. Так же исключительно важно, что программа, работающая быстрее и эффективнее остальных на одном компьютере, вполне может оказаться не самой быстродействующей на другом. Существуют даже специальные программы с общим названием benchmark, предназначенные для оценки архитектур персональных компьютеров [2].
Во-вторых, не совсем понятно, что такое сложность задачи. Ее можно было бы обозначить как минимальную из возможных сложностей алгоритмов, которые решают эту задачу. Но можно ли вычислить алгоритм минимальной сложности (как найти доказательства тому, что полученный алгоритм действительно минимальный или, напротив, не соответствует требованиям)? Есть ли возможности усовершенствовать алгоритм и насколько сложен поиск этого минимума – эти вопросы связаны с нижней оценкой сложности алгоритмов (а не верхней, как в предыдущих шагах) [8, C.67].
Существует несколько самостоятельных способов оптимизации программ, из которых можно выделить два:
– оптимизация, которая напрямую связана с выбором метода построения алгоритма;
– оптимизация, связанная с выбором методов представления исходных данных в программе [2].
Графически способ оптимизации программ представлен на рис. 2.1.
Способы оптимизации программ
Оптимизация, напрямую связанная с выбором метода построения алгоритма
Оптимизация, связанная с выбором методов представления исходных данных в программе
Рис.2.1 Способы оптимизации программ
Первый способ оптимизации имеет более глобальный характер и ведет к уменьшению порядка функции сложности. Он зависит от того, как поставленная в программе задача разбивается на подзадачи, насколько это разбиение подходит самой задаче или является только искусственным приемом. Общим руководящим подходом здесь является последовательность действий, обратная анализу алгоритмов.
Следующий вид оптимизации, не меняя целиковую структуры программы, приводит к экономии памяти и ресурсов, и/или упрощению работы со структурами вводных данных, повышению эффективности работы вспомогательных процедур, обеспечивающих «интерфейс» между прикладным уровнем (на котором мыслим в терминах высокоуровневых объектов – то графов, матриц, текстов и т. д.) и машинным уровнем, использующих простейшие типы данных (цифры, символы, указатели) [2].
Результатом данного процесса как правило является уменьшение коэффициентов при некоторых слагаемых в функции сложности (при удачной оптимизации – при наиболее значимом слагаемом), но порядок функции сложности остается тем же.
Оба вида оптимизации дополняют друг друга и могут применяться совместно.
Глава 3. Примеры известных алгоритмов
3.1 Алгоритм Евклида
Древнегреческие математики называли этот алгоритм ἀνθυφαίρεσις или ἀνταναίρεσις – «взаимное вычитание». Этот алгоритм не был открыт Евклидом, так как упоминание о нём имеется уже в Топике Аристотеля (IV век до н. э.). В «Началах» Евклида он описан дважды – в VII книге для нахождения наибольшего общего делителя двух натуральных чисел и в X книге для нахождения наибольшей общей меры двух однородных величин. В обоих случаях дано геометрическое описание алгоритма, для нахождения «общей меры» двух отрезков [15, C.7].
Историками математики было выдвинуто предположение, что именно с помощью алгоритма Евклида (процедуры последовательного взаимного вычитания) в древнегреческой математике впервые было открыто существование несоизмеримых величин (стороны и диагонали квадрата, или стороны и диагонали правильного пятиугольника). Впрочем, это предположение не имеет достаточных документальных подтверждений. Алгоритм для поиска наибольшего общего делителя двух натуральных чисел описан также в I книге древнекитайского трактата Математика в девяти книгах.
Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел [4].
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД [13, C.93].
Описание алгоритма нахождения НОД делением:
- Большее число делим на меньшее.
- Если делится без остатка, то меньшее число и есть НОД (следует выйти из цикла).
- Если есть остаток, то большее число заменяем на остаток от деления.
- Переходим к пункту 1.
Приведем пример алгоритма Евклида:
Найти НОД для 30 и 18.
30/18 = 1 (остаток 12)
18/12 = 1 (остаток 6)
12/6 = 2 (остаток 0)
Конец: НОД – это делитель. НОД (30, 18) = 6.
Графически алгоритм Евклида представлен на рис. 3.1
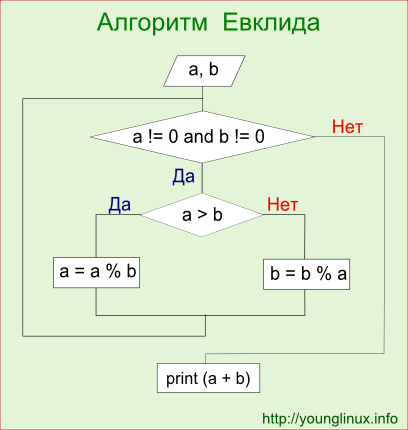
Рис. 3.1 Алгоритм Евклида [14]
Геометрический алгоритм Евклида можно представляет собой: Пусть даны два отрезка длины a и b. Вычтем из большего отрезка меньший и заменим больший отрезок полученной разностью. Повторяем эту операцию, пока отрезки не станут равны. Если это произойдёт, то исходные отрезки соизмеримы, и последний полученный отрезок есть их наибольшая общая мера. Если общей меры нет, то процесс бесконечен. В таком виде алгоритм описан Евклидом и реализуется с помощью циркуля и линейки.
Для иллюстрации алгоритм Евклида будет использован, чтобы найти НОД a = 1071 и b = 462. Для начала от 1071 отнимем кратное значение 462, пока не получим разность меньше, чем 462. Мы должны дважды отнять 462, (q0 = 2), оставаясь с остатком 147:
1071 = 2 × 462 + 147.
Затем от 462 отнимем кратное значение 147, пока не получим разность меньше, чем 147. Мы должны трижды отнять 147 (q1 = 3), оставаясь с остатком 21:
462 = 3 × 147 + 21.
Затем от 147 отнимем кратное значение 21, пока не получим разность меньше, чем 21. Мы должны семь раз отнять 21 (q2 = 7), оставаясь без остатка:
147 = 7 × 21 + 0.
Таким образом последовательность a > b >r1>r2>r3> … >rn в данном конкретном случае будет выглядеть так:
1071 > 462> 147 > 21.
Так как последний остаток равен нулю, алгоритм заканчивается числом 21 и НОД(1071, 462) = 21.
В табличной форме шаги были следующие (таблица 3.1):
Таблица 3.1 Последовательность решения алгоритма Евклида
|
Шаг k |
Равенство |
Частное и остаток |
|
0 |
1071 = q0 462 + r0 |
q0 =2 и r0 = 147 |
|
1 |
462 = q1 147 + r1 |
q1 = 3 и r1 = 21 |
|
2 |
147 = q2 21 + r2 |
q2 = 7 и r2 = 0 алгоритм заканчивается |
Для данного алгоритма существует множество теоретических и практических применений. В частности, он является основой для криптографического алгоритма с открытым ключом RSA, широко распространённого в электронной коммерции. Также алгоритм используется при решении линейных диофантовых уравнений, при построении непрерывных дробей, в методе Штурма. Алгоритм Евклида является основным инструментом для доказательства теорем в современной теории чисел, например, таких как теорема Лагранжа о сумме четырёх квадратов и основная теорема арифметики.
3.2 Алгоритм перебора делителей
Перебор делителей – это алгоритм, предназначенный для определения, какое число перед нами: простое или составное [4].
Алгоритм заключается в последовательном делении заданного натурального числа на все целые числа, начиная с двойки и заканчивая значением меньшим или равным квадратному корню тестируемого числа. Если хотя бы один делитель делит тестируемое число без остатка, то оно является составным. Если у тестируемого числа нет ни одного делителя, делящего его без остатка, то такое число является простым [5, C.119].
Для иллюстрации проведем перебор делителей числа n = 29. i – возможные делители n.
[n1/2] = 5
Решение задачи представим в таблице 3.2.
Таблица 3.2 Решение алгоритмом «перебора делителей» для числа 29
|
i |
n % i |
|
2 |
1 |
|
3 |
2 |
|
4 |
1 |
|
5 |
4 |
Так как ни один из остатков деления 29 не равен 0, то 29 объявляется простым.
Пусть теперь n = 7399, тогда[n1/2] = 86
Решение задачи представим в таблице 3.3.
Таблица 3.3 Решение алгоритмом «перебора делителей» для числа 7399
|
i |
n % i |
|
2 |
1 |
|
3 |
1 |
|
4 |
3 |
|
5 |
4 |
|
6 |
1 |
|
7 |
0 |
[ n 1 / 2 ] = 86 {\displaystyle [n^{1/2}]=86}
Так как остаток деления 7399 на 7 равен 0, то 7399 не является простым. Графически алгоритм перебора делителей представлен на рис. 3.2.
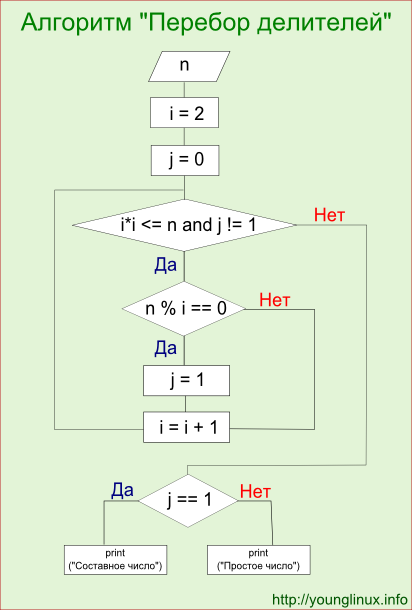
Рис. 3.2 Алгоритм «перебора делителей» [14]
В практических задачах данный алгоритм применяется редко ввиду его большой вычислительной сложности, однако его применение оправдано в случае, если проверяемые числа относительно невелики, так как данный алгоритм довольно легко реализуем.
3.3 Алгоритм решето Эратосфена
Решето Эратосфена – это алгоритм нахождения простых чисел до заданного числа n. В процессе выполнения данного алгоритма постепенно отсеиваются составные числа, кратные простым, начиная с 2.
Название «решето» метод получил потому, что, согласно легенде, Эратосфен писал числа на дощечке, покрытой воском, и прокалывал дырочки в тех местах, где были написаны составные числа. Поэтому дощечка являлась неким подобием решета, через которое «просеивались» все составные числа, а оставались только числа простые. Эратосфен дал таблицу простых чисел до 1000 (см. Приложение 3).
Схематично алгоритм «Решето Эратосфена» представлен на рис. 3.3.

Рис. 3.3 Алгоритм «Решето Эратосфена» [14]
Приведем пример алгоритма «Решето Эратосфена».
Для нахождения всех простых чисел не больше заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
- Выписать подряд все целые числа от двух до n (2, 3, 4, …, n).
- Пусть переменная p изначально равна двум – первому простому числу.
- Зачеркнуть в списке числа от 2p до n считая шагами по p (это будут числа кратные p: 2p, 3p, 4p, …).
- Найти первое не зачеркнутое число в списке, большее чем p, и присвоить значению переменной p это число.
- Повторять шаги 3 и 4, пока возможно.
Теперь все не зачеркнутые числа в списке – это все простые числа от 2 до n.
На практике, алгоритм можно улучшить следующим образом. На шаге № 3 числа можно зачеркивать начиная сразу с числа p2, потому что все составные числа меньше него уже будут зачеркнуты к этому времени. И, соответственно, останавливать алгоритм можно, когда p2 станет больше, чем n. Также, все простые числа (кроме 2) – нечётные числа, и поэтому для них можно считать шагами по 2p, начиная с p2.
Приведем пример алгоритма «Решето Эратосфена» для n = 30.
Запишем натуральные числа, начиная от 2, до 30 в ряд:
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Первое число в списке, 2 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 2 (то есть, каждое второе, начиная с 22 = 4):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачеркнутое число, 3 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 3 (то есть, каждое третье, начиная с 32 = 9):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачёркнутое число, 5 – простое. Пройдём по ряду чисел, зачёркивая все числа, кратные 5 (то есть, каждое пятое, начиная с 52 = 25):
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Следующее не зачеркнутое число –7. Его квадрат, 49– больше 30, поэтому на этом работа завершена. Все составные числа уже зачеркнуты:
2 3 5 7 11 13 17 19 23 29
Подобно всем алгоритмам, решето Эратосфена имеет ограничения. Например, оно неэффективно при поиске очень больших простых чисел. Но в то же время цель этого алгоритма – поиск всех простых меньших, чем определенная верхняя граница. Ясно, что такой поиск невыполним, если граница слишком велика.
Суммируя ограничения, накладываемые назначением алгоритма, отметим два его слабых места: решето требует уйму компьютерной памяти и должно проделать слишком много витков цикла. К его достоинствам можно отнести простоту программирования и, кроме того, нам не нужно вычислять отдельные делители.
Заключение
Целью данной курсовой работы являлось изучение базовых структур алгоритмов, проведения их сравнительного анализа и изучения их применения на практике.
На проведенной проделанной работы можно сделать следующие выводы.
Во всех сферах своей деятельности, и частности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата – мы можем трактовать это как первоначальное или интуитивное определение алгоритма. Некоторые дополнительные требования приводят к определению алгоритма.
Алгоритм – это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных.
Понятие алгоритма – одно из основных в программировании и информатике. Это последовательность команд, предназначенная исполнителю, в результате выполнения которой он должен решить поставленную задачу. Алгоритм должен описываться на формальном языке, исключающем неоднозначность толкования. Исполнитель может быть человеком или машиной. Исполнитель должен уметь выполнять все команды, составляющие алгоритм. Множество возможных команд конечно и изначально строго
Алгоритм обладает следующими основными свойствами: дискретностью; определенностью (детерминированностью, точностью); массовостью; результативностью; формальностью.
При всем разнообразии решаемых задач в них можно выделить три основных (канонических) вида алгоритмических структур: линейную, разветвленную и циклическую. С помощью этих трех видов структур можно построить алгоритм любой сложности.
Запись алгоритма на формальном языке называется программой. Иногда само понятие алгоритма отождествляется с его записью, так что слова «алгоритм» и «программа» — почти синонимы. Небольшое различие заключается в том, что под алгоритмом, как правило, понимают основную идею его построения. Программа же всегда связана с записью алгоритма на конкретном формальном языке.
Благодаря развитию информационных технологий и алгоритмам мы сегодня имеем возможность быстро находить информацию в интернете (в частности, искать по картинкам), находить кратчайшие пути, анализировать геномы и так далее. Алгоритмы используются практически во всех областях жизни.
Список использованной литературы
- Ахо А., Хопкрофт Дж., Ульман Дж. Структуры данных и алгоритмы: Пер. с англ.: – М.: Издательский дом «Вильямс», 2001 г. –384 с., ил.
- Библиотека программиста // http://www.programmer-lib.ru/assemw_page.php?id=1 (дата обращения 27.07.2018)
- Брой, М. Информатика. Основополагающее введение: В 4-х ч. Ч.1. / М. Брой. – М.: Диалог-МИФИ, 1996. – 299 с.
- Википедия // https://ru.wikipedia.org/wiki (дата обращения 11.08.2018)
- Вирт, Н. Алгоритмы и структуры даны учебник / Н. Вирт. – М.: Мир, 1989. – 360 с.
- Информатика: базовый курс: учебник для студентов вузов, бакалавров, магистров, обучающихся по направлению «Информатика» / О.А. Акулов, Н.В. Медведев. 6-е изд., испр. и доп. – М.: Издательство «Омега-Л», 2009. – 574 с.
- Кадырова, Г.Р. Основы алгоритмизации и программирования: учебное пособие / Г.Р. Кадырова. – Ульяновск, УлГТУ, 2014 – 95 с.
- Каймин, В.А. Информатика: учебник / В.А. Каймин. – М.: Проспект, 2011. – 272 с.
- Кормен Т., Лейзерсон Ч., Ривест Р. Алгоритмы: построение и анализ. – М.: МЦНМО, 2001 г. – 960 с., 263 ил.
- Макконнел Дж. Анализ алгоритмов. Вводный курс. – М.: Техносфера, 2002 г. –304 с.
- Самуйлов С.В. Методика сравнительного анализа алгоритмов на примере алгоритмов последовательного поиска // Концепт, 2014. – №9. // https://e-koncept.ru/2014/14236.htm (Дата обращения 15.08.2018)
- Семакин, И.Г. Основы алгоритмизации и программирования: учебник для студ. учреждений сред. проф. Образования / И.Г. Семакин, А.П. Шестаков. – 3-е изд. стер. – М.: Издательский центр «Академия», 2012. – 400 с.
- Соболь, Б.В. Информатика и программирование: учебное пособие / Б.В. Соболь. – Ростов н/Д: Феникс, 2006 – 354 с.
- Теория алгоритмов // https://inf1.info (дата обращения 01.08.2018)
- Тихомиров, В. М. Великие математики прошлого и их великие теоремы. – 2-е изд., испр. – МЦНМО, 2003. – 16 с.
Приложение 1. Основные элементы блок--схемы
Приложение 2. Структура разветвляющегося алгоритма
Начало
Объявление переменных
Ввод данных
Действия
Условие
Действия 1
Действия 2
Окончание
Вывод данных
Окончание
Приложение 3. Таблица алгоритма «Решето Эратосфена»
|
2 |
3 |
5 |
7 |
11 |
13 |
17 |
19 |
|
23 |
29 |
31 |
37 |
41 |
43 |
47 |
53 |
|
59 |
61 |
67 |
71 |
73 |
79 |
83 |
89 |
|
97 |
101 |
103 |
107 |
109 |
113 |
127 |
131 |
|
137 |
139 |
149 |
151 |
157 |
163 |
167 |
173 |
|
179 |
171 |
191 |
193 |
197 |
199 |
211 |
223 |
|
227 |
229 |
233 |
239 |
241 |
251 |
257 |
263 |
|
269 |
271 |
277 |
281 |
283 |
293 |
307 |
311 |
|
313 |
317 |
331 |
337 |
347 |
349 |
353 |
359 |
|
367 |
373 |
379 |
383 |
389 |
397 |
401 |
409 |
|
419 |
421 |
431 |
433 |
439 |
443 |
449 |
457 |
|
461 |
463 |
467 |
479 |
487 |
491 |
499 |
503 |
|
509 |
521 |
523 |
541 |
547 |
557 |
563 |
569 |
|
571 |
577 |
587 |
593 |
599 |
601 |
607 |
613 |
|
617 |
619 |
631 |
641 |
643 |
647 |
653 |
659 |
|
661 |
673 |
677 |
683 |
691 |
701 |
709 |
719 |
|
727 |
733 |
739 |
743 |
751 |
757 |
761 |
769 |
|
773 |
787 |
797 |
809 |
811 |
821 |
823 |
827 |
|
829 |
839 |
853 |
857 |
859 |
863 |
877 |
881 |
|
883 |
887 |
907 |
911 |
919 |
929 |
937 |
941 |
|
947 |
953 |
967 |
971 |
977 |
983 |
991 |
997 |
- «Приемка товаров по качеству и количеству на примере ИП “Земрау”
- «Анализ конкурентов на рынке и определение собственной конкурентоспособности на примере OOO Вавилон)»
- Сетевая форма организации бизнеса (Теоретические основы построения сетевого бизнеса)
- "Бренд как конкурентное преимущество компании"
- Баланс и отчетность (ОАО «Маслодельно – сыродельный комбинат «Михайловский»)
- «Налоговая система РФ и проблемы еe совершенствования
- «Анализ конкурентов на рынке и определение собственной конкурентоспособности (на примере конкретной организации)
- Рекурсивные и итерационные алгоритмы: особенности и примеры использования (Структура итерационного алгоритма)
- «Право собственности на землю
- Особенности сервиса в гостинично-ресторанном бизнесе города Краснодар на примере ресторана Камелот
- Теоретические аспекты рекламы
- Реклама в современном маркетинге

