Оптимизация решений по Парето (Теоретические аспекты решений Парето)

Содержание:

Введение

В течение многих лет экономисты старались определить понятие эффективности и разработать критерии для оценки экономической эффективности. Под эффективностью понимается улучшение одного состояния по сравнению с другим. В теории благосостояния сравниваются уровни благосостояния, которые связаны с тем или иным размещением каких-либо благ в экономике.

В ординалистской теории полезности предполагается, что человек обладает способностью ранжировать (упорядочивать) свои предпочтения определенным образом.

Но в реальной экономике действуют миллионы людей. В этом случае мы сталкиваемся с серьезной проблемой Учета и суммирования всех индивидуальных предпочтении. Для того чтобы представить, о чем идет речь, допустим, что принимается кардиналистский подход к измерению полезностей, а общественное благосостояние - это результат прямого суммирования их значений у всех членов общества. В результате одно состояние будет считаться более эффективным по сравнению с другим, если оно дает большую сумму индивидуальных полезностей, и наоборот.

Однако такой подход никак не считается с ухудшением положения части общества (причем, возможно, большей его части), если такое ухудшение с избытком перекрывается улучшением положения другой, возможно, меньшей его части.

Решение этой проблемы предложил итальянский экономист и социолог Вильфредо Парето (1848-1923). Он предложил считать, что одно состояние предпочтительнее другого, если хотя бы для одного индивида первое состояние приносит больший уровень полезности, чем второе состояние, не снижая уровень полезности ни у одного из остальных индивидов.

Таким образом, при переходе из одного состояния в другое никто ничего не теряет, а кто-то что-нибудь еще и выигрывает. При этом более эффективное состояние называется Парето-предпочтительным (лучшим) по сравнению с менее эффективным, которое, соответственно, является Парето-худшим. Переход из менее эффективного состояния считается Парето-улучшением, наоборот - Парето-ухудшением. Все вышесказанное обуславливает актуальность данной курсовой работы по теме «Оптимизация решений по Парето».

Объект исследования: эффективность Парето.

Предмет исследования: оптимальность решений.

Целью курсовой работы является изучение оптимизации решений по Парето.

Задачи курсовой работы:

1. Рассмотреть теоретические аспекты решений Парето;

2. Проанализировать оптимизацию решений по Парето;

3. Сделать вывод по изученной теме.

Структурно работа состоит из введения, двух глав, заключения и списка литературы

Глава 1. Теоретические аспекты решений Парето

1.1 Понятие эффективности

Эффективность по Парето - уровень организации экономики, при котором:

- уже невозможно осуществить какие-либо изменения в пользу одного лица либо группы лиц, не ухудшив положение другого лица либо группы лиц;

- входные ресурсы используются наиболее эффективно (эффективность производства), а результат обеспечивает максимально возможную полезность для потребителей (эффективность распределения ресурсов).

Оптимальность по Парето — такое состояние системы, при котором значение каждого частного критерия, описывающего состояние системы, не может быть улучшено без ухудшения положения других элементов.

Принцип, по словам самого Парето гласит так: «Всякое изменение, которое не приносит убытков, а которое некоторым людям приносит пользу (по их собственной оценке), является улучшением». Таким образом признаётся право на все изменения, которые не приносят никому дополнительного вреда [7, с.76].

Множество состояний системы, оптимальных по Парето, называют «множеством Парето», «множеством альтернатив, оптимальных в смысле Парето», либо «множеством оптимальных альтернатив».

Ситуация, когда достигнута эффективность по Парето — это ситуация, когда все выгоды от обмена исчерпаны.

Эффективность по Парето является одним из центральных понятий для современной экономической науки. На основе этого понятия строятся первая и вторая фундаментальные теоремы благосостояния. Одним из приложений Парето-оптимальности является т.н. Парето-распределение ресурсов (трудовых ресурсов и капитала) при международной экономической интеграции, т.е. экономическом объединении двух и более государств. Интересно, что Парето-распределение до и после международной экономической интеграции было адекватно математически описано (Далимов Р.Т., 2008). Анализ показал, что добавленная стоимость секторов и доходы трудовых ресурсов движутся противонаправленно в соответствии с хорошо известным уравнением теплопроводности аналогично газу или жидкости в пространстве, что дает возможность применить методику анализа, используемую в физике, в отношении экономических задач по миграции экономических параметров.

Оптимум по Парето гласит, что благосостояние общества достигает максимума, а распределение ресурсов становится оптимальным, если любое изменение этого распределения ухудшает благосостояние хотя бы одного субъекта экономической системы.

Парето-оптимальное состояние рынка - ситуация, когда нельзя улучшить положение любого участника экономического процесса, одновременно не снижая благосостояния как минимум одного из остальных.

Согласно критерию Парето (критерию роста общественного благосостояния), движение в сторону оптимума возможно лишь при таком распределении ресурсов, которое увеличивает благосостояние по крайней мере одного человека, не нанося ущерба никому другому.

По своим экономическим взглядам В.Парето (1848-1923) можно отнести к представителям Лозаннской экономической школы. Как и Вальрас, Парето считал политическую экономию своеобразной механикой, раскрывающей процессы экономических взаимодействий на основе теории равновесия. По его мнению, данная наука должна исследовать Механизм, устанавливающий равновесие между потребностями людей и ограниченными средствами их удовлетворения. Существенный вклад внес В.Парето в разработку теории потребительского поведения, введя вместо количественного понятия субъективной полезности - порядковые, что означало переход от кардиналисткой к ординалисткой версии теории предельной полезности. Далее, вместо сопоставления порядковой полезности отдельных благ Парето предложил сопоставление их наборов, где равно предпочтительные наборы описывались кривыми безразличия.

По мнению Парето, всегда существует такая комбинация ценностей, при которой потребителю безразлично, в какой пропорции он их получит, лишь бы сумма этих ценностей не подвергалась изменениям и приносила максимум удовлетворения. Эти положения В.Парето легли в основу современной теории потребительского поведения [5, с.6].

Но наиболее известен Парето своим принципом оптимальности, который получил название "оптимум по Парето", который лег в основу так называемой новой экономики благосостояния. Оптимум по Парето гласит, что благосостояние общества достигает максимума, а распределение ресурсов становится оптимальным, если любое изменение этого распределения ухудшает благосостояние хотя бы одного субъекта экономической системы. В ситуации, оптимальной по Парето, нельзя улучшить положение любого участника экономического процесса, одновременно не снижая благосостояния как минимум одного из остальных. Такое состояние рынка называется Парето-оптимальным состоянием. Согласно критерию Парето (критерию роста общественного благосостояния), движение в сторону оптимума возможно лишь при таком распределении ресурсов, которое увеличивает благосостояние по крайней мере одного человека, ни нанося ущерба никому другому.

Исходной посылкой теоремы Парето стали взгляды Бентама и других ранних представителей утилитаризма из числа экономистов о том, что счастье (рассматриваемое как удовольствие или полезность) разных людей сравнимы и аддитивны, то есть могут суммироваться в некое общее счастье всех. И, по Парето, критерием оптимальности является не общая максимизация полезности, а ее максимизация для каждого отдельного индивида в пределах обладания определенным исходным запасом благ.

Исходя из посылки о рациональном поведении индивида, мы предполагаем, что фирма при производстве продукции использует такой набор производственных возможностей, который обеспечит ей максимальное расхождение между валовой выручкой и издержками. Потребитель, в свою очередь, приобретает такой набор товаров, который обеспечит ему максимизацию полезности. Равновесное состояние системы предполагает оптимизацию целевых функций (у потребителя - максимизация полезности, у предпринимателя - максимизация прибыли). Это и есть Парето-оптимальное состояние рынка. Оно означает, что, когда все участники рынка, стремясь каждый к своей выгоде, достигают взаимного равновесия интересов и выгод, суммарное удовлетворение (общая функция полезности) достигает своего максимума. И это почти то, о чем говорил А. Смит в своем знаменитом пассаже о "невидимой руке" (правда, не в терминах полезности, а в терминах богатства). Впоследствии действительно была доказана теорема о том, что общее рыночное равновесие и есть Парето-оптимальное состояние рынка [4, с.22-23].

Итак, суть взглядов Парето может быть сведена к двум утверждениям:

- любое конкурентное равновесие является оптимальным (прямая теорема),

- оптимум может быть достигнут конкурентным равновесием, что означает, что выбранный исходя из некоторых критериев оптимум наилучшим способом достигается через рыночный механизм (обратная теорема).

Другими словами, состояние оптимума целевых функций и обеспечивает сбалансированность на всех рынках. Оптимизация целевых функций, по Парето, означает выбор наилучшей альтернативы из всех возможных всеми участниками экономического процесса. Однако необходимо отметить, что выбор каждого индивида зависит от цен и начального объема благ, которым он располагает, и варьируя начальное распределение благ мы изменяем и равновесное распределение, и цены. Отсюда следует, что рыночное равновесие - это наилучшее положение в рамках уже сформировавшейся системы распределения и модель Парето предполагает невосприимчивость общества к неравенству. Такой подход станет более понятен, если принять во внимание "закон Парето", или закон распределения доходов. На основе изучения статистики ряда стран в различные исторические эпохи Парето установил, что распределение доходов выше определенной величины сохраняет значительную устойчивость, и это свидетельствует, по его мнению, о неравномерном распределении природных человеческих способностей, а не о несовершенстве социальных условий. Отсюда вытекало крайне скептическое отношение Парето к вопросам социального переустройства общества.

Однако трудно оспаривать положение, что оптимальное, по Парето, очень часто является социально неприемлемым. Поэтому даже в русле неоклассического направления политической экономии формируются иные теории благосостояния.

1.2 Признаки Парето-эффективности

Концепция Парето базировалась на порядковой теории полезности, не предполагала межперсоналъных сравнений уровня полезности, а ограничивалась обычным ранжированием потребителями собственных предпочтений [3, с.45-46].

Отсутствие необходимости межличностных сравнений в критерии Парето сделало его наименее оспариваемым из всех предлагавшихся критериев. Этим и было обусловлено его широкое применение в экономической теории, хоть он и не является совершенным и поиски других критериев не прекращаются до сих пор.

Выработанный критерий сопоставления состояний выводит на определение экономической эффективности (Парето-эффективности).

Парето-эффективное состояние заключается в том, что никакое другое возможное размещение благ не может повысить уровень полезности ни для одного из индивидов без того, чтобы понизить его для кого-нибудь другого [1, с.7].

Теория эффективности Парето построена на следующих ценностных суждениях, которые принимаются в качестве аксиом:

1. Безразличие к процессу. Сосредоточив внимание исключительно на сравнении различных состояний, теория Парето тем самым вносит достаточно жесткое ценностное утверждение о безразличии к процессу (механизму), благодаря которому достигается определенное состояние. То есть абсолютно безразлично, достигается ли эффективное распределение рыночным механизмом или же централизованной плановой экономикой.

2. Индивидуализм. В соответствии с критериями Парето единственное, что имеет значение при оценке того или иного размещения, - это его воздействие на людей в обществе.

3. Отсутствие патернализма. Предполагается, что люди - лучшие судьи (оценщики) собственного благосостояния. Это также очень жесткое ценностное суждение, которое принимается далеко не всеми людьми. С этой позиции, например, ничем не оправдан запрет на торговлю наркотиками и их потребление; его введение явно ведет к парето-ухудшению, и при его наличии парето-эффективное состояние недостижимо в принципе.

4. Благожелательность. Подход Парето предполагает благожелательность к человеку поскольку, при прочих равных условиях, увеличение благосостояния одного индивида рассматривается как улучшение.

5. Атомистичность. Общество представляется только как простая совокупность отдельных людей, а не как сложный организм. Подход к обществу основан на ценностном представлении, что нет ничего выше интересов человека.

Эффективность экономики по Парето предполагает выполнение трех условий:

- эффективность распределения

- эффективность производства

- эффективность выпуска

Глава 2. Анализ оптимизации решений по Парето

2.1 Оптимальность по Парето

Для облегчения результатов полезно всё время проводить аналогию с однокритериальным (классическим) случаем. Пусть имеется область D и задана функция f – целевая функция (критерий). Задача оптимизации имеет вид

min f(X)

X∈D

Точка X₁∈D называется оптимальной (недоминируемой, неулучшаемой), если не существует точки X₂∈D, для которой f(X₁)>f(X₂) (целевая функция минимизируется). Аналогично в МЗО можно исключить из области D точки, которые заведомо не могут оказаться наилучшими.

Очевидно, что в обобщённом смысле определение оптимальности можно трактовать как описание (выделение) в подмножестве D некоторого нового подмножества D₀, т.е. некоторое сужение D до D₀ ⊂D. В зависимости от характера описания, подмножество D₀ может оказаться пустым, состоять из одного элемента, содержать более одного элемента. Описание D₀ можно проводить либо только с помощью критериев Fi, либо использовать дополнительные условия. Здесь мы рассмотрим направление, которое связано с определением оптимальности по Парето.

Как было сказано раньше для всякого решения X∈D набор его оценок по всем критериям, т.е. набор (F₁(X), F₂(X), . . .,Fm(X)), есть векторная оценка решения X. Векторная оценка X содержит полную информацию о ценности (полезности) этого решения для ЛПР и сравнение любых двух решений заменяется сравнение их векторных оценок. Пусть в МЗО требуется получить меньшие значения каждого частного критерия (минимизировать частные критерии) Fi(X).

Опр. Пусть имеются два решения X₁ и X₂. Говорят, что решение X₁ лучше (предпочтительнее, эффективнее, доминирует) решения X₂, если F_i(X₁)<=F_i(X₂) для всех i=1,m, и хотя бы для одного j - го критерия выполняется строгое неравенство F_i(X₁)<F_i(X₂). или

Опр. Решение X₂ называется доминируемым, если существует решение X₁, не хуже чем X₂, т.е. для любой оптимизируемой функции Fi, I=1, 2, …, m,

Fi(X₂)≤Fi(X₁) при максимизации функции Fi,

Fi(X₂)≥Fi(X₁) при минимизации Fi.

В случае доминирования при переходе от X₂ к X₁ ничего не будет проиграно ни по одному из частных критериев, но в отношении j - го частного критерия точно будет получен выигрыш. Говорят, что решение X₁ лучше (предпочтительнее) решения X₂.

Опр. Стратегия X₁∈D называется эффективной (оптимальной по Парето), если не существует стратегии X₂∈D такой, что Fi(X₂) ≤Fi(X₁), i=1, . . ., m, F(X₂)≠F(X₁), или

Опр. Если решение не доминируемо никаким другим решением, то оно называется недоминируемым или оптимальным в смысле Парето.

Очевидно, тогда в составе множества D нет смысла сохранять решение X₂, оно вытесняется (или, как говорят, “доминируется”) решением X₁. Ладно, выбросим, решение X₂ как неконкурентоспособное и перейдём к сравнению других решений по всем критериям. В результате такой процедуры отбрасывания заведомо непригодных, невыгодных решений множество D обычно сильно уменьшается: в нём сохраняются только так называемые эффективные (иначе “паретовские”) решения, характерные тем, что ни для одного из них не существует доминирующего решения. Множество таких точек и называется множеством точек оптимальных по Парето. Множество точек оптимальных по Парето лежат между точками оптимумов, полученных при решении задачи математического программирования для каждого частного критерия. В литературе множество точек оптимальных по Парето, как правило, обозначают буквой P (P⊂D).

Опр. Множество векторных оценок, соответствующих множеству эффективных точек, называют областью компромиссов (переговорным множеством) или множеством Парето в области критериев. Будем обозначать Y_P (Y_P ⊆Y_D).

Опр. Множество векторных оценок, соответствующих множеству неэффективных точек (доминируемых решений), называют областью согласия Y_c.

В области Y_c нет противоречия между частными критериями оптимальности, т.к. каждая точка X∈D может быть изменена таким образом, что будет одновременно улучшены все частные критерии.

Если область критериев Y_D состоит только из области согласия Y_c, то существует единственная точка X_opt∈D, в которой все частные критерии согласованны между собой в том смысле, что при движении к точке X_opt все F_i(X) i=1, 2, . . ., m, одновременно улучшаются. Все частные критерии достигают минимума в т. X_opt (см. рис. 1). Такую точку называют оптимальным решение и при этом значения всех частных критериев достигают в ней минимума.

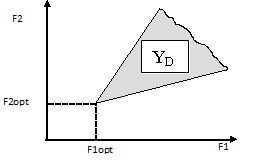
Рис. 1. Критерии F₁ и F₂ непротиворечивы

Однако такая ситуация встречается крайне редко. Наиболее типичным является случай, когда частные критерии являются противоречивыми и минимум по каждому из них достигается в различных точках. В этом случае уменьшение одного частного критерия приводит к увеличению других частных критериев (рис. 2).

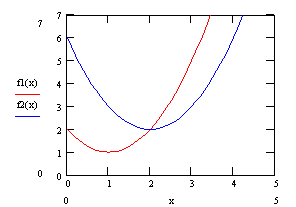
Рис. 2. Критерии F₁ и F₂ противоречивы на отрезке [1; 2]

Оптимальность Парето что дальше значение критерия, ухудшая этом бы из

Проиллюстрируем выделения решений примере с критериями ₁ F₂ требуется Множество состоит 11 решений. решению определённые показателей ₁ F₂. имеются векторные F(X₁)=(2;4), ₂)=(3;5), ₃)=(3;3), ₄)=(5;2), ₅)=(4;3), ₆)=(1;3), ₇)=(2;3), ₈)=(3;2), ₉)=(2;2), ₁₀)=(3;1), ₁₁)=(2;1). оценки представим координатной (по абсцисс значения F₁, по ординат значения F₂). принцип по для эффективных Решение ₁ решением ₂, X₂ решений ₃, ₇, ₈, ₉, ₁₀ X₁₁. X₄ первому лучше X₅, по наоборот, имеем решения, т.д. проведённого у остались решения ₂,X₄, ₅ по [7,

Построим пространство нашей Как паре соответствует на Занумеруем соответственно решения 3). рисунка что точки на верхней области решений решить задачу, оба нужно

Рис. Множество Y_k

Когда множества решений эффективные, могут уже пределах "эффективного" На 3 три X₂, ₄, ₅; них ₄ по F₁, решение ₂ критерию ₂. ЛПР, тот который него и по критериям.

Замечание. Y₁ в _D том только том когда другая Y₂ Y_D хотя по координате больше Y₁ минимизируются).

Замечание. определения точек правило Уголок ∟ для компромиссных в пространстве, критерии а ┐когда минимизируются [6,

В когда допустимых является их оценки некоторую Y_D плоскости получается вроде на 4. этом множество оценок линия) собой границы _D, говоря, "юго-западную" Если максимизируются – границу Y_D.

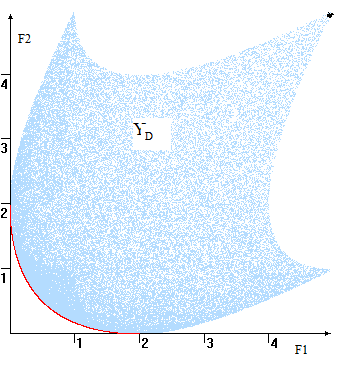
Рис. Пространство Y_D и кривая цвет)

Замечание. случае области Парето-оптимальная может более вид, состоять отдельных и/или Для примера максимизируются) это пик.

Замечание. так оптимальность Парето. называется по если следующее ничьё не быть без благосостояния другого (см. экономических /Под В. Учеб. – ИНФА М, – с. 242)).

Таким под оптимально-компромиссным понимать из точек, предпочтительней точки ЛПР. векторной не однозначно на получено оптимальное Положительный на вопрос от информации важности критериев, имеется ЛПР.

Компромиссная [2,

Особый для — В случае паретовских представляет одномерное на и удобное представление.

Опр. паретовских в пространстве называют компромиссной .

Она состоять несвязных и изолированные (см. 5). кривая строго убывает следующем Пусть ₁ и ₂ точки, КК. их Y₁(y1,y2) Y₂(y3,y4), y1<y3, y2>y4. образом, не ни ни отрезков её может представлено форме ₂=u(F₁) F₁=v(F₂).

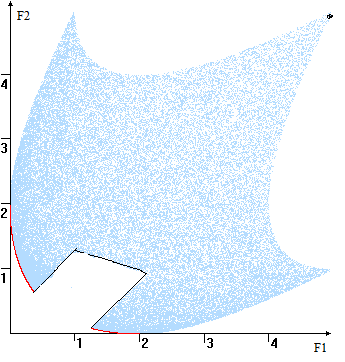
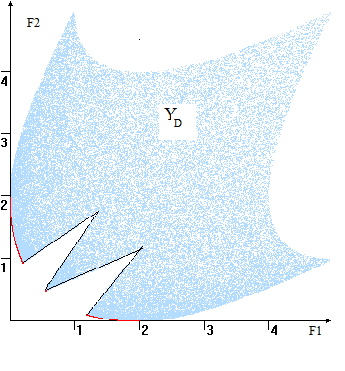
Рис. Примеры (компромиссная выделена цветом)

Аналитический . функции ₁(X) F₂(X) то попытаться геометрическое точек поверхностей F₁(X)=b1 F₂(X)=b2. таких gradF₁=-gradFλ₂, .≤λ<∞

Последнее уравнение n алгебраическим которые кривую пространстве x₁=ϕ₁(), xλ_n=ϕ_n(). участок кривой, котором принадлежит D, он и P - Парето). КК этом определяется уравнениями:λλ≥

F₁=F₁(ϕ₁(), λϕ_n()),λ

F₂=F₁(ϕ₁(), λϕ_n()), λλ≥

Пример В D={-1 ≤₁ ≤ -1 ≤₂ ≤ заданы критерия

которые минимизировать.

1. минимумы F₁ F₂ Абсолютные находятся точках и и области

2. частные

составляем уравнений

4x₁=- λ₁+1)

x₂=- λ₂-1).

Отсюда параметрическое кривой пространстве

В случае получить этой в прямоугольных Для решаем уравнения параметра Получимλ

Приравнивая части разрешая x₂, уравнение кривой .

Параметрическое КК иметь вид

F₁()=λ

F₂()=.λ

Закономерность F₁ от до а ₂ от до

Построим паретовских в D пространстве (рис. и

Рис. Область D множество P 7. кривая

Пример . области x≤₁ ≤ 0 ≤₂ ≤ заданы критерия

которые минимизировать учетом ограничений ⎥₂-x₁-0.375 ⎥≥

а) сначала без ограничений

1. минимумы F₁ и ₂. минимумы в X_1opt=(0,0) X_2opt=(-1,1) первая принадлежат а нет. условный для F₂: X_2услов=(-0.5, находим F2(-0.5,1)=0.25, F1(-0.5,1)=4.25.

2. частные

составляем уравнений

2x₁=- λ₁+1),

8x₂=- λ₂-1).

Отсюда параметрическое кривой пространстве

В случае получить этой в прямоугольных Для решаем уравнения параметра Получимλ

Приравнивая части разрешая x₂, уравнение кривой . точку кривой x₁=-0.5. Xп=(-0.5; Это случаю, λ от до (0≤

Параметрическое КК иметь вид точки X_1opt=(0,0) X_2opt=(-1,1) области

F₁()=λ

F₂()=.λ

Закономерность F₁ от до а ₂ от до

Построим паретовских в D пространстве (рис. и [7,

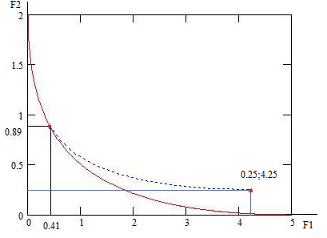
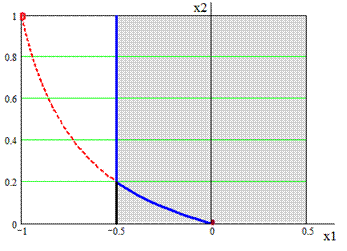
Xп

Рис. Область D множество P Рис. Компромиссная

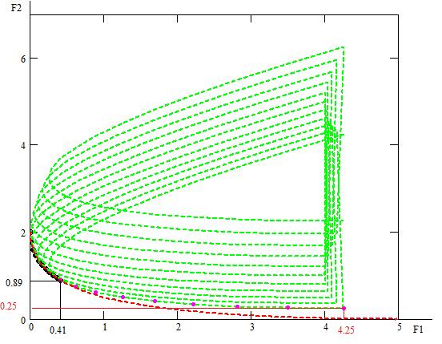
Рис. Пространство и кривая

б) функциональные Область в случае иметь (рис. Находим минимум функции ₁ F₂ Они в X_1opt=(0,0) X_2opt=(-0.5, Как из результатов минимумов изменились.

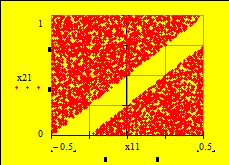
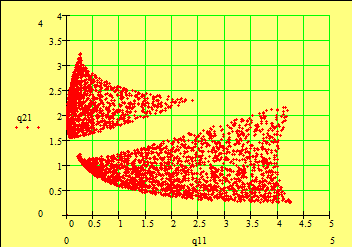
Рис. Область Рис. Пространство

Из примера что множества в виде сложной Поэтому настоящее широко численные построения оптимальных Парето раздел методы множеств

Выделение Парето часто является решением. связано тем, при большом множестве множество оказывается большим того, ЛПР бы состоянии выбор Таким выделение Парето рассматривать как этап и проблема сокращения множества.

Для одной стратегии множества решений каждой многокритериальной необходимо дополнительную о операции, ту которая задании критерия неформализованной потому

Наиболее и представляется построения отношения более чем Парето, сузить выбираемых до с зрения размеров. для потребуется дополнительная которую получить ЛПР. может информация критериях, самих вариантах т.п. стоящая создателями заключается том, с этой обосновать действия сужению и ЛПР того, ни из представляющих него не потерян процессе [5,

Необходимо что сужения Парето существенным многих многокритериальной Многокритериальная Математические /Б.А Ю.М. и - Наука, - с.

Таким общая исследования принятия на математического для может реализована рамках из подходов.

Первый . заданной задачи находится её решений, выбор оптимального из Парето-оптимальных ЛПР.

Второй . уже сказано производится множества исходов идеале до элемента) помощью формализованных что окончательный для Отметим, такое может произведено при дополнительной о или оптимального

Рассмотрим простейшие сужения множества, при внимание необходимость информации. что многокритериальная оптимизации.

Указание границ . информация оптимальном X_opt∈D этом имеет

(1)

Число C_i здесь верхняя по i му

Отметим, указание границ критериям может "извлечено" математической задачи решения; ограничений C₁, C₂, C_m) собой информацию, от

Задача. Выбор работы

Предположим, Вам выбрать работы девяти представленных табл.1. качестве критериев зарплата длительность Д, поездки работу Из задачи что З Д максимизировать, критерий – Какой является

Таблица

Варианты	Критерий
	Зарплата,	Длительность (дни)	Время (мин)
1	900	20	60
2	500	30	20
3	700	36	40
4	800	40	50
5	400	60	15
6	600	30	10
7	900	35	60
8	600	24	10
9	650	35	40

Решение. вначале варианты. доминируемые Парето {1, 8, получаем множество 4, 6, При информации относительной рассматриваемых а о дополнительных оптимального дальнейшее Парето-оптимального произвести Тогда анализ указанием множества окончательный оптимального производится из пяти на каких-то соображений.

Рассмотрим второй который к Парето-оптимального на дополнительной получаемой ЛПР.

а) Указание границ . например, ограничения оптимальное

зарплата не 600

длительность — менее дней;

время — более минут.

Варианты, этим ограничения: 6, из оптимальными Парето варианты и Остаётся окончательный между 3 6.

б) . в выделенного важнейшего) выступает зарплата; длительность — менее дней, поездки не 40 Отбросим которые удовлетворяют ограничениям; варианты: 3, 6, Из максимальную имеет 3. вариант будет

в) Лексикографическая . критерии относительной Например, образом: важнейший — зарплата, за по время , важный длительность ). значение критерию имеют 1 7. сравниваем варианты второму важности В. как поездки этих одинакова, к критерию по длительность является 7, и здесь

2.2 Методы множеств

Часто следующий Во D некоторая например, которой с датчика чисел, по закону. вычисляют векторного F точках сетки, чего конечное сравнений, функцию по строится Парето указанной являющееся большом приближением Парето D – точек

В выше оптимизации выбора решения плана) при требования скалярной которая образом степень целей и часто целевой [7,

Однако такой функции реального объекта собой, правило, трудную Причины связаны многообразным целей влиянием только но социальных сложностью полезности результатов деятельности т.п. некая общая производственного часто быть лишь словесной но не формулировке помощи выраженной целевой В с оказывается считать, объект перед задачу не общей но в систему каждой которой частная функция. подход поставить выбора решения проблему оптимизации множестве Z допустимых интенсивностей способов.

Пусть f _l ( z ) l = ..., L ) функции, системе L целей объекта, на Z . этом значению f _l отвечает высокая достижения l -той Можно что найти задачи оптимизации

В ситуации целевая f ( z ) в компромисса различными и условно некоторую, говоря, математическую в требуется план, был точкой для различных Для чтобы бы устранить неправильность, некоторые определения многокритериальной

Вообще оптимум не единственным. всех оптимумов множество которое иметь структуру. всего о Парето при графического в частных функций

Проблема множества в задаче оптимизации обычно сложной решается последовательного серии однокритериальных При используется, частности, факт, оптимальный всякой вида оптимумом Следовательно, коэффициенты, построить набор множества

Заключение

Процедура многокритериальной методом уступок в что частные располагают нумеруют порядке относительной максимизируют наиболее критерий; назначают допустимого значения критерия максимизируют по частный при что первого не отличаться максимального чем величину снижения снова величину но по критерию находят третьего важности при чтобы первых критериев отличались ранее максимальных больше на соответствующих далее же поочередно все частные оптимальной считают стратегию, получена решении отыскания максимума по критерия.

Таким при метода уступок задача к максимизации критериев выбору уступок. уступок отклонение одних критериев другими лексикографического: уступки тем жестче.

Порядок детерминированных задач последовательных

При многокритериальной методом уступок производится анализ важности критериев; основании анализа располагаются нумеруются порядке важности, что является , важен затем остальные критерии Максимизируется по критерий определяется наибольшее . назначается «допустимого» (уступки) и наибольшее второго при что первого должно не чем Снова величина , уже второму которая с используется нахождении максимума критерия, т.д. максимизируется по критерий условии, значение критерия предыдущих быть меньше величины; в стратегии оптимальными.

Список литературы

1. Вэриан Микроэкономика. уровень. Юнити, с.
2. Гальперин Игнатьев Моргунов Микроэкономика. 2. СПбГУЭиФ, с.
3. Казаков П., Н. Экономика. ЦИПКК 2016.-632
4. Носова Экономическая - изд. 2015.-541
5. Чепурин Курс теории. Юнити-Дана, с.
6. Орехов Методы исследований пособие. ИНФРА-М, с.
7. Плоткин Щербаков Экономико-математическое коммерческих (оптимизация Парето). СПбГУЭФ, с.
8. «Анализ равновесия экономическая (Электронный – доступа:
9. «Парето (Электронный – доступа:
10. «Общественное и эффективность» ресурс). Режим /micro27.htm