Алгоритмы сортировки данных, блочная сортировка

Содержание:

ВВЕДЕНИЕ

Часто нужно упорядочить предметы по какому-то признаку: записать данные числа в порядке возрастания, слова сгруппировать по алфавиту, или выстроить любые другие данные в заданном порядке. Если можно сравнить любые два предмета из данного набора, то этот набор всегда можно упорядочить. Процесс упорядочивания информации и называют «сортировкой».

Алгоритм сортировки – это алгоритм для упорядочивания элементов в списке, массиве и т.д по какому-либо признаку. Существует множество алгоритмов сортировки, имеющих разную эффективность, требующие разные количества ресурсов и разные области применения. При работе с алгоритмами следует знать эти характеристики алгоритма. Актуальность темы заключается в том, что следует не только рассмотреть существующие алгоритмы сортировки, но и сгруппировать их по этим характеристикам.

Теоретическая и практическая значимость выбранной темы заключается в том, что изложенный в работе материал будет полезен для студентов изучающих информационные технологии и стремящихся стать специалистами этой области.

Целью курсовой работы является рассмотрение и изучение некоторых алгоритмов сортировки, их свойства, способы оценки, разновидности и оласти применения.

Задачи:

1. Изучение свойств алгоритмов.
2. Изучение способа оценки алгоритмов.
3. Сгруппировать алгоритмы по быстродействию.
4. Описать результаты работы.
5. Сделать вывод.

1. Свойства и оценка алгоритмов сортировки

Для сравнения и анализа алгоритмов сортировки существуют следующие свойства:

Устойчивость – устойчивая сортировка не меняет взаимного расположения элементов с одинаковыми ключами.

Естественность поведения – эффективность метода при обработке уже упорядоченных или частично упорядоченных данных. Алгоритм ведёт себя естественно, если учитывает эту характеристику входной последовательности и работает лучше.

Использование операции сравнения. Алгоритмы, использующие для сортировки сравнение элементов между собой, называются основанными на сравнениях. Минимальная трудоемкость худшего случая для этих алгоритмов составляет , но они отличаются гибкостью применения. Для специальных случаев (типов данных) существуют более эффективные алгоритмы.

Время – основной параметр, характеризующий быстродействие алгоритма. Называется также вычислительной сложностью. Для упорядочения важны худшее, среднее и лучшее поведение алгоритма в терминах мощности входного множества A. Если на вход алгоритму подаётся множество A, то обозначим n = |A|. Для типичного алгоритма хорошее поведение — это O(n log(n)) и плохое поведение – это O(). Идеальное поведение для упорядочения – O(n). Алгоритмы сортировки, использующие только абстрактную операцию сравнения ключей всегда нуждаются по меньшей мере в сравнениях.;

Память – ряд алгоритмов требует выделения дополнительной памяти под временное хранение данных. Как правило, эти алгоритмы требуют O(log(n)) памяти. При оценке не учитывается место, которое занимает исходный массив и независящие от входной последовательности затраты, например, на хранение кода программы (так как всё это потребляет O(1)). Алгоритмы сортировки, не потребляющие дополнительной памяти, относят к сортировкам на месте.

1.1 Оптимальность O(n log(n))

Задача сортировки в общем случае предполагает, что единственной обязательно наличествующей операцией для элементов является сравнение. Это делает невозможным реализацию алгоритма Хана, использующего арифметические действия. Рассмотрим схему алгоритма, когда единственным возможным действием над элементами является их сравнение.

Пусть по ходу работы алгоритмом производится k сравнений. Ответом на сравнение двух элементов a и b может быть один из двух вариантов a<b или a>b. Значит, всего возможно вариантов комбинаций ответов на k вопросов.

Количество перестановок из n элементов равно n!. Для того, чтобы можно было провести сюръекцию из множества ответов на сравнения на множество перестановок, количество сравнений должно быть не меньше, чем .

Прологарифмировав формулу Стирлинга, можно обнаружить, что .

В следующем разделе будет описано несколько различных алгоритмов сортировки. Одни из них – сортировка вставкой, выбором и слиянием – более сложные, но зато быстро действенные. Другие, например сортировка подсчетом, не используют сравнение элементов и могут преодолевать ограничение , работая удивительно эффективно при правильных условиях. В следующем разделе алгоритмы распределены по категориям с учетом их производительности.

2. Алгоритмы O()

Алгоритмы O() являются относительно медленными, зато простыми. Последнее качество позволяет им иногда превосходить сравнительно быстрые, но более сложные алгоритмы для очень малых массивов.

2.1 Сортировка вставкой

Основная идея сортировки вставкой заключается в выборе элемента из списка ввода и его вставке в соответствующую позицию отсортированного списка вывода, который изначально пуст.

Аналогичную технологию можно использовать и для сортировки массива.

Листинг 1 – Псевдокод сортировки вставками

Insertionsort(Data: values[])

For i = 0 To <количество значений> - 1

// Перемещаем элемент i в соответствующую позицию

// в отсортированной части массива.

<Находим первый индекс j, при котором j < i

и values[j] > values[i].>

<Помещаем элемент в позицию j.>

Next i

End Insertionsort

При циклическом прохождении по элементам массива на основе индекса i наблюдается следующее разделение: элементы с индексом менее i признаются отсортированными, а с индексом более или равным i — неотсортированными. После того как код пересмотрит все индексы массива (от 0 до последнего), он перемещает элемент с индексом i в соответствующую позицию во второй части массива. Чтобы обнаружить эту позицию, перебираются уже отсортированные элементы и находится первый элемент, который больше, чем values[i]. Перемещение может занять какое-то время. Ведь если новый индекс элемента должен быть j, код должен сдвинуть все элементы между индексами j и i на одну позицию вправо, чтобы освободить место.

На рисунке 1 показаны основные шаги алгоритма. Верхний фрагмент представляет собой исходный не отсортированный массив. На среднем фрагменте первые четыре элемента (они обведены толстой линией) уже отсортированы, а алгоритм готовится добавить к ним следующий со значением 3. Код пересматривает отсортированные элементы, пока не определит, что число 3 нужно вставить перед числом 4. На нижнем фрагменте видно, что алгоритм передвинул значения 5, 6 и 7 вправо, чтобы освободить место для значения 3. Вставив его, он продолжит цикл For, чтобы упорядочить следующий элемент со значением 2.

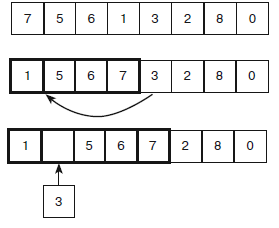
Рисунок 1 – Основные шаги алгоритма сортировки вставками

2.2 Сортировка выбором

Суть этого алгоритма сортировки состоит в том, чтобы найти в списке ввода наибольший элемент и добавить его в конец отсортированного списка. Как вариант, можно искать наименьший элемент и перемещать его в начало отсортированного списка. В следующем псевдокоде представлен алгоритм, работающий с массивами.

Листинг 2 – Псевдокод сортировки выбором

Selectionsort(Data: values[])

For i = 0 To <количество значений> - 1

// Находим элемент, принадлежащий позиции i.

<Находим наименьший элемент, у которого индекс j >= i.>

<Меняем местами values[i] и values[j].>

Next i

End Selectionsort

Код проходит в рамках цикла по массиву и выбирает наименьший элемент, который еще не добавлен в отсортированную часть списка, затем меняет его местами с элементом в позиции i.

Основные шаги алгоритма представлены на рисунке 2. На верхнем фрагменте виден исходный не отсортированный массив. На среднем первые три элемента уже отсортированы (они обведены толстой линией), а алгоритм готовится поменять позицию следующего элемента. Он ищет не отсортированные элементы, чтобы выявить среди них тот, который имеет наименьшее значение, – в данном случае это 3. Найденное число перемещается в следующую не отсортированную позицию. На нижнем фрагменте показан массив после того, как новый элемент был добавлен в отсортированную часть. Цикл For приступает к следующему элементу со значением 5.

Как и в случае сортировки вставкой, алгоритм располагает упорядоченные элементы в исходном массиве, поэтому дополнительной памяти ему не требуется (кроме нескольких переменных для контроля над циклами и перемещения элементов).

Если в массиве содержится N элементов, алгоритм изучает каждый из них. Для начала он должен пересмотреть N – i еще не отсортированных элементов, чтобы найти принадлежащий позиции i, а затем передвинуть сортируемый элемент на последнюю позицию за малое количестве шагов. Таким образом, для перемещения всех элементов потребуется (n – 1) + (n – 2) + ... + 2 + 1 = (+ n)/2 шагов. Это значит, что алгоритм обладает временем работы O(), как и алгоритм сортировки вставкой.

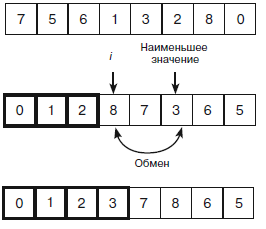
Рисунок 2 – Пример сортировки выбором

Сортировка выбором также является достаточно быстрой для относительно малых массивов (менее 10 000 элементов). Кроме того, она проста и если элементов совсем немного (от 5 до 10), работает эффективнее, чем более сложные алгоритмы

2.3 Пузырьковая сортировка

Пузырьковая сортировка предполагает следующее: если массив не отсортирован, любые два смежных элемента в нем находятся в неправильном положении. Из-за этого алгоритм должен проходить по массиву несколько раз, меняя местами все неправильные пары.

Листинг 3 – Псевдокод пузырьковой сортировки

Bubblesort(Data: values[])

// Повторяем, пока не отсортируем массив.

Boolean: not_sorted = True

While (not_sorted)

// Предполагаем, что неправильных пар нет.

not_sorted = False

// Ищем смежные элементы массива, стоящие в неправильном порядке.

For i = 0 To <количество значений> - 1

// Проверяем, стоят ли элементы i и i – 1

// в правильном порядке.

If (values[i] < values[i - 1]) Then

// Меняем их местами.

Data: temp = values[i]

values[i] = values[i - 1]

values[i - 1] = temp

// Массив еще не отсортирован.

not_sorted = True

End If

Next i

End While

End Bubblesort

В коде используется булевская переменная not_sorted, которая отслеживает перемещение элементов при прохождении через массив. Пока она истинна, цикл работает — ищет неправильные пары элементов и перестраивает их. Иллюстрацией этого алгоритма может служить рисунок 3. Первый массив выглядит по большей части отсортированным, но, пройдясь по нему, алгоритм выявит, что пара 6 – 3 находится в неправильном положении (число 6 должно следовать после 3). Код поменяет найденные элементы местами и получит второй массив, в котором в неправильном положении окажется пара 5 – 3. После ее исправления образуется третий массив, где неверна пара 4 – 3. Поменяв ее элементы местами, алгоритм сформирует четвертый массив, совершит еще один конечный проход и, не найдя пар, стоящих в неправильном положении, остановится.

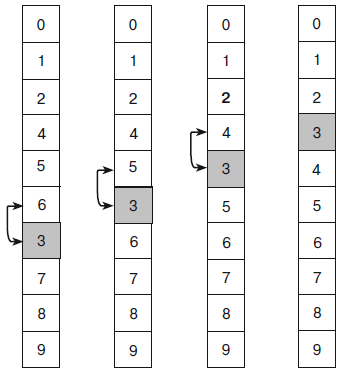
Рисунок 3 – Пузырьковая сортировка

В пузырьковой сортировке неупорядоченный элемент 3 как бы медленно «всплывает» на правильную позицию, отсюда и специфическое название метода. Каждое прохождение через массив ставит на нужное место как минимум один элемент. В массиве, приведенном на рисунке 3, при первом прохождении на правильной позиции оказывается число 6, при втором — 5, при третьем — 3 и 4.

Если предположить, что в массиве содержится N элементов и хотя бы один из них занимает свое место в результате однократного пересмотра значений, то алгоритм может совершить не более N прохождений. (Все N понадобятся, когда массив изначально отсортирован в обратном порядке.) Каждое такое прохождение включает N шагов, отсюда общее время работы алгоритма — O(N2).

Как и две предыдущие сортировки, пузырьковая является довольно медленной, но может показать приемлемую производительность в малых списках (менее 1000 элементов). Она также быстрее, чем более сложные алгоритмы для очень малых списков (около 5 элементов).

Можно несколько усовершенствовать пузырьковую сортировку. В массиве, приведенном на рисунке 3, элемент со значением 3 находится ниже своей конечной позиции. Но если он будет выше нее, алгоритм определит, что элемент не там, где ему положено находиться, и поменяет местами со следующим элементом, затем снова переставит, обнаружив неверный распорядок. Так продолжится вниз по списку до тех пор, пока не отыщется конечная позиция. Чередуя прохождения вверх и вниз по массиву, можно ускорить работу алгоритма: первые быстрее поставят на место те элементы, которые находятся слишком низко в списке, вторые – те, что слишком высоко.

Еще один способ усовершенствования – выполнять несколько перестановок за проход. Например, при движении вниз по массиву элемент (пусть он будет назван K) может сменить свою позицию не один раз, прежде чем займет нужное место. Можно сэкономите время, если он не будет передвигаться его по массиву, а сохранится во временной переменной и, при смещении других элементов вверх, будет найдена целевая позиция для K.

Предположим, что в массиве содержится наибольший элемент L, который стоит не на своем месте. Двигаясь вниз, алгоритм добирается до него (возможно, совершая другие перестановки) и затем перемещает вниз по списку, пока тот не достигнет конечной позиции. Во время последнего прохождения по массиву ни один элемент не может встать после L, поскольку этот элемент уже находится на нужном месте. Значит, алгоритм может остановиться, когда достигнет элемента L.

Если обобщить вышесказанное, получается, что алгоритм завершает прохождение через массив, добравшись до позиции последней перестановки, которую выполнил во время предыдущего прохождения. Таким образом, отследив последние перестановки при движении вниз и вверх по массиву, вы можете сократить путь. Рассмотренные усовершенствования проиллюстрированы на рисунке 4.

На крайнем левом фрагменте видно, что во время первого прохождения вниз по массиву алгоритм вставляет элемент 7 во временную переменную и меняет местами с элементами 4, 5, 6 и 3. Другими словами, алгоритму не требуется хранить элемент 7 в массиве до тех пор, пока он не займет конечную позицию.

Разместив 7 должным образом, алгоритм продолжает движение по массиву и не находит других элементов для перестановки. Теперь ему известно, что 7 и следующие за ним элементы стоят в своих конечных позициях и рассматривать их больше не нужно. Если бы какой-нибудь элемент, расположенный ближе к верху массива, оказался больше 7, то при первом же прохождении он переместился бы вниз, минуя 7.

На среднем фрагменте элементы на конечных позициях закрашены серым – во время последующих прохождений они не нуждаются в проверке.

На крайнем правом фрагменте алгоритм совершает второе прохождение по массиву вверх, начиная с элемента, стоящего перед 7. В нашем случае это 3. Алгоритм меняет его местами с элементами 6, 5 и 4, удерживая во временной переменной, пока не поставит на конечную позицию. Теперь 3 и предшествующие ему элементы находятся на своих местах – они закрашены серым цветом. Последнее прохождение осуществляется вниз по массиву, начиная со значения 4 и заканчивая значением 6. Во время него перестановки не выполняются, и алгоритм останавливается.

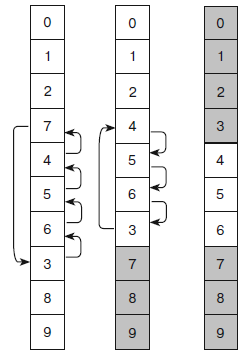
Рисунок 4 – Усовершенствованный алгоритм

Такие усовершенствования на практике ускоряют пузырьковую сортировку (время сортировки 10 000 элементов ускоряется в 4-5 раз). Но все же время работы подобного алгоритма остается O(), то есть он применим для списков с ограниченным размером.

3. Алгоритмы O(n log(n))

Алгоритмы O(n log(n)) намного быстрее алгоритмов O(), по крайней мере, при работе с большими массивами. Например, если n = 1000, то время работы O(n log(n)) покажет результат 1 x , а – 1 x , то есть примерно в 100 раз больше. Такая разница в скорости делает алгоритмы первого рода более полезными на практике.

3.1 Пирамидальная сортировка

Пирамидальная сортировка подходит для работы с полными бинарными деревьями в массиве. В ней используется структура данных, называемая кучей.

Бинарное дерево – это дерево, в котором каждая вершина соединена с хотя бы двумя дочерними записями. Если все его уровни заполнены, кроме, возможно, последнего (где все вершины сдвинуты влево), то такое дерево называется полным.

На рисунке 5 показано полное бинарное дерево с 12 вершинами: первые три уровня полные, четвертый содержит пять вершин, сдвинутых влево.

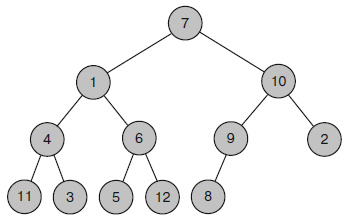
Рисунок 5 – Бинарное дерево

Полные бинарные деревья легко сохранить в массив: присвойте корневому узлу индекс 0, а дочерним записям любого узла с индексом i — индексы 2i + 1 и 2i + 2 и т. д.

Если узлу присвоен индекс j, то родительская запись для него будет иметь индекс |(j – 1)/2|, где | | - означают округление результата до следующего меньшего целого числа. Например, |2,9| = 2 и |2| = 2.

На рисунке 6 показано дерево (рис. 5), переведенное в массив. Сверху указаны входные индексы. Так, узлу 6 присвоен индекс 4. Значит, его дочерние записи 5 и 12 будут иметь индексы 4 х 2 + 1 = 9 и 4 х 2 + 2 = 10 соответственно.

Рисунок 6 – Дерево, переведённое в массив

Если индекс какой-либо дочерней записи превышает наибольший индекс массива – такой записи в дереве нет. Например, узел 9 имеет индекс 5, тогда его дочерняя запись справа должна носить индекс 2 х 5 + 2 = 12. Но это число выходит за пределы массива, и если посмотреть на рисунок 5, то можно убедиться, что у элемента со значением 9 справа дочерней записи нет. Рассмотрим также получение индекса родительской записи для элемента со значением 12, которому присвоен индекс 10.

Согласно вышеприведенной формуле, родительская запись должна иметь индекс |(10 – 1)/2| = |4,5| = 4. В массиве ему соответствует элемент 6. На нашем дереве (рис. 5) это и есть родительский узел для вершины со значением 12.

Двоичная куча (рис. 7) – это полное бинарное дерево, где каждая вершина содержит значение, которое не меньше тех, что находятся в его дочерних записях. На рисунке 5 изображена не куча. Если взять для примера корневой узел 7, можно заметить, что его правая дочерняя запись имеет значение 10, то есть она больше родительской.

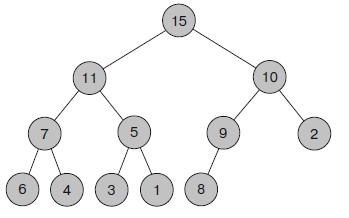
Рисунок 7 – Двоичная куча

На рисунке 8 показан процесс, в ходе которого к дереву, изображенному на рисунке 7, добавляют новую запись 12. Обновленную кучу можно увидеть на рисунке 9.

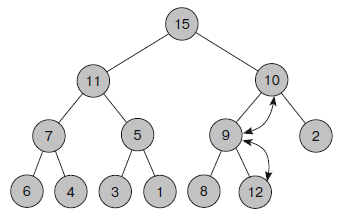
Рисунок 8 – Добавление нового элемента в кучу

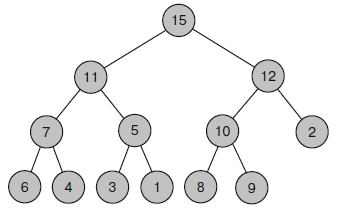
Рисунок 9 – Новая куча

Если куча хранится в массиве, ее обновление выполнить еще проще. Очередной элемент, присоединяемый к концу дерева, автоматически занимает соответствующую позицию в массиве.

Следующий псевдокод превращает массив в кучу.

Листинг 4 – Псевдокод образования кучи

MakeHeap(Data: values[])

// Добавляем каждый элемент в кучу (по одному).

For i = 0 To <количество значений> - 1

// Начинаем с нового элемента и работаем до корня.

Integer: index = i

While (index != 0)

// Находим индекс родительской записи.

Integer: parent = (index - 1) / 2

// Если дочерняя запись меньше или равна родительской,

// мы закончили и выходим из цикла While.

If (values[index] <= values[parent]) Then Break

// Меняем местами родительскую и дочернюю записи.

Data: temp = values[index]

values[index] = values[parent]

values[parent] = temp

// Переходим к родительской записи.

index = parent

End While

Next i

End MakeHeap

Кучи хороши для создания очередей с приоритетом, поскольку чем больше элемент в дереве, тем ближе он к корневому узлу. Следовательно, при удалении элемента из очереди достаточно убрать тот, что является корневым. К сожалению, такая операция разрушает пирамидальную структуру кучи. Но ситуацию легко исправить, если переместить последний элемент дерева в корень. На следующем этапе понадобится восстановить основное свойство кучи. Для этого можно использовать тот метод, который фигурирует и при построении: если новое значение меньше какого-то дочернего, поменяйте их местами. Исправив текущий узел, проверьте тот, что идет на уровень ниже. Продолжайте перестановку узлов вниз по дереву, пока не найдете точку, в которой свойство кучи уже будет выполненным, либо не достигните конца дерева.

В следующем псевдокоде представлен алгоритм удаления элемента из кучи и восстановления ее основного свойства.

Листинг 5 – Псевдокод удаление элемента из кучи

Data: RemoveTopItem (Data: values[], Integer: count)

// Сохраняем верхний элемент, чтобы вернуться к нему позднее.

Data: result = values[0]

// Перемещаем последний элемент к корню.

values[0] = values[count - 1]

// Восстанавливаем свойство кучи.

Integer: index = 0

While (True)

// Находим индексы дочерних записей.

Integer: child1 = 2 * index + 1

Integer: child2 = 2 * index + 2

// Если индекс дочерней записи выпадает из дерева,

// используем индекс родительской записи.

If (child1 >= count) Then child1 = index

If (child2 >= count) Then child2 = index

// Если свойство кучи выполнено,

// мы закончили и выходим из цикла While.

If ((values[index] >= values[child1]) And

(values[index] >= values[child2])) Then Break

// Получаем индекс дочерней записи с большим значением.

Integer: swap_child

If (values[child1] > values[child2]) Then

swap_child = child1

Else

swap_child = child2

// Меняем местами с большим дочерним элементом.

Data: temp = values[index]

values[index] = values[swap_child]

values[swap_child] = temp

// Переходим на дочернюю ветку.

index = swap_child

End While

// Возвращаем значение, которое удалили из корня.

return result

End RemoveTopItem

Приведенный алгоритм в качестве параметра берет размер дерева, поэтому он может найти место, где заканчивается куча внутри массива. Значение сохраняется в корневом узле, чтобы потом была возможность к нему вернуться. Затем последний элемент дерева перемещается к корневому узлу. Для этого алгоритм назначает индексу корневого узла переменную index и вводит бесконечный цикл While. Внутри цикла алгоритм рассчитывает индексы дочерних записей текущего узла. Если они оба выпадают из дерева, то их значения приравниваются к родительскому. В таком случае дальнейшее сравнение индекса происходит с самим собой.

А поскольку любое значение больше или равно самому себе, подобный подход удовлетворяет свойству кучи и недостающий узел не заставляет алгоритм менять значения местами. После того как алгоритм рассчитает дочерние индексы, он проверяет, сохраняется ли свойство кучи в текущем месте. Если да, то алгоритм покидает цикл While.

То же самое происходит, если нет обеих дочерних записей или в отсутствии одной из них другая соответствует свойству кучи. Если свойство кучи не выполняется, алгоритм устанавливает swap_child на индекс дочерней записи, содержащий большее значение, и меняет местами значения родительского и дочернего узлов. Затем он обновляет переменную index, чтобы сдвинуть ее вниз к переставленному дочернему узлу, и продолжает спускаться по дереву.

Теперь, после описания кучи, следует рассмотреть алгоритм сортировки. Приведенный ниже алгоритм строит кучу. Он несколько раз меняет ее первый и последний элементы местами и перестраивает все дерево, исключая последний элемент. При каждом прохождении один элемент удаляется из кучи и добавляется в конец массива, где расположены элементы в отсортированном порядке.

Листинг 6 – Псевдокод сортировки

Heapsort(Data: values)

<Преобразуем массив в кучу.>

For i = <количество значений> - 1 To 0 Step -1

// Меняем местами корневой и последний элементы.

Data: temp = values[0]

values[0] = values[i]

values[i] = temp

<Определяем элемент в позиции i, который нужно удалить из

кучи. Теперь куча содержит i - 1 элементов. Опускаем значение

нового узла вниз, чтобы восстановить свойство кучи.>

Next i

End Heapsort

Представленный алгоритм начинает свою работу с того, что превращает массив в кучу. Затем он несколько раз удаляет верхний элемент, самый большой и перемещает его в конец кучи. Количество элементов в куче при этом сокращается и восстанавливается ее основное свойство, а переставленный элемент занимает правильную позицию в конце кучи.

На завершающем этапе алгоритм удаляет элементы из кучи в порядке от наибольшего к наименьшему и помещает их в конец постоянно сокращающейся кучи. Массив продолжает содержать значения в порядке возрастания. Объем памяти, требуемый для пирамидальной сортировки, легко рассчитать. Алгоритм хранит все данные внутри исходного массива и использует лишь определенное количество дополнительных переменных для расчета значений и их перестановки. Если в массиве содержится n значений, алгоритм использует O(n) памяти.

Сложнее определить время работы алгоритма. Чтобы построить исходную кучу, ему приходится прибавлять каждый элемент к растущей куче. Всякий раз он размещает его в конце дерева и просматривает структуру данных до самого верха, чтобы убедиться, что она является кучей. Поскольку дерево полностью бинарное, количество его уровней равно O(log(n)). Таким образом, передвижение элемента вверх по дереву может занять максимум O(log(n)) шагов. Алгоритм осуществляет шаг, при котором добавляется элемент и восстанавливается свойство кучи, n раз, поэтому общее время построения исходной кучи составит O(n log(n)).

Для завершения сортировки алгоритм удаляет каждый элемент из кучи, а затем восстанавливает ее свойства. Для этого он меняет местами последний элемент кучи и корневой узел, а затем передвигает новый корень вниз по дереву. Дерево имеет высоту O(log(n)) уровней, поэтому процесс может занять O(log(n)) времени. Алгоритм повторяет такой шаг n раз, отсюда общее количество нужных шагов – O(n log(n)). Суммирование времени, необходимого для построения исходной кучи и окончания сортировки, дает следующее: O(n log(n)) + O(n log(n)) = O(n log(n)).

Пирамидальная сортировка представляет собой так называемую сортировку на месте и не нуждается в дополнительной памяти. На ее основе хорошо видно,как работают кучи и как происходит сохранение полного бинарного дерева в массиве. И хотя производительность O(nlog(n)) высока для алгоритма, сортирующего путем сравнений, далее пойдет речь об алгоритме, который показывает еще более быстрые результаты.

3.2 Быстрая сортировка

Приведенный ниже алгоритм делит массив на две части и впоследствии рекурсивно вызывает сам себя для их сортировки.

Листинг 7 – Псевдокод быстрой сортировки

Quicksort(Data: values[], Integer: start, Integer: end)

<Выбираем элемент из массива. Называем его разделяющим элементом.>

<Переносим элементы, которые меньше разделяющего, в начало массива.>

<Переносим элементы, которые больше разделяющего или равны ему, в конец массива. >

<Пусть серединой будет индекс, где помещен разделяющий элемент.>

// Рекурсивно сортируем две части массива.

Quicksort(values, start, middle - 1)

Quicksort(values, middle + 1, end)

End Quicksort

В верхней части рисунка 10 показан массив для сортировки. В качестве разделяющего элемента выбрано первое значение 6. На среднем фрагменте значения, которые меньше, чем разделяющий элемент, были перемещены в начало массива, а значения, которые больше или равны ему, – в конец. Разделяющий элемент с индексом 6 закрашен темно-серым Обратите внимание, что еще один элемент массива со значением 6 следует за разделителем.

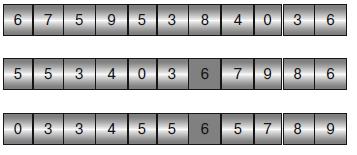
Рисунок 10 – Быстрая сортировка

Далее алгоритм рекурсивно вызывает сам себя, чтобы отсортировать части массива до и после разделяющего элемента. Результат этого процесса показан на нижнем фрагменте рисунка 10.

Перед тем как приступить к подробному анализу алгоритма, изучим время его работы.

Для начала рассмотрим особый случай, когда при каждом шаге разделяющий элемент делит анализируемый массив пополам (рис. 11).

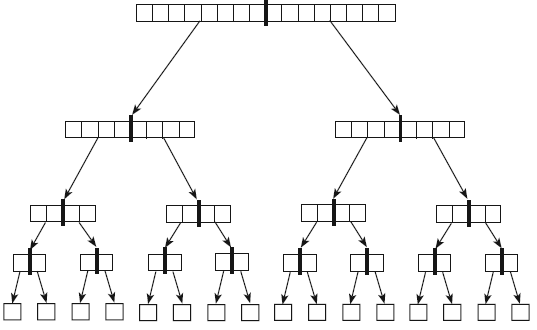
Рисунок 11 – Разделение массива

В каждой вершине дерева, изображенного на рисунке 11, происходит обращение к алгоритму быстрой сортировки. Толстыми линиями отмечено разделение массива надвое. Стрелки символизируют алгоритм быстрой сортировки, он вызывает себя дважды – для каждой половины массива. Внизу дерева вызов осуществляется единожды (и возвращается, ничего не сделав), поскольку список из одного элемента уже отсортирован. Достигнув последнего уровня в пирамидальной структуре данных, вызовы начинают возвращаться к собственным методам – так происходит контроль снизу вверх.

Если изначально в массиве содержится n элементов и они разделены четко по-полам, дерево вызовов быстрой сортировки имеет высоту log(n) уровней. При каж-дом вызове проверяются элементы в той части массива, которая подвергаетсясортировке. Например, в массиве из четырех элементов будут исследованы все четыре элемента с целью последующего разделения их значений.

Все элементы из исходного массива представлены на каждом уровне дерева. Та-ким образом, любой уровень содержит n элементов. Если добавить те, которые должен проверять каждый вызов быстрой сортировки на определенном уровне дерева, получится n элементов. Это значит, что вызовы быстрой сортировки потребуют n шагов. Поскольку дерево имеет высоту log(n) уровней и для каждого из них нужно n шагов, общее время работы алгоритма составит O(n log(n)).

Подобный алгоритм предполагает разделение массива на две равные части прикаждом шаге, что выглядит не очень правдоподобно. Однако в большинстве случаевразделяющий элемент будет отстоять недалеко от середины — не точно по центру,но и не с самого края. Например, на рисунке 10 на среднем фрагменте разделяющий элемент 6 находится хотя и не ровно посередине, но близко к ней. В этом случае алгоритм быстрой сортировки все еще обладает временем работы O(n log(n)). В худшем случае разделяющий элемент может оказаться меньше любого другого в той части массива, которую делит, либо все они будут иметь равные значения.

Тогда ни один из элементов не перейдет в левую часть массива — все, кроме разделяющего, окажутся в правой. Первый рекурсивный вызов вернется немедленно, поскольку сортировка не понадобится, зато в ходе второго потребуется обработать почти каждый элемент. Если первому вызову быстрой сортировки надо отсортировать n элементов, то рекурсивному – n – 1.

Если разделяющий элемент всегда меньше остальных в сортируемой части массива, алгоритм вызывается для сортировки вначале n элементов, затем n – 1, n – 2 и т. д. В таком случае дерево вызовов, изображенное на рисунке 11, является очень тонким и имеет высоту n.

Вызовы быстрой сортировки на уровне i в дереве должны проверить n – i элементов. Суммирование всех элементов, проверяемых на всех вызовах, даст n + (n – 1) + (n – 2) + ... + 1 = n(n + 1)/2, что равняется O(). Таким образом, в худшем случае время работы алгоритма составит O(). Кроме вышесказанного, следует обратить внимание на требуемый объем памяти. Он частично зависит от метода, с помощью которого массив делится на части, а также от глубины рекурсии алгоритма. Если последовательность рекурсивных вызовов слишком глубока, программа расходует стековое пространство и зависнет.

В примере с деревом, изображенным на рисунке 11, алгоритм быстрой сортировки рекурсивно вызывает сам себя до глубины n. Таким образом, в ожидаемом случае стек вызова программы будет иметь глубину O(log(n)) уровней. Для большинства компьютеров это не проблема. Даже если в массиве содержится 1 млрд элементов, в log(n) их всего 30, а стек вызова должен обладать возможностью работать с 30 рекурсивными вызовами. Однако в худшей ситуации, когда дерево высокое и тонкое, глубина рекурсии составит n. Немногие программы способны создать стек вызова с 1 млрд рекурсивных вызовов. Вы можете избежать наихудшего сценария, если заставите алгоритм работать в течение разумного времени и с разумной глубиной рекурсии путем тщательного выбора разделяющего элемента. В следующих подразделах рассматриваются необходимые для этого стратегии, приводятся два метода разделения массива на части, а также резюмируются сведения по использованию быстрой сортировки на практике.

В качестве разделяющего элемента можно использовать первый элемент из той части массива, которая сортируется. Это простой и, как правило, эффективный способ. К сожалению, если массив изначально отсортирован в прямом или обратном порядке, ситуация окажется наихудшей. Лучше всего, если элементы располагаются в случайном порядке, но чаще сортировка является частичной или полной. Решить проблему поможет предварительная рандомизация массива перед вызовом быстрой сортировки. Если элементы расположены в случайном порядке,

маловероятно, что описанный метод каждый раз будет выбирать плохой разделяющий элемент, и мы получим худший вариант его работы. В главе 2 рассказывалось, как рандомизировать массив за время O(n) и не увеличить при этом ожидаемую производительность алгоритма быстрой сортировки O(n log (n)). Однако на практике для работы с большим массивом требуется довольно много времени, поэтому опытные программисты не используют такой метод.

Можно прибегнуть к другому варианту: определить первый, последний и средний элементы в сортируемой части массива и использовать в качестве разделителя элемент, чье значение находится между любыми двумя значениями из этого трио. Нет абсолютной гарантии, что результат не будет приближаться к наибольшему или наименьшему элементу в данной части массива, однако незначительная вероятность есть.

И наконец, последний метод заключается в том, чтобы выбрать случайный индекс из сортируемой части массива, а затем использовать в качестве разделителя значение элемента с данным индексом. Маловероятно, что каждый такой выбор приведет к плохому результату и худшему варианту работы алгоритма.

3.3 Сортировка слиянием

Подобно быстрой сортировке, сортировка слиянием использует стратегию «разделяй и властвуй». Если в первом случае выбирается разделитель, а оставшиеся элементы делятся на две группы — большие и меньшие его, то во втором разделение происходит на две равные части, а затем алгоритм рекурсивно вызывает сам себя для их сортировки. Потом отсортированные половины сливаются в комбинированный отсортированный список. Описанный алгоритм представлен в следующем псевдокоде.

Листинг 8 – Псевдокод сортировки слиянием

Mergesort(Data: values[], Data: scratch[], Integer: start, Integer: end)

// Если в массиве только один элемент — он отсортирован.

If (start == end) Then Return

// Разбиваем массив на левую и правую половины.

Integer: midpoint = (start + end) / 2

// Вызываем Mergesort для сортировки двух половин.

Mergesort(values, scratch, start, midpoint)

Mergesort(values, scratch, midpoint + 1, end)

// Соединяем отсортированные половины.

Integer: left_index = start

Integer: right_index = midpoint + 1

Integer: scratch_index = left_index

While ((left_index <= midpoint) And (right_index <= end))

If (values[left_index] <= values[right_index]) Then

scratch[scratch_index] = values[left_index]

left_index = left_index + 1

Else

scratch[scratch_index] = values[right_index]

right_index = right_index + 1

End If

scratch_index = scratch_index + 1 End While

// Завершаем копирование из непустой половины.

For i = left_index To midpoint

scratch[scratch_index] = values[i]

scratch_index = scratch_index + 1

Next i

For i = right_index To end

scratch[scratch_index] = values[i]

scratch_index = scratch_index + 1

Next i

// Копируем значения в исходный массив.

For i = start To end

values[i] = scratch[i]

Next i

End Mergesort

Кроме сортируемых массивов, начального и конечного индексов, алгоритм также берет в качестве параметра рабочий массив, который использует для объединения отсортированных половин.

Код начинает работу с проверки общего количества элементов в части массива. Если элемент один, значит, массив отсортирован и алгоритм прекращает выполняться. Если элементов несколько, алгоритм рассчитывает индекс того, что находится в середине части, и рекурсивно вызывает сам себя для сортировки половин. Затем отсортированные половины объединяются. Они пересматриваются в цикле, при этом меньший элемент копируется в рабочий массив. Если одна половина пуста, алгоритм копирует остальные элементы из другой половины. На завершающем этапе объединенные элементы из рабочего массива переносятся обратно в исходный массив values

Анализ времени работы для быстрой сортировки применим и для сортировки слиянием. Таким образом, производительность рассмотренного выше алгоритма составит O(n log(n)). Как и в случае пирамидальной сортировки, она не зависит от изначального расположения элементов, поэтому всегда одинакова. Нет здесь и худшего варианта, как в быстрой сортировке. Сортировку слиянием тоже можно распараллелить. Когда алгоритм рекурсивно вызывает сам себя, он вправе передать один из таких вызовов другому процессору. Однако это требует некоторой координации: исходный вызов должен подождать, пока оба рекурсивных вызова закончатся, чтобы объединить их результаты. Быстрая сортировка, напротив, может приказать рекурсивным вызовам отсортировать определенную часть массива и не ждать их возвращения.

Сортировка слиянием особенно полезна, когда данные не содержатся в памяти единовременно. Например, программе нужно отсортировать 1 млн записей о клиентах, каждая из которых занимает 1 Мбайт. Для комплексной загрузки данных ей понадобится 1018 байт памяти, или 1000 Тбайт, что намного больше, чем в основной массе компьютеров. Сортировка слиянием не требует такого количества ресурсов, алгоритму даже не нужно обращаться к элементам массива, пока не вернутся его рекурсивные вызовы. Он проходит через отсортированные половины линейным способом и объединяет их, что сокращает необходимость разбивать память компьютера на страницы. В противоположность вышесказанному быстрая сортировка, перемещая элементы в разные половины массива, перепрыгивает с одного места на другое, увеличивая разбивку на страницы и очень сильно замедляя алгоритм.

4. Алгоритмы быстрее O(N log(N))

В работе уже упоминалось, что самому быстрому алгоритму, использующему сравнение, для сортировки n элементов требуется как минимум O(n log(n)) времени. Рассмотренные сортировки (пирамидальная, слиянием и быстрая) в ожидаемом случае достигают такого предела, поэтому может показаться, что тема исчерпана. Но если заострить внимание на словах «алгоритму, использующему сравнения» и воспользоваться другим методом, то указанная производительность не предел. В следующих подразделах будет рассмотрено ещё два алгоритма, где сортировка осуществляется за время, которое значительно меньше, чем O(n log(n)).

4.1 Сортировка подсчетом

Подобный метод удобно использовать в том случае, если сортировать приходится целые числа, лежащие в относительно небольшом диапазоне. Например, вам нужно упорядочить 1 млн целых чисел от 0 до 1000. Основная идея заключается в том, чтобы установить количество элементов массива с определенным значением, а затем скопировать это значение по порядку нужное количество раз обратно в массив. Реализацию такого метода показывает следующий код.

Листинг 9 – Псевдокод сортировки подсчётом

Countingsort(Integer: values[], Integer: max_value)

// Создаем массив счетчиков.

Integer: counts[0 To max_value]

// Инициализируем массив счетчиков

// (требуется не во всех языках программирования).

For i = 0 To max_value

counts[i] = 0

Next i

// Считаем количество элементов для каждого значения.

For i = 0 To <количество значений> - 1

// Прибавляем 1 к счетчику данного значения.

counts[values[i]] = counts[values[i]] + 1

Next i

// Копируем значения в исходный массив.

Integer: index = 0

For i = 0 To max_value

// Копируем значение i в массив counts[i] раз.

For j = 1 To counts[i]

values[index] = i

index = index + 1

Next j

Next i

End Countingsort

Параметр max_value содержит наибольшее значение из массива (если оно не задано, алгоритм определит его, просмотрев массив); M — общее количество элементов в массиве counts (M = max_value + 1), а N — в массиве values. Если используемый вами язык программирования не инициализирует массив counts так, чтобы он содержал нули, алгоритм затратит на это М шагов, после чего выполнит еще N шагов, чтобы посчитать значения

В завершение работы алгоритм копирует значения обратно в исходный массив (каждое один раз), поэтому данная часть процесса займет N шагов. Если какая-либо из записей в массиве counts все еще равна 0, программа потратит определенное время на перепрыгивание через нее. В худшем случае, когда все значения одинаковы, а массив counts содержит в основном нули, для аналогичного действия понадобится M шагов. Отсюда общее время работы алгоритма: O(2N + M) = O(N + M).

Если M относительно мало по сравнению с N, полученная производительность окажется лучше O(N _ log N), которую демонстрирует пирамидальная сортировка и другие описанные выше алгоритмы.

На практике для тестового массива с 1 млн элементов и диапазоном значений от 0 до 1000, быстрая сортировка заняла в несколько сот раз больше времени, чем сортировка подсчетом.

Следует отметить, что для быстрой сортировки выбранный пример оказался не самым лучшим, поскольку среди значений было множество дубликатов (приблизительно 1000), а данный алгоритм справляется с ними плохо. Пирамидальная сортировка аналогичного массива показала себя эффективнее быстрой сортировки, но все равно значительно уступила сортировке подсчетом.

4.2 Блочная сортировка

Алгоритм блочной, или, как ее еще называют, корзинной, сортировки делит элементы на блоки, а затем сортирует их с помощью рекурсивного вызова блочной сортировки либо другого алгоритма и присоединяет содержимое блоков к исходному массиву. В следующем псевдокоде представлен высокоуровневый алгоритм, демонстрирующий этот метод.

Листинг 10 – Псевдокод блочной сортировки

Bucketsort(Data: values[])

<Создаем блоки.>

<Распределяем элементы по блокам.>

<Сортируем блоки.>

<Собираем элементы блоков в исходный массив.>

End Bucketsort

Если при использовании M блоков значения в массиве из N элементов распределены относительно равномерно и их диапазон делится поровну, можно ожидать, что в каждый блок попадет N/M элементов.

В качестве примера возьмем массив, изображенный вверху на рисунке 12. Он содержит 10 элементов со значениями от 0 до 99. На первом этапе алгоритм делит элементы на блоки, которые в нашем случае состоят из 20 значений: от 0 до 19, от 20 до 39 и т. д. На втором этапе алгоритм сортирует каждый блок, а на третьем объединяет их значения для построения результата сортировки.

Блоками могут выступать стеки, связные списки, очереди, массивы или любые другие структуры данных.

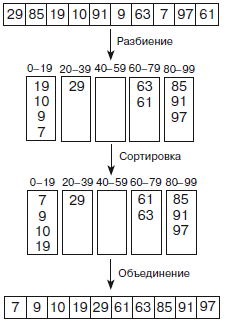
Рисунок 12 – Блочная сортировка

Чтобы разбить N равномерно распределенных элементов по блокам, алгоритму понадобится N шагов, если не учитывать перенос элемента в блок. Обычно такое преобразование занимает фиксированный отрезок времени. Предположим, в массиве находятся целые числа от 0 до 99, как в примере на рисунке 12. Вам надо перенести элемент со значением v в блок номер |v/20|. Этот номер можно рассчитать за определенное время, таким образом, для распределения элементов потребуется O(N) шагов.

Если таких блоков M, для сортировки каждого из них понадобится F(N/M) шагов, где F — функция времени работы алгоритма, который вы используете при сортировке блоков. Получается, что общее время сортировки всех блоков составит O(M x F(N/M)).

Чтобы собрать все отсортированные значения назад в массив, надо выполнить N основных шагов и, возможно, O(M) дополнительных, чтобы пропустить пустые блоки. Но если M < N, для всей операции потребуется O(N) шагов.

При суммировании всех этапов получим следующее: O(N) + O(M _ F(N/M)) + + O(N) = O(N + M _ F(N/M)). Если M является фиксированной долей N, то N/M, а следовательно, и F(N/M) — константы. Тогда формула упрощается до O(N + M).

На практике число M должно составлять относительно большую долю N, чтобы алгоритм мог хорошо работать. Если у вас 10 млн записей и 10 блоков, то в каждом из них будет в среднем по 1 млн записей. В отличие от сортировки подсчетом, производительность блочной сортировки не зависит от количества используемых блоков.

Заключение

Алгоритмы сортировки, описанные в работе, используют разные методы и обладают различными характеристиками. Все они сведены в таблицу 1.

Таблице 1 – Алгоритмы сортировки

Сортировка	Время работы	Метод	Область использования
Вставкой	O(N2)	Вставка	Очень малые массивы
Выбором	O(N2)	Выбор	Очень малые массивы
Пузырьковая	O(N2)	Двусторонние прохождения, ограничения рассматриваемых пределов	Очень малые и частично сортированные
Пирамидальная	O(N log N)	Кучи, хранение полных деревьев в массиве	Крупные массивы с неизвестным распределением
Быстрая	O(N log N) ожидаемое, O(N2) в худшем случае	«Разделяй и властвуй», перемещение элементов в позицию, рандомизация во избежание худшего случая	Крупные массивы без большого количества дубликатов, параллельная сортировка
Слиянием	O(N log N)	«Разделяй и властвуй»,объединение, внешняя сортировка	Крупные массивы с неиз вестным распределением, большие объемы данных, параллельная сортировка
Подсчетом	O(N + M)	Счет	Крупные массивы с достаточно единообразным распределением значений

Рассмотренные алгоритмы демонстрируют набор полезных методов и обеспечивают хорошую производительность для решения широкого спектра задач, но это далеко не все. Существуют десятки других способов сортировки. Некоторые из них являются модификациями приведенных алгоритмов, в других используются совершенно иные методы.

список использованной литературы

1. Р. Стивенс. Алгоритмы. Теория и практическое применение [Текст]: Перевод с английского – М.: Издательство «Э», 2016. — 544 с.
2. Р. Седжвик. Фундаментальные алгоритмы на С++ [Текст]: Перевод с английского – М.: «ДиасСофт», 2002. — 688 с.
3. Википедия, свободная энциклопедия [Электронный ресурс]. – Режим доступа: https://ru.wikipedia.org