Рекурсивные и итерационные алгоритмы: особенности и примеры использования (ПОНЯТИЕ РЕКУРСИВНОГО АЛГОРИТМА)

Содержание:

ВВЕДЕНИЕ

При разработке современного программного обеспечения широко используются различные алгоритмы. Они применяются при решении математических и логических задач, для нахождения решений уравнений численными методами и много другого.

Выделяют такие отдельные алгоритмы, как рекурсивные и итерационные. Рекурсивный алгоритм (или функция в функциональном программировании) – это вызов участка кода или функции самой себя. В отличии от цикла, рекурсия для определения момента выхода должна выполнять сравнение результатов, а цикл используют для подсчета числа исполнений итератор.

Итерационный алгоритм – это разновидность рекурсивного алгоритма, в котором используется параметр, задающий степень приближения к вычисляемому значению или цели.

Основными целями написания курсовой работы является исследование рекурсивных и итерационных алгоритмов, их сфера применения в современном программирование, изучение результатов работы программного обеспечения, использующего данные алгоритмы.

Объектом исследования являются особенности применения рекурсивных алгоритмов при написании программ.

Предметом исследования является процесс реализации математической или логической задачи при помощи рекурсивного и итерационного алгоритмов.

Этапами разработки курсовой работы будут теоретические исследования, описание математических задач, имеющих решения при помощи рекурсивных и итерационных алгоритмов и изучение примеров программного кода.

ГЛАВА 1. ПОНЯТИЕ РЕКУРСИВНОГО АЛГОРИТМА

При программировании множества задач из реальной жизни часто используются рекурсивные алгоритмы. Классическим определением рекурсии является приведенное в [4] - «Рекурсия - это такой способ организации вычислительного процесса, при котором подпрограмма в ходе выполнения составляющих ее операторов обращается сама к себе».

Программы, использующие рекурсию отличаются компактностью и простотой. Такие качества рекурсивных алгоритмов вытекают из того, что рекурсивная процедура указывает что нужно делать, а нерекурсивная больше акцентирует внимание на том, как нужно делать.

Однако за эту простоту приходится расплачиваться неэкономным использованием оперативной памяти, так как выполнение рекурсивных процедур требует значительно большего размера оперативной памяти во время выполнения, чем нерекурсивных. При каждом рекурсивном вызове для локальных переменных, а также для параметров процедуры, которые передаются по значению, выделяются новые ячейки памяти [4].

В отличии от циклических алгоритмов, в которых группа операторов выполняется несколько раз подряд [1], рекурсивные алгоритмы осуществляют вызов самих себя с различными параметрами и не содержат в своем составе счетчиков повторений (итераций).

Вопрос о желательности использования рекурсивных функций в программировании неоднозначен: с одной стороны, рекурсивная форма может быть структурно проще и нагляднее, в особенности, когда сам реализуемый алгоритм по сути рекурсивен. Кроме того, в некоторых декларативных или чисто функциональных языках (таких как Пролог или Haskell) просто нет синтаксических средств для организации циклов, и рекурсия в них — единственный доступный механизм организации повторяющихся вычислений. С другой стороны, обычно рекомендуется избегать рекурсивных программ, которые приводят (или в некоторых условиях могут приводить) к слишком большой глубине рекурсии.

Имеется специальный тип рекурсии, называемый «хвостовой рекурсией» (структура рекурсивного алгоритма такова, что рекурсивный вызов является последней выполняемой операцией в функции, а его результат непосредственно возвращается в качестве результата функции). Интерпретаторы и компиляторы функциональных языков программирования, поддерживающие оптимизацию кода (исходного или исполняемого), автоматически преобразуют хвостовую рекурсию к итерации, благодаря чему обеспечивается выполнение алгоритмов с хвостовой рекурсией в ограниченном объёме памяти. Такие рекурсивные вычисления, даже если они формально бесконечны (например, когда с помощью рекурсии организуется работа командного интерпретатора, принимающего команды пользователя), никогда не приводят к исчерпанию памяти. Однако далеко не всегда стандарты языков программирования чётко определяют, каким именно условиям должна удовлетворять рекурсивная функция, чтобы транслятор гарантированно преобразовал её в итерацию. Одно из редких исключений — язык Scheme (диалект языка Lisp), описание которого содержит все необходимые сведения.

Теоретически, любую рекурсивную функцию можно заменить циклом и стеком. Однако такая модификация, как правило, бессмысленна, так как приводит лишь к замене автоматического сохранения контекста в стеке вызовов на ручное выполнение тех же операций с тем же расходом памяти. Исключением может быть ситуация, когда рекурсивный алгоритм приходится моделировать на языке, в котором рекурсия запрещена.

Рекурсивный алгоритм всегда разбивает задачу на части, которые по своей структуре являются такими же как исходная задача, но более простыми. Для решения подзадач функция вызывается рекурсивно, а их результаты каким-либо образом объединяются. Разделение задачи происходит лишь тогда, когда ее не удается решить сразу (она является слишком сложной).

Например, задачу обработки массива нередко можно свести к обработке его частей. Деление на части выполняется до тех пор, пока они не станут элементарными, то есть достаточно простыми чтобы получить результат без дальнейшего упрощения.

Для более строгого описания рекурсии можно ввести набор описывающих ее параметров [4]:

1. Локальной переменной А на разных уровнях рекурсии будут соответствовать различные ячейки памяти, которые могут иметь разные значения.

2. Глубиной рекурсии называется максимальное число рекурсивных вызовов процедуры без возвратов, которое происходит во время выполнения программы.

В общем случае любая рекурсивная процедура Rec включает в себя некоторое множество операторов S и один или несколько операторов рекурсивного вызова.

Безусловные рекурсивные процедуры приводят к бесконечным процессам, и на эту проблему нужно обратить особое внимание, так как практическое использование процедур с бесконечным самовызовом невозможно.

Следовательно, главное требование к рекурсивным процедурам заключается в том, что вызов рекурсивной процедуры должен выполняться по условию, которое на каком-то уровне рекурсии станет ложным.

Анализ трудоемкости рекурсивных функций значительно сложнее аналогичной оценки циклов, но основной причиной, по которой циклы предпочтительнее являются высокие затраты на вызов функции.

После вызова управление передается другой функции. Для передачи управления достаточно изменить значение регистра программного счетчика, в котором процессор хранит номер текущей выполняемой команды – аналогичным образом передается управление ветвям алгоритма, например, при использовании условного оператора. Однако, вызов – это не только передача управления, ведь после того, как вызванная функция завершит вычисления, она должна вернуть управление в точку, и которой осуществлялся вызов, а также восстановить значения локальных переменных, которые существовали там до вызова.

Для реализации такого поведения используется стек (стек вызовов, call stack) – в него помещаются номер команды для возврата и информация о локальных переменных. Стек не является бесконечным, поэтому рекурсивные алгоритмы могут приводить к его переполнению, в любом случае на работу с ним может уходить значительная часть времени.

В ряде случаев рекурсивную функцию достаточно легко заменить циклом, например, алгоритмы поиска и бинарного поиска [9]. В некоторых случаях требуется более творческий подход, но чаще всего такая замена оказывается возможной. Кроме того, существует особый вид рекурсии, когда рекурсивный вызов является последней операцией, выполняемой функцией. Очевидно, что в таком случае вызывающая функция не будет каким-либо образом изменять результат, а значит ей нет смысла возвращать управление. Такая рекурсия называется хвостовой – компиляторы автоматически заменяют ее циклом.

Зачастую сделать рекурсию хвостовой помогает метод накапливающего параметра [8], который заключается в добавлении функции дополнительного аргумента-аккумулятора, в котором накапливается результат. Функция выполняет вычисления с аккумулятором до рекурсивного вызова.

Рассмотрим функцию вычисления чисел Фибоначчи.

Числа Фибоначчи определяются рекуррентным выражением, т.е. таким, что вычисление элемента которого выражается из предыдущих элементов:

F₀=0,F₁=1,Fn=Fn−1+Fn−2,n>2

Основная функция вызывает вспомогательную, использующую метод накапливающего параметра, при этом передает в качестве аргументов начальное значение итератора и два аккумулятора (два предыдущих числа Фибоначчи).

Код:

int (Fibonacci int number){

return (fibonacci(number, 1, 1, 0))}:

int fibonacci(int number, int iterator, int fib1, int fib2){

if (iterator == number) return fib1;

else {fibonacci(number, iterator + 1, fib1 + fib2, fib1)}};

Функция с накапливающим параметром возвращает накопленный результат, если рассчитано заданное количество чисел, в противном случае – увеличивает счетчик, рассчитывает новое число Фибоначчи и производит рекурсивный вызов. Оптимизирующие компиляторы могут обнаружить, что результат вызова функции без изменений передается на выход функции и заменить его циклом. Такой прием особенно актуален в функциональных и логических языках программирования, т.к. в них программист не может явно использовать циклические конструкции.

Для подобранного анализа выполнения программ рекурсивных алгоритмов в памяти ПК воспользуемся источником [2].

Рекурсивные алгоритмы в программировании реализованы в механизме так называемых рекурсивных подпрограмм. Рекурсивной считается подпрограмма, которая прямо или косвенно, через другие подпрограммы, обращается к себе, быть может с иными фактическими параметрами. В современных системах программирования корректное функционирование подпрограмм, особенно рекурсивных, обеспечивается с помощью стека.

Стек – связная структура данных, построенная на принципе «первый пришёл – первый вышел» (Fiгst In – Fiгst Out, FIFO). То есть вновь добавляемые объекты помещаются в начало, вершину стека, и выбираются они также только из вершины.

Стек является чрезвычайно удобной структурой данных для многих задач вычислительной техники. Наиболее типичной из таких задач является обеспечение вложенных вызовов процедур. Предположим, имеется процедура A, которая вызывает процедуру B, а та в свою очередь – процедуру C. Когда выполнение процедуры A дойдет до вызова B, процедура A приостанавливается и управление передается на входную точку процедуры B. Когда B доходит до вызова C, B приостанавливается и управление передается на процедуру C. Когда заканчивается выполнение процедуры C, управление должно быть возвращено в B, причем в точку, следующую за вызовом C. При завершении B управление должно возвращаться в A, в точку, следующую за вызовом B. Правильную последовательность возвратов легко обеспечить, если при каждом вызове процедуры записывать адрес возврата в стек. Так, когда процедура A вызывает процедуру B, в стек заносится адрес возврата в A; когда B вызывает C, в стек заносится адрес возврата в B. Когда C заканчивается, адрес возврата выбирается из вершины стека – а это адрес возврата в B. Когда заканчивается B, в вершине стека находится адрес возврата в A, и возврат из B произойдет в A.

Механизм вызова функции или процедуры в языке высокого уровня существенно зависит от архитектуры компьютера и операционной системы. В рамках IBM PC совместимых компьютеров, в микропроцессорах семейства Intel, как и в большинстве современных процессорных архитектур, поддерживается аппаратный стек. Аппаратный стек расположен в ОЗУ, указатель стека содержится в паре специальных регистров SS:SP доступных для программиста. Аппаратный стек расширяется в сторону уменьшения адресов, указатель его адресует первый свободный элемент. Схематично этот механизм иллюстрирован на рисунке 1.

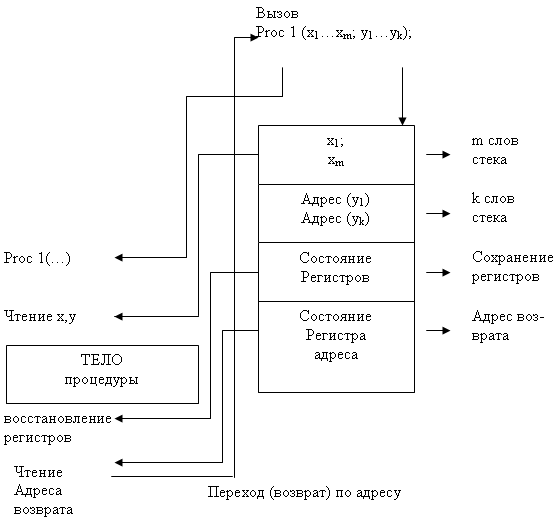
Рисунок 1 - Механизм вызова функции в аппаратном стеке

Языки PASCAL, C, C++ используют стек для размещения в нем локальных переменных процедур и иных программных блоков. Стек разбит на фрагменты, представляющие собой блоки последовательных ячеек. Каждый вызов подпрограммы использует фрагмент стека, длина которого зависит от вызывающей подпрограммы. При каждой активизации процедуры память для ее локальных переменных выделяется в стеке; при завершении процедуры эта память освобождается. Поскольку при вызовах процедур всегда строго соблюдается вложенность, то в вершине стека всегда находится память, содержащая локальные переменные активной в данный момент процедуры.

Таким образом, в общем случае при вызове процедурой A процедуры B происходит следующее:

В вершину стека помещается фрагмент нужного размера. В него входят следующие данные:

- указатели фактических параметров вызова процедуры В;

- пустые ячейки для локальных переменных, определенных в процедуре В;

- адрес возврата, т.е. адрес команды в процедуре A, которую следует выполнить после того, как процедура B закончит свою работу.

Если B – функция, то во фрагмент стека для B помещается указатель ячейки во фрагменте стека для A, в которую надлежит поместить значение этой функции (адрес значения).

Управление передается первому оператору процедуры B.

При завершении работы процедуры B управление передается процедуре A с помощью следующей последовательности шагов:

- адрес возврата извлекается из вершины стека;

- если B – функция, то ее значение запоминается в ячейке, предписанной указателем на адрес значения;

- фрагмент стека процедуры B извлекается из стека, в вершину ставится фрагмент процедуры A;

- выполнение процедуры A возобновляется с команды, указанной в адресе возврата.

При вызове подпрограммой самой себя, т.е. в рекурсивном случае, выполняется та же самая последовательность действий.

Этот прием делает возможной легкую реализацию рекурсивных процедур. Когда процедура вызывает сама себя, то для всех ее локальных переменных выделяется новая память в стеке, и вложенный вызов работает с собственным представлением локальных переменных. Когда вложенный вызов завершается, занимаемая его переменными область памяти в стеке освобождается и актуальным становится представление локальных переменных предыдущего уровня.

Рекурсия использует стек в скрытом от программиста виде, но все рекурсивные процедуры могут быть реализованы и без рекурсии, но с явным использованием стека.

Рассмотрим пример для функции вычисления факториала: дерево рекурсии при вычислении 5! (рисунок 2).

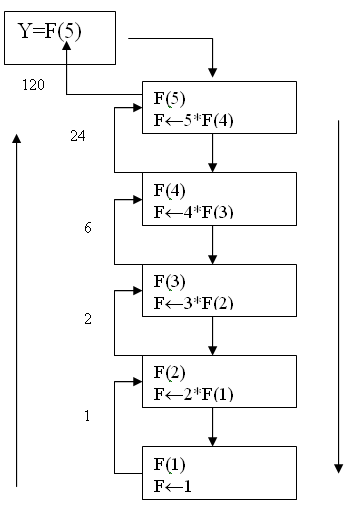
Рисунок 2 - Дерево рекурсии при вычислении факториала числа 5

Дерево рекурсивных вызовов может иметь и более сложную структуру, если на каждом вызове порождается несколько обращений – фрагмент дерева рекурсий для чисел Фибоначчи представлен на рисунке 3.

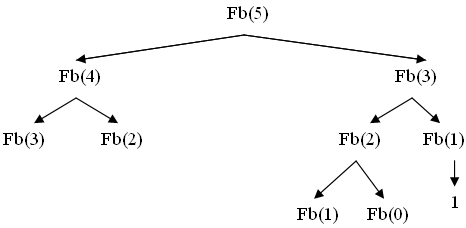
Рисунок 3 - Вычисление 5 – ого числа Фибоначчи (Fb(5)).

Упомянутый анализ практической сложности программ показывает, что часто асимптотически более сложные итеративные алгоритмы, на практике становятся более эффективными. Сравнивая скорость вычисления чисел Фибоначчи с помощью итеративной и рекурсивной функции можно заметить, что итеративная функция выполняется почти «мгновенно», не зависимо от значения n. При использовании же рекурсивной функции уже при n=40 заметна задержка при вычислении, а при больших n результат появляется весьма не скоро. Причина, как уже было сказано, кроется в том, что в теории не учтена зависимость времени работы программы от количества вызовов вложенных подпрограмм. Неэффективность рекурсии проявляется в том, что одни и те же вычисления производятся много раз. Особенно сильно это проявляется в методе, который был самым востребованным при построении теоретически быстрых рекурсивных алгоритмов, – методе бинарного разбиения на независимые подзадачи. Когда подзадачи независимы, это часто приводит к недопустимо большим затратам времени, так как одни и те же подзадачи решаются многократно.

Обходить подобные ситуации позволяет подход, известный как динамическое программирование [5]. Этот подход для реализации рекурсивных программ дает возможность получать эффективные и элегантные решения для обширного класса задач.

Технология, называемая восходящим динамическим программированием (bottom – up dynamic pгogгamming) основана на том, что значение рекурсивной функции можно определить, вычисляя все значения этой функции, начиная с наименьшего, используя на каждом шаге ранее вычисленные значения для подсчета текущего значения. Она применима к любому рекурсивному вычислению при условии, что мы можем позволить себе хранить все ранее вычисленные значения. Это в результате позволит уменьшить временную зависимость с экспоненциальной на линейную.

Нисходящее динамическое программирование (top – down dynamic pгogгamming). Оно позволяет выполнять рекурсивные функции при том же количестве итераций, что и восходящее динамическое программирование. Технология требует введения в рекурсивную программу неких средств, обеспечивающих сохранение каждого вычисленного значения и проверку сохраненных значений во избежание их повторного вычисления.

Таким образом, современные информационные технологии содержат достаточно средств, чтобы сделать теоретически эффективные рекурсивные алгоритмы, также эффективными и широко используемыми на практике. Преимущества рекурсии заключаются в следующих аспектах:

- часто это наиболее легкий метод написания алгоритма для задач, которые можно решить с помощью рекурсии (число фибоначчи, факториал);

- рекурсивно реализованные алгоритмы, при правильных на то основаниях, имеют лаконичную запись и менее трудоёмки при последующей отладке и модификации, они сокращают временные затраты на разработку, отладку и модификацию программных средств;

- целый ряд структур данных и многие объекты современных язы­ков программирования рекурсивны по самой своей сути (фрактальные объекты, иерархия классов в объектно – ориентированном программировании, древовидные регулярные структуры данных) и программы для работы с такими структурами выглядят намного более естественно в рекурсивной реализации;

- рекурсия делает код более читабельным (позволяет читать код с любого места, не просматривая его весь, отслеживая все изменения переменной), что облегчает отладку;

- рекурсия защищает от ошибок типа: «действия выполнены в не верном порядке», «использована неинициализированная переменная» и других аналогичных.

Недостатки рекурсии заключаются в следующем:

- велика возможность войти в бесконечный цикл;

- при использовании некоторых формул слишком большие затраты памяти компьютера (к примеру, при вычислении числа Фибоначчи или факториалов, необходимо запоминать все значения чисел и вычислять одни и те же значения по многу раз);

- в случае, если вызываемых функций будет очень много, может произойти переполнение стека;

- следует избегать использования рекурсии в случаях, когда требуется высокая эффективность, так как они требуют времени и дополнительных затрат памяти и обладают худшей временной эффективностью.

Обслуживание рекурсивных вызовов влечет определенные накладные расходы, но при этом рекурсивные алгоритмы, разработанные методом декомпозиции, имеют лучшие асимптотические оценки. Это означает, что, начиная с некоторой длины входа, достаточно часто соответствующей области практического использования, программная реализация рекурсивного алгоритма будет иметь лучшие временные показатели.

ГЛАВА 2. ПОНЯТИЕ ИТЕРАЦИОННОГО АЛГОРИТМА

Практически все численные методы основаны на последовательном приближении вычисленного значения к искомому результату.

Итерационными (пошаговыми) алгоритмами называются алгоритмы, в которых на каждом шаге используется одна и та же формула, выраженная через значения, полученные на предыдущих шагах алгоритма. Выполнение такого алгоритма сводится к генерации некоторой числовой последовательности результатов.

В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет "зацикливание" алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность [1].

Метод хорд, или метод итерационных приближений, широко используется при решении различных алгебраических задач. В общих словах, сущность метода заключается в последовательном нахождении корней уравнения, с приближением найденного значения к заданному отклонению «эпсилон».

Изучение полиномиальных уравнений и их решений связан целый ряд преобразований в математике. Техническая простота вычислений, связанных с многочленами, по сравнению с более сложными классами функций, а также тот факт, что множество многочленов плотно в пространстве непрерывных функций на компактных подмножествах евклидова пространства (аппроксимационная теорема Вейерштрасса), способствовали развитию методов разложения в ряды и полиномиальной интерполяции в математическом анализе.

При программной реализации данного метода скорость работы программы будет завысить от степени полинома, заданного отрезка для нахождения корня и точности его нахождения.

Рассмотрим метод коротких итераций для нахождения корней полиноминального уравнения.

Многочлен (или полином) от n переменных — это сумма одночленов или, строго, — конечная формальная сумма вида:

, (1)

где k – первый показатель степени полинома;

N – конечный показатель степени полинома;

а – коэффициенты перед неизвестными.

Более традиционная формула представления полинома n-ой степени будет выглядеть следующим образом:

(2)

Корень многочлена (не равного тождественно нулю), над полем k это элемент , (либо элемент расширения поля k), такой, что выполняются два следующих равносильных условия:

1 Данный многочлен делится на многочлен x-c;

2 Подстановка элемента c вместо x обращает уравнение:

(3)

в тождество.

Равносильность двух формулировок следует из теоремы Безу. В различных источниках любая одна из двух формулировок выбирается в качестве определения, а другая выводится в качестве теоремы.

Свойства корней многочлена:

1. Число корней многочлена степени n не превышает n даже в том случае, если кратные корни учитывать кратное количество раз.

2. Корни многочлена связаны с его коэффициентами формулами Виета.

Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время (следует упомянуть метод, предложенный Омаром Хайямом), пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.

То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов, было доказано норвежским математиком Нильсом Абелем в 1826 году. Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, в частных случаях, при некоторых комбинациях коэффициентов, корни уравнения всё же могут быть определены. Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие специальные функции — эллиптические или гипергеометрические (например, корень Бринга).

В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера, причем при нахождении целых корней перебор может быть существенно уменьшен приемом чистки корней. Также в этом случае можно использовать полиномиальный LLL-алгоритм [10].

Для приблизительного нахождения (с любой требуемой точностью) вещественных корней многочлена с вещественными коэффициентами используются итерационные методы.

ГЛАВА 3. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ ИТЕРАЦИОННОГО АЛГОРИТМА НАХОЖДЕНИЯ КОРНЕЙ УРАВНЕНИЯ

Итерация в программировании — организация обработки данных, при которой действия повторяются многократно, не приводя при этом к вызовам самих себя.

Метод секущих — итерационный численный метод приближённого нахождения корня уравнения.

Алгебраическое описание метода секущих.

Пусть задан диапазон абсцисс, находящийся между x₁ и x₂. Уравнение, содержащее хорду, имеет вид:

y = kx+b (4)

Найдем значения коэффициентов k и b и выразим через них первое приближение к корню.

(5)

Теперь возьмем координаты x₂ и x₃ и повторим все проделанные операции, найдя новое приближение к корню. Таким образом, итерационная формула метода секущих имеет вид:

(6)

Повторять операцию следует до тех пор, пока |x_i-x_i-1| не станет меньше или равно заданному значению погрешности .

Иногда методом секущих называют метод с итерационной формулой:

(7)

Этот метод можно считать разновидностью метода простой итерации, и он имеет меньшую скорость сходимости.

Итерации метода секущих сходятся к корню f(x), если начальные величины x₁ и x₂ достаточно близки к корню. Метод секущих является быстрым.

На рисунке 4 представлена блок-схема алгоритма.

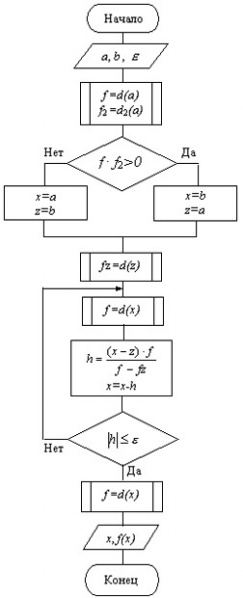
Рисунок 4 - Схема алгоритма нахождения корня методом хорд

Так как для решения поставленной задачи требуется отыскание функции F(x), метод хорд и касательных достаточно трудно реализуем на программном уровне. Связано это с тем, что перед передачей функции в цикл, необходимо аналитически определить ее форму – представить коэффициенты перед соответствующими переменными. Если человек выполняет такую работу легко, то для ПК этот процесс будет трудным, нужно предусмотреть в программе алгоритм «отсеивания» незначащих коэффициентов перед соответствующими степенями и алгоритм передачи значений из одной функции в другую. Поэтому, ограничимся для данного задания полиномом 10-ой степени со всеми значащими коэффициентами.

В данном случае, алгоритм вычисления корня уравнения, лежащего в заданном отрезке с определённой точностью, будет выглядеть следующим образом:

1 Ввод коэффициентов перед переменными полинома;

2 Ввод границ значений корня;

3 Ввод необходимой точности;

4 Формирование полинома и передача его в вычисляемом виде в функцию;

5 Передача границ и полинома в функцию вычисления корней;

6 Вычисление корней необходимое количество раз;

7 Вывод результатов.

Функция определения полинома:

1. double f(double x)
2. {
3. return a[0]*x^[0]+ a[1]*x^[1]+ a[2]*x^[2]+…+ a[n]*x^[n];// функция, для
4. //которой определяются корни, где n – порядок полинома
5. }

Функция итерационного приближения:

1. // a, b - пределы хорды, epsilon - необходимая погрешность
2. double findRoot(double a, double b, double epsilon)
3. {
4. while(fabs(b - a) > epsilon)
5. {
6. a = b - (b - a) * f(b)/(f(b) - f(a));
7. b = a - (a - b) * f(a)/(f(a) - f(b));
8. }
9. // a - i-1, b - i-тый члены
10. return b;
11. }

Исходный код:

1. //
2. /*подключим необходимые библиотеки*/
3. #include "stdafx.h"
4. #include "stdio.h"
5. #include <iostream>
6. #include <conio.h>
7. /*объявляем необходимые переменные*/
8. int N_polinom; //порядок полинома
9. float a, b; //начало и конец хорды
10. float epsilon; //погрешность нахождения корня
11. int polinom_massiv_length;
12. float *polinom_mas = 0;
13. using namespace std;
14. /*прототипы функций*/
15. float f_polinom(float x);
16. float f_iteration(float a, float b, float epsilon);
17. int _tmain(int argc, _TCHAR* argv[])
18. {
19. setlocale(LC_ALL, "Russian"); //подключение русского языка
20. /*блок получения значений*/
21. puts("Введите порядок полинома\n");
22. std::cin >> N_polinom;
23. polinom_mas = new float[N_polinom+1]; //резервируем память под массив (не забыть потом подчистить за собой!!!)
24. /*принимаем из входного потока коэффициенты*/
25. /*для упрощения последующего программирования введем переменную длины массива, так как длина массива длиньше полинома на +1*/
26. polinom_massiv_length = N_polinom + 1;
27. std::cout << "Введите коэффициенты полинома, начиная с a0 и далее" << endl;
28. for (int count = 0; count < polinom_massiv_length; count++){
29. /*приглашение на ввод*/
30. std::cout << "Введите значение " << "a" << count << ": ";
31. std::cin >> polinom_mas[count];
32. }
33. /*получаем интервал и эпсилон*/
34. std::cout << "Введите начальный интервал поиска корня" << endl;
35. std::cin >> a;
36. std::cout << "Введите конечный интервал поиска корня" << endl;
37. std::cin >> b;
38. std::cout << "Введите допустимую погрешность" << endl;
39. std::cin >> epsilon;
40. /*вычисление корня*/
41. float koren = f_iteration(a, b, epsilon);
42. /*вывод значений корня*/
43. cout <<"X="<< koren << endl;
44. delete[] polinom_mas; //подчищаем за собой память
45. _gettch();
46. return 0;
47. }
48. /*функция построения полинома*/
49. float f_polinom(float x){
50. float temp_x=0;
51. for (int count = 0; count < polinom_massiv_length; count++){
52. temp_x += (pow(x, count))*polinom_mas[count]; //вычисление значения полинома
53. }
54. return(temp_x);
55. }
56. /*функция итерации*/
57. float f_iteration(float a, float b, float epsilon)
58. {
59. while (fabs(b - a) > epsilon)
60. {
61. a = b - (b - a) * f_polinom(b) / (f_polinom(b) - f_polinom(a));
62. b = a - (a - b) * f_polinom(a) / (f_polinom(a) - f_polinom(b));
63. }
64. // a - i-1, b - i-тый члены
65. return b;
66. }

Разберем подробно работу программы. В строках с 1 по 7 происходит подключение стандартных библиотек.

В строках с 8 по 12 объявляются необходимые переменные, такие как значение порядка полинома, начало и конец интервала приближений и необходимая точность.

В 13 строке подключается стандартное пространство имен, необходимое для корректной работы операторов cin и cout.

16 и 17 строчка – это объявление прототипов функций, необходимое для того, чтобы компилятор зарезервировал для них память.

С 20 по 37 строчку происходит получение входных значений, необходимых для работы программы – степеней полинома, коэффициентов перед этими степенями, интервала расчёта и допустимой погрешности.

39 строка вычисление корня, 41 строка – вывод результата.

42-44 строки необходимы для корректной работы программы, здесь очищается память, ставится задержка в консоли, возвращается значение нормального завершения программы.

Разберем более подробно работу функций, вызываемых в строках 47-52 и 54-60.

Первая функция – это функция построения полинома. Она начинает работать с присвоения нулевого значения временной переменной temp. после этого, в каждой итерации цикла происходит увеличение значения этой переменной на величину, полученную умножением значения x в степени, совпадающей со значением номера элемента массива на значение этого элемента. Последним значением счётчика служит порядок полинома.

Эта функция рекурсивно вызывается во второй функции, которая производит вычисления двух значений a и b, где a – нижнее значение границы ходы, а b – верхнее. После этого, корень полинома считается за b и проверяется равенство – попадает ли этот корень в заданное значение точности. Если попадает – то значение b возвращается как корень полинома, если нет – то происходит еще одна итерация цикла.

Результат работы готового программного продукта представлен на рисунках 5 и 6. Это случайные наборы значений. Кроме этого, подобраны такие значения полинома, которые не могут иметь корень.

На случайных параметрах программа отрабатывает без ошибок.

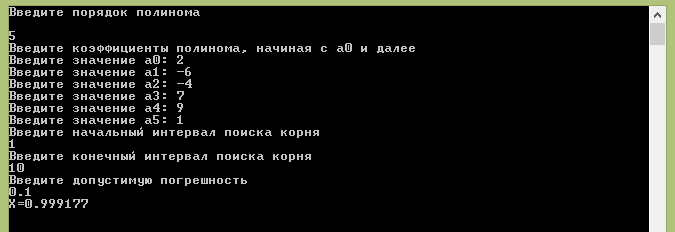
Рисунок 5 – Набор случайных входных параметров.

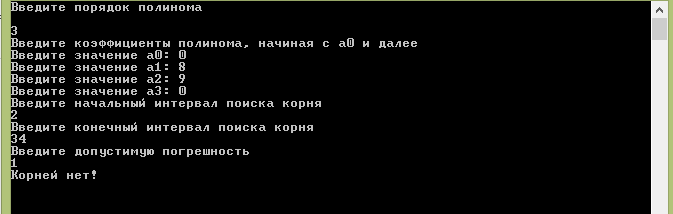
Рисунок 6 – Набор параметров для полинома, не имеющего корней.

ГЛАВА 4. ПРАКТИЧЕСКАЯ РЕАЛИЗАЦИЯ РЕКУРСИВНЫХ АЛГОРИТМОВ

Рекурсия аналогична методу математической индукции. Базе индукции соответствует база рекурсии. Предположению индукции соответствует предположение о том, что нужная процедура уже написана. Шагу индукции соответствует вызов создаваемой рекурсивной процедуры. В любой рекурсии необходимо предусмотреть условие завершения процесса, т.е. когда вызова больше не происходит.

Рассмотрим – вычисление N – ого по счёту числа Фибоначчи. Числа Фибоначчи составляют последовательность, очередной элемент которой вычисляется по двум предыдущим значениям:

F_­n=F_n – 1 + F_n – 2

1. #include <iostream>
2. int fib(int n) {
3. if(n < 3)
4. return 1;
5. return fib(n – 2) + fib(n – 1);
6. }
7. int main() {
8. int n = 0;
9. std::cout << "Vvedite nomer chisla:\n";
10. std::cin >> n;
11. std::cout << "Result: chislo " << fib(n) << " eto " << n << "th po schetu chislo v ryade Fibonacci.\n";
12. return 0;
13. }

Результат работы программы представлен на рисунке 7.

Рассмотрим задачу нахождение факториала.

1. #include <iostream>
2. int factorial(int n)
3. {
4. if(n==1 || n==0) return 1;
5. return n* factoгial (n – 1);
6. }
7. int main() {
8. int n = 0;
9. std::cout << "Vvedite chislo:\n";
10. std::cin >> n;
11. std::cout << "Factorial " << n << " raven " << factorial(n) << "\n";
12. return 0;
13. }

Результат работы программы представлен на рисунке 8.

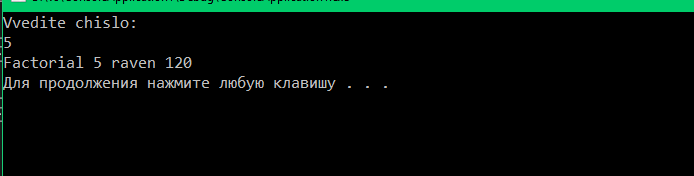
Рисунок 8 – Результат работы программы.

Рассмотрим нахождение наибольшего общего делителя.

1. #include <iostream>
2. int nod(int m, int n)
3. {
4. if (n == 0) return m;
5. else
6. return nod(n, m % n);
7. }
8. int main() {
9. int n = 0;
10. int m = 0;
11. std::cout << "Vvedite pervoe chislo:\n";
12. std::cin >> n;
13. std::cout << "Vvedite vtoroe chislo:\n";
14. std::cin >> m;
15. std::cout << "NOD raven "<< nod(m, n) << "\n";
16. return 0;
17. }

Результат работы программы представлен на рисунке 9.

Рисунок 9 – Результат работы программы.

Рассмотрим реальную задачу из экономической теории.

Одной и наиболее востребованной операцией в экономической сфере является расчет процентов по вкладу. Пример задачи: вкладчик положил в банк сумму в sum денежных единиц под pr процентов за один период времени (год, месяц, неделя и т.д.). Составить программу, возвращающую величину вклада по истечении m периодов времени (m = 24).

Для чего человек несет свои сбережения в банк? Конечно же, чтобы обеспечить их сохранность, и самое главное - получить доходы. И вот здесь знание формулы простых или сложных процентов, а также умение составить предварительный расчет процентов по депозиту как никогда пригодится. Ведь прогнозирование процентов по вкладам или процентов по кредитам относится к одной из составляющих разумного управления своими финансами. Такое прогнозирование хорошо осуществлять до подписания договоров и совершения финансовых операций, а также в периоды очередного начисления процентов и причисления их к вкладу по уже оформленному депозитному договору.

Воспользуемся источником [11], для составления методики расчета.

Для начисления процентов по вкладам (депозитам), да и кредитам тоже, применяются следующие формулы:

- формула простых процентов;

- формула сложных процентов.

Порядок начисления процентов по вышеперечисленным формулам осуществляется с использованием фиксированной или плавающей ставки. Чтобы не возвращаться к данному вопросу в дальнейшем, сразу поясним значение слов и отличия фиксированной ставки и плавающей ставки.

Фиксированная ставка, это когда установленная по вкладу банка процентная ставка, закреплена в депозитном договоре и остается неизменной весь срок вложения средств, т.е. фиксируется. Такая ставка может измениться только в момент автоматической пролонгации договора на новый срок или при досрочном расторжении договорных отношений и выплате процентов за фактический срок вложения по ставке «до востребования», что оговаривается условиями.

Плавающая ставка, это когда первоначально установленная по договору процентная ставка может меняться в течение всего срока вложения. Условия и порядок изменения ставок оговариваются в депозитном договоре. Процентные ставки могут изменяться: в связи с изменениями ставки рефинансирования, с изменением курса валюты, с переходом суммы вклада в другую категорию, и другими факторами.

Для начисления процентов с применением формул, необходимо знать параметры вложения средств на депозитный счет, а именно:

- сумму вклада (депозита);

- процентную ставку по выбранному вкладу (депозиту);

- цикличность начисления процентов (ежедневно, ежемесячно, ежеквартально и т.д.);

- срок размещения вклада (депозита);

- иногда требуется и вид используемой процентной ставки - фиксированной или плавающей.

Теперь рассмотрим названные выше стандартные формулы процентов, которые применяются для расчета процентов по вкладам (депозитам).

1. Формула простых процентов.

Формула простых процентов применяется, если начисляемые на вклад проценты причисляются к вкладу только в конце срока депозита или вообще не причисляются, а переводятся на отдельный счет, т.е. расчет простых процентов не предусматривает капитализации процентов.

При выборе вида вклада, на порядок начисления процентов стоит обращать внимание. Когда сумма вклада и срок размещения значительные, а банком применяется формула простых процентов, это приводит к занижению суммы процентного дохода вкладчика. Формула простых процентов по вкладам выглядит так:

(7)

где S — сумма денежных средств, причитающихся к возврату вкладчику по окончании срока депозита. Она состоит из первоначальной суммы размещенных денежных средств, плюс начисленные проценты;

I – годовая процентная ставка;

t – количество дней начисления процентов по привлеченному вкладу;

K – количество дней в календарном году (365 или 366);

P – первоначальная сумма привлеченных в депозит денежных средств;

Sp – сумма процентов (доходов).

2. Формула сложных процентов.

Формула сложных процентов применяется, если начисление процентов по вкладу, осуществляется через равные промежутки времени (ежедневно, ежемесячно, ежеквартально) а начисленные проценты причисляются к вкладу, т. е. расчет сложных процентов предусматривает капитализацию процентов (начисление процентов на проценты).

Большинство банков, предлагают вклады с поквартальной капитализацией (Сбербанк России, ВТБ и т. д.), т.е. с начислением сложных процентов. А некоторые банки, в условиях по вкладам предлагают капитализацию по окончанию срока вложения, т.е. когда вклад пролонгируется на следующий срок, что, мягко говоря, относится к рекламному трюку, который подталкивает вкладчика не забирать начисляемые проценты, но само начисление процентов фактически осуществляется по формуле простых процентов. И повторюсь, когда сумма вклада и срок размещения значительные, такая «капитализация» не приводит к увеличению суммы процентного дохода вкладчика, ведь начисления процентов на полученные в предыдущих периодах процентные доходы нет.

Формула сложных процентов выглядит так:

(8)

где I – годовая процентная ставка;

j – количество календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов;

K – количество дней в календарном году (365 или 366);

P – первоначальная сумма привлеченных в депозит денежных средств;

n — количество операций по капитализации начисленных процентов в течение общего срока привлечения денежных средств;

Sp – сумма процентов (доходов).

При начислении процентов необходимо учитывать и еще один маленький нюанс. При определении количества дней начисления процентов по вкладу (t) или количества календарных дней в периоде, по итогам которого банк производит капитализацию начисленных процентов (j), не учитывается день закрытия (снятия) вклада. Так, например, 02.11.17 банк принял депозит сроком на 7 дней. Полный срок депозита с 02.11.17 по 09.11.17, т.е. 8 календарных дней. А период начисления процентов по депозиту будет с 02.11.17 по 08.11.17, т.е. – 7 календарных дней. День 09.11.17 в расчет не принимается т.к. депозит возвращен клиенту.

Исходный кол:

1. #include <iostream>
2. #include <windows.h>
3. using namespace std;
4. double rec_fun(double sum, double per, int m, int i)
5. {
6. if(m==i)
7. return sum;
8. sum+=(sum/100.)*per;
9. return rec_fun(sum, per, m, i+1);
10. }
12. int main ()
13. {
14. int m;
15. double sum, per;
16. SetConsoleCP(1251);
17. SetConsoleOutputCP(1251);
18. cout<<"Введите начальную сумму вклада (например: 124.34): "<< endl;
19. cin>>sum;
20. cout<<"Введите ежемесячный процент начисления по вкладу (например: 12.42): "<< endl;
21. cin>>per;
22. cout<<"Введите количество месяцев: "<< endl;
23. cin>>m;
24. cout<<"За "<<m<<" месяцев сумма вклада составит: "<<rec_fun(sum, per, m, 0)<<endl;
25. return 0;

Результат работы программы представлен на рисунке 10.

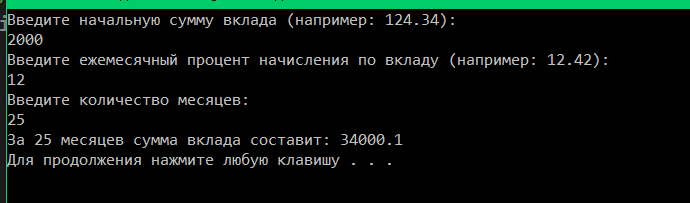
Рисунок 10 – Результат работы программы.

ЗАКЛЮЧЕНИЕ

В результате работы над курсовой работой было исследовано понятие рекурсии и итерационных алгоритмов.

В первой главе было показано, что рекурсивные алгоритмы есть распространенное средство решения разнообразных алгоритмических проблем. Любая разрешимая задача такого рода имеет рекурсивное решение, которое при этом отличается изяществом и простотой для восприятия человеком, но при этом имеет набор недостатков.

Во второй главе рассмотрены итерационные алгоритмы, как средство нахождения корней уравнения методом хорд.

В третей главе представлен практический результат использования итерационных алгоритмов, а в четвертой результат использования рекурсивных алгоритмов.

Общим выводом по проделанной работе является то, что рекурсивные алгоритмы часто имеют более низкую асимптотическую сложность, чем эквивалентные им итерационные. То есть теоретически они быстрее и развитие современных программных средств сделало практическое использование рекурсии достаточно несложным делом, а новые концепции и технологии программирования преодолели проблему низкой эффективности рекурсивных и итерационных программ.

Рекурсия отражает черту абстрактного мышления, проявляющуюся в самых различных приложениях (в математике, синтаксическом анализе и трансляции, древовидной сортировке и обработке данных с динамической структурой, шахматных задачах и т.д.). Именно в задачах такого рода лучше применять рекурсивные алгоритмы, так как они, избавляют от необходимости последовательного описания процессов, к тому же, большинство языков программирования поддерживают рекурсию.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1. Основы алгоритмизации и программирования: учеб. пособие / Т.А. Жданова, Ю.С. Бузыкова. – Хабаровск : Изд-во Тихоокеан. гос.ун-та, 2011. – 56 с. Режим доступа:

http://pnu.edu.ru/media/filer_public/2013/02/25/book_basics.pdf.

2. Программирование и основы алгоритмизации: Для инженерных специальностей технических университетов и вузов. /А.Г. Аузяк, Ю.А. Богомолов, А.И. Маликов, Б.А. Старостин. Казань: Изд-во Казанского национального исследовательского технического ун-та - КАИ, 2013, 153 с. Режим доступа: http://au.kai.ru/documents/Auzyak_Progr_osn_alg_C_2013.pdf.

3. Основы алгоритмизации и программирования : учебное пособие / Г.Р. Кадырова. – Ульяновск : УлГТУ, 2014. – 95 с. . Режим доступа:

http://venec.ulstu.ru/lib/disk/2014/137.pdf

4. Основы алгоритмизации и программирования. Курс лекций. Режим доступа: http://lib.ssga.ru/fulltext/UMK/исходные%20для%20Кацко/заменить%20полностью/Информатика/лекции/13%20Основы%20алгоритмизации%20и%20программирования.pdf

5. Белов П.М. Основы алгоритмизации в информационных системах: Учебн. Пособие.- Спб.: СЗТУ, 2003. – 85с. Режим доступа:

http://www.ict.edu.ru/ft/005406/nwpi225.pdf

6. Основы алгоритмизации и программирования: Метод. указ. / Сост.: И.П. Рак, А.В. Терехов, А.В. Селезнев. Тамбов: Изд-во Тамб. гос. техн. ун-та. Режим доступа: http://www.ict.edu.ru/ft/004758/terehov.pdf.

7. Макаров В.Л. Программирование и основы алгоритмизации.: учебн. пособие.-Спб., СЗТУ, 2003, - 110с. Режим доступа: http://window.edu.ru/resource/126/25126/files/nwpi223.pdf

8. Сергиевский Г.М. Функциональное и логическое программирование : учеб. пособие для студентов высш. учеб. заведений / Г.М. Сергиевский, Н.Г. Волченков. — М.: Издательский центр «Академия», 2010.- 320с.

9. Миллер, Р. Последовательные и параллельные алгоритмы: Общий подход / Р. Миллер, Л. Боксер ; пер. с англ. — М. : БИНОМ. Лаборатория знаний, 2006. — 406 с.

10. Плис, А.И. Математический практикум для инженеров и программистов[Текст]: Учеб. пособие. – 2-е изд. перераб. и доп. / А.И. Плис, Н.А. Сливина. – М.: Финансы и Статистика, 2003. – 565 с.

11. Формула расчета процентов по вкладам (депозитам). Банкирша.сом - Режим доступа:

https://bankirsha.com/formula-calculate-of-interest-on-deposit.html