
Психологическая готовность к школьному обучению
Содержание:
ВВЕДЕНИЕ
Актуальность темы исследования. Психологическая готовность к школе возникает не ранее 7 лет, на границе дошкольного и младшего школьного возраста по периодизации отечественных психологов. Этот возраст совпадает с кризисом 7 лет. Дошкольники, которых систематически готовят к школьному обучению в ущерб традиционным детским занятиям, оказываются не только психологически не готовы к школе, но и недостаточно психически развиты. К концу дошкольного детства складывается важнейшее новообразование в психике ребенка - готовность к школьному обучению. Оно обеспечивает переход к позиции школьника, которая предполагает не только усвоение знаний, но и кардинальную перестройку всего образа жизни ребенка. Готовность включает в себя несколько компонентов: личностный, познавательный, коммуникативный. К 6-7 годам формируются общее положительное отношение к школе, интерес к школьному содержанию занятий, признание авторитета учителя, развиваются познавательные интересы, появляются собственно учебные мотивы деятельности. Все это составляет новообразование личности и самосознания ребенка - внутреннюю позицию, которая выражается в стремлении к поступлению в школу.
Проблема психологической готовности к школьному обучению широко разрабатывается в трудах отечественных и зарубежных психологов (Л. И. Божович, А. Н. Леонтьев, Д. Б. Эльконин, А. Л. Венгер, Н. И. Гуткина, Е. Е. Кравцова, Н. Г. Салмина, Й. Йирасек, Г. Витцлак, Ж. Пиаже и др.). Специалисты в области возрастной психологии (Л. С. Выготский, Е. Е. Кравцова, Н. Г. Салмина, М. И. Лисина, Н. Н. Поддьяков и др.) считают, что о готовности ребенка к школе следует судить по критериям, которые отражают особенности его психики в целом и являются новообразованиями, возникшими в его игровой деятельности, но подготовившими переход к учебной.
Целью курсовой работы является исследование формирования готовности детей к школе
Задачи:
1. Формирование готовности детей к обучению в школе: теоретические аспекты
2. Исследовать формирования готовности детей к обучению в школе на примере ДОУ "Эрудит"
1. Формирование готовности детей к обучению в школе: теоретические аспекты
1.1 Понятие готовности ребёнка к обучению в школе. Основные теоретические подходы в рассмотрении проблемы подготовки детей к школе
Одним из важных вопросов вступления ребёнка в школьную жизнь является его готовность к школе. В настоящее время существует большое количество определений и классификаций готовности ребёнка к обучению в школе. Наиболее основательной нам представляется классификация, предложенная Р.В. Овчаровой [8]. Она выделяет специальную, психологическую и физическую готовность. К психологической относит: личностную и социально-психологическую, интеллектуальную, эмоционально-волевую. В нашей работе мы рассмотрим психологическую готовность к обучению в школе.
Большой интерес к этому вопросу связан с тем, что готовность к школьному обучению – это важнейшее новообразование дошкольного возраста. Являясь итогом развития ребёнка на протяжении первых семи лет жизни, она обеспечивает переход к позиции школьника и выступает необходимым фундаментом для усвоения школьной программы.
В историческом аспекте проблема готовности к обучению первоначально рассматривалась как проблема педагогическая. Педагоги занимались рассмотрением этой проблемы с тех пор, как появились общественные учебные заведения (Я.А. Коменский, К.Д. Ушинский, А.С. Симонович и др.)
Одним из первых к проблеме формирования готовности детей к школе обратился Я.Коменский [10]. Он считал, что систематическое школьное обучение следует начинать с семилетнего возраста, если у ребёнка сформированы прочные знания в различных областях окружающего мира: математике, грамматике, географии; способность к логическому рассуждению, умение правильно ставить вопросы и давать точные ответы; интерес к школе и учебной деятельности. К.Ушинский [21] также в своих работах писал о том, что основные направления подготовки к началу систематического обучения должны способствовать развитию у ребёнка способности сосредоточивать внимание на одном предмете, слушать то, что ему говорят, выражать свои мысли полными предложениями.
Но ни Я.Коменский, ни К.Ушинский, ни другие педагоги понятие «готовность к обучению» не вводили. Впервые понятие «психологическая готовность к обучению» было предложено А.Н.Леонтьевым.
А.Леонтьев считал, что основой психологической готовности является «управляемое» поведение, то есть не просто закреплённое в навыке, а сознательно контролируемое поведение. Этот контроль, по А.Леонтьеву, не требует специально направленного внимания. «Ученик должен вести себя на уроке надлежащим образом – правильно сидеть за партой, не вертеться не болтать ногами, словом, ни на минуту «не забываться», как бы ни было поглощено его внимание тем, что рассказывает учитель в классе» [13].
Согласно А.Леонтьеву, «управляемое» поведение предполагает три момента:
- чтобы действия ребёнка направлялись мотивами;
- чтобы в поведении устанавливалась иерархия мотивов, их соподчинение;
- чтобы важные, общественно ценные мотивы стали сильнее и подавляли бы, подчиняли случайные побуждения и желания.
Проблема готовности к школе изучалась как у нас в стране, так и за рубежом.
У зарубежных авторов, изучающих школьную зрелость нет чёткого и однозначного определения этого понятия. Так, по мнению А.Анастази [1], школьная зрелость представляет собой овладение умениями, знаниями, способностями и другими поведенческими характеристиками, необходимыми для оптимального уровня усвоения школьной программы.
Й. Шванцара более ёмко определяет школьную зрелость – как достижение такой степени в развитии, когда ребёнок «становится способным принимать участие в школьном обучении». В качестве компонентов готовности к обучению в школе Й. Шванцара выделяет умственный, социальный и эмоциональный компоненты. По мнению С. Штребела [23] и А.Керна, поступающий в школу ребёнок должен быть зрелым в умственном, эмоциональном и социальном отношениях. Они выделяют несколько признаков, определяющих выделенные ими компоненты школьной зрелости. С.Штребел и А.Керн считают, что об интелектуальной зрелости можно судить по следующим признакам:
- дифференцированное восприятие (перцептивная зрелость), включающее выделение фигуры и фона;
- концентрация внимания ;
- аналитическое мышление, выражающееся в способности постижения основных связей между явлениями;
- логическое запоминание;
- сенсомоторная координация;
- умение воспроизводить образец;
- развитие тонких движений руки.
Об эмоциональной зрелости говорят:
- уменьшение импульсивных реакций;
- возможность длительное время выполнять не очень привлекательное занятие.
О социальной зрелости свидетельствуют:
- потребности ребёнка в общении со сверстниками и умение подчинять своё поведение законам детских групп;
- способность исполнять роль ученика в ситкации школьного обучения.
По мнению Я.Йирасека, достижение школьной зрелости во всех компонентах психологической структуры зависит от факторов, которые оказывают воздействие на соматическое и психическое развитие ребёнка.
Это органические (стимулирующий характер среды, эмоциональная атмосфера, собственно психическая активность, систематическое воспитание и обучение) факторы.
Таким образом, можно сказать, что в рассмотренных выше работах зарубежных психологов ребёнок, готовый к школе, представляет не только как обладающий достаточным для усвоения школьной программы набором знаний и умений, но и как способный взаимодействовать в группе сверстников, подчиняться требованиям школьного распорядка и учителя. То есть поступающий в школу ребёнок, по мнению зарубежных психологов, обладает достаточной социальной, интелектуальной и эмоциональной зрелостью.
1.2 Готовность ребёнка к школе
Готовность к школе – это не «программа», которой можно просто обучить (натренировать). Скорее, это интегральное свойство личности ребёнка, которое развивается при общих благоприятных условиях в многообразных ситуациях жизненного опыта и общения, в которые включен ребёнок в семье и других социальных группах. Она развивается не путём специальных занятий, а непрямым образом – через «участие в жизни».
Если мы вспомним требования, которые предъявляет к ребёнку школьная жизнь, и постараемся проанализировать компетентности, которыми должен обладать ребёнок, то их можно сгруппировать в четыре большие группы.
Эмоциональная готовность к школе подразумевает совокупность качеств, которые позволяют ребёнку преодолевать эмоциональную неуверенность, различные блокады, которые мешают воспринимать учебные импульсы или ведут к тому, что ребёнок замыкается в себе.
Понятно, что не со всеми заданиями и ситуациями ребёнок может справиться легко. Трудные задания, а также объяснения учителя могут вызывать у ребёнка ощущения: «с этим я никогда не справлюсь» или «я не понимаю вообще, чего она (учительница) от меня хочет». Подобные переживания могут быть нагрузкой на детскую психику и привести к тому, что ребёнок вообще перестает верить в свои силы и прекращает активно учиться. Устойчивость к подобным нагрузкам, умение конструктивно обходиться с ними — важная составная часть эмоциональной компетентности.
Когда ребёнок что-то знает, хочет показать свои знания и тянет руку, то, естественно, не всегда получается так, что его действительно вызывают. Когда учитель вызывает другого, а ребёнок хочет непременно показать свои знания, это может стать сильным разочарованием. Ребёнок может подумать: «Если меня не вызывают, то и стараться не стоит» – и перестать активно принимать участие на уроках. В школьной жизни существуют самые разные ситуации, в которых ему приходится испытывать разочарования. На эти ситуации ребёнок может реагировать пассивностью или агрессией. Умение адекватно переносить разочарования и справляться с ними – еще одна сторона эмоциональной компетентности.
Социальная готовность к школе тесно связана с эмоциональной. Школьная жизнь включает в себя участие ребёнка в различных сообществах, вступление и поддерживание многообразных контактов, связей и отношений.
Прежде всего это сообщество класса. Ребёнок должен быть готов к тому, что он не сможет больше следовать только своим желаниям и импульсам независимо от того, мешает ли он благодаря своему поведению другим детям или учителю. От отношений в классном сообществе во многом зависит, насколько ваш ребёнок сможет успешно воспринимать и перерабатывать учебный опыт, то есть извлекать из него пользу для своего развития.
Представим себе это более конкретно. Если каждый, кто хочет что-то сказать или задать вопрос, будет в ту же минуту говорить или спрашивать, возникнет хаос, и никто никого не сможет слушать. Для нормальной продуктивной работы важно, чтобы дети слушали друг друга, давали бы собеседнику договорить до конца. Поэтому способность воздерживаться от собственных импульсов и выслушивать других – это важный компонент социальной компетентности.
Важно, чтобы ребёнок мог чувствовать себя членом группы, группового сообщества, в случае школьного обучения – класса. Учитель не может обращаться к каждому ребёнку в отдельности, но обращается ко всему классу. В этом случае важно, чтобы каждый ребёнок понимал и чувствовал, что учитель, обращаясь к классу, обращается и лично к нему. Поэтому чувствовать себя членом группы – это еще одно важное свойство социальной компетентности.
Дети все разные, с разными интересами, импульсами, желаниями и т.д. Эти интересы, импульсы и желания должны реализовываться сообразно ситуации и не в ущерб другим. Для того чтобы разнородная группа смогла успешно функционировать, создаются различные правила общей жизни. Поэтому к социальной готовности к школе относится способность ребёнка понимать смысл правил поведения и обхождения людей друг с другом и готовность следовать этим правилам.
К жизни любой социальной группы относятся конфликты. Жизнь класса не представляет здесь исключения. Дело не в том, появляются ли конфликты или нет, а в том, как они решаются. Важно научить их другим, конструктивным моделям решения конфликтных ситуаций: говорить друг с другом, вместе искать решения конфликтов, привлекать третьих лиц и т.д. Способность конструктивно решать конфликты и социально приемлемо вести себя в спорных ситуациях является важной частью социальной готовности ребёнка к школе.
Моторная готовность к школе. Под моторной готовностью к школе понимается не только то, насколько ребёнок владеет своим телом, но и его способность воспринимать свое тело, ощущать и произвольно направлять движения (владеть внутренней подвижностью), выражать при помощи тела и движения свои импульсы.
Когда говорят о моторной готовности к школе, то имеют в виду координацию системы «глаз–рука» и развитие тонкой моторики, необходимой для обучения письму. Здесь надо сказать, что скорость овладения движениями руки, связанными с письмом, может быть у разных детей различной. Это связано с неравномерным и индивидуальным созреванием соответствующих участков головного мозга человека. Многие современные методики обучения письму учитывают этот факт и не требуют от ребёнка с самого начала мелкого письма в разлинованных тетрадях со строгим соблюдением границ. Дети сначала «пишут» буквы и «рисуют» формы в воздухе, потом – карандашом на больших листах, и лишь на следующем этапе переходят к написанию букв в тетрадях. Такой щадящий метод учитывает, что ребёнок может поступить в школу, имея недостаточно развитую руку. Однако в большинстве школ до сих пор требуют писать сразу маленьким шрифтом (по прописи) и соблюдать соответствующие границы. Это для многих детей сложно. Поэтому хорошо, если уже до школы ребёнок овладел до известной степени движением руки, кисти и пальцев. Владение тонкой моторикой является важной характеристикой моторной готовности ребёнка к школе.
Проявление воли, собственной инициативы и активности во многом зависит от того, насколько ребёнок владеет своим телом в целом и способен выразить свои импульсы в форме телесного движения.
Участие в общих играх и радость от движения – это нечто большее, чем способ утверждения себя в детском коллективе (социальные отношения). Дело в том, что учебный процесс протекает ритмически. Периоды концентрации, внимания, работы, требующей известного напряжения, должны сменяться периодами активности, приносящими радость и отдых. Если ребёнок не может полноценно проживать такие периоды телесной активности, то нагрузка, связанная с учебным процессом, и общее напряжение, связанное со школьной жизнью, не смогут найти полноценного противовеса. Вообще развитость так называемой «крупной моторики», без которой ребёнок не может прыгать через скакалку, играть в мяч, держать равновесие на перекладине и т.д., а также получать удовольствие от разных видов движения, является важной составной частью готовности к школе.
Восприятие собственного тела и его возможностей («Это я могу, я сумею с этим справиться!») сообщает ребёнку общее позитивное ощущение жизни. Позитивное чувство жизни выражается в том, что детям доставляет удовольствие воспринимать препятствия, преодолевать трудности и испытывать свои умения и ловкость (забираться на деревья, прыгать с высоты и т.д.). Уметь адекватно воспринимать препятствия и взаимодействовать с ними – важная составная часть моторной готовности ребёнка к школе.
Когнитивная готовность к школе, которая долгое время считалась и до сих пор многими считается основной формой готовности к школе, играет хоть и не основную, но все же весьма существенную роль.
Важно, чтобы ребёнок мог некоторое время концентрироваться на какой-либо задаче и выполнять ее. Это не так-то просто: в каждый момент времени мы подвержены воздействиям раздражителей самого различного рода. Это шумы, оптические впечатления, запахи, другие люди и т.д. В большом классе постоянно происходят какие-либо отвлекающие события. Поэтому способность некоторое время концентрироваться и удерживать внимание на поставленной задаче является важнейшей предпосылкой успешного обучения. Считается, что хорошая концентрация внимания развита у ребёнка, если он может в течение 15–20 минут внимательно выполнять поставленную перед ним задачу, не утомляясь.
Учебный процесс устроен так, что при объяснении или демонстрации каких-либо явлений часто возникает необходимость связать то, что происходит в данный момент, с тем, что объяснялось или демонстрировалось недавно. Поэтому наряду со способностью внимательно слушать необходимо, чтобы ребёнок запоминал услышанное и увиденное и хотя бы некоторое время удерживал это в памяти. Поэтому способность к краткосрочной аудитивной (слуховой) и визуальной (зрительной) памяти, позволяющей мысленно переработать поступающую информацию, является важной предпосылкой успеха учебного процесса. Само собой разумеется, что слух и зрение тоже должны быть хорошо развиты.
Дети с удовольствием занимаются тем, что им интересно. Поэтому, когда тема или задание, которое дает учитель, соответствует их склонностям, тому, что им нравится, проблем не возникает. Когда же им неинтересно, они часто просто ничего не делают, начинают заниматься своими делами, то есть перестают учиться. Однако требовать от учителя, чтобы он предлагал детям только интересные для них темы, интересные всегда и для всех, совершенно нереально. Что-то для одних детей интересно, для других же нет. Невозможно, да и неправильно строить все преподавание исключительно на основе интереса ребёнка. Поэтому школьное обучение всегда содержит такие моменты, когда детям приходится делать что-то, что им неинтересно и скучно, по крайней мере сначала. Предпосылкой того, что ребёнок будет заниматься содержанием, которое для него поначалу чуждо, является общий интерес к учению, любопытство и любознательность по отношению к новому. Такое любопытство, любознательность, желание учиться и чему-то научиться является важной предпосылкой успешного обучения.
Учение – это в значительной мере систематическое накопление знаний. Такое накопление может протекать по-разному. Одно дело, когда я запоминаю отдельные элементы информации, не связывая их между собой, не пропуская их через индивидуальное понимание. Это ведет к механическому заучиванию. Такая стратегия обучения опасна, так как может стать привычкой. К сожалению, приходится констатировать, что в последние годы увеличилось количество студентов вузов, понимающих обучение именно так – как механическое воспроизведение непонятого материала, определений, схем и конструкций без всякой взаимосвязи, в отрыве от отношения к реальности. Такое «знание» не служит развитию мышления и личности в целом, быстро забывается.
Причина этого – неправильные привычки учения, закрепленные школьным обучением. Стратегия зубрежки (механического заучивания) устанавливается тогда, когда ребёнку предлагается материал, который он еще не может понять, или в результате непродуманной методики, не учитывающей актуального уровня развития ребёнка. Важно, чтобы знания, которые ребёнок получает в школе и вне школы, складывались в разветвленную сеть взаимосвязанных элементов, пропущенных через индивидуальное понимание. В этом случае знание служит развитию и может быть применено в естественных ситуациях. Такое знание является непременной составной частью компетентности – умения успешно справляться с проблемами в различных ситуациях жизни. Интеллигентное знание выстраивается шаг за шагом не только в процессе школьного обучения, но и из многообразной информации и опыта, получаемого ребёнком вне стен школы.
Для того чтобы ребёнок мог получаемую информацию интегрировать в уже имеющуюся и выстраивать на ее основе разветвленную сеть взаимосвязанных знаний, необходимо, чтобы он к моменту обучения уже владел начатками логического (последовательного) мышления и понимал взаимосвязи и закономерности (выражаемые словами «если», «то», «потому что»). При этом речь идет не о каких-то специальных «научных» понятиях, а о простых взаимосвязях, встречающихся в жизни, в языке, в человеческой деятельности. Если мы утром видим, что на улице лужи, то естественно заключить, что ночью шел дождь или рано утром улицу полила поливальная машина. Когда мы слышим или читаем какую-то историю (сказку, рассказ, слышим сообщение о событии), то в этой истории отдельные высказывания (предложения) выстраиваются во взаимосвязанную нить благодаря языку. Язык сам по себе логичен.
И, наконец, наши повседневные действия, употребление простых орудий в домашнем хозяйстве тоже подчиняются логической закономерности: для того чтобы налить воду в чашку, мы ставим чашку дном вниз, а не вверх и т.д. Логические связи в природных явлениях, языке и повседневных действиях являются согласно современной логике и психологии основанием логических законов и их понимания. Поэтому способность к последовательному логическому мышлению и пониманию взаимосвязей и закономерностей на уровне обыденной жизни является важной предпосылкой когнитивной готовности ребёнка к обучению.
Представим теперь все названные нами элементы в виде общей таблицы «базовых компетентностей» готовности к школе.
Возникает вопрос: должен ли ребёнок обладать всеми этими качествами в полной мере, чтобы быть «готовым к школе»? Детей, которые бы полностью соответствовали всем описанным характеристикам, практически не бывает. Но готовность ребёнка к школе все-таки можно определить.
Таблица 1.1 Эмоциональная готовность к школе
|
Эмоциональная готовность к школе: · Способность выдерживать нагрузки; · Способность выдерживать разочарования; · Не бояться новых ситуаций; · Уверенность в себе и своих силах |
Социальная готовность к школе: · Умение слушать; · Чувствовать себя членом группы; · Понимать значение правил и умение соблюдать их; · Конструктивно решать конфликтные ситуации |
|
Полезность парных сравнений. Прокоп О.М. Научный руководитель проф. На множестве элементов Х={х1,...,хт} определена семья отношений преобладания ={,,,,}, первым из которых является отношение «не хуже» (). Функция полезности удовлетворяет условию:). Это означает, что элемент x1X не хуже элемента x2X, если полезность f(x1) элемента х1 не меньше полезности f(x2) элемента х2. Таким образом, функция полезности f отображает отношение преобладания на множестве X. Можно убедиться, что она отображает и все другие отношения семьи . В частности, отображение основных отношений «равноценно» () и «лучшее» ():),). Всегда ли бинарное отношение преобладания можно отобразить функцией? Утвердительный ответ для счетного множества дал Кантор, а для несчетного – Милграм и Биркгоф. Очень важную теорему доказал Дебре: отношение преобладания «не хуже» на компактном множестве XRn можно отобразить функцией полезности, если оно непрерывно на X. Если множество допустимых элементов X представляет собой компакт в Rn, то непрерывная на этом множестве функция достигает наибольшего значения (теорема Вейєрштрасса). Множество элементов, доставляющих максимум функции f на множестве X, не пусто. Поскольку эти элементы являются максимальными по отношению преобладания , что отображается функцией полезности f, то множество преобладающих элементов не пусто. Вместе с функцией ценности f все отношения преобладания семьи отображает другая функция, полученная возрастающим преобразованием. Если u=f(х), хX – функция полезности, а v=g(и) – возрастающая функция переменной u, то сложная функция v=g(f(x)), хX также является функцией полезности. Функция полезности, заданная с точностью до произвольного монотонно возрастающего преобразования, называется порядковой. Если же функция полезности задана с точностью до произвольного положительного линейного преобразования v=f(x)+, где ,>0, ее называют интервальной. Особенность интервальной функции полезности состоит в том, что она (в отличие от порядковой) позволяет не только определять, что один элемент преобладает над другим, а и то, как различаются элементы по преобладанию. Если функция полезности f положительна и задана с точностью до любого множителя , то есть w=f(x), >0, то ее называют относительной. Она показывает, в сколько раз один элемент преобладает над другим. При сравнении двух элементов xі и xj множества важно знать, в какой степени один элемент преобладает над другим. Если при сравнении элемента xі с элементом xj первый элемент получил указанный в таблице 1 ранг, то другой элемент получает ранг, обратный к рангу первого элемента. Таблица 1. Шкала относительной важности объектов Степень важности Определение 1 Объекты равноценны 3 Объект немного лучше другого 5 Объект лучше другого 7 Объект намного лучше другого 9 Объект гораздо лучше другого 2,4,6,8 Промежуточные суждения По результатам парных сравнений образуем mm-матрицу A=(aij), элемент которой aij дает оценку преобладания элемента хi в сравнении с элементом xj (i,j=1,…,т). Пусть (w1,...,wт) – набор истинных полезностей элементов множества X. Если парные сравнения будут взаимно согласованы, должны выполняться соотношения aij=wi/wj для i,j=1,…,т. Это означает, что аii=1 и аji=1/aij для i,j=1,…,т. Последнее соотношение означает, что если элемент xі лучше элемента xj в >1 раз, то полезность xj составит 1/ часть от ценности xj. Взаимная согласованность парных сравнений означает также, что должны выполняться соотношения аij=akj/aki для i,j,k=1,…,m. Если хk лучше хi в раз, а хi лучше xj в раз, то хk лучше xj в раз. Для заполнения матрицы A достаточно задать одну строку (один столбец). В самом деле, если заполнена первая строка этой матрицы (а11,...,а1i,...,а1т), то ее i-ая строка (i=2,…,т) заполняется по правилу aij=a1j/a1i (j=1,…,n). При полной согласованности элементов выполняется соотношение: Вектор относительной полезности (w1,…,wm)T – собственный вектор матрицы А для ее собственного значения =т. Для согласованной матрицы – это наибольшее собственное значение (спектральный радиус матрицы), а другие собственные значения равны нулю. Это свойство согласованных парных сравнений можно использовать в случае, если допущены ошибки. После построения матрицы парных сравнений относительные полезности элементов можно получить как компоненты собственного вектора w для собственного значения max. Чем ближе max к т, тем лучше согласованы парные сравнения элементов. Индекс согласованности (индекс Саати). Если значение индекса меньше 10 % от эталонных значений таблицы 2, то результаты парного сравнения считают удовлетворительными. Если значение индекса больше 10 %, то результаты считают неудовлетворительными, и тогда нужно уточнить оценки относительной важности элементов в парных сравнениях. Таблица 2. Эталонные значения индекса согласованности. Способ приближенного вычисления относительной полезности элементов состоит в использовании среднего геометрического элементов каждой строки матрицы:, i=1,…,m. Предположим, что вы решаете, в каком кафе провести свободное время. Выбор ограничен тремя кафе 1, 2 и 3. Они обеспечивают качественное обслуживание клиентов. В кафе 1 свободен доступ в «Интернет», а в кафе 3 много посетителей. Кафе 2 находится ближе к вашему дому. Результаты парного сравнения кафе: <1:2>=3 – есть некоторые основания считать кафе 1 лучше кафе 2; <1:3>=7 – уровень обслуживания в кафе 1 значительно лучше, чем в кафе 3; <2:3>=3 – уровень обслуживания в кафе 2 и 3 почти одинаков, но число посетителей в кафе 2 меньше, и оно расположено ближе к дому. По этим результатам составляем матрицу парных сравнений:. По методу среднего геометрического, находим,,. Оценим собственное значение, которому отвечает этот вектор полезностей. Для этого вычислим произведение. Чтобы оценить max, делим покомпонентно вектор Аw=(2,013;0,73;0,264)T на вектор относительных полезностей w=(0,669;0,243;0,088)T. Получим вектор (3,007;3,007;3,007)T. Собственное значение:. Индекс согласованности. составляет 0,6 % от эталонного значения показателя согласованности:. Уровень согласованности достаточно высок, а относительными полезностями кафе 1, 2 и 3 можно считать: w1=0,669; w2=0,243; w3=0,088. Если принять <1:2>=3 – есть основания считать кафе 1 лучше кафе 2; <1:3>=9 – уровень обслуживания в кафе 1 гораздо лучше, чем в кафе 3; <2:3>=3 – есть основания считать кафе 2 лучше кафе 3, то согласие парных сравнений полное max=3 и J=0: w1=0,692; w2=0,231; w3=0,077. При большом числе объектов этот метод слишком громоздок, что присуще всем методам, основанным на парном сравнении элементов. 2. Потоки и запасы В экономике три категории агентов: предприятия E, домохозяйства H и все другие агенты V. Агенты E производят товары и услуги. Агенты H их потребляют. Агенты V оказывают услуги по распределению созданных благ. Стоимость произведенной в стране конечной продукции равна расходам по ее приобретению, а валовой внутренний продукт (ВВП) можно получить как сумму конечных расходов Y=C+I (C – потребление, I – инвестиции). Добавленная стоимость – доходы агентов, а ВВП равен сумме факторных доходов Y=L+K (L и K – оплата труда и капитала). Плата за капитал включает амортизационные расходы, арендную плату, проценты, страховку и прибыль. Потоки Y, C и I связывают агентов с рынком товаров и услуг MP. Другие потоки связывают их с рынком ресурсов MR и другими рынками M. Отобразим агентов и рынки вершинами графа, потоки – дугами. Модель взаимодействия агентов E, H и V на рынках MP, MR и M дана на рис.1. Доход MP|E=Y предприятия E получают на рынке товаров и услуг MP, где H и V несут расходы C(MP|H) и I(MP|F). Домохозяйства получают доход R(MR|H) на рынке ресурсов MR, где предприятия несут расходы L(E|MR). Другие агенты V получают доход W(M|V) на рынках M, где несут расходы предприятия K(E|M) и домохозяйства S(H|M). Условия баланса рынков, и. Условия баланса агентов, и. Здесь I – инвестиции в товары и услуги, Q – инвестиции в ресурсы. Рис.1. Потоки доходов и расходов. Направленный граф рис.1 на шести вершинах содержит девять дуг потоков. Если удалить вершину графа V и инцидентные ей дуги, оставшаяся часть графа не сбалансирована. Удаленная часть графа становится деревом графа, если ее дополнить дугами V|E и V|H с нулевыми потоками. На рис.2 ветви дерева изображены пунктирными линиями, а хорды дополнения дерева – сплошными линиями. Множество дуг замкнутого графа – объединение его ветвей и хорд. Для графа рис.2 вектор потоков ветвей Ib=(I,Q,–W,0,0), а запасы ветвей Vb=(I,Q,W,0,0). Потоки хорд Ic=(Y,R,L,C,K,S). Матрица потоков хорд Icc=diag(Ic). Рис.2. Дерево графа и его дополнение. Топологические свойства дополнения дерева описывают матрицы инцидентности таблиц 1. Элемент матрицы Dbc равен 1, если i-ая вершина начальная для j-ой хорды, и 0 в противном случае. Элемент матрицы Cbc равен 1, если i-ая вершина конечная для j-ой хорды, и 0 в противном случае. Унимодулярная матрица инцидентности Abc=Cbc–Dbc. Таблица 1. Матрицы инцидентности дополнения дерева. Dbc MP|E MR|H E|MR H|MP E|M H|M Cbc MP|E MR|H E|MR H|MP E|M H|M MP 1 0 0 0 0 0 MP 0 0 0 1 0 0 MR 0 1 0 0 0 0 MR 0 0 1 0 0 0 MF 0 0 0 0 0 0 MF 0 0 0 0 1 1 E 0 0 1 0 1 0 E 1 0 0 0 0 0 H 0 0 0 1 0 1 H 0 1 0 0 0 0 Потоки ветвей и запасы хорд и выражают законы Кирхгофа: алгебраическая сумма потоков в вершине графа и запасов в контуре графа равна нулю. Потоки и запасы дуг даны на рис.2. Мощность дуги – произведение ее потока на запас. Дуги с положительной мощностью – ресурсы, дуги с отрицательной мощностью – использования. Мощность ветвей и хорд и. Сравнение дает теорему Тевенина: Mb+Mc=0 – мощность замкнутого графа равна нулю. В таблице 2 представлена матрица потоков и матрица сальдо и. Таблица 2. Матрица проводок и матрица сальдо. Pbb MP MR M E H Sbb MP MR M E H Ib MP 0 0 0 Y 0 MP 0 0 0 Y –C I MR 0 00 0 R MR 0 0 0 –L R Q M 0 0 0 0 0 M 0 0 0 –K –S –W E 0 L K 0 0 E –Y LK 0 0 0 H C0 S 0 0 H C –R S 0 0 0 –Ib –I –Q W 0 0 0 Если I=Y–C>0, то рынок товаров и услуг MP находится в активном состоянии (I – инвестиции в товары и услуги). Если Q=R–L>0, то рынок ресурсов MR находится в активном состоянии (Q – инвестиции в ресурсы). Поскольку W+I+Q=0 и W<0, то рынки M находятся в пассивном состоянии. Агенты E и H сбалансированы. Потоки ресурсов направлены от агентов к рынкам, а потоки использования – от рынков к агентам. Выделяя в матрице потоков Icc потоки использования Ucc и потоки ресурсов Rcc, можно получить матрицу использования и ресурсов. Эта матрица сбалансирована по столбцам, но не сбалансирована по строкам. Чтобы построить граф использования ресурсов, нужно дуги положительных элементов матрицы Qbb направить от рынков к агентам, а отрицательных – от агентов к рынкам. Таблица 3. Матрица использования и ресурсов. Балансовые модели описывают взаимосвязи выходных и входных переменных (потоки или запасы). Сложение добавленной стоимости ячеек производства дает валовой внутренний продукт Y. В системе национальных счетов (СНС) доход предприятий Y=C+I+G равен сумме потребления C, инвестиции I, государственных расходов G (закрытая система) и чистого экспорта NX= EX–IM (открытая система). Если Y – валовой внутренний продукт (GDP), то NX включает только товары и услуги. Если Y – валовой национальный продукт (GNP), то NX включает доход из-за рубежа (YF): GNP=C+I+G+(EX–IM+YF). Валовой национальный доход (доход резидентов, идущий на потребление и накопление) учитывает трансферты из-за рубежа (TRF): GNDI=C+I+G+(EX–IM+YF+TRF). В круглых скобках счет текущих операций NX. Если T – выплачиваемые налоги, то частные сбережения Sp=GNDI–C–T, излишек государственного бюджета BS=T–G, сбережения S=Y–C–G. Макромодель IS-LM связывает Y со ставкой процента R. Кривая IS описывает зависимость дохода от ставки процента при равновесии на рынке товаров и услуг Y=C(Y,T)+I(R)+G+NX(Y,RER). Здесь потребление C зависит от дохода Y и налога T, инвестиция I – от ставки процента, а чистый экспорт NX – от Y и обменного курса RER. Кривая IS имеет отрицательный наклон, так как увеличение ставки R уменьшает инвестиции и снижает доходы. Кривая LM описывает связь Y и R при равновесии на денежном рынке M/P=L(R,Y). Здесь M/P – отношение денежной массы M к уровню цен P (предложение денег), а L(R,Y) – спрос на деньги. Кривая LM имеет положительный наклон, поскольку R и Y оказывают противоположное влияние на денежный спрос. Пересечение кривых IS и LM дает величины Y* и R* при равновесии на товарном и денежном рынке. Кривая BP описывает взаимосвязь Y и R при внешнем равновесии (баланс официальных расчетов). Платежный баланс включает счет текущих операций и счет операций с активами KA: NX=EX(RER)–IM(Y,RER) и KA(ΔR)=IM(Y,RER)–EX(RER), где ΔR=R–R* – разность внутренней и мировой ставки процента. Внутренняя ставка R зависит от мировой ставки R*: можно получать любые кредиты на международных рынках, не влияя на R* (малая открытая экономика). Если сальдо платежного баланса не равно нулю, точка пересечения кривых IS и LM не лежит на кривой BP. Кривая BP имеет положительный наклон: увеличение Y приводит к росту импорта и к дефициту по текущему счету NX. Равновесие восстановит положительное сальдо счета KA: для привлечения иностранного капитала нужен рост внутренней ставки процента. Наклон кривой BP зависит от склонности к импортированию и мобильности капитала: при низкой мобильности она круче, чем кривая LM. На потоки капитала между странами влияют многие факторы, но самым важным является доход резидентов. Ставки дохода на активы в стране равны номинальной ставке R. Разность номинальной и мировой ставок – это причина оттока (или притока) капитала из страны. Если внутренняя ставка процента выше мировой, иностранные инвесторы найдут привлекательными внутренние активы и приобретут их, резиденты же воздержатся от покупки иностранных активов и станут заимствовать кредиты за границей (приток капитала). Неравновесное состояние баланса текущих операций и платежного баланса, внешние долги неблагоприятно повлияют на состоянии экономики, вызывая экономические спады и финансовые кризисы. Равновесный рост предприятия – движение с оптимизацией цены, выпуска и ресурсов для роста прибыли. Экономика находится в равновесии, если достигается всеми субъектами одновременно, если спрос на товары и услуги равен предложению, если все секторы сбалансированы. Потребитель находится в равновесии, если его доходы и расходы приносят максимальное удовлетворение. Предприятие находится в равновесии, если цена продуктов, выпуск и количество используемых им ресурсов сбалансировано. Владелец ресурсов в равновесии, если использует ресурсы с максимальной выгодой. 14. Потоки Эрланга. Интервалы времени между 1-ым и 2-ым, 2-ым и 3-им,…, n-ым и n+1-ым событием,…T1,T2,…,Tn,… в потоках с ограниченным последействием независимы. Стационарный поток с ограниченным последействием называют потоком Пальма. Случайные интервалы времени T1,T2,…,Tn,… в потоках Пальма имеют один закон распределения. Простейший поток – это поток Пальма. Нестационарный пуассоновский поток не является потоком Пальма. Поток Эрланга k-го порядка получают из простейшего потока путем сохранения каждого k-го события. Промежуток времени T(k) между двумя событиями в потоке Эрланга имеет плотность распределения , t>0, k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение , и, k=1,2,3,… При k=1 закон Эрланга k-го порядка превращается в экспоненциальный закон f(t)=exp(–t) с параметром . Интенсивность потока Эрланга k-го порядка, k=1,2,3,… определяет его основные характеристики, t>0, k=1,2,3,…, и, k=1,2,3,… Интенсивность нормированного потока Эрланга, k=1,2,3,… Промежуток времени между соседними состояниями k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение, , , k=1,2,3,… Плотность распределения нормированного потока Эрланга, t>0, k=1,2,3,… Случайная величина промежутка времени – это среднее арифметическое k независимых случайных величин Ti, i=1,…,k, распределенных по одному и тому же закону распределения (экспоненциальному с параметром ). В силу центральной предельной теоремы она будет иметь распределение, близкое к нормальному с математическим ожиданием 1/ и дисперсией 1/k2. Поскольку дисперсия уменьшается с ростом k, промежуток времени между соседними событиями нормированного потока Эрланга становится все менее случайным и по закону больших чисел приближается по вероятности к математическому ожиданию 1/. Поток Эрланга приближается с ростом k к регулярному потоку с промежутком времени 1/ между событиями. Это свойство потоков Эрланга выявляет роль k как меры «последействия»: от полного отсутствия последействия при k=1 (простейший поток) до жесткого последействия при k (регулярный поток). Для моделирования реального потока с последействием применяется нормированный поток Эрланга с почти тем же математическим ожиданием и дисперсией интервала времени между соседними событиями. С помощью потоков Эрланга немарковские процессы можно сводить к марковским процессам. Пример 7. Наблюдения за работой рекламного агентства показали, что среднее значение интервала времени T между соседними поступлениями заказов M[T]=1 неделя и стандартное отклонение T=4 дня. Интенсивность и стандартное отклонение нормированного потока Эрланга (заказ в неделю) и. Отсюда k=(7/4)2=3,067. Ближайшее целое число – порядок k=3. Плотность распределения вероятностей случайного интервала времени, t>0. Вероятность, что интервал времени между двумя заказами больше 3 и меньше 5 дней. Интегрируя по частям, получим, и. Интегрируя по частям, получим. Таким образом, p=0,189. Пуассоновские потоки событий и дискретные марковские процессы с непрерывным временем тесно связаны. Случайный процесс с непрерывным временем в системе с дискретными состояниями будет марковским, если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими (стационарными или нестационарными). Такие системы с непрерывным временем называются пуассоновскими. Исследование случайного процесса проводится по алгоритму: (1) Описать каждое состояние системы; (2) Составить граф состояний, указать возможные переходы из состояния в состояние; (3) Задать интенсивности потоков событий, под влиянием которых осуществляются эти переходы; (4) Указать начальное состояние системы (при t=0). Пример 8. Банкоматы B1 и B2 могут «отказывать» независимо друг от друга (выходить из строя). Потоки отказов B1 и B2 с интенсивностями 1=4 и 2=3 (отказа в неделю) – пуассоновские. После отказа каждый банкомат сразу ремонтируется (восстанавливается). Потоки восстановлений B1 и B2 с интенсивностями 1=5 и 2=2 (восстановлений в неделю) – пуассоновские. Потоки с постоянными интенсивностями являются простейшими. Система S может находиться в четырех состояниях: s11 – оба банкомата исправны; s12 – банкомат B1 исправен, а B2 ремонтируется; s21 – банкомат B1 ремонтируется, а B2 исправен; s22 – банкоматы ремонтируются. Размеченный граф состояний системы изображен на рис.10, а матрица плотностей вероятностей переходов дана в таблице 5. Рис.10. Граф состояний системы двух банкоматов. Таблица 5. Матрица плотности вероятностей. Составим систему уравнений Колмогорова: В начальный момент времени t=0 система находилась в состоянии s12:, , ,. Условие нормировки p11(t)+p12(t)+p21(t)+p22(t)=1 (t0). С учетом условия нормировки получаем неоднородную систему трех линейных дифференциальных уравнений первого порядка:, ,. Общее решение однородной системы, ,. Для нахождения решений неоднородной системы применим метод вариации постоянных, рассматривая c1,c2,c3 как неизвестные функции от t. Подставляя решение однородной системы, получим систему линейных уравнений для dc1/dt, dc2/dt и dc3/dt. После ее решения и интегрирования найдем функции,, , где b1, b2 и b3 – постоянные интегрирования. Для их определения используем начальные условия:, ,. Решение этой системы уравнений методом Крамера дает, ,. Подставив эти значения, получим общее решение неоднородной системы:, ,. Функцию p22(t) находят из условия нормировки:. При t=2 будем иметь, , ,. Во втором квартале система S будет находиться вероятнее всего в состоянии s12: банкомат B1 будет работать, а B2 – ремонтироваться. Дискретный процесс с непрерывным временем является марковским, если каждый из потоков, переводящих систему из состояния в состояние, является пуассоновским потоком. Преобразование Лапласа Спектральная плотность сигнала v(t). Это преобразование Фурье сигнала v(t). Обратное преобразование Фурье. Сигналу v(t) можно сопоставить спектральную плотность V() в том случае, если сигнал абсолютно интегрируем:. Если экономическую систему возбуждают источники потока y(t), а искомые переменные x(t) являются запасами, то ее поведение описывается уравнением, где квадратная матрица T(p)=G+pC, а G и C не зависят от комплексной частоты p. Допустим, что система уравнений решена, а выходная функция F(p)=cTX(p). Формальное решение, где T+(p) – присоединенная матрица. Линейные выходные функции имеют общий знаменатель, равный определителю матрицы T(p). Определитель и любой элемент присоединенной матрицы T+ – это полиномы от p, а F(p) – рациональная функция комплексной переменной p вида F(p)=N(p)/D(p). Знаменатель функции системы D(p)=|T|, а числитель N(p)=|Tcy|. Если изображение есть дробь F(p)=K1/(p–p1) с полюсом p1 и вычетом K1, то. Обращение преобразования Лапласа заключается в вычислении для. Нужно найти условие, при котором интеграл можно представить в виде. Замкнем контур интегрирования в левой полуплоскости полуокружностью с радиусом, которой растет с пределами интегрирования. Если выполнить условие равенства нулю интеграла вдоль этой бесконечной полуокружности, то интеграл равен сумме вычетов. Введем p=Rexp(i) с dp=iRexp(i)d:. На полуокружности в левой полуплоскости, ограниченной точками iR и –iR, величина R постоянна. При больших R преобладают члены старших степеней и выражение для интеграла можно упростить. Интеграл конечный. Чтобы обеспечить равенство нулю выражения при R, нужно выбрать M и N, чтобы R в знаменателе имел положительную степень. Интеграл от рациональной функции I(p) по бесконечной полуокружности равен нулю, если число полюсов MN+2 функции на два больше, чем число ее нулей. Интегрирование рациональной функции при MN+2 вдоль линии, параллельной мнимой оси, дает 2i{сумма вычетов для полюсов слева от линии}, если контур интегрирования замкнуть через левую полуплоскость. Если замкнуть контур через правую полуплоскость, то следует взять сумму вычетов для полюсов справа от линии, а умножить на (–2i). Если f(z) определена в точке ветвления, то значение f(a) является общим для ветвей, полученных при обходе. Если, описывая кривую вокруг точки z=a сколь угодно раз в том же направлении, мы каждый раз будем получать новые ветви, то точка a называется точкой ветвления бесконечного порядка (логарифмическая точка ветвления). Определение коэффициентов полиномов N(p) и D(p) по ряду чисел (pi,N(pi)) и (pi,D(pi)) составляет интерполяционную задачу. Пусть известны значения qi в n+1 точке pi. Нужно найти коэффициенты полинома, проходящего через эти точки. Подставив pi, получим систему уравнений. Наилучшим выбором pj являются равноотстоящие точки, лежащие на единичной окружности комплексной плоскости. Обозначим P=(pij), где i и j принимают значения от 0 до n. Если обозначить, то pk=wk и P=(wij), а решение принимает вид. Исходный полином, определенный в точках pk, представлен в виде,. Это дискретное преобразование Фурье. Оно эффективно при выборе n+1=2m и целом числе m (быстрое преобразование). Дисконтирование достигается преобразованием Лапласа, которое переводит функцию f(t) действительной переменной t в функцию f(p) комплексной переменной p=r+is (r=Rep, s=Imp, i – мнимая единица). При ограниченном росте |f(t)|<exp(r0t) с абсциссой абсолютной сходимости r0>0 этот интеграл сходится при Rep<r0: область определения функции f(p) лежит слева от r=r0. Изображение запаздывающего импульса Хевисайда h(t–) с амплитудой h=1:. Изображение импульса g(t)=[h(t)–h(t–)]/ длительностью :. В пределе 0 получается изображение импульса Дирака (p)=1. Таблица оригиналов f(t) и изображений f(p). (для преобразования Карсона p используется интеграл Бромвича) Изображения являются рациональными функциями p:, и, где pl – нули, а pk – полюса функции f(p). На комплексной плоскости они изображаются соответственно кружками и крестиками. Функцию можно представить суммой простых множителей с вычетами, , ,. Функцию можно представить суммой. При k=1 имеем pk=1 и nk=2, а [(p–pk)f(p)]=p-3:, и,. При k=2 имеем pk=0 и nk=3, а [(p–pk)f(p)]=(p–1)-2:, , , и,. Если f(p)=c(p)/d(p), а c(p) и d(p) – аналитические функции в простом полюсе p1, то resf(p1)=c(p1)/d(p1). Формула Хевисайда применима, если m различных полюсов pk имеют кратности mk:, Если все полюсы простые, то Через компоненты матрицы Прибыль в рыночном сегменте Экономические рынки удобно рассматривать в виде множества секторов, элементы которых имеют общие признаки. Хозяйствующие субъекты сектора более однородны по своему поведению, чем субъекты всего рынка. Устойчивость сегменту придают прибыльные субъекты. Рыночный сегмент характеризуется какими-то свойствами и параметрами. Экстенсивные свойства пропорциональны размеру сегмента (совокупный доход, энтропия, число субъектов). Интенсивные свойства не зависят от размеров сегмента: скорость обращения полезности V определяет условия обмена между сектором и рынком, а уровень цен p отражает издержки рыночного сегмента. Если экономические параметры изменяются во времени, то в секторе протекает экономический процесс. Самопроизвольный процесс приводит рыночный сегмент в такое состояние, когда его экономические свойства больше не изменяются: в секторе установится полное равновесие. Равновесные рыночные сегменты характеризуются распределением Гиббса [3]. Сейчас кажется тривиальным, что при нехватке некоторого блага его цена растет. Однако между эмпирическим фактом и математическим доказательством дистанция огромного размера [1]. В основе доказательства лежит предположение о детерминированности процессов производства товаров и услуг. Оно попросту не учитывает неопределенность будущего, тем самым не затрагивая финансовую сторону экономической деятельности. Такие явления, как денежная инфляция и спекуляция, нельзя объяснить в рамках детерминированного подхода [2]. Предметом нашего исследования является экономическая система ячеек, которые находятся в состояниях полезности. При этом ячейка «погружена» во внешнюю среду, формируемую другими ячейками. Основное занятие ячейки – это распределение товаров и услуг. Совокупность ячеек и среды образует замкнутую экономическую систему. Нас интересует товарные отношение в этой системе. Пусть индекс n нумерует товары полезностями un. Согласно основному принципу статистической механики, если известна вероятность и статистическая сумма то можно найти внутреннюю полезность системы U, накопление W и свободную полезность F как функции скорости обращения полезности V: Эти функции связаны условием баланса U=F+W. Энтропия n-го состояния Энтропия закрытого региона. Экстенсивная переменная S – мера накопления VS, а интенсивная переменная V – ее оценка. И V и S неотрицательны. Изменения Q и Pn с V описываются производными где U зависит от V. Производные энтропии по V зависят от дисперсии и асимметрии дохода: Поскольку 2>0, то S увеличивается со скоростью V, достигая насыщения при V=V3μ3/3μ2, если μ3>0. При 3<0 энтропия ограничена. Производные по V:, и, Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом V. Производные по S:, и Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом S. Скорость обращения полезности V и энтропия S сопряжены на внутренней и свободной полезности: U(S) является потенциалом для скорости обращения полезности V, а F(V) – потенциалом для энтропии S. Накопление W не является потенциалом ни для скорости обращения, ни энтропии. Для учета доходов используем экстенсивную переменную благосостояния Y. Полезность товара un уменьшается с ростом Y, а производные pn(Y)=–dun/dY>0 определяют уровень цен, где вероятность Pn(V,Y) зависит от Y, так как un зависит от Y. Рыночный сегмент имеет две пары сопряженных переменных (S,V), (Y,p) и четыре потенциала F(V,Y), G(V,p), H(S,p) и U(S,Y) с дифференциалами, , и. Свободная полезность F вычисляется по статистической сумме Q(V,Y). Внутренняя полезность U=F+W включает F и W. Свободная полезность G=F+pY включает F и pY, а внутренняя полезность H=F+VS+pY. Переменные S и Y являются экстенсивными факторами, а V и p – интенсивные факторы. Частные производные статистической суммы выражаются в виде: Свободная полезность F(V,Y) является функцией V и Y: Свободная полезность G(V,p)=F+pY является функцией V и p: Внутреняя полезность H(S,p)=G+VS является функцией S и p: Внутреняя полезность U(S,Y)=H–pY является функцией S и Y: Внутрення полезность U растет с энтропией S и уменьшается с доходом Y. Потенциалы полезности F(V,Y), G(V,p), H(S,p) и U(S,Y) аддитивны, а V и p одинаковы для всех всех субъектов сегмента. Поэтому потенциалы должны быть однородными функциями первого порядка по переменным S и Y: где ψ, μ, ν и φ – некоторые функции. Будем рассматривать N как независимую переменную. Тогда в дифференциалы нужно добавить μdN с потенциалом. Оценка μ(V,p) резидентов в открытой экономической зоне оказывается функцией скорости обращения полезности V и уровня цен p. Дифференцируя G по N, получаем (V,p) – оценка μ числа субъектов в сегменте оказывается функцией V и p. Большой потенциал открытой зоны Ω=F–G является функцией V, Y и μ: dΩ=–SdV–pdY–Ndμ. Если полезность n-го резидента в зоне обозначить unN, то вероятность. Накопление полезности в открытой экономической зоне:, , и. Открытая экономическая зона является большим каноническим ансамблем. При описании экономических явлений используют понятие эластичности фактора и показателя [4]. Пусть взаимозависимые переменные x, y и z отвечают любой тройке неповторяющихся факторов S, V, Y и p. Тогда y-ой эластичностью фактора x при неизменном факторе z называется величина xyz=y(x/y)z. Только 16 эластичностей независимы в закрытой системы. Свободная полезность F(V,Y) вычисляется с помощью статистической суммы Q, а другие потенциалы в переменных V и Y – из выражений: Дифференцирование дает Потенциалы в переменных V и p выражаются через G(V,p): Дифференцирование дает Потенциалы в переменных S и p выражаются через H(S,p): Дифференцирование дает Потенциалы в переменных S и Y выражаются через U(S,Y): Дифференцирование дает Эти производные легко вычисляются, если учесть свойства якобианов: Доход Y(F,V) как функция свободной полезности F и скорости обращения имеет частные производные: Скорость обращения полезности V(G,p) как функция свободной полезности G и уровня цен имеет частные производные: Уровень цен p(H,S) как функция внутренней полезности H и энтропии имеет частные производные: Энтропия S(U,Y) как функция внутренней полезности U и благосостояния имеет частные производные: Статистическая оценки важных эластичностей дает: где означает усреднение с учетом вероятности Pn. Экономические процессы в закрытом сегменте сопровождаются ростом энтропии, пока она не достигнет наибольшего значения при полном равновеси. С ростом числа субъектов энтропия растет при фиксированной скорости V и уровне цен p. Это означает, что норма накопления увеличивается с числом субъектов, т.е. с переходом от большого к малому бизнесу. Субъекты малого бизнеса слабо взаимодействуют друг с другом в идеальном сегменте и представляют собой однородную массу, а их прибыль линейно зависит от конъюнктуры. Замечательным достижением статистической экономики является точная формулировка условий равновесия с внешней средой. Процессы, протекающие в замкнутой неравновесной системе, идут таким образом, что система переходит из состояний с меньшей энтропией в состояния с большей энтропией, пока она не достигнет своего наибольшего значения, соответствующего полному равновесию. Энтропия замкнутой системы – сумма энтропий резидентов и внешней среды. Равенство нулю первых производных суммарной энтропии является только необходимым условием экстремума и не дает того, чтобы энтропия имела именно максимум. Для выяснения достаточных условий необходимо вычислить второй дифференциал суммарной энтропии. Это исследование удобнее провести, исходя не из условия максимума суммарной энтропии, а из эквивалентного ему условия. Выделим из системы некоторую малую часть, а остаток будем рассматривать как внешнюю среду со скоростью обращения V0 и уровнем цен p0. Тогда в равновесии имеет минимум величина U–V0S+p0Y с внутренней полезностью U, энтропией S и доходом Y. При всяком малом отклонении от равновесия ее изменение должно быть положительным: Разлагая δU в ряд, получаем с точностью до членов второго порядка: где производные взяты в состоянии равновесия. Но поскольку то члены первого порядка сокращаются. Это необходимые условия равновесия: скорость обращения полезности V и уровень цен p для резидентов равны этим же величинам внешней среды. Достаточное условие равновесия имеет вид: Для того, чтобы такое неравенство имело место при произвольных δS и δY, нужно удовлетворить два неравенства: Поскольку то первое неравенство удовлетворяется при Второе неравенство можно записать в виде якобиана Переходя к переменным V и Y, имеем Поскольку p=p0>0 и SV0,Y>0, то это равносильно условию Уровень цен должен уменьшаться с ростом благосостояния при постоянной скорости обращения полезности. Эти экономические неравенства гарантируют устойчивость равновесной системы. Для SV0,Y>0 нужно, чтобы средний квадрат внутренней полезности u2 превышал квадрат среднего U2, а дисперсия была положительной. Поскольку для устойчивости равновесия необходимо, чтобы dp/dY было отрицательным и по модулю превышало отношение дисперсии уровня цен к скорости обращения. При любом начальном состоянии закрытой системы с течением времени в ней установится единственное состояние – равновесие. Эта тенденция означает монопольное возрастание энтропии во времени и увеличение разности энтропий S=S–S0 от отрицательных значений до нуля. Эти утверждения эквивалентны, и они отражают тот факт, что равновесие является глобальным асимптотически устойчивым состоянием, энтропия – функцией Ляпунова. Если только свободная полезность F(V,Y) будет иметь несколько минимумов при неизменных V, Y и различных значениях N, то стабильному состоянию будет отвечать наименьшее значение F, а метастабильному – самый мелкий минимум с наибольшим F. Такие состояния легко разрушаются переходом системы в устойчивое состояние с наименьшей свободной полезностью. Если системы переходит из одного состояния в другое с изменением ее внутренней полезности при неизменном накоплении, то обратный переход нельзя осуществить без воображаемого внешнего источника R. Прямому переходу с совершением максимальной работы |Rmax| отвечает обратный переход c работой Rmin внешнего источника. Изменение внешней полезности ΔU при изменении состояния состоит из трех частей: из произведенной работы внешнего источника R, из работы внешней среды p0ΔY0 и из полученной из нее V0ΔS0: где индекс 0 относится к внешней среде. Поскольку затраты среды равны доходу ΔY0=–ΔY, а в силу закона возрастания энтропии S0–S, то где знак равенства достигается при обратимом процессе. Переход совершается с минимальной работой, если он происходит обратимо: Обратный переход также совершается с минимальной работы, если происходит обратимо: Пусть SΣ есть полная энтропия. Если резиденты находятся в равновесии с внешней средой, то SΣ является функция их внутренней полезности UΣ.. Если же резиденты не находятся в равновесии с внешней средой, то суммарная энтропия отличается от SΣ(UΣ) на величину Но dU/dS является равновесной скоростью обращения полезности V0. Таким образом, получаем Эта формула определяет, как отличается энтропия замкнутой системы от своего возможного значения, если резиденты не находятся в равновесии со средой. Рассмотрим закрытую систему с энтропией SΣ. Пусть β – некоторый фактор, обеспечивающий ее внутреннее равновесие, т.е. S/=0. Пусть α – другой фактор, обеспечивающий при внутреннем равновесии системы и ее равновесие с внешней средой, т.е. S/=0. Введем обозначения Энтропия SΣ замкнутой системы максимальна при полном равновесии. Чтобы энтропия была максимальной, кроме необходимых условий А=0 и В=0, должны выполняться неравенства Уже незначительные изменения фактора α при некотором воздействии на закрытую систему приводят к изменению A на величину Изменение α при постоянном β приводит к нарушению условия внутреннего равновесия системы B=0. После того, как это равновесие восстановится, величина ΔA будет иметь значение Используя свойства якобиана, находим С учетом неравенств получаем новое неравенство Это неравенство выражает принцип Ла Шателье [6]. Рассмотрим изменение Δα фактора α как меру внешнего воздействия на систему, а ΔΑ – κак меру изменения системы под его влиянием. Тогда Значение ΔΑ уменьшается при восстановлении внутреннего равновесия системы после внешнего воздействия, выводящего ее из равновесия. Другими словами, внешнее воздействие, выводящее систему из равновесия, стимулирует в системе процессы, стремящиеся ослабить его влияние. Изменение энтропии системы –Rmin/V0 зависит от скорости обращения полезности во внешней среде V0 и минимальной работы Rmin, необходимой для приведения системы из состояния равновесия с внешней средой в данное состояние. Поэтому можно написать где для бесконечно малого изменения состояния системы резидентов Все величины без индекса относятся к резидентам, а с индексом 0 – к среде. Пусть α есть энтропия S. Тогда A=V/V0–1 и в равновесии V=V0, неравенства принимают вид Рост энтропии означает, что в систему инвестируется оборотный капитал. В итоге нарушается равновесие резидентов и, в частности, увеличивается скорость обращения полезности на величину (V). Восстановление равновесия резидентов приводит к тому, что изменение скорости обращения уменьшится до (V)B=0. т.е. как бы ослабляется результат воздействия, выводящего резидентов из равновесия. Если в неравенстве в качестве фактора β взять доход Y, то будем иметь поскольку условие В=0 означает, что случае p=p0. Подстановка дает неравенство Используя свойства якобиана, можно получить Пусть α есть налог Y. Тогда A=1–V/V0 и в равновесии V=V0, а неравенства принимают вид Если в неравенстве в качестве фактора β взять энтропию S, то условие В=0 означает, что V=V0 и В устойчивой системе величина (p/Y)V должна быть отрицательной. Используя свойства якобиана, можно получить В устойчивой системе величина (S/V)p должна быть положительной. Основной недостаток идеального сегмента состоит в том, что полезность расходится при Y=0. Этот коллапс не должен допускаться государством, которое может установить минимальный предел Y0. Рассмотрим процесс L в экономической системе, которая не находится в равновесии с внешней средой. Пусть B – накопление, полученное системой из внешней среды со скоростью обращения полезности V0. Процесс L перехода из состояния 1 в состояние 2 нельзя реализовать, если нарушается неравенство где S1 и S2 – энтропии состояний, а интегрирование проводится по траектории процесса. Равенство применимо только при обратимом процессе. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы и не зависит от ее промежуточных состояний Дифференциал внутренней полезности в замкнутой системе содержит малое накопление B и малое потребление A, которые не являются дифференциалами в общем случае. Переведем идеальную систему из начального состояния 1 в промежуточное состояние 2 при неизменной энтропии: где. Выпуск и потребление положительны, если. Переведем теперь систему из состояния 2 в промежуточное состояние 3 при неизменной ренте: Переведем далее систему из состояния 3 в промежуточное состояние 4 при неизменной конъюнктуре: Наконец, переведем систему из состояния 4 в начальное состояние 1 при неизменной ренте: При этот цикл оказывается замкнутым. В начальном состоянии 1 идеальная система имеет низкую конъюнктуру и низкую ренту. Переход в состояние 2 при низкой конъюнктуре сопровождается увеличением ренты и цены, а капитал убывает потому, что выпуск равен потреблению (накопление не меняется). Переход в состояние 3 при высокой ренте сопровождается увеличением конъюнктуры и капитала, а цена уменьшается, потому что выпуск отсутствует (инвестиция накоплений в производство повышает его конъюнктуру). Переход в состояние 4 при высокой конъюнктуре сопровождается уменьшением ренты и цены, а капитал увеличивается, потому что потребление равно выпуску (накопление не изменяется). Переход в начальное состояние 1 при низкой ренте сопровождается уменьшением конъюнктуры и капитала, а цена увеличивается, потому что выпуск отсутствует (конфискация накопления из производства понижает его конъюнктуру). Коэффициент полезного действия этого замкнутого экономического цикла определяется следующим образом: Инвестиция S2=S23>0 и конфискация S1=S41<0 удовлетворяют соотношению Это соотношение справедливо только для замкнутого цикла. Макроскопическая теория выпусков и затрат использована для описания экономических циклов системы многих резидентов на основе модели В.В.Леонтьева. Основные понятия макроэкономики развиты в русле детерминированного подхода, дополненного соображениями оптимальности и полезности [1,2]. Может быть поэтому нет строгого определения конъюнктуры как меры эффективной деятельности экономической системы. Вместе с тем, этот термин используется [3]. Эвристические соображения известных экономистов о конъюнктуре близки к определению температуры как производной внутренней энергии системы по ее энтропии [4,5]. Аналогом внутренней энергии в экономике является внутренняя полезность, но она должна быть определена в рамках вероятностного подхода. Необходимость такого подхода отмечалась в связи с инфляционными процессами современной экономической жизни [6]. Полезность un зависит от индекса благосостояния Y, причем при Y=1 она равна нулю, а цена благосостояния pn(Y)–dun/dY не может быть отрицательной, так как un уменьшается с ростом Y. Согласно основного принципа статистической экономики, если известны статистическая сумма Q, вероятность Pn, энтропия S и уровень цен p, , и, то можно найти макроскопические показатели закрытой системы при скорости обращения полезности V и индексе благосостояния Y. Показателями закрытой системы являются внутренняя полезность U=F+W, свободная полезность F и накопление W, и, а ее факторами являются скорость обращения полезности V, энтропия S, индекс благосостояния Y и уровень цен p. Для простой закрытой системы, а свободная полезность (потребление) выражается в виде, где f(V)=VlnL(V). Энтропия и уровень цен простой системы даются уравнениями состояния и. Полуэластичности этих двух факторов и. Для устойчивости закрытой системы необходимо и достаточно иметь =const, =const и SV,Y>0, pY,V<0. Простая система устойчива, если d2f/dV2<0. Свободная полезность G=F+pY в простой системе определяется с учетом уравнения состояния:, а энтропия и индекс благосостояния выражаются в виде и. Полуэластичности этих факторов и. Идеальной называется простая система с SV,Y=N0>0 и, где f0 и – постоянные интегрирования. Внутренняя полезность U=F+W такой системы определяется с учетом уравнения состояния:, где =1+N/N0>1. Удобно выбрать f0=–S0 и, чтобы внутренняя полезность исчезала при энтропии S11=S(V=1,Y=1) и индексе Y=1:. В этом случае и, а внутренняя полезность являются линейной функцией скорости обращения полезности U=N0(V–1). Свободная полезность идеальной системы и ее энтропия – нелинейные функции скорости обращения полезности и индекса благосостояния и. Зависимость энтропии идеальной системы S(V,Y) от конъюнктуры V приводится на рис.1 для двух значений индекса благосостояния Y. Рис.1. Зависимость энтропии от конъюнктуры. Используются данные для высокоэластичной экономики с небольшим числом резидентов, представляющих отрасли народного хозяйства [3] (N0=10, S11=3 и N=10). Рост энтропии с конъюнктурой свидетельствует о структурных изменениях системы, сопровождаемых линейным увеличением внутренней полезности. Этот рост замедляется с уменьшением индекса благосостояния. Уравнение состояния pY=NV связывает большую полезность pY с числом резидентов N и конъюнктурой V идеальной системы. При неизменной конъюнктуре уровень цен уменьшается с ростом индекса благосостояния (деинфляция). Рассмотрим квазистатический процесс L в системе резидентов, которые не находятся в равновесии с внешней средой. Малое накопление B система резидентов получит из окружающей среды с равновесной конъюнктурой V0. Переход системы резидентов из состояния 1 с энтропией S1 в состояние 2 с энтропией S2 нельзя реализовать, если нарушается неравенство, где интегрирование проводится по траектории процесса L. Равенство применимо при обратимых процессах. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы. Дифференциал внутренней полезности закрытой системы dU=B+A=VdS–pdY содержит малое накопление B и малое потребление А, которые не являются дифференциалами. В состоянии 1 система имеет энтропию S1 и конъюнктуру V1. Переведем систему из начального состояния 1 в состояние 2 при неизменной энтропии: и. Переход в состояние 2 с конъюнктурой V2>V1 сопровождается уменьшением индекса благосостояния Y и увеличением уровня цен p, потому что прирост полезности потребляется (рис.1). Переведем систему из состояния 2 в состояние 3 при неизменной конъюнктуре:, и. Переход в состояние 3 с энтропией S3>S1 сопровождается увеличением Y и уменьшением p, потому что внутренняя полезность не изменяется (инвестиция накоплений в систему повышает энтропию). Зависимость индекса благосостояния Y от уровня цен p приводится на рис.2 для той же высокоэластичной системы при S1=1, V1=1, V2=3 и S3=3. Рис.2. Зависимость индекса от ставки затрат. Переведем систему из состояния 3 в состояние 4 при неизменной энтропии: и. Переход в состояние 4 с конъюнктурой V4<V2 сопровождается увеличением Y и уменьшением p. Переведем систему из состояния 4 в состояние 1 при неизменной конъюнктуре:, и. Переход в состояние 1 с энтропией S1 и конъюнктурой V4=V1 сопровождается уменьшением Y и увеличением p из-за конфискации накоплений окружающей средой. Коэффициент полезного действия экономического цикла. Инвестиция B2=B23>0 и конфискация B1=B41<0 удовлетворяют соотношению. Это соотношение справедливо только для замкнутого цикла. Современному состоянию экономики Украины отвечает одна из нижних точек на траектории L12 c энтропией S1 и конъюнктурой VV2. Движение по этой траектории с падением индекса благосостояния Y и увеличением уровня цен p разогревает экономику до такой конъюнктуры V2, при которой возможны структурные изменения отношений резидентов на траектории L23. Движение по траектории с ростом Y и уменьшением p хаотизирует экономику до значения энтропии S3, которое зависит от инвестиции накоплений. Определению кризисной точки более отвечает состояние экономики с энтропией S1 и конъюнктурой V1, а квазистатический процесс L41 имеет периода застоя. Ему предшествует движение по траектории L34, которое ведет к охлаждению экономических отношений. |
|
|
Моторная готовность к школе: · Координация системы «рука–глаз», ловкость пальцев и рук; · Способность проявлять собственную инициативу и активность; · Воспринимать равновесие, тактильные и кинестетические ощущения; · Уметь воспринимать препятствия и активно взаимодействовать с ними |
Когнитивная готовность к школе: · Способность к концентрации внимания в течение некоторого времени; · Краткосрочная слуховая память, понимание на слух, визуальная память; · Любознательность и интерес к учению; · Логически связное мышление, способность усматривать взаимосвязи и закономерности |
Главное – это психологическая готовность ребёнка к школе. Это понятие означает сформированность необходимых психологических предпосылок учебной деятельности, помогающих ребёнку приспособиться к условиям школы и приступить к систематической учебе.
Набор психологических свойств и качеств многообразен, поскольку понятие психологической готовности к школе включает в себя несколько аспектов. Все они между собой тесно взаимосвязаны.
Функциональная готовность ребёнка свидетельствует об уровне общего развития, его глазомера, пространственной ориентации, способности к подражанию, а также о степени развития сложно-координированных движений руки.
Интеллектуальная готовность предполагает приобретение ребёнком определенного запаса конкретных знаний, понимание общих связей, принципов, закономерностей; развитость наглядно-образного, наглядно-схематического мышления, творческого воображения, наличие основных представлений о природе и социальных явлениях.
Оценка готовности к школе по уровню интеллектуального развития – наиболее распространенная ошибка родителей. Старание родителей направляется на "запихивание" в ребёнка всевозможной информации. Но важен не столько объем знаний, сколько их качество, степень осознанности, четкость представлений. Желательно развивать способность слушать, понимать смысл прочитанного, пересказывать услышанный материал, умение сопоставлять, сравнивать, выражать свое отношение к прочитанному, проявлять интерес к неизвестному.
Интеллектуальная готовность имеет и другой аспект – формирование у ребёнка определенных умений. К ним прежде всего относится умение выделить учебную задачу и превратить ее в самостоятельную цель деятельности.
К 6 годам происходит постепенное оформление основных элементов волевого действия: ребёнок способен поставить: цель, принять решение, наметить план действия, исполнить его, проявить определенное усилие для преодоления препятствия. Но все эти компоненты еще недостаточно развиты: волевое поведение и процессы торможения слабы. Сознательное управление собственным поведением дается пока ребёнку с большим трудом. Помощь родителей в этом направлении может выражаться в формировании у детей умения преодолевать трудности, в высказывании одобрения и похвалы, в создании для него ситуаций успеха.
Возможность управлять своим поведением тесно связана с уровнем развития способности контролировать свои поступки усилием воли. Это выражается в умении слушать, понимать и точно выполнять указания взрослого, действовать в соответствии с правилом, использовать образец, сосредоточивать и удерживать внимание на определенной деятельности в течение длительного времени.
2. Исследование формирования готовности детей к обучению в школе на примере ДОУ "Эрудит"
2.1. Цель эксперимента
Целью экспериментальной работы является выявить влияние состава семьи на формирование психологической готовности детей подготовительной группы к обучению в школе.
В эксперименте участвовало 25 дошкольников 6-7 лет, посещающие подготовительную группу в ДОУ «Эрудит».
Обследование будущих первоклассников проводилось в детском саду, при этом они находились в привычной им обстановке.
Нами было проведено четыре диагностики по выявлению психологической готовности детей: «Ориентационный тест школьной зрелости» Керна - Йирасека, тест А.Л. Венгера , «Мотивационная готовность», собеседование С.А. Банкова, «Психосоциальное развитие», графический диктант Д.Б. Эльконина, а также анкетирование родителей для выявления состава семьи и занятости родителей.
2.2. Описание и результаты методик
«Ориентационный тест школьной зрелости» Керна - Йирасека.
Ориентационный тест школьной зрелости Я. Йирасека, являющийся модификацией теста А.Керна, состоит из 3-х заданий: подражание письменным буквам, срисовывание группы точек, рисование мужской фигуры по представлению. Результат оценивается по пятибалльной системе, а затем вычисляется суммарный итог по всем трем заданиям. Данная методика позволяет определить уровень развития мелкой моторики, предрасположенность к овладению навыками письма, уровень развития координации движений руки и пространственной ориентации.
Выявляет общий уровень психического развития, уровень развития мышления, умение слушать, выполнять задания по образцу, произвольность психической деятельности.
Я. Йирасек провел исследование по установлению связи между успешностью выполнения теста школьной зрелости и успешностью в дальнейшем обучении. Оказалось, что дети, хорошо справляющиеся с тестом, как правило, хорошо учатся в школе, но дети, плохо справляющиеся с тестом, в школе могут хорошо успевать. Поэтому Я. Йирасек подчеркивает, что результат тестового испытания можно рассматривать как основание для заключения о школьной зрелости и нельзя интерпретировать как школьную незрелость (например, бывают случаи, когда способные дети схематично рисуют человека, что существенно отражается на полученном ими суммарном балле).

|
В данной работе мы рассмотрели очень важную тему, которая является на сегодняшний день очень актуальной. Эта тема уже давно раскрыта в иностранных трудах. У нас она начала исследоваться относительно недавно, но очень плодотворно. Написано уже немало книг и статей по этой тематике. |
Высокий – 21
Средний – 4
Низкий – 0
Детей охвачено: 25
Тест А.Л. Венгера «Мотивационная готовность».
Целью данного исследования является диагностика внутренней позиции будущего школьника. Ребенку дается набор вопросов, предлагающих выбор одного из двух вариантов поведения.
Послушай меня внимательно. Я тебе сейчас буду задавать вопросы, а ты должен отвечать, какой вариант тебе нравится больше.
Проведение теста:
Детям читают вслух вопросы, причем время на ответ не ограничивается. Каждый ответ фиксируют, так же как и все дополнительные замечания детей.
При анализе за каждый правильный ответ дается 1 балл, за неправильный – 0 баллов. Внутренняя позиция считается сформированной, если ребёнок набрал 5 баллов и больше.
В результате исследования по данной методике были получены следующие результаты:
Сформирована - 25
Не сформировано - 0
Детей охвачено: 25
Собеседование «Психосоциальное развитие» по С.А. Банкову.
Определяет степень психосоциальной зрелости (кругозор) - тестовая беседа, предложенная С. А. Банковым. Ребенок должен ответить на следующие вопросы .
Оценка ответов за правильный ответ на все подвопросы одного пункта ребенок получает 1 балл (за исключением контрольных). На правильные, но неполные ответы на подвопросы ребенок получает 0,5 балла. Например, правильные ответы: «Папа работает инженером», «У собаки лап больше, чем у петуха»; неполные ответы: «Мама Таня», «Папа работает на работе». К контрольным заданиям относятся вопросы 5, 8, 15,22. Они оцениваются так: №5 – ребенок может вычислить, сколько ему лет -1 балл, называет год с учетом месяцев – 3 балла. №8 – за полный домашний адрес с названием города- 2 балла, неполный – 1 балл. № 15 – за каждое правильно указанное применение школьной атрибутики – 1 балл. № 22 – за правильный ответ -2 балла. № 16 оценивается совместно с №15 и № 22. Если в № 15 ребенок набрал 3 балла, и в №16 – положительный ответ, то считается, что у него положительная мотивация к обучению в школе. Оценка результатов: ребенок получил 24-29 баллов, он считается школьно-зрелым, 20-24 – средне-зрелым, 15-20 – низкий уровень психосоциальной зрелости.
В результате исследования по данной методике были получены следующие результаты, которые отражены на рис. 2.3..
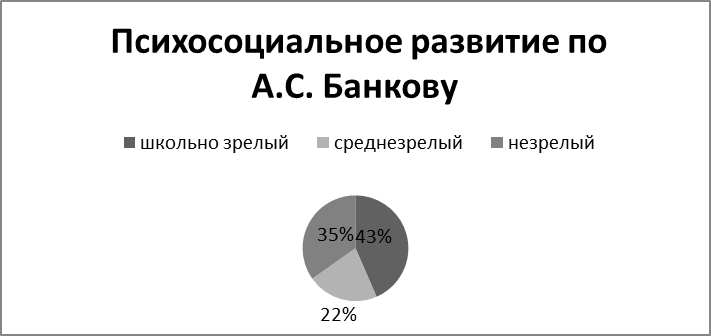
Рис. 2.3. Психосоциальное развитие
Школьно–зрелый –5 детей
Средне–зрелый –15 детей
Не зрелый – 4 ребенка
Детей охвачено: 24
Графический диктант Д.Б. Эльконина.
Методика предназначена для исследования ориентации в пространстве.
С ее помощью также определяется умение внимательно слушать и точно выполнять указания взрослого, правильно воспроизводить заданное направление линии, самостоятельно действовать по указанию взрослого.
Для проведения методики ребенку выдается тетрадный лист в клеточку, с нанесенными на нем друг под другом четырьмя точками. Расстояние между точками около 8 клеточек.
Сначала ребенку дается предварительное объяснение: «Сейчас мы с тобой будем рисовать разные узоры. Надо постараться, чтобы они получились красивыми и аккуратными. Для этого нужно внимательно слушать меня, я буду говорить, на сколько клеточек и в какую сторону ты должен проводить линию. Проводится только та линия, которую я скажу. Следующую линию надо начинать там, где кончается предыдущая, не отрывая карандаша от бумаги». После этого исследователь вместе с ребенком выясняют, где у него правая, где левая рука, показывают на образце как проводить линии вправо и влево. Затем начинается рисование тренировочного узора.
«Начинаем рисовать первый узор. Поставь карандаш на самую верхнюю точку. Внимание! Рисуем линию: одна клеточка вниз. Не отрываем карандаш от бумаги. Теперь одна клеточка вправо. Одна клетка вверх. Одна клетка направо. Одна клетка вниз. Одна клетка направо. Одна клетка вверх. Одна клетка направо. Одна клетка вниз. Дальше продолжай рисовать узор сам».
При диктовке делаются достаточно длительные паузы. На самостоятельное продолжение узора ребенку дается 1–1,5 минуты. Во время выполнения тренировочного узора исследователь помогает ребенку исправлять допущенные ошибки. В дальнейшем такой контроль снимается.
«Теперь поставь карандаш на следующую точку. Внимание! Одна клетка вверх. Одна клетка вправо. Одна клетка вверх. Одна клетка вправо. Одна клетка вниз. Одна клетка вправо. Одна клетка вниз. Одна клетка вправо. А теперь продолжай рисовать этот узор сам».
«Поставь карандаш на следующую точку. Внимание! Три клетки вверх. Две клетки вправо. Одна клетка вниз. Одна клетка влево (слово «влево выделяется голосом). Две клетки вниз. Две клетка вправо. Три клетки вверх. Две клетки вправо. Одна клетка вниз. Одна клетка влево. Две клетки вниз. Две клетки вправо. Три клетки вверх. Теперь продолжай сам».
«Теперь поставь карандаш на самую нижнюю точку. Внимание! Три клетки вправо. Одна клетка вверх. Одна клетка влево. Две клетки вверх. Три клетки вправо. Две клетки вниз. Одна клетка влево. Одна клетка вниз. Три клетки вправо. Одна клетка вверх. Одна клетка влево. Две клетки вверх. Теперь продолжай рисовать узор сам».
Оценка результатов. Результаты выполнения тренировочного узора не оцениваются. В основных узорах отдельно оценивается выполнение диктанта и самостоятельное рисование:
4 балла – точное воспроизведение узора (неровность линии, «грязь» не учитываются);
3 балла – воспроизведение, содержащее ошибку в одной линии;
2 балла – воспроизведение, содержащее несколько ошибок;
1 балл – воспроизведение, в котором имеется лишь сходство отдельных элементов с узором;
0 баллов – отсутствие сходства.
За самостоятельное выполнение задания оценка идет по каждой шкале. Таким образом, ребенок получает 2 оценки за каждый узор, колеблющиеся от 0 до 4 баллов. Итоговая оценка за выполнение диктанта выводится из суммирования минимальной и максимальной оценки за выполнение 3 узоров (средняя не учитывается). Аналогично подсчитывается средний балл за самостоятельную работу. Сумма этих оценок дает итоговый балл, который может колебаться от 0 до 16 баллов. В дальнейшем анализе используется только итоговый показатель, который интерпретируется следующим образом:
0–3 баллов – низкий;
3–6 баллов – ниже среднего;
7–10 баллов – средний;
11–13 баллов – выше среднего;
14–16 баллов – высокий.
Результаты этой методики приведены на рис. 2.4.

Рис. 2.4. Графический диктант
Детей охвачено – 20, из них
Высокий – 17,
Средний -2,
Низкий – 1.
2.3. Анализ результатов исследования
Таблица 2.2
Результаты готовности к школе
|
Психосоциальный тест по Банкову |
Тест Керна -Йирасека |
Мотивационная готовность |
Графический диктант |
Общий итог |
|
|
Полезность парных сравнений. Прокоп О.М. Научный руководитель проф. На множестве элементов Х={х1,...,хт} определена семья отношений преобладания ={,,,,}, первым из которых является отношение «не хуже» (). Функция полезности удовлетворяет условию:). Это означает, что элемент x1X не хуже элемента x2X, если полезность f(x1) элемента х1 не меньше полезности f(x2) элемента х2. Таким образом, функция полезности f отображает отношение преобладания на множестве X. Можно убедиться, что она отображает и все другие отношения семьи . В частности, отображение основных отношений «равноценно» () и «лучшее» ():),). Всегда ли бинарное отношение преобладания можно отобразить функцией? Утвердительный ответ для счетного множества дал Кантор, а для несчетного – Милграм и Биркгоф. Очень важную теорему доказал Дебре: отношение преобладания «не хуже» на компактном множестве XRn можно отобразить функцией полезности, если оно непрерывно на X. Если множество допустимых элементов X представляет собой компакт в Rn, то непрерывная на этом множестве функция достигает наибольшего значения (теорема Вейєрштрасса). Множество элементов, доставляющих максимум функции f на множестве X, не пусто. Поскольку эти элементы являются максимальными по отношению преобладания , что отображается функцией полезности f, то множество преобладающих элементов не пусто. Вместе с функцией ценности f все отношения преобладания семьи отображает другая функция, полученная возрастающим преобразованием. Если u=f(х), хX – функция полезности, а v=g(и) – возрастающая функция переменной u, то сложная функция v=g(f(x)), хX также является функцией полезности. Функция полезности, заданная с точностью до произвольного монотонно возрастающего преобразования, называется порядковой. Если же функция полезности задана с точностью до произвольного положительного линейного преобразования v=f(x)+, где ,>0, ее называют интервальной. Особенность интервальной функции полезности состоит в том, что она (в отличие от порядковой) позволяет не только определять, что один элемент преобладает над другим, а и то, как различаются элементы по преобладанию. Если функция полезности f положительна и задана с точностью до любого множителя , то есть w=f(x), >0, то ее называют относительной. Она показывает, в сколько раз один элемент преобладает над другим. При сравнении двух элементов xі и xj множества важно знать, в какой степени один элемент преобладает над другим. Если при сравнении элемента xі с элементом xj первый элемент получил указанный в таблице 1 ранг, то другой элемент получает ранг, обратный к рангу первого элемента. Таблица 1. Шкала относительной важности объектов Степень важности Определение 1 Объекты равноценны 3 Объект немного лучше другого 5 Объект лучше другого 7 Объект намного лучше другого 9 Объект гораздо лучше другого 2,4,6,8 Промежуточные суждения По результатам парных сравнений образуем mm-матрицу A=(aij), элемент которой aij дает оценку преобладания элемента хi в сравнении с элементом xj (i,j=1,…,т). Пусть (w1,...,wт) – набор истинных полезностей элементов множества X. Если парные сравнения будут взаимно согласованы, должны выполняться соотношения aij=wi/wj для i,j=1,…,т. Это означает, что аii=1 и аji=1/aij для i,j=1,…,т. Последнее соотношение означает, что если элемент xі лучше элемента xj в >1 раз, то полезность xj составит 1/ часть от ценности xj. Взаимная согласованность парных сравнений означает также, что должны выполняться соотношения аij=akj/aki для i,j,k=1,…,m. Если хk лучше хi в раз, а хi лучше xj в раз, то хk лучше xj в раз. Для заполнения матрицы A достаточно задать одну строку (один столбец). В самом деле, если заполнена первая строка этой матрицы (а11,...,а1i,...,а1т), то ее i-ая строка (i=2,…,т) заполняется по правилу aij=a1j/a1i (j=1,…,n). При полной согласованности элементов выполняется соотношение: Вектор относительной полезности (w1,…,wm)T – собственный вектор матрицы А для ее собственного значения =т. Для согласованной матрицы – это наибольшее собственное значение (спектральный радиус матрицы), а другие собственные значения равны нулю. Это свойство согласованных парных сравнений можно использовать в случае, если допущены ошибки. После построения матрицы парных сравнений относительные полезности элементов можно получить как компоненты собственного вектора w для собственного значения max. Чем ближе max к т, тем лучше согласованы парные сравнения элементов. Индекс согласованности (индекс Саати). Если значение индекса меньше 10 % от эталонных значений таблицы 2, то результаты парного сравнения считают удовлетворительными. Если значение индекса больше 10 %, то результаты считают неудовлетворительными, и тогда нужно уточнить оценки относительной важности элементов в парных сравнениях. Таблица 2. Эталонные значения индекса согласованности. Способ приближенного вычисления относительной полезности элементов состоит в использовании среднего геометрического элементов каждой строки матрицы:, i=1,…,m. Предположим, что вы решаете, в каком кафе провести свободное время. Выбор ограничен тремя кафе 1, 2 и 3. Они обеспечивают качественное обслуживание клиентов. В кафе 1 свободен доступ в «Интернет», а в кафе 3 много посетителей. Кафе 2 находится ближе к вашему дому. Результаты парного сравнения кафе: <1:2>=3 – есть некоторые основания считать кафе 1 лучше кафе 2; <1:3>=7 – уровень обслуживания в кафе 1 значительно лучше, чем в кафе 3; <2:3>=3 – уровень обслуживания в кафе 2 и 3 почти одинаков, но число посетителей в кафе 2 меньше, и оно расположено ближе к дому. По этим результатам составляем матрицу парных сравнений:. По методу среднего геометрического, находим,,. Оценим собственное значение, которому отвечает этот вектор полезностей. Для этого вычислим произведение. Чтобы оценить max, делим покомпонентно вектор Аw=(2,013;0,73;0,264)T на вектор относительных полезностей w=(0,669;0,243;0,088)T. Получим вектор (3,007;3,007;3,007)T. Собственное значение:. Индекс согласованности. составляет 0,6 % от эталонного значения показателя согласованности:. Уровень согласованности достаточно высок, а относительными полезностями кафе 1, 2 и 3 можно считать: w1=0,669; w2=0,243; w3=0,088. Если принять <1:2>=3 – есть основания считать кафе 1 лучше кафе 2; <1:3>=9 – уровень обслуживания в кафе 1 гораздо лучше, чем в кафе 3; <2:3>=3 – есть основания считать кафе 2 лучше кафе 3, то согласие парных сравнений полное max=3 и J=0: w1=0,692; w2=0,231; w3=0,077. При большом числе объектов этот метод слишком громоздок, что присуще всем методам, основанным на парном сравнении элементов. 2. Потоки и запасы В экономике три категории агентов: предприятия E, домохозяйства H и все другие агенты V. Агенты E производят товары и услуги. Агенты H их потребляют. Агенты V оказывают услуги по распределению созданных благ. Стоимость произведенной в стране конечной продукции равна расходам по ее приобретению, а валовой внутренний продукт (ВВП) можно получить как сумму конечных расходов Y=C+I (C – потребление, I – инвестиции). Добавленная стоимость – доходы агентов, а ВВП равен сумме факторных доходов Y=L+K (L и K – оплата труда и капитала). Плата за капитал включает амортизационные расходы, арендную плату, проценты, страховку и прибыль. Потоки Y, C и I связывают агентов с рынком товаров и услуг MP. Другие потоки связывают их с рынком ресурсов MR и другими рынками M. Отобразим агентов и рынки вершинами графа, потоки – дугами. Модель взаимодействия агентов E, H и V на рынках MP, MR и M дана на рис.1. Доход MP|E=Y предприятия E получают на рынке товаров и услуг MP, где H и V несут расходы C(MP|H) и I(MP|F). Домохозяйства получают доход R(MR|H) на рынке ресурсов MR, где предприятия несут расходы L(E|MR). Другие агенты V получают доход W(M|V) на рынках M, где несут расходы предприятия K(E|M) и домохозяйства S(H|M). Условия баланса рынков, и. Условия баланса агентов, и. Здесь I – инвестиции в товары и услуги, Q – инвестиции в ресурсы. Рис.1. Потоки доходов и расходов. Направленный граф рис.1 на шести вершинах содержит девять дуг потоков. Если удалить вершину графа V и инцидентные ей дуги, оставшаяся часть графа не сбалансирована. Удаленная часть графа становится деревом графа, если ее дополнить дугами V|E и V|H с нулевыми потоками. На рис.2 ветви дерева изображены пунктирными линиями, а хорды дополнения дерева – сплошными линиями. Множество дуг замкнутого графа – объединение его ветвей и хорд. Для графа рис.2 вектор потоков ветвей Ib=(I,Q,–W,0,0), а запасы ветвей Vb=(I,Q,W,0,0). Потоки хорд Ic=(Y,R,L,C,K,S). Матрица потоков хорд Icc=diag(Ic). Рис.2. Дерево графа и его дополнение. Топологические свойства дополнения дерева описывают матрицы инцидентности таблиц 1. Элемент матрицы Dbc равен 1, если i-ая вершина начальная для j-ой хорды, и 0 в противном случае. Элемент матрицы Cbc равен 1, если i-ая вершина конечная для j-ой хорды, и 0 в противном случае. Унимодулярная матрица инцидентности Abc=Cbc–Dbc. Таблица 1. Матрицы инцидентности дополнения дерева. Dbc MP|E MR|H E|MR H|MP E|M H|M Cbc MP|E MR|H E|MR H|MP E|M H|M MP 1 0 0 0 0 0 MP 0 0 0 1 0 0 MR 0 1 0 0 0 0 MR 0 0 1 0 0 0 MF 0 0 0 0 0 0 MF 0 0 0 0 1 1 E 0 0 1 0 1 0 E 1 0 0 0 0 0 H 0 0 0 1 0 1 H 0 1 0 0 0 0 Потоки ветвей и запасы хорд и выражают законы Кирхгофа: алгебраическая сумма потоков в вершине графа и запасов в контуре графа равна нулю. Потоки и запасы дуг даны на рис.2. Мощность дуги – произведение ее потока на запас. Дуги с положительной мощностью – ресурсы, дуги с отрицательной мощностью – использования. Мощность ветвей и хорд и. Сравнение дает теорему Тевенина: Mb+Mc=0 – мощность замкнутого графа равна нулю. В таблице 2 представлена матрица потоков и матрица сальдо и. Таблица 2. Матрица проводок и матрица сальдо. Pbb MP MR M E H Sbb MP MR M E H Ib MP 0 0 0 Y 0 MP 0 0 0 Y –C I MR 0 00 0 R MR 0 0 0 –L R Q M 0 0 0 0 0 M 0 0 0 –K –S –W E 0 L K 0 0 E –Y LK 0 0 0 H C0 S 0 0 H C –R S 0 0 0 –Ib –I –Q W 0 0 0 Если I=Y–C>0, то рынок товаров и услуг MP находится в активном состоянии (I – инвестиции в товары и услуги). Если Q=R–L>0, то рынок ресурсов MR находится в активном состоянии (Q – инвестиции в ресурсы). Поскольку W+I+Q=0 и W<0, то рынки M находятся в пассивном состоянии. Агенты E и H сбалансированы. Потоки ресурсов направлены от агентов к рынкам, а потоки использования – от рынков к агентам. Выделяя в матрице потоков Icc потоки использования Ucc и потоки ресурсов Rcc, можно получить матрицу использования и ресурсов. Эта матрица сбалансирована по столбцам, но не сбалансирована по строкам. Чтобы построить граф использования ресурсов, нужно дуги положительных элементов матрицы Qbb направить от рынков к агентам, а отрицательных – от агентов к рынкам. Таблица 3. Матрица использования и ресурсов. Балансовые модели описывают взаимосвязи выходных и входных переменных (потоки или запасы). Сложение добавленной стоимости ячеек производства дает валовой внутренний продукт Y. В системе национальных счетов (СНС) доход предприятий Y=C+I+G равен сумме потребления C, инвестиции I, государственных расходов G (закрытая система) и чистого экспорта NX= EX–IM (открытая система). Если Y – валовой внутренний продукт (GDP), то NX включает только товары и услуги. Если Y – валовой национальный продукт (GNP), то NX включает доход из-за рубежа (YF): GNP=C+I+G+(EX–IM+YF). Валовой национальный доход (доход резидентов, идущий на потребление и накопление) учитывает трансферты из-за рубежа (TRF): GNDI=C+I+G+(EX–IM+YF+TRF). В круглых скобках счет текущих операций NX. Если T – выплачиваемые налоги, то частные сбережения Sp=GNDI–C–T, излишек государственного бюджета BS=T–G, сбережения S=Y–C–G. Макромодель IS-LM связывает Y со ставкой процента R. Кривая IS описывает зависимость дохода от ставки процента при равновесии на рынке товаров и услуг Y=C(Y,T)+I(R)+G+NX(Y,RER). Здесь потребление C зависит от дохода Y и налога T, инвестиция I – от ставки процента, а чистый экспорт NX – от Y и обменного курса RER. Кривая IS имеет отрицательный наклон, так как увеличение ставки R уменьшает инвестиции и снижает доходы. Кривая LM описывает связь Y и R при равновесии на денежном рынке M/P=L(R,Y). Здесь M/P – отношение денежной массы M к уровню цен P (предложение денег), а L(R,Y) – спрос на деньги. Кривая LM имеет положительный наклон, поскольку R и Y оказывают противоположное влияние на денежный спрос. Пересечение кривых IS и LM дает величины Y* и R* при равновесии на товарном и денежном рынке. Кривая BP описывает взаимосвязь Y и R при внешнем равновесии (баланс официальных расчетов). Платежный баланс включает счет текущих операций и счет операций с активами KA: NX=EX(RER)–IM(Y,RER) и KA(ΔR)=IM(Y,RER)–EX(RER), где ΔR=R–R* – разность внутренней и мировой ставки процента. Внутренняя ставка R зависит от мировой ставки R*: можно получать любые кредиты на международных рынках, не влияя на R* (малая открытая экономика). Если сальдо платежного баланса не равно нулю, точка пересечения кривых IS и LM не лежит на кривой BP. Кривая BP имеет положительный наклон: увеличение Y приводит к росту импорта и к дефициту по текущему счету NX. Равновесие восстановит положительное сальдо счета KA: для привлечения иностранного капитала нужен рост внутренней ставки процента. Наклон кривой BP зависит от склонности к импортированию и мобильности капитала: при низкой мобильности она круче, чем кривая LM. На потоки капитала между странами влияют многие факторы, но самым важным является доход резидентов. Ставки дохода на активы в стране равны номинальной ставке R. Разность номинальной и мировой ставок – это причина оттока (или притока) капитала из страны. Если внутренняя ставка процента выше мировой, иностранные инвесторы найдут привлекательными внутренние активы и приобретут их, резиденты же воздержатся от покупки иностранных активов и станут заимствовать кредиты за границей (приток капитала). Неравновесное состояние баланса текущих операций и платежного баланса, внешние долги неблагоприятно повлияют на состоянии экономики, вызывая экономические спады и финансовые кризисы. Равновесный рост предприятия – движение с оптимизацией цены, выпуска и ресурсов для роста прибыли. Экономика находится в равновесии, если достигается всеми субъектами одновременно, если спрос на товары и услуги равен предложению, если все секторы сбалансированы. Потребитель находится в равновесии, если его доходы и расходы приносят максимальное удовлетворение. Предприятие находится в равновесии, если цена продуктов, выпуск и количество используемых им ресурсов сбалансировано. Владелец ресурсов в равновесии, если использует ресурсы с максимальной выгодой. 14. Потоки Эрланга. Интервалы времени между 1-ым и 2-ым, 2-ым и 3-им,…, n-ым и n+1-ым событием,…T1,T2,…,Tn,… в потоках с ограниченным последействием независимы. Стационарный поток с ограниченным последействием называют потоком Пальма. Случайные интервалы времени T1,T2,…,Tn,… в потоках Пальма имеют один закон распределения. Простейший поток – это поток Пальма. Нестационарный пуассоновский поток не является потоком Пальма. Поток Эрланга k-го порядка получают из простейшего потока путем сохранения каждого k-го события. Промежуток времени T(k) между двумя событиями в потоке Эрланга имеет плотность распределения , t>0, k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение , и, k=1,2,3,… При k=1 закон Эрланга k-го порядка превращается в экспоненциальный закон f(t)=exp(–t) с параметром . Интенсивность потока Эрланга k-го порядка, k=1,2,3,… определяет его основные характеристики, t>0, k=1,2,3,…, и, k=1,2,3,… Интенсивность нормированного потока Эрланга, k=1,2,3,… Промежуток времени между соседними состояниями k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение, , , k=1,2,3,… Плотность распределения нормированного потока Эрланга, t>0, k=1,2,3,… Случайная величина промежутка времени – это среднее арифметическое k независимых случайных величин Ti, i=1,…,k, распределенных по одному и тому же закону распределения (экспоненциальному с параметром ). В силу центральной предельной теоремы она будет иметь распределение, близкое к нормальному с математическим ожиданием 1/ и дисперсией 1/k2. Поскольку дисперсия уменьшается с ростом k, промежуток времени между соседними событиями нормированного потока Эрланга становится все менее случайным и по закону больших чисел приближается по вероятности к математическому ожиданию 1/. Поток Эрланга приближается с ростом k к регулярному потоку с промежутком времени 1/ между событиями. Это свойство потоков Эрланга выявляет роль k как меры «последействия»: от полного отсутствия последействия при k=1 (простейший поток) до жесткого последействия при k (регулярный поток). Для моделирования реального потока с последействием применяется нормированный поток Эрланга с почти тем же математическим ожиданием и дисперсией интервала времени между соседними событиями. С помощью потоков Эрланга немарковские процессы можно сводить к марковским процессам. Пример 7. Наблюдения за работой рекламного агентства показали, что среднее значение интервала времени T между соседними поступлениями заказов M[T]=1 неделя и стандартное отклонение T=4 дня. Интенсивность и стандартное отклонение нормированного потока Эрланга (заказ в неделю) и. Отсюда k=(7/4)2=3,067. Ближайшее целое число – порядок k=3. Плотность распределения вероятностей случайного интервала времени, t>0. Вероятность, что интервал времени между двумя заказами больше 3 и меньше 5 дней. Интегрируя по частям, получим, и. Интегрируя по частям, получим. Таким образом, p=0,189. Пуассоновские потоки событий и дискретные марковские процессы с непрерывным временем тесно связаны. Случайный процесс с непрерывным временем в системе с дискретными состояниями будет марковским, если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими (стационарными или нестационарными). Такие системы с непрерывным временем называются пуассоновскими. Исследование случайного процесса проводится по алгоритму: (1) Описать каждое состояние системы; (2) Составить граф состояний, указать возможные переходы из состояния в состояние; (3) Задать интенсивности потоков событий, под влиянием которых осуществляются эти переходы; (4) Указать начальное состояние системы (при t=0). Пример 8. Банкоматы B1 и B2 могут «отказывать» независимо друг от друга (выходить из строя). Потоки отказов B1 и B2 с интенсивностями 1=4 и 2=3 (отказа в неделю) – пуассоновские. После отказа каждый банкомат сразу ремонтируется (восстанавливается). Потоки восстановлений B1 и B2 с интенсивностями 1=5 и 2=2 (восстановлений в неделю) – пуассоновские. Потоки с постоянными интенсивностями являются простейшими. Система S может находиться в четырех состояниях: s11 – оба банкомата исправны; s12 – банкомат B1 исправен, а B2 ремонтируется; s21 – банкомат B1 ремонтируется, а B2 исправен; s22 – банкоматы ремонтируются. Размеченный граф состояний системы изображен на рис.10, а матрица плотностей вероятностей переходов дана в таблице 5. Рис.10. Граф состояний системы двух банкоматов. Таблица 5. Матрица плотности вероятностей. Составим систему уравнений Колмогорова: В начальный момент времени t=0 система находилась в состоянии s12:, , ,. Условие нормировки p11(t)+p12(t)+p21(t)+p22(t)=1 (t0). С учетом условия нормировки получаем неоднородную систему трех линейных дифференциальных уравнений первого порядка:, ,. Общее решение однородной системы, ,. Для нахождения решений неоднородной системы применим метод вариации постоянных, рассматривая c1,c2,c3 как неизвестные функции от t. Подставляя решение однородной системы, получим систему линейных уравнений для dc1/dt, dc2/dt и dc3/dt. После ее решения и интегрирования найдем функции,, , где b1, b2 и b3 – постоянные интегрирования. Для их определения используем начальные условия:, ,. Решение этой системы уравнений методом Крамера дает, ,. Подставив эти значения, получим общее решение неоднородной системы:, ,. Функцию p22(t) находят из условия нормировки:. При t=2 будем иметь, , ,. Во втором квартале система S будет находиться вероятнее всего в состоянии s12: банкомат B1 будет работать, а B2 – ремонтироваться. Дискретный процесс с непрерывным временем является марковским, если каждый из потоков, переводящих систему из состояния в состояние, является пуассоновским потоком. Преобразование Лапласа Спектральная плотность сигнала v(t). Это преобразование Фурье сигнала v(t). Обратное преобразование Фурье. Сигналу v(t) можно сопоставить спектральную плотность V() в том случае, если сигнал абсолютно интегрируем:. Если экономическую систему возбуждают источники потока y(t), а искомые переменные x(t) являются запасами, то ее поведение описывается уравнением, где квадратная матрица T(p)=G+pC, а G и C не зависят от комплексной частоты p. Допустим, что система уравнений решена, а выходная функция F(p)=cTX(p). Формальное решение, где T+(p) – присоединенная матрица. Линейные выходные функции имеют общий знаменатель, равный определителю матрицы T(p). Определитель и любой элемент присоединенной матрицы T+ – это полиномы от p, а F(p) – рациональная функция комплексной переменной p вида F(p)=N(p)/D(p). Знаменатель функции системы D(p)=|T|, а числитель N(p)=|Tcy|. Если изображение есть дробь F(p)=K1/(p–p1) с полюсом p1 и вычетом K1, то. Обращение преобразования Лапласа заключается в вычислении для. Нужно найти условие, при котором интеграл можно представить в виде. Замкнем контур интегрирования в левой полуплоскости полуокружностью с радиусом, которой растет с пределами интегрирования. Если выполнить условие равенства нулю интеграла вдоль этой бесконечной полуокружности, то интеграл равен сумме вычетов. Введем p=Rexp(i) с dp=iRexp(i)d:. На полуокружности в левой полуплоскости, ограниченной точками iR и –iR, величина R постоянна. При больших R преобладают члены старших степеней и выражение для интеграла можно упростить. Интеграл конечный. Чтобы обеспечить равенство нулю выражения при R, нужно выбрать M и N, чтобы R в знаменателе имел положительную степень. Интеграл от рациональной функции I(p) по бесконечной полуокружности равен нулю, если число полюсов MN+2 функции на два больше, чем число ее нулей. Интегрирование рациональной функции при MN+2 вдоль линии, параллельной мнимой оси, дает 2i{сумма вычетов для полюсов слева от линии}, если контур интегрирования замкнуть через левую полуплоскость. Если замкнуть контур через правую полуплоскость, то следует взять сумму вычетов для полюсов справа от линии, а умножить на (–2i). Если f(z) определена в точке ветвления, то значение f(a) является общим для ветвей, полученных при обходе. Если, описывая кривую вокруг точки z=a сколь угодно раз в том же направлении, мы каждый раз будем получать новые ветви, то точка a называется точкой ветвления бесконечного порядка (логарифмическая точка ветвления). Определение коэффициентов полиномов N(p) и D(p) по ряду чисел (pi,N(pi)) и (pi,D(pi)) составляет интерполяционную задачу. Пусть известны значения qi в n+1 точке pi. Нужно найти коэффициенты полинома, проходящего через эти точки. Подставив pi, получим систему уравнений. Наилучшим выбором pj являются равноотстоящие точки, лежащие на единичной окружности комплексной плоскости. Обозначим P=(pij), где i и j принимают значения от 0 до n. Если обозначить, то pk=wk и P=(wij), а решение принимает вид. Исходный полином, определенный в точках pk, представлен в виде,. Это дискретное преобразование Фурье. Оно эффективно при выборе n+1=2m и целом числе m (быстрое преобразование). Дисконтирование достигается преобразованием Лапласа, которое переводит функцию f(t) действительной переменной t в функцию f(p) комплексной переменной p=r+is (r=Rep, s=Imp, i – мнимая единица). При ограниченном росте |f(t)|<exp(r0t) с абсциссой абсолютной сходимости r0>0 этот интеграл сходится при Rep<r0: область определения функции f(p) лежит слева от r=r0. Изображение запаздывающего импульса Хевисайда h(t–) с амплитудой h=1:. Изображение импульса g(t)=[h(t)–h(t–)]/ длительностью :. В пределе 0 получается изображение импульса Дирака (p)=1. Таблица оригиналов f(t) и изображений f(p). (для преобразования Карсона p используется интеграл Бромвича) Изображения являются рациональными функциями p:, и, где pl – нули, а pk – полюса функции f(p). На комплексной плоскости они изображаются соответственно кружками и крестиками. Функцию можно представить суммой простых множителей с вычетами, , ,. Функцию можно представить суммой. При k=1 имеем pk=1 и nk=2, а [(p–pk)f(p)]=p-3:, и,. При k=2 имеем pk=0 и nk=3, а [(p–pk)f(p)]=(p–1)-2:, , , и,. Если f(p)=c(p)/d(p), а c(p) и d(p) – аналитические функции в простом полюсе p1, то resf(p1)=c(p1)/d(p1). Формула Хевисайда применима, если m различных полюсов pk имеют кратности mk:, Если все полюсы простые, то Через компоненты матрицы Прибыль в рыночном сегменте Экономические рынки удобно рассматривать в виде множества секторов, элементы которых имеют общие признаки. Хозяйствующие субъекты сектора более однородны по своему поведению, чем субъекты всего рынка. Устойчивость сегменту придают прибыльные субъекты. Рыночный сегмент характеризуется какими-то свойствами и параметрами. Экстенсивные свойства пропорциональны размеру сегмента (совокупный доход, энтропия, число субъектов). Интенсивные свойства не зависят от размеров сегмента: скорость обращения полезности V определяет условия обмена между сектором и рынком, а уровень цен p отражает издержки рыночного сегмента. Если экономические параметры изменяются во времени, то в секторе протекает экономический процесс. Самопроизвольный процесс приводит рыночный сегмент в такое состояние, когда его экономические свойства больше не изменяются: в секторе установится полное равновесие. Равновесные рыночные сегменты характеризуются распределением Гиббса [3]. Сейчас кажется тривиальным, что при нехватке некоторого блага его цена растет. Однако между эмпирическим фактом и математическим доказательством дистанция огромного размера [1]. В основе доказательства лежит предположение о детерминированности процессов производства товаров и услуг. Оно попросту не учитывает неопределенность будущего, тем самым не затрагивая финансовую сторону экономической деятельности. Такие явления, как денежная инфляция и спекуляция, нельзя объяснить в рамках детерминированного подхода [2]. Предметом нашего исследования является экономическая система ячеек, которые находятся в состояниях полезности. При этом ячейка «погружена» во внешнюю среду, формируемую другими ячейками. Основное занятие ячейки – это распределение товаров и услуг. Совокупность ячеек и среды образует замкнутую экономическую систему. Нас интересует товарные отношение в этой системе. Пусть индекс n нумерует товары полезностями un. Согласно основному принципу статистической механики, если известна вероятность и статистическая сумма то можно найти внутреннюю полезность системы U, накопление W и свободную полезность F как функции скорости обращения полезности V: Эти функции связаны условием баланса U=F+W. Энтропия n-го состояния Энтропия закрытого региона. Экстенсивная переменная S – мера накопления VS, а интенсивная переменная V – ее оценка. И V и S неотрицательны. Изменения Q и Pn с V описываются производными где U зависит от V. Производные энтропии по V зависят от дисперсии и асимметрии дохода: Поскольку 2>0, то S увеличивается со скоростью V, достигая насыщения при V=V3μ3/3μ2, если μ3>0. При 3<0 энтропия ограничена. Производные по V:, и, Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом V. Производные по S:, и Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом S. Скорость обращения полезности V и энтропия S сопряжены на внутренней и свободной полезности: U(S) является потенциалом для скорости обращения полезности V, а F(V) – потенциалом для энтропии S. Накопление W не является потенциалом ни для скорости обращения, ни энтропии. Для учета доходов используем экстенсивную переменную благосостояния Y. Полезность товара un уменьшается с ростом Y, а производные pn(Y)=–dun/dY>0 определяют уровень цен, где вероятность Pn(V,Y) зависит от Y, так как un зависит от Y. Рыночный сегмент имеет две пары сопряженных переменных (S,V), (Y,p) и четыре потенциала F(V,Y), G(V,p), H(S,p) и U(S,Y) с дифференциалами, , и. Свободная полезность F вычисляется по статистической сумме Q(V,Y). Внутренняя полезность U=F+W включает F и W. Свободная полезность G=F+pY включает F и pY, а внутренняя полезность H=F+VS+pY. Переменные S и Y являются экстенсивными факторами, а V и p – интенсивные факторы. Частные производные статистической суммы выражаются в виде: Свободная полезность F(V,Y) является функцией V и Y: Свободная полезность G(V,p)=F+pY является функцией V и p: Внутреняя полезность H(S,p)=G+VS является функцией S и p: Внутреняя полезность U(S,Y)=H–pY является функцией S и Y: Внутрення полезность U растет с энтропией S и уменьшается с доходом Y. Потенциалы полезности F(V,Y), G(V,p), H(S,p) и U(S,Y) аддитивны, а V и p одинаковы для всех всех субъектов сегмента. Поэтому потенциалы должны быть однородными функциями первого порядка по переменным S и Y: где ψ, μ, ν и φ – некоторые функции. Будем рассматривать N как независимую переменную. Тогда в дифференциалы нужно добавить μdN с потенциалом. Оценка μ(V,p) резидентов в открытой экономической зоне оказывается функцией скорости обращения полезности V и уровня цен p. Дифференцируя G по N, получаем (V,p) – оценка μ числа субъектов в сегменте оказывается функцией V и p. Большой потенциал открытой зоны Ω=F–G является функцией V, Y и μ: dΩ=–SdV–pdY–Ndμ. Если полезность n-го резидента в зоне обозначить unN, то вероятность. Накопление полезности в открытой экономической зоне:, , и. Открытая экономическая зона является большим каноническим ансамблем. При описании экономических явлений используют понятие эластичности фактора и показателя [4]. Пусть взаимозависимые переменные x, y и z отвечают любой тройке неповторяющихся факторов S, V, Y и p. Тогда y-ой эластичностью фактора x при неизменном факторе z называется величина xyz=y(x/y)z. Только 16 эластичностей независимы в закрытой системы. Свободная полезность F(V,Y) вычисляется с помощью статистической суммы Q, а другие потенциалы в переменных V и Y – из выражений: Дифференцирование дает Потенциалы в переменных V и p выражаются через G(V,p): Дифференцирование дает Потенциалы в переменных S и p выражаются через H(S,p): Дифференцирование дает Потенциалы в переменных S и Y выражаются через U(S,Y): Дифференцирование дает Эти производные легко вычисляются, если учесть свойства якобианов: Доход Y(F,V) как функция свободной полезности F и скорости обращения имеет частные производные: Скорость обращения полезности V(G,p) как функция свободной полезности G и уровня цен имеет частные производные: Уровень цен p(H,S) как функция внутренней полезности H и энтропии имеет частные производные: Энтропия S(U,Y) как функция внутренней полезности U и благосостояния имеет частные производные: Статистическая оценки важных эластичностей дает: где означает усреднение с учетом вероятности Pn. Экономические процессы в закрытом сегменте сопровождаются ростом энтропии, пока она не достигнет наибольшего значения при полном равновеси. С ростом числа субъектов энтропия растет при фиксированной скорости V и уровне цен p. Это означает, что норма накопления увеличивается с числом субъектов, т.е. с переходом от большого к малому бизнесу. Субъекты малого бизнеса слабо взаимодействуют друг с другом в идеальном сегменте и представляют собой однородную массу, а их прибыль линейно зависит от конъюнктуры. Замечательным достижением статистической экономики является точная формулировка условий равновесия с внешней средой. Процессы, протекающие в замкнутой неравновесной системе, идут таким образом, что система переходит из состояний с меньшей энтропией в состояния с большей энтропией, пока она не достигнет своего наибольшего значения, соответствующего полному равновесию. Энтропия замкнутой системы – сумма энтропий резидентов и внешней среды. Равенство нулю первых производных суммарной энтропии является только необходимым условием экстремума и не дает того, чтобы энтропия имела именно максимум. Для выяснения достаточных условий необходимо вычислить второй дифференциал суммарной энтропии. Это исследование удобнее провести, исходя не из условия максимума суммарной энтропии, а из эквивалентного ему условия. Выделим из системы некоторую малую часть, а остаток будем рассматривать как внешнюю среду со скоростью обращения V0 и уровнем цен p0. Тогда в равновесии имеет минимум величина U–V0S+p0Y с внутренней полезностью U, энтропией S и доходом Y. При всяком малом отклонении от равновесия ее изменение должно быть положительным: Разлагая δU в ряд, получаем с точностью до членов второго порядка: где производные взяты в состоянии равновесия. Но поскольку то члены первого порядка сокращаются. Это необходимые условия равновесия: скорость обращения полезности V и уровень цен p для резидентов равны этим же величинам внешней среды. Достаточное условие равновесия имеет вид: Для того, чтобы такое неравенство имело место при произвольных δS и δY, нужно удовлетворить два неравенства: Поскольку то первое неравенство удовлетворяется при Второе неравенство можно записать в виде якобиана Переходя к переменным V и Y, имеем Поскольку p=p0>0 и SV0,Y>0, то это равносильно условию Уровень цен должен уменьшаться с ростом благосостояния при постоянной скорости обращения полезности. Эти экономические неравенства гарантируют устойчивость равновесной системы. Для SV0,Y>0 нужно, чтобы средний квадрат внутренней полезности u2 превышал квадрат среднего U2, а дисперсия была положительной. Поскольку для устойчивости равновесия необходимо, чтобы dp/dY было отрицательным и по модулю превышало отношение дисперсии уровня цен к скорости обращения. При любом начальном состоянии закрытой системы с течением времени в ней установится единственное состояние – равновесие. Эта тенденция означает монопольное возрастание энтропии во времени и увеличение разности энтропий S=S–S0 от отрицательных значений до нуля. Эти утверждения эквивалентны, и они отражают тот факт, что равновесие является глобальным асимптотически устойчивым состоянием, энтропия – функцией Ляпунова. Если только свободная полезность F(V,Y) будет иметь несколько минимумов при неизменных V, Y и различных значениях N, то стабильному состоянию будет отвечать наименьшее значение F, а метастабильному – самый мелкий минимум с наибольшим F. Такие состояния легко разрушаются переходом системы в устойчивое состояние с наименьшей свободной полезностью. Если системы переходит из одного состояния в другое с изменением ее внутренней полезности при неизменном накоплении, то обратный переход нельзя осуществить без воображаемого внешнего источника R. Прямому переходу с совершением максимальной работы |Rmax| отвечает обратный переход c работой Rmin внешнего источника. Изменение внешней полезности ΔU при изменении состояния состоит из трех частей: из произведенной работы внешнего источника R, из работы внешней среды p0ΔY0 и из полученной из нее V0ΔS0: где индекс 0 относится к внешней среде. Поскольку затраты среды равны доходу ΔY0=–ΔY, а в силу закона возрастания энтропии S0–S, то где знак равенства достигается при обратимом процессе. Переход совершается с минимальной работой, если он происходит обратимо: Обратный переход также совершается с минимальной работы, если происходит обратимо: Пусть SΣ есть полная энтропия. Если резиденты находятся в равновесии с внешней средой, то SΣ является функция их внутренней полезности UΣ.. Если же резиденты не находятся в равновесии с внешней средой, то суммарная энтропия отличается от SΣ(UΣ) на величину Но dU/dS является равновесной скоростью обращения полезности V0. Таким образом, получаем Эта формула определяет, как отличается энтропия замкнутой системы от своего возможного значения, если резиденты не находятся в равновесии со средой. Рассмотрим закрытую систему с энтропией SΣ. Пусть β – некоторый фактор, обеспечивающий ее внутреннее равновесие, т.е. S/=0. Пусть α – другой фактор, обеспечивающий при внутреннем равновесии системы и ее равновесие с внешней средой, т.е. S/=0. Введем обозначения Энтропия SΣ замкнутой системы максимальна при полном равновесии. Чтобы энтропия была максимальной, кроме необходимых условий А=0 и В=0, должны выполняться неравенства Уже незначительные изменения фактора α при некотором воздействии на закрытую систему приводят к изменению A на величину Изменение α при постоянном β приводит к нарушению условия внутреннего равновесия системы B=0. После того, как это равновесие восстановится, величина ΔA будет иметь значение Используя свойства якобиана, находим С учетом неравенств получаем новое неравенство Это неравенство выражает принцип Ла Шателье [6]. Рассмотрим изменение Δα фактора α как меру внешнего воздействия на систему, а ΔΑ – κак меру изменения системы под его влиянием. Тогда Значение ΔΑ уменьшается при восстановлении внутреннего равновесия системы после внешнего воздействия, выводящего ее из равновесия. Другими словами, внешнее воздействие, выводящее систему из равновесия, стимулирует в системе процессы, стремящиеся ослабить его влияние. Изменение энтропии системы –Rmin/V0 зависит от скорости обращения полезности во внешней среде V0 и минимальной работы Rmin, необходимой для приведения системы из состояния равновесия с внешней средой в данное состояние. Поэтому можно написать где для бесконечно малого изменения состояния системы резидентов Все величины без индекса относятся к резидентам, а с индексом 0 – к среде. Пусть α есть энтропия S. Тогда A=V/V0–1 и в равновесии V=V0, неравенства принимают вид Рост энтропии означает, что в систему инвестируется оборотный капитал. В итоге нарушается равновесие резидентов и, в частности, увеличивается скорость обращения полезности на величину (V). Восстановление равновесия резидентов приводит к тому, что изменение скорости обращения уменьшится до (V)B=0. т.е. как бы ослабляется результат воздействия, выводящего резидентов из равновесия. Если в неравенстве в качестве фактора β взять доход Y, то будем иметь поскольку условие В=0 означает, что случае p=p0. Подстановка дает неравенство Используя свойства якобиана, можно получить Пусть α есть налог Y. Тогда A=1–V/V0 и в равновесии V=V0, а неравенства принимают вид Если в неравенстве в качестве фактора β взять энтропию S, то условие В=0 означает, что V=V0 и В устойчивой системе величина (p/Y)V должна быть отрицательной. Используя свойства якобиана, можно получить В устойчивой системе величина (S/V)p должна быть положительной. Основной недостаток идеального сегмента состоит в том, что полезность расходится при Y=0. Этот коллапс не должен допускаться государством, которое может установить минимальный предел Y0. Рассмотрим процесс L в экономической системе, которая не находится в равновесии с внешней средой. Пусть B – накопление, полученное системой из внешней среды со скоростью обращения полезности V0. Процесс L перехода из состояния 1 в состояние 2 нельзя реализовать, если нарушается неравенство где S1 и S2 – энтропии состояний, а интегрирование проводится по траектории процесса. Равенство применимо только при обратимом процессе. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы и не зависит от ее промежуточных состояний Дифференциал внутренней полезности в замкнутой системе содержит малое накопление B и малое потребление A, которые не являются дифференциалами в общем случае. Переведем идеальную систему из начального состояния 1 в промежуточное состояние 2 при неизменной энтропии: где. Выпуск и потребление положительны, если. Переведем теперь систему из состояния 2 в промежуточное состояние 3 при неизменной ренте: Переведем далее систему из состояния 3 в промежуточное состояние 4 при неизменной конъюнктуре: Наконец, переведем систему из состояния 4 в начальное состояние 1 при неизменной ренте: При этот цикл оказывается замкнутым. В начальном состоянии 1 идеальная система имеет низкую конъюнктуру и низкую ренту. Переход в состояние 2 при низкой конъюнктуре сопровождается увеличением ренты и цены, а капитал убывает потому, что выпуск равен потреблению (накопление не меняется). Переход в состояние 3 при высокой ренте сопровождается увеличением конъюнктуры и капитала, а цена уменьшается, потому что выпуск отсутствует (инвестиция накоплений в производство повышает его конъюнктуру). Переход в состояние 4 при высокой конъюнктуре сопровождается уменьшением ренты и цены, а капитал увеличивается, потому что потребление равно выпуску (накопление не изменяется). Переход в начальное состояние 1 при низкой ренте сопровождается уменьшением конъюнктуры и капитала, а цена увеличивается, потому что выпуск отсутствует (конфискация накопления из производства понижает его конъюнктуру). Коэффициент полезного действия этого замкнутого экономического цикла определяется следующим образом: Инвестиция S2=S23>0 и конфискация S1=S41<0 удовлетворяют соотношению Это соотношение справедливо только для замкнутого цикла. Макроскопическая теория выпусков и затрат использована для описания экономических циклов системы многих резидентов на основе модели В.В.Леонтьева. Основные понятия макроэкономики развиты в русле детерминированного подхода, дополненного соображениями оптимальности и полезности [1,2]. Может быть поэтому нет строгого определения конъюнктуры как меры эффективной деятельности экономической системы. Вместе с тем, этот термин используется [3]. Эвристические соображения известных экономистов о конъюнктуре близки к определению температуры как производной внутренней энергии системы по ее энтропии [4,5]. Аналогом внутренней энергии в экономике является внутренняя полезность, но она должна быть определена в рамках вероятностного подхода. Необходимость такого подхода отмечалась в связи с инфляционными процессами современной экономической жизни [6]. Полезность un зависит от индекса благосостояния Y, причем при Y=1 она равна нулю, а цена благосостояния pn(Y)–dun/dY не может быть отрицательной, так как un уменьшается с ростом Y. Согласно основного принципа статистической экономики, если известны статистическая сумма Q, вероятность Pn, энтропия S и уровень цен p, , и, то можно найти макроскопические показатели закрытой системы при скорости обращения полезности V и индексе благосостояния Y. Показателями закрытой системы являются внутренняя полезность U=F+W, свободная полезность F и накопление W, и, а ее факторами являются скорость обращения полезности V, энтропия S, индекс благосостояния Y и уровень цен p. Для простой закрытой системы, а свободная полезность (потребление) выражается в виде, где f(V)=VlnL(V). Энтропия и уровень цен простой системы даются уравнениями состояния и. Полуэластичности этих двух факторов и. Для устойчивости закрытой системы необходимо и достаточно иметь =const, =const и SV,Y>0, pY,V<0. Простая система устойчива, если d2f/dV2<0. Свободная полезность G=F+pY в простой системе определяется с учетом уравнения состояния:, а энтропия и индекс благосостояния выражаются в виде и. Полуэластичности этих факторов и. Идеальной называется простая система с SV,Y=N0>0 и, где f0 и – постоянные интегрирования. Внутренняя полезность U=F+W такой системы определяется с учетом уравнения состояния:, где =1+N/N0>1. Удобно выбрать f0=–S0 и, чтобы внутренняя полезность исчезала при энтропии S11=S(V=1,Y=1) и индексе Y=1:. В этом случае и, а внутренняя полезность являются линейной функцией скорости обращения полезности U=N0(V–1). Свободная полезность идеальной системы и ее энтропия – нелинейные функции скорости обращения полезности и индекса благосостояния и. Зависимость энтропии идеальной системы S(V,Y) от конъюнктуры V приводится на рис.1 для двух значений индекса благосостояния Y. Рис.1. Зависимость энтропии от конъюнктуры. Используются данные для высокоэластичной экономики с небольшим числом резидентов, представляющих отрасли народного хозяйства [3] (N0=10, S11=3 и N=10). Рост энтропии с конъюнктурой свидетельствует о структурных изменениях системы, сопровождаемых линейным увеличением внутренней полезности. Этот рост замедляется с уменьшением индекса благосостояния. Уравнение состояния pY=NV связывает большую полезность pY с числом резидентов N и конъюнктурой V идеальной системы. При неизменной конъюнктуре уровень цен уменьшается с ростом индекса благосостояния (деинфляция). Рассмотрим квазистатический процесс L в системе резидентов, которые не находятся в равновесии с внешней средой. Малое накопление B система резидентов получит из окружающей среды с равновесной конъюнктурой V0. Переход системы резидентов из состояния 1 с энтропией S1 в состояние 2 с энтропией S2 нельзя реализовать, если нарушается неравенство, где интегрирование проводится по траектории процесса L. Равенство применимо при обратимых процессах. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы. Дифференциал внутренней полезности закрытой системы dU=B+A=VdS–pdY содержит малое накопление B и малое потребление А, которые не являются дифференциалами. В состоянии 1 система имеет энтропию S1 и конъюнктуру V1. Переведем систему из начального состояния 1 в состояние 2 при неизменной энтропии: и. Переход в состояние 2 с конъюнктурой V2>V1 сопровождается уменьшением индекса благосостояния Y и увеличением уровня цен p, потому что прирост полезности потребляется (рис.1). Переведем систему из состояния 2 в состояние 3 при неизменной конъюнктуре:, и. Переход в состояние 3 с энтропией S3>S1 сопровождается увеличением Y и уменьшением p, потому что внутренняя полезность не изменяется (инвестиция накоплений в систему повышает энтропию). Зависимость индекса благосостояния Y от уровня цен p приводится на рис.2 для той же высокоэластичной системы при S1=1, V1=1, V2=3 и S3=3. Рис.2. Зависимость индекса от ставки затрат. Переведем систему из состояния 3 в состояние 4 при неизменной энтропии: и. Переход в состояние 4 с конъюнктурой V4<V2 сопровождается увеличением Y и уменьшением p. Переведем систему из состояния 4 в состояние 1 при неизменной конъюнктуре:, и. Переход в состояние 1 с энтропией S1 и конъюнктурой V4=V1 сопровождается уменьшением Y и увеличением p из-за конфискации накоплений окружающей средой. Коэффициент полезного действия экономического цикла. Инвестиция B2=B23>0 и конфискация B1=B41<0 удовлетворяют соотношению. Это соотношение справедливо только для замкнутого цикла. Современному состоянию экономики Украины отвечает одна из нижних точек на траектории L12 c энтропией S1 и конъюнктурой VV2. Движение по этой траектории с падением индекса благосостояния Y и увеличением уровня цен p разогревает экономику до такой конъюнктуры V2, при которой возможны структурные изменения отношений резидентов на траектории L23. Движение по траектории с ростом Y и уменьшением p хаотизирует экономику до значения энтропии S3, которое зависит от инвестиции накоплений. Определению кризисной точки более отвечает состояние экономики с энтропией S1 и конъюнктурой V1, а квазистатический процесс L41 имеет периода застоя. Ему предшествует движение по траектории L34, которое ведет к охлаждению экономических отношений. |
|||||
|
А.Володя |
Школьно-зрелый |
высокий |
сформирована |
Высокий |
|
|
А. Толя |
Школьно зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Б. Егор |
средний |
сформирована |
Средний |
||
|
В. Андрей |
Средне зрелый |
высокий |
сформирована |
Высокий |
Средний |
|
Г. Лана |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Д. Катя |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Д. Артур |
незрелый |
высокий |
средний |
Средний |
|
|
Е. Аня |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
И.-А. Карина |
Школьно-зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
К. Витя |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Л. Маша |
Средне зрелый |
высокий |
сформирована |
Высокий |
|
|
Л. Аня |
незрелый |
высокий |
сформирована |
Высокий |
Средний |
|
М. Айсен |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
М. Даша |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Н. Юля |
Школьно-зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
Н. Маша |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
О. Алена |
Средне зрелый |
высокий |
сформирована |
Высокий |
|
|
П. Валя |
Средне зрелый |
средний |
сформирована |
Средний |
Средний |
|
П. Семен |
незрелый |
средний |
сформирована |
Низкий |
Низкая |
|
Полезность парных сравнений. Прокоп О.М. Научный руководитель проф. На множестве элементов Х={х1,...,хт} определена семья отношений преобладания ={,,,,}, первым из которых является отношение «не хуже» (). Функция полезности удовлетворяет условию:). Это означает, что элемент x1X не хуже элемента x2X, если полезность f(x1) элемента х1 не меньше полезности f(x2) элемента х2. Таким образом, функция полезности f отображает отношение преобладания на множестве X. Можно убедиться, что она отображает и все другие отношения семьи . В частности, отображение основных отношений «равноценно» () и «лучшее» ():),). Всегда ли бинарное отношение преобладания можно отобразить функцией? Утвердительный ответ для счетного множества дал Кантор, а для несчетного – Милграм и Биркгоф. Очень важную теорему доказал Дебре: отношение преобладания «не хуже» на компактном множестве XRn можно отобразить функцией полезности, если оно непрерывно на X. Если множество допустимых элементов X представляет собой компакт в Rn, то непрерывная на этом множестве функция достигает наибольшего значения (теорема Вейєрштрасса). Множество элементов, доставляющих максимум функции f на множестве X, не пусто. Поскольку эти элементы являются максимальными по отношению преобладания , что отображается функцией полезности f, то множество преобладающих элементов не пусто. Вместе с функцией ценности f все отношения преобладания семьи отображает другая функция, полученная возрастающим преобразованием. Если u=f(х), хX – функция полезности, а v=g(и) – возрастающая функция переменной u, то сложная функция v=g(f(x)), хX также является функцией полезности. Функция полезности, заданная с точностью до произвольного монотонно возрастающего преобразования, называется порядковой. Если же функция полезности задана с точностью до произвольного положительного линейного преобразования v=f(x)+, где ,>0, ее называют интервальной. Особенность интервальной функции полезности состоит в том, что она (в отличие от порядковой) позволяет не только определять, что один элемент преобладает над другим, а и то, как различаются элементы по преобладанию. Если функция полезности f положительна и задана с точностью до любого множителя , то есть w=f(x), >0, то ее называют относительной. Она показывает, в сколько раз один элемент преобладает над другим. При сравнении двух элементов xі и xj множества важно знать, в какой степени один элемент преобладает над другим. Если при сравнении элемента xі с элементом xj первый элемент получил указанный в таблице 1 ранг, то другой элемент получает ранг, обратный к рангу первого элемента. Таблица 1. Шкала относительной важности объектов Степень важности Определение 1 Объекты равноценны 3 Объект немного лучше другого 5 Объект лучше другого 7 Объект намного лучше другого 9 Объект гораздо лучше другого 2,4,6,8 Промежуточные суждения По результатам парных сравнений образуем mm-матрицу A=(aij), элемент которой aij дает оценку преобладания элемента хi в сравнении с элементом xj (i,j=1,…,т). Пусть (w1,...,wт) – набор истинных полезностей элементов множества X. Если парные сравнения будут взаимно согласованы, должны выполняться соотношения aij=wi/wj для i,j=1,…,т. Это означает, что аii=1 и аji=1/aij для i,j=1,…,т. Последнее соотношение означает, что если элемент xі лучше элемента xj в >1 раз, то полезность xj составит 1/ часть от ценности xj. Взаимная согласованность парных сравнений означает также, что должны выполняться соотношения аij=akj/aki для i,j,k=1,…,m. Если хk лучше хi в раз, а хi лучше xj в раз, то хk лучше xj в раз. Для заполнения матрицы A достаточно задать одну строку (один столбец). В самом деле, если заполнена первая строка этой матрицы (а11,...,а1i,...,а1т), то ее i-ая строка (i=2,…,т) заполняется по правилу aij=a1j/a1i (j=1,…,n). При полной согласованности элементов выполняется соотношение: Вектор относительной полезности (w1,…,wm)T – собственный вектор матрицы А для ее собственного значения =т. Для согласованной матрицы – это наибольшее собственное значение (спектральный радиус матрицы), а другие собственные значения равны нулю. Это свойство согласованных парных сравнений можно использовать в случае, если допущены ошибки. После построения матрицы парных сравнений относительные полезности элементов можно получить как компоненты собственного вектора w для собственного значения max. Чем ближе max к т, тем лучше согласованы парные сравнения элементов. Индекс согласованности (индекс Саати). Если значение индекса меньше 10 % от эталонных значений таблицы 2, то результаты парного сравнения считают удовлетворительными. Если значение индекса больше 10 %, то результаты считают неудовлетворительными, и тогда нужно уточнить оценки относительной важности элементов в парных сравнениях. Таблица 2. Эталонные значения индекса согласованности. Способ приближенного вычисления относительной полезности элементов состоит в использовании среднего геометрического элементов каждой строки матрицы:, i=1,…,m. Предположим, что вы решаете, в каком кафе провести свободное время. Выбор ограничен тремя кафе 1, 2 и 3. Они обеспечивают качественное обслуживание клиентов. В кафе 1 свободен доступ в «Интернет», а в кафе 3 много посетителей. Кафе 2 находится ближе к вашему дому. Результаты парного сравнения кафе: <1:2>=3 – есть некоторые основания считать кафе 1 лучше кафе 2; <1:3>=7 – уровень обслуживания в кафе 1 значительно лучше, чем в кафе 3; <2:3>=3 – уровень обслуживания в кафе 2 и 3 почти одинаков, но число посетителей в кафе 2 меньше, и оно расположено ближе к дому. По этим результатам составляем матрицу парных сравнений:. По методу среднего геометрического, находим,,. Оценим собственное значение, которому отвечает этот вектор полезностей. Для этого вычислим произведение. Чтобы оценить max, делим покомпонентно вектор Аw=(2,013;0,73;0,264)T на вектор относительных полезностей w=(0,669;0,243;0,088)T. Получим вектор (3,007;3,007;3,007)T. Собственное значение:. Индекс согласованности. составляет 0,6 % от эталонного значения показателя согласованности:. Уровень согласованности достаточно высок, а относительными полезностями кафе 1, 2 и 3 можно считать: w1=0,669; w2=0,243; w3=0,088. Если принять <1:2>=3 – есть основания считать кафе 1 лучше кафе 2; <1:3>=9 – уровень обслуживания в кафе 1 гораздо лучше, чем в кафе 3; <2:3>=3 – есть основания считать кафе 2 лучше кафе 3, то согласие парных сравнений полное max=3 и J=0: w1=0,692; w2=0,231; w3=0,077. При большом числе объектов этот метод слишком громоздок, что присуще всем методам, основанным на парном сравнении элементов. 2. Потоки и запасы В экономике три категории агентов: предприятия E, домохозяйства H и все другие агенты V. Агенты E производят товары и услуги. Агенты H их потребляют. Агенты V оказывают услуги по распределению созданных благ. Стоимость произведенной в стране конечной продукции равна расходам по ее приобретению, а валовой внутренний продукт (ВВП) можно получить как сумму конечных расходов Y=C+I (C – потребление, I – инвестиции). Добавленная стоимость – доходы агентов, а ВВП равен сумме факторных доходов Y=L+K (L и K – оплата труда и капитала). Плата за капитал включает амортизационные расходы, арендную плату, проценты, страховку и прибыль. Потоки Y, C и I связывают агентов с рынком товаров и услуг MP. Другие потоки связывают их с рынком ресурсов MR и другими рынками M. Отобразим агентов и рынки вершинами графа, потоки – дугами. Модель взаимодействия агентов E, H и V на рынках MP, MR и M дана на рис.1. Доход MP|E=Y предприятия E получают на рынке товаров и услуг MP, где H и V несут расходы C(MP|H) и I(MP|F). Домохозяйства получают доход R(MR|H) на рынке ресурсов MR, где предприятия несут расходы L(E|MR). Другие агенты V получают доход W(M|V) на рынках M, где несут расходы предприятия K(E|M) и домохозяйства S(H|M). Условия баланса рынков, и. Условия баланса агентов, и. Здесь I – инвестиции в товары и услуги, Q – инвестиции в ресурсы. Рис.1. Потоки доходов и расходов. Направленный граф рис.1 на шести вершинах содержит девять дуг потоков. Если удалить вершину графа V и инцидентные ей дуги, оставшаяся часть графа не сбалансирована. Удаленная часть графа становится деревом графа, если ее дополнить дугами V|E и V|H с нулевыми потоками. На рис.2 ветви дерева изображены пунктирными линиями, а хорды дополнения дерева – сплошными линиями. Множество дуг замкнутого графа – объединение его ветвей и хорд. Для графа рис.2 вектор потоков ветвей Ib=(I,Q,–W,0,0), а запасы ветвей Vb=(I,Q,W,0,0). Потоки хорд Ic=(Y,R,L,C,K,S). Матрица потоков хорд Icc=diag(Ic). Рис.2. Дерево графа и его дополнение. Топологические свойства дополнения дерева описывают матрицы инцидентности таблиц 1. Элемент матрицы Dbc равен 1, если i-ая вершина начальная для j-ой хорды, и 0 в противном случае. Элемент матрицы Cbc равен 1, если i-ая вершина конечная для j-ой хорды, и 0 в противном случае. Унимодулярная матрица инцидентности Abc=Cbc–Dbc. Таблица 1. Матрицы инцидентности дополнения дерева. Dbc MP|E MR|H E|MR H|MP E|M H|M Cbc MP|E MR|H E|MR H|MP E|M H|M MP 1 0 0 0 0 0 MP 0 0 0 1 0 0 MR 0 1 0 0 0 0 MR 0 0 1 0 0 0 MF 0 0 0 0 0 0 MF 0 0 0 0 1 1 E 0 0 1 0 1 0 E 1 0 0 0 0 0 H 0 0 0 1 0 1 H 0 1 0 0 0 0 Потоки ветвей и запасы хорд и выражают законы Кирхгофа: алгебраическая сумма потоков в вершине графа и запасов в контуре графа равна нулю. Потоки и запасы дуг даны на рис.2. Мощность дуги – произведение ее потока на запас. Дуги с положительной мощностью – ресурсы, дуги с отрицательной мощностью – использования. Мощность ветвей и хорд и. Сравнение дает теорему Тевенина: Mb+Mc=0 – мощность замкнутого графа равна нулю. В таблице 2 представлена матрица потоков и матрица сальдо и. Таблица 2. Матрица проводок и матрица сальдо. Pbb MP MR M E H Sbb MP MR M E H Ib MP 0 0 0 Y 0 MP 0 0 0 Y –C I MR 0 00 0 R MR 0 0 0 –L R Q M 0 0 0 0 0 M 0 0 0 –K –S –W E 0 L K 0 0 E –Y LK 0 0 0 H C0 S 0 0 H C –R S 0 0 0 –Ib –I –Q W 0 0 0 Если I=Y–C>0, то рынок товаров и услуг MP находится в активном состоянии (I – инвестиции в товары и услуги). Если Q=R–L>0, то рынок ресурсов MR находится в активном состоянии (Q – инвестиции в ресурсы). Поскольку W+I+Q=0 и W<0, то рынки M находятся в пассивном состоянии. Агенты E и H сбалансированы. Потоки ресурсов направлены от агентов к рынкам, а потоки использования – от рынков к агентам. Выделяя в матрице потоков Icc потоки использования Ucc и потоки ресурсов Rcc, можно получить матрицу использования и ресурсов. Эта матрица сбалансирована по столбцам, но не сбалансирована по строкам. Чтобы построить граф использования ресурсов, нужно дуги положительных элементов матрицы Qbb направить от рынков к агентам, а отрицательных – от агентов к рынкам. Таблица 3. Матрица использования и ресурсов. Балансовые модели описывают взаимосвязи выходных и входных переменных (потоки или запасы). Сложение добавленной стоимости ячеек производства дает валовой внутренний продукт Y. В системе национальных счетов (СНС) доход предприятий Y=C+I+G равен сумме потребления C, инвестиции I, государственных расходов G (закрытая система) и чистого экспорта NX= EX–IM (открытая система). Если Y – валовой внутренний продукт (GDP), то NX включает только товары и услуги. Если Y – валовой национальный продукт (GNP), то NX включает доход из-за рубежа (YF): GNP=C+I+G+(EX–IM+YF). Валовой национальный доход (доход резидентов, идущий на потребление и накопление) учитывает трансферты из-за рубежа (TRF): GNDI=C+I+G+(EX–IM+YF+TRF). В круглых скобках счет текущих операций NX. Если T – выплачиваемые налоги, то частные сбережения Sp=GNDI–C–T, излишек государственного бюджета BS=T–G, сбережения S=Y–C–G. Макромодель IS-LM связывает Y со ставкой процента R. Кривая IS описывает зависимость дохода от ставки процента при равновесии на рынке товаров и услуг Y=C(Y,T)+I(R)+G+NX(Y,RER). Здесь потребление C зависит от дохода Y и налога T, инвестиция I – от ставки процента, а чистый экспорт NX – от Y и обменного курса RER. Кривая IS имеет отрицательный наклон, так как увеличение ставки R уменьшает инвестиции и снижает доходы. Кривая LM описывает связь Y и R при равновесии на денежном рынке M/P=L(R,Y). Здесь M/P – отношение денежной массы M к уровню цен P (предложение денег), а L(R,Y) – спрос на деньги. Кривая LM имеет положительный наклон, поскольку R и Y оказывают противоположное влияние на денежный спрос. Пересечение кривых IS и LM дает величины Y* и R* при равновесии на товарном и денежном рынке. Кривая BP описывает взаимосвязь Y и R при внешнем равновесии (баланс официальных расчетов). Платежный баланс включает счет текущих операций и счет операций с активами KA: NX=EX(RER)–IM(Y,RER) и KA(ΔR)=IM(Y,RER)–EX(RER), где ΔR=R–R* – разность внутренней и мировой ставки процента. Внутренняя ставка R зависит от мировой ставки R*: можно получать любые кредиты на международных рынках, не влияя на R* (малая открытая экономика). Если сальдо платежного баланса не равно нулю, точка пересечения кривых IS и LM не лежит на кривой BP. Кривая BP имеет положительный наклон: увеличение Y приводит к росту импорта и к дефициту по текущему счету NX. Равновесие восстановит положительное сальдо счета KA: для привлечения иностранного капитала нужен рост внутренней ставки процента. Наклон кривой BP зависит от склонности к импортированию и мобильности капитала: при низкой мобильности она круче, чем кривая LM. На потоки капитала между странами влияют многие факторы, но самым важным является доход резидентов. Ставки дохода на активы в стране равны номинальной ставке R. Разность номинальной и мировой ставок – это причина оттока (или притока) капитала из страны. Если внутренняя ставка процента выше мировой, иностранные инвесторы найдут привлекательными внутренние активы и приобретут их, резиденты же воздержатся от покупки иностранных активов и станут заимствовать кредиты за границей (приток капитала). Неравновесное состояние баланса текущих операций и платежного баланса, внешние долги неблагоприятно повлияют на состоянии экономики, вызывая экономические спады и финансовые кризисы. Равновесный рост предприятия – движение с оптимизацией цены, выпуска и ресурсов для роста прибыли. Экономика находится в равновесии, если достигается всеми субъектами одновременно, если спрос на товары и услуги равен предложению, если все секторы сбалансированы. Потребитель находится в равновесии, если его доходы и расходы приносят максимальное удовлетворение. Предприятие находится в равновесии, если цена продуктов, выпуск и количество используемых им ресурсов сбалансировано. Владелец ресурсов в равновесии, если использует ресурсы с максимальной выгодой. 14. Потоки Эрланга. Интервалы времени между 1-ым и 2-ым, 2-ым и 3-им,…, n-ым и n+1-ым событием,…T1,T2,…,Tn,… в потоках с ограниченным последействием независимы. Стационарный поток с ограниченным последействием называют потоком Пальма. Случайные интервалы времени T1,T2,…,Tn,… в потоках Пальма имеют один закон распределения. Простейший поток – это поток Пальма. Нестационарный пуассоновский поток не является потоком Пальма. Поток Эрланга k-го порядка получают из простейшего потока путем сохранения каждого k-го события. Промежуток времени T(k) между двумя событиями в потоке Эрланга имеет плотность распределения , t>0, k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение , и, k=1,2,3,… При k=1 закон Эрланга k-го порядка превращается в экспоненциальный закон f(t)=exp(–t) с параметром . Интенсивность потока Эрланга k-го порядка, k=1,2,3,… определяет его основные характеристики, t>0, k=1,2,3,…, и, k=1,2,3,… Интенсивность нормированного потока Эрланга, k=1,2,3,… Промежуток времени между соседними состояниями k=1,2,3,… Математическое ожидание, дисперсия и стандартное отклонение, , , k=1,2,3,… Плотность распределения нормированного потока Эрланга, t>0, k=1,2,3,… Случайная величина промежутка времени – это среднее арифметическое k независимых случайных величин Ti, i=1,…,k, распределенных по одному и тому же закону распределения (экспоненциальному с параметром ). В силу центральной предельной теоремы она будет иметь распределение, близкое к нормальному с математическим ожиданием 1/ и дисперсией 1/k2. Поскольку дисперсия уменьшается с ростом k, промежуток времени между соседними событиями нормированного потока Эрланга становится все менее случайным и по закону больших чисел приближается по вероятности к математическому ожиданию 1/. Поток Эрланга приближается с ростом k к регулярному потоку с промежутком времени 1/ между событиями. Это свойство потоков Эрланга выявляет роль k как меры «последействия»: от полного отсутствия последействия при k=1 (простейший поток) до жесткого последействия при k (регулярный поток). Для моделирования реального потока с последействием применяется нормированный поток Эрланга с почти тем же математическим ожиданием и дисперсией интервала времени между соседними событиями. С помощью потоков Эрланга немарковские процессы можно сводить к марковским процессам. Пример 7. Наблюдения за работой рекламного агентства показали, что среднее значение интервала времени T между соседними поступлениями заказов M[T]=1 неделя и стандартное отклонение T=4 дня. Интенсивность и стандартное отклонение нормированного потока Эрланга (заказ в неделю) и. Отсюда k=(7/4)2=3,067. Ближайшее целое число – порядок k=3. Плотность распределения вероятностей случайного интервала времени, t>0. Вероятность, что интервал времени между двумя заказами больше 3 и меньше 5 дней. Интегрируя по частям, получим, и. Интегрируя по частям, получим. Таким образом, p=0,189. Пуассоновские потоки событий и дискретные марковские процессы с непрерывным временем тесно связаны. Случайный процесс с непрерывным временем в системе с дискретными состояниями будет марковским, если все потоки событий, переводящие систему из состояния в состояние, являются пуассоновскими (стационарными или нестационарными). Такие системы с непрерывным временем называются пуассоновскими. Исследование случайного процесса проводится по алгоритму: (1) Описать каждое состояние системы; (2) Составить граф состояний, указать возможные переходы из состояния в состояние; (3) Задать интенсивности потоков событий, под влиянием которых осуществляются эти переходы; (4) Указать начальное состояние системы (при t=0). Пример 8. Банкоматы B1 и B2 могут «отказывать» независимо друг от друга (выходить из строя). Потоки отказов B1 и B2 с интенсивностями 1=4 и 2=3 (отказа в неделю) – пуассоновские. После отказа каждый банкомат сразу ремонтируется (восстанавливается). Потоки восстановлений B1 и B2 с интенсивностями 1=5 и 2=2 (восстановлений в неделю) – пуассоновские. Потоки с постоянными интенсивностями являются простейшими. Система S может находиться в четырех состояниях: s11 – оба банкомата исправны; s12 – банкомат B1 исправен, а B2 ремонтируется; s21 – банкомат B1 ремонтируется, а B2 исправен; s22 – банкоматы ремонтируются. Размеченный граф состояний системы изображен на рис.10, а матрица плотностей вероятностей переходов дана в таблице 5. Рис.10. Граф состояний системы двух банкоматов. Таблица 5. Матрица плотности вероятностей. Составим систему уравнений Колмогорова: В начальный момент времени t=0 система находилась в состоянии s12:, , ,. Условие нормировки p11(t)+p12(t)+p21(t)+p22(t)=1 (t0). С учетом условия нормировки получаем неоднородную систему трех линейных дифференциальных уравнений первого порядка:, ,. Общее решение однородной системы, ,. Для нахождения решений неоднородной системы применим метод вариации постоянных, рассматривая c1,c2,c3 как неизвестные функции от t. Подставляя решение однородной системы, получим систему линейных уравнений для dc1/dt, dc2/dt и dc3/dt. После ее решения и интегрирования найдем функции,, , где b1, b2 и b3 – постоянные интегрирования. Для их определения используем начальные условия:, ,. Решение этой системы уравнений методом Крамера дает, ,. Подставив эти значения, получим общее решение неоднородной системы:, ,. Функцию p22(t) находят из условия нормировки:. При t=2 будем иметь, , ,. Во втором квартале система S будет находиться вероятнее всего в состоянии s12: банкомат B1 будет работать, а B2 – ремонтироваться. Дискретный процесс с непрерывным временем является марковским, если каждый из потоков, переводящих систему из состояния в состояние, является пуассоновским потоком. Преобразование Лапласа Спектральная плотность сигнала v(t). Это преобразование Фурье сигнала v(t). Обратное преобразование Фурье. Сигналу v(t) можно сопоставить спектральную плотность V() в том случае, если сигнал абсолютно интегрируем:. Если экономическую систему возбуждают источники потока y(t), а искомые переменные x(t) являются запасами, то ее поведение описывается уравнением, где квадратная матрица T(p)=G+pC, а G и C не зависят от комплексной частоты p. Допустим, что система уравнений решена, а выходная функция F(p)=cTX(p). Формальное решение, где T+(p) – присоединенная матрица. Линейные выходные функции имеют общий знаменатель, равный определителю матрицы T(p). Определитель и любой элемент присоединенной матрицы T+ – это полиномы от p, а F(p) – рациональная функция комплексной переменной p вида F(p)=N(p)/D(p). Знаменатель функции системы D(p)=|T|, а числитель N(p)=|Tcy|. Если изображение есть дробь F(p)=K1/(p–p1) с полюсом p1 и вычетом K1, то. Обращение преобразования Лапласа заключается в вычислении для. Нужно найти условие, при котором интеграл можно представить в виде. Замкнем контур интегрирования в левой полуплоскости полуокружностью с радиусом, которой растет с пределами интегрирования. Если выполнить условие равенства нулю интеграла вдоль этой бесконечной полуокружности, то интеграл равен сумме вычетов. Введем p=Rexp(i) с dp=iRexp(i)d:. На полуокружности в левой полуплоскости, ограниченной точками iR и –iR, величина R постоянна. При больших R преобладают члены старших степеней и выражение для интеграла можно упростить. Интеграл конечный. Чтобы обеспечить равенство нулю выражения при R, нужно выбрать M и N, чтобы R в знаменателе имел положительную степень. Интеграл от рациональной функции I(p) по бесконечной полуокружности равен нулю, если число полюсов MN+2 функции на два больше, чем число ее нулей. Интегрирование рациональной функции при MN+2 вдоль линии, параллельной мнимой оси, дает 2i{сумма вычетов для полюсов слева от линии}, если контур интегрирования замкнуть через левую полуплоскость. Если замкнуть контур через правую полуплоскость, то следует взять сумму вычетов для полюсов справа от линии, а умножить на (–2i). Если f(z) определена в точке ветвления, то значение f(a) является общим для ветвей, полученных при обходе. Если, описывая кривую вокруг точки z=a сколь угодно раз в том же направлении, мы каждый раз будем получать новые ветви, то точка a называется точкой ветвления бесконечного порядка (логарифмическая точка ветвления). Определение коэффициентов полиномов N(p) и D(p) по ряду чисел (pi,N(pi)) и (pi,D(pi)) составляет интерполяционную задачу. Пусть известны значения qi в n+1 точке pi. Нужно найти коэффициенты полинома, проходящего через эти точки. Подставив pi, получим систему уравнений. Наилучшим выбором pj являются равноотстоящие точки, лежащие на единичной окружности комплексной плоскости. Обозначим P=(pij), где i и j принимают значения от 0 до n. Если обозначить, то pk=wk и P=(wij), а решение принимает вид. Исходный полином, определенный в точках pk, представлен в виде,. Это дискретное преобразование Фурье. Оно эффективно при выборе n+1=2m и целом числе m (быстрое преобразование). Дисконтирование достигается преобразованием Лапласа, которое переводит функцию f(t) действительной переменной t в функцию f(p) комплексной переменной p=r+is (r=Rep, s=Imp, i – мнимая единица). При ограниченном росте |f(t)|<exp(r0t) с абсциссой абсолютной сходимости r0>0 этот интеграл сходится при Rep<r0: область определения функции f(p) лежит слева от r=r0. Изображение запаздывающего импульса Хевисайда h(t–) с амплитудой h=1:. Изображение импульса g(t)=[h(t)–h(t–)]/ длительностью :. В пределе 0 получается изображение импульса Дирака (p)=1. Таблица оригиналов f(t) и изображений f(p). (для преобразования Карсона p используется интеграл Бромвича) Изображения являются рациональными функциями p:, и, где pl – нули, а pk – полюса функции f(p). На комплексной плоскости они изображаются соответственно кружками и крестиками. Функцию можно представить суммой простых множителей с вычетами, , ,. Функцию можно представить суммой. При k=1 имеем pk=1 и nk=2, а [(p–pk)f(p)]=p-3:, и,. При k=2 имеем pk=0 и nk=3, а [(p–pk)f(p)]=(p–1)-2:, , , и,. Если f(p)=c(p)/d(p), а c(p) и d(p) – аналитические функции в простом полюсе p1, то resf(p1)=c(p1)/d(p1). Формула Хевисайда применима, если m различных полюсов pk имеют кратности mk:, Если все полюсы простые, то Через компоненты матрицы Прибыль в рыночном сегменте Экономические рынки удобно рассматривать в виде множества секторов, элементы которых имеют общие признаки. Хозяйствующие субъекты сектора более однородны по своему поведению, чем субъекты всего рынка. Устойчивость сегменту придают прибыльные субъекты. Рыночный сегмент характеризуется какими-то свойствами и параметрами. Экстенсивные свойства пропорциональны размеру сегмента (совокупный доход, энтропия, число субъектов). Интенсивные свойства не зависят от размеров сегмента: скорость обращения полезности V определяет условия обмена между сектором и рынком, а уровень цен p отражает издержки рыночного сегмента. Если экономические параметры изменяются во времени, то в секторе протекает экономический процесс. Самопроизвольный процесс приводит рыночный сегмент в такое состояние, когда его экономические свойства больше не изменяются: в секторе установится полное равновесие. Равновесные рыночные сегменты характеризуются распределением Гиббса [3]. Сейчас кажется тривиальным, что при нехватке некоторого блага его цена растет. Однако между эмпирическим фактом и математическим доказательством дистанция огромного размера [1]. В основе доказательства лежит предположение о детерминированности процессов производства товаров и услуг. Оно попросту не учитывает неопределенность будущего, тем самым не затрагивая финансовую сторону экономической деятельности. Такие явления, как денежная инфляция и спекуляция, нельзя объяснить в рамках детерминированного подхода [2]. Предметом нашего исследования является экономическая система ячеек, которые находятся в состояниях полезности. При этом ячейка «погружена» во внешнюю среду, формируемую другими ячейками. Основное занятие ячейки – это распределение товаров и услуг. Совокупность ячеек и среды образует замкнутую экономическую систему. Нас интересует товарные отношение в этой системе. Пусть индекс n нумерует товары полезностями un. Согласно основному принципу статистической механики, если известна вероятность и статистическая сумма то можно найти внутреннюю полезность системы U, накопление W и свободную полезность F как функции скорости обращения полезности V: Эти функции связаны условием баланса U=F+W. Энтропия n-го состояния Энтропия закрытого региона. Экстенсивная переменная S – мера накопления VS, а интенсивная переменная V – ее оценка. И V и S неотрицательны. Изменения Q и Pn с V описываются производными где U зависит от V. Производные энтропии по V зависят от дисперсии и асимметрии дохода: Поскольку 2>0, то S увеличивается со скоростью V, достигая насыщения при V=V3μ3/3μ2, если μ3>0. При 3<0 энтропия ограничена. Производные по V:, и, Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом V. Производные по S:, и Внутреняя полезность и накопление увеличиваются, а свободная полезность уменьшается с ростом S. Скорость обращения полезности V и энтропия S сопряжены на внутренней и свободной полезности: U(S) является потенциалом для скорости обращения полезности V, а F(V) – потенциалом для энтропии S. Накопление W не является потенциалом ни для скорости обращения, ни энтропии. Для учета доходов используем экстенсивную переменную благосостояния Y. Полезность товара un уменьшается с ростом Y, а производные pn(Y)=–dun/dY>0 определяют уровень цен, где вероятность Pn(V,Y) зависит от Y, так как un зависит от Y. Рыночный сегмент имеет две пары сопряженных переменных (S,V), (Y,p) и четыре потенциала F(V,Y), G(V,p), H(S,p) и U(S,Y) с дифференциалами, , и. Свободная полезность F вычисляется по статистической сумме Q(V,Y). Внутренняя полезность U=F+W включает F и W. Свободная полезность G=F+pY включает F и pY, а внутренняя полезность H=F+VS+pY. Переменные S и Y являются экстенсивными факторами, а V и p – интенсивные факторы. Частные производные статистической суммы выражаются в виде: Свободная полезность F(V,Y) является функцией V и Y: Свободная полезность G(V,p)=F+pY является функцией V и p: Внутреняя полезность H(S,p)=G+VS является функцией S и p: Внутреняя полезность U(S,Y)=H–pY является функцией S и Y: Внутрення полезность U растет с энтропией S и уменьшается с доходом Y. Потенциалы полезности F(V,Y), G(V,p), H(S,p) и U(S,Y) аддитивны, а V и p одинаковы для всех всех субъектов сегмента. Поэтому потенциалы должны быть однородными функциями первого порядка по переменным S и Y: где ψ, μ, ν и φ – некоторые функции. Будем рассматривать N как независимую переменную. Тогда в дифференциалы нужно добавить μdN с потенциалом. Оценка μ(V,p) резидентов в открытой экономической зоне оказывается функцией скорости обращения полезности V и уровня цен p. Дифференцируя G по N, получаем (V,p) – оценка μ числа субъектов в сегменте оказывается функцией V и p. Большой потенциал открытой зоны Ω=F–G является функцией V, Y и μ: dΩ=–SdV–pdY–Ndμ. Если полезность n-го резидента в зоне обозначить unN, то вероятность. Накопление полезности в открытой экономической зоне:, , и. Открытая экономическая зона является большим каноническим ансамблем. При описании экономических явлений используют понятие эластичности фактора и показателя [4]. Пусть взаимозависимые переменные x, y и z отвечают любой тройке неповторяющихся факторов S, V, Y и p. Тогда y-ой эластичностью фактора x при неизменном факторе z называется величина xyz=y(x/y)z. Только 16 эластичностей независимы в закрытой системы. Свободная полезность F(V,Y) вычисляется с помощью статистической суммы Q, а другие потенциалы в переменных V и Y – из выражений: Дифференцирование дает Потенциалы в переменных V и p выражаются через G(V,p): Дифференцирование дает Потенциалы в переменных S и p выражаются через H(S,p): Дифференцирование дает Потенциалы в переменных S и Y выражаются через U(S,Y): Дифференцирование дает Эти производные легко вычисляются, если учесть свойства якобианов: Доход Y(F,V) как функция свободной полезности F и скорости обращения имеет частные производные: Скорость обращения полезности V(G,p) как функция свободной полезности G и уровня цен имеет частные производные: Уровень цен p(H,S) как функция внутренней полезности H и энтропии имеет частные производные: Энтропия S(U,Y) как функция внутренней полезности U и благосостояния имеет частные производные: Статистическая оценки важных эластичностей дает: где означает усреднение с учетом вероятности Pn. Экономические процессы в закрытом сегменте сопровождаются ростом энтропии, пока она не достигнет наибольшего значения при полном равновеси. С ростом числа субъектов энтропия растет при фиксированной скорости V и уровне цен p. Это означает, что норма накопления увеличивается с числом субъектов, т.е. с переходом от большого к малому бизнесу. Субъекты малого бизнеса слабо взаимодействуют друг с другом в идеальном сегменте и представляют собой однородную массу, а их прибыль линейно зависит от конъюнктуры. Замечательным достижением статистической экономики является точная формулировка условий равновесия с внешней средой. Процессы, протекающие в замкнутой неравновесной системе, идут таким образом, что система переходит из состояний с меньшей энтропией в состояния с большей энтропией, пока она не достигнет своего наибольшего значения, соответствующего полному равновесию. Энтропия замкнутой системы – сумма энтропий резидентов и внешней среды. Равенство нулю первых производных суммарной энтропии является только необходимым условием экстремума и не дает того, чтобы энтропия имела именно максимум. Для выяснения достаточных условий необходимо вычислить второй дифференциал суммарной энтропии. Это исследование удобнее провести, исходя не из условия максимума суммарной энтропии, а из эквивалентного ему условия. Выделим из системы некоторую малую часть, а остаток будем рассматривать как внешнюю среду со скоростью обращения V0 и уровнем цен p0. Тогда в равновесии имеет минимум величина U–V0S+p0Y с внутренней полезностью U, энтропией S и доходом Y. При всяком малом отклонении от равновесия ее изменение должно быть положительным: Разлагая δU в ряд, получаем с точностью до членов второго порядка: где производные взяты в состоянии равновесия. Но поскольку то члены первого порядка сокращаются. Это необходимые условия равновесия: скорость обращения полезности V и уровень цен p для резидентов равны этим же величинам внешней среды. Достаточное условие равновесия имеет вид: Для того, чтобы такое неравенство имело место при произвольных δS и δY, нужно удовлетворить два неравенства: Поскольку то первое неравенство удовлетворяется при Второе неравенство можно записать в виде якобиана Переходя к переменным V и Y, имеем Поскольку p=p0>0 и SV0,Y>0, то это равносильно условию Уровень цен должен уменьшаться с ростом благосостояния при постоянной скорости обращения полезности. Эти экономические неравенства гарантируют устойчивость равновесной системы. Для SV0,Y>0 нужно, чтобы средний квадрат внутренней полезности u2 превышал квадрат среднего U2, а дисперсия была положительной. Поскольку для устойчивости равновесия необходимо, чтобы dp/dY было отрицательным и по модулю превышало отношение дисперсии уровня цен к скорости обращения. При любом начальном состоянии закрытой системы с течением времени в ней установится единственное состояние – равновесие. Эта тенденция означает монопольное возрастание энтропии во времени и увеличение разности энтропий S=S–S0 от отрицательных значений до нуля. Эти утверждения эквивалентны, и они отражают тот факт, что равновесие является глобальным асимптотически устойчивым состоянием, энтропия – функцией Ляпунова. Если только свободная полезность F(V,Y) будет иметь несколько минимумов при неизменных V, Y и различных значениях N, то стабильному состоянию будет отвечать наименьшее значение F, а метастабильному – самый мелкий минимум с наибольшим F. Такие состояния легко разрушаются переходом системы в устойчивое состояние с наименьшей свободной полезностью. Если системы переходит из одного состояния в другое с изменением ее внутренней полезности при неизменном накоплении, то обратный переход нельзя осуществить без воображаемого внешнего источника R. Прямому переходу с совершением максимальной работы |Rmax| отвечает обратный переход c работой Rmin внешнего источника. Изменение внешней полезности ΔU при изменении состояния состоит из трех частей: из произведенной работы внешнего источника R, из работы внешней среды p0ΔY0 и из полученной из нее V0ΔS0: где индекс 0 относится к внешней среде. Поскольку затраты среды равны доходу ΔY0=–ΔY, а в силу закона возрастания энтропии S0–S, то где знак равенства достигается при обратимом процессе. Переход совершается с минимальной работой, если он происходит обратимо: Обратный переход также совершается с минимальной работы, если происходит обратимо: Пусть SΣ есть полная энтропия. Если резиденты находятся в равновесии с внешней средой, то SΣ является функция их внутренней полезности UΣ.. Если же резиденты не находятся в равновесии с внешней средой, то суммарная энтропия отличается от SΣ(UΣ) на величину Но dU/dS является равновесной скоростью обращения полезности V0. Таким образом, получаем Эта формула определяет, как отличается энтропия замкнутой системы от своего возможного значения, если резиденты не находятся в равновесии со средой. Рассмотрим закрытую систему с энтропией SΣ. Пусть β – некоторый фактор, обеспечивающий ее внутреннее равновесие, т.е. S/=0. Пусть α – другой фактор, обеспечивающий при внутреннем равновесии системы и ее равновесие с внешней средой, т.е. S/=0. Введем обозначения Энтропия SΣ замкнутой системы максимальна при полном равновесии. Чтобы энтропия была максимальной, кроме необходимых условий А=0 и В=0, должны выполняться неравенства Уже незначительные изменения фактора α при некотором воздействии на закрытую систему приводят к изменению A на величину Изменение α при постоянном β приводит к нарушению условия внутреннего равновесия системы B=0. После того, как это равновесие восстановится, величина ΔA будет иметь значение Используя свойства якобиана, находим С учетом неравенств получаем новое неравенство Это неравенство выражает принцип Ла Шателье [6]. Рассмотрим изменение Δα фактора α как меру внешнего воздействия на систему, а ΔΑ – κак меру изменения системы под его влиянием. Тогда Значение ΔΑ уменьшается при восстановлении внутреннего равновесия системы после внешнего воздействия, выводящего ее из равновесия. Другими словами, внешнее воздействие, выводящее систему из равновесия, стимулирует в системе процессы, стремящиеся ослабить его влияние. Изменение энтропии системы –Rmin/V0 зависит от скорости обращения полезности во внешней среде V0 и минимальной работы Rmin, необходимой для приведения системы из состояния равновесия с внешней средой в данное состояние. Поэтому можно написать где для бесконечно малого изменения состояния системы резидентов Все величины без индекса относятся к резидентам, а с индексом 0 – к среде. Пусть α есть энтропия S. Тогда A=V/V0–1 и в равновесии V=V0, неравенства принимают вид Рост энтропии означает, что в систему инвестируется оборотный капитал. В итоге нарушается равновесие резидентов и, в частности, увеличивается скорость обращения полезности на величину (V). Восстановление равновесия резидентов приводит к тому, что изменение скорости обращения уменьшится до (V)B=0. т.е. как бы ослабляется результат воздействия, выводящего резидентов из равновесия. Если в неравенстве в качестве фактора β взять доход Y, то будем иметь поскольку условие В=0 означает, что случае p=p0. Подстановка дает неравенство Используя свойства якобиана, можно получить Пусть α есть налог Y. Тогда A=1–V/V0 и в равновесии V=V0, а неравенства принимают вид Если в неравенстве в качестве фактора β взять энтропию S, то условие В=0 означает, что V=V0 и В устойчивой системе величина (p/Y)V должна быть отрицательной. Используя свойства якобиана, можно получить В устойчивой системе величина (S/V)p должна быть положительной. Основной недостаток идеального сегмента состоит в том, что полезность расходится при Y=0. Этот коллапс не должен допускаться государством, которое может установить минимальный предел Y0. Рассмотрим процесс L в экономической системе, которая не находится в равновесии с внешней средой. Пусть B – накопление, полученное системой из внешней среды со скоростью обращения полезности V0. Процесс L перехода из состояния 1 в состояние 2 нельзя реализовать, если нарушается неравенство где S1 и S2 – энтропии состояний, а интегрирование проводится по траектории процесса. Равенство применимо только при обратимом процессе. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы и не зависит от ее промежуточных состояний Дифференциал внутренней полезности в замкнутой системе содержит малое накопление B и малое потребление A, которые не являются дифференциалами в общем случае. Переведем идеальную систему из начального состояния 1 в промежуточное состояние 2 при неизменной энтропии: где. Выпуск и потребление положительны, если. Переведем теперь систему из состояния 2 в промежуточное состояние 3 при неизменной ренте: Переведем далее систему из состояния 3 в промежуточное состояние 4 при неизменной конъюнктуре: Наконец, переведем систему из состояния 4 в начальное состояние 1 при неизменной ренте: При этот цикл оказывается замкнутым. В начальном состоянии 1 идеальная система имеет низкую конъюнктуру и низкую ренту. Переход в состояние 2 при низкой конъюнктуре сопровождается увеличением ренты и цены, а капитал убывает потому, что выпуск равен потреблению (накопление не меняется). Переход в состояние 3 при высокой ренте сопровождается увеличением конъюнктуры и капитала, а цена уменьшается, потому что выпуск отсутствует (инвестиция накоплений в производство повышает его конъюнктуру). Переход в состояние 4 при высокой конъюнктуре сопровождается уменьшением ренты и цены, а капитал увеличивается, потому что потребление равно выпуску (накопление не изменяется). Переход в начальное состояние 1 при низкой ренте сопровождается уменьшением конъюнктуры и капитала, а цена увеличивается, потому что выпуск отсутствует (конфискация накопления из производства понижает его конъюнктуру). Коэффициент полезного действия этого замкнутого экономического цикла определяется следующим образом: Инвестиция S2=S23>0 и конфискация S1=S41<0 удовлетворяют соотношению Это соотношение справедливо только для замкнутого цикла. Макроскопическая теория выпусков и затрат использована для описания экономических циклов системы многих резидентов на основе модели В.В.Леонтьева. Основные понятия макроэкономики развиты в русле детерминированного подхода, дополненного соображениями оптимальности и полезности [1,2]. Может быть поэтому нет строгого определения конъюнктуры как меры эффективной деятельности экономической системы. Вместе с тем, этот термин используется [3]. Эвристические соображения известных экономистов о конъюнктуре близки к определению температуры как производной внутренней энергии системы по ее энтропии [4,5]. Аналогом внутренней энергии в экономике является внутренняя полезность, но она должна быть определена в рамках вероятностного подхода. Необходимость такого подхода отмечалась в связи с инфляционными процессами современной экономической жизни [6]. Полезность un зависит от индекса благосостояния Y, причем при Y=1 она равна нулю, а цена благосостояния pn(Y)–dun/dY не может быть отрицательной, так как un уменьшается с ростом Y. Согласно основного принципа статистической экономики, если известны статистическая сумма Q, вероятность Pn, энтропия S и уровень цен p, , и, то можно найти макроскопические показатели закрытой системы при скорости обращения полезности V и индексе благосостояния Y. Показателями закрытой системы являются внутренняя полезность U=F+W, свободная полезность F и накопление W, и, а ее факторами являются скорость обращения полезности V, энтропия S, индекс благосостояния Y и уровень цен p. Для простой закрытой системы, а свободная полезность (потребление) выражается в виде, где f(V)=VlnL(V). Энтропия и уровень цен простой системы даются уравнениями состояния и. Полуэластичности этих двух факторов и. Для устойчивости закрытой системы необходимо и достаточно иметь =const, =const и SV,Y>0, pY,V<0. Простая система устойчива, если d2f/dV2<0. Свободная полезность G=F+pY в простой системе определяется с учетом уравнения состояния:, а энтропия и индекс благосостояния выражаются в виде и. Полуэластичности этих факторов и. Идеальной называется простая система с SV,Y=N0>0 и, где f0 и – постоянные интегрирования. Внутренняя полезность U=F+W такой системы определяется с учетом уравнения состояния:, где =1+N/N0>1. Удобно выбрать f0=–S0 и, чтобы внутренняя полезность исчезала при энтропии S11=S(V=1,Y=1) и индексе Y=1:. В этом случае и, а внутренняя полезность являются линейной функцией скорости обращения полезности U=N0(V–1). Свободная полезность идеальной системы и ее энтропия – нелинейные функции скорости обращения полезности и индекса благосостояния и. Зависимость энтропии идеальной системы S(V,Y) от конъюнктуры V приводится на рис.1 для двух значений индекса благосостояния Y. Рис.1. Зависимость энтропии от конъюнктуры. Используются данные для высокоэластичной экономики с небольшим числом резидентов, представляющих отрасли народного хозяйства [3] (N0=10, S11=3 и N=10). Рост энтропии с конъюнктурой свидетельствует о структурных изменениях системы, сопровождаемых линейным увеличением внутренней полезности. Этот рост замедляется с уменьшением индекса благосостояния. Уравнение состояния pY=NV связывает большую полезность pY с числом резидентов N и конъюнктурой V идеальной системы. При неизменной конъюнктуре уровень цен уменьшается с ростом индекса благосостояния (деинфляция). Рассмотрим квазистатический процесс L в системе резидентов, которые не находятся в равновесии с внешней средой. Малое накопление B система резидентов получит из окружающей среды с равновесной конъюнктурой V0. Переход системы резидентов из состояния 1 с энтропией S1 в состояние 2 с энтропией S2 нельзя реализовать, если нарушается неравенство, где интегрирование проводится по траектории процесса L. Равенство применимо при обратимых процессах. Изменение внутренней полезности при обратимом процессе определяется начальным 1 и конечным 2 состоянием системы. Дифференциал внутренней полезности закрытой системы dU=B+A=VdS–pdY содержит малое накопление B и малое потребление А, которые не являются дифференциалами. В состоянии 1 система имеет энтропию S1 и конъюнктуру V1. Переведем систему из начального состояния 1 в состояние 2 при неизменной энтропии: и. Переход в состояние 2 с конъюнктурой V2>V1 сопровождается уменьшением индекса благосостояния Y и увеличением уровня цен p, потому что прирост полезности потребляется (рис.1). Переведем систему из состояния 2 в состояние 3 при неизменной конъюнктуре:, и. Переход в состояние 3 с энтропией S3>S1 сопровождается увеличением Y и уменьшением p, потому что внутренняя полезность не изменяется (инвестиция накоплений в систему повышает энтропию). Зависимость индекса благосостояния Y от уровня цен p приводится на рис.2 для той же высокоэластичной системы при S1=1, V1=1, V2=3 и S3=3. Рис.2. Зависимость индекса от ставки затрат. Переведем систему из состояния 3 в состояние 4 при неизменной энтропии: и. Переход в состояние 4 с конъюнктурой V4<V2 сопровождается увеличением Y и уменьшением p. Переведем систему из состояния 4 в состояние 1 при неизменной конъюнктуре:, и. Переход в состояние 1 с энтропией S1 и конъюнктурой V4=V1 сопровождается уменьшением Y и увеличением p из-за конфискации накоплений окружающей средой. Коэффициент полезного действия экономического цикла. Инвестиция B2=B23>0 и конфискация B1=B41<0 удовлетворяют соотношению. Это соотношение справедливо только для замкнутого цикла. Современному состоянию экономики Украины отвечает одна из нижних точек на траектории L12 c энтропией S1 и конъюнктурой VV2. Движение по этой траектории с падением индекса благосостояния Y и увеличением уровня цен p разогревает экономику до такой конъюнктуры V2, при которой возможны структурные изменения отношений резидентов на траектории L23. Движение по траектории с ростом Y и уменьшением p хаотизирует экономику до значения энтропии S3, которое зависит от инвестиции накоплений. Определению кризисной точки более отвечает состояние экономики с энтропией S1 и конъюнктурой V1, а квазистатический процесс L41 имеет периода застоя. Ему предшествует движение по траектории L34, которое ведет к охлаждению экономических отношений. |
|||||
|
П. Кирилл |
Школьно зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
С. Спартак |
незрелый |
высокий |
сформирована |
Высокий |
Средний |
|
С. Витя |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |
|
С. Настя |
Средне зрелый |
высокий |
сформирована |
Высокий |
|
|
С. Катя |
Средне зрелый |
средний |
сформирована |
Высокий |
Средний |
|
Ч. Слава |
Средне зрелый |
высокий |
сформирована |
Высокий |
Высокий |

Рис. 2.5. Общий итог
Анализируя составленную по результатам всех методик сводную гистограмму, мы видим, что большинство дошкольников психологически готовы к поступлению в школу. Низкий уровень готовности выявлен у одного ребенка. Средний уровень у семи детей из общих 25 детей.
Но если рассматривать психологическую готовность к школе по отдельности по составу семьи, получились такие результаты:
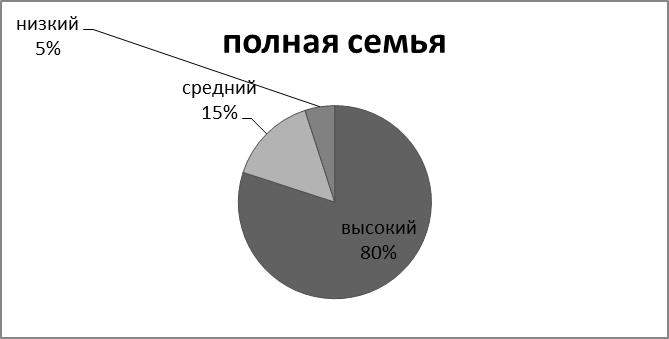
Рис. 2.6. Психологическая готовность к школе по отдельности по составу семьи
Количество детей из полной семьи – 20, из них
Высокий уровень показали – 16
Средний – 3
Низкий - 1.
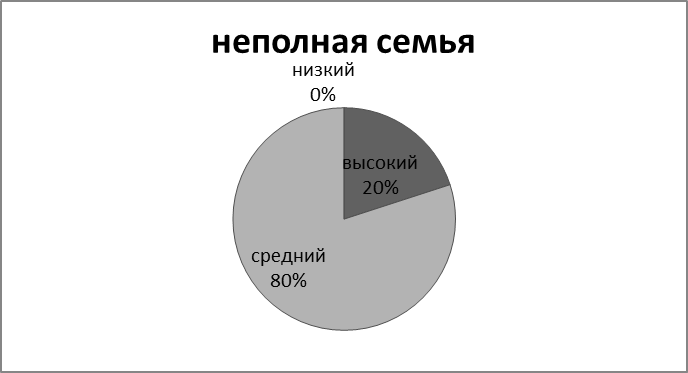
Рис. 2.7. Психологическая готовность к школе по отдельности по составу семьи
Количество детей из неполной семьи – 5, из них
Высокий уровень показали – 1
Средний -4,
Низкий – 0.
Таким образом, с помощью интерпретации данных, мы установили, что высокая психологическая готовность к школе доминирует у детей из полной семьи. Что доказывает наши предположения, о том, что уровень развития психологической готовности к обучению в школе у исследуемой группы выше у детей из полных семей, так как в неполной семье один родитель в силу своей занятости не может уделить должное внимание воспитанию ребенка, а в полной семье такая возможность есть.
ЗАКЛЮЧЕНИЕ
Одна из проблем подготовки детей к школе, посещающих детские образовательные учреждения, состоит в том, что эти образовательные организации работают по разным программам; при этом каждая из них разрабатывает свои показатели и критерии развития, тесно связанные с образовательным содержанием, заложенным в программе. При таком разнообразии показатели развития в программах несоотносимые друг с другом. К тому же списки этих показателей весьма обширны, что приводит к многочисленным процедурам проверки или к формальному приписыванию их детям, которое искажает настоящее состояние качества подготовленности.
В системе российского образования большое значение придается дошкольному образованию и воспитанию, которое дети получают в системе дошкольных образовательных учреждений или под руководством родителей, являющихся их первыми учителями. Именно в этот период необходимо заложить основы физического, нравственного, духовного и интеллектуального развития детей. Важной задачей системы дошкольного образования выступает формирование физически здоровой, социально активной, духовно богатой, творческой личности ребенка.
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
- Аверина, И. Е. Физкультурные минутки и динамические паузы в ДОУ: практическое пособие / И. Е. Аверина. - 2-е изд. - М.: Айрис-Пресс; Айрис-дидактика, 2016. - 136 с.
- Атемаскина, Ю.В. Современные педагогические технологии в ДОУ / Ю.В. Атемаскина, Л.Г.Богословец.- Спб.: Изд-во «Детство-Пресс», 2018.- 112 с.
- Веракса, Н. Е. Веракса А. Н. Проектная деятельность дошкольников : пособие для педагогов дошкольных учреждений для работы с детьми 5-7 лет / Н. Е. Веракса, А. Н Веракса.- М.: Мозаика – Синтез, 2017.- 110 с.
- Григорьева Г.Г. Практикум по изобразительной деятельности дошкольников: учебное пособие для студ. сред. пед. учеб. заведений .- М.: Академия, 2017.- 128 с.
- Губанова, Н.Ф. Игровая деятельность в детском саду. Программа и методические рекомендации / Н.Ф.Губанова.- М.: Мозаика-Синтез, 2016.- 128 с.
- Губанова, Н.Ф. Развитие игровой деятельности. Система работы в средней группе детского сада: методическое пособие для воспитателей / Н.Ф.Губанова. - М.: Академия, 2015.- 160 с.
- Гуткин, Н. И. Психологическая готовность к школе / Н. И.Гуткина. – СПб.: Питер, 2014. – 208 с.
- Доскин, В. А. Растем здоровыми: пособие для воспитателей, родителей и инструкторов физкультуры / В. А. Доскин, Л. Г. Голубева. - 3-е изд. - М.: Просвещение, 2014. - 109 с.
- Дошкольная педагогика. Обзорные лекции по подготовке студентов к итоговому междисциплинарному экзамену: учеб. пособие / Н.А. Виноградова и др.; под ред. Н.В. Миклевой. – М.: Форум, 2016. – 255 с.
- Дыбина, О.В. Образовательная среда и организация самостоятельной деятельности детей старшего дошкольного возраста. Методические рекомендации – М., Центр педагогического образования, 2018. – 64 с.
- Елжова, Н. В. Методическая копилка для педагогов дошкольного образовательного учреждения / Н.В. Елжова; Нац. проект "Образование". – 3-е изд. – Ростов н/Д : Феникс, 2017. – 251 с.
- Елжова, Н. В. Здоровый образ жизни в дошкольном образовательном учреждении / Н.В. Елжова. – Ростов н/Д : Феникс, 2016. – 216 с.
- Здоровьесберегающие технологии воспитания в детском саду: примерные планы и конспекты занятий / Ред. Т. С. Яковлева. - М.: Школьная Пресса, 2016. - 46 с.: ил., фото. - (Здоровый образ жизни). - (Дошкольное воспитание и обучение: Прилож. к ж. Воспитание школьников; Вып. 148)
- Из детства - в отрочество: программа для родителей и воспитателей по формированию здоровья и развитию детей 4-7 лет / Т. Н. Доронова, Л. Г. Голубева, Н. А. Гордова. - 3-е изд. - М.: Просвещение, 2014. - 142 с.
- Кожухова, Н. Н. Питание, режим и здоровье ребенка: практические советы педагога / Н. Н. Кожухова. - М.: Школьная Пресса, 2015. - 40 с. - (Ребенок XXI века от рождения до школы: Я - человек)
- Козлова С.А., Куликова Т.А. Дошкольная педагогика: учебник для студ. сред. пед. учеб. заведений/ С.А. Козлова, Т.А. Куликова. – 5-е изд., испр.- М.: Академия, 2014. – 416 с.
- Комарова Т.С. Трудовое воспитание в детском саду. Программа и методические рекомендации / Т.С.Комарова, Л.В.Куцакова, Л.Ю.Павлова – М.: Мозаика-Синтез, 2016. - 90 с.
- Комарова, Т.С. Эстетическая развивающая среда в ДОУ. учебно-методическое пособие / Т.С. Комарова, О.Ю. Филлипс. - М.: Педагогическое общество России, 2015. -128 с.
- Корепанова, М. В. Педагогика дошкольного детства: учебное пособие по дошкольной педагогике для слушателей курсов повышения квалификации / М. В. Корепанова. - Волгоград, 2016. - 93 с.
- Морозова Л.Д. Педагогическое проектирование в ДОУ: от теории к практике / Л.Д. Морозова. – М.: Сфера, 2017.- 128 с.
- Николаева С. Н. Теория и методика экологического образования дошкольников. М.: Академия, 2017.- 224 с.
- Николаева С.Н. Теория и методика экологического образования детей. - М.: Издательский центр «Академия», 2016. - 336 с.
- Николаева, С. Н. Методика экологического воспитания дошкольников: учебное пособие для средних педагогических учебных заведений / С. Н. Николаева - 3-е изд., перераб. - Москва: Академия, 2015. - 220, [1] с.
- Погодина С.В. Теория и методика развития детского изобразительного творчества / С.В. Погодина. – М., 2018.
- Полякова, М.Н. Создание моделей предметно-развивающей среды в ДОУ: методические рекомендации: учебно-методическое пособие / М.Н. Полякова. – М.. Центр педагогического образования, 2018.- 96 с.
- Предметно-пространственная развивающая среда в детском саду. Принципы построения, советы, рекомендации / Сост. Н.В. Нищева. – СПб., «ДЕТСТВО-ПРЕСС», 2016.-128 с.
- Репина, Г.А. Математическое развитие дошкольников: современные направления / Г.А. Репина.- М. ТЦ Сфера, 2018.- 128 с.
- Савенков, А.И. Методика исследовательского обучения дошкольников / А.И. Савенков. – Самара: Учебная литература, 2017.- 128 с.
- Руководство, стили руководства (Теоретические основы анализа различных стилей руководства в современной организации)
- Руководство, стили руководства (Теоретические основы изучения современных подходов стилям управления)
- Управление приемом, размещением и хранением товаров. Классификация запасов. На примере реально существующей организации
- Проблемы профессиональных стрессов. Профессиональное выгорание (Исследование профессионального выгорания в зарубежной и отечественной психологии)
- Понятие и основные признаки правовой нормы (Анализ понятия норма права)
- Понятие правонарушения (НЕКОТОРЫЕ АКТУАЛЬНЫЕ ПРОБЛЕМЫ ПРАВОНАРУШЕНИЙ В ЮРИДИЧЕСКОЙ НАУКЕ)
- Понятие и классификация функций государства (Понятие и признаки функции государства)
- Психологические и организационные основы обеспечения профессионального обучения персонала (психолого – организационные аспекты обучения персонала)
- Методические возможности повышения эффективности профессионального обучения (Теоретические основы изучения профессионального образования)
- Общая характеристика валютно-финансовой системы ЕС
- Оказание финансовой помощи группой Всемирного банка (Структура Всемирного Банка)
- Взаимодействие школы и семьи в нравственном воспитании младших школьников (Семейное воспитание)

