Преподаватель который помогает студентам и школьникам в учёбе.

Методы кодирования данных (Физическое кодирование данных)

Содержание:

Введение

В настоящее время по каналам связи передаются данные со столь высокими требованиями к достоверности передаваемой информации, что удовлетворить эти требования традиционным методами - совершенствованием антенно-фидерных устройств, увеличением излучаемой мощности, снижением собственного шума приемника - оказывается экономически невыгодным или просто невозможным.

Хотя существующие на данный момент системы передачи данных отвечают всем основным стандартам и требованиям, они все же не являются совершенными. Причины тому влияние помех в канале связи. При передаче сообщений по каналам связи могут возникать помехи, способные привести к искажению принимаемых знаков.

Одним из средств решения подобных несоответствий в системах передачи цифровой информации, является применение помехоустойчивых кодов, лежащих в основе устройств кодирования/декодирования. Высокоэффективным средством решения данной проблемы является применение помехоустойчивого кодирования, основанного на введении искусственной избыточности в передаваемое сообщение. Помехоустойчивое кодирование передаваемой информации позволяет в приемной части системы обнаруживать и исправлять ошибки.

Работа подавляющего числа современных систем связи основана на передаче сообщений в цифровом виде. Сбой при приеме любого элемента цифровых данных способен вызвать значительное искажение всего сообщения в целом, что, в свою очередь, может привести к полной потере информации, содержащейся в нем. В данной работе будут рассмотрены основные методы кодирования, а также практическое применение наиболее распространённых кодов.

Объект: Методы кодирования данных

Предмет: Теория кодирования данных

Цель исследования: Выявить актуальность развития теории кодирования данных.

Задачи:

1) Рассмотреть методы физического кодирования данных.

2) Рассмотреть основные методы помехоустойчивого кодирования.

3) Рассмотреть практическую реализацию помехоустойчивого кодирования в современных сетях передачи данных.

Физическое кодирование данных.

2.1 Физическое и логическое кодирование данных

Каждый вид компьютеров имеет индивидуальный вид кодирования для представления данных – текстовой и символьной информации. Наиболее часто используются коды ASCII (American Standard Code for Information Interchange, американский стандартный код для обмена информацией) и EBCDIC (Extended Binary Coded Decimal Interchange Code, расширенный двоично-десятичный код обмена информацией).

ASCII представляет собой 8-битную кодировку для представления десятичных цифр, латинского и национального алфавитов, знаков препинания и управляющих символов. Первую половину кодовой таблицы (0 — 127) занимают символы US-ASCII, которые включают 95 печатаемых и 33 управляющих символа (разработана ANSI – Американским институтом национальных стандартов). Вторая половина таблицы (128 — 255) содержит национальные шрифты (кириллица) и символы псевдографики. Этот код используется в персональных компьютерах и в несовместимых с IBM больших машинах. В мейнфреймах используется 8-битовый код EBCDIC, разработанный компанией IBM. При передаче данных от одного компьютера к другому может потребоваться перекодировка символов, которая осуществляется системным МО передающего или принимающего компьютеров. Эти действия являются функциями уровня представления модели OSI. Рассмотрим наиболее часто применяемые методы кодирования на физическом уровне.

Большинство компьютеров для представления «0» и «1» оперирует стандартными уровнями бинарных сигналов (логическими уровнями), которые определяются видом микросхем. TTL-логика представляет 0,5В как «0», и 5В как «1». ECL и CMOS-логики представляют -1,75В как «0», и -0,9В как «1». Для передачи данных, например, в оптоволоконных системах, в трансивере устанавливается специальный чип, обрабатывающий любую логику и выдающий управляющий сигнал источнику света с конвертацией 0,5В и 5В TTL в 0 мA и 50 мА соответственно (on, off).

В большинстве компьютерных сетей цифровые данные передаются при помощи цифрового сигнала, то есть последовательностью импульсов. Для передачи данных может использоваться более двух уровней сигнала, при этом единичный импульс сигнала может представлять не один бит, а группу бит. Возможна обратная ситуация, когда для передачи одного бита может использоваться два импульса.[6,9,13,2]

При цифровой передаче используют потенциальные и импульсные коды. В потенциальных кодах для представления логических единиц и нулей используется только значение сигнала в течение битового интервала, а фронты сигнала, формирующие законченные импульсы, во внимание не принимаются. Импульсные коды представляют логический ноль и логическую единицу перепадом потенциала определенного направления. В значение импульсного кода включается весь импульс вместе с его фронтами.

Сигнал в виде импульсной последовательности имеет бесконечный спектр. Основная энергия сигнала сосредоточена в диапазоне частот от нуля до частоты f=1/t_о(первый лепесток энергетического спектра сигнала), где t_о – бодовый интервал, то есть длительность единичного импульса линейного сигнала.

Теоретически в соответствии с пределом Найквиста максимально допустимая скорость изменения значений дискретного сигнала (B=1/t_о, скорость передачи в Бодах) при передаче последовательности прямоугольных импульсов по каналу связи, эквивалентом которого является идеальный ФНЧ с прямоугольной АЧХ и линейной ФЧХ и с частотой среза f_гр, равна B_max=2f_гр. Указанное ограничение связано с наличием переходных процессов на выходе ФНЧ, при этом время нарастания/спада фронта сигнала определяется как

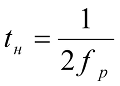
При максимально допустимой скорости передачи сигнала t_о=t_н. Если интервал t_о < t_н, происходит недопустимое искажение формы сигнала на выходе канала и, как следствие, ошибки при приеме. Таким образом, скорость передачи информации N (Бит/с) зависит от скорости передачи сигнала В (Бод) и выбранного метода кодирования сигнала на физическом уровне.[6]

Используемый метод физического цифрового кодирования должен достигать несколько целей:

Обеспечивать наименьшую ширину спектра сигнала при заданной скорости передачи информации N (Бит/с). Минимизировать величину постоянной составляющей в спектре линейного сигнала.
Обеспечивать приемнику возможность тактовой синхронизации (clocking). Так называемые самосинхронизирующиеся коды позволяют приемнику выделять из принимаемого цифрового потока колебание тактовой частоты и затем формировать из него тактовые импульсы при любой статистике битового потока на входе передатчика.
Обладать способностью распознавать ошибки
Обладать низкой стоимостью реализации.

Рассмотрим методы физического цифрового кодирования сигналов.

2.2 Потенциальный код без возвращения к нулю NRZ (Non Return to Zero)

Сигнал в линии имеет два уровня: нулю соответствует нижний уровень, единице - верхний. Переходы происходят на границе битового интервала. При передаче последовательности единиц сигнал не возвращается к нулю в течение битового интервала.

Рассмотрим частные случаи передачи данных кодом NRZ (рис. 1.1): чередующаяся последовательность нулей и единиц, последовательность нулей и последовательность единиц. Определим частоту основной гармоники спектра сигнала в каждом из этих случаев.

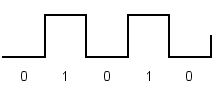
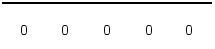
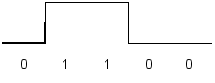
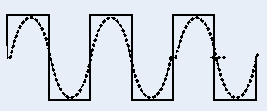
Рис. 1.1. Кодирование по методу NRZ

При чередовании единиц и нулей и скорости передачи N (Бит/с) период основной гармоники в спектре сигнала равен T=2t₀=2/N (с). Частота основной гармоники f₀равна f_о=N/2 (Гц).

При передаче только единиц, или только нулей сигнал в линии представляет собой постоянный ток.

Спектр реального сигнала постоянно меняется в зависимости от того, какова структура данных, передаваемых по линии связи. При передаче длинных последовательностей нулей или единиц, спектр сигнала сдвигается в сторону низких частот. Линейный сигнал NRZ обычно содержит постоянную составляющую и не всегда обеспечивает приемнику возможность синхронизироваться с поступающим сигналом. С другой стороны код NRZ прост в реализации, обладает хорошей помехоустойчивостью (из-за двух резко отличающихся уровней сигнала). Основная энергия сигнала в коде NRZ сосредоточена на частотах от 0 до N/2 (Гц).

В чистом виде код NRZ в сетях не используется. Тем не менее, используются его различные модификации, в которых с успехом устраняют как плохую самосинхронизацию, так и наличие постоянной составляющей.

Потенциальный код с инверсией при единице NRZI (Non Return to Zero with ones Inverted, NRZI)

При этом методе кодирования передаче нуля соответствует уровень сигнала, который был установлен в предыдущем битовом интервале (уровень сигнала не меняется), а при передаче единицы – уровень изменяется на противоположный.

Код используется при передаче по оптоволоконным кабелям, где приемник устойчиво распознает два состояния сигнала - свет и темнота.

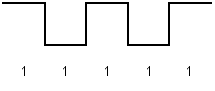
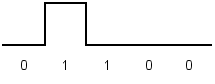
Рис.1.2. Кодирование по методу NRZI

Определим частоты основных гармоник линейного сигнала для частных случаев битовых последовательностей.

Для последовательности чередующихся единиц и нулей период сигнала равен T=4t₀ (с), основная частота сигнала f_о=N/4 (Гц), при последовательности единиц – f_о=N/2 (Гц), при передаче последовательности нулей f_о=0 - постоянный ток в линии (или отсутствие света).

Код NRZI использует только два уровня сигнала и поэтому обладает хорошей помехоустойчивостью. Максимальную энергию имеют спектральные составляющие сигнала около частоты N/4 (Гц). Следует отметить, что код NRZI стал основным при разработке улучшенных методов кодирования для систем передачи данных.[13]

2.3 Метод биполярного кодирования с альтернативной инверсией (Bipolar Alternate Mark Inversion, AMI, квазитроичный код)

В этом методе используются три значения сигнала –«-1», «0» и «+1». Для различения трех уровней необходимо лучшее соотношение сигнал/шум на входе приемника. Дополнительный уровень требует увеличение мощности передатчика примерно на 3 дБ для обеспечения той же достоверности приема бит на линии. Это общий недостаток кодов с несколькими состояниями сигнала по сравнению с двухуровневыми кодами.

Для кодирования логического нуля используется нулевой потенциал, логическая единица кодируется попеременно либо положительным потенциалом, либо отрицательным.

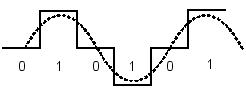
Рис.1.3. Квазитроичное кодирование (AMI)

При передаче любой битовой последовательности сигнал в линии не содержит постоянную составляющую. При передаче единиц основная гармоника сигнала находится на частоте f_o=N/2 (Гц). В случае чередующегося набора единиц и нулей основная гармоника находится на частоте f_o=N/4 (Гц), что в два раза меньше чем у кода NRZ. Но остается проблема синхронизации при передаче последовательности нулей.

В целом, для различных комбинаций бит использование кода AMI приводит к более узкому спектру сигнала, чем для кода NRZ. Код AMI предоставляет также некоторые возможности по распознаванию ошибочных сигналов. Так, нарушение строгого чередования полярности сигналов говорит о ложном импульсе или исчезновении корректного импульса.[9]

2.4 Манчестерский код (Manchester)

Манчестерский код относится к самосинхронизирующимся кодам и имеет два уровня, что обеспечивает хорошую помехозащищенность. Каждый битовый интервал делится на две части. Информация кодируется перепадом уровня, происходящим в середине каждого интервала.

Единица кодируется перепадом от высокого уровня сигнала к низкому, а ноль - обратным перепадом. В начале каждого битового интервала может происходить служебный перепад сигнала (при передаче несколько единиц или нулей подряд).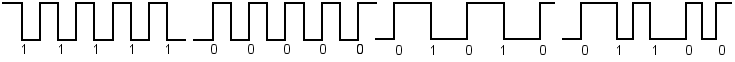

Рис.1.4. Манчестерское кодирование

При передаче любой битовой последовательности сигнал не содержит постоянную составляющую. Длительность единичного импульса линейного сигнала t₀ равна половине битового интервала, то есть B=2N. Частота основной гармоники сигнала зависит от характера битовой последовательности и находится в диапазоне f_о=N/2 – N (Гц).

Манчестерский код используется в сетях Ethernet со скоростью передачи 10 Мбит/с (спецификация 10Bаsе-Т).

В настоящее время разработчики пришли к выводу, что во многих случаях рациональнее применять потенциальное кодирование, ликвидируя его недостатки с помощью, так называемого логического кодирования.

2.5 Потенциальный код 2B1Q

Это потенциальный код с четырьмя уровнями сигнала для кодирования данных. Название отражает суть кодирования – каждые два бита (2В) передаются за один такт сигналом определенного уровня (1Q). Линейный сигнал имеет четыре состояния.

Дибиту «00» соответствует потенциал -2,5 В (-3), «01» - потенциал -0,833 В (-1), «11» - потенциал +0,833 В (+1), «10» - потенциал +2,5 В (+3). Скорость передачи сигнала В при таком кодировании в 2 раза меньше скорости передачи информации N. На рис.1.5 изображен сигнал, соответствующий последовательности бит: 01 01 10 00.

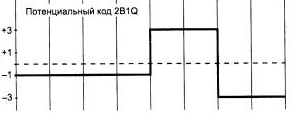
Рис.1.5 Сигнал в коде 2B1Q

Основная частота сигнала не превышает f_о=N/4 Гц. Однако для реализации этого метода кодирования мощность передатчика должна быть выше, чтобы четыре значения потенциала четко различались приемником на фоне помех.[6]

2.6 Код MLT3 (Multi Level Transmission - 3).

Используются три уровня линейного сигнала: «-1», «0», «+1». Логической единице соответствует обязательный переход с одного уровня сигнала на другой. При передаче логического нуля изменение уровня линейного сигнала не происходит.

При передаче последовательности единиц период изменения уровня сигнала включает четыре бита. В этом случае f_о=N/4 (Гц). Это максимальная основная частота сигнала в коде MLT-3. В случае чередующейся последовательности нулей и единиц основная гармоника сигнала находится на частоте f_о=N/8 (Гц).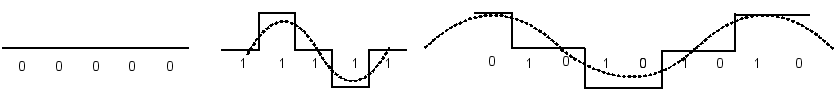

Рис.1.6 Сигнал в коде MLT-3

Логическое кодирование выполняется передатчиком до физического кодирования, рассмотренного выше, обычно средствами физического уровня. На этапе логического кодирования борются с недостатками методов физического цифрового кодирования - отсутствие синхронизации, наличие постоянной составляющей. Таким образом, сначала с помощью средств логического кодирования формируются исправленные последовательности данных, которые потом с помощью методов физического кодирования передаются по линиям связи.

Логическое кодирование подразумевает замену бит исходной информационной последовательности новой последовательностью бит, несущей ту же информацию, но обладающей, кроме этого, дополнительными свойствами.

Различают два метода логического кодирования:

избыточные коды;
скремблирование.

Избыточные коды основаны на разбиении исходной последовательности бит на группы и замене каждой исходной группы в соответствии с заданной таблицей кодовым словом, которое содержит большее количество бит.

Логический код 4В/5В заменяет исходные группы (слова) длиной 4 бита словами длиной 5 бит. В результате, общее количество возможных битовых комбинаций 25=32 больше, чем для исходных групп 24=16. В кодовую таблицу включают 16 кодовых слов, которые не содержат более двух нулей подряд, и используют их для передачи данных. Код гарантирует, что при любом сочетании кодовых слов на линии не могут встретиться более трех нулей подряд.

Остальные комбинации кода используются для передачи служебных сигналов (синхронизация передачи, начало блока данных, конец блока данных, управление передачей). Неиспользуемые кодовые слова могут быть задействованы приемником для обнаружения ошибок в потоке данных. Цена за полученные достоинства при таком способе кодирования данных - снижение скорости передачи полезной информации на 25%.

Имеются также коды и с тремя состояниями сигнала, например, в коде 8В/6Т для кодирования 8 бит исходной информации используются кодовые слова из 6 элементов, каждый из которых может принимать одно из трех значений. Избыточность кода 8В/6Т выше, чем кода 4В/5В, так как на 28=256 исходных комбинаций приходится 36=729 результирующих комбинаций.[6]

Методы кодирования в программировании

3.1 Код Шеннона

Оптимальным кодом можно определить тот, в котором каждый двоичный символ будет передавать максимальную информацию. В силу формул Хартли и Шеннона максимум энтропии достигается при равновероятных событиях, следовательно, двоичный код будет оптимальным, если в закодированном сообщении символы 0 и 1 будут встречаться одинаково часто.[2]

Рассмотрим в качестве примера оптимальное двоичное кодирование букв русского алфавита вместе с символом пробела «-». Полагаем, что известны вероятности появления в сообщении символов русского алфавита, например, приведенные в таблице.

Таблица 1.Частота букв русского языка (предположение)

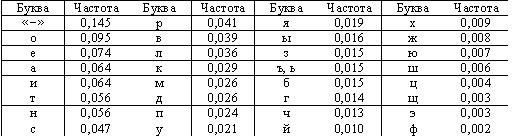
К. Шеннон и Р. Фано независимо предложили в 1948-1949 гг. способ построения кода, основанный на выполнении условия равной вероятности символов 0 и 1 в закодированном сообщении. [11]

Все кодируемые символы (буквы) разделяются на две группы так, что сумма вероятностей символов в первой группе равна сумме вероятностей символов второй группы (то есть вероятность того, что в сообщении встретится символ из первой группы, равна вероятности того, что в сообщении встретится символ из второй группы).

Для символов первой группы значение первого разряда кода присваивается равным «0», для символов второй группы – равными «1».

Далее каждая группа разделяется на две подгруппы, так чтобы суммы вероятностей знаков в каждой подгруппе были равны. Для символов первой подгруппы каждой группы значение второго разряда кода присваивается равным «0», для символов второй подгруппы каждой группы – «1». Такой процесс разбиения символов на группы и кодирования продолжается до тех пор, пока в подгруппах не остается по одному символу.

Пример кодирования символов русского алфавита приведен в табл.(2)

Таблица 2.

Пример кодирования букв русского алфавита с помощью кода Шеннона-Фано. [5]

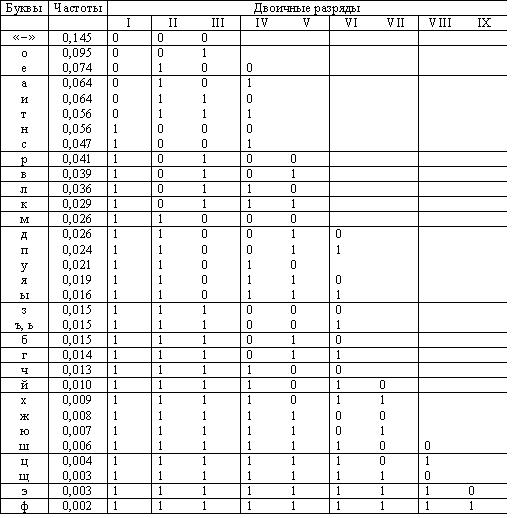
(Таблица 2)

Анализ приведенных в таблице кодов приводит к выводу, что часто встречающиеся символы кодируются более короткими двоичными последовательностями, а редко встречающиеся - более длинными. Значит, в среднем для кодирования сообщения определенной длины потребуется меньшее число двоичных символов 0 и 1, чем при любом другом способе кодирования.

Вместе с тем процедура построения кода Шеннона-Фано удовлетворяет критерию различимости Фано. Код является префиксным и не требует специального символа, отделяющего буквы друг от друга для однозначного него декодирование двоичного сообщения.

Таким образом, проблема помехоустойчивого кодирования представляет собой обширную область теоретических и прикладных исследований. Основными задачами при этом являются следующие: отыскание кодов, эффективно исправляющих ошибки требуемого вида; нахождение методов кодирования и декодирования и простых способов их реализации.

Наиболее разработаны эти задачи применительно к систематическим кодам. Такие коды успешно применяются в вычислительной технике, различных автоматизированных цифровых устройствах и цифровых системах передачи информации.

3.2 Метод Хафмана

Алгоритм Хаффмана — адаптивный жадный алгоритм оптимального префиксного кодирования алфавита с минимальной избыточностью. Был разработан в 1952 году аспирантом Массачусетского технологического института Дэвидом Хаффманом при написании им курсовой работы. В настоящее время используется во многих программах сжатия данных.[1]

В отличие от алгоритма Шеннона — Фано, алгоритм Хаффмана остаётся всегда оптимальным и для вторичных алфавитов m₂ с более чем двумя символами.

Этот метод кодирования состоит из двух основных этапов:

Построение оптимального кодового дерева.
Построение отображения код-символ на основе построенного дерева.

Один из первых алгоритмов эффективного кодирования информации был предложен Д. А. Хаффманом в 1952 году. Идея алгоритма состоит в следующем: зная вероятности символов в сообщении, можно описать процедуру построения кодов переменной длины, состоящих из целого количества битов. Символам с большей вероятностью ставятся в соответствие более короткие коды. Коды Хаффмана обладают свойством префиксности, что позволяет однозначно их декодировать.[1]

Классический алгоритм Хаффмана на входе получает таблицу частот встречаемости символов в сообщении. Далее на основании этой таблицы строится дерево кодирования Хаффмана (Н-дерево).

Символы входного алфавита образуют список свободных узлов. Каждый лист имеет вес, который может быть равен либо вероятности, либо количеству вхождений символа в сжимаемое сообщение.
Выбираются два свободных узла дерева с наименьшими весами.
Создается их родитель с весом, равным их суммарному весу.
Родитель добавляется в список свободных узлов, а два его потомка удаляются из этого списка.
Одной дуге, выходящей из родителя, ставится в соответствие бит 1, другой — бит 0.
Шаги, начиная со второго, повторяются до тех пор, пока в списке свободных узлов не останется только один свободный узел. Он и будет считаться корнем дерева.[12]

Допустим, у нас есть следующая таблица частот:

15	7	6	6	5
A	B	C	D	E

Этот процесс можно представить как построение дерева, корень которого — символ с суммой вероятностей объединенных символов, получившийся при объединении символов из последнего шага, его n₀ потомков — символы из предыдущего шага и т. д.

Чтобы определить код для каждого из символов, входящих в сообщение, мы должны пройти путь от листа дерева, соответствующего этому символу, до корня дерева, накапливая биты при перемещении по ветвям дерева. Полученная таким образом последовательность битов является кодом данного символа, записанным в обратном порядке.

Для данной таблицы символов коды Хаффмана будут выглядеть следующим образом.

A	B	C	D	E
0	100	101	110	111

Поскольку ни один из полученных кодов не является префиксом другого, они могут быть однозначно декодированы при чтении их из потока. Кроме того, наиболее частый символ сообщения А закодирован наименьшим количеством бит, а наиболее редкий символ Д — наибольшим.

При этом общая длина сообщения, состоящего из приведённых в таблице символов, составит 87 бит (в среднем 2,2308 бита на символ). При использовании равномерного кодирования общая длина сообщения составила бы 117 бит (ровно 3 бита на символ). Заметим, что энтропия источника, независимым образом порождающего символы с указанными частотами составляет ~2,1858 бита на символ, т.е. избыточность построенного для такого источника кода Хаффмана, понимаемая, как отличие среднего числа бит на символ от энтропии, составляет менее 0,05 бит на символ.

Классический алгоритм Хаффмана имеет ряд существенных недостатков. Во-первых, для восстановления содержимого сжатого сообщения декодер должен знать таблицу частот, которой пользовался кодер. Следовательно, длина сжатого сообщения увеличивается на длину таблицы частот, которая должна посылаться впереди данных, что может свести на нет все усилия по сжатию сообщения. Кроме того, необходимость наличия полной частотной статистики перед началом собственно кодирования требует двух проходов по сообщению: одного для построения модели сообщения (таблицы частот и Н-дерева), другого для собственно кодирования. Во-вторых, избыточность кодирования обращается в ноль лишь в тех случаях, когда вероятности кодируемых символов являются обратными степенями числа 2. В-третьих, для источника с энтропией, не превышающей 1, непосредственное применение кода Хаффмана не имеет смысла.

3.3 Адаптивное сжатие

Адаптивное сжатие позволяет не передавать модель сообщения вместе с ним самим и ограничиться одним проходом по сообщению как при кодировании, так и при декодировании.[1,12]

В создании алгоритма адаптивного кодирования Хаффмана наибольшие сложности возникают при разработке процедуры обновления модели очередным символом. Теоретически можно было бы просто вставить внутрь этой процедуры полное построение дерева кодирования Хаффмана, однако, такой алгоритм сжатия имел бы неприемлемо низкое быстродействие, так как построение Н-дерева — это слишком большая работа и производить её при обработке каждого символа неразумно. К счастью, существует способ модифицировать уже существующее Н-дерево так, чтобы отобразить обработку нового символа.

Обновление дерева при считывании очередного символа сообщения состоит из двух операций.

Первая — увеличение веса узлов дерева. Вначале увеличиваем вес листа, соответствующего считанному символу, на единицу. Затем увеличиваем вес родителя, чтобы привести его в соответствие с новыми значениями веса потомков. Этот процесс продолжается до тех пор, пока мы не доберемся до корня дерева. Среднее число операций увеличения веса равно среднему количеству битов, необходимых для того, чтобы закодировать символ.

Вторая операция — перестановка узлов дерева — требуется тогда, когда увеличение веса узла приводит к нарушению свойства упорядоченности, то есть тогда, когда увеличенный вес узла стал больше, чем вес следующего по порядку узла. Если и дальше продолжать обрабатывать увеличение веса, двигаясь к корню дерева, то дерево перестанет быть деревом Хаффмана.

Чтобы сохранить упорядоченность дерева кодирования, алгоритм работает следующим образом. Пусть новый увеличенный вес узла равен W+1. Тогда начинаем двигаться по списку в сторону увеличения веса, пока не найдем последний узел с весом W. Переставим текущий и найденный узлы между собой в списке, восстанавливая таким образом порядок в дереве (при этом родители каждого из узлов тоже изменятся). На этом операция перестановки заканчивается.

После перестановки операция увеличения веса узлов продолжается дальше. Следующий узел, вес которого будет увеличен алгоритмом, — это новый родитель узла, увеличение веса которого вызвало перестановку.[1]

3.4 Переполнение

В процессе работы алгоритма сжатия вес узлов в дереве кодирования Хаффмана неуклонно растет. Первая проблема возникает тогда, когда вес корня дерева начинает превосходить вместимость ячейки, в которой он хранится. Как правило, это 16-битовое значение и, следовательно, не может быть больше, чем 65535. Вторая проблема, заслуживающая ещё большего внимания, может возникнуть значительно раньше, когда размер самого длинного кода Хаффмана превосходит вместимость ячейки, которая используется для того, чтобы передать его в выходной поток. Декодеру все равно, какой длины код он декодирует, поскольку он движется сверху вниз по дереву кодирования, выбирая из входного потока по одному биту. Кодер же должен начинать от листа дерева и двигаться вверх к корню, собирая биты, которые нужно передать. Обычно это происходит с переменной типа «целое», и, когда длина кода Хаффмана превосходит размер типа «целое» в битах, наступает переполнение.[1]

Можно доказать, что максимальную длину код Хаффмана для сообщений с одним и тем же входным алфавитом будет иметь, если частоты символов образует последовательность Фибоначчи. Сообщение с частотами символов, равными числам Фибоначчи до Fib (18), — это отличный способ протестировать работу программы сжатия по Хаффману.

3.5 Масштабирование весов узлов дерева Хаффмана

Уделяя внимание сказанному выше, алгоритм обновления дерева Хаффмана должен быть изменен следующим образом: при увеличении веса нужно проверять его на достижение допустимого максимума. Если мы достигли максимума, то необходимо «масштабировать» вес, обычно разделив вес листьев на целое число, а потом пересчитав вес всех остальных узлов.

Однако при делении веса пополам возникает проблема, связанная с тем, что после выполнения этой операции дерево может изменить свою форму. Объясняется это тем, что мы делим целые числа и при делении отбрасываем дробную часть.[1]

Правильно организованное дерево Хаффмана после масштабирования может иметь форму, значительно отличающуюся от исходной. Это происходит потому, что масштабирование приводит к потере точности нашей статистики. Но со сбором новой статистики последствия этих «ошибок» практически нивелируются.[14] Масштабирование веса — довольно дорогостоящая операция, так как она приводит к необходимости заново строить все дерево кодирования. Но, так как необходимость в ней возникает относительно редко, то с этим можно смириться.[12]

Выигрыш от масштабирования

Масштабирование веса узлов дерева через определенные интервалы дает неожиданный результат. Несмотря на то, что при масштабировании происходит потеря точности статистики, тесты показывают, что оно приводит к лучшим показателям сжатия. Это можно объяснить тем, что текущие символы сжимаемого потока больше «похожи» на своих близких предшественников, чем на тех, которые встречались намного раньше. Масштабирование приводит к уменьшению влияния «давних» символов на статистику и к увеличению влияния на неё «недавних» символов. Это очень сложно измерить количественно, но, в принципе, масштабирование оказывает положительное влияние на степень сжатия информации. Эксперименты с масштабированием в различных точках процесса сжатия показывают, что степень сжатия сильно зависит от момента масштабирования веса, но не существует правила выбора оптимального момента масштабирования для программы, ориентированной на сжатие любых типов информации.[1,12,14]

Сжатие данных по Хаффману применяется при сжатии фото- и видеоизображений (JPEG, стандарты сжатия MPEG), в архиваторах (PKZIP, LZH и др.), в протоколах передачи данных MNP5 и MNP7.

3.6 Коды БЧХ

Коды Боуза-Чоудхури-Хоквингема (БЧХ) – класс циклических кодов, исправляющих кратные ошибки, т. е. две и более (d₀≥ 5). Кодирование этой группой методов является одним из самых распространённых в современном мире. Коды БЧХ применяются для исправления ошибок при передаче больших пакетов данных.[8,4]

Теоретически коды БЧХ могут исправлять произвольное количество ошибок, но при этом существенно увеличивается длительность кодовой комбинации, что приводит к уменьшению скорости передачи данных и усложнению приемо-передающей аппаратуры (схем кодеров и декодеров).

Методика построения кодов БЧХ отличается от обычных циклических, в основном, выбором определяющего полинома P(х). Коды БЧХ строятся по заданной длине кодового слова n и числа исправляемых ошибок S , при этом количество информационных разрядов k не известно пока не выбран определяющий полином. [8]

3.6.1 Декодирование кодов БЧХ

Коды БЧХ представляют собой циклические коды и, следовательно, к ним применимы любые методы декодирования циклических кодов. Открытие кодов БЧХ привело к необходимости поиска новых алгоритмов и методов реализации кодеров и декодеров. Получены существенно лучшие алгоритмы, специально разработанные для кодов БЧХ. Это алгоритмы Питерсона, Бэрлекэмпа и др. [3]

Рассмотрим алгоритм ПГЦ (Питерсона-Горенстейна-Цирлера). Пусть БЧХ код над полем GF(q) длины n и с конструктивным расстоянием d задается порождающим полиномом g(x), который имеет среди своих корней элементы 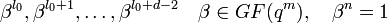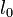$\beta^{l_0},\beta^{l_0+1},\ldots,\beta^{l_0+d-2} \quad \beta \in GF(q^m), \quad \beta^n=1$ , $\quad l_0$ — целое число (например 0 или 1). Тогда каждое кодовое слово обладает тем свойством, что 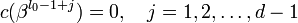$c(\beta^{l_0-1+j}) = 0, \quad j=1,2,\ldots,d-1$ . Принятое слово r(x) можно записать как r(x) = c(x) + e(x), где e(x) — полином ошибок. 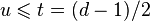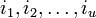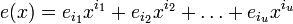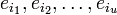Пусть произошло $u \leqslant t = (d-1)/2$ ошибок на позициях $i_1,i_2,\ldots,i_u$ (t максимальное число исправляемых ошибок), значит $e(x) = e_{i_1}x^{i_1}+e_{i_2}x^{i_2}+\ldots+e_{i_u}x^{i_u}$ , а $e_{i_1}, e_{i_2},\ldots, e_{i_u}$ — величины ошибок.

Можно составить j-ый синдром Sj принятого слова r(x):

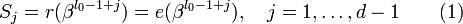$S_j = r(\beta^{l_0-1+j}) = e(\beta^{l_0-1+j}), \quad j=1,\ldots,d-1\quad\quad (1)$ .

Задача состоит в нахождений числа ошибок u, их позиций 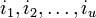$i_1,i_2,\ldots,i_u$ и их значений 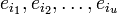$e_{i_1}, e_{i_2},\ldots, e_{i_u}$ при известных синдромах Sj.

Предположим, для начала, что u в точности равно t. Запишем (1) в виде системы нелинейных уравнений в явном виде:

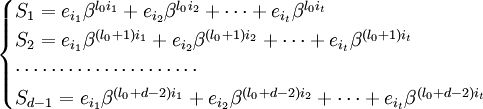
${ \begin{cases}S_1 = e_{i_1} \beta^{l_0 i_1} + e_{i_2} \beta^{l_0 i_2} + \dots + e_{i_t} \beta^{l_0 i_t} \\S_2 = e_{i_1} \beta^{(l_0+1) i_1} + e_{i_2} \beta^{(l_0+1) i_2} + \dots + e_{i_t} \beta^{(l_0+1) i_t} \\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \\S_{d-1} = e_{i_1} \beta^{(l_0+d-2) i_1} + e_{i_2} \beta^{(l_0+d-2) i_2} + \dots + e_{i_t} \beta^{(l_0+d-2) i_t} \\\end{cases} }$

Обозначим через 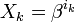$X_k = \beta^{i_k}$ локатор k-ой ошибки, а через 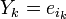$Y_k = e_{i_k}$ величину ошибки, 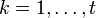$k=1,\ldots,t$ . При этом все Xk различны, так как порядок элемента β равен n, и поэтому при известном Xk можно определить ik как ik = logβXk.

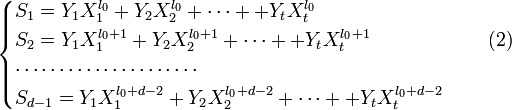
${ \begin{cases}S_1 = Y_1 X_1^{l_0} + Y_2 X_2^{l_0} + \dots + + Y_t X_t^{l_0} \\S_2 = Y_1 X_1^{l_0+1} + Y_2 X_2^{l_0+1} + \dots + + Y_t X_t^{l_0+1} \quad \quad \quad \quad \quad\quad(2) \\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \\S_{d-1} = Y_1 X_1^{l_0+d-2} + Y_2 X_2^{l_0+d-2} + \dots + + Y_t X_t^{l_0+d-2} \end{cases} }$

Составим полином локаторов ошибок:

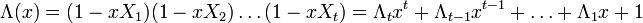
$\Lambda (x) = (1-xX_1)(1-xX_2)\dots (1-xX_t) = \Lambda_t x^t + \Lambda_{t-1} x^{t-1} + \dots + \Lambda_1 x + 1$

Корнями этого полинома являются элементы, обратные локаторам ошибок. Помножим обе части этого полинома на 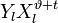$Y_l X_{l}^{\vartheta+t}$ . Полученное равенство будет справедливо для

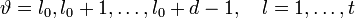$\vartheta = l_0,l_0+1,\dots,l_0+d-1,\quad l=1,\ldots,t$ :

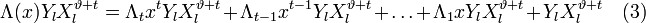
$\Lambda (x) Y_l X_{l}^{\vartheta+t} = \Lambda_t x^t Y_l X_{l}^{\vartheta+t} + \Lambda_{t-1} x^{t-1} Y_l X_{l}^{\vartheta+t} + \dots + \Lambda_1 x Y_l X_{l}^{\vartheta+t} + Y_l X_{l}^{\vartheta+t} \quad (3)$

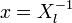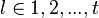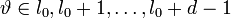Положим $x=X_l^{-1}$ и подставим в (3). Получится равенство, справедливое для каждого $l \in {1,2,...,t}$ и при всех $\vartheta \in { l_0,l_0+1,\dots,l_0+d-1 }$ :

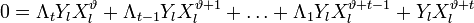
$0 = \Lambda_t Y_l X_{l}^{\vartheta} + \Lambda_{t-1} Y_l X_{l}^{\vartheta+1} + \dots + \Lambda_{1} Y_l X_{l}^{\vartheta+t-1} + Y_l X_{l}^{\vartheta+t}$

Таким образом, для каждого l можно записать свое равенство. Если их просуммировать по l, то получиться равенство, справедливое для каждого

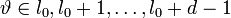$\vartheta \in { l_0,l_0+1,\dots,l_0+d-1 }$ :

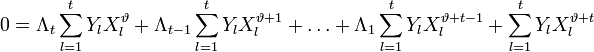$0 = \Lambda_t \sum_{l=1}^t Y_l X_{l}^{\vartheta} + \Lambda_{t-1} \sum_{l=1}^t Y_l X_{l}^{\vartheta+1} + \dots + \Lambda_{1} \sum_{l=1}^t Y_l X_{l}^{\vartheta+t-1} + \sum_{l=1}^t Y_l X_{l}^{\vartheta+t}$ .

Учитывая (2) и то, что

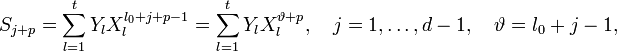
$S_{j+p} = \sum_{l=1}^t Y_l X_{l}^{l_0+j+p-1} = \sum_{l=1}^t Y_l X_{l}^{\vartheta+p}, \quad j=1,\ldots,d-1, \quad \vartheta = l_0+j-1,$

(то есть 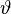$\vartheta$ меняется в тех же пределах, что и ранее) получаем систему линейных уравнений:

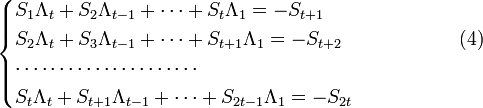
${ \begin{cases}S_1 \Lambda_t + S_2 \Lambda_{t-1} + \dots + S_t \Lambda_1 = -S_{t+1} \\S_2 \Lambda_t + S_3 \Lambda_{t-1} + \dots + S_{t+1} \Lambda_1 = -S_{t+2} \quad \quad \quad \quad \quad\quad(4) \\\cdots \cdots \cdots \cdots \cdots \cdots \cdots \\S_t \Lambda_t + S_{t+1} \Lambda_{t-1} + \dots + S_{2t-1} \Lambda_1 = -S_{2t}\end{cases} }$

Или в матричной форме

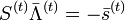$S^{(t)} \bar\Lambda^{(t)} = -\bar s^{(t)}$ ,

Где

$S^{(t)}={ \left[ \begin{matrix}S_1 & S_2 & \dots & S_t \\S_2 & S_3 & \dots & S_{t+1} \\\cdots & \cdots & \cdots & \\S_t & S_{t+1} & \dots & S_{2t-1} \end{matrix} \right] }, \quad \quad \quad \quad \quad\quad(5)$

$\bar\Lambda^{(t)} = { \left[ \begin{matrix}\Lambda_t \\\Lambda_{t-1} \\\cdots \\\Lambda_1\end{matrix} \right] }, \quad \quad \bar s^{(t)}{ \left[ \begin{matrix}S_{t+1} \\S_{t+2} \\\cdots \\S_{2t}\end{matrix} \right] }$

Если число ошибок и в самом деле равно t, то система (4) разрешима, и можно найти значения коэффициентов 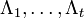$\Lambda_{1},\ldots,\Lambda_{t}$ . Если же число u < t, то определитель матрицы S(t) системы (4) будет равен 0. Это есть признак того, что количество ошибок меньше t. Поэтому необходимо составить систему (4), предполагая число ошибок равным t − 1. Высчитать определитель новой матрицы S(t − 1) и т. д., до тех пор, пока не установим истинное число ошибок.

После этого можно решить систему (4) и получить коэффициенты полинома локаторов ошибок. Его корни (элементы, обратные локаторам ошибок) можно найти простым перебором по всем элементам поля GF(qm). К ним найти элементы, обратные по умножению, — это локаторы ошибок 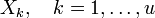$X_k, \quad k=1,\ldots,u$ . По локаторам можно найти позиции ошибок (ik = logβXk), а значения Yk ошибок из системы (2), приняв t = u. Декодирование завершено.[3]

3.7 Коды Рида-Соломона

Широко используемым подмножеством кодов БЧХ являются коды Рида-Соломона, которые позволяют исправлять пакеты ошибок. Пакет ошибок длины b представляет собой последовательность из таких b ошибочных символов, что первый и последний из них отличны от нуля. Существуют классы кодов Рида-Соломона, позволяющие исправлять многократные пакеты ошибок.

Коды Рида-Соломона широко используются в устройствах цифровой записи звука, в том числе на компакт-диски. Данные, состоящие из отсчетов объединяются в кадр, представляющий кодовое слово. Кадры разбиваются на блоки по 8 бит. Часть блоков являются контрольными.

Обычно 1 кадр (кодовое слово) = 32 символа данных +24 сигнальных символа +8 контрольных бит = 256 бит.

Сигнальные символы это вспомогательные данные, облегчающие декодирование: сигналы синхронизации, служебные сигналы, и т. д.

При передаче данных производится перемежение блоков с различным сдвигом во времени, в результате чего расчленяются сдвоенные ошибки, что облегчает их локализацию и коррекцию. При этом используются коды Рида-Соломона с минимальным кодовым расстоянием d0 = 5.

4. Реализация методов кодирования данных

В современном мире с постоянно развивающейся отраслью информационных технологий многие методы теории кодирования реализовать до сих пор невозможно по тем или иным причинам, но основные методы кодирования данных всё же нашли своё применение.

4.1 Реализация метода Хаффмана и Шеннона-Фано для сжатия данных

Сжимая файл по алгоритму Хаффмана первое что мы должны сделать - это необходимо прочитать файл полностью и подсчитать сколько раз встречается каждый символ из расширенного набора ASCII. Если мы будем учитывать все 256 символов, то для нас не будет разницы в сжатии текстового и EXE файла.

После подсчета частоты вхождения каждого символа, необходимо просмотреть таблицу кодов ASCII и сформировать мнимую компоновку между кодами по убыванию. То есть не меняя местонахождение каждого символа из таблицы в памяти отсортировать таблицу ссылок на них по убыванию. Каждую ссылку из последней таблицы назовем "узлом". В дальнейшем ( в дереве ) мы будем позже размещать указатели которые будут указывает на этот "узел

Данный метод используется в формировании архивов *.zip;Применяется во множестве программ архиваторов. Так же метод Хаффмана применяется для сжатия изображений. Для сжатия данных так же используется алгоритм Шеннона-Фано.

4.2 Реализация метода Рида – Соломона

Благодаря кодам Рида-Соломона можно прочитать компакт-диск с множеством царапин, либо передать информацию в условиях связи с большим количеством помех. В среднем для компакт-диска избыточность кода (т.е. количество дополнительных символов, благодаря которым информацию можно восстанавливать) составляет примерно 25%. Восстановить при этом можно количество данных, равное половине избыточных. Если емкость диска 700 Мб, то, получается, теоретически можно восстановить до 87,5 Мб из 700. При этом нам не обязательно знать, какой именно символ передан с ошибкой. Так же заметим, что вместе с кодированием используется перемежевание, когда байты разных блоков перемешиваются в определенном порядке, что в результате позволяет читать диски с обширными повреждениями, локализированными близко друг к другу (например, глубокие царапины), так как после операции, обратной перемежеванию, обширное повреждение оборачивается единичными ошибками во множестве блоков кода, которые поддаются восстановлению.

4.3 Реализация Физических методов кодирования данных

Все рассмотренные избыточные коды применяются в сетях Ethernet, которые нашли самое широкое распространение. Так, код 4B/5B используется в стандартах 100Base-TX/FX, а код 8B/6T — в стандарте 100Base-T4, который в настоящее время практически уже не используется. Код 8B/10В используется в стандарте 1000Base-Х, код 64/66 в стандарте 10 GbE (когда в качестве среды передачи данных используется оптоволокно).

Осуществляют логическое кодирование сетевые адаптеры. Поскольку, использование таблицы перекодировки является очень простой операцией, метод логического кодирования избыточными кодами не усложняет функциональные требования к этому оборудованию.

Для обеспечения заданной пропускной способности линии передатчик, использующий избыточный код, должен работать с повышенной скоростью (тактовой частотой). Так, для обеспечения скорости передачи информации 100 Мбит/с с использованием кодирования 4В/5В + NRZI передатчик должен работать на скорости 125 МБод. При этом спектр линейного сигнала расширяется. Тем не менее, спектр сигнала избыточного потенциального кода уже спектра сигнала в манчестерском коде, что оправдывает дополнительный этап логического кодирования, а также работу приемника и передатчика на повышенной скорости.

5. Заключение

Таким образом, рассмотрев основные методы кодирования данных, мы можем прийти к выводу, что проблема помехоустойчивого кодирования и оптимизация кодов актуальна в современном мире. Кодирование данных в той или иной степени связано со всей структурой информационных технологий, и играет в ней основополагающую роль. Рассмотренные в работе методы являются основными для современных методов кодирования, на их основе реализованы каскадное кодирование данных, а так же другие методы, и алгоритмы программирования.

Особую роль в кодировании данных занимают физические методы кодирования данных они широко применяются в проводных ,а так же беспроводных сетях передачи данных. Без их применения на практике стали бы не возможны такие технологии как интернет, телеграф, факс. Так же методы физического кодирования широко применяются в прогнозировании погоды и передачи данных со спутников.

6. Список используемой литературы

Ананий В. Левитин. Глава 9. Жадные методы: Алгоритм Хаффмана // Алгоритмы: введение в разработку и анализ = Introduction to The Design and Analysis of Aigorithms. — М.: Вильямс, 2006. — С. 392—398. — ISBN 0-201-74395-7
Берлекэмп Э., Алгебраическая теория кодирования, Москва, “Мир”, 1971.
Блейхут Р. Теория и практика кодов, контролирующих ошибки = Theory and practice of error control codes. — М.: Мир, 1986. — С. 576
Дмитриев В.И. Прикладная теория информации: Учебник для вузов. М.: Высшая школа , 1989. 320 c.
Жоголев Е.А. Ж.78 Технология программирования. – М., Научный Мир, 2004, 216 с.
Колесник В.Д., Полтырев Г.Ш. Курс теории информации. – М.: Наука, 1982.
Коломоец Г.П. "Моделирование сигналов передаваемых в компьютерных сетях данных"/Сборник научных трудов 9-й Международной научно-практической конференции «Современные информационные и электронные технологии», Одесса, Одесский национальный политехнический университет, 19–23 мая 2008 г, т.1.–с 118.
Кудряшов Б.Д. Теория информации. Учебник для вузов Изд-во ПИТЕР, 2008. – 320с.
Олифер В.Г., Олифер Н.А. Компьютерные сети. Принципы, технологии, протоколы: Учебник для вузов. –3-е изд. – СПб.: Питер, 2006. – 958с.
Питерсон У., Уэлдон Э. Коды, исправляющие ошибки. — М.: Мир, 1976. — С. 596.
Семенюк В. В. Экономное кодирование дискретной информации. – СПб.: СПб ГИТМО (ТУ), 2001
Сэломон Д., Сжатие данных, изображения и звука. — М.: Техносфера, 2004. — 368 с. — 3000 экз. — ISBN 5-94836-027-X
Таненбаум Э. Компьютерные сети. 4-е изд. /. – СПб.: Питер, 2003. – 992с.
Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ = Introduction to Algorithms. — 2-е изд. — М.: Вильямс, 2006. — 1296 с. — ISBN 0-07-013151-1
Фундаментальные алгоритмы на C++. Анализ/Структуры данных/Сортировка/Поиск: Пер. с англ./Роберт Седжвик. - К.: Издательство «ДиаСофт», 2001.- 688 с.
4. IEEE Standard 802.3–2005: Information technology – Telecommunications and information exchange between systems – Local and metropolitan area networks – Specific requirements. Part3: Carrier Sense Multiple Access with Collision Detection (CSMA/CD) access method and physical layer specifications – http://www.ieee.org.