Рекурсивные и итерационные алгоритмы: особенности и примеры использования (Определение итерационного алгоритма)

Содержание:

Введение

С развитием средств связи и компьютерных технологий встал вопрос хранения, обработки информации с использованием современных технических средств и методов программирования. Информационные системы различного уровня сложности и трудоемкости используются для хранения и обработки информационных потоков данных. При создании информационных систем требуются нестандартные решения программистов.

Часто программисту не известно количество шагов при выполнении каких-либо вычислений. Такие задачи решаются с использованием итерационного цикла или рекурсии.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.

Объект называется рекурсивным, если для своего определения или функционирования он прямо или косвенно обращается к объекту в некотором смысле такого же типа. [5, 67] Правильность работы рекурсивных алгоритмов зависит от технических возможностей процессора, что рассмотрено в настоящей работе.

Рекурсия существует вокруг нас практически везде: в литературных произведениях, математике, биологии, физике и соответственно, в программировании. Рекурсия является общим методом научного познания, эффективно применяется во многих научных дисциплинах и стала неотъемлемой их частью.

Актуальность темы исследования заключается в том, что любую задачу можно решить с использованием итерационного алгоритма и рекурсии. Рекурсия позволяет создавать "понятные" и "читаемые" алгоритмы, быстро сходящиеся, но необходимо грамотно использовать рекурсивные методы вместо простых итерационных алгоритмов. Правильность работы рекурсии зависит от технических характеристик компьютера. Процессор не может обеспечить бесконечный рекурсивный спуск вниз, необходимо создавать промежуточные точки выхода из рекурсии, позволяющие проводить анализ правильности работы алгоритма. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса).

Объект исследования – алгоритмы.

Предметом исследования являются– рекурсивные и итерационные алгоритмы.

Цель курсовой работы заключается в расширении систематизации теоретических знаний по теме: "Рекурсивные и итерационные алгоритмы: особенности и примеры использования".

Задачи исследования

• провести анализ научных источников по теме «Рекурсивные и итерационные алгоритмы: особенности и примеры использования»;
• описать принципы написания итерационных алгоритмов;
• описать принципы написания рекурсивных алгоритмов;
• привести примеры задач с итерационным методом решения;
• привести примеры использования рекурсии;
• сравнить работу итерационных алгоритмов и рекурсии.

При проведении исследования были изучены научные труды по основам алгоритмизации и программирования, приведенные в списке литературы.

В научных трудах описаны алгоритмические конструкци, принципы написания итерационных и рекурсивных алгоритмов.

Итерационные алгоритмы используются при вычислении значений с некоторой необходимой точностью, например, при нахождении корня уравнения, приближенного значения функции. Рекурсия является средством программирования, при котором процедура или функция прямо или косвенно вызывает сама себя. Рекурсия бывает прямой и косвенной (сложной). Прямая рекурсия вызывает ту же процедуру или функцию, но с другими параметрами (вызывает саму себя). Косвенная рекурсия вызывается через несколько подпрограмм. Механизм вызова рекурсивных функции или процедуры на языке программирования зависит от архитектуры компьютера и операционной системы. В рамках персональных компьютеров механизм использования рекурсии реализован через программный стек. Все промежуточные значения рекурсии помещаются в программный стек встроенными командами процессора. При этом, сохраняется адрес возврата в вызывающую подпрограмму и отслеживается количество вызовов рекурсивной подпрограммы. Рекурсия вызывается согласно составленной формуле, в которой обязательно должны быть определены начальные значения, позволяющие завершить алгоритм на определенном шаге.

1. Итерационные алгоритмы

1.1. Определение итерационного алгоритма

Алгоритм - это точное, сформулированное на определенном языке, конечное описание того или иного способа действия, основанного на применении исполнимых элементарных однозначно трактуемых шагов. [8, 42]

Любой алгоритм имеет пять особенностей.

1) Конечность алгоритма (финитность). Означает, что алгоритм всегда должен заканчиваться после конечного числа шагов.

2) Определенность алгоритма. Каждый шаг алгоритма должен быть точно определен, то есть действия, которые необходимо произвести должны быть недвусмысленно определены в каждом возможном случае.

3) Наличие входных данных. Алгоритм имеет некоторое число входных величин, заданных ему до начала работы.

4) Наличие выходных данных. Результатом выполнения любого алгоритма всегда будет обработанная информация, выдаваемая в том или ином виде и, следовательно, алгоритм обязательно имеет одну или несколько выходных величин, являющихся результатом обработки входных данных.

5) Эффективность алгоритма. Алгоритм, который выполняет действие за меньшее число шагов признается более эффективным.

Алгоритм является абстракцией и поэтому один и тот же алгоритм можно представить многими способами. Если с алгоритмом работает человек, то это может быть традиционный язык (русский, английский), язык картинок и пиктограмм, а также математические формулы. [7, 12]

В программировании эти проблемы решают путем создания четко определенного набора составных блоков, называемых примитивами, из которых могут конструироваться представления алгоритмов. Набор примитивов вместе с набором правил, устанавливающих, как эти примитивы могут комбинироваться для представления более сложных идей, образуют язык программирования.[8, 43]

Для организации алгоритмов иногда используются способы дополнительные, позволяющие решение той или иной задачи [1, 34]. Среди них выделяют:

1. Итерация – циклическая управляющая структура, которая содержит композицию и ветвление, предназначенное для организации повторяющихся процессов обработки последовательности значений переменных.

2.Рекурсия – организация алгоритма, при которой процедура, состоящая из набора шагов, обращается к самой себе (рекурсивная процедура).

Рассмотрим подробнее способ итерации:

Итерационный цикл -оператор цикла, для которого число повторений тела цикла заранее неизвестно. В итерационных циклах на каждом шаге вычислений происходит последовательное приближение и проверка условия достижения искомого результата. Выход из итерационного цикла осуществляется в случае выполнения заданного условия. Различают итерационные циклы с предусловиями и с постусловиями.[11, 19]

Итерационный процесс – процесс последовательного вычисления значений по формулам; процесс последовательных приближений.

Алгоритм, в состав которого входит итерационный цикл, называется итерационным алгоритмом. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса). В противном случае произойдет зацикливание алгоритма, т.е. не будет выполняться основное свойство алгоритма — результативность.

Примером такого рода алгоритмов, могут служить алгоритмы и методы приближенного вычисления функций и решения различного рода уравнений [3,120].

1.2. Примеры использования итерационного алгоритма

В итерационных алгоритмах решение задачи реализуется путем последовательного приближения к искомому результату^[1]. Процесс является циклическим, поскольку заключается в многократных вычислениях. Начальное приближение Y₀ выбирается заранее или задается по определенным правилам. Заканчивается итерационное вычисление при выполнении условия |Y_i –Y_i-1| <d

где d - допустимая ошибка вычисления.

Типовая структура алгоритма итерационных вычислений имеет вид, показанный на рисунке 1.

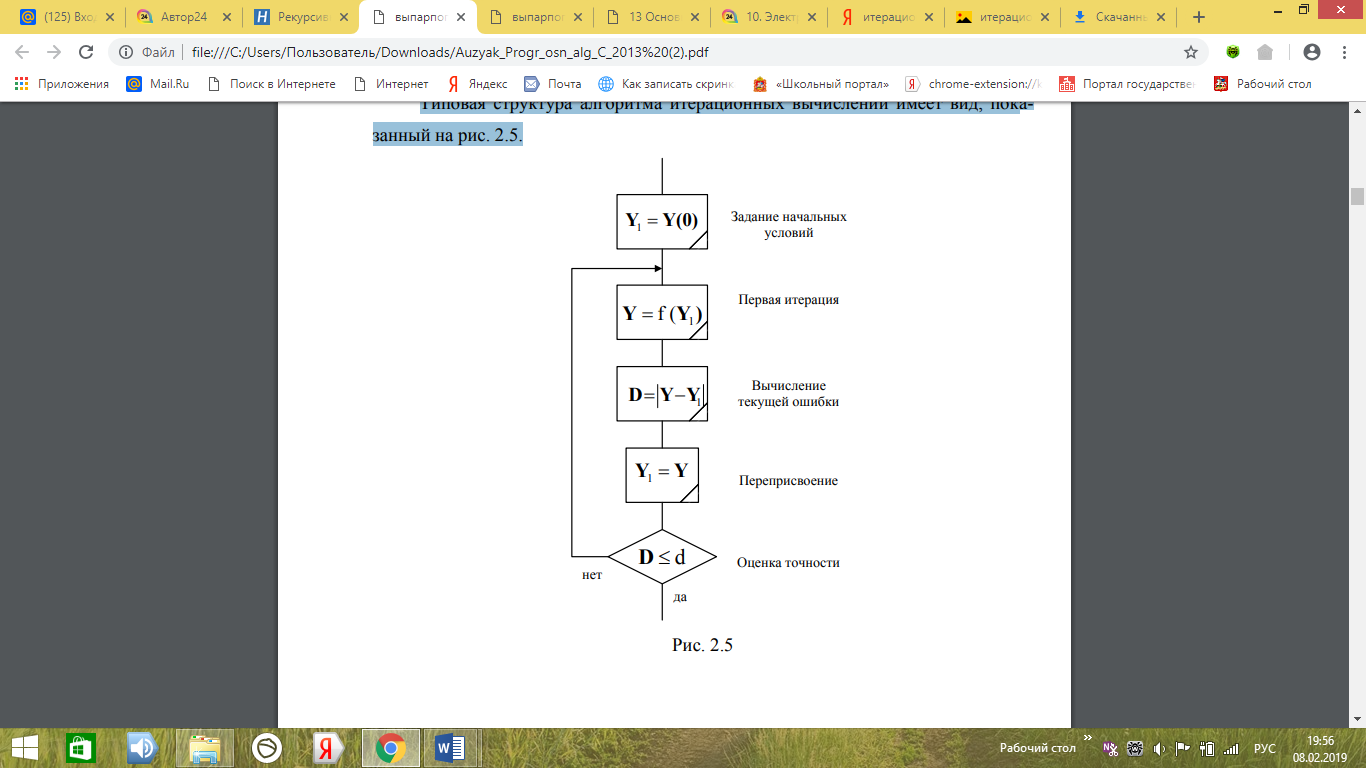
Рисунок 1 – Структура итерационного алгоритма

Пример итерационного алгоритма

Составить алгоритм вычисления функции y= √x c точностью d, используя рекуррентную формулу

y _i+1=0.5*(x/y_i+y_i).

Этот метод называется методом Ньютона, но начало получил из Древней Греции и приписывается Герону Александрийскому. Герон жил в I веке н.э. и описал в своих книгах механизмы извлечения квадратного корня из чисе. Данный метод настолько прост, понятен и есть возможность проводить вычисления с заданной точностью. Интересно, что и в наше время метод Герона используется в вычислительных машинах и калькуляторах.

Заслуга метода Ньютона в том, что он описал данный механизм нахождения квадратного корня с использованием формул, которые в дальнейшем стали называться как итерационными формулами. Проиллюстрируем на следующем примере метод Герона^[2].

Найдем приближенное значение квадратного корня из 720.

Ближайшее к 720 число, из которого извлекается квадратный корень, есть число 729, оно имеет корнем 27. Разделив 720 на 27, получаем 26. Найдем среднее арифметическое чисел 27 и 26.

Получаем (26 + 27) : 2 = 53 : 2 =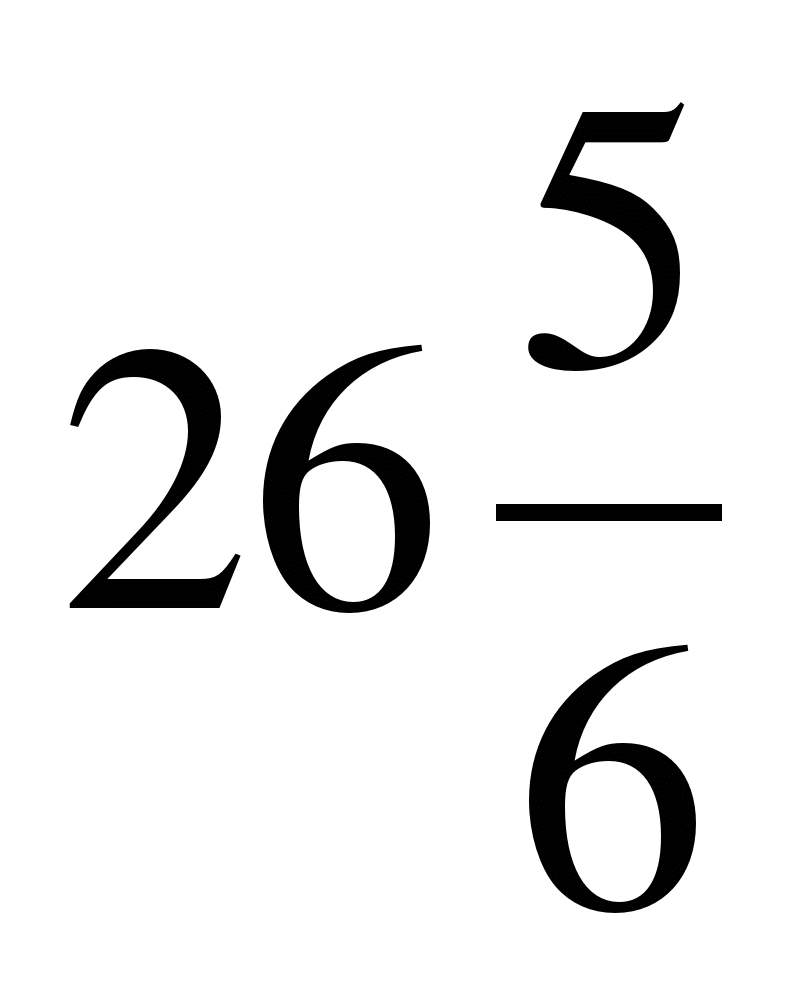 

Это и есть результат. Если возвести это число в квадрат, получим 720.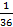

Где 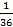-это погрешность алгоритма.

Если начальное приближение y₁ = x , тогда на первом цикле вычисления будем иметь

y ₁=0.5*(x/y₁+y₁)

Блок - схема алгоритма решения примера 4 приведена на рисунке 2.

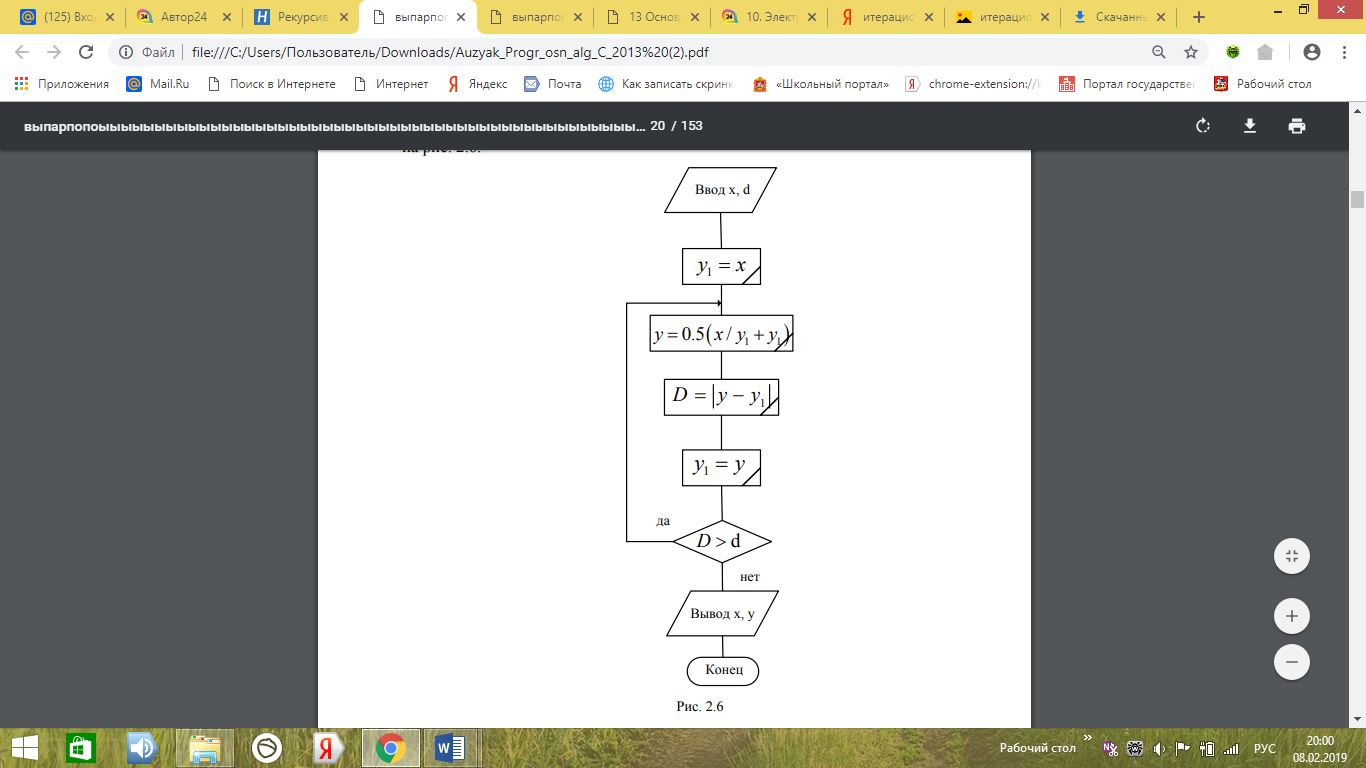
Рисунок 2-Блок-схема алгоритма

Приведем пример вычисления корня уравнения методом дихотомии или половинного деления.

Изложение метода, приведенное в работе Окулова С.М. [4, 451]

Перед применением метода для поиска корней функции необходимо отделить корни одним из известных способов, например, графическим методом. Отделение корней необходимо в случае, если неизвестно на каком отрезке нужно искать корень.

Будем считать, что корень 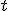 функции  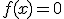отделён на отрезке 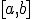. Задача заключается в том, чтобы найти и уточнить этот корень методом половинного деления. Другими словами, требуется найти приближённое значение корня с заданной точностью .

Пусть функция 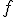 непрерывна на отрезке ,

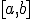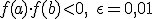 и 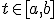 - единственный корень уравнения .

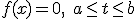(Мы не рассматриваем случай, когда корней на отрезке 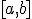 несколько, то есть более одного. В качестве  можно взять и другое достаточно малое положительное число, например, .)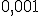

Поделим отрезок 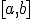 пополам. Получим точку  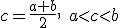и два отрезка .

• Если 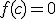, то корень  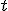найден ().
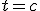• Если нет, то из двух полученных отрезков 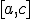 и 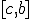 надо выбрать один  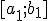такой, что 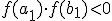, то есть
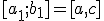  • , ес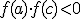ли  или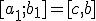
  • , если .

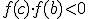Новый отрезок 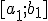 делим пополам. Получаем середину этого отрезка  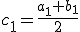и так далее.

Для того, чтобы найти приближённое значение корня с точностью до 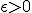, необходимо остановить процесс половинного деления на таком шаге 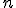, на котором  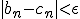и вычислить 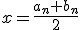. Тогда можно взять .

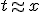Начало

e:=0.001

c:=(a+b)/2

F(a)*F(c)<=0

Да

b:=c

a:=c

abs(b-a)<e ;

Да

x:=(a+b)/2

x

Конец

Ввод а,b

Рисунок 3-Блок-схема метода дихотомии

2. Рекурсивные алгоритмы

2.1. Определение рекурсии

Рекурсия – определение некоторого понятия через самое себя.[6, 115]

С рекурсией мы постоянно сталкиваемся в повседневной жизни. Иллюстрации примеров рекурсии вокруг нас приведены на рисунках 5- 10.

Бесконечный процесс рождения цыпленка из яйца, бабочки из гусеницы, рыбы из икры. На рисунке 4 приведен пример рекурсии в животном мире.

Рисунок 4 - Что появилось раньше, яйцо или цыпленок?

Рекурсия в поэзии, музыке и литературе применяется часто. Повторяющие фразы в стихах и мелодии, которые в определенный момент воспроизведения одинакового фрагмента интерпретируются человеком по разному. Самый распространенный пример рекурсии в литературе приведен на рисунке 5^[3].

Рисунок 5 - Рекурсия в литературе

Рекурсия в геометрии и математике широко применяется и изучается и по сей день. Фракталы, кривые различные множества. Наиболее распространенные приведены на рисунке 6.

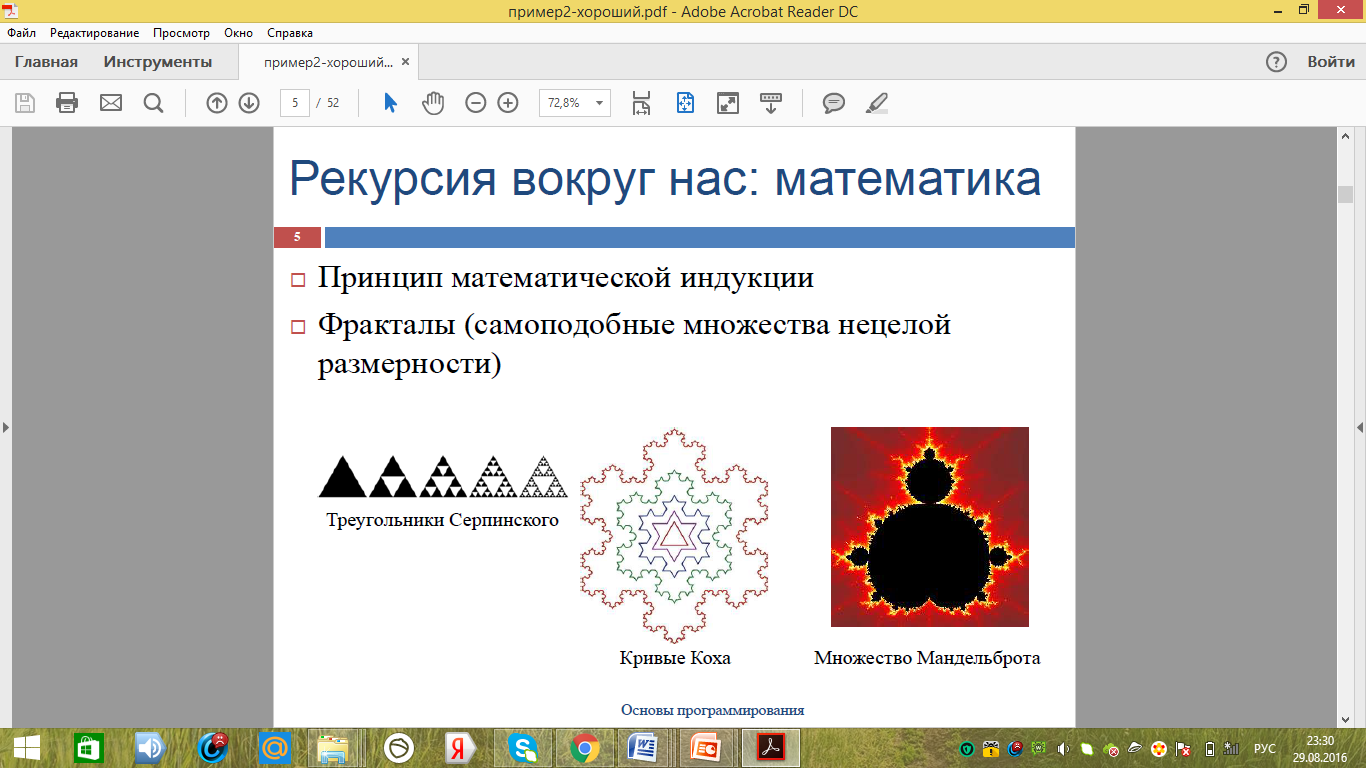
Рисунок 6 - Рекурсивная математика

Если обратиться к древним обычаям, то рекурсивность была и в древности. Построение пирамид из колец буддийскими монахами наблюдали еще тысячу лет назад. Описание древнего обычая приведено на рисунке 7.

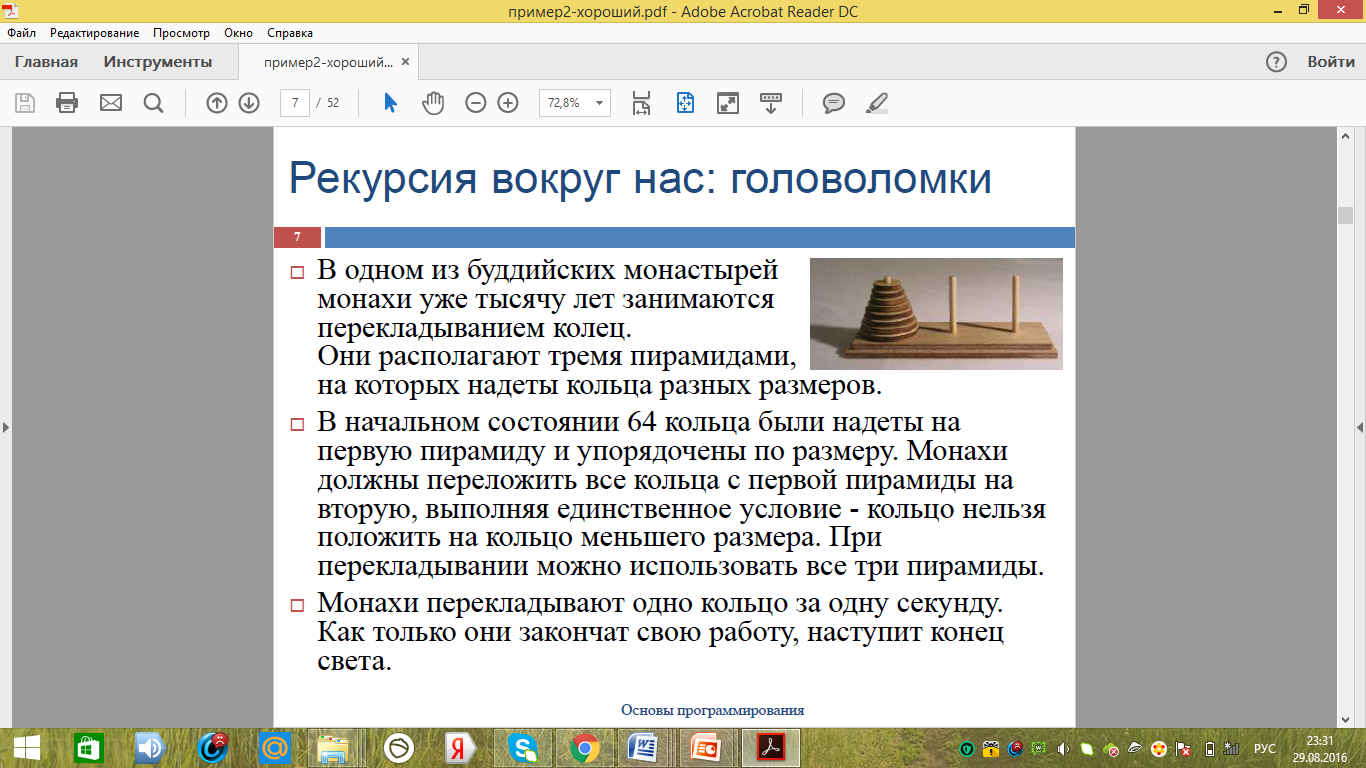
Рисунок 7 - Рекурсия в древности

Треугольник Серпинского составлен по геометрическим закономерностям: внутри каждого треугольника чертится перевернутый такой же треугольник меньшего размера. Такой процесс можно продолжать до бесконечности. На рисунке 8 приведен пример треугольника Серпинского.

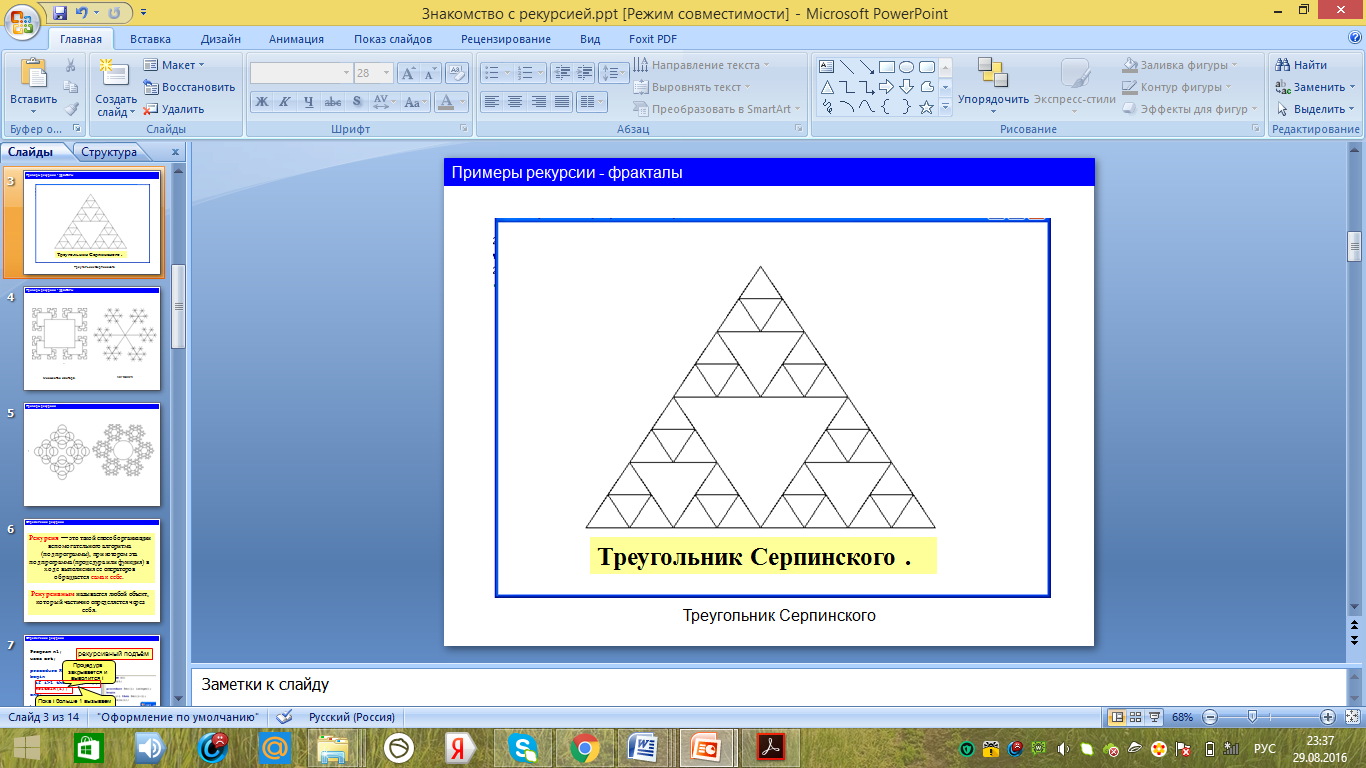
Рисунок 8 - Треугольник Серпинского-геометрические закономерности

Фракталы, как и треугольник Серпинского имеют различные закономерности, но состоят из кругов или фигур, полученных при использовании кривых Безье. Рисунок 9 показывает различные формы фракталов.

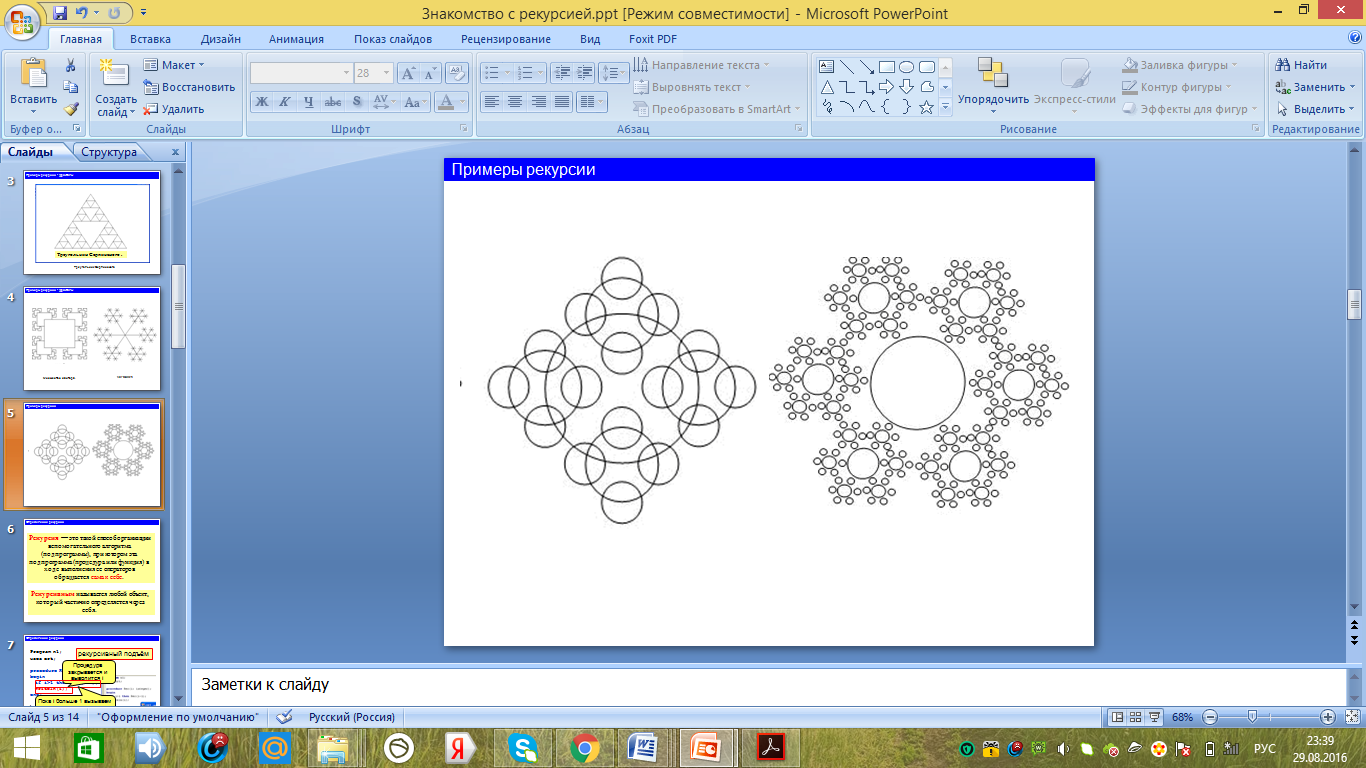
Рисунок 9 - Фракталы

Рекурсия является средством программирования, при котором процедура или функция прямо или косвенно вызывает сама себя. При прямой рекурсии в описании функции или процедуры используется обращение к ней же самой, но с другим набором параметров. При косвенной рекурсии подпрограмма вызывает какую-либо другую подпрограмму, в описании которой содержится вызов исходной подпрограммы (например, процедура V вызывает процедуру X, а процедура X вызывает процедуру V). Косвенный вызов может быть организован c использованием нескольких подпрограмм.

В книге^[4] Вьюковой Н.И. приведена интересная иллюстрация, показывающая разницу между рекурсивным и итерационным алгоритмом. Приведем её с небольшими изменениями.

Пусть в эксперименте "Позвони другу" участвуют n человек, причем k-й (0<k<n) знает только телефон следующего (k+1)-го человека, а n-й знает только то, что он последний. И возникла ситуация, когда некто, знающий телефон первого человека, решил выяснить, чему равно n. Если он будет действовать не рекурсивно, и на бумаге будет вести подсчеты. Сначала он напишет 0 и позвонит первому. Затем он прибавит 1 и спросит у первого телефон второго человека, повесит трубку, наберет номер второго, прибавит ещё 1 и получит 2, далее - спросит телефон третьего и т.д., пока не дойдет до человека, который сообщит, что он последний. Подсчитав сумму единиц, получит ответ.

Если же упомянутый некто захочет действовать рекурсивно, то он позвонит первому и прикажет: "Алло, не вешайте трубку! Сообщите мне, сколько вас". Поскольку первый не знает, сколько их, а трубку вешать нельзя, то ему предстоит взять трубку мобильного телефона и позвонить второму на домашний, сказав те же слова. Здесь рекурсия пошла вниз. Эти же действия повторит второй и далее все остальные по цепочке. Наконец последний сообщит предпоследнему, что он один. Рекурсия достигла точки выхода и пошла вверх. Предпоследний передаст предпредпоследнему что их двое, прибавив 1, предпредпоследний скажет что их трое, прибавив 1 к двойке и т.д. И, в конечном счете, первый услышит число, к которому нужно прибавить 1 и получится ответ.

При не рекурсивном способе для каждой пары абонентов необходим листок бумаги. Переполнение стека можно сравнить с ситуацией, когда АТС окажется перегруженной и нельзя будет дозвониться до абонентов.

Приведем пример программной реализации процедуры прямой рекурсии, написанной на языке Паскаль.

procedure Rec(х: intеger);

bеgin

if х>0 thеn

Rec (х-1);

writеln(х);

еnd;

Данная процедура в виде блок-схемы приведена на рисунке 10. Она вызывается в программе Rec(3).

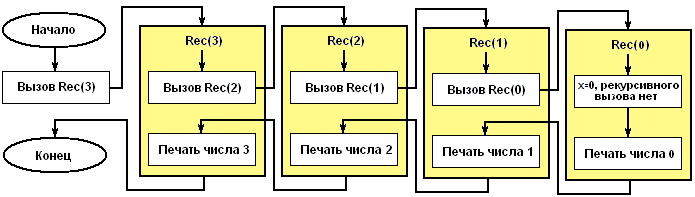
Рисунок 10 - Пошаговая блок-схема работы процедуры

Спуск "вниз" осуществляется до х=0 и по итогам происходит подъём "вверх" до печати числа 3.

Иллюстрация работы данной процедуры приведена на рисунке 11.

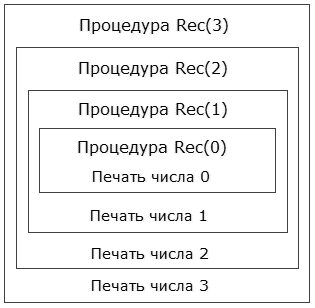
Рисунок 11 - Визуальный образ работы процедуры

Приведем пример сложной рекурсии.

Сложная рекурсия может быть представлена в виде следующего алгоритма:

procedure A(n: longint); {Опережающее описание первой процедуры}

prоcеdure B(n: longint); {Опережающее описание второй процедуры}

prоcеdure A(n: longint); {Описание блока процедуры A}

begin

writeln('Из процедуры А ',n);

B(n-1);

end;

prоcеdure B(n: longint); {Описание блока процедуры B}

begin

writeln('Из процедуры В ',n);

if n<10 then

A(n+2);

end;

begin

A(3);

end.

Приведенный алгоритм схематично изображен на рисунке 12.

Процедура А Процедура В

Рисунок 12 -Работа сложной рекурсии

После тестирования программы, вызова процедуры А(3) имеем следующую последовательность чисел:

Из процедуры В 3

Из процедуры А 2

Из процедуры В 4

Из процедуры А 3

Из процедуры В 5

Из процедуры А 4

Из процедуры В 6

Из процедуры А 5

Из процедуры В 7

Из процедуры А 6

Из процедуры В 8

Из процедуры А 7

Из процедуры В 9

Из процедуры А 8

Из процедуры В 10

Из процедуры А 9

Из процедуры В 11

Из процедуры А 10

Ответ: 10.

2.2. Механизм рекурсивных выводов

Рассмотрим механизм рекурсивных выводов прямой рекурсии на примере считалочки про 10 негритят.

Вот текст стихотворения:

«10 негритят пошли купаться в море,

10 негритят резвились на просторе,

Один из них пропал и вот вам результат:

9 негритят пошли купаться в море,

9 негритят резвились на просторе,

Один из них пропал – и вот вам результат:

…

1 (из) негритят пошли(ел) купаться в море,

1 (из) негритят резвились(ся)на просторе,

Один из них пропал – и вот вам результат:

Нет больше негритят!»

Программная реализация на Паскале представлена на рисунке 13. Механизм вывода виден в окне вывода оболочки Паскаля. Механизм работы процедуры приведен на рисунке 14.

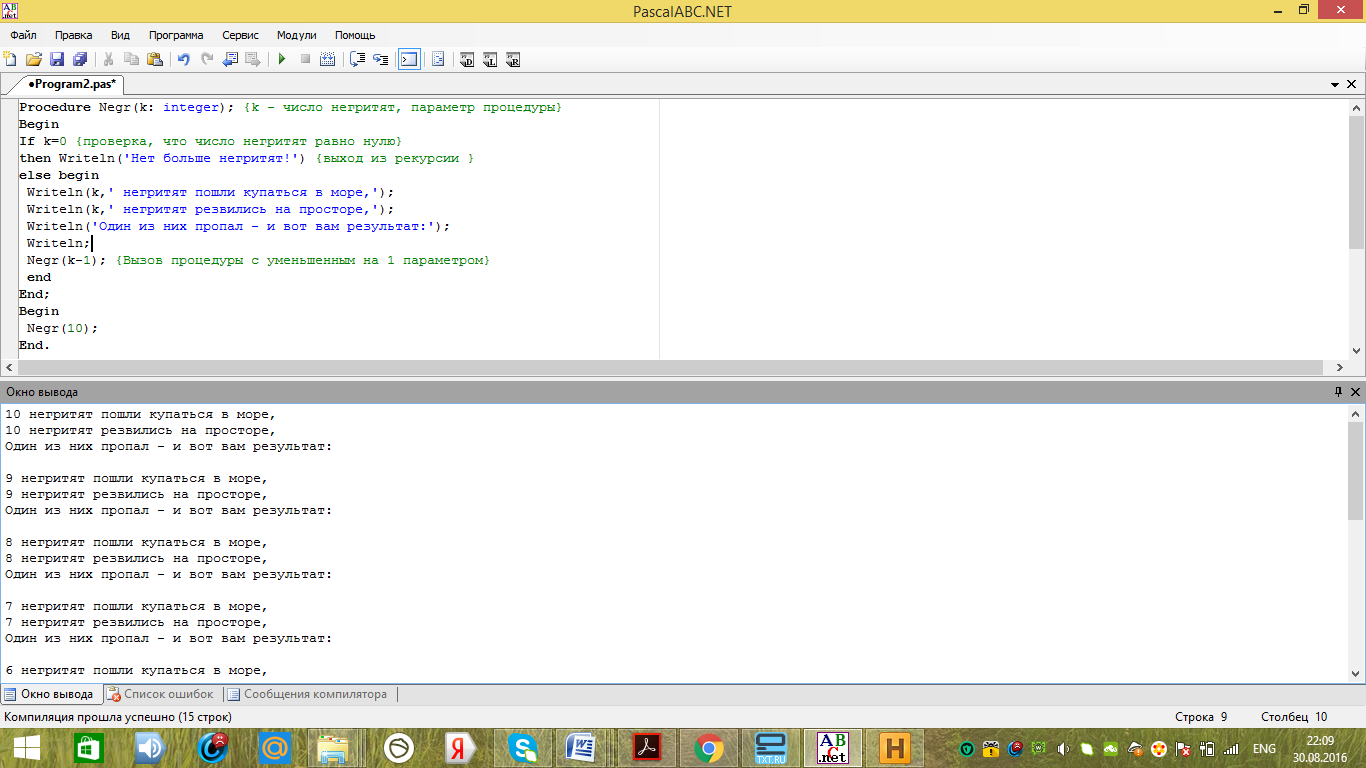
Рисунок 13 - Иллюстрация работы программы

Для вызова три раза процедуры необходимо в теле программы вызвать процедуру от трех (Negr(3))^[5].

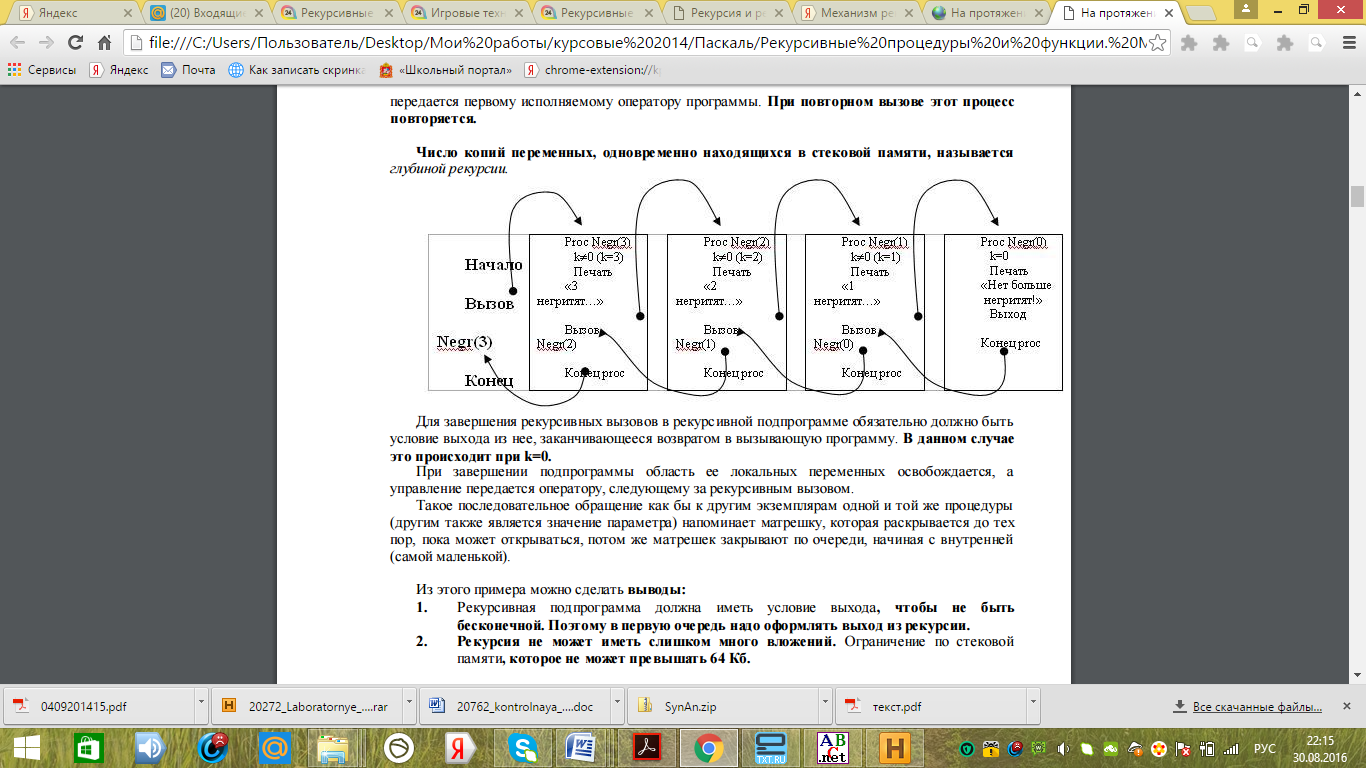
Рисунок 14 - Механизм работы рекурсивной процедуры

Из примера можно сделать выводы:

1. Рекурсивная подпрограмма должна быть конечной и иметь условие выхода. Поэтому в самом начале подпрограммы оформляют выход из рекурсии путем определения границ или диапазона для переменных.

2. Рекурсия не может иметь слишком много вызовов саму себя или вложений. Работа рекурсии зависит от объема стековой памяти компьютера. Объем стековой памяти зависит от архитектуры компьютера.

Рекурсивные определения представляют собой мощный аппарат в математике.

Например:

1. Натуральные числа:

а) 1 есть натуральное число;

б) число, следующее за натуральным, - есть натуральное число.

2. Деревья:

а) 0 есть дерево ("пустое дерево");

б) если А1 и А2 - деревья, то построение, содержащее вершину с двумя ниже расположенными деревьями, опять дерево.

3. Функция n! "факториал" (для неотрицательных целых чисел):

а) 0!=1;

б) n>0: n!=n·(n-1)!

Хорошей иллюстрацией механизма рекурсии является функция для вычисления факториала натурального числа. Факториал вычисляется следующим образом:

N! = 1 * 2 * 3 * … * (N-1) * N (1)

Факториал представляет собой произведение натуральных чисел от 1 до N включительно. Запишем формулу (1) в виде рекурсии.

N! = N * (N-1)! (2)

Факториал определяется через сам факториал. Для определения выхода из бесконечного вызова функции необходимо задать соответствующее условие:

если N>0, то N! = N * (N-1)! иначе функция равна 1.

В примере с факториалом, нахождение неизвестной функции сводится к вычислению той же неизвестной функции от другого аргумента, на единицу меньшего, чем исходный. Таким образом, есть надежда, что каждая следующая задача будет решаться чуть легче предыдущей.

2.3. Сравнение механизма работы рекурсивных и итерационных алгоритмов

Рассмотрим примеры алгоритмов, записанных рекурсивным и итерационным способом. На рисунке 15 приведена функция, вычисляющая числа Фибоначчи. Запись функции с использованием рекурсивного алгоритма короче и понятнее для восприятия, т.к. записывается при помощи формулы. Запись итерационного алгоритма гораздо длиннее и вычисление чисел Фибоначчи происходит в цикле.

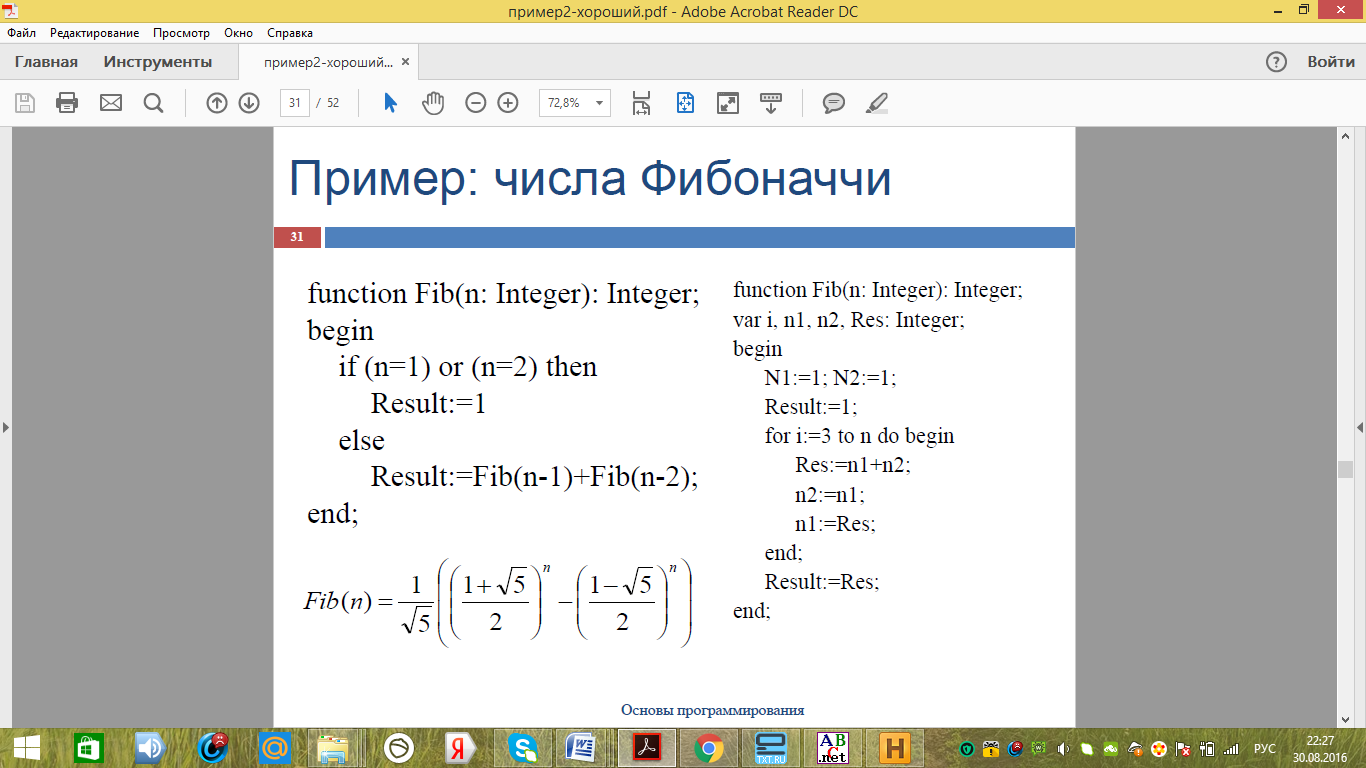
Рисунок 15 - Вычисление чисел Фибоначчи

Аналогично числам Фибоначчи вычисляется НОД двух чисел. На рисунке 16 приведены алгоритмы рекурсивного и итерационного способов нахождения НОД. Итерационный способ длинее в написании, рекурсивный способ более понятен, т.к. визуально написана математическая формула.

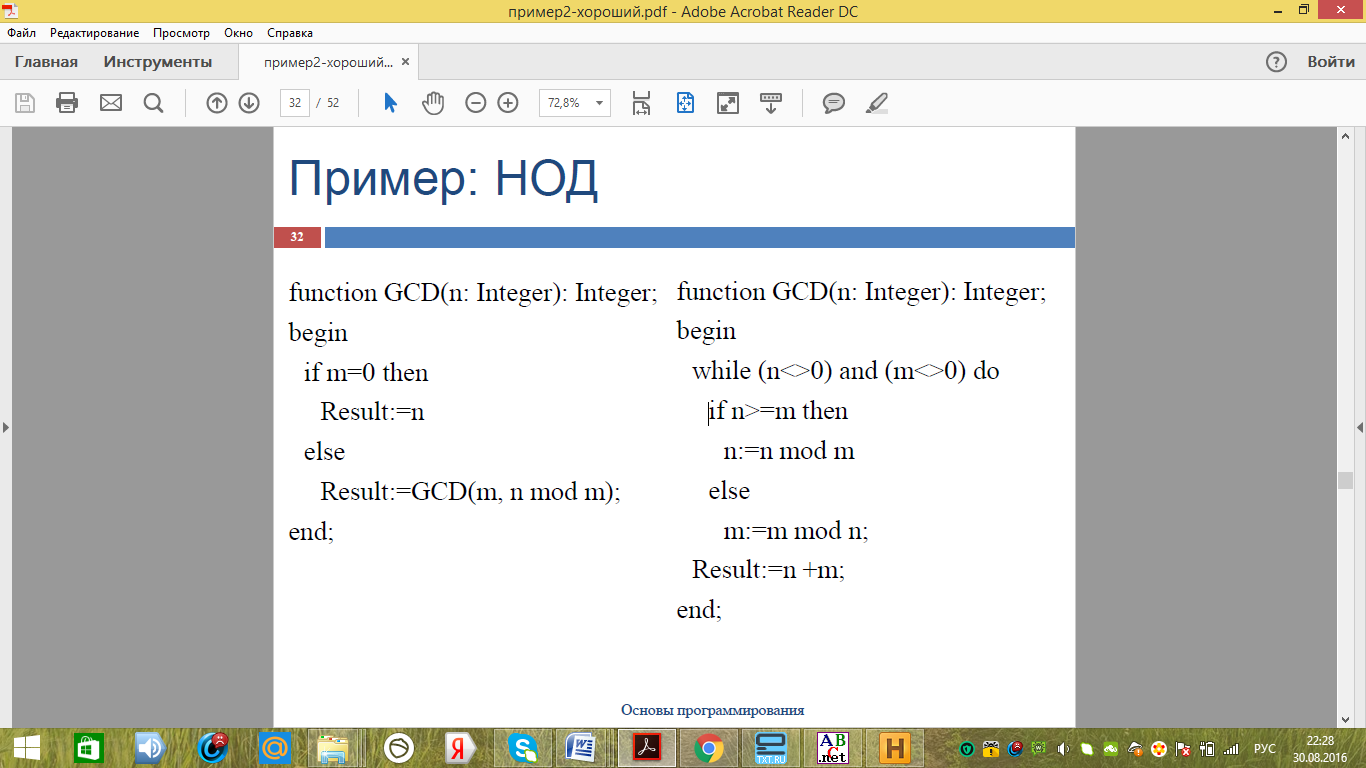
Рисунок 16 - Определение НОД числа

При итерационном нахождении биномиальных коэффициентов используются вложенные циклы, что делают алгоритм громоздким и трудным для восприятия. Рекурсивный алгоритм состоит из одного условного оператора. Для сравнения, алгоритмы приведены на рисунке 17.

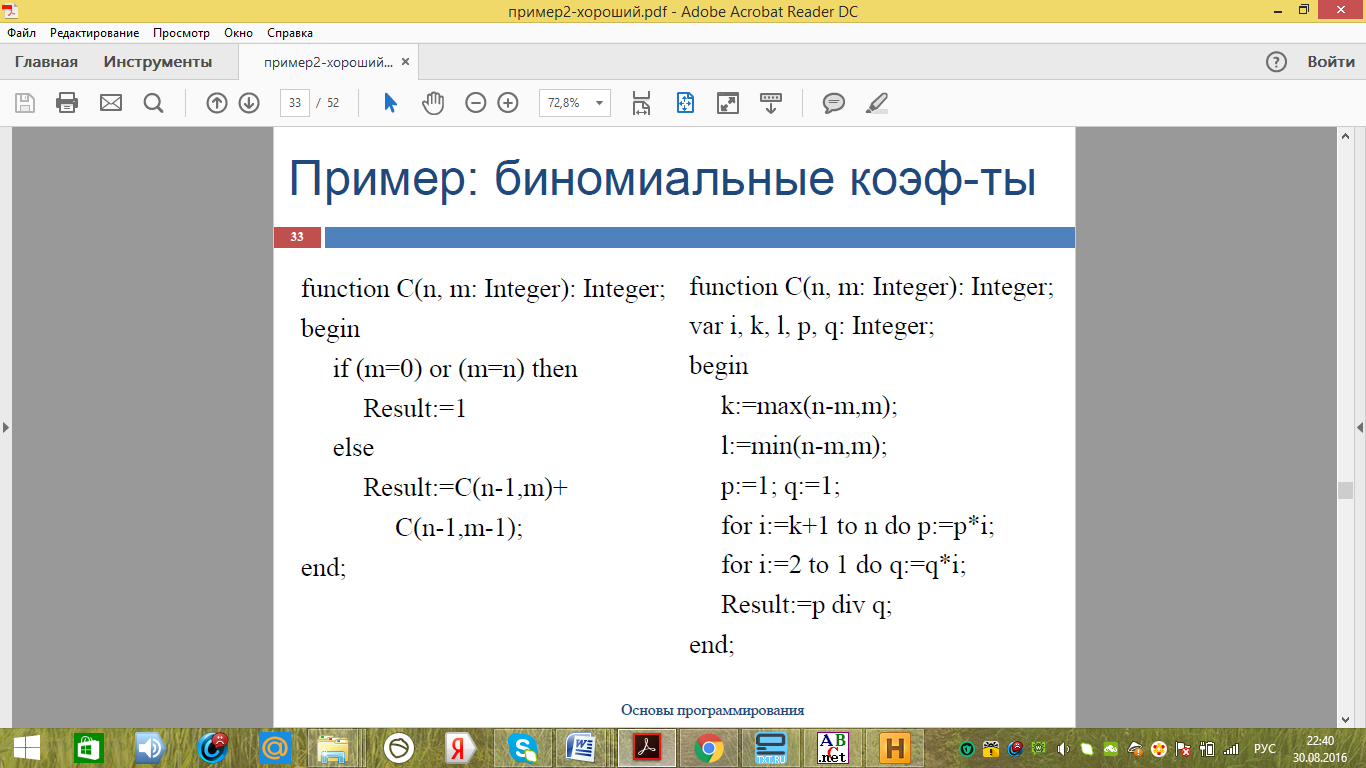
Рисунок 17 - Вычисление Биноминальных коэффициентов

Рекурсия имеет много недостатков. Повторный запуск рекурсивного механизма вызовов функции приводит к росту накладных расходов: к нарастающим затратам процессорного времени или требуемого объема памяти. Каждый рекурсивный вызов приводит к созданию новой копии функции (в самом деле, копируются только переменные данной функции); для этого может потребоваться значительная память. Итерации обычно не связаны с функциями, так что в них отсутствуют накладные расходы на повторные вызовы функции и дополнительные затраты памяти. Тогда для чего же применять рекурсию?

Любые задачи можно решить рекурсивно и итеративно (без рекурсии). Рекурсивный подход предпочтителен итеративному, если он более естественно отражает задачу и ее результаты, более нагляден и легче отлаживается и очевиден. Но, рекурсия не применяется когда требуется высокая эффективность.

3. Практика использования рекурсии и итерации

3.1. Практическое применение рекурсии на примере решения экономической задачи

Применим рекурсивный алгоритм к расчету банковских процентов по вкладу.

Вкладчик кладет в банк некоторую сумму под некоторые проценты на некоторый период. Требуется найти ту сумму, которую вкладчик сможет получить по окончании срока вклада.

Обозначим:

s-начальная сумма вклада

p-процентная ставка банка

per-период, на который положен вклад

Рекурсия расчета:

Если pеr=0, то gеt_totаl_sum := sum

Иначе sum := sum + gеt_pеrсents(sum, perс);

get_tоtal_sum := gеt_totаl_sum(sum, perс, per - 1);

В нашем случае get_total_sum-рекурсивная функция.

Код программы

var s,p,per:integer;

function get_perc(const val, perc: Single): Single;

begin

get_perc:= perc * val/100;

end;

function get_total_sum(sum, perc: Single; period: Integer): Single;

begin

if period = 0 then

get_total_sum := sum

else begin

sum := sum + get_perc(sum, perc);

get_total_sum := get_total_sum(sum, perc, period - 1);

end;

end;

begin

write ('введите начальную сумму вклада ');

readln(s);

write ('введите процентную ставку ');

readln(p);

write ('введите период ');

readln(per);

writeln('вклад достигнет суммы = ',get_total_sum(s, p, per):0:2);

readln;

end.

Блок-схема алгоритма

get_total_sum

period = 0

Да

get_total_sum := sum

sum := sum + get_percents(sum, percent)

get_total_sum := get_total_sum(sum, percent, period - 1)

Конец

Рисунок 18 - Блок-схема рекурсивной функции get_total_sum

get_percents

get_percents := percent * value / 100

Конец

Рисунок 19 - Блок-схема get_percent

Начало

'введите начальную сумму вклада '

s

'введите процентную ставку '

p

'введите период '

per

'вклад достигнет суммы = ',get_total_sum(s, p, per):0:2

Конец

Рисунок 20 - Блок-схема основной программы

Тестирующий пример

введите начальную сумму вклада 10000

введите процентную ставку 15

введите период 5

вклад достигнет суммы = 20113.57

Демонстрация работы программы представлена на рисунке 21.

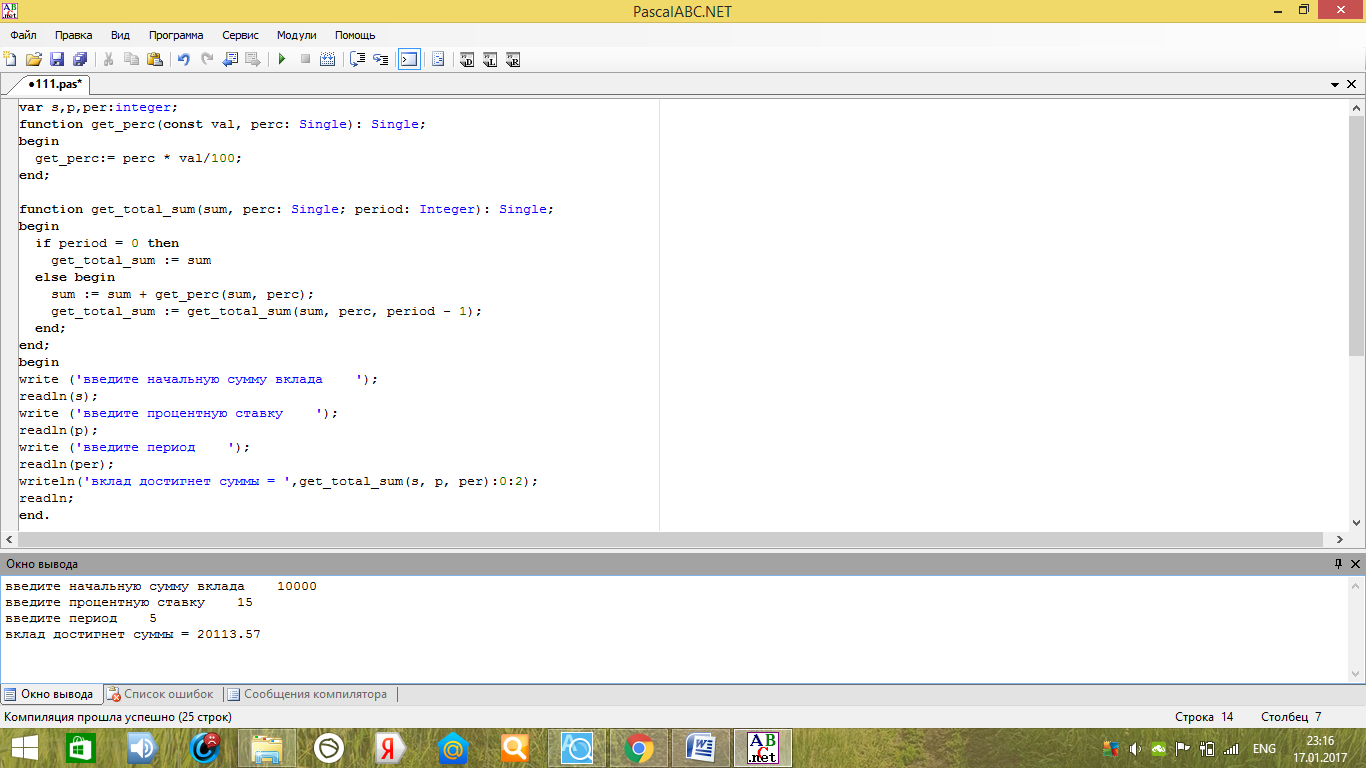
Рисунок 21 - Демонстрация работы тестового примера в программе

Разработанная программа показывает, что запись алгоритма с использованием рекурсии компактен, понятен и прост при чтении. При расчете банковских процентов на любом современном компьютере будет достаточно стековой памяти для развертывания рекурсии. Приведенный рекурсивный алгоритм является оптимальным.

3.2. Практическое применение рекурсии на примере нахождения корней квадратного уравнения методом половинчатого деления (Дихотомии)

Приведем пример решения уравнения y=x²-1 методом Дихотомии.

Для решения данной задачи необходимо знать интервал, в котором корень существует. Функция y(x)= x²-1 непрерывна на всей области своего определения и в частности, на интервале [a,b]. Для простоты считать, что отрезок [a,b] задается таким образом, что корень на нем есть (иначе основная программа должна содержать проверку наличия корня).

Метод половинного деления для непрерывных функций заключается в следующем:

Базисное утверждение: Если абсолютная величина функции в середине отрезка не превышает заданного значения точности, то координата середины отрезка и есть корень.

Проверка наличия корня осуществляется по смене знака функции на концах отрезка. Если знаки функции на концах отрезка различны, то на отрезке корень есть.

Рекурсивное утверждение: Корень расположен между серединой отрезка и тем концом, значение функции в котором по знаку не совпадает со значением функции в середине отрезка.

Код программы

program dixotomi;

var a,b,e,x:real;

procedure ro(a,b,e:real;var r:real);

var f,x:real;

begin x:=(a+b)/2;

f:=x*x-1;

if abs(f)>e then

begin

if (a*a-1)*f>0 then ro(x,b,e,r)

else ro(a,x,e,r)

end;

end;

begin

readln(a,b,e);

ro(a,b,e,x);

writeln(x);

end.

Тестирующий пример

0 3

0.0001

1

Корень существует на данном отрезке и равен 1.

Блок-схема алгоритма приведена на рисунке 22.

ro

x:=(a+b)/2

f:=x*x-1

abs(f)>e

Да

(a*a-1)*f>0

Да

ro(x,b,e,r)

ro(a,x,e,r)

Конец

Рисунок 22 Метод Дихотомии

Фрагмент кода рекурсии приведен ниже:

procedure ro(a,b,e:real;var r:real);

var f,x:real;

begin x:=(a+b)/2;

f:=x*x-1;

if abs(f)>e then

begin

if (a*a-1)*f>0 then ro(x,b,e,r)

else ro(a,x,e,r)

end;

end;

Рекурсивная процедура ro вызывает сама себя в процессе обработки данных.

3.3. Практическое применение рекурсии на примере фракталов

Применение рекурсии в построении геометрических фракталов началось в конце 70-х годов. Все фигуры самоподобны, т.е. увеличенные части объекта походят на сам объект и друг на друга.

Фрактал является сложной геометрической фигурой, которая составлена из бесконечной последовательности одинаковых частей. Каждая часть подобна всей фигуре целиком, и повторяется при уменьшении масштаба. Такой процесс бесконечен.

На рисунке 23 приведен пример программы, рисующей фракталы.

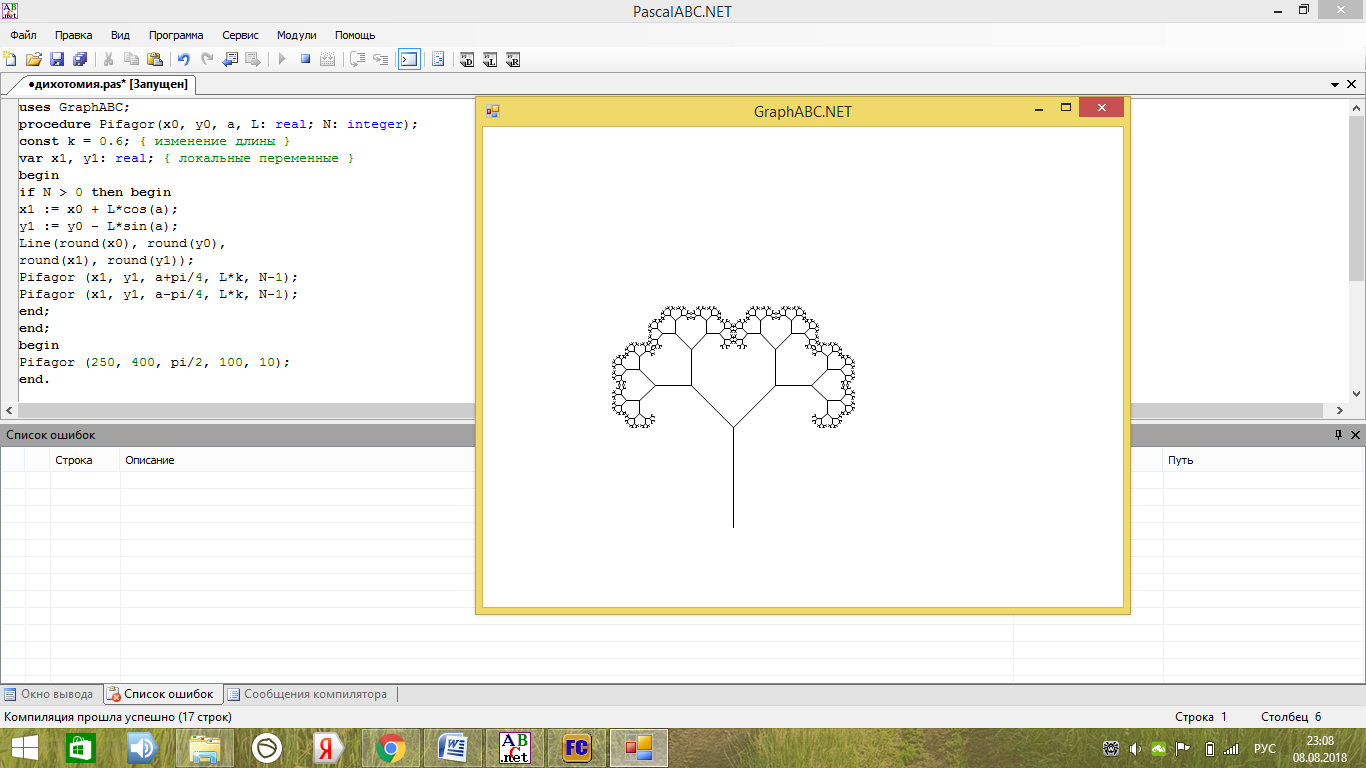
Рисунок 23 Фракталы (N=10)

Код программы

uses GraphABC;

procedure Pifagor(x0, y0, a, L: real; N: integer);

const k = 0.6; { изменение длины }

var x1, y1: real; { локальные переменные }

begin

if N > 0 then begin

x1 := x0 + L*cos(a);

y1 := y0 - L*sin(a);

Line(round(x0), round(y0),

round(x1), round(y1));

Pifagor (x1, y1, a+pi/4, L*k, N-1);

Pifagor (x1, y1, a-pi/4, L*k, N-1);

end;

end;

begin

Pifagor (250, 400, pi/2, 100, 10);

end.

На рисунке 18 приведена блок-схема алгоритма.

Pifagor

N > 0

Да

x1 := x0 + L*cos(a)

y1 := y0 - L*sin(a)

Line(round(x0), round(y0),

round(x1), round(y1))

Pifagor (x1, y1, a+pi/4, L*k, N-1)

Pifagor (x1, y1, a-pi/4, L*k, N-1)

Конец

Рисунок 24 Блок-схема фрактала

Рекурсивная процедура вызывается один раз в теле программы

Pifagor (250, 400, pi/2, 100, 10) и алгоритм выполняется 10 раз.

На рисунке 25 приведен пример выполнения алгоритма 5 раз.

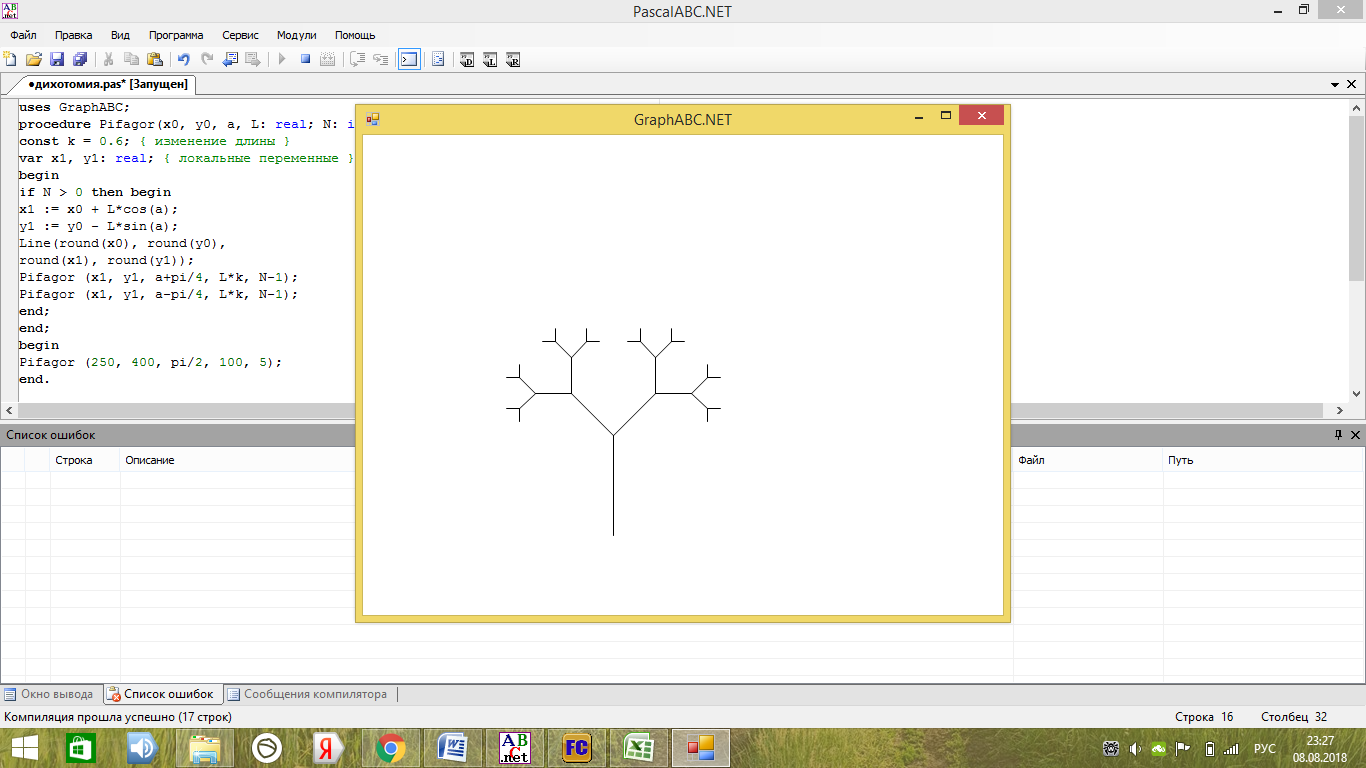
Рисунок 25 Фрактал (N=5 )

3.4. Практическое применение итерации на примере применения метода Дихотомии

Вычислим корень уравнения y= cos x-x с заданной точностью e=0.001.

Код программы:

function F(x:real):real;

begin

F:=x*x-1;

end;

var a,b,c,x,e:real;

begin

a:=0;

b:=1;

e:=0.0001;

repeat

c:=(a+b)/2;

if F(a)*F(c)<=0 then b:=c

else a:=c;

until abs(b-a)<e;

x:=(a+b)/2;

writeln('Для уравнения y=x*x-1');

writeln ('В интервале от 0 до 1 с погрешностью 0.0001');

writeln ('x=',x:0:4);

end.

Вывод программы

Для уравнения y=x*x-1

В интервале от 0 до 1 с погрешностью 0.0001

x=1.0000

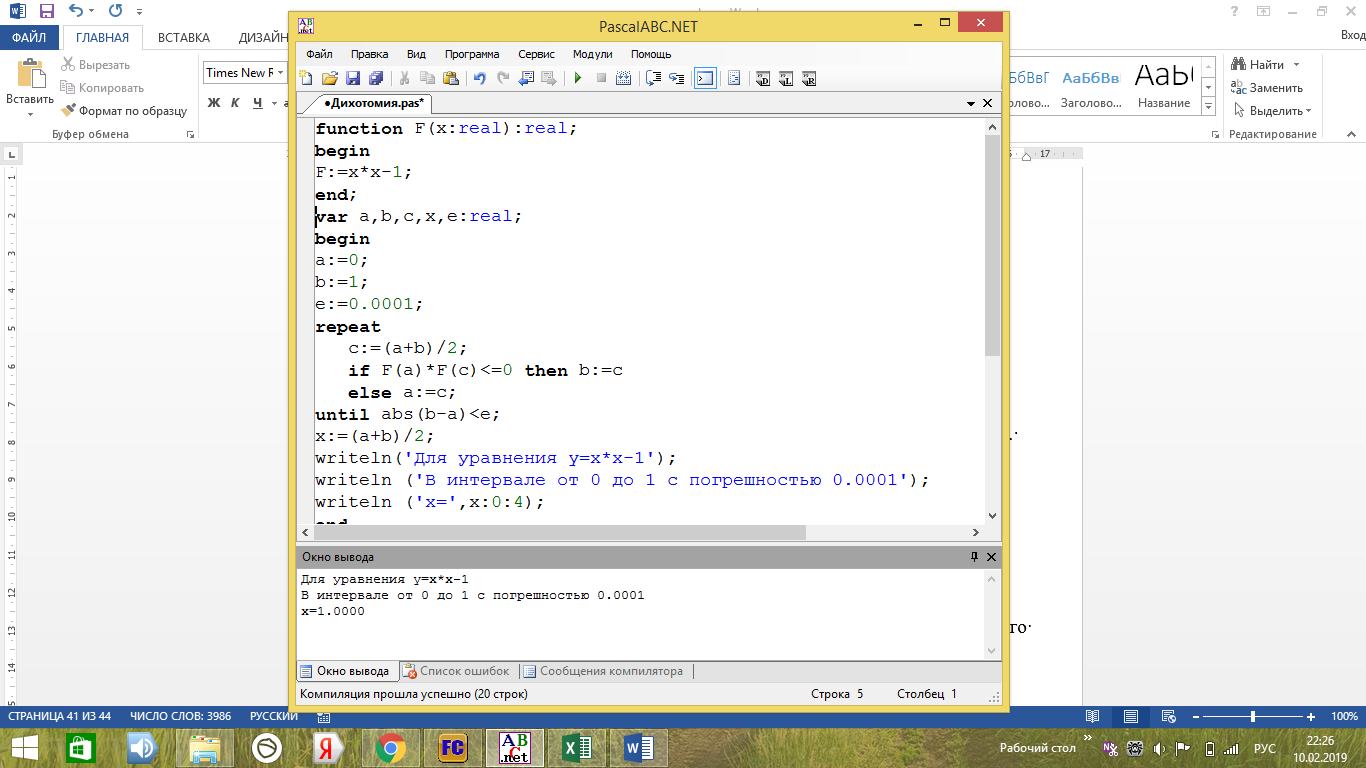
Рисунок 26 - Тестирующий пример

В пункте 3.2. приведено решение этого примера с помощью рекурсии. Ответы совпадают с точностью е=0.0001.

3.5. Практическое применение итерации на примере вычисления факториала

Приведем механизм итераций для вычисления факториала натурального числа. Факториал вычисляется следующим образом:

N! = 1 * 2 * 3 * … * (N-1) * N (1)

Факториал представляет собой произведение натуральных чисел от 1 до N включительно. Запишем формулу (1) в виде итерации.

N_i=N_i-1*N

Где N₀=1

Код программы

var

n, i, s: integer;

begin

read(n);

s := 1;i:=1;

while i <=n do

begin

s := s * i;

i:=i+1;

end;

writeln(s);

end.

Тестирующий пример

5

120

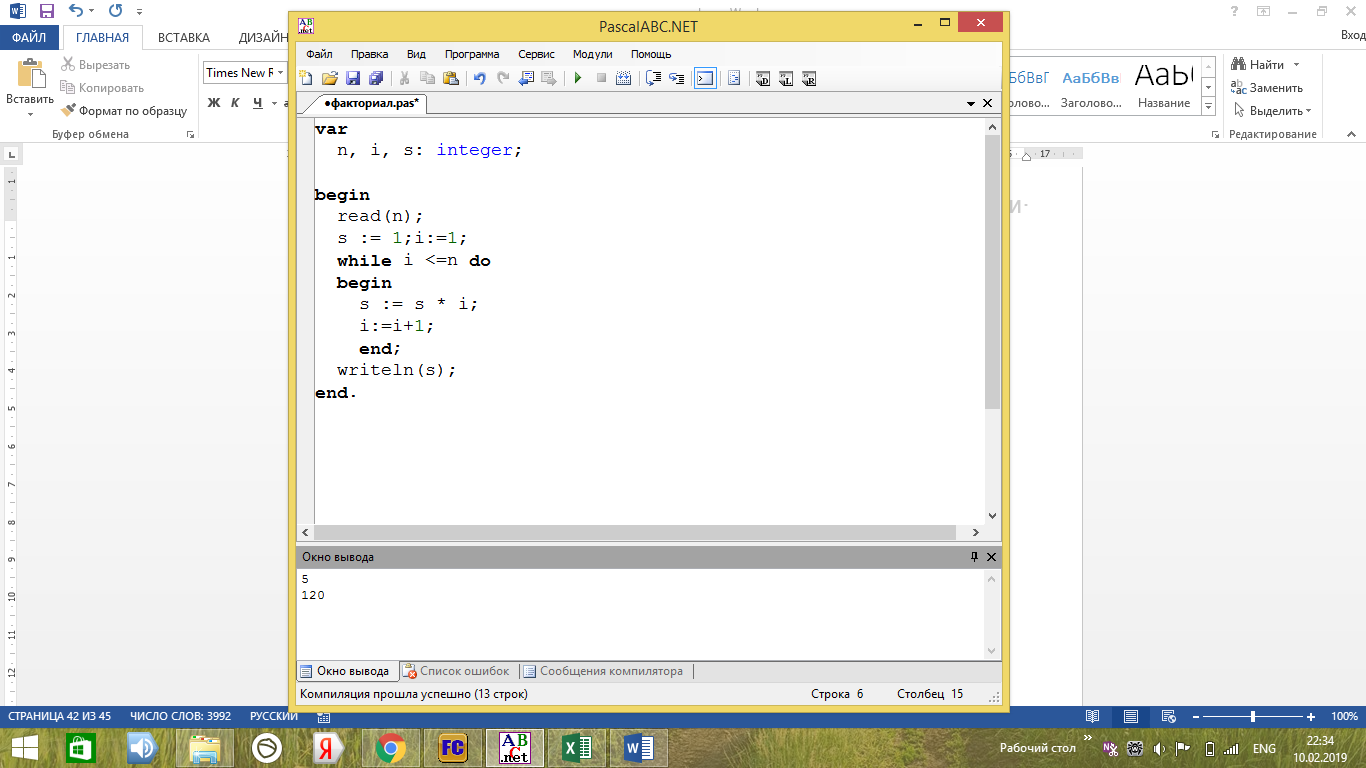
Рисунок 27 - Вычисление факториала

Заключение

При работе с информацией требуются нестандартные решения программистов. Исследование заключается в том, что бы сравнить итерационные методы решения с рекурсивным подходом в программировании.

Вывод: любую задачу можно решить с использованием итерационного алгоритма и рекурсии. Рекурсия позволяет создавать "понятные" и "читаемые" алгоритмы, быстро сходящиеся, но необходимо грамотно использовать рекурсивные методы вместо простых итерационных алгоритмов. Правильность работы рекурсии зависит от технических характеристик компьютера. Процессор не может обеспечить бесконечный рекурсивный спуск вниз, необходимо создавать промежуточные точки выхода из рекурсии, позволяющие проводить анализ правильности работы алгоритма. Итерационные алгоритмы используются при реализации итерационных численных методов. В итерационных алгоритмах необходимо обеспечить обязательное достижение условия выхода из цикла (сходимость итерационного процесса).

В работе проведен анализ научных источников по теме «Рекурсивные и итерационные алгоритмы: особенности и примеры использования»; описаны принципы написания итерационных алгоритмов; описаны принципы написания рекурсивных алгоритмов; разобраны примеры задач с итерационным методом решения и рекурсии; проведено сравнение работы итерационных алгоритмов и рекурсии.

Само понятие рекурсии отражает черту абстрактного мышления, проявляющуюся в самых различных областях науки: математике, геометрии, биологии, физике, синтаксическом анализе и трансляции, древовидной сортировке и обработке данных с динамической структурой, шахматных задачах, задачах с лабиринтами, генетических алгоритмах. Рекурсия избавляет программиста от необходимости последовательного описания процессов, благодаря чему уменьшается код программы и трудоемкость программиста по созданию алгоритма. Большим успехом в программировании считается то, что практически все современные языки программирования поддерживают рекурсию. Недостатком рекурсивного алгоритма может быть нехватка свободной оперативной памяти компьютера для развертывания всего рекурсивного механизма задачи. Но, с этим недостатком можно справиться, если производить промежуточный вывод результата и проводить его анализ.

Итерационные методы при не сходимости приводят к зацикливанию программы, что сразу видит программист.

Любую задачу можно решить как с рекурсией, так и с итерацией, но иногда встречаются такие задачи, что без рекурсии решить их чрезвычайно сложно и стоит больших усилий в описании алгоритма.

Выбор метода решения задачи зависит от программиста.

Список использованной литературы

1. Белов П.М. Основы алгоритмизации в информационных системах: Учебн. Пособие.- Спб.: СЗТУ, 2003. – 85с. Режим доступа: http://www.ict.edu.ru/ft/005406/nwpi225.pdf
2. Кетков Ю., Кетков А. Свободное программное обеспечение. – Санкт-Петербург: «БХВ-Петербург», 2011. – С. 370.
3. Макаров В.Л. Программирование и основы алгоритмизации.: учебн. пособие.-Спб., СЗТУ, 2003, - 110с. Режим доступа: http://window.edu.ru/resource/126/25126/files/nwpi223.pdf
4. Окулов С.М. Задачи по программированию. - М.: Бином. Лаборатория знаний, 2006.- С. 820.
5. Окулов С.М. Основы программирования. 2-еизд. Испр. – М.: Бином. Лаборатория знаний, 2005.- С. 440.
6. Окулов С.М. Программирование в алгоритмах. 2-еизд. Испр. – М.: Бином. Лаборатория знаний, 2006.- С. 424.
7. Основы алгоритмизации и программирования : учебное пособие / Г. Р. Кадырова. – Ульяновск : УлГТУ, 2014. – 95 с. Режим доступа: http://venec.ulstu.ru/lib/disk/2014/137.pdf
8. Основы алгоритмизации и программирования. Курс лекций. Режим доступа: http://lib.ssga.ru/fulltext/UMK/исходные%20для%20Кацко/заменить%20полно стью/Информатика/лекции/13%20Основы%20алгоритмизации%20и%20прог раммирования.pdf
9. Основы алгоритмизации и программирования: Метод. указ. / Сост.: И.П. Рак, А.В. Терехов, А.В. Селезнев. Тамбов: Изд-во Тамб. гос. техн. ун-та. Режим доступа: http://www.ict.edu.ru/ft/004758/terehov.pdf.
10. Основы алгоритмизации и программирования: учеб. пособие / Т.А. Жданова, Ю.С. Бузыкова. – Хабаровск : Изд-во Тихоокеан. гос.ун-та, 2011. – 56 с. Режим доступа: http://pnu.edu.ru/media/filer_public/2013/02/25/book_basics.pdf.
11. Программирование и основы алгоритмизации: Для инженерных специальностей технических университетов и вузов. /А.Г. Аузяк, Ю.А. Богомолов, А.И. Маликов, Б.А. Старостин. Казань: Изд-во Казанского национального исследовательского технического ун-та - КАИ, 2013, 153 с. Режим доступа: http://au.kai.ru/documents/Auzyak_Progr_osn_alg_C_2013.pdf.
12. Роберт В Себеста. Основные концепции языков программирования. 5-е издание. - Диалектика, 2011. –С. 672.
13. Роберт С. Сиакорд. Безопасное программирование на С и С++.- М.: Вильямс, 2014. — С. 496.

1. Основы алгоритмизации и программирования. Курс лекций. (http://lib.ssga.ru/fulltext/UMK/исходные%20для%20Кацко/заменить%20полно стью/Информатика/лекции/13%20Основы%20алгоритмизации%20и%20прог раммирования.pdf) ↑

2. http://genius.pstu.ru/file.php/1/pupils_works/Bursuk.pdf (стр.11) ↑

3. http://proekt-obrazovanie.ru/public/users/62/PDF/0409201415.pdf ↑

4. Вьюкова Н.И., Галатенко В.А., Ходулева А.Б. "Систематический подход к программированию" ↑

5. http://proekt-obrazovanie.ru/public/users/62/PDF/0409201415.pdf ↑