Методы сортировки данных

Содержание:

Введение

Можно считать, что в любом из существующих программных проектов однажды возникнет необходимость в обработки большого количества единообразно организованных данных. В подобных ситуациях удобно прибегнуть к обработке данных как единого целого, для чего стоит представить их в виде единого массива — а именно формального объединения какого-то количества однотипных строк, объектов или символов, что будут рассматриваться как единое целое.

При решении любых экономических и научно-технических задач обработки большого количества заданий так или иначе придется столкнуться с понятием «массив». Именно массивы значительно упрощают процесс управления данными, где необходимо использование большего количества элементов данных схожего типа, что дает отличное ыыедение в разнообразные методики работы с базами данных. Они полезны в частности в вопросах обработки большого количества информации способами, кажущимися невозможными к реализации при использовании традиционных переменных.

Также одним из важнейших свойств алгоритма можно считать сферу его применения. Здесь классифицируется два типа упорядочивания:

Сортировка внутренняя — та, что оперирует лишь теми массивами, что занимают все место в оперативной памяти, сохраняя при этой совершенно свободный доступ к каждой из ячеек. ВА данном случае упорядочивание данных будет происходить в том же месте, но при этом не произведет особых незапланированных затрат.

В нынешних архитектурах ПК (персональных компьютеров) популярно прибегать к кэшировании памяти и подкачке. Именно поэтому крайне важно, чтоб алгоритм сортировки правильно считался с применяемыми алгоритмами подкачки и кэширования памяти.

В свою очередь, сортировка внешняя использует уже запоминающие устройства большего объема, но при этом имеют доступ с последовательным, а не произвольным, упорядочивающем файлов. Это значит, что в определенный момент мы можем увидеть лишь один элемент, хоть затраты на перемотку в сравнении с затратами на память слишком велики. Из-за того, что это имеет за собой последствия в виде дополнительных ограничений на алгоритм, приходится прибегать к специальным методам упорядочивания, которые обычно используют не основное, а дополнительное пространство дисков. Помимо этого, доступ к тем данным, которые хранятся на носителе, будет производиться гораздо медленнее, чем производились бы операции непосредственно с оперативной памятью.

Таким образом, доступ к носителям информации может быть обеспечен последовательным образом: в новый момент позволено учитывать и записывать лишь тот элемент, что идет вслед за текущим.

• объём данных не позволяет им разместиться в ОЗУ.

«Сортировкой» принято называть процесс, в который входит перестановка объектов какого-то множества в фиксированном порядке. Цель процесса сортировки — облегчение дальнейшего поиска элементов в заранее отсортированном множестве. В таком смысле присутствие элементов сортировки можно заметить почти в любых задачах. В оглавлениях, ведомостях, библиотеках, словарях и складах содержатся упорядоченные объекты, но их необходимо искать и изучать.

В наше время существует колоссальное количество различных вариантов сортировки, но их большая часть имеет сходства. Каждый из возможных методов имеет определенные особенности. От выбора метода будет зависеть эффективность каждого конкретного случая.

Таким образом, методы сортировки имеют колоссальную важность, особенно при обработке данных. Казалось бы, что легче рассортировать, чем набор данных? Однако с сортировкой связаны многие фундаментальные приемы построения алгоритмов, которые и будут нас интересовать в первую очередь. Практически каждый из таких приемов можно встретить в связи с алгоритмами сортировки. В частности, сортировка является идеальным примером огромного разнообразия алгоритмов, выполняющих одну и ту же задачу, многие из которых, в некотором смысле являются оптимальными, а большинство имеет какие-либо преимущества по сравнению с остальными. В настоящее время разработано достаточно много различных методов сортировки. Одни из них относятся к методам простых сортировок, другие к улучшенным.

Данная курсовая работа будет состоять из введения, двух глав, заключения и списка литературы.

Глава 1 Методы сортировки массивов

Алгоритмы устойчивой сортировки (самые медленные алгоритмы сортировки, принадлежащие к классу О(n²)):

Пузырьковая сортировка (метод простых обменов).

Шейкер-сортировка.

Сортировка методом выбора (метод простого выбора).

Сортировка методом вставок.

Сортировка парным (бинарным) деревом.

Сортировка слиянием.

В дальнейших разделах, используя пример колоды карт, мы рассмотрим и опишем методы пузырьковой сортировки, шейкер-сортировки, сортировки выбором и сортировки вставок. Для начала работы выбираем из колоды абсолютно все карты одной масти, к примеру, пики, перемешиваем (тасуем) их. То, что на руках мы имеем лишь тринадцать карт, значительно упростит предстоящую работу, а также сделает ее куда более наглядной. Детальное описание представленных методов изложено в книге Джулиан М. Бакнелла: «Фундаментальные алгоритмы и структуры данных в Delphi».^[1]

1.1 Пузырьковая сортировка (метод простых обменов)

Алгоритм, с которого следует начинать — пузырьковая сортировка, ведь именно с ним сталкивается каждый программист, приступая к изучению азов языка программирования.

Из всех существующий в наше время, пузырьковая сортировка является самым времязатратным методом. Однако, в нем есть и преимущества: его незначительно, но проще запрограммировать.

Номинальное значение карты
5	Король	4	2	Валет	Туз	9	8	3	10	Дама	6	7
5	Король	4	2	Валет	Туз	9	8	3	10	Дама	6	7
5	Король	4	2	Валет	Туз	9	8	3	10	6	Дама	7
5	Король	4	2	Валет	Туз	9	8	3	6	10	Дама	7
5	Король	4	2	Валет	Туз	9	8	3	6	10	Дама	7
5	Король	4	2	Валет	Туз	9	3	8	6	10	Дама	7
5	Король	4	2	Валет	Туз	3	9	8	6	10	Дама	7
5	Король	4	2	Валет	Туз	3	9	8	6	10	Дама	7
5	Король	4	2	Туз	Валет	3	9	8	6	10	Дама	7
5	Король	4	Туз	2	Валет	3	9	8	6	10	Дама	7
5	Король	Туз	4	2	Валет	3	9	8	6	10	Дама	7
5	Туз	Король	4	2	Валет	3	9	8	6	10	Дама	7
Туз	5	Король	4	2	Валет	3	9	8	6	10	Дама	7

Рис. 1. Один проход с помощью алгоритма пузырьковой сортировки 

Пузырьковая сортировка работает следующим образом. Разложите ваши карты (помните, их всего 13). Посмотрите на двенадцатую и тринадцатую карту. Если двенадцатая карта старше тринадцатой, поменяйте их местами. То же сделайте и для пар (10, 11), (9, 10), и т.д., пока не дойдетё до первой и второй карты. После первого прохода по всей колоде туз окажется на первой позиции. Фактически когда вы «зацепились» за туз он «выплыл» на первую позицию, как показано на рисунке 1. Продолжайте процесс сортировки, уменьшая с каждым новым циклом количество просматриваемых карт и поступая так до тех пор, пока вся колода не будет отсортирована.

Идея данного метода заключается в том, что весь массив вариантов будет рассматриваться лишь один раз, а при каждом рассмотрении в сравнение будут идти лишь знаки 2-х соседних элементов. В том случае, если они находились в неверном порядке, произведется их перестановка. Так будет происходить долгое время, пока пока не останется ни одной перестановки для выполнения системой. Этот метод зовут именно «пузырьковой» сортировкой, ведь меньшие значения элементов всплывают подобно пузырькам воздуха в жидкости, в то время как более тяжелые элементы оседают на дно.

Имеет смысл предположение о том, что такого рода сортировки являются через чур утомительными и занимают слишком много времени. Именно медленной скоростью выполнения работы и выражается утомительность данного метода при его воспроизведении на языке Паскаль. Однако, придуман еще один вариант метода описания «пузырьковой» сортировки: в том случае, когда при выполнении не производится ни одной перестановки, мы можем предположить, что карты уже были рассортированы в необходимой последовательности.

Эффективность сортировки. За один проход непосредственно среднее число сравнений равно С=size/2. При этом среднее число всех возможных пересылок М=1.5*С (в предположении, что проверяемое условие выполняется в половине случаев). Минимальное количество проходов равняется 1, максимальное − size -1, а среднее − size/2.

Лидирующая проблема метода пузырьковой сортировки заключается в том, что перестановка будет производиться лишь в соседних элементах отдельного избранного массива. В том случае, если этот элемент с минимальным значением случайно окажется в конце массива, он будет тратить довольно много времени, меняясь с каждым последующим элементом ровно столько времени, сколько потребуется ему для достижения первой позиции.

Исходя из вышеописанных проблем, метод пузырьковой сортировки можно отнести к наиболее нестабильным, ведь из двух элементов с одинаковыми значениями в уже готовом сортированном списке окажется тот, что стоял в первоначальном массиве дальше от начала. Если менять тип сравнения на«меньше чем» или «равен», а не просто «меньше», то метод пузырьковой сортировки будет устойчивее, однако и количество перестановок резко возрастет, так что эта оптимизация бессмысленна, ведь она не даст никакого выигрыша в скорости.

00000000000000000000000000000000000000000000000000000000000000000000099999

1.2 Шейкер-сортировка

Помимо базового алгоритма, у метода пузырьковой сортировки имеется и еще один вариант, дающую на практике увеличение скорости, хоть и незначительное. Это и есть так называемая в мире шейкер-сортировка (shake sort).^[2]

Вернёмся к картам. Выполним первый проход согласно алгоритму сортировки, как показано на рисунке 2.1. Туз попадает на первую позицию.

Номинальное значение карты
5	Король	4	2	Валет	Туз	9	8	3	10	Дама	6	7
5	Король	4	2	Валет	Туз	9	8	3	10	Дама	6	7
5	Король	4	2	Валет	Туз	9	8	3	10	6	Дама	7
5	Король	4	2	Валет	Туз	9	8	3	6	10	Дама	7
5	Король	4	2	Валет	Туз	9	8	3	6	10	Дама	7
5	Король	4	2	Валет	Туз	9	3	8	6	10	Дама	7
5	Король	4	2	Валет	Туз	3	9	8	6	10	Дама	7
5	Король	4	2	Валет	Туз	3	9	8	6	10	Дама	7
5	Король	4	2	Туз	Валет	3	9	8	6	10	Дама	7
5	Король	4	Туз	2	Валет	3	9	8	6	10	Дама	7
5	Король	Туз	4	2	Валет	3	9	8	6	10	Дама	7
5	Туз	Король	4	2	Валет	3	9	8	6	10	Дама	7
Туз	5	Король	4	2	Валет	3	9	8	6	10	Дама	7

Рис. 2.1. Выполнение первого прохода с помощью шейкер-сортировкииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииииии

Номинальное значение карты
Туз	5	Ко роль	4	2	Валет	3	9	8	6	10	Дама	7
Туз	5	Ко роль	4	2	Валет	3	9	8	6	10	Дама	7
Туз	5	4	Ко роль	2	Валет	3	9	8	6	10	Дама	7
Туз	5	4	2	Ко роль	Валет	3	9	8	6	10	Дама	7
Туз	5	4	2	Валет	Ко роль	3	9	8	6	10	Дама	7
Туз	5	4	2	Валет	3	Ко роль	9	8	6	10	Дама	7
Туз	5	4	2	Валет	3	9	Ко роль	8	6	10	Дама	7
Туз	5	4	2	Валет	3	9	8	Ко роль	6	10	Дама	7
Туз	5	4	2	Валет	3	9	8	6	Ко роль	10	Дама	7
Туз	5	4	2	Валет	3	9	8	6	10	Ко роль	Дама	7
Туз	5	4	2	Валет	3	9	8	6	10	Дама	Ко роль	7
Туз	5	4	2	Валет	3	9	8	6	10	Дама	7	Ко роль

Рис. 2.2. Выполнение второго прохода с помощью шейкер-сортировки

Теперь же, вместо того, чтоб колода карт проходила справа налево, произведем движение слева направо: сравнивая вторую и третью карты, а также старшую карту, их необходимо переместить на третью позицию. Теперь же, сравнивая третью и четвертую карту, их можно поменять местами, если в этом есть необходимость. Стоит продолжить сравнения до тех пор, пока не будет достигнута пара двенадцать и тринадцать. Стоит отметить, что, направляясь к правому краю колоды карт, вы «захватили» короля и переместили его на последнюю позицию, как показано на рисунке 2.2.

По аналогии мы имеем возможность заново пройти всю карточную колоду справа налево вплоть до второй карты. Во вторую позицию попадёт двойка. Продолжайте чередовать направления проходов до тех пор, пока не будет отсортирована вся колода.

Невзирая на тот факт, что шейкер-сортировка принадлежит к алгоритмам класса О(n2), выполнение мероприятий, предписанных этим методом, займет куда меньше времени, чем пузырьковая сортировка. А назван этот алгоритм был шейкер-сортировкой по той причине, что элементы, находящиеся в массиве, все время колебались вокруг своих позиций, пока весь массив е был окончательно отсортирован.

Как и в случае с пузырьковой сортировкой, шейкер-сортировка относится к неустойчивым алгоритмам.

1.3 Сортировка методом выбора (метод простого выбора)

Сортировка методом выбора (selection sort).

Номинальное значение карты
5	Король	4	4	Валет	Туз	9	8	3	10	Дама	6	7
Туз	Король	4	2	Валет	5	9	8	3	10	Дама	6	7
Туз	2	4	Король	Валет	5	9	8	3	10	Дама	6	7
Туз	2	3	Король	Валет	5	9	8	4	10	Дама	6	7
Туз	2	3	4	Валет	5	9	8	Король	10	Дама	6	7
Туз	2	3	4	5	Валет	9	8	Король	10	Дама	6	7
Туз	2	3	4	5	6	9	8	Король	10	Дама	Валет	7
Туз	2	3	4	5	6	7	8	Король	10	Дама	Валет	9
Туз	2	3	4	5	6	7	8	9	10	Дама	Валет	Король
Туз	2	3	4	5	6		8	9	10	Валет	Дама	Король

Рис. 3. Сортировка методом выбора

В данном случае мы приступим к работе, начиная с правого края колоды. Необходимо пересмотреть все имеющиеся карты и обнаружить среди них самую младшую, которой, само собой, будет туз. Теперь, полностью игнорируя карту под номером один, заново пересмотрите колоду полностью справа налево в попытках найти наиболее младшую карту. Измените местоположение младшей карты со второй картой. Теперь, не обращая никакого внимания на первые две карты их всех, пересмотрите снова полностью всю колоду справа налево, разыскивая младшую карту, и производите ее перемену с картой под номером три. Продолжайте до тех пор, пока вся колода не будет отсортирована, как показано на рисунке 3. Очевидно, что одиннадцатый цикл не понадобится, поскольку он будет манипулировать только с одной картой, которая к тому времени будет находиться в требуемой позиции.

Сортировка методом выбора относится к алгоритмам класса О(n²). Количество выполняемых сравнений непосредственно для первого прохода равно n, для второго n-1 и т.д. общее количество сравнений будет равно n(n+1)/2-1, т.е. сортировка принадлежит к классу О(n²). Тем не менее, количество перестановок намного меньше: при каждом выполнении внешнего цикла производится всего одна перестановка. Таким образом, общее количество перестановок (n-1), т.е. О(n). Что это означает на практике? Если время и требуемые ресурсы перестановки элементов массива намного больше, чем время сравнения, то сортировка методом выбора оказывается достаточно эффективной.

В свою очердь, данный тип сортировки мы можем отнести к устойчивым алгоритмам. Ведь именно поиск минимального значения будет снова и снова первое из нескольких присутствующих наименьших значений. Поэтому ровные значения и вынуждены присутствовать в уже отсортированном списке ровно в том же порядке, в котором они и находились в первоначальном списке.

Идея метода выбора заключается в том, что весь взятый массив просматривается несколько раз и непосредственно на каждом шаге ищется минимальный элемент и запоминается его порядковый номер. Затем найденный минимальный элемент меняется значением с первым, вторым, третьим и т.д. предпоследним элементом массива и исключается из рассмотрения.

1.4 Сортировка методом вставок

В свою очередь, сортировка методом вставок может производиться простыми вставками, что мы подробнее рассмотрим ниже, используя все ту же колоду карт:

Номинальное значение карты
5	Ко роль	4	2	Валет	Туз	9	8	3	10	Дама	6	7
4	5	Ко роль	2	Валет	Туз	9	8	3	10	Дама	6	7
2	4	5	Ко роль	Валет	Туз	9	8	3	10	Дама	6	7
2	4	5	Валет	Ко роль	Туз	9	8	3	10	Дама	6	7
Туз	2	4	5	Валет	Ко роль	9	8	3	10	Дама	6	7
Туз	2	4	5	9	Валет	Ко роль	8	3	10	Дама	6	7
Туз	2	4	5	8	9	Валет	Ко роль	3	10	Дама	6	7
Туз	2	3	4	5	8	9	Валет	Ко роль	10	Дама	6	7
Туз	2	3	4	5	8	9	10	Валет	Ко роль	Дама	6	7
Туз	2	3	4	5	8	9	10	Валет	Дама	Ко роль	6	7
Туз	2	3	4	5	6	8	9	10	Валет	Дама	Ко роль	7
Туз	2	3	4	5	6	7	8	9	10	Валет	Дама	Ко роль

Рис. 4. Сортировка методом вставок

Приступаем к работу с левого края исходной колоды. Сравним первые две карты и расположим их в необходимом порядке. Далее смотрим на карту под номером три. Необходимо поставить ее так, чтоб она встала на свое место по отношению к тем двум картам, которые мы уже обработали. Далее обратим внимание на четвертую карту, переставив ее в правильное место относительно прошлых трех карт. Операции стоит повторять, переходя к новым картам, пока они не подойдут к концу. При перемещении слева направо часть колоды будет отсортирована, как показано на рисунке 4.

Однако, имеется и любопытная особенность в предложенном методе реализации сортировки, а именно то, что значение текущего элемента будет сохранено в локальной переменной, а после, выполняя поиск необходимого места его вставки, мы будем перемещать каждый новый элемент со значением выше текущего, на одну позицию в правую сторону, а, выполняя эти действия, мы переместим ту самую «дыру» списка в левую сторону. По итогу, мы обнаруживаем необходимое место и переносим сохраненное значение в то место, которое только что освободилось.

Идея метода заключается в том, что делается предположение, что первый n элемент массива уже упорядочен и рассматривается n+1 элемент. Если окажется, что он меньше чем какой либо из первых n, то он занимает место большего, а участок массива ограниченный его новым местом и старым смещается вправо.

Не отличаясь от прошлых алгоритмов, данная сортировка (методом вставок) принадлежит к классу алгоритмов О(n²). Как и в случае с пузырьковой сортировкой, если исходный массив уже отсортирован, сортировка методом вставок практически не выполняет никак действий помимо сравнения пар двух соседних элементов. Худшим случаем для сортировки методом вставок является ситуация, когда исходный список отсортирован в обратном порядке и для попадания в требуемое место массива каждому элементу нужно пройти максимальное расстояние.

Именно сортировку методом вставок мы можем отнести к той группе алгоритмов, которые называют устойчивыми. Это происходит от того, что она может сохранить относительное положение элементов массива с равными значениями, поскольку поиск требуемой позиции для элемента завершается, когда найден элемент, значение которого меньше или равно значению текущего элемента. Следовательно, относительное положение элементов с равными значениями сохраняется.

Так же, как это происходит в методе пузырьковой сортировки, в методе сортировки вставками все элементы непосредственного массива попадут в необходимые им позиции лишь за счет их перемены с соседствующими элементами. В том случае, когда элемент находился на отдалении от необходимой позиции, его перемещение в нужное место занимает немало времени.

1.5 Сортировка двоичным (бинарным) деревом

Двоичным (бинарным) деревом называют уже упорядоченную структуру данных, в которой каждому элементу, который является предшественником или корнем (под)дерева - поставлены в соответствие по крайней мере два других элемента (преемника). Причем для каждого предшественника выполнено следующее правило: левый преемник всегда меньше, а правый преемник всегда больше или равен предшественнику.

Описание метода сортировки двоичным деревом детально рассмотрено в книге Н. Вирта: «Алгоритмы и структуры данных».^[3]

Вместо «предок» и «преемник» также непосредственно употребляют термины «родитель» и «потомок». Все элементы дерева также называют «узлами». При добавлении в дерево нового элемента его последовательно сравнивают с нижестоящими узлами, таким образом, вставляя на место. Если элемент >= корня - он идет в правое поддерево, сравниваем его уже с правым сыном, иначе - он идет в левое поддерево, сравниваем с левым, и так далее, пока есть сыновья, с которыми можно сравнить.

Вот процесс построения дерева из последовательности 44 55 12 42 94 18 06 67:

44 44 44 44 44

\ / \ / \ / \

55 12 55 12 55 12 55

\ \ \

42 42 94

(**) 44 44 (*) 44

/ \ / \ / \

12 55 12 55 12 55

\ \ / \ \ / \ \

42 94 06 42 94 06 42 94

/ / / /

18 18 18 67

Дерево может быть и более-менее ровным, как на (*), может и иметь всего две основные ветви (**), а если входная последовательность уже непосредственно отсортирована, то дерево выродится в линейный список.

Рекурсивно обходя полученное дерево по правилу "левый сын - родитель - правый сын", то, записывая все встречающиеся элементы в массив, мы будем получать упорядоченное в порядке возрастания множество. Hа этом и основана идея сортировки деревом.

Куда подробнее правила обхода мы можем сформулировать, как обойти левое поддерево - непосредственно вывести корень - обойти правое поддерево, где рекурсивная процедура 'обойти' вызывает себя еще раз, если сталкивается с узлом-родителем и выдает очередной элемент, если у узла нет сыновей.

Общее быстродействие метода O(n×logn). Поведение неестественно, устойчивости, вообще говоря, нет.

Основной недостаток этого метода - большие требования к памяти под дерево. Очевидно, нужно n места под ключи и, кроме того, память на 2 указателя для каждого из них.

Поэтому данная сортировка обычно применяют там, где:

- построенное дерево можно с успехом применить для других задач;

- данные уже построены в 'дерево';

- данные можно считывать непосредственно в дерево.

Так как не тратится лишняя память, например, при потоковом вводе с консоли или из файла.

1.6 Сортировка слиянием

Сортировка слиянием (merge sort) привлекает своей простотой и наличием некоторых особенностей (например, она принадлежит к алгоритмам класса O(n×log(n)) и не имеет худших случаев), но если приступить к его реализации, можно натолкнуться на большую проблему. Тем не менее, сортировка слиянием очень широко используется при необходимости сортировки содержимого файлов, размер которых слишком велик, чтобы поместиться в памяти. Данный метод также рассмотрен в книге Джулиан М. Бакнелла: «Фундаментальные алгоритмы и структуры данных в Delphi».^[4]

В качестве примера мы не будем пользоваться картами - алгоритм легко понять и без карт.

Представьте себе, что имеется два уже отсортированных массива и необходимо сформировать один массив, объединяющий в себе все элементы исходных массивов. Путь № 1 состоит в том, чтобы скопировать оба массива в результирующий и выполнить его сортировку. но в этом случае, к сожалению, мы не воспользуемся тем, что исходные массивы уже отсортированы. Путь № 2 предусматривает слияние.

Смотрим на первые элементы обоих массивов. Элемент с меньшим значением переносим в результирующий массив. Снова смотрим на первые элементы в обоих массивах и снова переносим в результирующий массив элемент с меньшим значением, удаляя его из исходного массива. описанный процесс продолжается до тех пор, пока не исчёрпываются элементы одного из исходных массивов. После этого непосредственно в результирующий массив можно перенести все оставшиеся элементы в исходном массиве. Такой алгоритм формально известен под названием алгоритма двухпутевого слияния (two-way merge algorithm).

Конечно, на практике элементы не удаляются из массивов, вместо удаления используются указатели на текущие начальные элементы массивов, которые при копировании передвигаются на следующий элемент.

Время выполнения алгоритма двухпутевого слияния зависит от количества элементов в обоих исходных массивах. Если в первом из них находится - nэлементов, а во втором - m, нетрудно придти к выводу, что в худшем случае будет произведено (n+m) сравнений. Следовательно, алгоритм двухпутевого слияния принадлежит к классу O(n).

Так каким же образом алгоритм двухпутевого слияния помогает выполнить сортировку? Ведь для его работы необходимо иметь два отсортированных массива меньшей длины, из которых создаётся один большой массив.

На основе такого описания можно придти к рекурсивному определению сортировки слиянием: разделите исходный массив на две половины, примените к каждой половине алгоритм сортировки слиянием, а затем с помощью алгоритма слияния объедините подписки в один отсортированный массив.

Сортировка слиянием обладает только одним недостатком - алгоритм слияния требует наличия третьего массива, в котором будут храниться результаты слияния.

В отличие от ранее рассмотренных методов сортировки, которые сортируют элементы непосредственно в самом исходном массиве, сортировка слиянием для работы непосредственно требует большого дополнительного объёма памяти. В самой простой реализации может показаться, что для выполнения сортировки понадобится новый вспомогательный массив, размер которого равен сумме размеров двух исходных массивов. Элементы из обоих массивов будут помещаться во вспомогательный массив, а затем после слияния - в основной массив. Несмотря на то, что можно разработать алгоритм, который выполняет операцию слияния, не требуя вспомогательного массива, на практике его выполнение занимает намного больше времени. Поэтому при необходимости применения сортировки слиянием, нужно смириться с дополнительными требованиями в отношении памяти.

Что касается устойчивости, то поскольку элементы массива перемещаются только при процедуре слияния, устойчивость всей сортировки слиянием будет зависеть от устойчивости самого слияния двух половин массива. Если в обеих половинах исходного массива имеются элементы с одинаковым значением, то оператор сравнения гарантирует, что первым в результирующий список попадёт элемент из первой половины исходного массива. Это означает, что операция слиянием сохраняет относительный порядок элементов, и, следовательно, сортировка слиянием будет устойчивой.

Идея метода состоит в том, что сортировка слиянием используется для содержимого файлов, размер которых слишком велик, чтобы поместиться в памяти. В этой ситуации выполняется сортировка частей файла, запись этих частей в отдельные файлы, а затем их слияние в один файл.

Несмотря на то, что сортировка слиянием требует дополнительной памяти (объём которой пропорционален количеству элементов в исходном массиве), она обладает некоторыми интересными свойствами:

• сортировка непосредственно слиянием принадлежит к классу O(n×log(n)).
• она устойчива.
• для сортировки слиянием не имеет значения ни порядок элементов в исходном массиве (будь то массив, отсортированный в прямом порядке или обратном), ни повторения значений в массиве, то есть сортировка слиянием не имеет худшего случая.

Очевидно, требуется n операций на создание первоначального дерева, а затем n шагов, каждый по logn сравнений для выбора нового наименьшего.

Глава 2 Алгоритмы неустойчивой сортировки

Сортировка методом Шелла.

Сортировка методом прочёсывания.

Пирамидальная сортировка (сортировка деревом).

Быстрая сортировка.

Можно считать, что быстрые методы сортировки срабатывают лучше и чаще, чем те методы, что рассматривались нами ранее. Однако выполнение их математического анализа оказалось непростым занятием. Невзирая на тот факт, что в практике алгоритмы группы производятся с достаточно высокой скоростью, они бывают использованы относительно редко.

Сортировку методом Шелла и сортировку методом прочёсывания также рассмотрим непосредственно на примере сортировки колоды карт, из которой выберем все карты одной масти, перетасуем их (манипулирование только 13 картами позволит упростить нашу работу, сделав её более наглядной).

Более подробное описание сортировки методом Шелла, сортировки методом прочёсывания и быстрой сортировки также изложено в книге Джулиан М. Бакнелла: «Фундаментальные алгоритмы и структуры данных в Delphi».^[5]

2.1 Сортировка методом прочесывания

Сортировку методом прочёсывания (comb sort) нельзя отнести к обычным и общепринятым алгоритмам. На сегодняшний день он малоизвестен, тем не менее, он отличается достаточно быстрым уровнем быстродействия и удобной реализацией. Метод был разработан Стефаном Лейси (Stephan Lacey) и Ричардом Боксом (Richard Box) в 1991 году. Фактически он использует пузырьковую сортировку таким же образом, как и сортировка методом Шелла сортировку методом вставок.

Номинальное значение карты
5	Король	4	2	Валет	Туз	9	8	3	10	Дама	6	7
3	Король	4	2	Валет	Туз	9	8	5	10	Дама	6	7
3	10	2	4	Валет	Туз	9	8	5	Король	Дама	6	7
3	10	4	2	7	Туз	9	8	5	Король	Дама	6	Валет
3	8	4	2	7	Туз	9	10	5	Король	Дама	6	Валет
3	Туз	4	2	7	8	9	10	5	Король	Дама	6	Валет
3	Туз	4	2	5	8	9	6	7	Король	Дама	10	Валет
2	Туз	4	3	5	8	9	6	7	Король	Дама	10	Валет
2	Туз	4	3	5	7	9	6	8	Король	Дама	10	Валет
2	Туз	4	3	5	7	9	6	8	Валет	Дама	10	Король
2	Туз	4	3	5	6	9	7	8	Валет	Дама	10	Король
2	Туз	4	3	5	6	8	7	9	Валет	Дама	10	Король
2	Туз	4	3	5	6	8	7	9	10	Дама	Валет	Король
Туз	2	4	3	5	6	8	7	9	10	Дама	Валет	Король
Туз	2	3	4	5	6	8	7	9	10	Дама	Валет	Король
Туз	2	3	4	5	6	7	8	9	10	Дама	Валет	Король
Туз	2	3	4	5	6	7	8	9	10	Дама	Валет	Король

Рис. 6 Сортировка методом прочёсывания

Перетасуйте карты и разложите на столе. Выделите 1 и 9 карту (расстояние между картами 8), если они находятся в неправильном порядке - поменяйте их местами. Выделите 2 и 10 карты (расстояние между картами 6) и, при необходимости, поменяйте их местами. То же самое проделайте для 3 и 11 карты (расстояние между картами 4), 4 и 12 карты (расстояние между картами 3), а затем 5 и 13 (расстояние между картами 2). Далее сравнивайте и переставляйте пары карт (1, 7), (2, 8), (3, 9), (4, 10), (5, 11), (6, 12) и (7, 13), т.е. карты непосредственно отстоящие друг от друга на шесть позиций. А теперь выполните проход по разложенным картам, отстоящим друг от друга на четыре позиции, затем на три и две позиции, как показано на рисунке 6. После этого выполните стандартную пузырьковую сортировку.^[6]

Суть изложенного метода заключается в том, что во время выполнения метода прочесывания вам потребуется только два цикла — первый, служащий для минимализации размера «прыжков», и второй, который необходим для выполнения сортировки пузырьковым методом.

Каким образом были получены значения расстояний 8, 6, 4 ,3, 2, 1? Разработчики этого метода сортировки провели большое количество экспериментов и эмпирическим путём пришли к выводу, что значение каждого последующего расстояния «прыжка» должно быть получено в результате деления предыдущего значения расстояния на 1,3.

Разработчики метода выявили, что сортировка методом причёсывания немного быстрее сортировки методом Шелла (на последовательности Д. Кнута). Очевидно, что данный вид сортировки также принадлежит к группе неустойчивых алгоритмов.

2.2 Сортировка методом Шелла

Данный метод разработал Дональд Л.Шелл в 1959 году. Он основан на сортировке методом вставок. Сортировка методом Шелла (Shell sort) призвана значительно повысить скорость выполнения работы, жертвуя скоростью перемещения элементов исходного массива, которые находятся достаточно далеко от необходимых позиций. Сортировка методом Шелла включает в себя необходимость перемещения непосредственно таких элементов «прыжками» через несколько элементов одновременно, уменьшая размер «прыжков» и, в конце концов, завершительная установка элементов в нужные позиции выполняется с помощью классической сортировки методом вставок.

Рассмотрим выполнение сортировки методом Шелла на примере карточной колоды. Разложив карты в тянущуюся линию, извлеките из этой линии карт первую и каждую четвёртую карту, следующую после первой (т.е. пятую, девятую и тринадцатую). Выполните сортировку выбранных карт методом вставок и снова поместите их в линию. Извлеките из колоды вторую и четвёртую карту после второй, а именно — шестую и девятую. Выполните сортировку выбранных карт методом вставок и снова поместите их в линию. Выполните те же операции над третей и каждой четвёртой картой после третей, а затем над четвёртой и каждой четвёртой картой после четвёртой.

После первого прохода карты будут находиться в отсортированном порядке по 4, какую бы карту не выбрали, карты, которые находятся на количество позиций, кратном 4 вперёд и назад, будут отсортированы в требуемом порядке.

Стоит обратить свое внимание на тот факт, что карты с первого взгляда кажутся не отсортированными, но, несмотря на это, невзирая а исходное положение карт, по завершению первого прохода они переместятся не так далеко от своих мест, которые должны занять в непосредственно отсортированной последовательности.

Теперь выполним стандартную сортировку методом вставок, в результате чего получим отсортированную колоду карт, как показано на рисунке 5. При небольших расстояниях между элементами в массиве и их позициями в отсортированной последовательности быстродействие сортировки методом вставок линейно зависит от числа элементом массива.

Сортировка методом Шелла работает путём вставки отсортированных подмножеств основного списка. Каждое подмножество формируется за счёт выборки каждого n-ной части массива, начиная с любой позиции в списке. В результате будет получено n подмножеств, которые отсортированы методом вставок. Полученная последовательность элементов массива называется отсортированной по n. Затем значение n уменьшается и снова выполняется сортировка. Уменьшение значений n происходит до тех пор, пока n не будет равно 1, после чего последний проход будет представлять собой стандартную сортировку методом вставок.

Суть данной методы заключается в том, что сортировка по n быстро переносит элементы массива в область, где они обязаны находиться в отсортированной последовательности, а уменьшение значений n позволяет уменьшать объем «прыжков» и в конце концов поместить элемент в требуемую позицию. Плавному перемещению элементов предшествуют большие «прыжки», сводящиеся к простой сортировке методом вставок.

Какие значения n лучше использовать?

Дональд Л.Шелл предложил значения 1, 2, 4, 8, 16, 32 и т.д. (естественно в обратном порядке), но с этими значениями связана одна проблема: до последнего прохода элементы массива с чётными индексами никогда не сравниваются с элементами нечётного индексами. И, следовательно, при выполнении последнего прохода всё ещё возможны перемещения элементов на большие расстояния.

В 1969 году Дональд Кнут (Donald Knuth) предложил последовательность 1, 4, 13, 40, 121 и т.д. (каждое последующее значение на единицу больше, чем утроенное предыдущее значение). Для массивов средних размеров эта последовательность позволяет получить достаточно высокие характеристики быстродействия.

Сортировка методом Шелла относится к группе неустойчивых алгоритмов, так как при перестановке элементов массива, далеко стоящих друг от друга, возможно нарушение порядка следования элементов с равными значениями.

2.3 Пирамидальная сортировка

В случае с сортировкой, которую зовут пирамидальной, элементы начального массива будут представлены в виде листьев дерева. Их попарное сравнение позволит определить минимальный и максимальный элемент, т.е. от каждого прохода получать большее количество информации, чем просто указание на один, наименьший элемент.

Метод пирамидальной сортировки более подробно изложен в книге Т. Кормена, Ч. Лейзерсона, Р. Ривеста и К. Штайн: «Алгоритмы: построение и анализ, 2-издание» и в учебном пособии для студентов вузов Л.Г. Гагариной и В.Д. Колдаева «Алгоритмы и структуры данных».

Метод сортирующего дерева основывается на повторяющихся поисках наименьшего значения среди n элементов массива, среди оставшихся n-1 элементов и т.д. К примеру, сделав n/2 сравнений, можно определить в каждой паре значений меньшее значение. С помощью n/4 сравнений — меньшее значение из пары уже выбранных меньших и т. д. Проделав n - 1 сравнений, мы можем построить дерево выбора, по аналогии представленного на рисунке 7.1 и идентифицировать его корень как нужное нам наименьшее значение.

06

06

06

06

12

12

12

44

44

55

42

94

18

18

67

Рис. 7.1. Повторяющиеся выборы среди двух значений

Второй этап сортировки — это спуск вдоль пути, отмеченного наименьшим элементом, и непосредственное исключение его из дерева путем замены на пустой элемент (дырку), как показано на рисунке 7.2. ^[7]

12

12

12

44

44

55

42

94

18

18

67

Рис. 7.2. Исключение наименьшего значения

Элемент, передвинувшийся в корень дерева, как показано на рисунке 7.3, вновь будет наименьшим (теперь уже вторым) элементом, и его можно исключить. После n таких шагов дерево станет пустым (т. е. в нем останутся только пустые элементы - «дырки»), и процесс сортировки заканчивается.

12

18

67

12

12

12

44

44

55

42

94

18

18

67

Рис.7.3. Сдвигание элементов и заполнение пустых элементов (дырок)

Обратите внимание - на каждом из n шагов выбора требуется только log₂ n сравнений. Поэтому на весь процесс понадобится порядка n×log₂ n элементарных операций плюс еще n шагов на построение дерева. Естественно, сохранение дополнительной информации делает задачу более изощренной, поэтому в сортировке по дереву увеличилась сложность отдельных шагов. Ведь для сохранения избыточной информации, получаемой при начальном проходе, создается некоторая древообразная структура.

Стоит сперва избавиться от нужды в пустых элементах (дырах), которые заполняют всё дерево и приводят к большому количеству ненужных сравнений. Дж. Уильямс в 1964 году предложил метод, названный пирамидальной сортировкой.

Пирамида определяется как последовательность ключей h_l, h_l+1,...,h_r, такая, что hi <= h_2i. и hi< =h_2i+1, для i =l,..., r/2.

Если любое двоичное дерево рассматривать как массив, представленный на рисунке 7.4, то можно говорить, что деревья сортировок, представленными на рисунках 7.5 и 7.6 являются пирамидами, а элемент h_l её наименьший элемент: h_l = min(h₁, h₂,…, h_n).

h₁

h₃

h₇

h₂

h₅

h₁₀

h₄

h₈

h₉

h₁₁

h₁₂

h₆

h₁₃

h₁₅

h₁₄

Рис. 7.4. Массив h, представленный в виде двоичного дерева

h₁

06

12

42

94

55

18

Рис.7.5. Пирамида из семи элементов.

Представим, что существует некоторая пирамида с заданными элементами hi,.., hr. Возьмем, в качестве примера, непосредственно исходной пирамиду h1, ...,h7, показанную на рисунке 7.5, и расширим эту пирамиду влево, добавив к ней элемент h1 = 44.

Каждый последующий элемент, в нашем случае это - h1 = 44, сначала помещается в вершину дерева, а затем «просеивается» по своему пути, на котором находятся меньшие по сравнению с ним элементы, которые, в свою очередь, поднимутся наверх, так как их значение меньше помещаемого в дерево элемента. В нашем случае 44 меняется местами с 06, затем с 12, и так формируется дерево, показанное на рисунке 7.6.

06

122

44

42

94

55

18

Рис.7.6.Просеивание ключа - 44 через пирамиду.

2.4 Быстрая сортировка

Куда эффективнее остальных может сработать метод сортировки К. Хора, который получил также название «быстрая сортировка» или же «сортировка с разделением». В базу этого метода сортировки положено последовательное дробление взятого множества на части. Перед тем, как приступить к работе, необходимо определить тот элемент, что стоит в середине взятого массива, а после массив стоит разделить на две равные части. Глядя на левую часть массива с левой стороны на правую, выполним поиск такого элемента массива, что M[I] > X, затем при просмотре правой части справа налево отыскивается такой элемент, что M[I] X, не будут обменены с элементами, расположенными справа от середины и удовлетворяющими условию M[I] < X . По окончанию таких действий мы получим массив из двух частей. Далее левая часть в свою очередь дробится на две части и сортируется описанным выше способом. Этот процесс происходит до тех пор, пока в каждой из частей не останется по одному элементу. Затем аналогично сортируется правая часть первоначального массива.

Таким образом, алгоритм быстрой сортировки дает лучшие результаты, чем пузырьковый метод, однако следует учесть, что в некоторых случаях это преимущество снижается. Например, если применить эту сортировку непосредственнок массиву, содержащему несколько одинаковых элементов.

Заключение

Подводя итоги проделанной работы, мы делаем вывод, что экономия в использовании памяти является основополагающим требованием к методам сортировки массивов. Это значит, что переупорядочение элементов нужно выполнять in situ, что означает «на том же месте», а также, что те из методов, которые перемещали элементы из одного массива в другой, не имеют для нас никакой ценности, а также не представляют и малейшего интереса. Это значит, что, подходя к выбору метода сортировки, необходимо руководствоваться критерием экономии памяти, проводя непосредственную классификацию алгоритмов в соответствии с той эффективностью, которую они имеют, т. е. экономией времени или быстродействием.

Детальный анализ продемонстрировал нам, что сортировка методом обмена и ее маленькие улучшения проигрывают сортировке выбором или включениями, что правда, ведь есть сомнения в том, что сортировка пузырьковым методом будет иметь хоть малейшие преимущества помимо любопытного на слух и приятного для запоминания названия. В свою очередь, метод шейкер-сортировки может быть полезен в сортировке лишь тогда, когда ясно, что элементы в исходном массиве практически упорядочены, что является крайне редким случаем на практике.

Мы имеем возможность продемонстрировать, что среднее расстояние, на которое необходимо выполнить перемещение каждого из n элементов во время сортировки, - это n/3 мест. Это число дает ключ к поиску усовершенствованных, т. е. более эффективных, методов сортировки. Все простые методы в принципе перемещают каждый элемент на одну позицию на каждом элементарном шаге. По этой причине они требуют порядка 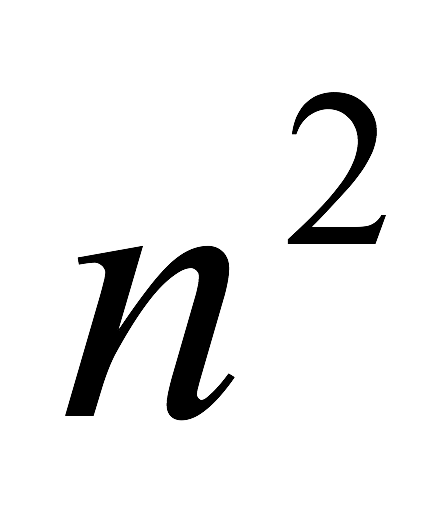таких шагов. Любое улучшение должно основываться на принципе пересылки элементов за один цикл на большее расстояние.

Теперь, подведя итоги изучения усовершенствованных методов сортировки, мы можем сравнить их эффективность. Как и раньше, n — число сортируемых элементов, а С и М — соответственно число необходимых сравнений ключей и число обменов. Для всех прямых методов сортировки можно дать точные аналитические формулы. Для усовершенствованных методов нет сколько-либо осмысленных, простых и точных формул. Но, в то же время, возвращаясь к теме сортировки методом Шелла, нельзя не обратить внимание на вычислительные затраты, которые составят с×n^1.2, а для пирамидальной сортировки и метода быстрой сортировки — с×n×logn, где с — соответствующие коэффициенты.

Данные формулы дают нам грубую меру для производительности как функции n и позволяют разбить методы сортировки на примитивные, прямые методы (n²) и на усложненные или "логарифмические" методы (n×log(n)).

Теперь, изучив различные усложненных методы сортировки и их вариации, легко заметить их основной недостаток — слишком низкая производительность при имеющихся небольших n. И правда, эти сортировки не рекомендуется применять для небольшого числа элементов (для этого существуют простые методы сортировки). Хоть и это можно изменить, прибегнув к пути включения простых методов сортировки для небольших n.

Итак, подведем итог: мы выяснили, что алгоритмы устойчивой сортировки являются самыми медленными из возможным алгоритмов сортировки массивов, принадлежащих к классу О(n²), применяются при небольшом n. Алгоритмы неустойчивой сортировки – наиболее быстрые, принадлежащие к классу О(n×log(n)), применяются при большом n. Выбор наиболее подходящего метода сортировки первоначальных массивов будет зависеть от структуры обрабатываемых данных и от количества элементов. Подходя к решению новой задачи, стоит подобрать тот метод сортировки массивов, что окажется максимально эффективным.

Список использованной литературы

1. Бакнелл Джулиан М. Книга: Фундаментальные алгоритмы и структуры данных в Delphi. [Текст] / Д.М. Бакнелл. Перевод с английского. - ООО "ДиаСофтЮП", 2003.- 560 с.
2. Вирт Н. Книга: Алгоритмы и структуры данных. [Текст] / Н.Вирт. Перевод с английского – М. Издательство «Мир», 1989. -358 с.
3. Кормен Т., Лейзерсон Ч., Ривест Р., Штайн К. [Текст] = Алгоритмы: построение и анализ, 2-издание. / Т. Кормен, Ч. Лейзерсон, Р. Ривест, К. Штайн. Перевод с английского – М. Издательский дом «Вильямс», 2005. – 1296 с.
4. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с.

1. Бакнелл Джулиан М. Книга: Фундаментальные алгоритмы и структуры данных в Delphi. [Текст] / Д.М. Бакнелл. Перевод с английского. - ООО "ДиаСофтЮП", 2003.- 560 с. ↑

2. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с. ↑

3. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с. ↑

4. Бакнелл Джулиан М. Книга: Фундаментальные алгоритмы и структуры данных в Delphi. [Текст] / Д.М. Бакнелл. Перевод с английского. - ООО "ДиаСофтЮП", 2003.- 560 с. ↑

5. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с. ↑

6. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с. ↑

7. Гагарина Л.Г., Колдаев В.Д. Алгоритмы и структуры данных. [Текст] : учебное пособие для студентов вузов / Л.Г. Гагарина, В.Д. Колдаев. - Издательство "Финансы и статистика"; Издательский дом ИНФРА-М, 2009. - 304 с. ↑