Разработка модуля для выполнения операций с натуральными числами в 16-ричной системе счисления (Теоретически основы выполнения вычислительных операций в 16-ричной системе счисления)

Содержание:

Введение

Современный человек в повседневной жизни постоянно сталкивается с числами. Числа, цифры... они с нами везде. Историки показали, что и пять тысяч лет назад люди могли записывать числа и производить над ними арифметические действия. Конечно, принципы записи были совсем не такими, как сейчас. Но в любом случае число изображалось с помощью одного или нескольких символов. Эти символы, участвующие в записи числа, в математике и информатике принять называть цифрами.

Первоначально понятие отвлечённого числа отсутствовало, число было "привязано" к тем конкретным предметам, которые пересчитывали. Отвлечённое понятие натурального числа появляется вместе с развитием письменности. Дробные же числа изобрели тогда, когда возникла необходимость производить измерения. Измерение, как известно, это сравнение с другой величиной того же рода, выбираемой в качестве эталона. Эталон называется ещё единицей измерения. Понятно, что единица измерения не всегда укладывалась целое число раз в измеряемой величине. Отсюда и возникла практическая потребность ввести более "мелкие" числа, чем натуральные. Дальнейшее развитие понятия числа было обусловлено уже развитием математики. Понятие числа – фундаментальное понятие, как математики, так и информатики. В дальнейшем при изложении материала под числом мы будем понимать его величину, а не его символьную запись. Сегодня, в самом конце XX века, для записи чисел человечество использует в основном десятичную систему счисления.

Под системой счисления понимается способ записи (изображения) чисел. Различные системы счисления, которые существовали раньше и которые используются в настоящее время, делятся на две группы: позиционные и непозиционные. Наиболее совершенными являются позиционные системы счисления, т.е. системы записи чисел, в которых вклад каждой цифры в величину числа зависит от её положения (позиции) в последовательности цифр, изображающей число. Системы счисления, в которых каждой цифре соответствует величина, не зависящая от её места в записи числа, называются непозиционными. Существуют также смешанные системы счисления. В настоящее время конечно используются позиционные системы счисления. Позиционные системы счисления – результат длительного исторического развития непозиционных систем счисления.

В настоящей работе рассмотрим одну из разновидностей позиционной системы счисления – 16-ричную систему счисления, а также реализуем программное приложение на языке C#, позволяющее выполнять простейшие арифметические операции.

1. Теоретически основы выполнения вычислительных операций в 16-ричной системе счисления

Разновидности позиционных систем счисления

В позиционных системах счисления один и тот же числовой знак (цифра) в записи числа имеет различные значения в зависимости от того места (разряда), где он расположен. Изобретение позиционной нумерации, основанной на поместном значении цифр, приписывается шумерам и вавилонянам; развита была такая нумерация индусами и имела неоценимые последствия в истории человеческой цивилизации. К числу таких систем относится современная десятичная система счисления, возникновение которой связано со счётом на пальцах. В средневековой Европе она появилась через итальянских купцов, в свою очередь заимствовавших её у арабов.

Под позиционной системой счисления обычно понимается b-ричная система счисления, которая определяется целым числом b > 1, называемым основанием системы счисления. Целое число без знака x в b-ричной системе счисления представляется в виде конечной линейной комбинации степеней числа b: , где a_k – это целые числа, называемые цифрами, удовлетворяющие неравенству

Каждая степень b^k в такой записи называется весовым коэффициентом разряда. Старшинство разрядов и соответствующих им цифр определяется значением показателя k (номером разряда). Обычно в записи ненулевых чисел начальные нули опускаются.

Если не возникает разночтений (например, когда все цифры представляются в виде уникальных письменных знаков), число x записывают в виде последовательности его b-ричных цифр, перечисляемых по убыванию старшинства разрядов слева направо: x=a_n-2a_n-1….a₀.

Например, число тридцать три представляется в десятичной системе счисления в виде: 33₁₀=3*10¹+3*10⁰.

Наиболее часто употребляемыми в настоящее время позиционными системами являются:

2 – двоичная (в дискретной математике, информатике, программировании);

3 – троичная;

8 – восьмеричная;

10 – десятичная (используется повсеместно);

12 – двенадцатеричная (счёт дюжинами);

16 – шестнадцатеричная (используется в программировании, информатике);

20 – двадцатеричная;

60 – шестидесятеричная (единицы измерения времени, измерение углов и, в частности, координат, долготы и широты).

В позиционных системах чем больше основание системы счисления, тем меньшее количество разрядов (то есть записываемых цифр) требуется при записи числа.

1.2 Особенности 16-ричной системы счисления

Шестнадцатеричная система счисления – позиционная система счисления по целочисленному основанию 16. В качестве цифр этой системы счисления обычно используются цифры от 0 до 9 и латинские буквы от A до F. Буквы A, B, C, D, E, F имеют значения 10₁₀, 11₁₀, 12₁₀, 13₁₀, 14₁₀, 15₁₀ соответственно.

Широко используется в низкоуровневом программировании и компьютерной документации, поскольку в современных компьютерах минимальной адресуемой единицей памяти является 8-битный байт, значения которого удобно записывать двумя шестнадцатеричными цифрами. Такое использование началось с системы IBM/360, где вся документация использовала шестнадцатеричную систему, в то время как в документации других компьютерных систем того времени (даже с 8-битными символами, как, например, PDP-11 или БЭСМ-6) использовали восьмеричную систему.

В стандарте Юникода номер символа принято записывать в шестнадцатеричном виде, используя не менее 4 цифр (при необходимости – с ведущими нулями).

Для перевода шестнадцатеричного числа в десятичное необходимо это число представить в виде суммы произведений степеней основания шестнадцатеричной системы счисления на соответствующие цифры в разрядах шестнадцатеричного числа.

Например, требуется перевести шестнадцатеричное число «3A5» в десятичное. В этом числе 3 цифры. В соответствии с вышеуказанным правилом представим его в виде суммы степеней с основанием 16:

3A5₁₆ = 3·16²+10·16¹+5·16⁰= 3·256+10·16+5·1 = 768+160+5 = 93310.

При переводе чисел, следует помнить, что в шестнадцатеричной системе счисления: A=10; B=11; C=12; D=13; E=14; F=15.

Шестнадцатеричное представление чисел получило популярность вследствие того, что двоичные числа очень трудно читать, особенно если они очень большие. При этом перевод двоичного числа в десятичное достаточно труден, а в шестнадцатеричное – нет, так как в последнем случае существует ускоренные методы перевода многозначного двоичного числа в шестнадцатеричную систему на основе разбиения его на тетрады, справа налево и замены каждой тетрады соответствующей шестнадцатеричной цифрой. Для перевода числа из шестнадцатеричной системы в двоичную нужно заменить каждую его цифру на соответствующую тетраду из нижеприведённой таблицы перевода (таблица 1.1). К примеру, для числа 010110100011₂ получим:

010110100011₂ = 0101 1010 0011 = 5A3₁₆.

Чтобы перевести десятичное число в шестнадцатеричное, необходимо выполнить следующие действия:

1.Проверяем, не меньше ли 16 наше число: если да, то результат достигнут. Действительно, такое десятичное число необходимо лишь заменить соответствующей ему шестнадцатеричной цифрой из таблицы 1. Если же наше десятичное число больше 16, переходим к шагу 2.

2.Делим наше число «нацело» на 16 и запоминаем целочисленный остаток от этого деления. Результат этого деления снова сравниваем с 16. Если результат деления меньше 16, то его стоит тоже запомнить как последний из остатков.

3.Шаг 2 повторяем до тех пор, пока результат деления не будет меньше 16. Целочисленные остатки на всех этапах запоминаем. Они понадобятся в шаге 4.

4.Все остатки записываем в обратном порядке и заменяем в них числа от 10 до 15 шестнадцатеричными цифрами от A до F.

Таблица 1.1

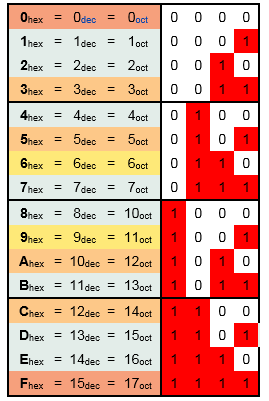
К примеру, переведем десятичное число 89 в шестнадцатеричное. Оно больше 16, поэтому разделим его на 16. Частное равно 5 и 9 в остатке. 5 меньше 16, значит, деление прекращается и 5 запомним как последний остаток. То есть у нас есть два остатка: 9 и 5. Теперь их надо записать в обратном порядке, получаем: 89 = 59₁₆. Проверим, действительно ли 0×59 равно 89? Распишем его по привычной уже схеме: 59₁₆= 5×16¹ + 9×16⁰ = 5×16 + 9 = 89.

Действительно, получилось. Но в выбранном примере число 89 очень быстро закончилось, если так можно сказать. В противном случае деление потребовалось бы продолжить. Покажем это на более сложном примере. Возьмем число 3728: 3728 / 16 = 233 и 0 в остатке. Затем 233 / 16 = 14 и 9 в остатке. Результат этого деления равен 14, он меньше 16. Деление заканчиваем и запоминаем этот результат деления как последний остаток. Нам осталось лишь записать эти остатки в обратном порядке и заменить десятичное число 14 на шестнадцатеричную цифру E. Итак, искомое число E90.

На рисунке 1.1. представлен пример перевода десятичного числа 500 в шестнадцатеричную систему счисления на основе деления в столбик.

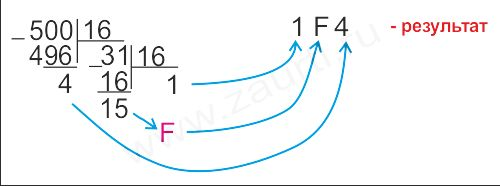
Рис.1.1.

Результат перевода 1F4₁₆.

1.3 Арифметические операции с 16-ричными числами

Сначала рассмотрим необходимые правила. Самое первое – всегда стоит помнить о том, что шестнадцатеричная система счисления позиционная. Об этом я писал в самом начале, но не грех и повторить. Просто из этого правила следует очень важный момент, складывая числа, нужно делать это только с цифрами, находящимися в одинаковых разрядах.

Для начала рассмотрим, как складывать числа в столбик в привычной нам десятичной системе счисления и применим эти знания на шестнадцатеричные числа.

Предположим, нам необходимо сложить числа 234 и 49. Для этого мы запишем эти числа одно под другим так, чтобы разряды в них совпадали – единицы под единицами, десятки под десятками и так далее. И складывать будем цифры из одинаковых разрядов, начиная с единиц и идя влево.

234

+

49

283

Помня о том, что мы пока складываем десятичные числа (10 является основанием системы счисления), складываем разряды по очереди справа налево. 4 + 9 = 13. Наш результат – 13, он больше 10 – нашего основания. В случае, когда результат больше или равен основанию, это самое основание нужно вычесть из результата. В нашем примере от 13 необходимо отнять 10, а новый результат записать под цифрами 4 и 9, отнятую же здесь десятку, перенести в левый разряд как единицу старшего разряда (десять единиц равно одному десятку). В разряде с десятков мы складываем 3 + 4 и добавляем к ним перенесенный 1 десяток. Результат – 8. Он меньше нашего основания, значит под десятками просто записываем 8. Далее складываем сотни. Но двойку не с чем складывать, значит просто переносим ее в результат. Итак: 234 + 49 = 283.

Ровно те же правила сложения чисел действуют в любой позиционной системе счисления. Единственное отличие заключается в том, что результаты сложения цифр в разрядах придется сравнивать с другими основаниями систем счисления.

Переходим к шестнадцатеричным числам. Вспомним, что основание здесь равно 16. И неприятной особенностью являются цифры обозначенные буквами латинского алфавита. Чтобы нам было проще складывать, вспомним, чему они равны:

A = 10, B = 11, C = 12, D = 13, E = 14, F = 15.

Переходим собственно, к примеру, на сложение. Давайте сложим 0xA15 и 0xBC.

A15

+

BC

AD1

Сначала складываем единицы – 5 + С. Вспоминаем, что С = 12, получаем 5 + 12 = 17. Результат больше основания системы счисления, который равен 16. Значит, вычитаем 16 из 17 – равно 1, записываем этот новый результат под правым разрядом, а в левый старший разряд переносим единичку (16 единиц равно одному десятку в шестнадцатеричной системе). Там же складываем 1 + B. Добавляем к этой сумме 1 перенесенный разряд и вспоминаем, что B = 11, получаем: 1 + 1 + 11 = 13. Во-первых: этот результат меньше 16, значит его можно просто записать под складываемыми цифрами, а во-вторых: Число 13 в шестнадцатеричной арифметике записывается буквой D. В разряд сотен при этом ничего не переносится, а цифра A из верхнего слагаемого просто переносится в результат. Несложно заметить, что A15 + BC = AD1. На рисунке 1.2 представлены результаты сложения двух чисел 1С52₁₆ и 891₁₆.

Рис. 1.2

Рассмотри операцию вычитания 16-ричных чисел. Начнем мы снова с привычной нам десятичной системы счисления. Давайте решим пример: 123-85.

123

–

85

38

Вычитание снова происходит поразрядно, но переносы делаются на сей раз слева направо. Поясню. В нашем примере необходимо из 3 отнять 5. Этого сделать нельзя, поэтому мы занимаем один десяток из левого разряда. Теперь 5 нужно отнять от 13. В результате мы получим 8, запишем этот результат под разрядом единиц. От десятков в уменьшаемом (число 123) мы один десяток заняли в разряд единиц. Теперь здесь только 1 десяток. Нам нужно из одного вычесть 8. Для этого снова приходится занять единицу из левого разряда (теперь уже сотен). Значит нужно из 11 вычесть 8. В результате получаем – 3 и записываем его под разрядом десятков. А единственную сотню мы заняли для вычитания десятков. Пример решён: 123-85 = 38.

Перейдем к вычитанию шестнадцатеричных чисел. Все делается аналогично, надо только помнить, что в случае необходимости из левых разрядов мы будем занимать не 10, а 16.

Давайте решим пример BC4-AF.

BC4

–

AF

B15

Из 4 нельзя вычесть F, значит, из левого разряда мы займем 16. Теперь F надо вычитать из 20. В результате – 5, записываем его под разрядом единиц. Цифра C уменьшилась на 1, теперь это B. Значит надо A вычесть из B. Нетрудно догадаться, что в результате будет 1. Записываем этот результат в разряде десятков. Из сотен в этот раз мы ничего не занимали и в вычитаемом только 2 цифры – сотен нет, то есть сносим B из уменьшаемого в результат. Итак: BC4-AF = B15, пример решен.

На рисунке 1.3 представлены результаты вычитания двух чисел С5B₁₆ и A7E₁₆.

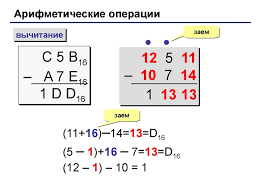
Рис.1.3.

Умножение и деление проводится также, как и десятичной системе. На рисунке 1.4 представлены результаты перемножения двух чисел 20A4₁₆ и B15₁₆.

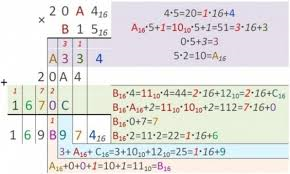
Рис.1.4.

Для того, чтобы легче было проводить эти действия, лучше воспользоваться таблицей умножения, которая приведена в таблице 1.2.

Таблица 1.2

	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
1	1	2	3	4	5	6	7	8	9	A	B	C	D	E	F
2	2	4	6	8	A	C	E	10	12	14	16	18	1A	1C	1E
3	3	6	9	C	F	12	15	18	1B	1E	21	24	27	2A	2D
4	4	8	C	10	14	18	1C	20	24	28	2C	30	34	38	3C
5	5	A	F	14	19	1E	23	28	2D	32	37	3C	41	46	4B
6	6	C	12	18	1E	24	2A	30	36	3C	42	48	4E	54	5A
7	7	E	15	1C	23	2A	31	38	3F	46	4D	54	5B	62	69
8	8	10	18	20	28	30	38	40	48	50	58	60	68	70	78
9	9	12	1B	24	2D	36	3F	48	51	5A	63	6C	75	7E	87
A	A	14	1E	28	32	3C	46	50	5A	64	6E	78	82	8C	96
B	B	16	21	2C	37	42	4D	58	63	6E	79	84	8F	9A	A5
C	C	18	24	30	3C	48	54	60	6C	78	84	90	9C	A8	B4
D	D	1A	27	34	41	4E	5B	68	75	82	8F	9C	A9	B6	C3
E	E	1C	2A	38	46	54	62	70	7E	8C	9A	A8	B6	C4	D2
F	F	1E	2D	3C	4B	5A	69	78	87	96	A5	B4	C3	D2	E1

Операция умножения довольно просто выполняется при использовании этой таблицы. Например, при умножении чисел 4А x C сначала выполним операцию умножения для 4 х С = 30 и затем А х С = 78. Для этого нужно найти числа, находящиеся на пересечении строк и столбцов чисел 4 и С, а затем А и С. Затем нужно сложить 300 и 78, в результате получим 378.

На рисунке 1.5 представлены результаты деления двух чисел 6F78₁₆ и 8₁₆ в столбик.

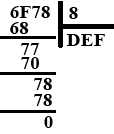
Рис. 1.5.

При этом также можем воспользоваться данными из таблицы 1.2. Для операции деления нужно найти число в строке, в которой слева находится делитель или близкое к нему число. Например, при делении 378 на С, найдем в строке, где слева находится С, максимальное число, которое не превышает 37 – это будет 30. Запишем верхнее число, которое находится в этом столбце, это будет 4. 37 – 30 = 7. Далее найдем в этой же строке число 78 и запишем верхнее значение столбца, где оно находится. Получим А, значит, наше число 4A.

Разработка модуля для выполнения операций с натуральными числами в 16-ричной системе счисления в языке C#

Разрабатываемый модуль представляет собой калькулятор, позволяющий реализовать операции сложения и вычитания двух натуральных 16-ричных чисел.

Описание интерфейса модуля

Интерфейс представлен на рисунке 2.1 и включает: поле ввода, набор кнопок для ввода натуральных чисел в шестнадцатеричной системе счисления (от 0 до F), кнопки арифметических операций («+», «–»,«=») и очистки поля ввода.

Рис. 2.1.

Порядок выполнения вычислений

Для выполнения вычислений необходимо ввести первое число в поле ввода, к примеру, число 2 (рис. 2.2).

Рис. 2.2.

Далее нажимаем необходимую операцию, например сложения (рис.2.3).

Рис. 2.3.

Далее выбираем операцию равно (рис. 2.4) и получаем результат вычислений (рис. 2.5).

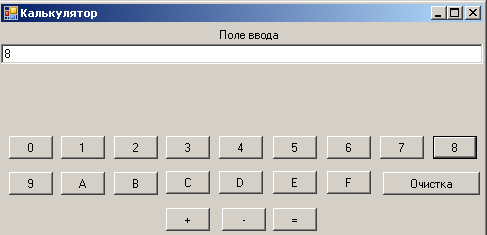
Рис. 2.4.

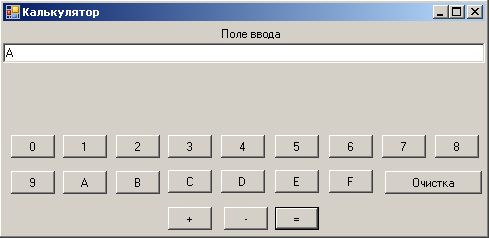
Рис. 2.5.

Исследование работы модуля

Проверим работу модуля при выполнении операций сложения на числах, приведенных ранее в разделе 1. На рисунке 2.6 и 2.7 представлен результат сложения двух натуральных чисел A15 и BC. Получен результат AD1.

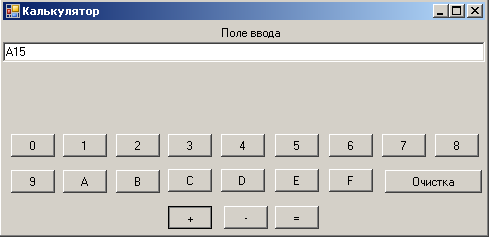
Рис. 2.6.

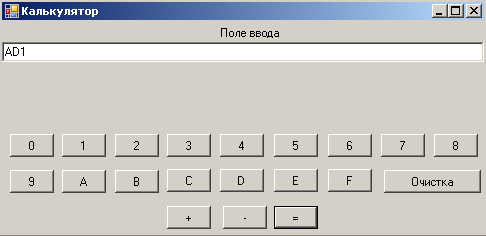
Рис. 2.7.

На рисунке 2.8 и 2.9 представлен результат сложения двух натуральных чисел 1С52₁₆ и 891₁₆ . Получен результат 24E3.

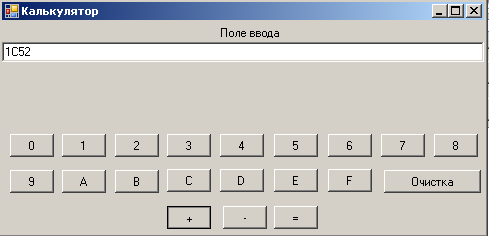
Рис. 2.8

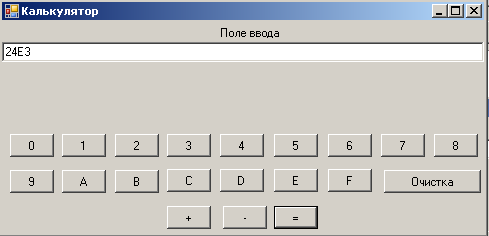
Рис. 2.9.

Далее рассмотрим операции вычитания.

На рисунке 2.10 и 2.11 представлен результат вычитания двух натуральных чисел BC4₁₆ и AF₁₆ . Получен результат B15₁₆.

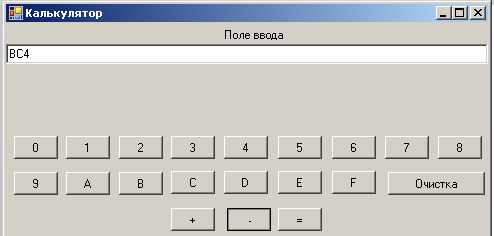
Рис. 2.10

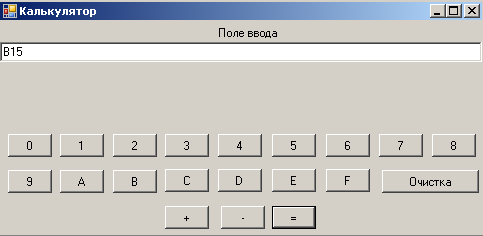
Рис. 2.11.

На рисунке 2.12 и 2.13 представлен результат вычитания двух натуральных чисел С5B₁₆ и A7E₁₆ . Получен результат 1DD₁₆.

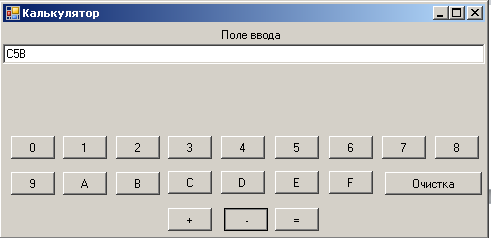
Рис. 2.12.

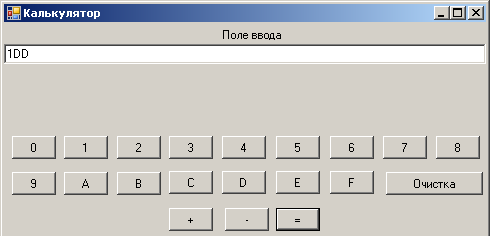
Рис. 2.13.

Проверим правильность работы модуля в дополнительных ситуациях.

Сложим числа FF₁₆ и B₁₆ (рис.2.14, 2.15, 2.16). Получим 10A₁₆, что легко проверяется, так как сумма F и B дает 26₁₀=1*16+10=1*16+A, запоминаем 1. А сумма F и 1 дает 16₁₀ или 10₁₆. Итого получается 10A₁₆.

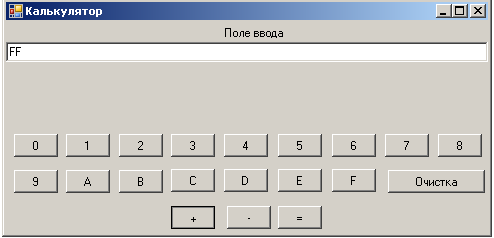
Рис. 2.14.

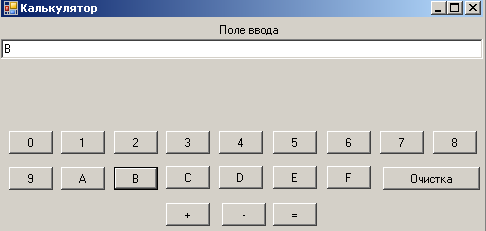
Рис. 2.15.

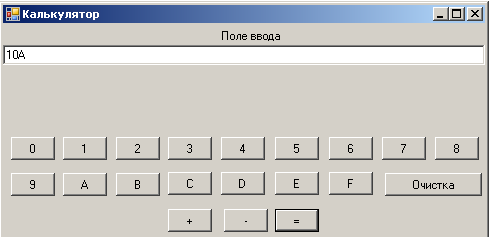
Рис. 2.16.

Вычтем из числа FF₁₆ число F₁₆ (рис. 2.17, 2.18, 2.19). Получаем верное число F0₁₆.

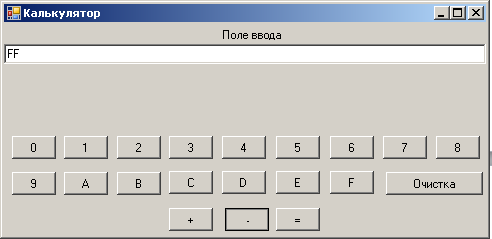
Рис. 2.17.

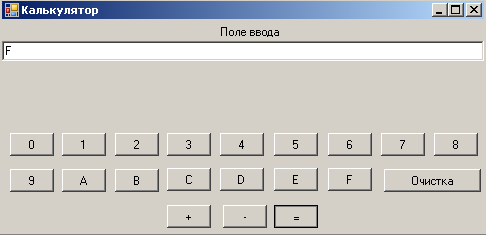
Рис. 2.18.

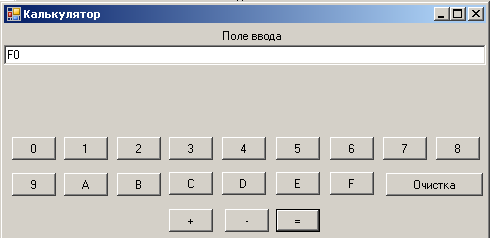
Рис. 2.19.

Таким образом, разработанный модуль удовлетворяет всем необходимым требованиям при выполнении операций сложения и вычитания. Така

Заключение

Вопросы изучения систем счисления являются одними из базовых вопросов информатики и теории программирования, так как один разряд двоичной системы представляет собой не что иное, как один бит, а два разряда шестнадцатеричной системы представляют собой один байт. В современных компьютерах информация кодируется в байтах, поэтому во многих случаях удобно использовать шестнадцатеричную систему счисления. Помимо прочего, шестнадцатеричную систему используют в низкоуровневом программировании, в компьютерном дизайне при кодировании цветов изображений, в некоторых системах кодировки информационных символов и т.п.

В представленной курсовой работе проанализированы основные существующие системы позиционного счисления. Подробно исследованы вопросы выполнения арифметических операций над натуральными числами в шестнадцатеричной системе счисления. Разработан программный модуль на языке C# в среде Visual Studio 2017, позволяющий реализовать сложение и вычитание натуральных чисел в шестнадцатеричной системе счисления. Проведены исследования разработанного модуля на примерах, рассмотренных в теоретической части и дополнительных примерах, позволяющих сделать вывод о надежности разработанного программного обеспечения в различных нестандартных ситуациях.

Список используемой литературы

1. Гашков С. Б. Системы счисления и их применение. – М.: МЦНМО, 2004. – 52 с.
2. Микушин А.В., Сажнев А.М., Сединин В.И. Цифровые устройства и микропроцессоры. СПб, БХВ-Петербург, 2010. – 832 с.
3. Стахов А. Роль систем счисления в истории компьютеров // https://mirznanii.com/a/118900/rol-sistem-schisleniya-v-istorii-kompyuterov
4. Двоичная и шестнадцатиричная системы счисления// https://microkontroller.ru/programmirovanie-mikrokontrollerov-avr/dvoichnaya-i-shestnadtsatirichnaya-sistemyi-schisleniya.
5. Смирнов В. Шестнадцатеричная арифметика // http://www.vsmirnov. ru /articles/hexmetric.html.
6. Шилдт Г. C# 4.0: полное руководство. : Пер. с англ. – М. : ООО "И.Д. Вильямс", 2011. – 1056 с.

Приложение. Листинг программы

namespace WindowsFormsApp4

{

public partial class Form1 : Form

{

String str1 = "";

String str2 = "";

String Pr="";

String Vis = "";

public Form1()

{

InitializeComponent();

}

private void button1_Click(object sender, EventArgs e)

{

str1 = str1 + 0;

textBox1.Text = str1;

}

private void panel2_Paint(object sender, PaintEventArgs e)

{

}

private void button2_Click(object sender, EventArgs e)

{

str1 = str1 + "1";

textBox1.Text = str1;

}

private void button3_Click(object sender, EventArgs e)

{

str1 = str1 + "2";

textBox1.Text = str1;

}

private void button4_Click(object sender, EventArgs e)

{

str1 = str1 + "3";

textBox1.Text = str1;

}

private void button5_Click(object sender, EventArgs e)

{

str1 = str1 + "4";

textBox1.Text = str1;

}

private void button6_Click(object sender, EventArgs e)

{

str1 = str1 + "5";

textBox1.Text = str1;

}

private void button7_Click(object sender, EventArgs e)

{

str1 = str1 + "6";

textBox1.Text = str1;

}

private void button8_Click(object sender, EventArgs e)

{

str1 = str1 + "7";

textBox1.Text = str1;

}

private void button9_Click(object sender, EventArgs e)

{

str1 = str1 + "8";

textBox1.Text = str1;

}

private void button10_Click(object sender, EventArgs e)

{

str1 = str1 + "9";

textBox1.Text = str1;

}

private void button11_Click(object sender, EventArgs e)

{

str1 = str1 + "A";

textBox1.Text = str1;

}

private void button12_Click(object sender, EventArgs e)

{

str1 = str1 + "B";

textBox1.Text = str1;

}

private void button13_Click(object sender, EventArgs e)

{

str1 = str1 + "C";

textBox1.Text = str1;

}

private void button14_Click(object sender, EventArgs e)

{

str1 = str1 + "D";

textBox1.Text = str1;

}

private void button15_Click(object sender, EventArgs e)

{

str1 = str1 + "E";

textBox1.Text = str1;

}

private void button16_Click(object sender, EventArgs e)

{

str1 = str1 + "F";

textBox1.Text = str1;

}

private void button17_Click(object sender, EventArgs e)

{

str1 = str1 + "10";

textBox1.Text = str1;

}

private void button18_Click(object sender, EventArgs e)

{

str2 = str1;

str1 = "";

textBox1.Text = "";

Pr = "+";

}

private void button19_Click(object sender, EventArgs e)

{

str2 = str1;

str1 = "";

textBox1.Text = "";

Pr = "-";

}

private void button20_Click(object sender, EventArgs e)

{

if (str1 != "")

{

if (str2 != "")

{

if (Pr == "+")

{

Vis = Summer(str2, str1);

textBox1.Text = Vis;

}

if (Pr == "-")

{

Vis = Minuser(str2, str1);

textBox1.Text = Vis;

}

}

}

}

public string Summer(String s2, String s1)

{

int n2 = s2.Length;

int n1 = s1.Length;

int prr = 0;

String pmj = "";

if (n2>n1)

{

int m = n2 - n1;

for (int j=1;j<=m;j++)

{

s1 = 0 + s1;

}

}

if (n1 > n2)

{

int m = n1 - n2;

for (int j = 1; j <= m; j++)

{

s2 = 0 + s2;

}

}

for (int j = 1; j <= s2.Length; j++)

{

String s2j = s2[s2.Length-j].ToString();

String s1j = s1[s1.Length - j].ToString();

if (s1j == "A") { s1j = "10"; }

if (s1j == "B") { s1j = "11"; }

if (s1j == "C") { s1j = "12"; }

if (s1j == "D") { s1j = "13"; }

if (s1j == "E") { s1j = "14"; }

if (s1j == "F") { s1j = "15"; }

if (s2j == "A") { s2j = "10"; }

if (s2j == "B") { s2j = "11"; }

if (s2j == "C") { s2j = "12"; }

if (s2j == "D") { s2j = "13"; }

if (s2j == "E") { s2j = "14"; }

if (s2j == "F") { s2j = "15"; }

int s2ji = Convert.ToInt32(s2j);

int s1ji = Convert.ToInt32(s1j);

int mj = s2ji + s1ji+prr;

if (mj >= 16)

{

int pmji = mj - 16;

if (pmji == 10) { pmj = "A" + pmj; }

if (pmji == 11) { pmj = "B" + pmj; }

if (pmji == 12) { pmj = "C" + pmj; }

if (pmji == 13) { pmj = "D" + pmj; }

if (pmji == 14) { pmj = "E" + pmj; }

if (pmji == 15) { pmj = "F" + pmj; }

if (pmji < 10) { pmj = pmji.ToString() + pmj; }

prr = 1;

}

if (mj < 16)

{

int pmji = mj;

if (pmji<10) { pmj = pmji.ToString()+pmj;}

if (pmji == 10) { pmj = "A" + pmj; }

if (pmji == 11) { pmj = "B" + pmj; }

if (pmji == 12) { pmj = "C" + pmj; }

if (pmji == 13) { pmj = "D" + pmj; }

if (pmji == 14) { pmj = "E" + pmj; }

if (pmji == 15) { pmj = "F" + pmj; }

prr = 0;

}

}

if (prr>0) { pmj = prr.ToString() + pmj; }

Vis = pmj;

return Vis;

}

public string Minuser(String s2, String s1)

{

int n2 = s2.Length;

int n1 = s1.Length;

int prr = 0;

String pmj = "";

if (n2 > n1)

{

int m = n2 - n1;

for (int j = 1; j <= m; j++)

{

s1 = 0 + s1;

}

}

if (n1 > n2)

{

int m = n1 - n2;

for (int j = 1; j <= m; j++)

{

s2 = 0 + s2;

}

}

for (int j = 1; j <= s2.Length; j++)

{

String s2j = s2[s2.Length - j].ToString();

String s1j = s1[s1.Length - j].ToString();

if (s1j == "A") { s1j = "10"; }

if (s1j == "B") { s1j = "11"; }

if (s1j == "C") { s1j = "12"; }

if (s1j == "D") { s1j = "13"; }

if (s1j == "E") { s1j = "14"; }

if (s1j == "F") { s1j = "15"; }

if (s2j == "A") { s2j = "10"; }

if (s2j == "B") { s2j = "11"; }

if (s2j == "C") { s2j = "12"; }

if (s2j == "D") { s2j = "13"; }

if (s2j == "E") { s2j = "14"; }

if (s2j == "F") { s2j = "15"; }

int s2ji = Convert.ToInt32(s2j);

int s1ji = Convert.ToInt32(s1j);

int mj = s2ji - s1ji - prr;

if (mj < 0)

{

int pmji = mj + 16;

if (pmji == 10) { pmj = "A" + pmj; }

if (pmji == 11) { pmj = "B" + pmj; }

if (pmji == 12) { pmj = "C" + pmj; }

if (pmji == 13) { pmj = "D" + pmj; }

if (pmji == 14) { pmj = "E" + pmj; }

if (pmji == 15) { pmj = "F" + pmj; }

if (pmji < 10) { pmj = pmji.ToString() + pmj; }

prr = 1;

}

if (mj >=0)

{

int pmji = mj;

if (pmji < 10) { pmj = pmji.ToString() + pmj; }

if (pmji == 10) { pmj = "A" + pmj; }

if (pmji == 11) { pmj = "B" + pmj; }

if (pmji == 12) { pmj = "C" + pmj; }

if (pmji == 13) { pmj = "D" + pmj; }

if (pmji == 14) { pmj = "E" + pmj; }

if (pmji == 15) { pmj = "F" + pmj; }

prr = 0;

}

}

if (prr > 0) { pmj = "-" + pmj; }

Vis = pmj;

return Vis;

}

private void button21_Click(object sender, EventArgs e)

{

str1 = "";

str2 = "";

textBox1.Text = "";

}

}

}