Оптимизация решений по Парето

Содержание:

ВВЕДЕНИЕ

Человек ежедневно сталкивается с трудностями и проблемами, перед ним ставятся задачи, которые необходимо выполнить для продолжения нормальной или более успешной жизнедеятельности. Простые задачи обычно не требуют затраты больших усилий для поиска решений: организму нужна жидкость - выпей стакан воды, организму нужна пища – поешь. Однако даже для решения таких задач может быть несколько альтернатив решения, из которых человек будет выбирать наиболее оптимальное для себя. Разберем как пример ту же нужду в жидкости. Если для решения данной проблемы человек пришел в магазин, то число возможных вариантов для решения резко увеличивается на n- возможных. Можно взять обычной воды, сок, газированную воду, сладкую воду, йогурт и т.д. У каждого из напитка есть свои критерии, по которым человек выберет оптимальный для себя способ освежиться: цена, объем, вкус, коэффициент утоления жажды и т.д. сравнивая критерии каждого напитка человек выбирает для себя оптимальный исходя из личных предпочтений, то есть значений параметра, который, по его мнению, является ключевым, и характеристик самого себя. Так скажем если человек очень хочет пить, у него есть деньги и неважен вкус, ключевым критерием будет являться объем тары жидкости, если у него мало денег, то ключевым критерием будет являться стоимость продукта и т.д.

Так же и предприятие, оно так же является единым организмом. У него свои проблемы, свои бизнес – задачи, которые необходимо решить для продолжения нормальной или более успешной жизнедеятельности: закупка оборудования, работа с клиентами, набор работников и т.д. Только у предприятия, в отличии от человека, поиск решений подразумевает анализ огромного количества критериев различных сред. Для успешного поиска оптимальных решений предприятий были разработаны механизмы выбора оптимальных решений, одним из которых является «Оптимизация решений по Парето».

Целью данной работы является исследование метода оптимизации решений по Парето и получения навыков по его применению на примере бизнес – задач предприятия.

Объектом данного исследования являются механизмы выбора оптимальных решений.

Предметом исследования является метод оптимизации решений по Парето.

Для достижения поставленной цели необходимо решить следующие задачи:

- провести анализ выбранной сущности;

- получить знания о механизме оптимизации решений по Парето;

- получить навыки по применению исследуемого метода;

- применить полученные навыки на практике.

1. ПОНЯТИЕ МНОГОКРИТЕРИАЛЬНАЯ ОПТИМИЗАЦИЯ

Достаточно часто в реальных ситуациях качество эксплуатации исследуемого объекта или системы оценивается не единственным критерием или показателем качества, а совокупностью таких критериев, причем представляющих одинаково значимыми. Пусть уже выделено N критериев, формализующих издержки или потери применительно к указанным процессам. Такие исходно заданные критерии называют частными критериями (чтобы отличать их от критерия выбора, на основе которого затем будет найдено оптимальное решение в формате задачи многокритериальной оптимизации).

Обозначим указанные частные критерии следующим образом:

^(k)(), k = 1,2,…,N.

Здесь

• – n-мерная векторная переменная, координаты которой представляют управляемые параметры для задачи многокритериальной оптимизации в рамках анализируемого звена/звеньев цепи поставок, т.е. = (x₁, x₂, … , x_n) ;
• считается заданной система ограничений є X , причем X представляет множество допустимых значений для в формате задачи многокритериальной оптимизации;
• ^(k)() - некоторая функция n переменных (при фиксированном значении k), формализуемая в качестве одного из частных критериев ( k=1, 2, …, N);

изменением знака функции ^(k)() всегда можно свести задачу максимизации к задаче минимизации частного критерия (и наоборот).

Поэтому далее достаточно рассматривать ситуации, когда соответствующие частные критерии формулируются именно как задачи минимизации (указанное допущение не ограничивает общности, но при этом позволит стандартизировать изложение последующего материала).

Задача многокритериальной оптимизации рассматривается как задача одновременной оптимизации всех частных критериев. Требуется найти точку X, которая в некотором смысле (будет уточняться) минимизирует все эти критерии. Другими словами, рассматривается следующая оптимизационная задача:

g^(k)()min, k=,

при условии X. При этом критерии ^(k)() называют частными критериями. Их совокупность можно рассматривать как векторный критерий G()=(g⁽¹⁾(), … , g^(N)()). Он и подлежит оптимизации (по каждой отдельной или частной компоненте).

Идеальной ситуацией при решении задач многокритериальной оптимизации является случай, когда пересечение множеств оптимальных решений для всех частных критериев не является пустым. Такое множество обозначают следующим образом: .

Если указанное множество не является пустым, то принадлежащие ему альтернативы называют абсолютными решениями. В реальных ситуациях на наличие элементов в данном множестве рассчитывать не приходиться. В практике не существует решения, минимизирующего (оптимизирующего) одновременно все частные критерии. Более того, одни частные критерии могут противоречить другим. Следовательно, нужно искать компромиссное решение, наилучшее в некотором смысле. Соответствующий подход к его нахождению и понятие наилучшего решения формализуют на основе дополнительно вводимого критерия выбора (чтобы отличать его от исходно заданных при постановке задачи частных критериев). Чем большим количеством таких подходов к формализации указанных критериев выбора владеет менеджер, тем более эффективно он может адаптировать оптимальный выбор применительно к предпочтениям лица принимающего решение.

Подводя итоги можно сказать что главная цель многокритериальной оптимизации системы — предоставить в распоряжение лица, принимающего решения, данные, наиболее полно характеризующие преимущества и недостатки каждого варианта решения.

1.1. МЕТОД АНАЛИЗА ИЕРАРХИЙ

Метод Анализа Иерархий (МАИ) – математический инструмент системного подхода к решению проблем принятия решений. МАИ не предписывает лицу, принимающему решение (ЛПР), какого-либо «правильного» решения, а позволяет ему в интерактивном режиме найти такой вариант (альтернативу), который наилучшим образом согласуется с его пониманием сути проблемы и требованиями к ее решению. Этот метод разработан американским ученым Томасом Л. Саати в 1970 году, с тех пор он активно развивается и широко используется на практике. Метод анализа иерархий можно применять не только для сравнения объектов, но и для решения более сложных проблем управления, прогнозирования и др.

Основным достоинством метода анализа иерархий является высокая универсальность – метод может применяться для решения самых разнообразных задач: анализа возможных сценариев развития ситуации, распределения ресурсов, составления рейтинга клиентов, принятия кадровых решений и др.

Недостатком метода анализа иерархий является необходимость получения большого объема информации от экспертов. Метод в наибольшей мере подходит для тех случаев, когда основная часть данных основана на предпочтениях лица, принимающего решения, в процессе выбора наилучшего варианта решения из множества существующих альтернатив.

В типичной ситуации принятия решения:

• рассматриваются несколько вариантов решения,
• задан критерий, по которому определяется в какой мере то или иное решение является подходящим,
• известны условия, в которых решается проблема, и причины, влияющие на выбор того или иного решения.

Постановка задачи в процессе применения метода анализа иерархий: Пусть имеется множество альтернатив (вариантов решений):  В₁, В₂, … В_k. Каждая из альтернатив оценивается списком критериев: К₁, К₂, … К_n. Требуется определить наилучшее решение.

Этапы применения метода анализа иерархий:

1. Предварительное ранжирование критериев, в результате которого они располагаются в порядке убывания важности (значимости).

2. Попарное сравнение критериев по важности по девятибалльной шкале с составлением соответствующей матрицы (таблицы) размера (n х n). Система парных сведений приводит к результату, который может быть представлен в виде обратно симметричной матрицы. Элементом матрицы a(i,j) является интенсивность проявления элемента иерархии i относительно элемента иерархии j, оцениваемая по шкале интенсивности от 1 до 9, где оценки имеют следующий смысл:

• равная важность – 1;
• умеренное превосходство – 3;
• значительное превосходство – 5;
• сильное превосходство – 7;
• очень сильное превосходство – 9;
• в промежуточных случаях ставятся четные оценки: 2, 4, 6, 8 (например, 4 – между умеренным и значительным превосходством).

При этом при проведении попарных сравнений в основном ставятся следующие вопросы при сравнении элементов А и Б:

• какой из них важнее или имеет большее воздействие ?
• какой из них более вероятен?
• какой из них предпочтительнее ?

Затем формируется матрица. В процессе заполнения матрицы если элемент i важнее элемента j, то клетка (i, j), соответствующая строке i и столбцу j , заполняется целым числом, а клетка (j, i),  соответствующая строке j и столбцу i, заполняется обратным числом (дробью).

Заполнение таблицы проводится построчно с наиболее важного критерия. Сначала проставляют целочисленные оценки, тогда соответствующие им дробные оценки получаются из них автоматически (как обратные к целым числам). Чем важнее критерий, тем больше целочисленных оценок будет в соответствующей ему строке матрицы, и сами оценки имеют большие значения. Так как каждый критерий равен себе по важности, то главная диагональ матрицы всегда будет состоять из единиц. Очевидно, что сумма компонентов равна единице. Каждый компонент НВП представляет собой оценку важности соответствующего критерия.

3.Проводиться расчет средней геометрической в каждой строке матрицы. Расчет суммы средних геометрическийх. Расчет компонентов нормализованного вектора приоритетов(НВП).

4.Проверка согласованности локальныз приоритетов путем расчета трех характеристик:

- собственного значения матрицы;

- индекса согласования;

- отношения согласованности.

5. Проводится попарное сравнение вариантов по каждому критерию аналогично тому, как это делалось для критериев, и заполняются соответствующие таблицы. Для каждой таблицы проводится проверка согласованности локальных приоритетов путем расчета трех характеристик.

6. Определяется общий критерий (приоритет) для каждого варианта:

К(В₁) = оценка В₁ по первому критерию х 1^й компонент НВП + оценка В₁ по второму критерию х 2^й компонент НВП + … + оценка В₁ по n^му критерию х n^й компонент НВП.

Аналогично подсчитываются К(В₂), К(В₃) и т.д., при этом в выражении В₁ заменяется на В₂ , В₃ и т.д. соответственно.

7. Определяется наилучшее решение, для которого значение К максимально.

8. Проверяется достоверность решения:

8.1. расчет обобщенного индекса согласования:

ОИС = ИС₁ х 1^й компонент НВП + ИС₂ х 2^й компонент НВП + … + ИС_nх n^й компонент НВП

8.2. расчет обобщенного отношения согласованности

Решение считается достоверным, если ООС≤10-15%, в противном случае нужно корректировать матрицы сравнения вариантов по критериям.

Основные понятия метода анализа иерархий

В соответствии с формулировкой задачи принятия решения структура модели принятия решения в методе анализа иерархий представляет собой схему (граф), которая включает:

• набор альтернативных решений,
• главный критерий рейтингования решений,
• набор групп однотипных факторов, влияющих на рейтинг,
• множество направленных связей, указывающих на влияния решений, критерия и факторов друг на друга.

Структура модели отражает результат анализа ситуации принятия решения. 

Основные группы понятий метода анализа иерархий:

• Первая группа понятий связана с описанием возможных структур моделей принятия решения. Для вычисления приоритетов альтернативных решений к структуре необходимо добавить информацию о силе влияний решений, критерия и факторов друг на друга.
• Вторая группа понятий связана с описанием данных для моделей принятия решения. После того как сформирована структура и собраны все данные, модель принятия решения готова, т.е. в ней могут быть получены рейтинги приоритетов решений и факторов. Знание приоритетов используется для поддержки принятия решения.
• Третья группа понятий связана с описанием результатов, получаемых в моделях принятия решения. Четвертая группа понятий связана с пояснением того, как организованы вычисления. Знание этих понятий необходимо лишь для понимания математических обоснований метода. Для применения метода знание этих понятий необязательно.

1.2. МЕТОД КУСОЧНО-ЛИНЕЙНОЙ АППРОКСИМАЦИИ

В тех случаях, когда ЛПР четко представляет себе "что за что он готов поменять"может быть использован метод кусочно-линейной аппроксимации. Метод позволяет осуществить линейное, а не групповое упорядочивание, но требует от ЛПР очень много информации. Тем не менее, в некоторых случаях, например при управлении очередями задач операционной системой ЭВМ, при решении задач численными методами, когда значение коэффициентов при неизвестных определяет эксперт или ЛПР, при принятии решений в чрезвычайных ситуациях и в некоторых других случаях метод может оказаться полезным. Пусть множество объектов А можно разбить на какие-то подмножества: А=u Bj которые можно рассортировать Bj=u Bji.J(-j пусть, далее, в каждом классе Bj выделяется некоторый представитель bB1(-Вi(-Вj(-А причем множество В°, состоящее из всех представителей также сортируемо и выбор лица, принимающего решение на любом наборе представителей соответствует охватывающей этот набор сортировке. Доказано, что в этом случае глобальная сортировка оказывается единственной для всех систем частичных сортировок. Этот метод реализует решение задачи классификации лицом, принимающим решение о состояниях объектов по совокупности качественных и/или количественных признаков. Приведем вначале алгоритм определения структуры предпочтения ЛПР путем построения поверхностей безразличия. Введем понятие кривой безразличия. Гиперповерхность уровня функции U(xi ,...,xm ) определяется как множество точек x=(xi , xz , ..., xm), для которых функция полезности U(x)=const. Гиперповерхности уровня функции полезности называются кривыми безразличия. Термин "кривая безразличия" связан с тем, что полезность альтернатив х и у, лежащих на одной кривой, одинакова U(x)=U(y). Норма замены между i-м и j-м критериями равна числу единиц по i-ому критерию, потеря которых может быть компенсирована одной единицей по j-ому критерию.

1.3. МЕТОД ПАРЕТО

Приведем соответствующее формальное определение. Решение ^*Х называется эффективным решением или оптимальным по Парето решением, если не существует другого решения X среди анализируемых альтернатив, такого, что g^(k)() g^(k)(^*), k=, причем хотя бы для одного k имеет место строгое неравенство. Другими словами, оптимальное по Парето решение ^*Х должно обладать следующим свойством. В множестве Х допустимых альтернативных решений не найдется ни одного другого решения, переход к которому (от ^*) позволит улучшить показатель хотя бы одного из частных критериев, чтобы при этом не ухудшились бы показатели других частных критериев. Если множество абсолютных решений не является пустым, то множество оптимальных по Парето решений совпадает с множеством абсолютных решений. Убедитесь в этом самостоятельно.

Если множество альтернативных решений является дискретным, то задачу выбора оптимального решения по многим критериям удобно представлять в табличной форме. При этом каждую альтернативу достаточно характеризовать оценками частных критериев. По строкам таблицы представляют альтернативы {}. В каждом столбце такой таблицы указывают оценки по конкретному частному критерию.

Понятие оптимального по Парето решения является основополагающим в теории многокритериальной оптимизации. Несмотря на то, что разные ЛПР могут иметь и разные предпочтения (и соответственно выбирать в качестве оптимальных решений разные альтернативы), тем не менее, в формате процедур их выбора всегда будет общим следующее. Любое ЛПР всегда будет выбирать оптимальное решение именно из множества решений оптимальных по Парето.

Графическая интерпретация. Понятие решения, оптимального по Парето имеет простую интерпретацию. Для графической интерпретации рассмотрим случай, когда задано только два частных критерия (N=2): G(g⁽¹⁾(), g⁽²⁾()). Кроме того, пусть каждый из указанных частных критериев будет представлен соответствующей функцией именно двух переменных. Для удобства изложения векторную переменную будем представлять как = (x, y), а частные критерии – как функции и , определенные в некоторой области D допустимых значений переменных. Итак, имеем следующий векторный критерий: G(g⁽¹⁾(), g⁽²⁾()) = G((x, y), (x, y)). Рассматриваем задачу оптимизации двух критериев:

(x, y)min

(x, y) min

при условии (x, y)D (см. рисунок 1.1).

Для интерпретации и графического представления множества решений, оптимальных по Парето, перейдем к двумерному пространству (U, V), в котором представим все возможные значения частных критериев (в формате анализируемых альтернатив). Такое пространство называют пространством значений частных критериев. Введем обозначения: U =(x, y), V=(x, y). На плоскости (U, V) изобразим все точки (для всех допустимых решений (x, y)D), координаты которых определяются по указанным формулам для U и V. Обозначим полученное множество через (см. рис. 1.2). Для представленного на рис. 1.2 множества всех возможных значений для частных критериев видно, что наименьшее значение первого частного критерия (значение U_min) и наименьшее значения второго частного критерия (значение V_min), вообще говоря, могут достигаться в разных точках пространства (U, V) и соответственно в разных точках пространства допустимых решений (x, y)D. При этом точка с координатами (U_min, V_min) лежит в пространстве значений частных критериев вне интересующего нас множества . Другими словами, для такой ситуации множество абсолютных решений будет пустым, а поставленная задача – неразрешима. Необходимо искать компромиссное решение. При этом множество Парето представляет собой такие точки (x, y)D, которым в пространстве (U, V) соответствует граничная область множества , обладающая следующим свойством. В указанном пространстве нельзя сдвинуться на «юг», на «запад» или на «юго-запад», чтобы при этом остаться в пределах множества .

УПРАЖНЕНИЕ. Рассмотрите самостоятельно интерпретацию множества оптимальных по Парето решений для случая, когда задача многокритериальной оптимизации является задачей максимизации соответствующих функций (x, y) и (x, y), причем менеджер не намерен использовать прием по замене знака критериальной функции для приведения таких частных критериев к оговоренному выше стандартному виду. Кроме того, рассмотрите также интерпретацию множества оптимальных по Парето решений для случая, когда задача многокритериальной оптимизации является задачей максимизации одной из этих функций и задачей минимизации другой из них.

УКАЗАНИЕ. Множеству оптимальных по Парето решений (x, y)D соответствуют в области значений частных критериев (при N=2) такие граничные точки, из которых:

• в задачах минимизации обоих частных критериев нельзя сдвинуться на «юг», «запад» или «юго-запад», чтобы при этом остаться в том же множестве ;
• в задачах максимизации обоих частных критериев нельзя сдвинуться на «север», «восток» или «северо-восток», оставаясь в том же множестве ;
• в задачах минимизации первого из них и максимизации второго нельзя сдвинуться на «север», «запад» или «северо-запад», чтобы при этом остаться в том же множестве ;
• в задачах максимизации первого из них и минимизации второго нельзя сдвинуться на «юг», «восток» или «юго-восток», оставаясь в том же множестве .

Некоторые примеры, иллюстрирующие аналог множества Парето (оптимальные по Парето границы множеств) в пространстве значений частных критериев для различных представлены ниже:

• • на рис. 1.3 (а-б) они представлены применительно к задачам многокритериальной оптимизации, когда оба частных критерия минимизируются;
  • на рис. 1.4 (а-б) – применительно к задачам многокритериальной оптимизации, когда оба частных критерия максимизируются.

На указанных рисунках соответствующие множества выделены жирным шрифтом (линиями / точками). При этом белые кружочки представляют выколотые точки, которые не принадлежат множеству решений, оптимальных по Парето.

Для более полного понимания оптимизации альтернативных решений рассмотрим еще несколько методов.

Сравнение альтернатив при многих критериях

Сначала проиллюстрируем особенности, которые соотносятся с процедурами сравнения альтернатив при многих критериях, следующим простым примером.

ПРИМЕР 1

При формализации многокритериальной задачи оптимизации заданы частные критерии для повышения эффективности работы некоторого звена цепи поставок. Все частные критерии минимизируются.

Анализируется 5 альтернатив . Оценки частных критериев в формате каждой альтернативы представлены в табл. 1.3. Какое из этих решений следует выбрать ЛПР, если никакой другой дополнительной информации (например, о важности этих оценок / показателей в формате работы соответствующего звена цепи поставок) не имеется?

Табл. 1.3.

Атрибуты задачи оптимизации для примера 1

Альтернативные решения	Оценки частных критериев
X1	50	40	30	30
X2	70	30	30	30
X3	10	80	20	70
X4	40	80	20	30
X5	60	20	50	30

РЕШЕНИЕ. В частности, можно предпочесть альтернативу X₁, так как при этом решении суммарный показатель по всем частным критериям является наименьшим (он равен 150). Никакая другая альтернатива не дает такого результата (хотя в формате отдельных показателей частных критериев потери, соотносимые с X1, при других альтернативных решениях могут быть меньшими). Но можно предпочесть, например, альтернативное решение X₂ , обратив внимание на следующее. Только по одному из частных критериев (показатель критерия ) альтернатива X₂ уступает альтернативе X₁, а применительно ко всем остальным частным критериям не уступает. Более того, по критерию она даже является более предпочтительной. Можно также предпочесть, например, альтернативу X₄, заметив, например, что только по одному из частных критериев (показатель критерия ) она уступает альтернативе X₂, а применительно ко всем остальным частным критериям она не уступает ей.

Если ЛПР считает, что самым важным из всех показателей является показатель частного критерия (причем, остальными частными критериями можно пренебречь), то наилучшей будет альтернатива X₃, т.к. этому решению соответствуют наименьшие потери (они равны 10) по критерию (например, это критерий минимизации расходов на поставку товара). Можно также предпочесть и решение X₅, в частности, если ЛПР считает, что в качестве наилучшего решения необходимо выбрать альтернативу с наименьшей суммой показателей частных критериев и (например, по сумме показателей критериев минимизации расходов на поставку товара и его хранение) и т.д.

Как видим, можно реализовать много различных подходов при сравнении этих альтернатив. А какой подход к оптимизации при этих критериях предпочли бы вы в формате задач вашего бизнеса? Попробуйте ответить на этот вопрос именно сейчас, пока вы не познакомились с рекомендациями теории (чтобы затем сделать соответствующие сравнения).

Интерпретация процедур сравнения альтернатив (N=2).

Для более глубокого понимания и иллюстрации особенностей принятия решений при нескольких критериях удобно выделить случай N=2. Это случай, когда в рамках рассматриваемой оптимизационной модели формализуются два частных критерия. Для такой ситуации таблица с оценками частных критериев имеет всего два столбца. Элементы первого из них (относящегося к частному критерию ) будем обозначать через , где i – индекс соответствующего решения . Элементы второго столбца (относящегося к оценкам частного критерия ) обозначаем через . Тогда каждое альтернативное решение характеризуется вектором соответствующих потерь по критериям и соответственно.

В декартовом пространстве значений частных критериев отдельное решение представляется точкой . При этом, представляя соответствующими точками все анализируемые решения , можно говорить о так называемом поле издержек/потерь в пространстве значений частных критериев. Оно представляет собой минимальный прямоугольник, включающий все допустимые альтернативные решения (см. рис. 1.7).

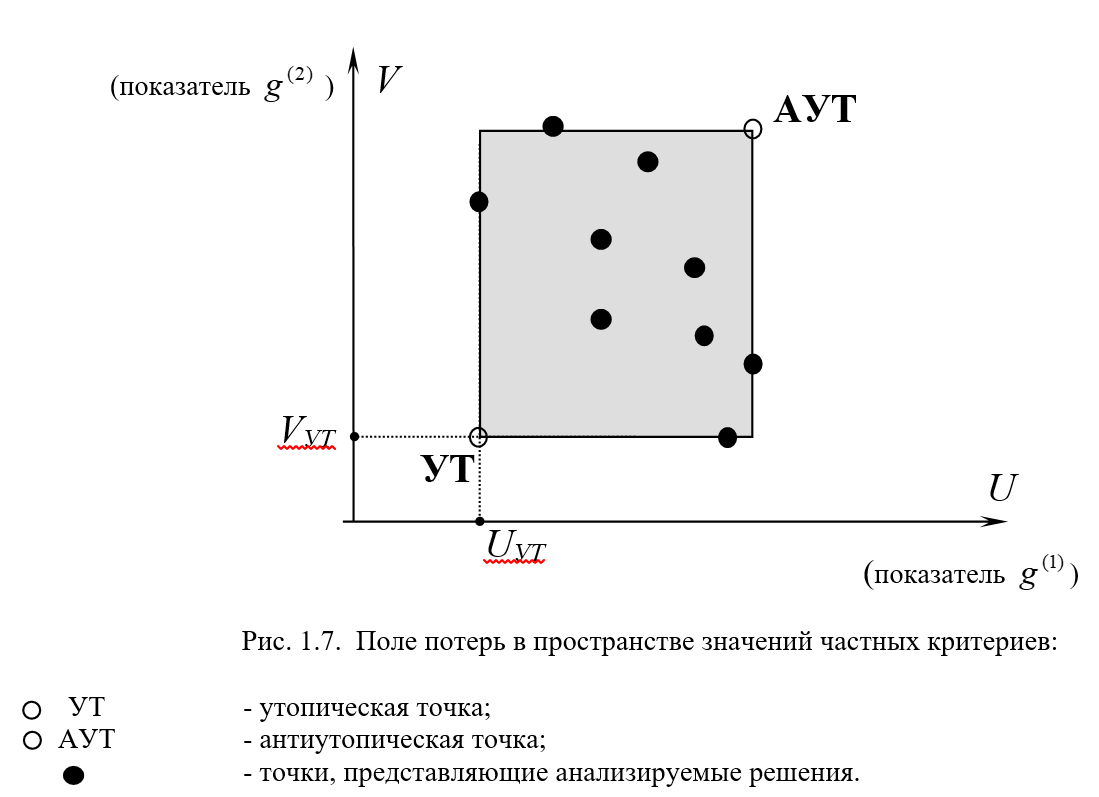
Поле издержек/потерь содержит все точки, представляющие анализируемые альтернативы . Дополнительно выделяют утопическую точку (УТ), которая соответствует условному (утопическому) решению , представленному вектором потерь с наилучшими (наименьшими) координатами: и . Название УТ обусловливается тем, что среди анализируемых решений указанного решения = УТ (как правило) не будет: иначе, не было бы проблемы выбора в формате задачи оптимизации при многих критериях. Любой участник рынка (любой менеджер или ЛПР) всегда предпочел бы указанное решение = УТ. Аналогично, говорят также и об антиутопической точке как точке с наихудшими координатами в формате поля потерь (ее обозначаем через АУТ), - см. рис. 1.7.

Выбор оптимального для ЛПР решения (из представленных в поле потерь) подразумевает, как минимум, необходимость сравнения имеющихся альтернатив. Рассмотрим особенности соответствующих процедур сравнения в пространстве значений частных критериев. Сравнивая какое-либо конкретное решение, например, решение с некоторыми другими альтернативами , возможны ситуации, которые представлены на рис. 1.8. Отметим эти ситуации.

1. Все другие альтернативные решения в поле потерь, которые отличаются от , причем такие, для которых ни одна из координат (U либо V) не является большей, чем соответственно U₀ либо V₀, образуют множество, которое называют конусом предпочтений по отношению к .
2. Кроме того, все другие отличные от альтернативные решения, для которых ни одна из координат (U либо V) не является меньшей, чем соответственно U₀ либо V₀, образуют множество альтернатив, которое называют антиконусом по отношению к .

На рис. 1.8 указанные множества заштрихованы с разным наклоном. Остальные области в соответствующем декартовом пространстве значений частных критериев называют конусами неопределенности (на рис 1.8 они отмечены как I и II). При сравнении решения с любым решением из конуса предпочтений и антиконуса никаких проблем не возникает.

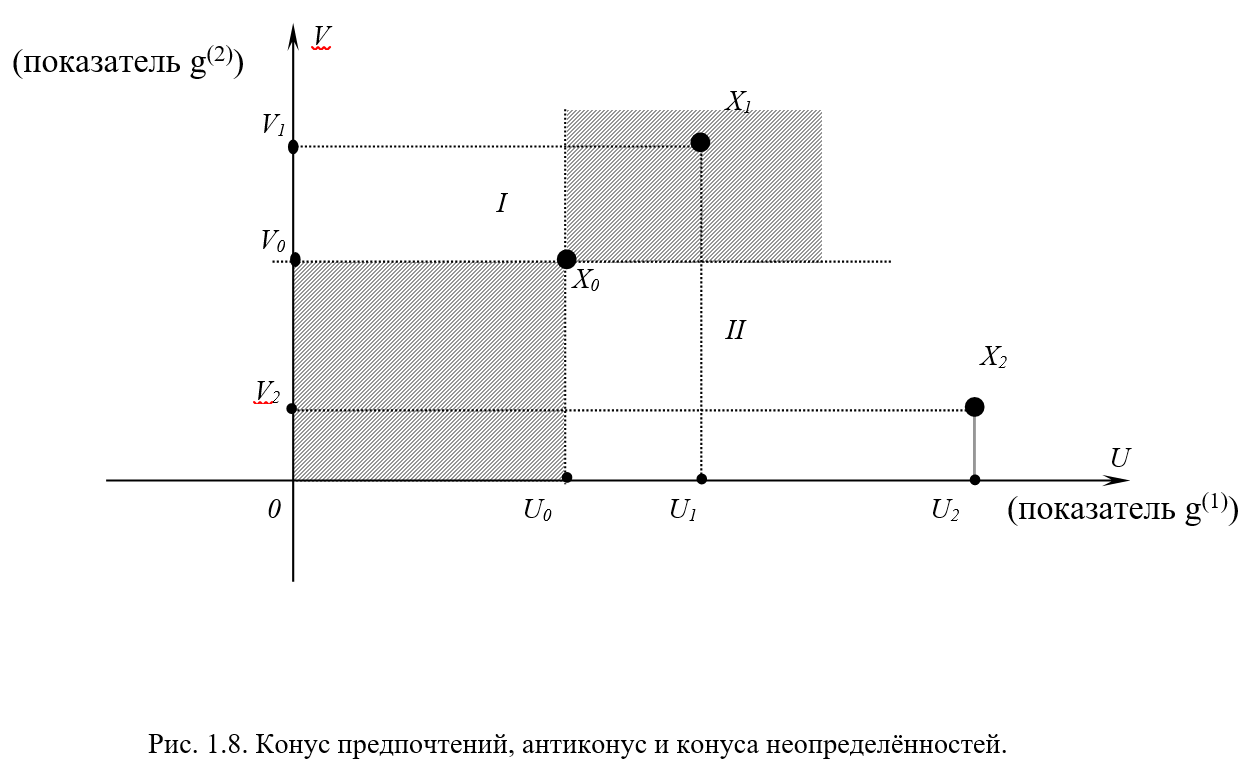
Здесь:

• - альтернативное решение из антиконуса (по отношению к );
• - альтернативное решение из конуса неопределенности (по отношению к ).

Применительно к рисунку 1.8 отметим, что решение из антиконуса (относительно ) будет для любого ЛПР худшим, чем решение , т.к. по любому из частных критериев соответствующий показатель потерь будет большим. Все решения, для которых каждая компонента соответствующего вектора потерь превосходит (или равна) аналогичную компоненту альтернативного решения , причем хотя бы по одному из частных критериев имеет место строгое неравенство, будут худшими, чем для всех ЛПР. Такие альтернативы называют доминируемыми по отношению к альтернативе и их можно заведомо отбросить при нахождении наилучшего решения.

Аналогично, для всех ЛПР любая альтернатива из конуса предпочтений будет лучше, чем , т.к. по каждому из частных критериев на рис. 1.8 потери для альтернативы из конуса предпочтений будут меньшими, чем для. Такие альтернативы из конуса предпочтений называют доминирующими по отношению к . Все решения, для которых каждая компонента вектора потерь меньше (или равна) аналогичной компоненте решения X₀, причём хотя бы для одного из частных критериев имеет место строгое неравенство, будут заведомо лучшими, чем для всех ЛПР.

Наконец, для решений из конусов неопределённости (I и II – на рис. 1.8) выбор по отношению к уже не является очевидным и не будет одинаковым / общим для всех ЛПР. Например, для решения на рис. 1.8 соответствующие потери по частному критерию будут большими, чем для решения по этому же критерию (), но зато соответствующие потери по критерию будут меньшими, чем аналогичные потери для решения . Поэтому нет однозначного ответа на вопрос о том, какая из этих альтернатив (или ) лучше. Надо учитывать предпочтения ЛПР: каждое ЛПР может ответить по-своему. Таким образом, при сравнении альтернатив по многим критериям может иметь место неопределённость (чаще всего именно так и бывает), характеризующая те особенности и затруднения, которые свойственны задачам интересующего нас типа. Каждое ЛПР реализует свои предпочтения в формате специфики соответствующей задачи многокритериальной оптимизации. Поэтому для различных ЛПР результат сравнения решения с альтернативой из конусов неопределённости (например, с альтернативой ) может оказаться различным. Менеджер должен уметь находить наилучшее решение для задач многокритериальной оптимизации систем логистики с учетом имеющихся предпочтений ЛПР. Каким образом это можно осуществить? Формальное задание соответствующих предпочтений для конкретного ЛПР можно реализовать на основе так называемого аппарата линий уровней. Далее представлены необходимые определения и пояснения, формализующие указанное понятие.

Формализация предпочтений ЛПР. Линии уровня критерия выбора.

Один из подходов для «раскрытия» неопределённостей указанного выше типа состоит в привлечении специального аппарата: линий уровня критерия выбора. С помощью указанного аппарата можно характеризовать специфику предпочтений конкретного ЛПР к показателям частных критериев в соответствующем поле издержек/потерь. Проиллюстрируем особенность такого аппарата применительно к ситуации, представленной на рис. 1.9. А именно, пусть требуется сравнить альтернативное решение с некоторой другой альтернативой (например, из области конуса неопределённости II), которая по частному критерию дает показатель , лучший, чем показатель решения (см. рис. 1.9). Другими словами, альтернатива сравнивается с некоторой альтернативой из области конуса неопределённости II, которая на рис. 1.9 будет представлена некоторой точкой, расположенной где-то на линии, параллельной оси “OU” и проходящей через точку с координатами .

Возможные ситуации, связанные с таким сравнением, охарактеризуем следующим образом.

1) С одной стороны, очевидно, следующее. В одном «крайнем» случае, когда такая альтернатива, сравниваемая с , будет представлена именно точкой (принадлежащей в этом крайнем случае конусу предпочтений по отношению к ), решение будет худшим, чем альтернатива . Подчеркнем, что такое сравнение будет иметь место для всех ЛПР (из-за дополнительных потерь величины по частному критерию при одинаковом показателе по критерию ).

2) С другой стороны, для любого ЛПР всегда найдется такая «своя» точка (см. рис. 1.9), лежащая на указанной выше линии, которая будет обладать следующим свойством. Соответствующая ей альтернатива будет для конкретного ЛПР худшей, чем альтернативное решение (за счет увеличения потерь по частному критерию ).

Если предпочтения ЛПР будут заданы корректно (отношение предпочтений будет транзитивным), то между точками и найдется единственная точка (на рис. 1.9 она выделена белым кружком), лежащая на указанной линии, для которой будет иметь место следующее. Любая другая альтернатива, представленная точкой на указанной линии, расположенной левее, чем , будет для ЛПР лучшей, чем решение . Любая другая альтернатива, представленная точкой на указанной линии, расположенной правее, чем , будет для ЛПР худшей, чем решение .

Таким образом, для любого альтернативного решения при его сравнении с альтернативой из конуса неопределённости на любой линии, параллельной оси “OU”, всегда найдётся эквивалентная альтернатива в конусе неопределённости, обладающая следующим свойством. Для данного ЛПР реализуется приемлемый “баланс” между потерей по частному критерию величины и требуемой этим ЛПР соответствующей минимально допустимой компенсации в виде выигрыша по частному критерию . Поскольку здесь в наших рассуждениях величина была произвольной, то эквивалентные по отношению к альтернативы для данного ЛПР, аналогичные , имеются при любом значении . Соединяя все такие эквивалентные между собой (и по отношению к альтернативе ) точки, получаем линию, представляющую одну из линий уровней для данного ЛПР в пространстве значений частных критериев: все точки на этой линии эквивалентны в рамках системы предпочтений этого ЛПР.

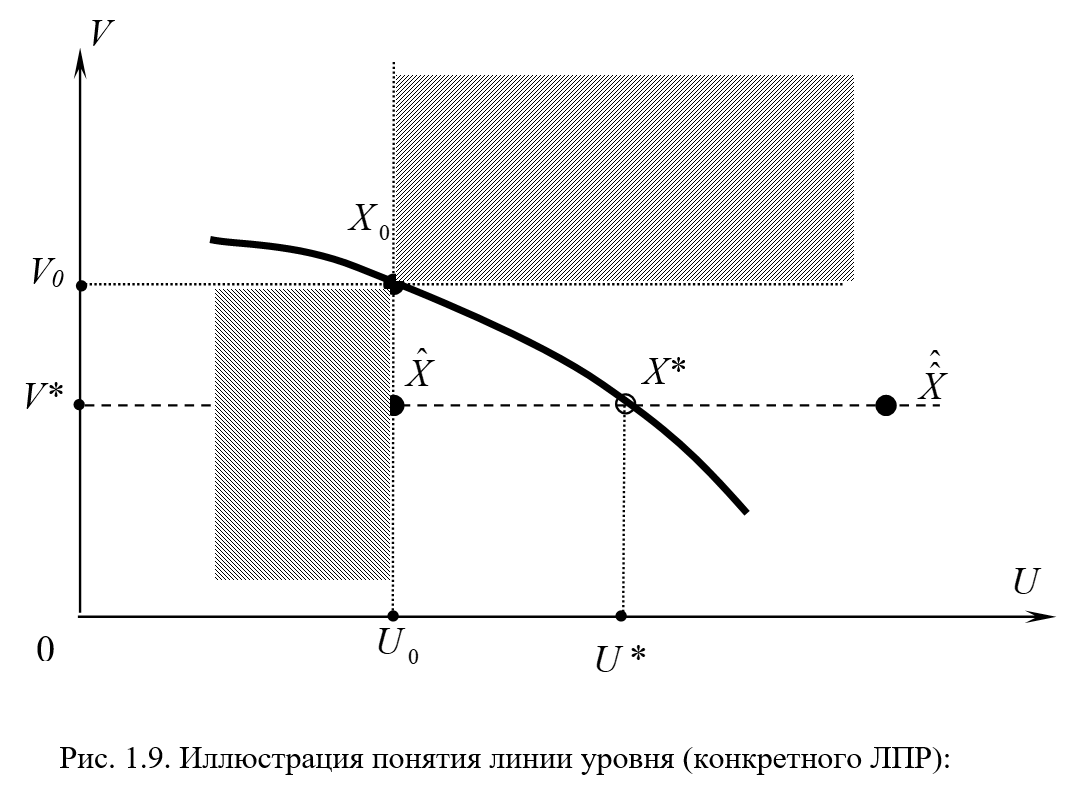
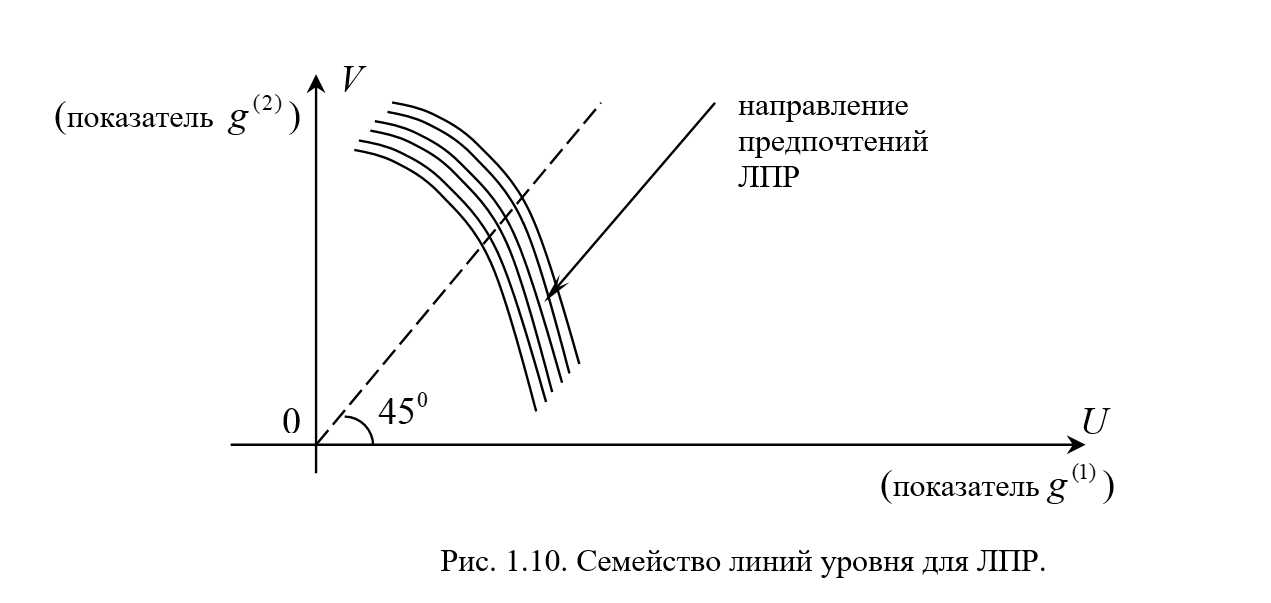
В приведённых выше рассуждениях, точка также была взята произвольно. Поэтому можно говорить о семействе линий уровня ЛПР, не привязываясь к отдельному решению (см. рис. 1.10). Все решения, лежащие на одной и той же линии (линии конкретного уровня) являются эквивалентными между собой (для ЛПР). Чем дальше от начала координат проходит линия, тем менее предпочтительные значения частных критериев она представляет: для иллюстрации сравните точки пересечения указанных линий уровня с биссектрисой первого координатного угла и дайте соответствующую интерпретацию.

На формальном уровне соответствующее семейство линий в двумерном пространстве задают на основе параметрического задания таких линий в пространстве значений частных критериев. А именно, под линией уровня K понимают линию, определяемую соотношением , где

• K – параметр, характеризующий отдельную линию семейства;
• - функция двух переменных, определённая в указанном пространстве и характеризующая отношение ЛПР к показателям частных критериев; она задается таким образом, чтобы большим значениям K соответствовали линии уровня семейства с меньшим предпочтением для данного ЛПР (напомним, что речь идет о минимизации всех частных критериев);
• - переменные, представляющие показатели частных критериев в пространстве .

Таким образом, на формальном уровне задача оптимального выбора наилучшего решения при двух критериях применительно к двумерному пространству значений частных критериев, может быть представлена как следующая задача: . В общем случае, когда модель задачи оптимизации решения при многих критериях учитывает произвольное число частных критериев , задача выбора наилучшей альтернативы представляется в следующем виде:

.

Здесь - функция m переменных, аргументами которой являются оценки частных критериев. Она задаётся так, чтобы выполнялось следующее положение. Меньшим значениям параметра «K» для “линии уровня K” (в -мерном пространстве это – соответствующие гиперплоскости), определяемой равенством , должны соответствовать более предпочтительные альтернативы (при минимизации частных критериев).

При нахождении наилучшего решения для дискретного множества альтернатив в формате заданного семейства “линий уровня” (т.е. при заданной критериальной функции ) удобно поступать следующим образом. К таблице с показателями частных критериев приписывают дополнительный столбец. Его элементы (показатели для решения ) определяются по алгоритму, задаваемому соответствующей критериальной функцией критерия выбора (учитываются показатели частных критериев по строке таблице). Элементы дополнительного столбца представляют соответствующие показатели “линий уровня” для альтернативных решений. Таким образом, по этому дополнительному столбцу далее остаётся выбрать наилучшее решение. Его укажет наименьший элемент дополнительного столбца. Разным алгоритмам (в формате критерия выбора) будут соответствовать разные семейства линий уровня. Менеджер должен знать и понимать особенности линий уровня любого критерия выбора, чтобы наилучшим образом адаптировать искомое решение к предпочтениям ЛПР. Чем большим будет арсенал соответствующих подходов к формализации критерия выбора в распоряжении менеджера, тем эффективнее будет адаптация найденного решения к предпочтениям ЛПР.

2. ПРИМЕНЕНИЕ МЕТОДА ПАРЕТО ДЛЯ ОПТИМИЗАЦИИ РЕШЕНИЙ ПРЕДПРИЯТИЯ

2.1. ЗАДАЧА ЗАКУПКИ ОБОРУДОВАНИЯ

Условие задачи.

Предприятию ООО «Солнышко» необходимо произвести закупку компьютерной техники для сотрудников. Для этого нужно выбрать фирму поставщика. Критериями выбора являются следующие параметры:

• стоимость;
• срок доставки;
• качество;
• наличие гарантии;
• страхование техники.

Построим матрицу частных критериев:

Альтернативные решения	Значения частных критериев
A	45	27	159	29	29
B	40	34	125	18	18
C	42	35	126	24	24
D	42	34	125	20	24

Где A,B,C,D – условные обозначения фирм поставщиков, g1- параметр «стоимость», g2- «срок доставки», g3- «Качество», g4- «наличие гарантии», g5- «страхование техники».

Решение. Альтернатива D доминирует альтернативу C, так как переход от альтернативы C к альтернативе D улучшит показатели частных критериев , и . Другими словами, вариант D является заведомо лучшим, чем вариант C. Так что альтернативу С выбирать нельзя в качестве наилучшей, она не является оптимальной по Парето. В свою очередь альтернатива B доминирует над альтернативой D. Так как переход от D к B улучшит показатели всех частных показателей.

Итого оптимальными альтернативами по методу Парето будут являться альтернативы A и B, так как переход от альтернативы A к альтернативе B ухудшит частный критерий , а переход от B к A ухудшит все частные критерии кроме .

Выбор между двумя данными альтернативами уже зависит от ЛПР и какие частные критерии будут ключевыми. Логичнее будет выбрать альтернативу B, так как она по всем частным критериями кроме срока доставки лучше критерия А.

2.2. ЗАДАЧА ВЫБОРА СОТРУДНИКА В IT- ОТДЕЛ РАЗРАБОТЧИКОВ.

Задача. Необходимо из кандидатов выбрать сотрудника для IT – отдела, занимающегося разработкой программного обеспечения предприятия. Критериями выбора служат:

- наличие высшего образования в области IT;

- опыт работы;

- уровень навыков программирования;

- уровень работы с SQL Server;

- знания в области IT технологий.

Ключевыми критериями являются опыт работы и уровень навыков программирования.

Альтернативные решения	Значения частных критериев
A	1	5	80	80	85
B	1	4	80	75	80
C	1	5	75	85	85
D	0	3	60	20	90

Где A,B,C,D – условные нахвания кандидатов, g1- параметр «наличие высшего образования в области IT », g2- «опыт работы», g3- «уровень навыков программирования», g4- «уровень работы с SQL Server», g5- «знания в области IT технологий».

Решение. Альтернатива A доминирует альтернативу B, так как переход от альтернативы B улучшит показатели частных критериев и не ухудшив при этом показатели других частных критериев. В связи с этим альтернативы A,C,D являются оптимальными так как нельзя улучшить показатель хотя бы одного из частных критериев, не ухудшив при этом показатель / показатели какого-нибудь из остальных частных критериев.

После нахождения оптимальных решений по Парето ЛПР необходимо из их множества выбрать наиболее подходящий. Для этого необходимо провести сравнительный анализ ключевых критериев оптимальных альтернатив:. и .

Альтернативные решения	Значения частных критериев
A	5	80
C	5	75
D	3	60

Альтернатива D не подходит, так как ее ключевые частные критерии уступают ключевым частным критериям альтернатив A и С. Сравнивая частные критерии альтернатив A и C можно увидеть что альтернатива A доминирует, так как переход от альтернативы C к альтернативе A улучшит показатель частного критерия не ухудшив показатели . Таким образом на работу необходимо взять кандидата A.

ЗАКЛЮЧЕНИЕ

При решении многокритериальных задач метод оптимизации решений по Парето является основополагающим, так как позволяет существенно уменьшить множество альтернатив решений. Далее ЛПР уже проще производить поиск единственно верного решения, используя уже только множество оптимальных решений.

В ходе данной работы было проведено исследование метода оптимизации решений по Парето, получены навыки по применению исследуемого метода. С помощью полученных навыков были решены 2 поставленные бизнес задачи.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

1. http://vamocenka.ru/metod-analiza-ierarxij-procedura-primeneniya/
2. Г.Л. Бродецкий: МЕТОДЫ ОПТИМИЗАЦИИ МНОГОКРИТЕРИАЛЬНЫХ РЕШЕНИЙ В ЛОГИСТИКЕ
3. http://e-biblio.ru/book/bib/geiti/sistemy_podderzhki_prinjatija_reshenii.pdf