Алгоритмы сортировки данных (Характеристика алгоритмов сортировки)

Содержание:

Введение

Сортировкой называют процесс перегруппировки заданного множества объектов в некотором определенном порядке. Сортировка (sorting) — распределение по сортам, деление на категории. Программисты используют более узкий термин — упорядочение (ordering), однако использование этого слова может привести к путанице из-за перегруженности слова «порядок». Ранжирование (sequencing) не всегда отражает суть дела, особенно если есть равные элементы. Часто используются все три термина с одним и тем же смыслом.

Алгоритм сортировки — это алгоритм для упорядочивания элементов в списке. В случае, когда элемент списка имеет несколько полей, поле, служащее критерием порядка, называется ключом сортировки. На практике в качестве ключа часто выступает число, а в остальных полях хранятся какие-либо данные, никак не влияющие на работу алгоритма.

Цель сортировки — облегчение последующего поиска элементов в отсортированном множестве во внутренней или внешней памяти. В последнем случае она особенно важна, если имеется только последовательный доступ к файлам (появляется возможность приемлемой замены прямого доступа). Сортировка и поиск в той или иной мере присутствуют во всех приложениях. При обработке больших объемов данных эффективность именно этих операций определяет эффективность, а иногда и работоспособность всей системы.

Объектом исследования являются направления реализации алгоритмов сортировки данных.

Предмет исследования – алгоритмы сортировки данных.

Целью исследования в работе является углубленное изучение основных алгоритмов сортировки данных.

Для достижения поставленной цели сформулированы следующие задачи:

1. изучить теоретические основы методов сортировки;
2. описать основные методы сортировки данных;
3. рассмотреть перспективы развития методов сортировки.

Методологической основой исследования являются учебная и методическая литература, статьи в периодической печати и Интернет-ресурсы.

1. Теоретические основы алгоритмов сортировки

1.1 Исторический аспект появления и развития методов сортировки

Первые прототипы современных методов сортировки появились уже в XIX веке. К 1890 году для ускорения обработки данных переписи населения в США американец Герман Холлерит создал первый статистический табулятор — электромеханическую машину, предназначенную для автоматической обработки информации, записанной на перфокартах^[1][3, с.416]. У машины Холлерита имелся специальный «сортировальный ящик» из 26 внутренних отделений. При работе с машиной от оператора требовалось вставить перфокарту и опустить рукоятку. Благодаря пробитым на перфокарте отверстиям замыкалась определенная электрическая цепь, и на единицу увеличивалось показание связанного с ней циферблата. Одновременно с этим открывалась одна из 26 крышек сортировального ящика, и в соответствующее отделение перемещалась перфокарта, после чего крышка закрывалась. Данная машина позволила обрабатывать около 50 карт в минуту, что ускорило обработку данных в 3 раза. К переписи населения 1900 года Холлерит усовершенствовал машину, автоматизировав подачу карт[3, с.417-418]. Работа сортировальной машины Холлерита основывалась на методах поразрядной сортировки. В патенте на машину обозначена сортировка «по отдельности для каждого столбца», но не определен порядок. В другой аналогичной машине, запатентованной в 1894 году Джоном Гором, упоминается сортировка со столбца десятков. Метод сортировки, начиная со столбца единиц, впервые появляется в литературе в конце 1930-х годов. К этому времени сортировальные машины уже позволяли обрабатывать до 400 карт в минуту[3, с.419].

В дальнейшем история алгоритмов оказалась связана с развитием электронно-вычислительных машин. По некоторым источникам, именно программа сортировки стала первой программой для вычислительных машин. Некоторые конструкторы ЭВМ, в частности разработчики EDVAC, называли задачу сортировки данных наиболее характерной нечисловой задачей для вычислительных машин. В 1945 году Джон фон Нейман для тестирования ряда команд для EDVAC разработал программы сортировки методом слияния. В том же году немецкий инженер Конрад Цузе разработал программу для сортировки методом простой вставки. К этому времени уже появились быстрые специализированные сортировальные машины, в сопоставлении с которыми и оценивалась эффективность разрабатываемых ЭВМ.

Первым опубликованным обсуждением сортировки с помощью вычислительных машин стала лекция Джона Мокли, прочитанная им в 1946 году. Мокли показал, что сортировка может быть полезной также и для численных расчетов, описал методы сортировки простой вставки и бинарных вставок, а также поразрядную сортировку с частичными проходами. Позже организованная им совместно с инженером Джоном Экертом[en]* компания «Eckert–Mauchly Computer Corporation» выпустила некоторые из самых ранних электронных вычислительных машин BINAC и UNIVAC. Наряду с отмеченными алгоритмами внутренней сортировки, появлялись алгоритмы внешней сортировки, развитию которых способствовал ограниченный объём памяти первых вычислительных машин. В частности, были предложены методы сбалансированной двухпутевой поразрядной сортировки и сбалансированного двухпутевого слияния[3, с.420].

К 1952 году на практике уже применялись многие методы внутренней сортировки, но теория была развита сравнительно слабо. В октябре 1952 года Даниэль Гольденберг привёл пять методов сортировки с анализом наилучшего и наихудшего случаев для каждого из них. В 1954 году Гарольд Сьюворд развил идеи Гольденберга, а также проанализировал методы внешней сортировки. Говард Демут в 1956 году рассмотрел три абстрактные модели задачи сортировки: с использованием циклической памяти, линейной памяти и памяти с произвольным доступом. Для каждой из этих задач автор предложил оптимальные или почти оптимальные методы сортировки, что помогло связать теорию с практикой[3, с.420-421]. Из-за малого числа людей, связанных с вычислительной техникой, эти доклады не появлялись в «открытой литературе». Первой большой обзорной статьёй о сортировке, появившейся в печати в 1955 году, стала работа Дж. Хоскена, в которой он описал всё имевшееся на тот момент оборудование специального назначения и методы сортировки для ЭВМ, основываясь на брошюрах фирм-изготовителей. В 1956 году Э. Френд в своей работе проанализировал математические свойства большого числа алгоритмов внутренней и внешней сортировки, предложив некоторые новые методы.

После этого было предложено множество различных алгоритмов сортировки: например, вычисление адреса в 1956 году; слияние с вставкой, обменная поразрядная сортировка, каскадное слияние и метод Шелла в 1959 году, многофазное слияние и вставки в дерево в 1960 году, осциллирующая сортировка и быстрая сортировка Хоара в 1962 году, пирамидальная сортировка Уильямса и обменная сортировка со слиянием Бэтчера в 1964 году. В конце 60-х годов произошло и интенсивное развитие теории сортировки[3, С.422]. Появившиеся позже алгоритмы во многом являлись вариациями уже известных методов. Получили распространение адаптивные методы сортировки, ориентированные на более быстрое выполнение в случаях, когда входная последовательность удовлетворяет заранее установленным критериям.

1.2 Математическая постановка задачи для сортировки данных

Пусть требуется упорядочить N элементов:  R₁,R_{2, …},R_n Каждый элемент представляет из себя запись R_j, содержащую некоторую информацию и ключ K_j, управляющий процессом сортировки. На множестве ключей определено отношение порядка «<» так, чтобы для любых трёх значений ключейa, b, cвыполнялись следующие условия[10]:

1. закон трихотомии: либоa<b, либо a>b, либо a=b;
2. закон транзитивности: если a<bи b<c, то  a<c.

Данные условия определяют математическое понятие линейного или совершенного упорядочения, а удовлетворяющие им множества поддаются сортировке большинством методов[10].

Задачей сортировки является нахождение такойперестановкизаписейp(1), p(2), …, p(n) с индексами1,2, … ,N, после которой ключи расположились бы в порядке неубывания[10]:

K_p(1)≤K_p(2)≤… ≤ K_p(n)

Сортировка называетсяустойчивой, если не меняет взаимного расположения элементов с одинаковыми ключами[10]:

p(i)<p(j)} длялюбых  K_p(i)=K_p(j) и  i<j.

Методы сортировки можно разделить на внутренние и внешние. Внутренняя сортировка используется для данных, помещающихся в оперативную память, за счёт чего является более гибкой в плане структур данных. Внешняя сортировка применяется, когда данные в оперативную память не помещаются, и ориентирована на достижение результата в условиях ограниченных ресурсов[11].

2. Характеристика алгоритмов сортировки

2.1 Алгоритм сортировки методом пузырька и прямым выбором

Одним из простейших алгоритмов сортировки является сортировка пузырьком (BubbleSort).

Название метода отражает его сущность: на каждом шаге самый «легкий» элемент поднимается до своего места («всплывает») (рис.1).

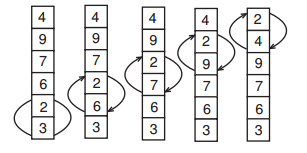
Рис.1. Нулевой проход. Сравниваемые пары и обмены выделены

Для этого мы просматриваем все элементыснизу вверх, берем пару соседних элементов и, в случае, если они стоят неправильно,меняем их местами.

Вместо поднятия самого «легкого» элемента можно «топить» самый «тяжелый».

Т.к. за каждый шаг на свое место встает ровно 1 элемент (самый «легкий» из оставшихся), то нам потребуется выполнить N шагов (рис.2).

Алгоритм не использует дополнительной памяти, т.е. все действия осуществляются на одном и том же массиве.

Сложность алгоритма сортировки пузырьком составляет О(N2), количество операций сравнения: N х (N — 1)/2. Это очень плохая сложность, но алгоритм имеет два плюса.

Во-первых, он легко реализуется, а значит, может и должен применяться в тех случаях, когда требуется однократная сортировка массива. При этом размер массива не должен быть больше 10000, т.к. иначе алгоритм сортировки пузырьком не будет укладываться в отведенное время.

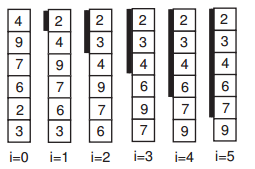
Рис.2. Номер прохода. Отсортированная часть выделена полосой

Во-вторых, сортировка пузырьком использует только сравнения и перестановки соседних элементов, а значит, может использоваться в тех задачах, где явно разрешен только такой обмен и для сортировки, например, списков.

Существуют разнообразные «оптимизации» сортировки пузырьком, которые усложняют (а нередко и увеличивают время работы алгоритма), но не приносят выгоды ни в плане сложности, ни в плане быстродействия.

На этом плюсы сортировки пузырьком заканчиваются. В дальнейшем мы еще более сузим область применения сортировки пузырьком.

Рассмотрим еще один квадратичный алгоритм, который, однако, является оптимальным по количеству присваиваний и может быть использован, когда по условию задачи необходимо явно минимизировать количество присваиваний.

Суть метода заключается в следующем: мы будем выбирать минимальный элемент в оставшейся части массива и приписывать его к уже отсортированной части. Повторив эти действия Nраз, мы получим отсортированный массив.

Количество сравнений составляет О(N²), а количество присваиваний всего О(N). В целом это плохой метод, и он должен быть использован только в случаях, когда явно необходимо минимизировать количество присваиваний.

2.2 Эффективные алгоритмы сортировки

Начнем рассмотрение эффективных алгоритмов сортировки (работающих за O(NlogN)) с пирамидальной сортировки, в которой используются знакомые нам идеи кучи.

Мы будем выбирать из кучи самый большой элемент, и записывать его в начало уже отсортированной части массива (сортировка выбором в обратном порядке). Т.е. отсортированный массив будет строиться от конца к началу. Такие ухищрения необходимы, чтобы не было необходимости в дополнительной памяти и для ускорения работы алгоритма — куча будет располагаться в начале массива, а отсортированная часть будет находиться после кучи.

Напомним свойство кучи максимумов: элементы с индексами i+ 1иi + 2не больше, чем элемент с индексом i(естественно, если i+ 1 и i+ 2 лежат в пределах кучи). Пусть n— размер кучи, тогда вторая половина массива (элементы от n/2 + 1 до n) удовлетворяют свойству кучи. Для остальных элементов вызовем функцию «проталкивания» по куче, начиная с n/2 до 0.

Эта функция получает указатель на массив, номер элемента, который необходимо протолкнуть и размер кучи. У нее есть небольшие отличия от обычных функций работы с кучей. Номер минимального предка хранится в переменнойy, если необходимость в обменах закончена, то мы выходим из цикла и записываем просеянную переменную на предназначенное ей место.

Сама сортировка будет состоять из создания кучи из массива и Nпереносов элементов с вершины кучи с последующим восстановлением свойства кучи:

Всего в процессе работы алгоритма будет выполнено 3 х N/2 — 2 вызова функции down_heap, каждый из которых занимает O(logN). Таким образом, мы и получаем искомую сложность в O(NlogN), не используя при этом дополнительной памяти. Количество присваиваний также составляет O(NlogN).

Пирамидальную сортировку следует осуществлять, если из условия задачи понятно, что единственной разрешенной операцией является «проталкивание» элемента по куче, либо в случае отсутствия дополнительной памяти.

Другим эффективным алгоритмом сортировки является метод быстрой сортировки. Мы уже рассматривали идеи, которые используются в быстрой сортировке, при поиске порядковых статистик. Точно так же, как и в том алгоритме, мы выбираем некий опорный элемент и все числа, меньшие его перемещаем в левую часть массива, а все числа большие его — в правую часть. Затем вызываем функцию сортировки для каждой из этих частей.

Таким образом, наша функция сортировки должна принимать указатель на массив и две переменные, обозначающие левую и правую границу сортируемой области.

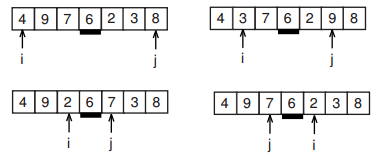
Рис. 3: Первый проход быстрой сортировки

Остановимся более подробно на выборе опорного элемента. В некоторых книгах рекомендуется выбирать случайный элемент между левой и правой границей. Хотя теоретически это красиво и правильно, но на практике следует учитывать, что функция генерации случайного числа достаточно медленная и такой метод заметно ухудшает производительность алгоритма в среднем.

Наиболее часто используется середина области, т.е. элемент с индексом (l + r)/2. При таком подходе используются быстрые операции сложения и деления на два, и в целом он работает достаточно неплохо. Однако в некоторых задачах, где сутью является исключительно сортировка, хитрое жюри специально подбирает тесты так, чтобы «завалить» стандартную быструю сортировку с выбором опорного элемента из середины. Стоит заметить, что это очень редкая ситуация, но все же стоит знать, что можно выбирать произвольный элемент с индексом m так, чтобы выполнялось неравенство l≤m≤r. Чтобы это условие выполнялось, достаточно выбрать произвольные два числа x и y и выбирать m исходя из следующего соотношения: m = (x*l + y*r)/(x + y). В целомтакой метод будет незначительно проигрывать выбору среднего элемента, т.к. требует двух дополнительных умножений.

Чтобы воспользоваться быстрой сортировкой, необходимо передать в функцию левую и правую границы сортируемого массива (т.е., например, вызов для массива a будет выглядеть как quick_sort(a, 0, n-1).

Алгоритм быстрой сортировки в среднем использует O(N log N) сравнений и O(N log N) присваиваний (на практике даже меньше) и использует O (log N) дополнительной памяти (стек для вызова рекурсивных функций). В худшем случае алгоритм имеет сложность O(N²) и использует O(N) дополнительной памяти, однако вероятность возникновения худшего случая крайне мала: на каждом шаге вероятность худшего случая равна 2/N, где N — текущее количество элементов.

Рассмотрим возможные оптимизации метода быстрой сортировки.

Во-первых, при вызове рекурсивной функции возникают накладные расходы на хранение локальных переменных (которые нам не особо нужны при рекурсивных вызовах) и другой служебной информацией. Таким образом, при замене рекурсии стеком мы получим небольшой прирост производительности и небольшое снижение требуемого объема дополнительной памяти.

Во-вторых, как мы знаем, вызов функции — достаточно накладная операция, а для небольших массивов быстрая сортировка работает не очень хорошо. Поэтому, если при вызове функции сортировки в массиве находится меньше, чем K элементов, разумно использовать какой-либо нерекурсивный метод, например, сортировку вставками или выбором. Число K при этом выбирается в районе 20, конкретные значения подбираются опытным путем. Такая модификация может дать до 15% прироста производительности.

Быструю сортировку можно использовать и для двусвязных списков (т.к. в ней осуществляется только последовательный доступ с начала и с конца), но в этом случае возникают проблемы с выбором опорного элемента — его приходится брать первым или последним в сортируемой области. Эту проблема можно решить неким набором псевдослучайных перестановок элементов списка, тогда даже если данные были подобраны специально, эффект нейтрализуется.

Сортировка слияниями также основывается на идее, которая уже была нами затронута при рассмотрении алгоритма поиска двух максимальных элементов. В этом алгоритме мы сначала разобьем элементы на пары и упорядочим их внутри пары. Затем из двух пар создадим упорядоченные четверки и т.д.

Рис.4. Алгоритм сортировки слияниями

Интерес представляет сам процесс слияния: для каждой из половинок мы устанавливаем указатели на начало, смотрим, в какой из частей элемент по указателю меньше, записываем этот элемент в новый массив и перемещаем соответствующий указатель.

Опишем функцию слияния следующим образом:

void merge(int a[], int b[], int c, int d, int e) {

int p1=c, p2=d, pres=c; while (p1 < d && p2 < e) if (a[p1] < a[p2])

b[pres++] = a[p1++]; else

b[pres++] = a[p2++]; while (p1 < d)

b[pres++]=a[p1++]; while (p2 < e)

b[pres++]=a[p2++]; }

Здесь a— исходный массив, b— массив результата, end— указатели на начало первой и второй части соответственно, е — указатель на конец второй части.

Далее опишем довольно хитрую нерекурсивную функцию сортировки слиянием:

void merge_sort(int a[], int n) {

int *temp, *a2=a, *b=(int*)malloc(n*sizeof(int)), *b2;

int c, k = 1, d, e;

b2=b;

while (k <= 2*n) {

for (c=0; c<n; c+=k*2) { d=c+k<n?c+k:n; e=c+2*k<n?c+2*k:n; merge(a2, b, c, d, e); }

temp = a2; a2 = b; b = temp; k *= 2;

}

for (c=0; c<n; c++)

a[c] = a2[c]; free(b2); }

Рекурсивная реализация сортировки слияними несколько проще, но обладает меньшей эффективностью и требует O(logN) дополнительной памяти.

Алгоритм имеет сложность O(NlogN) и требует O(N) дополнительной памяти.

В оригинале этот алгоритм был придуман для сортировки данных во внешней памяти (данные были расположены в файлах) и требует только последовательного доступа. Этот алгоритм применим для сортировки односвязных списков.

Сортировка подсчетомможет использоваться только для дискретных данных. Допустим, у нас есть числа от 0 до 99, которые нам следует отсортировать. Заведем массив размером в 100 элементов, в котором будем запоминать, сколько раз встречалось каждое число (т.е. при появлении числа будем увеличивать элемент вспомогательного массива с индексом, равным этому числу, на 1). Затем просто пройдем по всем числам от 0 до 99 и выведем каждое столько раз, сколько оно встречалось. Сортировкареализуетсяследующимобразом:

for (i=0; i<MAXV; i++)

c[i] = 0; for (i=0; i<n; i++)

c[a[i]]++; k=0; for (i=0; i<MAXV; i++)

for (j=0; j<c[i]; j++) a[k++]=i;

Здесь MAXV — максимальное значение, которое может встречаться (т.е. все числа массива должны лежать в пределах от 0 до MAXV — 1).

Алгоритм использует О (MAXV) дополнительной памяти и имеет сложность 0(N + MAXV). Его применение дает отличный результат, если MAXV намного меньше, чем количество элементов в массиве.

Алгоритм сортировки подсчетом чрезвычайно привлекателен своей высокой производительностью но она ухудшается при возрастании MAXV, также резко возрастают требования к дополнительной памяти. Фактически, невозможно осуществить сортировку подсчетом для переменных типа unsigned int (MAXV при этом равно 2³²).

В качестве развития идеи сортировки подсчетом рассмотрим поразрядную сортировку. Сначала отсортируем числа по последнему разряду (единиц). Затем повторим то жесамое для второго и последующих разрядов, полвзуюсь каким либо устойчивым алгоритмом сортировки (т.е. если числа с одинаковым значением в сортируемом разряде шли в одном порядке, то в отсортированной последовательности они будут идти в том же порядке).

Для примера приведем таблицу 1, в первом столбце которой расположены исходные данные, а в последующих — результат сортировки по разрядам.

Таблица 1

Пример для поразрядной сортировки

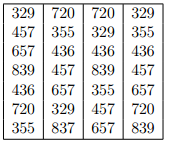
Для самой сортировки будем использовать сортировку подсчетом. После этого будем переделывать полученную таблицу так, чтобы для каждого возможного значения разряда сохранялась позиция, начиная с которой идут числа с таким значением в соответствующем разряде (т.е. сколько элементов имеют меньшее значение в этом разряде). Назовем этот массив с.

После этого будем проходить по всему исходному массиву, смотреть на текущее значение разряда (i), записывать текущее число во вспомогательный массив (b) на позицию с[i], а затем увеличивать с[i] (чтобы новое число с таким же значением текущего разряда не легло поверх уже записанного).

Пусть количество знаков в числе равно k, а количество возможных значений равно m (система счисления, использованная при записи числа). Тогда количество присваиваний, производимое алгоритмом, будет равно О(k*N + k*m), а количество дополнительной памяти — O(N + k*m).

Приведем эффективную реализацию поразрядной сортировки для беззнаковых 4-байтных чисел (unsigned int). Мы будем использовать 4 разряда, каждый из которых равен байту (система счисления с основанием 256). Эта реализация использует несколько хитростей, которые будут пояснены ниже.

voidradix_sort(unsignedinta[], intn) {

unsigned int *t, *a2=a;

unsigned int *b=(unsigned int*) malloc(n*sizeof(int));

unsigned int *b2;

unsigned char *bp;

int i, j, npos, temp;

int c[256][4];

b2 = b;

memset(c, 0, sizeof(int)*256*4);

bp = (unsigned char*) a;

For(i,n)

For (j,4) { c[*bp][j]++; bp++; } For(j,4) { npos = 0; For(i,256) { temp = c[i][j];

c[i][j] = npos; npos += temp; } } For(j,4) {

bp = (unsigned char*) a2 + j; For(i,n) {

b[c[*bp][j]++] = a2[i]; bp += 4; }

t=a2;a2=b;b=t; }

free(b2); }

Функция memset используется для заполнения заданной области памяти нулями (обнуление массива), она находится в библиотеке string.h. Всю таблицу сдвигов (с) мы будем строить заранее для всех 4 разрядов. Для эффективно доступа к отдельным байтам мы будем использовать указатель bpтипа unsigned char * (тип char как раз занимает 1 байт и может трактоваться как число). Затем мы формируем модифицированную таблицу и проводим собственно функцию расстановки чисел по всем 4 разрядам.

Внимательный читатель заметит в приведенной функции несколько мест, которые на первый взгляд кажутся ошибочными. Хотя в текстовом описании мы и говорили, что следует сортировать, начиная с последних разрядов, в реализации мы начинаем с первых байтов. Это объясняется тем, что в архитектуре x86 числа хранятся в «перевернутом» виде — это было сделано для совместимости с младшими моделями.

Второе возможное место для ошибки — массив а не ставится в соответствие указателю отсортированного массива и не осуществляется копирование отсортированных элементов в него в конце работы функции. Это связано с четным количеством разрядов, так что результат в итоге и так оказывается в массиве а.

Вообще говоря, далеко не обязательно так сильно связывать поразрядную сортировку с аппаратными средствами. Более того, основное удобство поразрядной сортировки состоит в там, что с ее помощью можно сортировать сложные структуры, такие как даты, строки (массивы) и другие структуры со многими полями.

2.3 Быстродействующие методы сортировки

Древовидными называют методы сортировки, реализацию которых можно представить в виде дерева. Узлы дерева отображают части сортируемого массива. Методом мы называем множество алгоритмов, объединенных общей идеей, различия которых второстепенны. Пред­метом исследования являются метод QuickSort (идея метода — разделение массива и незави­симое упорядочение его частей), метод слияния (идея — поэтапное объединение упорядочен­ных частей массива) и метод пирамидальной сортировки (идея — упорядоченный выбор запи­сей с помощью пирамиды). Эти три метода обладают наилучшей асимптотической оценкой времени сортировки T = O(n log2n) в классе алгоритмов, использующих сравнения ключей; n — число записей в массиве.

Большими будем называть массивы, занимающие область памяти размером D десятки мегабайт и более. Через R обозначим размер сортируемых запи­сей. Классический алгоритм QuickSort обозначен именем A. Ближайшее к Х целое, не меньшее Х, обозначается как ^┌x^┐.

Наши исследования свидетельствуют о том, что пирамидальная сортировка [4] не конкурен­тоспособна в случаях, когда D в несколько раз больше кеша самого нижнего уровня, т.е. именно при сортировке больших массивов. Это вызвано худшей локальностью, чем в методе QuickSort и методе слияния, выражающейся в большей частоте перезагрузки кешей всех уровней, поэтому среднее время доступа к данным существенно больше, чем в методе QuickSort. Чтобы изучить этот эффект, улучшенную пирамидальную сортировку сравнивали по времени с улучшенной реализацией метода QuickSort, обозначаемой ниже как алгоритм C. В табл. 2 для R = 16 и разных значений n приведено полученное экспериментально среднее время сорти­ровки, Tc в миллисекундах.

Таблица 2

Экспериментальное среднее время сорти­ровки

Время Tc работы алгоритма C хорошо аппроксимируется выражением k_cn log₂n, где k_c — коэффициент, зависящий от типа компьютера. Обозначим через g отношение T_p/T_c, где Tp — время пирамидальной сортировки. Значение g возрастает приблизительно от 1,6 до 4,5 для n = 10⁸. Это свидетельствует о том, что время T_p растет быстрее, чем число операций, котороесогласно теории определяется выражением k_pn log₂n, где k_p — коэффициент, т.е. сказываетсяувеличение удельного времени доступа к данным. Значение g и темп его изменения зависят от размера записи R и типа компьютера, точнее, от параметров иерархической структуры его памяти. В любом случае существует область больших значений n, где время T_p в несколько раз больше T_c. Это утверждение справедливо для всех разновидностей пирамидальной сортировки.

Чтобы сравнить метод слияния и метод QuickSort, рассмотрим последние результаты их оптимизации. Под оптимизацией сортировки [4] обычно понимается приближение среднего числа сравнений ключей к теоретико-информационному пределу log₂(n!). В [7] для сортировки был выведен нижний предел n + H_n – 2 среднего числа транспозиций записей — перемещений записей или обмена их местами (H_n — гармоническое число). Сокращение числа транспозицийтакже будем называть оптимизацией. Под всесторонней оптимизацией будем понимать умень­шение среднего числа как основных действий, так и массовых вспомогательных действий, для которых может быть известен теоретический минимум.

Метод QuickSort реализует разделение массива на внешне упорядоченные части (ВУЧ). Каж­дая запись может изменять положение лишь в рамках ВУЧ. Разделение можно изобразить дере­вом ВУЧ, узлы которого представляют ВУЧ, так как весь массив и каждая ВУЧ, содержащая более одной записи, разделяются на меньшие ВУЧ. В итоге, когда каждая ВУЧ содержит един­ственную запись, массив становится упорядоченным.

Исследованию и усовершенствованию метода QuickSort посвящено немало работ, остано­вимся на последних [2; 8; 12; 13]. В них по-разному реализуются две главные идеи:

а) отказ от разделения многочисленных малых ВУЧ (ведет к сильному сокращению множества вспомогательных действий);

б) улучшение формы дерева ВУЧ, выражающееся в уменьшении средней глубины листьев дерева.

Упорядочение малых ВУЧ выполняют алгоритмом вставки или иным алгоритмом. Длина внешнего пути [12] дерева ВУЧ определяет число сравнений ключей. В алгоритме, описанномв [12] и названном нами алгоритмом B, ВУЧ, как правило, разделяется на пять частей, дерево ВУЧ имеет меньшую длину внешнего пути, чем в алгоритме A, однако действия в алгоритме B сложнее, так как при разделении ВУЧ используются два опорных элемента. Средний выигрыш в числе сравнений приблизительно равен

2nlnn– (1,9nlnn – 2,46n) = 0,1nlnn + 2,46n

(для алгоритма A среднее число сравнений ключей равно 2nlnn). В [13] было показано, как этот выигрыш увеличить до значения 0,2nlnn (приблизительно). В алгоритме B среднее число транспозиций, примерно равное 0,6nlnn, существенно больше, чем в алгоритме A. Поэтому оптимизацию нельзя считать сбалансированной: уменьшение среднего числа сравнений клю­чей сопровождается ростом числа транспозиций сортируемых записей.

Алгоритм C предложен в МЭИ [2]. В нем упорядочение малых ВУЧ проводится специаль­ными алгоритмами, названными решетками, а форма дерева ВУЧ улучшается благодаря равно­мерному разделению ВУЧ, что достигается использованием в качестве опорного значения медианы пяти записей, взятых из разделяемой ВУЧ. Идея не нова, медиана трех элементов используется в известных реализациях QuickSort. Получение медианы — это дополнительные издержки времени, лишние операции. Важно их сократить и хотя бы частично совместить с операциями по разделению ВУЧ. Это было достигнуто при построении алгоритма C примени­тельно к медианам пяти элементов ВУЧ. Согласно [2] в алгоритме C среднее число K сравне­ний ключей с ростом n приближается к значению 1,62nlnn – 1,35n, т.е. по сравнению с алго­ритмом A выигрыш составляет примерно 0,38nlnn + 1,35n. Среднее число транспозиций составляет не более 0,5nlnn, и реализованы они как перемещения записей, тогда как в алго­ритме B используются более сложные операции — обмены записей местами. Поэтому время сортировки алгоритмом C при n = 10⁶ существенно меньше времени алгоритма B (рис. 5).

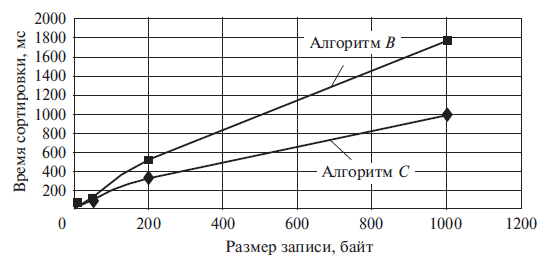
Рис.5. Сравнение времени сортировки алгоритмов В и С

Итак, по характеристикам алгоритм C лучше алгоритмов A и B. Однако достигнутые резуль­таты оптимизации метода QuickSort далеки от идеала: значение K заметно больше значения log2(n!) ≈ 1,44n (ln n – 1). Среднее число транспозиций записей относительно мало, но сущест­венно больше нижнего предела n + Hn – 2. Дальнейшее сокращение числа основных действий метода QuickSort, по-видимому, не имеет хорошей перспективы. Найдем альтернативу лучшим реализациям метода QuickSort.

Метод слияния обычно используется для сортировки файлов записей и редко применяется для сортировки массивов, так как требует значительной дополнительной памяти и выполняет больше транспозиций, чем метод QuickSort. Сильными сторонами слияния являются стабиль­ность времени сортировки и близость среднего числа сравнений к теоретическому минимуму. Так называемое t-арное слияние выполняет слияния t упорядоченных частей массива вплоть до получения единой части, т.е. упорядоченного массива. На рис. 6 для t = 3 показана схема слия­ния 30 упорядоченных частей (ими могут быть отдельные записи). На каждой фазе слияния (они обозначены штриховыми линиями) все сортируемые записи перемещаются в памяти. Число перемещений отдельно взятой записи равно числу фаз L = ┌logt(n/m)┐, где m — макси­мальное число записей в одной исходной части. При t = ┌n/m┐ каждая запись перемещается однажды. Итак, возможно рекордно малое число P перемещений записей. В дальнейшем будем исследовать процесс t-арного слияния при больших значениях t.

Сокращая числа перемещений записей P, важно сохранить указанные выше преимущества слияния. Массовая операция, во время которой сравниваются ключи, — это выбор очередной наименьшей записи из остающихся записей. Простой перебор при сравнении записей неприем­лем, он сильно снижает производительность метода при больших t. Найдем лучший вариант.

Обозначим X вычислительную сложность одной фазы слияния и выясним, каким должна быть X, чтобы получить приемлемую оценку сложности O(n log₂n) всего процесса слияния.

Выбирая эту оценку как ориентир, учитываем указанный выше теоретико-информационный предел и тот факт, что сравнения ключей являются самой массовой операцией при сортировке.

Возьмем m = 1 и запишем равенство X ┌logt n┐ = O(n log₂ n). Из него следует X = O(n log₂n/log_tn) = O(n log₂t), а сложность выбора одной записи, включая ее пересылку, получает оценку O(log₂t). Такую оценку имеет выбор среди t ключей экстремального ключа, реализуемый в простой пирамиде [4]. Асимптотическая оценка O(log₂t) скрывает коэффициент при величине log₂t, но если он будет велик, нельзя ожидать преимущества метода слияния по сравнению с методом QuickSort.

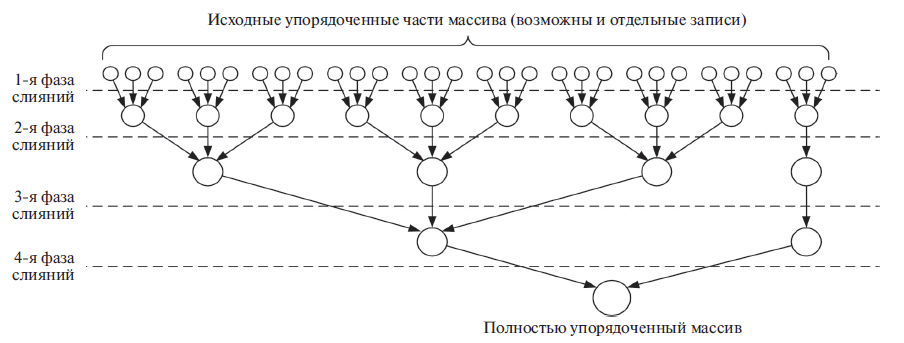
Рис.6. Реализация метода многопутевого слияния

Авторами был выполнен анализ использования (в качестве схемы выбора) простой и слабой [9] бинарных пирамид, 3-арной, 4-арной и 5-арной пирамид. Прежде всего определялся коэф­фициент k в формуле klog₂tчисла сравнений при выборе записи. Наименьшее значение k

имеет слабая пирамида, для нее k ~ 1. Поскольку в ней выполняются и пересылки, и много­численные вспомогательные операции, в целях сравнения проверялись улучшенные реализа­ции прочих пирамид. По затратам времени выбора лучшими оказались слабая пирамида и про­стая бинарная пирамида, в которой для уменьшения числа сравнений использована идея Р. Флойда [10].

Время тратится и на построение пирамид, выполняемое примерно столько же раз, сколько узлов в схеме слияния (рис. 6), исключая листья дерева. Время построения 4-арной и 5-арной пирамид наименьшее, но эти пирамиды проигрывают бинарным пирамидам по общим затра­там времени.

Таким образом, продолжена оптимизация t-арного слияния, начало которой было положено в [3]. В новых реализациях t-арного слияния помимо слабой пирамиды впервые используется схема выбора записей по принципу турнира.

Следующий шаг оптимизации — это выбор размера m исходных упорядоченных частей и способа их получения. Рассмотрим вариант, когда, неупорядоченный массив большой: пустьn = 10⁷, m=1. Если t = 100, то потребуется упорядочить на 1-й фазе слияния 10⁷/100 = 10⁵ час­тей и для этого 10⁵ раз построить схему выбора — пирамиду или турнирную схему, затратив больше времени. Для исключения такого рода фазы слияния описываемым ниже способом упо­рядочим части массива размером t(в последней части записей может быть меньше чем t). Для каждой части, сравнивая ключи, будем сортировать номера записей. Используя полученную последовательность номеров, переместим каждую запись (всего n пересылок записей, как и на исключенной фазе).

Были исследованы восемь способов упорядочения исходных частей. Алгоритмы естествен­ного и простого бинарного слияния [4] оказались наилучшими по времени сортировки исход­ных частей. Для сокращения числа машинных операций была проведена оптимизация их про­грамм. Для R = 48 среднее время сортировки одной части в условных единицах приведено в табл. 2. Оно зависит от размера записи R, но остается меньшим у алгоритмов слияния в рабо­чей области значений t. Например, для t = 1000 затрачивается примерно в 1,35 раза меньше вре­мени, если взамен первой фазы применяется простое бинарное слияние.

Заключение

Как можно было убедиться, практическая польза от описанных алгоритмов есть, со своей задачей они с переменным успехом справляются. Абсолютным лидером стал Timsort — дающий заметное ускорение при увеличении степени упорядоченности данных и работающий на уровне Quicksort в обычных случах. Не зря он признан и встроен в Python, OpenJDK и Android JDK.

Про Smoothsort в сети довольно немного информации (по сравнению с остальными алгоритмами) и не спроста: из-за сложности идеи и спорной производительности он скорее является алгоритмическим изыском, нежели применимым методом. Я нашел всего лишь одно реальное применение этого алгоритма — в библиотеке sofia-sip, предназначенной для построения IM- и VoIP-приложений.

Появление Shellsort в данном тесте является довольно спорным моментом, потому что его асимптотическая сложность несколько больше, чем у остальных двух алгоритмов. Но у него есть два больших преимущества: простота идеи и алгоритма, которая позволяет почти всегда обходить Smoothsort по скорости работы и простота реализации — работающий код занимает всего пару десятков строк, в то время как хорошие реализации Timsort и Smoothsort требуют более сотни строк.

Список использованных источников

1. Зубов В.С., Шевченко И.В. Об ускорении «быстрой сортировки» // Труды XXI международной НТК «Информационные средства и технологии». Т. 3. М.: Издательский дом МЭИ, 2013. С. 122—129.
2. Зубов В.С., Шевченко И.В. Новый алгоритм сортировки по методу многопутевого слияния //Вестник МЭИ. 2014. № 6. С. 49—56.
3. Кнут Д.Э. Искусство программирования. Т. 1. Основные алгоритмы: пер. с англ.; 3-е изд. — М.: Издательский дом «Вильямс», 2014. С. 449—451.
4. Кнут Д.Э. Искусство программирования. Т. 3. Сортировка и поиск: пер. с англ.; 2-е изд. — М.: Издательский дом «Вильямс», 2014. – 832 с.
5. Томас Х. Кормен, Чарльз И. Лейзерсон, Рональд Л. Ривест, Клиффорд Штайн. Алгоритмы: построение и анализ— 2-е изд. — М.: Вильямс, 2016. — С. 1296
6. Седжвик Р. Фундаментальные алгоритмы на C. Анализ/Структуры данных/Сортировка/Поиск— СПб.: ДиаСофтЮП, 2003. — С. 672.
7. Шевченко И.В. Композиции быстрых алгоритмов сортировки. Электронный журнал «Вычислитель­ные сети. Теория и практика» / Network-Journal. Theory and practice BC/NW. 2005. № 1 (6). http://network-journal.mpei.ac.ru/cgi-bit/main.pl?l=ru&n=6&pa=3&ar=4
8. Aumüller M., Dietzfelbinger M. Optimal Partitioning for Dual Pivot Quicksort. Automata, Languages and Programming // Lecture Notes in Computer Science. 2013. Vol. 7965. P. 33—44.
9. Dutton R.D. Weak-heap Sort // BIT. 2013. Vol. 33. P. 372—381.
10. Floyd R.W. Algorithm 245: treesort 3 // Comm. ACM. Vol. 7. No 12. P. 701.
11. Magnus Lie Hetland. Python Algorithms: Mastering Basic Algorithms in the Python Language. — Apress, 2015. — 336 с.
12. Yaroslavskiy V. Dual pivot quicksort. 2014. http://iaroslavski.narod.ru/quicksort/DualPivotQuicksort.pdf
13. Wild S., Nebel M.E. Average case analisys of Java 7’s dual pivot quicksort. Algorithms — ESA 2012 // Lecture Notes in Computer Science. 2012. Vol. 7501. P. 825—836.

1. Кнут Д. Э. Искусство программирования. Том 3. Сортировка и поиск  / под ред. Ю. В. Козаченко. — 2. — М.: Вильямс, 2007. — Т. 3. — 832 с. ↑