Методы кодирования данных (Теоретические сведения)

Содержание:

Введение

Цели и задачи данной курсовой работы – изучение способов и методов кодирования данных и разработки алгоритмов кодирования радиосигналов их источников в частности на языках программирования C\C++.

Объект исследования – радиосигналы и их кодирование.

Предметы исследования – алгоритмы распознавания и кодирования радиосигналов и их источников.

Рассмотрим для начала теоретически базовые понятия, способы и методы, работы с ними применительно к некоторым алгоритмам.

Кодирование – способ представления информации в удобном для хранения и передачи виде. В связи с развитием информационных технологий кодирование является центральным вопросом при решении самых разных задач программирования, таких как:

1.  представление данных произвольной структуры (числа, текст, графика) в памяти компьютера;

2.  обеспечение помехоустойчивости при передаче данных по каналам связи;

3.  сжатие информации в базах данных.

Далее на практике применим теоретические знания и во второй главе рассмотрим создание приложений, рассмотрим прикладные задачи.

Приступая к изучению любой предметной сферы, необходимо начать изучение с базовых понятий, архитектурных подходов и методологии разработки.

Базовыми понятиями будем считать: «сигнал», «алгоритм», «Частота», «фильтрация» и некоторые другие.

Понятно, что практически никакую программу невозможно создать без специальной теоретической подготовки, поэтому начнем с рассмотрения вышеупомянутых терминов, затем перейдем к рассмотрению алгоритмов, и затем к реализации в языках программирования на практике в том числе в С++.

Начиная изучать проблематику вопроса – начнем с простейших определений и описаний.

В данной курсовой работе рассмотрим основные виды работы через API и методы языков высокого уровня, и их применение на практике. Наша цель охватить как теоретические сведения (в первой части) о видах работы так и их применение в различных языках программирования в тех или иных алгоритмах (во второй части).

Список основных авторов -

1. Френкс Л.
2. Румянцев П. В.
3. Герберт Ш.
4. Йенсен К.
5. Вирт Н.
6. Перминов О.Н.
7. Шмидский Я.К.
8. Кормен Т.

Современная теория передачи сигналов является самостоятельной отраслью науки и учебной дисциплиной, смежной с рядом областей. К ним отно­сятся: общая теория линейных цепей и систем, теория информации, теория регулирования и управления, а также — в той мере, в которой теория сигналов затрагивает случайные процессы, теория обнаруже­ния и оценки параметров, теория статистических решений и т. п.

Математической основой теории сигналов является функциональ­ный анализ: важнейшая ее концепция опирается на понятие простран­ства сигналов, вполне соответствующее функциональному простран­ству в математической терминологии.

Часть 1. Теоретические сведения

• 1. Основные понятия теории сигналов.

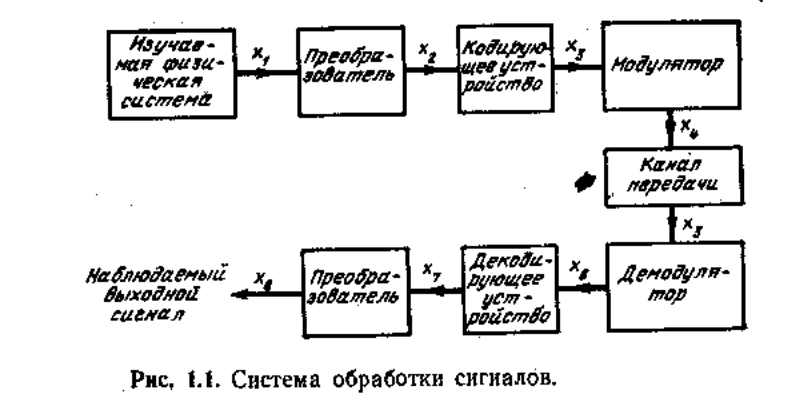
1. Обычно под сигналом понимают величину, отражающую каким-либо образом состояние физической системы. В этом смысле естест­венно рассматривать сигнал как результат некоторых измерений, проводимых над физической системой в процессе ее наблюдения. Уст­ройство обработки преобразует исходный сигнал в форму, понятную и удобную для наблюдателя. Поскольку такое устройство в целом обычно очень сложно, его для удобства расчленяют на блоки, вы­полняющие отдельные, частные преобразования. На рис. 1.1 пред­ставлена подобная модель, достаточно общая для наших целей. Изо­браженные блоки соответствуют, вообще говоря, произвольному рас­членению всего процесса на составные части; однако большинство применяемых систем обработки содержат такие блоки, хотя иногда и в упрощенном виде. Первичный преобразователь является «датчи­ком», преобразующим исходную физическую величину х₁ (механи­ческую, электрическую, оптическую, тепловую, химическую и т. д.) в другую физическую величину х_г , более удобную для дальнейшей обработки. Выбор типа «датчика» зависит в значительной степени от совершенства имеющихся технических средств. Например, при сегодняшнем уровне техники для телевидения более удобны электрон­но-оптические первичные преобразователь, чем чисто оптические.

1. Преобразовав исходные физические величины, скажем, в электри­ческие сигналы, мы можем произвести дальнейшее преобразование последних с тем, чтобы подчеркнуть наиболее важные свойства на­блюдаемой системы и ослабить, или полностью подавить, другие, не характеризующие ее состояние. Это и является в общем виде за­дачей кодирующего устройства. Назначение модуля/пора состоит в согласовании выходного сигнала х₄ со свойствами канала передачи, имеющегося при измерениях на расстоянии. Например, если исполь­зуется волноводный канал, сигналом х₃ обычно модулируют соответ­ствующее СВЧ колебание по амплитуде или по фазе. Демодулятор и декодирующее устройство служат для «расшифровки», они выпол­няют преобразования, обратные тем, которые производились на входе канала передачи. Пройдя демодулятор, декодирующее устройство и выходной преобразователь, сигнал приобретает желаемую струк­туру, удобную для наблюдателя. Читатель легко представит себе разнообразные реализации указанных блоков, если вспомнит извест­ные ему системы обработки сигналов. Примеры таких систем разно­образны--это телефония, телеметрия, локация, телеуправление, управление производственными процессами, телевидение, телегра­фия, медицинская диагностика, автоматическая классификация и рас­познавание образов, автоматическое обнаружение частиц и др. Сле­дует заметить, что показанная на рис. 1.1 система обработки может также быть блоком более сложной системы, например она может пред­ставлять собой цепь обратной связи, используемую для формирова­ния сигнала на автоматизированном заводе.
2. Мы стремились обратить внимание на большое разнообразие сиг­налов, встречающихся в различных системах. Теория сигналов долж­на быть достаточно общей, приспособленной для всех сигналов. Ис­ходя из этого, мы должны включить в нее методы аналитического представления сигналов, оценку числовых параметров сигналов и изу­чение преобразовании сигналов, осуществляемых различными уст­ройствами обработки. Применительно к этому кругу вопросов мы ис­следуем далее ряд аспектов проблемы, наиболее поддающихся мате­матической трактовке.
3. В предыдущих примерах сигналами обычно являются величины, изменяющиеся во времени. Удобно представлять сигнал как функцию времени даже в тех случаях, когда для этого приходится искусствен­но ввести временною зависимость. Оптическое изображение, напри­мер, следовало бы описать как функцию "пространственных коорди­нат. Однако методы, применяемые для рассмотрения функций вре­мени, пригодны и для функций других аргументов..
4. Рассмотрим способы представления временной функции х (t), позволяющие идентифицировать функции, различать их друг от дру­га. Хорошо знакомым и привычным способом является графическое изображение функции. График — это совокупность упорядоченных пар значений {t, х (t), взятых достаточно плотно и представленных в прямоугольной системе координат (рис. 1.2).

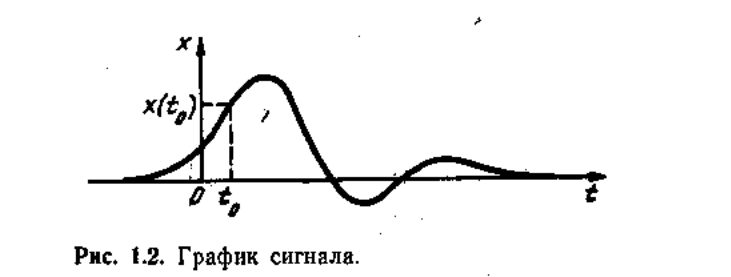
1. Заметим, что издавна существует двусмысленность в трактовке символа х(t). Строго говоря, х (t) — это просто величина, равная значению функции в момент времени t. Однако обычно мы обозна­чаем через х (t) также саму функцию, т. е. правило, по которому каж­дому значению / ставится в соответствие величина х.
2. Люди привыкли к графическому представлению сигналов и соз­дали для такого их изображения разнообразные осциллографические приборы. Имея достаточный навык, человек может успешно извлекать информацию из радиолокационной картинки, сейсмограммы, кардиограммы и т. д. Но способ анализа сигналов человеком — это область, достаточно «таинственная», не алгоритмизируемся не подда­ющаяся ни количественному анализу, ни автоматизации. Для проек­тировщика автоматической системы обработки графическое пред­ставление сигнала непригодно просто потому, что оно состоит из слиш­ком большого числа точек. Представление же сигнала в виде отдель­ных точек графика, т. е. набора значений х в равноотстоящие моменты времени — это лишь одни из простых способов представления сигналов.

1.2. Описание и классификация по признакам объектов и источников

Классификация сигналов

Рис. 1.3 Классификация сигналов

Классификация сигналов осуществляется на основании существенных признаков соответствующих математических моделей сигналов. Все сигналы разделяют на две крупных группы: детерминированные и случайные (рис. 1.1.4).

Классификация детерминированных сигналов. Обычно выделяют два класса детерминированных сигналов: периодические и непериодические.

К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... - любое целое число, Т - период, являющийся конечным отрезком независимой переменной.

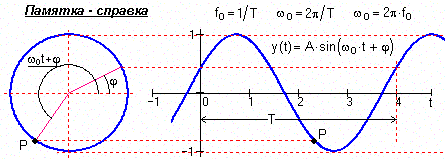
Гармонические сигналы (или синусоидальные), описываются следующими формулами:

s(t) = A sin (2pf_оt+f ) = A sin (w_оt+f ),

s(t) = A cos(w_оt+j),

где А, f_o, w_o, j, f - постоянные величины, которые могут исполнять роль информационных параметров сигнала: А - амплитуда сигнала, f_о - циклическая частота в герцах, w_о = 2pf_о - угловая частота в радианах, j и f - начальные фазовые углы в радианах. Период одного колебания T = 1/f_о = 2p/w_o. При j = f -p /2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты f_о (при t = 0).

Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:

s(t) =A_n sin (2pf_nt+j_n), (1.1.2)

или непосредственно функцией s(t) = y(t ± kT_p), k = 1,2,3,..., где Т_р - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение f_p =1/T_p называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (f_о=0) и произвольного (в пределе - бесконечного) числа гармонических составляющих с произвольными значениями амплитуд A_n и фаз j _n, с периодами, кратными периоду фундаментальной частоты f_p. Другими словами, на периоде фундаментальной частоты f_p, которая равна или кратно меньше минимальной частоты гармоник, укладывается кратное число периодов всех гармоник, что и создает периодичность повторения сигнала. Частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).

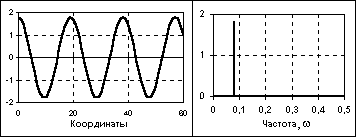
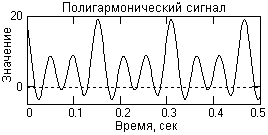
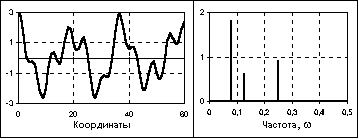
В качестве примера на рис. 1.1.6 приведен отрезок периодической сигнальной функции, которая получена суммированием постоянной составляющей (частота постоянной составляющей равна 0) и трех гармонических колебаний с разными значениями частоты и начальной фазы колебаний. Математическое описание сигнала задается формулой:

s(t) =A_k cos(2 p f_k t+j_k),

где: A_k = {5, 3, 4, 7} - амплитуда гармоник; f_k = {0, 40, 80, 120} - частота в герцах; j_k = {0, -0.4, -0.6, -0.8} - начальный фазовый угол колебаний в радианах; k = 0, 1, 2, 3.

Фундаментальная частота сигнала 40 Гц.

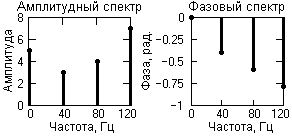Частотное представление данного сигнала (спектр сигнала) приведено на рис. 1.7. Обратим внимание, что частотное представление периодического сигнала s(t), ограниченного по числу гармоник спектра, составляет всего восемь отсчетов и весьма компактно по сравнению с временным представлением.

Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратными фундаментальной частоте колебаний f_р = 1/Т_р. Для этого достаточно разложить один период сигнала в ряд Фурье по тригонометрическим функциям синуса и косинуса с шагом по частоте, равным фундаментальной частоте колебаний Df = f_p:

s(t) = 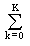(a_k cos 2pkDft + b_k sin 2pkDft),

a_o = (1/T)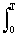s(t) dt, a_k = (2/T)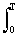s(t) cos 2pkDft dt,

b_k = (2/T)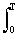s(t) sin 2pkDft dt.

Количество членов ряда Фурье K = k_max обычно ограничивается максимальными частотами f_max гармонических составляющих в сигналах так, чтобы f_max < K·f_p. Однако для сигналов с разрывами и скачками имеет место f_max ® Ґ , при этом количество членов ряда ограничивается по допустимой погрешности аппроксимации функции s(t).

Одночастотные косинусные и синусные гармоники можно объединить и представить разложение в более компактной форме:

s(t) = 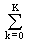S_k cos (2pkDft-j_k),

S_k =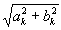, j_k = argtg (b_k/a_k).

Рис. 1.8. Прямоугольный периодический сигнал (меандр).

Пример представления прямоугольного периодического сигнала (меандра) в виде амплитудного ряда Фурье в частотной области приведен на рис. 1.1.8. Сигнал четный относительно t=0, не имеет синусных гармоник, все значения j_k для данной модели сигнала равны нулю.

Информационными параметрами полигармонического сигнала могут быть как определенные особенности формы сигнала (размах от минимума до максимума, экстремальное отклонение от среднего значения, и т.п.), так и параметры определенных гармоник в этом сигнале. Так, например, для прямоугольных импульсов информационными параметрами могут быть период повторения импульсов, длительность импульсов, скважность импульсов (отношение периода к длительности). При анализе сложных периодических сигналов информационными параметрами могут также быть:

- Текущее среднее значение за определенное время, например, за время периода:

(1/Т)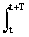s(t) dt.

- Постоянная составляющая одного периода:

(1/Т)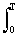s(t) dt.

- Среднее выпрямленное значение:

(1/Т)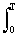|s(t)| dt.

- Среднее квадратичное значение:

.

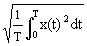К непериодическим сигналам относят почти периодические и апериодические сигналы. Основным инструментом их анализа также является частотное представление.

Почти периодические сигналы близки по своей форме к полигармоническим.

Они также представляют собой сумму двух и более гармонических сигналов (в пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Так, например, сумма двух гармоник с частотами 2f_o и 3.5f_o дает периодический сигнал (2/3.5 – рациональное число) с фундаментальной частотой 0.5f_o, на одном периоде которой будут укладываться 4 периода первой гармоники и 7 периодов второй. Но если значение частоты второй гармоники заменить близким значением 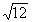f_o, то сигнал перейдет в разряд непериодических, поскольку отношение 2/ 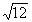не относится к числу рациональных чисел. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.

Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рис. 1.10 показан пример апериодического сигнала, заданного формулой на интервале (0, Ґ ):

s(t) = exp(-aЧ t) - exp(-bЧ t),

где a и b – константы, в данном случае a = 0.15, b = 0.17.

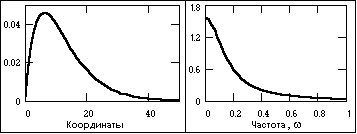
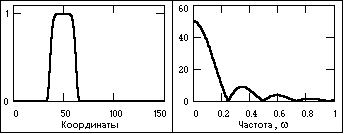
Рис. 1.10. Апериодический сигнал и модуль спектра.

Рис. 1.11. Импульсный сигнал и модуль спектра.

К апериодическим сигналам относятся также импульсные сигналы, которые в радиотехнике и в отраслях, широко ее использующих, часто рассматривают в виде отдельного класса сигналов. Импульсы представляют собой сигналы, как правило, определенной и достаточно простой формы, существующие в пределах конечных временных интервалов. Сигнал, приведенный на рис. 1.11, относится к числу импульсных.

Частотный спектр апериодических сигналов непрерывен и может содержать любые гармоники в частотном интервале [0, ].

Частотные функции a(f), b(f) и S(f) представляют собой не амплитудные значения соответствующих гармоник на определенных частотах, а распределения спектральной плотности амплитуд этих гармоник по частотной шкале.

Если нас не интересует поведение сигнала за пределами области его задания [0, Т], то эта область может восприниматься, как один период периодического сигнала, т.е. значение Т принимается за фундаментальную частоту периодический колебаний, при этом для частотной модели сигнала может применяться разложение в ряды Фурье по области его задания.

В классе импульсных сигналов выделяют подкласс радиоимпульсов. Пример радиоимпульса приведен на рис. 1.12.

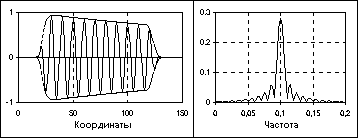Уравнение радиоимпульса имеет вид:

s(t) = u(t) cos(2pf_ot+j_o).

где cos(2pf_ot+j_o) – гармоническое колебание заполнения радиоимпульса, u(t) – огибающая радиоимпульса. Положение главного пика спектра радиоимпульса на частотной шкале соответствует частоте заполнения f_o, а его ширина определяется длительностью радиоимпульса. Чем больше длительность радиоимпульса, тем меньше ширина главного частотного пика.

С энергетических позиций сигналы разделяют на два класса: с ограниченной (конечной) энергией и с бесконечной энергией.

Для сигналов с ограниченной энергией (иначе – сигналов с интегрируемым квадратом) должно выполняться соотношение:

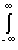|s(t)|²dt < ∞.

Как правило, к этому классу сигналов относятся апериодические и импульсные сигналы, не имеющие разрывов 2-го рода при ограниченном количестве разрывов 1-го рода. Любые периодические, полигармонические и почти периодические сигналы, а также сигналы с разрывами и особыми точками 2-го рода, уходящими в бесконечность, относятся к сигналам с бесконечной энергией. Для их анализа применяются специальные методы.

Иногда в отдельный класс выделяют сигналы конечной длительности, отличные от нуля только на ограниченном интервале аргументов (независимых переменных). Такие сигналы обычно называют финитными.

Классификация случайных сигналов. Случайным сигналом называют функцию времени, значения которой заранее неизвестны, и могут быть предсказаны лишь с некоторой вероятностью. Случайный сигнал отображает случайное физическое явление или физический процесс, причем зарегистрированный в единичном наблюдении сигнал не воспроизводится при повторных наблюдениях и не может быть описан явной математической зависимостью. При регистрации случайного сигнала реализуется только один из возможных вариантов (исходов) случайного процесса, а достаточно полное и точное описание процесса в целом можно произвести только после многократного повторения наблюдений и вычисления определенных статистических характеристик ансамбля реализаций сигнала. В качестве основных статистических характеристик случайных сигналов принимают:

а) закон распределения вероятности нахождения величины сигнала в определенном интервале значений;

б) спектральное распределение мощности сигнала.

Случайные сигналы подразделяют на стационарные и нестационарные. Случайные стационарные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса. Что касается случайных нестационарных сигналов, то их общепринятой классификации не существует. Как правило, из них выделяют различные группы сигналов по особенностям их нестационарности.

Алгоритмы распознавания

Алгоритм распознавания модуляции с использованием вейвлет - преобразования

Предлагается алгоритм распознавания модуляции в условиях присутствия белого шума с использованием вейвлет - преобразования и пика нормализованной гистограммы. Данный алгоритм позволяет определять ФМ-2, ФМ-4, ФМ-8, ФМ-16, КАМ-2, КАМ-4, КАМ-8, КАМ-16, ММС и ЧМ.

Математическая модель

Пусть принятый сигнал r(t), 0≤t≤T описывается уравнением

r(t)=s(t)+n(t) (1)

где s(t) – переданный сигнал, n(t)- аддитивный гауссовский белый шум. Сигнал s(t) может быть представлен в комплексной форме как

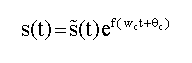(2)

где ω_с – несущая частота, а Ө_с– фаза несущей частоты. В общем виде комплексная огибающая s(t) в уравнении 1 может быть выражена для всех видов модуляции как

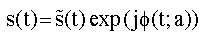(3)

где φ(t;a) представляет изменяющуюся во времени фазу несущей частоты, а – все возможные значения информационной последовательности {a_k}. В случае двоичных символов a_k =+/-1.

Для анализа нестационарного сигнала необходимо применение методов, позволяющих рассматривать частотные параметры на периоде времени. Использование преобразования Фурье позволяет рассматривать или частотные, или временные параметры. Вейвлет -преобразование позволяет провести многомасштабный анализ (multi-resolution analysis, MRA), рассматривая как частотные, так и временные составляющие. Вейвлет -преобразование уравнения (3) описывается уравнением

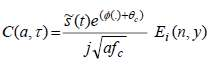(4)

Где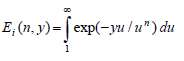

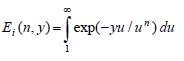- экспоненциальный интеграл, у=-jt(2πf-2πfc) и выражение (4) не сокращается до упрощенной формы и должно рассчитываться в численной величине по абсолютному значению |C(a,τ)|.

Распознавание классов сигналов

Для распознавания сигналов класса I (М-мерная ФМ и М-мерная КАМ) с сигналами класса II (ММС и М-мерная ЧМ) используется пик нормализованной гистограммы коэффициентов вейвлет -преобразования. Если ni – количество появления конкретной величины, тогда

нормализованная гистограмма (вероятность появления) процесса описывается уравнением.

Где n – общее количество появлений в частном процессе. Сигналы класса I имеют постоянные переходные характеристики и единичный пик нормализованной гистограммы. А сигналы класса II имеют многочастотные компоненты и, соответственно, множественные пики в нормализованной гистограмме. Основываясь на пиках гистограммы можно отнести тип модуляции к классу I или II.

Распознавание различных типов модуляции может быть сформулировано с использованием статистических параметров, таких как моменты и средние. Моменты статистики высшего порядка имеют основное значение в нестационарных сигналах. Таким образом, они могут быть использоваться как критерий классификации данных сигналов. Момент n-ого порядка для р(хi), где i=0,1,2…N-1 описывается уравнением

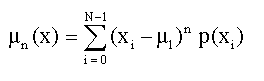(6)

Где:

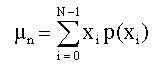- среднее статистического процесса. Момент второго порядка (дисперсия) дискретного вейвлет - преобразования может быть рассчитан по формуле:

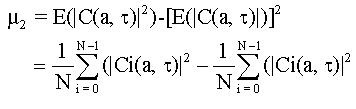(7)

Где N – длина анализируемого оцифрованного сигнала. Тогда задача распознавания может быть сформулирована как задача бинарного дерева испытания гипотез.

Пусть Нj будет i-й тип модуляции, отнесенный к принятому сигналу, где i относится к множеству {М-мерная ФМ,j}, а j относится к М-ной КАМ. Для статистического решения требуется функция распределения плотности вероятности тестовой статистики, обусловленной соответствующим сигналом с цифровой модуляцией. Принимая шум в уравнении (1) аддитивным белым гауссовским шумом, коэффициенты вейвлет -преобразования C(a,τ) носят характер случайных переменных, полученных линейной комбинацией синусоидального сигнала и гауссовского шума с гауссовской функцией плотности вероятности. Две условные гауссовские функции плотности вероятности позволяют установить пороговое значение принятия решения об отнесении модуляции к ФМ или КАМ при заданной вероятности ложного распознавания. Условная функция плотности вероятности описывается уравнением

Если гипотеза HM-PSK верна, вероятность ошибочного определения

ФМ является вероятностью того, что μ1, M-PSK - х> μ1, M-PSK – Т1, т.е. μ1 <Т1.

Вероятность ошибочного определения ФМ описывается уравнением

Где ercf(x) описывается, как

Таким же образом, если принято, что гипотеза HM-QAM верна,

вероятность ошибочного определения КАМ является вероятностью того, что х-μ1, M-PSK>Т1 - μ2, M-PSK, т.е. μ1>Т1. Вероятность ошибочного определения КАМ описывается уравнением

Где ercf(f) описывается той же формулой. Очевидно, что при увеличении гауссовского шума снижается значение среднего для ФМ и КАМ до точки, где вероятность ошибочного определения этих модуляций выравниваются. Таким образом, Р(е/ HM-PSK)= Р(е/ HM-QAM)=0.01 и условие для оптимального значения порога Т1 может быть получено приравниванием Гауссовского распределения к нулю. Тогда соответствующее значение порога получается равным

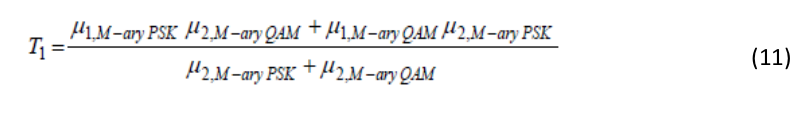
Основываясь на значении среднего может быть осуществлено

различение ФМ и КАМ.

Основные методики разработки алгоритмов

Высокоуровневые языки программирования очень похожи на естественные языки, так как они используют некоторые слова из них, а также общепринятые математические символы. Такие языки удобны для человека, с их помощью можно писать достаточно объёмные и масштабные программы. Однако без структурирования кода такие программы становились слишком нечитаемыми и мало управляемыми по сравнению с короткими программами. Эта проблема была решена вместе с изобретением языков структурного программирования, таких как Алгол (1958), Паскаль (1970), Си (1972).

Методология разработки ПО, основанная на предложенной в 1970-х годах Э. Дейкстрой представлении программы в виде иерархической структуры блоков, называется структурным программированием.

Опираясь на данную методологию, можно говорить о строении программы без участия оператора goto. Такого рода строение происходит из трех базовых структур: цикла, последовательности и ветвления. Помимо этого не стоит забывать об использовании подпрограмм: программа разбивается на более мелкие подпрограммы, и каждой из которых выполняется только одно действие, в соответствии с исходным заданием. Путем комбинирования различных подпрограмм, формируется итоговый алгоритм, состоящий из полностью завершенных блоков кода. Данные блоки имеют смысловую нагрузку, и обращаться к ним можно по названиям.

Структурное программирование - парадигма программирования, в которой предполагается наличие точно обозначенных управляющих структур, программных блоков и автономных подпрограмм. Суть такого подхода заключается в возможности разбиения программы на составляющие элементы.

– программирование «сверху вниз»;

– программирование «снизу вверх».

Программирование «сверху вниз», или нисходящее программирование - метод написания программ, в котором первым делом определяются цели решения проблемы, далее разрабатывается последовательная детализация, после чего создаётся детальная программа.

Сперва определяется несколько подпрограмм, служащих для решения глобальных задач (например, инициализация данных, главная часть и завершение), после чего каждый созданный модуль разделяется на несколько более детальных подпрограмм более низкого уровня, которые вновь делятся до тех пор, пока задача не будет выполнена полностью.

В представленном случае программа строится иерархически - сверху вниз: от основной/главной программы к подпрограммам нижнего уровня, важно заметить, что каждый уровень состоит из простых последовательностей инструкций, циклов и условных разветвлений.

Такой подход удобен тем, что позволяет человеку постоянно мыслить на предметном уровне, не опускаясь до конкретных операторов и переменных. Кроме того, появляется возможность некоторые подпрограммы не реализовывать сразу, а временно откладывать, пока не будут закончены другие части. Например, если имеется необходимость вычисления сложной математической функции, то выделяется отдельная подпрограмма такого вычисления, но реализуется она временно одним оператором, который просто присваивает заранее выбранное значение (например, 5). Когда все приложение будет написано и отлажено, тогда можно приступить к реализации этой функции.

Программирование «снизу вверх», или восходящее программирование – это методика разработки программ, начинающаяся с разработки подпрограмм (процедур, функций), в то время когда проработка общей схемы не закончилась.

Такая методика является менее предпочтительной по сравнению с нисходящим программированием так как часто приводит к нежелательным результатам, переделкам и увеличению времени разработки.

Достоинства структурного программирования:

– повышается надежность программ (благодаря хорошему структурированию при проектировании, программа легко поддается тестированию и не создает проблем при отладке);

– повышается эффективность программ (структурирование программы позволяет легко находить и корректировать ошибки, а отдельные подпрограммы можно переделывать (модифицировать) независимо от других);

– уменьшается время и стоимость программной разработки;

– улучшается читабельность программ.

Также создавались функциональные (аппликативные) языки (Пример: Lisp -- англ. LISt Processing, 1958) и логические языки (пример Prolog англ. Programming in LOGic, 1972).

Часть 2. Практическая часть

2.1. Алгоритмические части выбранных примеров

Ниже будут рассмотрены примеры реализации некоторых примеров программ.

Пока кратко опишем их алгоритмы:

Реализован класс генерации синусоидального сигнала заданной частоты и начальной фазы (амплитуды для простоты взяты за единицу), с добавлением белого Гауссовского шума с мат ожиданием равным нулю и единичным СКО.

Класс rnd_test:

Данные:

Целые:

testtime – число дискрет сигнала (порядка сотен тысяч миллионов, по умолчанию равно 1 млн).

colon_count – число столбцов гистограммы для отображения.

colors – цвет гистограммы,

*colons – агрегированные данные в вариационном ряду.

Вещественные:

*data – данные сигнала

mat – мат ожидание

disp – дисперсия

СКО – среднеквадратичное отклонение

timer – таймер затраченного на расчет времени

excess – коэффициент ексцесса,

assimetry – коэффициент ассиметрии,

freq – заданная частота сигнала,

phi – заданная начальная фаза сигнала.

Методы:

Приватные:

static double rnd_test::rnd(); - генератор случайныех чисел равномерного распределения на участве 0..1

static void rnd_test::srnd(int seed); - инициализатор генераторов случайных чисел

static double rnd_test::eyler(); - гернератор случайных чисел по распределению Эйлера

static double rnd_test::next_gauss(); - генератор Гауссовского распределения с парпаметрами (0,1)

static double rnd_test::uniform(double a,double b); - равномерное распределение от а до б.

static double rnd_test::normal(double m, double s); - гауссово распределение с параметрами (m,s)

static double rnd_test::erlang(double m, double s); - генератор потока Эрланга

static double rnd_test::erl();

void rnd_test::distrib_run(); - запуск теста, генерация данных , подсчет основных характеристик сигнала.

int rnd_test::getmax(int *data,int size); - получение минимума и максимума в сигнале

int rnd_test::getmin(int *data,int size);

double rnd_test::signal_func(double x); - функция сигнала (синусоида + гауссов шум).

Публичные методы:

rnd_test(void); - конструктор объекта по умолчанию

rnd_test(int test,int colons, int color, double fr, double ph); - конструктор объекта с параметрами, число дискрет сигнала, число столбцов гистограммы, цвет, частота, фаза.

~rnd_test(void); - деструктор объекта.

void rnd_test::draw(HWND hWnd); - отрисовка распределений, и его характеристик на окне , использован стандартный WIN API.

2.2. Оценка сложности алгоритма

Сложность всех алгоритмов генерации и подсчета характеристик - О(), n – число дискретных значений сигнала.

2.3. Руководство пользователя

Все разработанные программы просты в использовании и не требуют от пользователя особых усилий, данные либо считываются из файла, либо генерируются случайно автоматически. Программы написаны на языке программирования на С++ в среде разработки Microsoft Visual Studio.

Исполняемый файл - random_obj.exe. Исходный код - random_obj.срр и rnd_test.cpp.

При запуске программа автоматически по заданным параметрам генерирует сигнал, отображает первые 50 его значений,

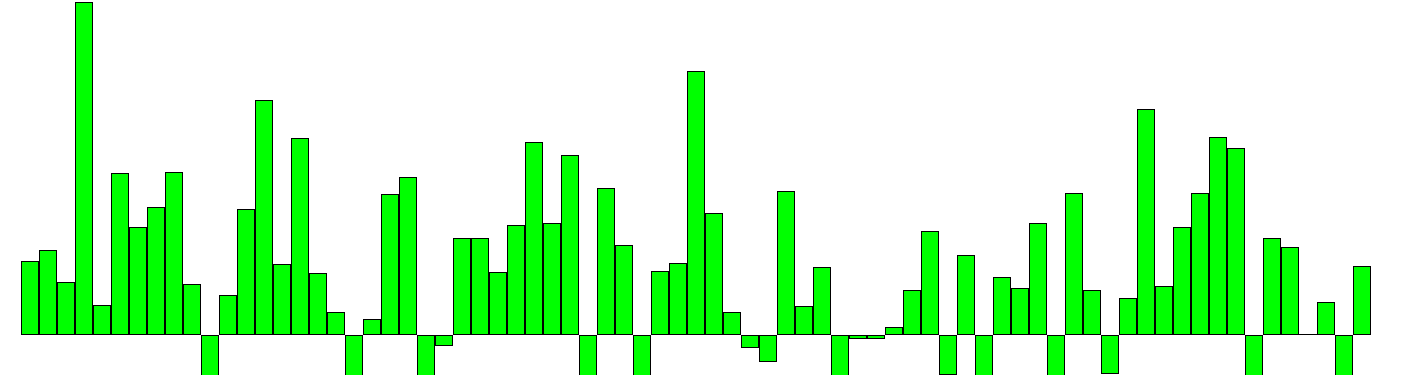
Рис 2.1.

И автоматически строит гистограмму сигнала:

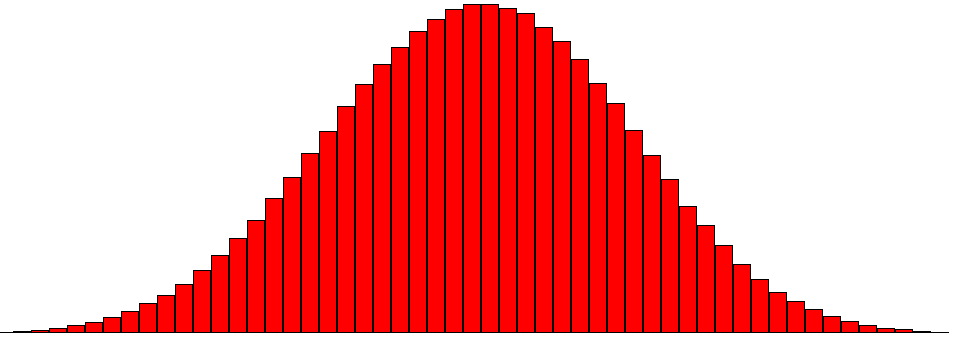
Рис 2.2.

и вычисляет его основные характеристики.

Рис 2.3.

2.4. Тестирование на различных данных

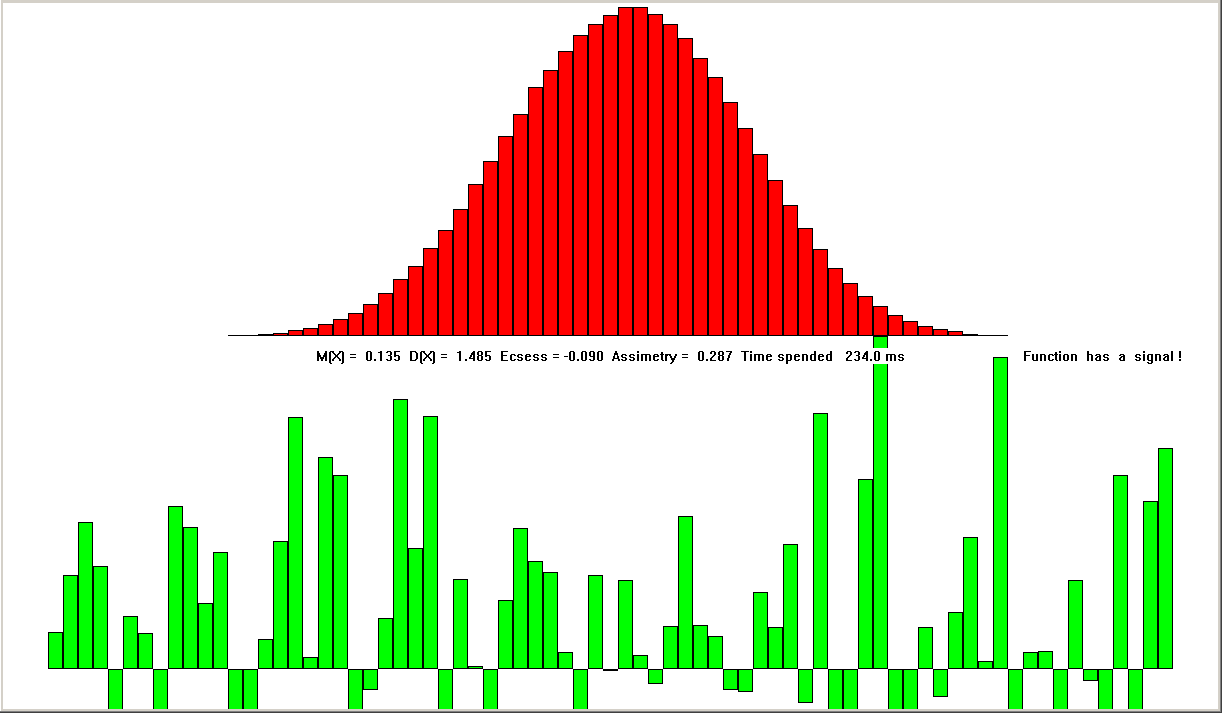
Рис 2.4.

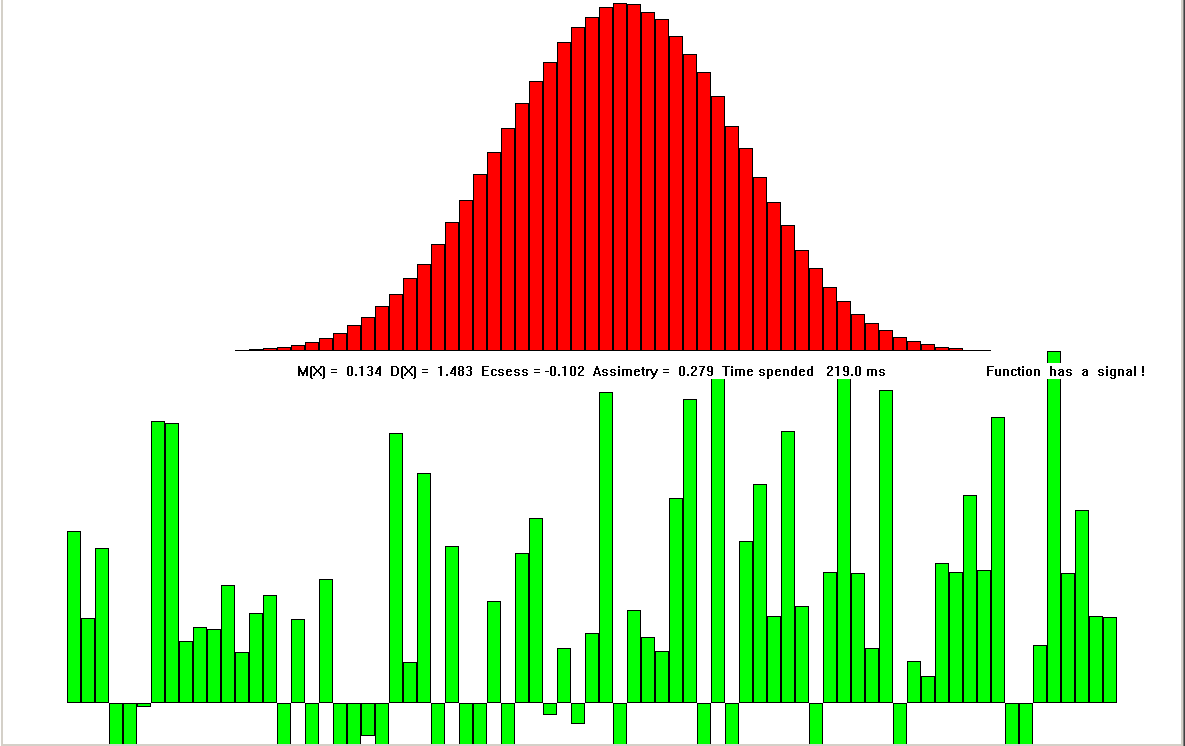
Рис 2.5.

2.5. Выводы

Нами были рассмотрены в том числе на практике, прикладные алгоритмы и методы генерации и моделирования сигналов, вероятностный алгоритм распознавания сигнала в белом Гауссовском шуме.

Получены практические навыки программирования тех или иных задач, оценена сложность алгоритмов.

Нами были рассмотрены, изучены и освоены основные методы использования графических библиотек Win32API в программировании на языках высокого уровня.

Заключение

Были рассмотрены теоретически понятия теории сигналов, классификация сигналов, алгоритмы распознавания сигналов в шуме и практическая реализация одного из них.

Были рассмотрены современные языки программирования, их достаточно мощный арсенал средств по организации и управлению графическими окнами и примитивами, а так же мат и стат. вычислениям.

Получены практические навыки программирования тех или иных задач по работе со случайными числами, генерацией сигналов, в том числе с аддитивным «белым шумом», оценена сложность алгоритмов.

Нами были рассмотрены, изучены и освоены основные методы работе с языками высокого уровня.

Были разработаны, протестированы и получены результаты по ряду программ с использованием API операционной системы.

Результаты проверены на корректность и соответствуют ожидаемым.

Получены практические навыки работы с указателями, ссылочными типами, и прочими динамическими и статическими структурами данных.

Приложение A. Текст тестирующей программы

// random_obj.cpp: определяет точку входа для приложения.

//

#include "stdafx.h"

#include "random_obj.h"

#include <time.h>

#include <stdlib.h>

#include <stdio.h>

#include <math.h>

#include <commctrl.h>

#include <string.h>

#include "rnd_test.h"

#define MAX_LOADSTRING 100

// Глобальные переменные:

HINSTANCE hInst; // текущий экземпляр

TCHAR szTitle[MAX_LOADSTRING]; // Текст строки заголовка

TCHAR szWindowClass[MAX_LOADSTRING]; // имя класса главного окна

int const maxobj = 100000;

// Отправить объявления функций, включенных в этот модуль кода:

ATOM MyRegisterClass(HINSTANCE hInstance);

BOOL InitInstance(HINSTANCE, int);

LRESULT CALLBACK WndProc(HWND, UINT, WPARAM, LPARAM);

INT_PTR CALLBACK About(HWND, UINT, WPARAM, LPARAM);

int WINAPI _tWinMain(HINSTANCE hInstance,

HINSTANCE hPrevInstance,

LPTSTR lpCmdLine,

int nCmdShow)

{

UNREFERENCED_PARAMETER(hPrevInstance);

UNREFERENCED_PARAMETER(lpCmdLine);

// TODO: разместите код здесь.

MSG msg;

HACCEL hAccelTable;

// Инициализация глобальных строк

LoadString(hInstance, IDS_APP_TITLE, szTitle, MAX_LOADSTRING);

LoadString(hInstance, IDC_RANDOM_OBJ, szWindowClass, MAX_LOADSTRING);

MyRegisterClass(hInstance);

// Выполнить инициализацию приложения:

if (!InitInstance (hInstance, nCmdShow))

{

return FALSE;

}

hAccelTable = LoadAccelerators(hInstance, MAKEINTRESOURCE(IDC_RANDOM_OBJ));

// Цикл основного сообщения:

while (GetMessage(&msg, NULL, 0, 0))

{

if (!TranslateAccelerator(msg.hwnd, hAccelTable, &msg))

{

TranslateMessage(&msg);

DispatchMessage(&msg);

}

}

return (int) msg.wParam;

}

//

// ФУНКЦИЯ: MyRegisterClass()

//

// НАЗНАЧЕНИЕ: регистрирует класс окна.

//

// КОММЕНТАРИИ:

//

// Эта функция и ее использование необходимы только в случае, если нужно, чтобы данный код

// был совместим с системами Win32, не имеющими функции RegisterClassEx'

// которая была добавлена в Windows 95. Вызов этой функции важен для того,

// чтобы приложение получило "качественные" мелкие значки и установило связь

// с ними.

//

ATOM MyRegisterClass(HINSTANCE hInstance)

{

WNDCLASSEX wcex;

wcex.cbSize = sizeof(WNDCLASSEX);

wcex.style = CS_HREDRAW | CS_VREDRAW;

wcex.lpfnWndProc = WndProc;

wcex.cbClsExtra = 0;

wcex.cbWndExtra = 0;

wcex.hInstance = hInstance;

wcex.hIcon = LoadIcon(hInstance, MAKEINTRESOURCE(IDI_RANDOM_OBJ));

wcex.hCursor = LoadCursor(NULL, IDC_ARROW);

wcex.hbrBackground = (HBRUSH)(COLOR_WINDOW+1);

wcex.lpszMenuName = MAKEINTRESOURCE(IDC_RANDOM_OBJ);

wcex.lpszClassName = szWindowClass;

wcex.hIconSm = LoadIcon(wcex.hInstance, MAKEINTRESOURCE(IDI_SMALL));

return RegisterClassEx(&wcex);

}

//

// ФУНКЦИЯ: InitInstance(HINSTANCE, int)

//

// НАЗНАЧЕНИЕ: сохраняет обработку экземпляра и создает главное окно.

//

// КОММЕНТАРИИ:

//

// В данной функции дескриптор экземпляра сохраняется в глобальной переменной, а также

// создается и выводится на экран главное окно программы.

//

BOOL InitInstance(HINSTANCE hInstance, int nCmdShow)

{

HWND hWnd;

hInst = hInstance; // Сохранить дескриптор экземпляра в глобальной переменной

hWnd = CreateWindow(szWindowClass, szTitle, WS_OVERLAPPEDWINDOW,

CW_USEDEFAULT, 0, CW_USEDEFAULT, 0, NULL, NULL, hInstance, NULL);

if (!hWnd)

{

return FALSE;

}

ShowWindow(hWnd, nCmdShow);

UpdateWindow(hWnd);

return TRUE;

}

//

// ФУНКЦИЯ: WndProc(HWND, UINT, WPARAM, LPARAM)

//

// НАЗНАЧЕНИЕ: обрабатывает сообщения в главном окне.

//

// WM_COMMAND - обработка меню приложения

// WM_PAINT -Закрасить главное окно

// WM_DESTROY - ввести сообщение о выходе и вернуться.

//

//

LRESULT CALLBACK WndProc(HWND hWnd, UINT message, WPARAM wParam, LPARAM lParam)

{

int wmId, wmEvent;

switch (message)

{

case WM_COMMAND:

wmId = LOWORD(wParam);

wmEvent = HIWORD(wParam);

// Разобрать выбор в меню:

switch (wmId)

{

case IDM_ABOUT:

DialogBox(hInst, MAKEINTRESOURCE(IDD_ABOUTBOX), hWnd, About);

break;

case IDM_EXIT:

DestroyWindow(hWnd);

break;

default:

return DefWindowProc(hWnd, message, wParam, lParam);

}

break;

case WM_PAINT:{

int colors = 255;

int test = 1000000,

col = 5 * int(log(5.0 + 5*test));

double freq = 1e-5, phi = 0.5;

rnd_test r = rnd_test(test, col , colors, freq, phi); //РАНДОМ ТЕСТ

r.draw(hWnd); //и ЕГО ОТРИСОВКА

break;

}

case WM_DESTROY:

PostQuitMessage(0);

break;

default:

return DefWindowProc(hWnd, message, wParam, lParam);

}

return 0;

}

// Обработчик сообщений для окна "О программе".

INT_PTR CALLBACK About(HWND hDlg, UINT message, WPARAM wParam, LPARAM lParam)

{

UNREFERENCED_PARAMETER(lParam);

switch (message)

{

case WM_INITDIALOG:

return (INT_PTR)TRUE;

case WM_COMMAND:

if (LOWORD(wParam) == IDOK || LOWORD(wParam) == IDCANCEL)

{

EndDialog(hDlg, LOWORD(wParam));

return (INT_PTR)TRUE;

}

break;

}

return (INT_PTR)FALSE;

}

#pragma once

#include<windows.h>

int static rnd_seed ;

static bool haveNextNextGaussian ;

static double nextNextGaussian;

class rnd_test

{

public:

rnd_test(void);

rnd_test(int test,int colons, int color, double fr, double ph);

~rnd_test(void);

void rnd_test::draw(HWND hWnd);

private:

static double rnd_test::rnd(); //0..1 uniform random generator

static void rnd_test::srnd(int seed); //init rnd

static double rnd_test::eyler(); // exp disrtibution with average = 1

static double rnd_test::next_gauss(); //normal (0,1)

static double rnd_test::uniform(double a,double b);//from a to b

static double rnd_test::normal(double m, double s); //normal light version

static double rnd_test::erlang(double m, double s); //erlang distrinbution

static double rnd_test::erl();

void rnd_test::distrib_run();

int rnd_test::getmax(int *data,int size);

int rnd_test::getmin(int *data,int size);

double rnd_test::signal_func(double x);

void rnd_test::distrib_test();

////////////////// данные

int testtime, colon_count,

colors, *colons;

double *data, mat,disp, timer, excess , assimetry , freq ,phi;

};

#include "StdAfx.h"

#include "rnd_test.h"

#include <math.h>

#include <stdlib.h>

#include <stdio.h>

#include <string.h>

#include <time.h>

rnd_test::rnd_test(void){

int defcol = 255,

defcolons = 50, deftest = 1000000 ;

double deffreq = 1e-5, def_phi = 0.5;

data = NULL;

colons = NULL;

rnd_test(deftest , defcolons , defcol, deffreq, def_phi);

}

rnd_test::~rnd_test(void){

if (data) free(data);

if (colons) free(colons);

}

rnd_test::rnd_test(int test,int colon, int color, double fr, double ph){

srnd(int(time(NULL)));

testtime = abs(test),

colon_count = abs(colon);

freq = fr;

phi = ph;

colors = color;

data = (double*)malloc(testtime*sizeof(double));

colons = (int*) calloc(colon_count,sizeof(int));

mat = disp = timer = 0;

excess = assimetry = 0;

haveNextNextGaussian = false;

nextNextGaussian = 0;

distrib_run();

}

double rnd_test::signal_func(double x){

return next_gauss() + 1.0 * sin(freq*x+phi);

}

void rnd_test::distrib_run(){

distrib_test();

}

void rnd_test::distrib_test(){

if ((colon_count<=0)||(testtime<=0)) return;

double begin = clock();

double min = 1e200 , max = -1e200 , s = 0 ,s2 = 0, s3=0, s4=0;

for (int i = 0;i<testtime;i++){

data[i] = signal_func(i); //сигнал по функции

if (min > data[i]) min = data[i]; //определение мин и макс сигнала

if (max < data[i]) max = data[i];

s+=data[i];

s2+=data[i]*data[i];

s3+=data[i]*data[i]*data[i];

s4+=data[i]*data[i]*data[i]*data[i];

}

double h = 1.000*(max-min)/colon_count;

for (int i = 0;i<testtime;i++){

int index = int((data[i]-min)/h);

if ((index>=colon_count)){

index = colon_count-1;

}

colons[index] ++;

}

int maxcol = 1;

for (int i = 0;i<colon_count;i++)

if (colons[i]>maxcol) maxcol = colons[i];

double end = clock();

mat = s/testtime ;

disp = s2/testtime - mat*mat;

double CKO = sqrt(disp);

excess = s4/(disp*disp)/testtime-3.0 , assimetry = s3/disp/CKO/testtime;

timer = double(end - begin);

}

int rnd_test::getmax(int *data,int size){

int m = data[0];

for (int i=1;i<size;i++)

if (m<data[i]) m = data[i];

return m;

}

int rnd_test::getmin(int *data,int size){

int m = data[0];

for (int i=1;i<size;i++)

if (m>data[i]) m = data[i];

return m;

}

void rnd_test::draw(HWND hWnd){

PAINTSTRUCT ps;

HDC hdc;

RECT Rect;

hdc = BeginPaint(hWnd, &ps);

GetClientRect(hWnd,&Rect);

int ey = Rect.bottom, by = Rect.top, ex = Rect.right, bx = Rect.left;

int maxy = (ey - by - 40 )/2 , maxx = int(0.95*(ex- bx));

int stepx = maxx / colon_count, minx = int(0.5*(ex- bx-stepx*colon_count));

if ((ex>=bx+colon_count)&&(ey>=16+by)){

int max = getmax(colons,colon_count);

int min = getmin(colons,colon_count);

for (int i=0;i<colon_count;i++){

HGDIOBJ hh = CreateSolidBrush(colors);

SelectObject(hdc,hh);

int curent_height = int(0.99*colons[i]*1.0/max*maxy);

Rectangle(hdc, minx + stepx*i,maxy,minx+stepx*(i+1),-curent_height + maxy);

DeleteObject(hh);

}

int *drawdata = (int*)malloc(sizeof(int)*colon_count);

for (int i=0;i<colon_count;i++) drawdata[i] = int(100*data[i]);

max = getmax(drawdata,colon_count);

min = getmin(drawdata,colon_count);

for (int i=0;i<colon_count;i++){

HGDIOBJ hh = CreateSolidBrush(colors*256);

SelectObject(hdc,hh);

int curent_height = int(99.99*data[i]*1.0/max*maxy);

Rectangle(hdc, minx + stepx*i,2*maxy,minx+stepx*(i+1),-curent_height + 2*maxy);

DeleteObject(hh);

}

}

int const charsize = 300;

TCHAR b[charsize]={0}, b1[charsize] = {0};

char a[charsize],a1[charsize]="Function has a signal ! \0";

sprintf_s(a,"M(X) = %6.3lf D(X) = %6.3lf Ecsess = %6.3lf Assimetry = %6.3lf Time spended %6.1lf ms\0",mat,disp,excess , assimetry , timer);

bool havesignal = (mat>0.1)||(fabs(excess)>0.1)||(fabs(assimetry)>0.1);

for (int i=0;i<charsize;i++){

if (a[i]>0) b[i] = 0 + a[i];

if (a1[i]>0) b1[i] = 0 + a1[i];

}

LPCWSTR A = (LPCWSTR)(&b) , A1 = (LPCWSTR)(&b1);

DrawText(hdc,A,-1,&Rect,DT_SINGLELINE|DT_CENTER|DT_VCENTER);

if (havesignal)

DrawText(hdc,A1,-1,&Rect,DT_SINGLELINE|DT_RIGHT|DT_VCENTER);

EndPaint(hWnd, &ps);

}

double rnd_test::rnd(){ //from 0 to 1

int iy = rnd_seed * 1220703125;

if (iy<0)

iy = iy +1073741824 + 1073741824;

rnd_seed = iy;

return iy * 0.4656613e-9;

}

double rnd_test::uniform(double a,double b){//from a to b

return a + (b-a)*rnd();

}

double rnd_test::normal(double m, double s){ //normal light version

double a = 0;

for (int i=0;i<12;i++)

a+=rnd();

return m+(a-6.0)*s;

}

double rnd_test::erl(){ //erlang distrinbution 1 1

return erlang(1,1);

}

double rnd_test::erlang(double m, double s){ //erlang distrinbution

int k = int(s);

double a = 0, b = s-k;

for (int i =0;i<k;i++)

a+=eyler()*m;

if(rnd()<b)

a+=eyler()*m;

return a;

}

void rnd_test::srnd(int seed){

if (seed%2==0) seed++;

rnd_seed = seed;

}

double rnd_test::eyler(){

double R = 0;

while (R==0) R = rnd();

return log(1.0/R);

}

double rnd_test::next_gauss(){

if (haveNextNextGaussian) {

haveNextNextGaussian = false;

return nextNextGaussian;

} else {

double v1, v2, s;

do {

v1 = 2*rnd()-1; // between -1 and 1

v2 = 2*rnd()-1; // between -1 and 1

s = v1 * v1 + v2 * v2;

} while (s >= 1 || s == 0);

double multiplier = sqrt(-2 * log(s)/s);

nextNextGaussian = v2 * multiplier;

haveNextNextGaussian = true;

return v1 * multiplier;

}

}

Список использованной литературы

1. Френкс Л. Теория сигналов.
2. Румянцев П. В. Азбука программирования в Win 32 API.
3. В.П. Цымбал Теория информации и кодирование. 1992, Издательское объединения «Высшая школа».
4. Э.Хант. Исскуственный интеллект. 1998.Москва. «Мир».
5. Б.Д. Кудряшов Теория информации. 2009, Учебник для ВУЗов.
6. В.М.Сидельников. Теория кодирования.
7. Герберт Шилдт - Полный справочник по Java SE 6 Edition Издательский дом «Вильямс» 2009
8. Зверева О.М., Саблина Н.Г. Среда Турбо Паскаль 7.0. Реализация простейших алгоритмов: Конспект лекций. Часть 1. - Екатеринбург: Изд-во УМЦ-УПИ, 2011. - с.112
9. Йенсен К., Вирт Н. Паскаль. Руководство для пользователя и описание языка.//Пер. с англ. и предисл. Д.Б.Подшивалова - М.: Финансы и статистика,1999. - с. 151
10. Ключарев А.А., Матьяш В.А., Щекин С.В. Структуры и алгоритмы обработки данных: Учебное пособие - СПбГУАП. СПб,2013 – с. 21-30
11. Краснов С.В. Программирование на языке высокого уровня TURBO PASCAL: Учебное пособие. - Ульяновск: УлГТУ, 2014. - с.27-31
12. Моргун А. Н. Программирование на языке Паскаль (Pascal). Основы обработки структур данных. - М.: Диалектика, 2012. — с. 576
13. Перминов О.Н. Программирование на языке Паскаль: Справочник.– М.: Радио и связь, 1999. – с.243-304
14. MSDN
15. Изучаем Java http://www.java-study.ru/java-uchebnik
16. Шмидский Я.К. Самоучитель по программированию на языке СИ++ 2013г.
17. Элементы теории графов. Ищенко М. Н. http://ppt4web.ru/matematika/ehlementy-teorii-grafov-sposoby-obkhodov-grafov.html
18. Вятский социально-экономический институт. Кафедра Информатики и вычислительной техники. Теория графов и сетей. Методические указания. Т.В. Волченская.
19. Научная библиотека http://edu.sernam.ru/book_p_math1.php?id=148
20. Портал Алгоритмы методы исходники http://algolist.manual.ru/
21. Портал Конспектов http://www.konspektov.net/
22. Алгоритмы и Структуры данных Кормен
23. http://www.intuit.ru/studies/courses/3505/747/lecture/26299
24. http://metodist.lbz.ru/authors/informatika/2/files/pk/kl11gl2.pdf
25. http://wm-help.net/lib/b/book/3683783285/34
26. http://java.novgorod.ru/lect/Java_COURSE_Lec11.pdf
27. http://www.cyberforum.ru/