
Методы кодирования данных (Процесс формирования цифровых сигналов)
Содержание:
Введение
В настоящее время по каналам связи передаются данные со столь высокими требованиями к достоверности передаваемой информации, что удовлетворить эти требования традиционным методами - совершенствованием антенно-фидерных устройств, увеличением излучаемой мощности, снижением собственного шума приемника - оказывается экономически невыгодным или просто невозможным.
Хотя существующие на данный момент системы передачи данных отвечают всем основным стандартам и требованиям, они все же не являются совершенными. Причин тому влияние помех в канале связи. При передаче сообщений по каналам связи могут возникать помехи, способные привести к искажению принимаемых знаков. Естественный язык обладает большой избыточностью (в европейских языках — до 7%), чем объясняется большая помехоустойчивость сообщений, составленных из знаков алфавитов таких языков. Примером, иллюстрирующим устойчивость русского языка к помехам, может служить предложение «в словох всо глосноо зомононо боквой о». Здесь 26% символов «поражены», однако это не приводит к потере смысла. Таким образом, в данном случае избыточность является полезным свойством. Избыточность могла бы быть использована и при передаче кодированных сообщений в технических системах. Например, каждый фрагмент текста («предложение») передается трижды, и верным считается та пара фрагментов, которая полностью совпала. Однако, больная избыточность приводит к большим временным затратам при передаче информации и требует большого объема памяти при ее хранении. Впервые теоретическое исследование эффективного кодирования предпринял К. Шеннон.
Одним из средств решения подобных несоответствий в системах передачи цифровой информации, является применение помехоустойчивых кодов, лежащих в основе устройств кодирования/декодирования. Высокоэффективным средством решения данной проблемы является применение помехоустойчивого кодирования, основанного на введении искусственной избыточности в передаваемое сообщение. Помехоустойчивое кодирование передаваемой информации позволяет в приемной части системы обнаруживать и исправлять ошибки.
Актуальность: Работа подавляющего числа современных систем связи основана на передаче сообщений в цифровом виде. Сбой при приеме любого элемента цифровых данных способен вызвать значительное искажение всего сообщения в целом, что, в свою очередь, может привести к полной потере информации, содержащейся в нем. В современных информационных системах важнейшей задачей является обеспечение информационной безопасности, связанной с методами криптографии и кодирования, теоретические основы которой заложил Шеннон в своих трудах. В данной работе будут рассмотрены основы задачи кодирования, а также практическое применение помехоустойчивых кодов.
Объект: процесс формирования цифровых сигналов
Предмет: кодирование информации
Цель исследования: разработать алгоритм на основе анализа задачи кодирования
Задачи:
- Проанализировать теоретические основы задачи кодирования
- Рассмотреть основные виды помехоустойчивых кодов
- Практическая реализация помехоустойчивого кодирования.
Теоретические основы задачи кодирования
1.1 Постановка задачи кодирования
Прежде чем рассмотреть задачу кодирования, необходимо рассмотреть ряд определений, использующихся в теории кодирования [1]:
Код – (1) правило, описывающее соответствие знаков или их сочетаний одного алфавита знакам или их сочетаниям другого алфавита; - (2) знаки вторичного алфавита, используемые для представления знаков или их сочетаний первичного алфавита.
Кодирование – перевод информации, представленной посредством первичного алфавита, в последовательность кодов.
Декодирование - операция, обратная кодированию, т.е. восстановление информации в первичном алфавите по полученной последовательности кодов.
Операции кодирования и декодирования называются обратимыми, если их последовательное применение обеспечивает возврат к исходной информации без каких-либо ее потерь.
Информационная энтропия - в теории связи энтропия используется как мера неопределенности ожидаемого сообщения, т.е. энтропия источника информации с независимыми сообщениями есть среднее арифметическое количеств информации сообщений
Примером обратимого кодирования является представление знаков в телеграфном коде и их восстановление после передачи. Примером кодирования необратимого может служить перевод с одного естественного языка на другой – обратный перевод, вообще говоря, не восстанавливает исходного текста. Безусловно, для практических задач, связанных со знаковым представлением информации, возможность восстановления информации по ее коду является необходимым условием применения кода, поэтому в дальнейшем изложении будет рассматриваться только обратимое кодирования.
Следовательно, процесс кодирования обязательно будет предшествовать процессам хранения и передачи данных. Процесс хранения данных неразрывно связан с фиксацией определенного состояния носителя данных, а процесс передачи связан с модификацией состояния с течением времени (т.е. процессом). Данные состояния (сигналы) следует называть элементарными сигналами. Совокупность этих сигналов составляет вторичный алфавит.
Без технических сторон передачи и хранения сообщения (т.е. того, каким образом фактически реализованы передача-прием последовательности сигналов или фиксация состояний) можно сформулировать следующую математическую постановку задачи кодирования. [5]
Пусть первичный алфавит A содержит N знаков со средней информацией на знак, определенной с учетом вероятностей их появления, I1(A) (нижний индекс отражает то обстоятельство, что рассматривается первое приближение, а верхний индекс в скобках указывает алфавит). Вторичный алфавит B пусть содержит M знаков со средней информационной емкостью I1(A). Пусть также исходное сообщение, представленное в первичном алфавите, содержит n знаков, а закодированное сообщение – m знаков. Если исходное сообщение содержит I(A) информации, а закодированное – I(B), то условие обратимости кодирования, т.е. неисчезновения информации при кодировании, очевидно, может быть записано следующим образом:
I(A) ≤ I(B), смысл которого в том, что операция обратимого кодирования может увеличить количество формальной информации в сообщении, но не может его уменьшить. Однако каждая из величин в данном неравенстве может быть заменена произведением числа знаков на среднюю информационную емкость знака, т.е.:
n*I1(A) ≤ n*I1 (B), или I1(A) ≤ m/n*I1 (B)
Таким образом, отношение m/n четко характеризует среднее число знаков вторичного алфавита, которое будет использоваться для кодирования одного знака первичного алфавита. Такой набор называется длиной кода или длиной кодовой цепочки. Обозначим его K(B) , при этом верхний индекс указывает алфавит кодов.
В конкретном случае, когда возникновение любых знаков вторичного алфавита оценивается равновероятно, согласно формуле Хартли I1(B)=log2M, и тогда I1(A) /log2M≤ K(B) (1)
По аналогии с величиной R, характеризующей избыточность языка, можно ввести относительную избыточность кода (Q):
Q= 1 – I(A) / I(B) = 1- I1(A) / K(B)*I1(B) (2)
Данная величина позволяет определить, насколько операция кодирования повысила длину исходного сообщения. Логично, чем меньше Q (т.е. чем ближе она к 0 или, что то же, I(B) ближе к I(A)), тем более выгодным будет считаться код и более рациональной будет считаться сама операция кодирования. Выгодность кодирования при передаче и хранении – это экономический фактор, поскольку более рациональный код дает возможность затратить на передачу сообщения меньшее количество энергии, а также времени и, таким образом, меньше времени занимать линию связи; при хранении применяется меньше площади поверхности (объема) носителя. Также важно сознавать, что выгодность кода не идентична временной выгодности всей цепочки «кодирование – передача – декодирование», так как возможна ситуация, когда за применение рационального кода при передаче данных потребуется расплачиваться тем, что операции кодирования и декодирования будут требовать больше времени и других ресурсов.
Выше давалась информация, что источник исходного сообщения включает в себя систему кодирования, формирующую сигналы по известным конечному получателю правилам. Ввиду независимости самого содержания сообщения от реализуемой формы его представления, допускается преобразование одного кода в другой, соблюдая правило обратного кодирования получателю сообщения. Рациональность этого дополнительного кодирования послания на передающей стороне и аналогичного декодирования на стороне приема получается из-за получающейся избыточности алфавита послания и модификации сигналов действующими в канале связи помехами. Кодирование предваряет процессы передачи и хранения данных.
Реализация базовых свойств канала связи кроме разработки технических средств, требует разработки информационных задач, то есть требуется выбор наиболее рационального способа кодирования.[11]
Базовыми целями кодирования являются:
1. Реализация характеристик экономичности передачи данных с помощью устранения избыточности.
2. Реализация характеристик помехоустойчивости передачи данных, то есть обеспечение надежности данного процесса.
3. Согласование скорости передачи данных с пропускной способностью передающих устройств и линий связи.
Согласование между компонентами дискретных сообщений и типом кодирования реализуется оптимальным подбором:
1. Длительности сигналов
2. Длины кодового слова
3. Алфавита знаков и метода кодирования. Например, может быть выбран блочный или побуквенный тип шифрования.
Примем, что сообщение источника данных составляется из знаков аi, i=1,2,.. Na внешнего (такой алфавит также называют «входным» или «первичным») алфавита А размером Na. Сообщения - это слова, образованные последовательностью nr символов: Ar =a1a2…anr. В устройстве кодировки слово Ar трансформируется в кодовое слово Br=b1b2…bmr, составленное из mr знаков bj, j=1,2,..Nb внутреннего (такой алфавит также называют «выходным» или «вторичным») алфавита В. Количество символов кодового алфавита является основанием кода. Число знаков в кодовом слове называют длиной кодового слова. Отображение G количества слов в алфавите А на количество слов в алфавите В является кодирующим отображением или кодом. Использование кодирующего отображения G к произвольному слову из входного алфавита называется процессом кодирования. То есть код представляет собой правило отображения символов одного алфавита в символы другого алфавита, а кодирование представляет собой процесс трансформации одной формы сообщения в другую с помощью указанного кода.
Следует различать побуквенное и блочное шифрование. При побуквенном (посимвольном) кодировании каждому символу вторичного алфавита ставится в соответствие кодовый символ из числа символа первичного алфавита. [2]
При блочном шифрования для слова из символов первичного алфавита ставится в соответствие кодовое слово из символов вторичного алфавита.
Слова из символов первичного алфавита В, сопоставленные словам из знаков вторичного алфавита А по определенному правилу G, являются так называемыми кодовыми комбинациями. Если ArE A и G(Ar)= Br, то считается, что слову Ar соответствует кодовая комбинация Br. Общность кодовых комбинаций применяемых для передач определенного объема дискретных сообщений именуют кодовым словарем.
Процесс, обратный кодированию, заключается в восстановлении из кодовой комбинации Br=b1b2…bmr слова Ar=a1a2…anr из входного алфавита и называется процессом декодирования. Если процесс кодирования выполняется с применением правила G, то процесс декодирования базируется на использовании правила G-1, где G-1 есть отображение, обратное отображению G.
Процессы кодирования и декодирования именуются обратимыми, если их последовательное использование обеспечивает возврат к начальной форме сообщения без утери данных.
Пусть Ar — слово в алфавите А и Br =G(Ar) — слово в алфавите В. Код называется обратимым, если для любого слова Br =G(Ar) в алфавите В существует единственное преобразование G-1(Br)= Ar . То есть, по слову Br в алфавите В, всегда однозначно восстанавливается слово Ar в алфавите А, из которого было образовано слово Br.
Образцом обратимого кодирования является представление символов в телеграфном коде при трансфере сообщений и восстановление их при приеме.
Образцом необратимого кодирования является модификация текста с одного естественного языка на другой, при этом обратный перевод посимвольно как правило не соответствует исходному тексту.
Для того, чтобы результирующий код был обратимым, требуется:
1) чтобы разным знакам входного алфавита А были сопоставлены различные кодовые комбинации;
2) чтобы всякая кодовая комбинация не составляла начальной части какой-либо другой кодовой комбинации.
Самым простым правилом кодирования считается сопоставление каждому знаку входного алфавита А слова итоговой длины во вторичном алфавите В. Код может быть задан в форме таблицы, графа, аналитического выражения, то есть в тех же формах, что и отображение.
Выражение (1) на данный момент считается как соотношение оценочного типа, из которого неочевидно, в какой степени при шифровании реализуется приближение к тождеству его правой и левой частей. Таким образом для теории связи существенное значение имеют две теоремы, сформулированные Шенноном. Первая теорема касается случая с кодированием при трансфере послания по каналам связи, в которой нет помех, искажающих данные. Другая теорема касается реальных каналов связи с соответствующим уровнем помех.
1.2. Первая теорема Шеннона
Очевидно, что при передаче посланий по линиям связи могут образовываться помехи, ведущие к нежелательной модификации передаваемых символов. К примеру, при передаче речевого сообщения в ветреную погоду собеседнику, находящемуся от вас на существенной дистанции, передаваемое сообщение будет в значительной степени искажено естественной помехой - ветром. В целом, трансфер данных при существующих помехах является значительной теоретической и практической задачей. Ее значимость существенно растет из-за многопланового внедрения компьютерных линий связи, в которых помехи представляют собой неизбежную проблему.[1]
При обработке кодированных данных, модифицированных помехами, следует определить такие базовые трудности: выявление самого факта модификации данных; определения того, на каком точно участке передаваемого сообщения это случилось; исправления ошибки с определенной теоретическим уровнем достоверности.
Помехи в процессе передачи данных характерны не только для сугубо технических систем. Они являются вполне обыденным эффектом в повседневной жизни. Как пример можно привести разговор по телефону с неудовлетворительным качеством линии связи. Как правило, человеческий организм довольно-таки эффективно справляется с любой из перечисленных выше задач, однако далеко не всегда сознательно отдает себе в этом отчет относительно внутренних механизмом осуществления. Таким образом, мозг человека действует неалгоритмически, а больше из неких ассоциативных нейронных связей. Очевидно, что натуральный язык характеризуется значительной избыточностью. Избыточность в европейских языках может составлять до 70 процентов. Таким образом, натуральный язык позволяет обеспечить существенную помехоустойчивость передачи данных, набранных из символов алфавитов такого типа языков. Устойчивость русского языка к помехам можно проиллюстрировать фразой "в словох всо глосноо зомононо боквой о", в которой 26 процентов знаков модифицированы «помехой», но сообщение все равно можно распознать. В такой ситуации избыточность является положительным качеством языка.
Также, любой участок текста передается три раза, и истинным можно считать ту пару участков, которые совпадают. Тем не менее, значительная избыточность может вести к существенным временным издержкам при трансфере данных, а также требует увеличенного размера памяти при ее обработке и хранении. Таким образом, появляется задача уменьшения избыточности, или рационального кодирования. К.Шеннон первым осуществил теоретическое изучение такого типа проблем.
Первая теорема Шеннона о передаче данных, которую также называют главной теоремой о кодировании при отсутствии помех, формулируется так:
«При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором среднее число знаков кода, приходящихся на один знак кодируемого алфавита, будет сколь угодно близко к отношению средних информаций на знак первичного и вторичного алфавитов.» [5]
Применяя понятие избыточности кодирования, можно сформулировать краткую формулировку данной теоремы:
«При отсутствии помех передачи всегда возможен такой вариант кодирования сообщения, при котором избыточность кода будет сколь угодно близкой к нулю.»
Такие тезисы рассматриваются как теоремы, а, значит, необходимо их доказывать. В рамках данной работы не будем приводить доказательства, так как в данном случае более важно то, что тезисы Шеннона предоставляют нам базу для практического обеспечения возможности кодирования с оптимальными параметрами.
Тем не менее важно сознавать, что из самой теоремы вовсе не следует конкретный способ реализации такого типа кодирования. Получается, что следует привлечь дополнительные изыскания для конкретной реализации алгоритма. Рациональное кодирование с оптимальными принципиально возможно на практике, однако средства реализации могут выбираться различные.
Самым важным в практическом смысле моментом является то, что информацию кодируют бинарно с помощью символов 1 и 0 при М=2. [1]
Шенноном была изучена определнная ситуация, когда при кодировании послания во внутреннем алфавите уже изначально закладывается различная вероятность возникновения символов знаков, а также равная вероятность возникновения символов в выходном алфавите. В такой ситуации справедливо равенство:
Кmin (А, В)= I (A) / log2 M= I (A) , где I (A) - средняя информация на символ внутреннего алфавита.
Гипотетически ограничимся случаем, когда M = 2, т.е. для создания кодов в канале связи применяется только два типа сигналов. Такой тип кодирования именуется двоичным. Символы двоичного алфавита обычно обозначают 0 и 1. Привлекательность двоичных кодов состоит также в том, что всякий элементарный сигнал (0 или 1) хранит в себе один бит данных (log2M = 1); тогда из (1), теоремы Шеннона получим:
I1(A)≤ K(2)
В таком случае первая теорема Шеннона обеспечивается новым объяснением:
«Если на канале связи нет помех, то средняя длина двоичного кода может быть сколь угодно близкой к средней информации, приходящейся на символ внутреннего алфавита.»
Вычисление объема переданных данных при двоичном кодировании может быть упрощено до банального подсчета количества импульсов (единиц) и пауз (нулей). В таком случае появляется новая трудность: необходимо выделять из потока сигналов дискретные коды. Приемник сигналов регистрирует интенсивность и длину сигналов. Простейшие сигналы (0 и 1) могут обладать одинаковыми или различными длинами.
Их общее число в коде (длина кодовой цепочки), который ставится в соответствие знаку внутреннего алфавита, тоже может быть одинаковым (равномерный код) или разным (неравномерный код). Также коды могут реализовываться для всякого символа первичного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, фраз, слов). В итоге при кодировании допустимы следующие варианты сочетаний:
Таблица 1. Варианты сочетаний
|
Длительности элементарных сигналов |
Кодировка первичных символов (слов) |
Ситуация |
|
Одинаковые |
Равномерная |
(1) |
|
Одинаковые |
Неравномерная |
(2) |
|
Разные |
Равномерная |
(3) |
|
Разные |
Неравномерная |
(4) |
В том случае, если применяется неравномерный тип кодирования или сигналы разной длительности (ситуации (2), (3) и (4)) для отделения кода одного символа от другого между ними требуется транслировать специфический сигнал – временной разделитель (признак конца символа) или использовать такие модификации кодов, которые являются уникальными, то есть несовпадающими с фрагментами других кодов. При равномерном кодировании одинаковыми по времени сигналами (ситуация (1)) в трансляции разделителя нет необходимости, поскольку отделение одного кода от другого выполняется по суммарной длительности, которая для всех кодов является одинаковой.
Длина двоичного простейшего сигнала показывает количество времени, которое потребуется для трансляции одного бита данных.
Характерно, что для трансляции данных, в среднем приходящихся на символ внутреннего алфавита, необходимо затратить определенное время. Проблему рационализации допустимо также сформулировать иначе: реализовать такой комплекс программно-аппаратных средств кодирования, чтобы суммарная длина кодов при трансляции определенного послания была бы минимальной.
Если есть в наличи источник данных, характеризующийся энтропией Н(х)), а также линия связи с пропускной способностью С, то если С > H(X), то есть возможность зашифровать большое послание таким способом, что она будет транслировано без временных задержек. Если же, наоборот, С < H(X), то трансляция данных без временных задержек нереальна.
Первая теорема Шеннона обеспечивает реализацию системы рационального шифрования дискретных посланий, в которых среднее число двоичных знаков на один знак послания асимптотически стремится к энтропии источника данных при отсутствии помех. [13]
Если нет помех, то средняя длина двоичного кода может быть сколь угодно близкой к среднему объему данных, приходящихся на символ изначального алфавита.
Перечислим характерные признаки внешнего алфавита при таком типе кодирования:
- Простейшие бинарные коды 0 и 1 могут характеризоваться одинаковыми или разными длинами;
- Длина кода может быть одинаковой для всех знаков первичного алфавита (код равномерный) или различной (неравномерный код)
- Коды могут реализовываться для отдельного символа исходного алфавита (алфавитное кодирование) или для их комбинаций (кодирование блоков, слов, фраз).
1.3 Вторая теорема Шеннона
Отношение характерной пропускной способности линии связи к скорости передачи знаков алфавита без помех транслируемого послания должно быть больше или равно энтропии трансляции одного знака.[5]
Вторая теорема Шеннона декларирует, что если в линии связи есть помехи, то всегда есть возможность реализовать такую схему кодирования, при которой послания будут транслированы с заданной достоверностью. Если есть какие-либо лимиты для пропускной способности линии связи, то пропускная способность линии связи должна обеспечивать производительность источника данных. Вторая теорема Шеннона реализует принципы помехоустойчивого кодирования. Для дискретного канала с помехами теорема декларирует, что, если скорость генерации посланий меньше или равна пропускной способности линии связи, то есть возможность создать такой код, который бы позволял обеспечить передачу со сколь угодно малой частотой возникновения ошибок.
Доказательство теоремы основывается на таких умозаключениях: изначально поток X={xi} записывается знаками из В таким образом, что получается наибольшая пропускная способность, так как линия связи без помех. После этого в поток из В длины n добавляется r знаков, по линии передачи данных передается вновь созданная последовательность из n + r знаков. Количество возможных комбинаций длины n + r превосходит количество комбинаций длины n. Общность всех комбинаций длины n + r может быть разбито на n подмножеств, любому из них сопоставлена одна из комбинаций длины n. При возникновении помех на линии связи последовательность из n + r выводит ее из такого подмножества с минимальной вероятностью. [12]
Данная теорема дает возможность выявлять на стороне-приемнике, какому из общностей принадлежит поврежденная помехами транслируемая комбинация n + r, и тем самым появляется возможность восстановить истинную последовательность длины n.
Такая теорема не предполагает определенной техники генерации кода, однако указывает на лимиты достижимого результата в сфере помехоустойчивого кодирования, а также стимулирует изыскание новых методик решения данной задачи.
1.4 Помехоустойчивые коды
1.4.1 Классификация помехоустойчивых кодов
На данный момент скорость эволюции передающих систем и линий связи дают предпосылки для возникновения совершенно других методик кодирования сообщений. Одной из важных задач кодирования становится не только безошибочная трансляция данных, но и их обработка в реальном времени. Несмотря на быстрое возрастание доступной производительности современной вычислительной техники, на первом рубеже решения данных проблем до сих пор остается задача реализации простых рациональных программных алгоритмов для осуществления эффективной коррекции ошибок. Одним из малоизученных вопросов в данной сфере можно считать применение кодов с иррациональным базисом.
Методология работы значительного количества актуальных комплексов передачи данных базируется на трансляции сообщений в цифровом виде. В таких системах технический или программный сбой при приеме блоков цифровых данных влечет за собой существенное искажение всего блока данных в целом, что ведет к полной утере данных, которые в нем находятся.
На данный момент по линиям связи транслируются данные со столь высокими требованиями к достоверности передаваемой информации, что реализовать эти требования стандартными техниками (то есть дальнейшим усовершенствованием приемо-передающих и антенно-фидерных комплексов, повышением излучаемой мощности, минимизацией собственного шума приемника) становится практически невозможным или невыгодным с финансовой точки зрения.
Методикой решения данной задачи, характеризующейся значительным коэффициентом эффективности, считается использование помехоустойчивого кодирования, базирующегося на интеграции повышенной избыточности в транслируемое сообщение. Теоретический базис и технологические способы помехоустойчивого шифрования прошли множество итераций в своем развитии. Первоначально это было только эмпирическое применение примитивных кодов с повторением, с постоянным весом, с единичной проверкой на четность и так далее.
Затем теория помехоустойчивого шифрования прошла длительный путь эволюции, в ходе которого для ее реализации применялись базовые понятия математической теории – сферы высшей алгебры и теории чисел в виде дополнения к реальным системам передачи данных.
Теория кодирования появилась в сороковых годах с появлением работ Голея, Хэмминга и Шеннона. Выдающиеся два ученые Голей и Хэмминг заложили базис алгебраическим техникам шифрования, которые применяются и в наше время, а Шеннон реализовал и исследовал понятие случайного кодирования. Важно заметить, что в актуальных информационных комплексах одной из важных проблем является практическая реализация информационной безопасности, связанной с методами криптографии и кодирования, теоретические базисы которой заложил Шеннон в своих работах.[3]
Написание работ Шеннона привело к бурному росту новых идей среди ученых и инженеров. В то время им казалось, что практическая реализация таких задач будет так же легко и просто, как Шеннон сделал это математически. Тем не менее эйфория стремительно прошла, так как реального решения в прямой постановке Шеннона отыскать так не сумели. Тогда же, сделанные Шенноном реализации задачи и доказательство базовых теорем теории информации дали толчок для поиска решения задач с использованием детерминированных (неслучайных) сигналов и алгебраических методов помехоустойчивого кодирования защиты от помех и шифрования для обеспечения секретности информации.
В 50-е-70-е годы было спроектировано и реализовано значительное число алгебраических кодов с поиском и исправлением ошибок, среди которых самыми удачными стали коды Боуза-Чоудхури-Хоквингема (БЧХ), Рида-Соломона (РС), Рида-Малера, Адамара, Юстенсена, Гоппы, циклические коды, сверточные коды с различными техниками декодирования (последовательное декодирование, алгоритм Витерби), арифметические коды.
Тем не менее, в практических реализациях используются довольно-таки малая группа алгебраических помехоустойчивых кодов: БЧХ, Рида-Соломона и сверхточные коды. Наиболее популярными являются циклические коды с обнаружением ошибок в стандартных протоколах HDLC, Х.25/2 (LAP-B, LAP-M). Коды Рида-Соломона с исправлением ошибок находят применение в каналах радиосвязи. В каналах спутниковой связи, которым свойственны независимые характеры возникающих ошибок, часто используются сверхточные коды .
Следует отметить тот факт, что хотя существующие на данный момент системы передачи данных отвечают всем основным стандартам и требованиям, они все же не являются совершенными. Причин тому влияние помех в канале связи. Одним из средств решения подобных несоответствий в системах передачи цифровой информации, является применение помехоустойчивых кодов, лежащих в основе устройств кодирования/декодирования.
Помехоустойчивое кодирование передаваемой информации позволяет в приемной части системы обнаруживать и исправлять ошибки. Коды, применяемые при помехоустойчивом кодировании, называются корректирующими кодами. Как правило, корректирующий код может исправлять меньше ошибок, чем обнаруживать. Число ошибок, которые корректирующий код может исправить в определенном интервале последовательности двоичных символов, например, в одной кодовой комбинации, называется исправляющей способностью кода.
Данные передаются в реальной физической среде, а она изначально не может быть 100% надежной. Кроме того, шумовой уровень также может быть довольно-таки большим. Ошибки при передаче данных – это реальные условия, которые следует непременно учитывать в расчетах.
Разные физические среды предполагают различных уровень и характер помех. Могут возникать как одиночные ошибки, так и по группам или даже несколькими блоками. Таким образом в ходе передаче теряются биты информации или же, напротив, появляются новые ошибочные биты.
Главным свойством интенсивности помех на линии связи является переменная шума — p. Это значения от 0 до 1, равное вероятности инвертирования бита данных.
Другая переменная величина— p2. Это вероятность того же события, но при условии, что предыдущий бит также был инвертирован.
Такими свойствами можно ограничиться при построении теории. Однако следовало было бы принимать во внимание похожие вероятности для пропадания бита информации, а также применять полные данные о пространственном взаимодействии ошибок, — то есть взаимодействии и схожести соседних ошибок, разделённых одним, двумя или более битами.
У групповых ошибок есть свои достоинства и недостатки. Пусть информация транслируется блоками по 1000 бит, а параметр ошибки 0,001 на бит. Если ошибки изолированные и независимые, то 60% блоков будут включать в себя ошибки. Если же они появятся группами по 100 сразу, то ошибки будут включать в себя 1% блоков.
Если же ошибки не группируются, то в любом кадре они малы, и их можно устранить. Групповые ошибки портят кадр безвозвратно. Требуется его повторная пересылка, но в некоторых системах это в принципе невозможно, — например, в телефонных системах, использующие цифровое кодирование, возникает эффект пропадания слов/слогов.
Для надёжной передачи кодов было предложено два основных метода.
Первый — добавить в передаваемый блок данных нескольких «лишних» бит так, чтобы, анализируя полученный блок, можно было бы сказать, есть в переданном блоке ошибки или нет. Это, так называемые, коды с обнаружением ошибок.
Второй — внести избыточность настолько, чтобы, анализируя полученные данные, можно не только замечать ошибки, но и указать, где именно возникли искажения. Это коды, исправляющие ошибки.
Под помехой понимается любое воздействие, накладывающееся на полезный сигнал и затрудняющее его прием.
Внешние источники помех вызывают в основном импульсные помехи, а внутренние - флуктуационные. Помехи, накладываясь на видеосигнал, приводят к двум типам искажений: краевые и дробления. Краевые искажения связаны со смещением переднего или заднего фронта импульса. Дробление связано с дроблением единого видеосигнала на некоторое количество более коротких сигналов. [4]
Помехоустойчивые коды делятся на блочные и непрерывные.
Блочными называются коды, в которых информационный поток символов разбивается на отрезки и каждый из них преобразуется в определённую последовательность (блок) кодовых символов. В блочных кодах кодирование при передаче (формирование проверочных элементов) и декодирование при приёме (обнаружение и исправление ошибок) выполняются в пределах каждой кодовой комбинации (блока) в отдельности по соответствующим алгоритмам.
Непрерывные или рекуррентные коды образуют последовательность символов, не разделяемую на отдельные кодовые комбинации. Кодирование и декодирование непрерывно совершаются над последовательностью элементов без деления их на блоки. Формирование проверочных символов ведётся по рекуррентным (возвратным) правилам, поэтому непрерывные коды часто называют рекуррентными или цепными.
В простейшем цепном коде каждый проверочный элемент формируется путём сложения по модулю 2 соседних или отстоящих друг от друга на определённое число позиций информационных элементов. В канал связи передаётся последовательность импульсов, в которой за каждым информационным следует проверочный.
К непрерывным кодам относятся и свёрточные коды, в которых каждый информационный символ, поступающий на вход кодирующего устройства, вызывает появление на его выходе ряда проверочных элементов, образованных суммированием по модулю 2 данного символа и " k-1 " предыдущих информационных символов. Рекуррентные коды позволяют исправлять групповые ошибки (" пачки ") в каналах связи.
Блочные коды делятся на равномерные и неравномерные. В равномерных кодах, в отличие от неравномерных, все кодовые комбинации содержат одинаковое число n - символов (разрядов) с постоянной длительностью τ0 импульсов символов кода. Равномерные коды в основном и применяются в системах связи, так как это упрощает технику передачи и приёма.
Классическими примерами неравномерного кода являются код Морзе, широко применяемый в телеграфии, и код Хафмена, применяемый для компрессии информации (факсимильная связь, ЭВМ).
Никаких специальных мер по исправлению и обнаружению ошибок в коде Морзе не предусматривается в связи с большой избыточностью самого передаваемого текста. В этом смысле код Морзе не относится к классу корректирующих кодов.
Почти все блочные корректирующие коды принадлежат к разделимым кодам, в которых кодовые комбинации состоят из двух частей: информационной и проверочной. Их символы всегда занимают одни и те же позиции, т.е. располагаются на определённых местах. Как правило, в таких кодах, все кодовые комбинации которых содержат n символов, первые k символов являются информационными, а за ними располагаются (n - k) проверочных символов. В соответствии с этим разделимые коды получили условное обозначение – (n , k) - коды.
В неразделимых кодах деление на информационные и проверочные символы отсутствует. К таким кодам относятся, в частности, коды с постоянным весом, так называемые равновесные коды. Например, Международным Консультативным Комитетом по телеграфии и телефонии (МККТТ) рекомендован для использования телеграфный код № 3 - семиразрядный код с постоянным весом, т.е. с числом единиц в каждой кодовой комбинации, равным 3 (W = 3).
Систематические коды образуют наиболее обширную группу (n, k)- разделимых кодов. Особенностью этих кодов является то, что проверочные (корректирующие) символы образуются с помощью линейных операций над информационными. Кроме того, любая разрешённая кодовая комбинация может быть получена в результате линейной операции над набором к линейно независимых кодовых комбинаций. В частности, суммирование по модулю 2 двух и более разрешённых комбинаций также дает разрешённую кодовую комбинацию.
Так как теоретическим базисом реализации такого рода совокупностей является математический аппарат линейной алгебры, то коды также именуются линейными. Блочные равномерные разделимые линейные коды содержат проверочные знаки, которые создаются по конкретным правилам, поэтому они носят название «систематические».
Использование аппарата линейной алгебры, в которой существенное значение имеет понятие "группа", породило и другое название этих типов кодов - групповые.
Эти коды получили наибольшее применение в системах передачи дискретной информации.
Несистематические (нелинейные) коды не характеризуются приведенными выше характеристиками, таким образом они используются существенно менее часто и только в специфических ситуациях. Удачным образцом нелинейного кода можно считать вышеупомянутый равновесный неразделимый код. Коды данного типа, как правило, применяются в асимметричных линиях связи, которые характеризуются вероятностью перехода «1 => 0» существенно больше вероятности перехода «0=>1» или в обратном порядке. В таких типах линии связи крайне маловероятно, чтобы в одном сегменте сосуществовали переходы двух типов, а, значит, практически все ошибки ведут к модификации веса сегмента, и, таким образом, достаточно эффективно обнаруживаются.
Иным образцом несистематического кода можно назвать код с контрольным суммированием, то есть, так называемый, итеративный тип кода. В таком виде кода проверочные разряды реализуются в виде сложения значений разрядов как в самой кодовой комбинации, так и одноимённых разрядов в списке соседних с ней совокупностей, образующих вместе общий сегмент.
Итеративные коды дают возможность реализовывать мощные коды. Мощные коды – это коды, содержащие сегменты большой длины и большое кодовое расстояние, при этом сохраняя достаточную простоту и рациональность процесса кодирования и декодирования. Такие коды могут реализовываться как комбинационные с помощью произведения двух или нескольких кодов систематического типа.
К комбинационным видам кодов следует также отнести специфические антифединговые коды, используемые для детектирования и исправления ошибок в линиях связи, характеризующихся федингом, то есть замиранием проходящих сигналов. Для такого типа линий связи используют технику перемежения знаков и систему декорелляции ошибок, чтобы нивелировать накопление и группирование ошибок при передачи пакетов данных.
Техника обработки заключается в том, что знаки, входящие в одну кодовую общность, транслируются не сразу по очереди, а перемежаются знаками иных кодовых общностей первичного систематического или иного кода. Если же расстояние между знаками, входящими в одну кодовую общность, сделать длиннее интервала корелляции канала с федингом, то в пределах длительности одной первичной кодовой общности группирования ошибок не возникнет. На принимающей стороне после обратной обработки в кодовых общностях следует осуществлять декодирование с поиском и исправлением ошибок.
В систематических кодах следует разделять два способа реализации проверочной группы знаков: поэлементный и в целом.
Самые популярные среди систематических кодов коды Хемминга, которые исторически были изучены ранее иных видов кодов и сыграли существенную роль в практической реализации теории корректирующих кодов. В такого рода кодах применяется техника проверки на чётность заранее определённого потока информационных знаков.
Проверочная группа из r знаков создается посимвольно по определенному алгоритму. Коды Хемминга, имеющие dmin = 3, дают возможность исправить одну ошибку
Циклические коды также относятся к виду линейных систематических кодов и обладают всеми их основными характеристиками. Коды названы циклическими благодаря использованию циклического сдвига. Такой сдвиг произвольной разрешённой кодовой общности также является разрешённой комбинацией. Теория построения циклических кодов основывается на понятиях высшей алгебры, оперирующей характеристиками бинарных многочленов.
Специфическую роль в данной теории выполняют неприводимые полиномы. Они не могут быть выполнены в виде произведения полиномов низших степеней. Таким образом, циклические коды относят к специфической разновидности полиномиальных кодов.
Среди циклических кодов важное место занимает специфическим тип кодов, предложенных Боузом и Рой-Чоудхури и независимо от них Хоквингемом. Коды Боуза-Чоудхури-Хоквингема получили аббревиатуру «БЧХ-коды» и характеризуются специфическим выбором образующего циклический код полинома, что ведет к упрощению процедуры декодирования.[7]
В циклических кодах "r" проверочных символов, добавляемых к исходным "k" информационным, могут быть получены сразу, то есть. в целом, в результате умножения исходной подлежащей передаче кодовой комбинации Q(x) простого кода на одночлен x r и прибавлением к этому произведению остатка R(x), выполненного в итоге деления произведения на порождающий полином P(x).
Во время кодирования при трансляции данных из информационных разрядов в соответствии с определёнными для каждого К. правилами реализуются дополнительные знаки — проверочные разряды. При расшифровке из принятых кодовых слов по тем же сценариям снова создают проверочные разряды и сравнивают их с изначально принятыми; если они не совпадают, то при передаче была допущена ошибка. Есть также такие коды, которые обнаруживают факт модификации послания, и коды, исправляющие ошибки, то есть такие, при помощи которых есть возможность восстановить исходные данные.
Ошибки в передаваемых словах могут возникать вследствие либо независимых искажений разрядов (в этом случае применяют, например, коды типа кода Хэмминга), либо искажений группы рядом стоящих разрядов (для таких случаев разработаны коды, исправляющие одиночные пачки ошибок, и коды, исправляющие более одной пачки ошибок); для обнаружения ошибок в процессе вычислений на ЭВМ разработаны так называемые арифметические коды.
1.4.2 Основные параметры и построение помехоустойчивых кодов
Проблема повышения верности обусловлена не соответствием между требованиями, предъявляемыми при передаче данных и качеством реальных каналов связи. В сетях передачи данных требуется обеспечить верность не хуже 10-6 - 10-9, а при использовании реальных каналов связи и простого (первичного) кода указанная верность не превышает 10-2 - 10-5.
Одним из путей решения задачи повышения верности в настоящее время является использование специальных процедур, основанных на применении помехоустойчивых (корректирующих) кодов.
Простые коды характеризуются тем, что для передачи информации используются все кодовые слова (комбинации), количество которых равно N=qn (q - основание кода, а n - длина кода). В общем случае они могут отличаться друг от друга одним символом (элементом). Поэтому даже один ошибочно принятый символ приводит к замене одного кодового слова другим и, следовательно, к неправильному приему сообщения в целом.
Помехоустойчивыми называются коды, позволяющие обнаруживать и (или) исправлять ошибки в кодовых словах, которые возникают при передаче по каналам связи. Эти коды строятся таким образом, что для передачи сообщения используется лишь часть кодовых слов, которые отличаются друг от друга более чем в одном символе. Эти кодовые слова называются разрешенными. Все остальные кодовые слова не используются и относятся к числу запрещенных.
Применение помехоустойчивых кодов для повышения верности передачи данных связанно с решением задач кодирования и декодирования.
Задача кодирования заключается в получении при передаче для каждой k - элементной комбинации из множества qk соответствующего ей кодового слова длиною n из множества qn.
Задача декодирования состоит в получении k - элементной комбинации из принятого n - разрядного кодового слова при одновременном обнаружении или исправлении ошибок. [6]
Основные параметры помехоустойчивых кодов
Длина кода - n;
Длина информационной последовательности - k;
Длина проверочной последовательности - r=n-k;
Кодовое расстояние кода - d0;
Скорость кода - R=k/n;
Избыточность кода - Rв;
Вероятность обнаружения ошибки (искажения) - РОО;
Вероятность не обнаружения ошибки (искажения) - РНО.
Кодовое расстояние между двумя кодовыми словами (расстояние Хэмминга) - это число позиций, в которых они отличаются друг от друга.
Кодовое расстояние кода - это наименьшее расстояние Хэмминга между различными парами кодовых слов.
Стиранием называется "потеря" значения передаваемого символа в некоторой позиции кодового слова, которая известна.
Код, в котором каждое кодовое слово начинается с информационных символов и заканчивается проверочными символами, называется систематическим.
Построение помехоустойчивых кодов в основном связано с добавлением к исходной комбинации (k-символов) контрольных (r-символов) Закодированная комбинация будет составлять n-символов. Эти коды часто называют (n,k) - коды.
k—число символов в исходной комбинации
r—число контрольных символов
Рассмотрим основные понятия помехоустойчивого кодирования. Двоичный (n,k)-код предполагает правило перехода от комбинации из k информационных символов, общее число которых 2k, к такому же числу кодовых комбинаций длиной n (причем n > k), общее число которых 2n , т.е. к введению избыточности (для систематических кодов избыточных символов). Для кода существует множество из 2k разрешенных кодовых комбинаций длиной n, каждая из которых соответствует одной из информационных комбинаций. Если сравнить пару кодовых комбинаций длиной n символов, то число двоичных символов в которых они не совпадают, называют расстоянием. Если попарно сравнить все кодовые комбинации, минимальное из полученных расстояний называют кодовым расстоянием d, которое описывает способность кода исправлять или обнаруживать искажения в канале кодовых комбинаций.
Декодирование кода может производиться либо в режиме обнаружения ошибки, либо в режиме исправления ошибок. Если полученная из канала кодовая комбинация является одной из разрешенных, то она считается принятой правильно, хотя на самом деле могла передаваться другая разрешенная комбинация. Если принятая комбинация не является одной из разрешенных комбинаций, то в режиме обнаружения ошибки фиксируется факт обнаружения ошибки, и кодовая комбинация, в общем случае, стирается, т.е. удаляется из дальнейшей обработки, а в режиме исправления ошибки предпринимается попытка исправить искажение (исправить ошибки).
Исправление ошибки выполняется по какому-то правилу или критерию выбора разрешенной комбинации, в которую преобразуется принятая искаженная комбинация (не равная передаваемой в канал связи). При декодировании двоичных алгебраических кодов используется принцип максимума правдоподобия, в основу которого положено предположение, что в канале связи вероятность ошибки большей кратности меньше вероятности меньшей кратности. Т. е. если в канале может исказиться один из символов кодовой комбинации (кратность ошибки t = 1 ), два символа ( t = 2), три символа (t = 3) и т.д., то справедливо для вероятностей искажения Р(t = 1) > Р(t = 2) > Р(t = 3) … Если такое предположение справедливо для используемого дискретного канала, то в декодере, который не знает, что было искажено в принятой кодовой комбинации, оправдано отождествить с передаваемой комбинацией ту из разрешенных комбинаций, которая ближе по расстоянию от комбинации, подлежащей исправлению. Самая близкая (отличающаяся в меньшем числе символов) разрешенная комбинация считается переданной и объявляется результатом исправления ошибки.
При декодировании по принципу максимума правдоподобия справедливо утверждение, что код с кодовым расстоянием d правильно исправляет число ошибок t =[(d-1)/2], где [a] – меньшее целое от а. В то же время ясно, что если реальное число искаженных символов в кодовом блоке превышает величину [(d-1)/2], то произойдет неверное исправление ошибки (ошибка декодирования с вероятностью Рош ). Таким образом, код правильно исправляет ошибки с кратностью не выше [(d-1)/2], при этом число искаженных символов в принимаемой информационной последовательности уменьшается, и вносит ошибки декодирования в результате исправления ошибок с кратностью, превышающей величину [(d-1)/2], когда число искажений в информационной последовательности увеличивается (остаются искажения, полученные в канале связи, и добавляется неверное исправление в декодере). Понятно, что если в канале связи число ошибок в кодовой последовательности может превышать величину [(d-1)/2] с достаточно большой вероятностью, то реализация режима исправления ошибок может быть бесполезной или даже вредной.
В реальном канале связи часто наблюдается группирование ошибок, когда искажается не один двоичный символ, а целый пакет, длина которого может превышать величину [(d-1)/2]. Это обстоятельство является одной из причин, ограничивающей широкое применение кодов с исправлением ошибок. Для широкого применения кодов с исправлением ошибок такой код в качестве одного из своих свойств должен обеспечивать гарантированную границу для вероятности ошибки декодирования в канале связи с произвольным распределением потока ошибок в канале связи.
Обычно оценка вероятности ошибки декодирования делается для q-ичного симметричного канала при вероятности искажения q-ичного символа Pq. В таком канале с вероятностыо 1 — Pq q-ичный символ принимается верно, после его искажения с вероятностью Рq каждое значение q-ичного символа отличается от переданного и появляется на входе декодера с одинаковой вероятностью
Pq/(q-1).
В таком канале в зависимости от кратности ошибки t вероятность ошибки декодирования
при
при (1)
В канале, не являющемся q-ичным симметричным для кода РС, получены следующие оценки для
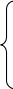 1/(q-1)i-2 + 1/(q-1)i при tРС =1
1/(q-1)i-2 + 1/(q-1)i при tРС =1
P (t) ≤ (2)
1/(q-1)i-2t -1/t! при tРС ≥ 2
При исправлении tРС ошибок в [9] предлагается оценка
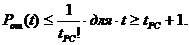 (3)
(3)
То есть, если кратность ошибки t превосходит исправляющую способность кода tpc, то в канале, не являющемся q-ичным симметричным, вероятность ошибки декодирования не зависит от основания кода q при исправлении tpc ошибок и достаточно близка к единице при малых tpc. Но q-ичный симметричный канал не существует в природе, особенно для больших q, свойство равновероятности (q—1) значений искаженного q-ичного символа для такого канала достигается применением стохастического преобразования q-ичных символов канала.[3]
Защита от ошибок в различных телекоммуникационных системах сводится к применению протоколов, содержащих описание двух основных функций: помехоустойчивого кодирования и управления передачей на конкретном протокольном уровне (для канального, сетевого и сеансового уровней) эталонной модели взаимодействия открытых систем (ЭМВОС). Защита информации в таких системах сводится не только к борьбе с независимыми искажениями в канале связи (в двоичном – симметричном канале ДСК), но и к защите от группирующихся искажений (пакетов ошибок) и от преднамеренных искажений. Выше было показано, что в канале с более сложным распределением потока ошибок, чем в ДСК, применение кодов, исправляющих ошибки, затруднено. Применение кодов с исправлением ошибок преднамеренного характера до последнего времени считалось в принципе невозможным, хотя бы для классических алгебраических кодов.
С учетом сказанного выше, можно сказать, что теория алгебраического кодирования с алгоритмом декодирования по принципу максимального правдоподобия для исправления независимых ошибок является примером того, как ошибочная постановка задачи о независимых ошибках в канале связи сводит практически на нет труды целого поколения исследователей.
Для обеспечения применения кодов, исправляющих ошибки, сформулируем два варианта постановки задачи. [4]
При этом будем учитывать требования к защите информации в современных информационных и телекоммуникационных системах.. Особенностями таких глобальных систем является передача очень больших массивов информации и использование различных каналов связи наиболее простым образом без проведения исследования их свойств, в том числе модели ошибок в них.
Первая постановка, являющаяся «мягкой», состоит в том, что применяемые коды с исправлением ошибок должны обеспечивать в канале с естественными помехами (ошибками) подвергаемую количественной оценке вероятность ошибки декодирования отдельно по следующим характерным интервалам кратности ошибки:
- кратность ошибки t меньше половины величины кодового расстояния d, т.е. t £ [(d-1)/2]
- кратность ошибки t меньше величины кодового расстояния d, т.е. t < d
- кратность ошибки t больше величины кодового расстояния d, t > d³
Вторая постановка, являющаяся сильной, состоит в том, что применяемые коды с исправлением ошибок должны обеспечивать в канале с произвольным характером ошибок гарантированную верхнюю границу для вероятности ошибки декодирование на всем интервале возможной кратности ошибки t £ n; причем эта граница должна устанавливаться при проектировании выбором параметров кода.
Из эвристических соображений сформулируем свойства помехоустойчивого кода с исправлением ошибок, которые позволили бы обеспечить его применение для защиты информации в современных информационных и телекоммуникационных системах в любых из существующих задачах применения.[14]
1. Код имеет режимы обнаружения и исправления ошибок с обеспечением в обоих режимах гарантированной (наперед заданной) вероятности декодирования с ошибкой в произвольном канале связи и надежным отказом от декодирования при невозможности исправления ошибки.
2. Код имеет такую исправляющую способность и позволяет выбрать такие параметры n и k, что использующий их алгоритм передачи информации характеризуется нехудшими вероятностно-временными характеристиками по сравнению с применением альтернативных кодов.
3. Код обеспечивает в режиме исправления ошибок выделение с заданной точностью части правильно принятых символов даже при кратности ошибки, превышающей исправляющую способность кода.
4. Код позволяет декодировать несколько копий (одинаковых по содержанию информации кодовых блоков) блока с эффективностью, превышающей эффективность декодирования исходного кода с обнаружением или исправлением ошибок. Это свойство может применяться для работы по параллельным каналам, при многократной передаче сообщения по одному каналу или в канале с обратной связью при обработке копий после приема повторенного блока.
5. Процедуры кодирования и декодирования кода содержат, в основном, операции по модулю 2.
6. Метод кодирования должен обладать свойствами случайности сигналов на выходе кодера, обеспечивающими совместное решение задач обеспечения помехоустойчивости и секретности в постановке К. Шеннона.
1.4.3 Код Шеннона
Оптимальным кодом можно определить тот, в котором каждый двоичный символ будет передавать максимальную информацию. В силу формул Хартли и Шеннона максимум энтропии достигается при равновероятных событиях, следовательно, двоичный код будет оптимальным, если в закодированном сообщении символы 0 и 1 будут встречаться одинаково часто.[8]
Рассмотрим в качестве примера оптимальное двоичное кодирование букв русского алфавита вместе с символом пробела «-». Полагаем, что известны вероятности появления в сообщении символов русского алфавита, например, приведенные в таблице 3.
Таблица 3.Частота букв русского языка (предположение)
|
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
Буква |
Частота |
|
«-» |
0,145 |
P |
0,041 |
Я |
0,019 |
X |
0,009 |
|
O |
0,095 |
B |
0,039 |
Ы |
0,016 |
Ж |
0,008 |
|
E |
0,074 |
Л |
0,036 |
З |
0,015 |
Ю |
0,007 |
|
A |
0,064 |
K |
0,029 |
Ъ, Ь |
0,015 |
Ш |
0,006 |
|
И |
0,064 |
M |
0,026 |
Б |
0,015 |
Ц |
0,004 |
|
T |
0,056 |
Д |
0,026 |
Г |
0,014 |
Щ |
0,003 |
|
H |
0,056 |
П |
0,024 |
Ч |
0,013 |
Э |
0,003 |
|
C |
0,047 |
У |
0,021 |
Й |
0,010 |
Ф |
0,002 |
К. Шеннон и Р. Фано независимо предложили в 1948-1949 гг. способ построения кода, основанный на выполнении условия равной вероятности символов 0 и 1 в закодированном сообщении. [10]
Все кодируемые символы (буквы) разделяются на две группы так, что сумма вероятностей символов в первой группе равна сумме вероятностей символов второй группы (то есть вероятность того, что в сообщении встретится символ из первой группы, равна вероятности того, что в сообщении встретится символ из второй группы).
Для символов первой группы значение первого разряда кода присваивается равным «0», для символов второй группы – равными «1».
Далее каждая группа разделяется на две подгруппы, так чтобы суммы вероятностей знаков в каждой подгруппе были равны. Для символов первой подгруппы каждой группы значение второго разряда кода присваивается равным «0», для символов второй подгруппы каждой группы – «1». Такой процесс разбиения символов на группы и кодирования продолжается до тех пор, пока в подгруппах не остается по одному символу.
Пример кодирования символов русского алфавита приведен в табл. 4
Таблица 4. Пример кодирования букв русского алфавита с помощью кода Шеннна-Фано.
|
Буквы |
Частоты |
Двоичные разряды |
||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
||
|
«-» |
0,145 |
0 |
0 |
0 |
||||||
|
O |
0,095 |
0 |
0 |
1 |
||||||
|
E |
0,074 |
0 |
1 |
0 |
0 |
|||||
|
A |
0,064 |
0 |
1 |
0 |
1 |
|||||
|
И |
0,064 |
0 |
1 |
1 |
0 |
|||||
|
T |
0,056 |
0 |
1 |
1 |
1 |
|||||
|
H |
0,056 |
1 |
0 |
0 |
0 |
|||||
|
C |
0,047 |
1 |
0 |
0 |
1 |
|||||
|
P |
0,041 |
1 |
0 |
1 |
0 |
0 |
||||
|
B |
0,039 |
1 |
0 |
1 |
0 |
1 |
||||
|
Л |
0,036 |
1 |
0 |
1 |
1 |
0 |
||||
|
K |
0,029 |
1 |
0 |
1 |
1 |
1 |
||||
|
M |
0,026 |
1 |
1 |
0 |
0 |
0 |
||||
|
Д |
0,026 |
1 |
1 |
0 |
0 |
1 |
0 |
|||
|
П |
0,024 |
1 |
1 |
0 |
0 |
1 |
1 |
|||
|
У |
0,021 |
1 |
1 |
0 |
1 |
0 |
||||
|
Я |
0,019 |
1 |
1 |
0 |
1 |
1 |
0 |
|||
|
Ы |
0,016 |
1 |
1 |
0 |
1 |
1 |
1 |
|||
|
З |
0,015 |
1 |
1 |
1 |
0 |
0 |
0 |
|||
|
Ъ, Ь |
0,015 |
1 |
1 |
1 |
0 |
0 |
1 |
|||
|
Б |
0,015 |
1 |
1 |
1 |
1 |
1 |
0 |
|||
|
Г |
0,014 |
1 |
1 |
1 |
1 |
0 |
1 |
|||
|
Ч |
0,013 |
1 |
1 |
1 |
1 |
1 |
0 |
|||
|
Й |
0,01 |
1 |
1 |
1 |
1 |
0 |
1 |
|||
|
X |
0,009 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
||
|
Ж |
0,008 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
||
|
Ю |
0,007 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
||
|
Ш |
0,006 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
||
|
Ц |
0,004 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
|
|
Щ |
0,003 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
|
|
Э |
0,003 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
|
Ф |
0,002 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
 Изучение данных в приведенной таблице кодов дает возможность сделать заключение, что наиболее часто встречающиеся буквы кодируются более краткими двоичными кодами, а редко встречающиеся - более длинными двоичными кодами. Соответственно, в среднем для кодирования послания определенной длины необходимо использовать меньшее количество двоичных знаков 0 и 1, чем при ином методе кодирования.
Изучение данных в приведенной таблице кодов дает возможность сделать заключение, что наиболее часто встречающиеся буквы кодируются более краткими двоичными кодами, а редко встречающиеся - более длинными двоичными кодами. Соответственно, в среднем для кодирования послания определенной длины необходимо использовать меньшее количество двоичных знаков 0 и 1, чем при ином методе кодирования.
Кроме того, процесс реализации кода Шеннона-Фано полностью удовлетворяет критерию различимости Фано. Данный вид кода считается префиксным и в нем нет потребности в использовании какого-либо специального символа, который будет отделять символы между собой для полностью однозначного декодирования двоичного послания.
Следовательно, задача помехоустойчивого шифрования представляет из себя довольно-таки большую сферу для теоретических и практических исследований. Главными целями в этом процессе можно считать: поиск кодов, с высокой эффективностью находящих и исправляющих ошибки определенного типа; поиск методик кодирования и декодирования и рациональных способов их программной реализации.
Данные задачи хорошо проработаны в области систематических кодов. Эти типы кодов эффективно используются в цифровой технике, различных автоматизированных комплексах и системах передачи данных.
2.Практическая реализация задачи кодирования
2.1 Пример к первой теореме Шеннона
Задача эффективного кодирования описывается триадой:
X = {X 4i 0} - кодирующее устройство - В.
Здесь Х, В - соответственно входной и выходной алфавит. Под множеством х 4i 0 можно понимать любые знаки (буквы, слова, предложения). В - множество, число элементов которого в случае кодирования знаков числами определяется основанием системы счисления 2 (например 2, m = 2 2) . Кодирующее устройство сопоставляет каждому сообщению x 4i 0 из Х кодовую комбинацию, составленную из n 4i символов множества В. Ограничением данной задачи является отсутствие помех. Требуется оценить минимальную среднюю длину кодовой комбинации.
Для решения данной задачи должна быть известна вероятность P 4i появления сообщения x 4i 0, которому соответствует определенное количество символов n 4i алфавита B. Тогда математическое ожидание количества символов из B определится следующим образом: n 4ср = n 4i P 4i (средняя величина).
Этому среднему количеству символов алфавита В соответствует максимальная энтропия H 4max = n 4ср log m. Для обеспечения передачи информации, содержащейся в сообщениях Х кодовыми комбинациями из В, должно выполняться условие H 4max >= H(x) 4, или n 4ср log m >= - P 4i log P 4i . В этом случае закодированное сообщение имеет избыточность
n 4ср >= H(x)/log m, n 4min = H(x)/log 4 m.
Коэффициент избыточности
Ku = (H 4max - H(x))/H 4max = (n 4ср - n 4min )/n 4ср .
Составим соответствующую таблицу. Имеем:
n 4min = H(x)/log 2 = 2.85, Ku = (2.92 - 2.85)/2.92 = 0.024,
т.е. код практически избыточности не имеет. Видно, что среднее количество двоичных символов стремится к энтропии источника сообщений.
2.2 Пример построения кода Шеннона
В таблице 2.2 приведены промежуточные вычисления и результат построения кода Шеннона. Средняя длина кодовых слов l = 2,95. В данном случае избыточность кода Шеннона на 0,5 бита больше, чем избыточность кода Хаффмена. Из этого рисунка понятно, почему код неэффективен. Кодовые слова для букв b , d , e , f могут быть укорочены на 1 бит без потери свойства однозначной декодируемой.
Таблица 2.2 Построение кода Шеннона
|
Буква |
Вероятность p m |
Кумулятивная вероятность q m |
Длина кодо- вого слова l m |
Двоичная запись [ q]2 |
Кодовое слово c m |
|
a |
0,35 |
0,00 |
2 |
0,00… |
00 |
|
b |
0,20 |
0,35 |
3 |
0,0101… |
010 |
|
c |
0,15 |
0,55 |
3 |
0,10001… |
100 |
|
d |
0,10 |
0,70 |
4 |
0,10110… |
1011 |
|
e |
0,10 |
0,80 |
4 |
0,11001… |
1100 |
|
f |
0,10 |
0,90 |
4 |
0,11100… |
1110 |
Докажем однозначную декодируемость кода Шеннона. Для этого выберем сообщения с номерами i и j , i < j . Кодовое слово ci для i заведомо короче, чем слово cj для j , поэтому достаточно доказать, что эти слова отличаются в одном из первых li символов.
Рассмотрим разность qj − qi =Σ pk − Σ pk =Σ pk ≥ pi
Вспомним, что длина слова и его вероятность связаны соотношением
li = [− log pi ]≥ − log pi .
Поэтому pi ≥2-li .
С учетом этого неравенства
q j − q i ≥ 2-li
В двоичной записи числа в правой части мы имеем после запятой li −1 нулей и единицу в позиции с номером li. Это означает, что по меньшей мере в одном из li разрядов слова ci и cj отличаются и, следовательно, ci не является префиксом для cj. Поскольку это верно для любой пары слов, то код является префиксным.
Заметим, что длины кодовых слов в коде Шеннона точно такие же, какие были выбраны при доказательстве прямой теоремы кодирования. Повторяя выкладки, получим уже известную оценку для средней длины кодовых слов
l ≤ H +1.
Примечательно, что при построении кода Шеннона мы выбрали длины кодовых слов приблизительно равными (чуть большими) собственной информации соответствующих сообщений. В результате средняя длина кодовых слов оказалось приблизительно равной (чуть большей) энтропии ансамбля.
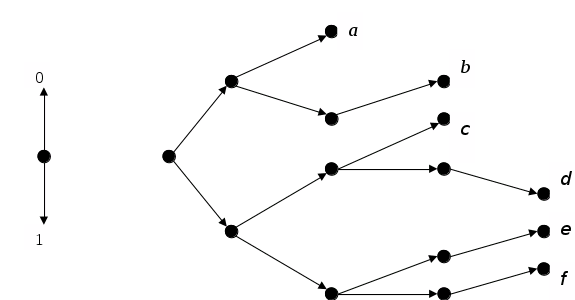
2.3 Пример Кода Шеннона
Допустим, нужно закодировать некоторое сообщение: AABCDAABC
Имеем :
A - 5 5/10 = 0.5
B - 2 2/10 = 0.2
C - 2 2/10 = 0.2
D - 1 1/10 = 0.1
Длина всего сообщения 10 (Вычисляется вероятность встречаемости каждого символа и располагаем их в столбик в порядке убывания вероятностей)
После этого строим кодовые комбинации простым методом. Делим столбик с вероятностями таким образом, чтобы сумма вероятностей верхней части равнялась приблизительно сумме вероятностей нижней части
0.5 - первая часть = 0.5
-----
0.2 \
0.2 | - вторая часть = 0.5
0.1 /
Напротив вероятностей верхней части проставляем нули, напротив нижней - единицы. В нашем примере получим.
0.5 0
0.2 1
0.2 1
0.1 1
Проделываем потом то же с разделёнными частями. В конце концов придём к тому, что делить больше нечего.
А 0.5 0
B 0.2 10
C 0.2 110
D 0.1 111
Итого - AABCDAABC = 0 0 10 110 111 0 0 10 110
Причём закодированное сообщение (это видно) не может быть раскодировано несколькими способами, хотя длина кодов символов отличается. Чтобы прочитать закодированное сообщение стpоится бинаpное деpево. В нашем слyчае оно бyдет такое.
()
/ \
0(A) 1
/ \
0(B) 1
/ \
0(C) 1(D)
Вот еще пример составления кодовых комбинаций по вероятностям:
0.3 00
0.25 01
--------------- (первое деление)
0.1 100
0.1 101
------------- (второе деление)
0.1 1100
0.05 1101
----------- (третье деление)
0.05 1110
0.05 1111
2.4 Пример кодирования и декодирования методом Шеннона-Фано
С помощью табл. 4 можно закодировать и декодировать любое сообщение. В виде примера запишем двоичным кодом фразу: "Теория информаций"
0 111 010000 11 01 000 11 011 11 0000
01101000111111 111 00110 100
11 0000 10111111 10101100110
Отметим, что здесь нет необходимости отделять буквы друг от друга специальным знаком, т.к. и без этого декодирование выполняется однозначно. Убедимся в этом, декодируя с помощью табл. 4 следующую фразу:
10011100110011001001111010000
1011100111001001101010000110101
010110000110110110
Результат декодирования - фраза "способ кодирования". При таком кодировании любая ошибка (случайное перепутывание знаков 0 и 1) губительна, т.к. декодирование всего следующего за ошибкой текста становится невозможным. Поэтому данный принцип кодирования используется тогда, когда ошибки при кодировании и передаче сообщения исключены.
Второй пример:
Построение кода Шеннона-Фано:
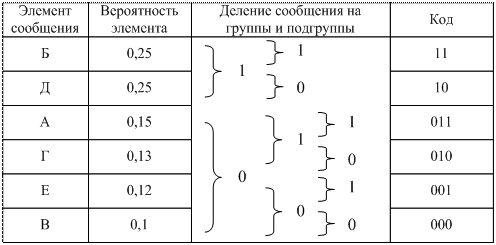
2. Образованный столбец символов делится на две группы таким образом, чтобы суммарные вероятности каждой группы мало отличались друг от друга.
3. Верхняя группа кодируется символом «1», а нижняя – «0».
4. Каждая группа делится на две подгруппы с близкими суммарными вероятностями; верхняя подгруппа кодируется символом «1», а нижняя – «0».
5. Процесс деления и кодирования продолжается до тех пор, пока в каждой подгруппе не окажется по одному символу сообщения источника.
6. Записывается код для каждого символа источника; считывание кода осуществляется слева направо.
При использовании простейшего равномерного кода для кодирования шести элементов алфавита источника потребуется по три двоичных символа на каждую букву сообщения. Если же используется код Шеннона – Фано, то среднее число символов на одну букву
|
|
что меньше, чем при простейшем равномерном коде и незначительно отличается от энтропии источника.
Заключение
В ходе курсовой работы была рассмотрена задача кодирования, которая включает в себя:
1.Обеспечение экономичности передачи информации посредством устранения избыточности.
2. Обеспечение надежности (помехоустойчивости) передачи информации
3.Согласование скорости передачи информации с пропускной способностью канала
Задача кодирования является одним из главных понятий информатики, так как кодирование предшествует передаче и хранению информации, и, соответственно, является основой их успешного осуществления.
При передаче сообщений по каналам связи могут возникать помехи, способные привести к искажению принимаемых знаков. Эта проблема решается с помощью помехоустойчивого кодирования. Помехоустойчивое кодирование передаваемой информации позволяет в приемной части системы обнаруживать и исправлять ошибки. Коды, применяемые при помехоустойчивом кодировании, называются корректирующими кодами. Впервые, исследование эффективного кодирования произвел Клод Шеннон. Для теории связи важнейшее значение имеют две теоремы, доказанные Шенноном.
В работе были рассмотрены эти теоремы, и можно прийти к выводу, что первая – затрагивает ситуацию с кодированием при передаче сообщения по линии связи, в которой отсутствуют помехи, искажающие информацию, т.е. эта теорема является эталоном, какими должны быть помехоустойчивые коды, Вторая теорема относится к реальным линиям связи с помехами.
В ходе курсовой работы были составлены примеры кодирования, на основе первой теоремы Шеннона. Это кодирования является достаточно эффективным, так как получаемый код практически не имеет избыточности, но, к сожалению, в реальных линиях связи множество помех, и такой результат недостижим. Поэтому код Шеннона не является таким же эффективным как, например код Хафмена. Но, несмотря на это нужно отметить, что Клод Шеннон был одним из основателей теории кодирования и его работы внесли огромный вклад в развитие информатики.
Список литературы
- Роль мотивации в поведении организации ( Сущность понятия мотивации. Мотивационный процесс)
- Финансы в макроэкономической системе (Анализ современной финансовой политики России в системе макроэкономического регулирования)
- Обзор языков программирования высокого уровня ( ЯЗЫКИ ПРОГРАММИРОВАНИЯ ВЫСОКОГО УРОВНЯ )
- Публичная власть (Общественный контроль: перспективы развития и современное состояние)
- Система управления качеством проекта (Процессы управления качеством проекта)
- Система управления качеством проекта (Краткая характеристика проекта)
- Гарантии прав и свобод человека и гражданина (История возникновения правовой системы и личности)
- Анализ прав и свобод человека и гражданина, закреплённых в Конституции Российской Федерации и других нормативно-правовых актах
- Соотношение системы права и системы законодательства (понятие и структура)
- Понятие и признаки государства (Территориальная организация населения, государственный суверенитет)
- Роль и перспективы развития розничной торговли в РФ
- Анализ деятельности спортивной организации на примере Национальной Баскетбольной Ассоциации

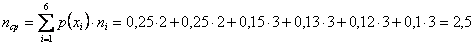 ,
,