Знакопеременные ряды - определение и вычисление с примерами решения

Содержание:

Абсолютная и условная сходимости:

Определение 28.1.1. Знакопеременным рядом называется ряд, членами которого являются вещественные числа произвольного знака.

Пусть

некоторый знакопеременный ряд. Составим ряд из модулей членов знакопеременного ряда:

Этот полученный ряд является рядом с положительными членами и поэтому его сходимость можно изучать методами, изложенными в лекции 27. А между сходимостью ряда (28.1.1) и сходимостью ряда (28.1.2) существует известная связь, т.е. справедливо следующее.

Определение 28.1.2. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов.

Знакопеременный ряд называется условно сходящимся, если он сходится, но не сходится абсолютно.

Заметим, что для условно сходящихся рядов некоторые привычные законы арифметики не имеют места.

Теорема 28.1.1. Всякий абсолютно сходящийся ряд сходится.

Доказательство. Пусть знакопеременный ряд (28.1.1) абсолютно сходится, т.е. это значит, что сходится ряд (28.1.2). В силу теоремы 27.2.2 ряд

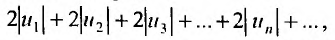полученный, умножением ряда (28.1.2) на число 2, сходится. Очевидно, что для любого n справедливо неравенство 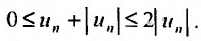Откуда, в силу I признака сравнения, следует сходимость ряда

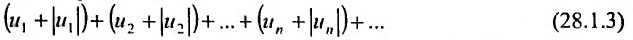
Вычитая из ряда (28.1.3) ряд (28.1.2), получим сходящийся ряд (28.1.1) в силу следствия из теоремы 27.2.3.

Теорема 28.1.2. Если 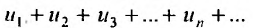абсолютно сходящийся ряд с суммой 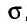, а сумма ряда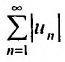

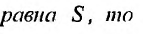
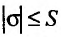
Доказательство. В силу свойства модулей, имеем 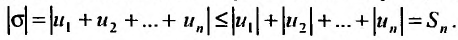Перейдем в этом неравенстве к пределу при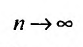 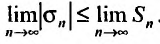. На основании свойства сходящейся последовательности², получим, что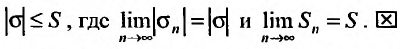

Следствие. Если n-ый остаток абсолютно сходящегося ряда (28.1.1) есть 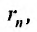, а n-ый остаток ряда (28.1.2) есть 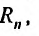то

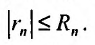
Если -элементы двух сходящихся последовательностей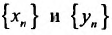 , начиная с некоторого номера, удовлетворяют неравенствам 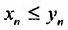, то и пределы этих последовательностей удовлетворяют такому же неравенству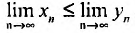

Пример:

Исследовать сходимость знакопеременного ряда

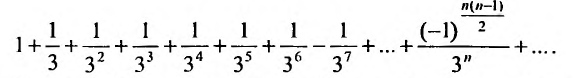
Решение:

Составляем ряд из абсолютных величин членов данного ряда:

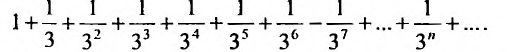
Построенный ряд сходится, так как является геометрическим рядом, со знаменателем 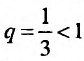Следовательно, данный ряд также сходится по теореме 28.1.1, (он является абсолютно сходящимся рядом в соответствии с определением 28.1.2).

Свойства условно сходящихся рядов

Теорема 28.2.1. Если знакопеременный ряд

сходится условно, то ряд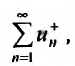 составленный из положительных членов, и ряд 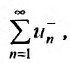, составленный из абсолютных величин отрицательных членов, расходятся.

Доказательство. Предположим сначала, что сходятся оба ряда

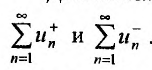Заменим в ряду 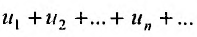все отрицательные члены нулями. Получим ряд, разбавленный нулями, который сходится, т.к. сходится ряд 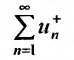по предположению. Заменяя в ряду 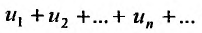все положительные члены нулями, а у отрицательных, изменяя знаки, получим сходящийся ряд 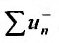. Сумма двух построенных «разбавленных» рядов есть ряд модулей членов ряда 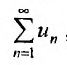, который по теореме о сумме сходящихся рядов, должен сходиться, что противоречит условию теоремы. Это означает, что оба ряда 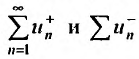расходятся.

Пусть теперь сходится один из рядов 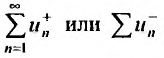Предположим для определенности, что ряд 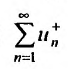сходится, а ряд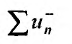расходится. Разбавим ряд 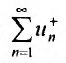нулями и вычтем полученный сходящийся ряд из ряда (28.1.1), изменив у оставшихся членов знаки.

Отбросив соответствующие нули, мы получим ряд 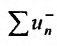который должен сходиться по теореме о вычитании рядов, что противоречит сделанному предположению.

Таким образом, учитывая оба предположения получаем, что оба ряда 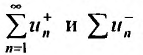расходятся.

Теорема 28.2.2. Пусть ряд (28.1.1) сходится условно. Тогда для любого числа S, можно так переставить его члены, что полученный сходящийся ряд 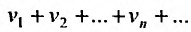имеет сумму S.

Доказательство. Будем выписывать подряд положительные члены ряда (28.1.1), пока их сумма не превзойдет S:

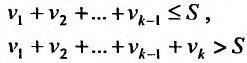
К имеющейся сумме припишем отрицательные члены ряда (28.1.1) пока новая сумма не опустится ниже S.

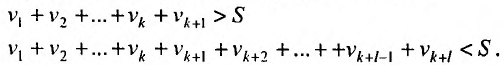
v, +v2 +...+V* +vA+l +vk+2 +... + +vi+M +vk+,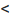S. Будем повторять этот процесс приписывания к сумме новых групп положительных и отрицательных членов, каждый раз минимально переходя через S. После каждого перехода частичная сумма ряда (28.1.1) будет по построению отличатся от S менее чем на абсолютную величину члена, последнего из приписанных в этом или предыдущем переходах. Но по необходимому признаку сходимости ряда эта абсолютная величина стремится к нулю. Следовательно, последовательность частичных сумм ряда (28.1.1) имеет пределом S. 

Определение знакочередующихся рядов

Определение 3.3. Знакопеременный ряд называется знакочередующимся, если его соседние члены имеют различные знаки, т.е.

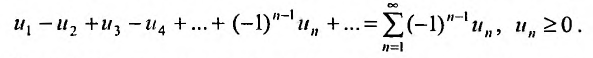
Примерами знакочередующихся рядов могут служить геометрические прогрессии с отрицательными знаменателями.

Для знакочередующихся рядов имеется достаточно общий, чувствительный и практичный признак сходимости Лейбница.

Теорема 28.3.1. (признак Лейбница). Если абсолютные величины членов знакочередующегося ряда

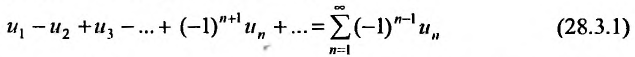
образуют монотонно убывающую последовательность, стремящуюся к нулю

и

то ряд (28.3.1) сходится.

Доказательство. Рассмотрим частичные суммы четного порядка ряда (28.3.1):

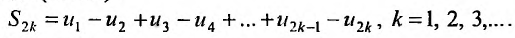Их можно записать в виде

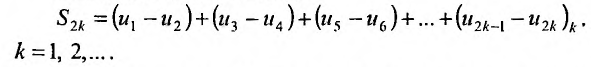
В силу условия (28.3.2) следует, что разности в круглых скобках неотрицательны и поэтому 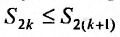, т.е. последовательность частичных сумм чётного порядка ряда (28.3.1) монотонно возрастастает. С другой стороны, частичные суммы можно записать и в виде:

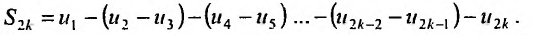
Разности в круглых скобках снова неотрицательны, т.к. выполняется (28.3.2), и 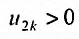. Поэтому,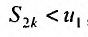, т.е. последовательность частичных сумм чётного порядка ограничена сверху. Из монотонного возрастания и ограниченности сверху, следует, что последовательность четных частичных сумм сходится, т.е.

Покажем, что и частичные суммы нечетного порядка ряда (28.3.1) стремятся к тому же пределу. Действительно, справедливо равенство 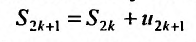и так как согласно (28.3.3) 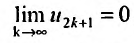, то, вычисляя предел левой и правой частей этого равенства, получим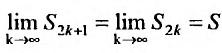, т.е.

Тогда из (28.3.4) и (28.3.5) следует, что 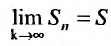. Следовательно, существует предел последовательности частичных сумм, что означает сходимость ряда (28.3.1).

Следствие. Для знакочередующегося ряда (28.3.1), удовлетворяющего признаку сходимости Лейбница, абсолютная величина остатка ряда не превышает абсолютной величины его первого члена, т.е.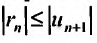

Действительно, остаток 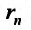можно рассматривать как сумму ряда 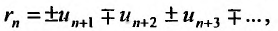которая, как следует из доказанной теоремы, не превышает по абсолютной величине своего первого члена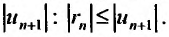

В заключение отмстим, что в признаке Лейбница все условия существенны и поэтому подлежат проверке.

• Заказать решение задач по высшей математике

Пример:

Исследовать сходимость ряда: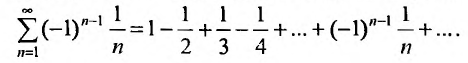

Решение:

Ряд, составленный из абсолютных величин членов данного ряда, является гармоническим рядом и, как правило, он расходится. Поэтому применим к данному ряду признак Лейбница. Условия признака выполнимы: ряд знакочередующийся; члены ряда убывают по модулю:

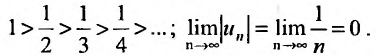
Следовательно, данный ряд сходится, причем сходится условно, так как ряд, составленный из модулей членов, расходится.

Пример:

Исследовать сходимость ряда:

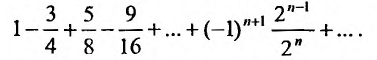
Решение:

Заданный ряд является знакочередующимся рядом. Абсолютные величины членов ряда убывают

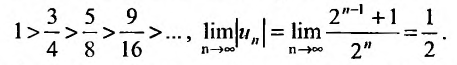
Следовательно, данный ряд расходится, так как не выполняется необходимый признак сходимости.

Из данного примера следует, что, применяя признак Лейбница, нужно проверять выполнимость всех условий.