
Замечательные пределы - определение и вычисление с примерами решения
Содержание:
Замечательные пределы
Сравнение бесконечно малых функций
Признак существования предела (теорема о 2-х милиционерах)
Теорема: Если значения функции 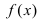
значениями функций 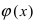
Рассмотрим геометрический смысл данной теоремы (Рис. 62). Из рисунка видно, что в случае, когда функции 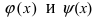 стягиваются к прямой у=А, то они “вынуждают” функцию
стягиваются к прямой у=А, то они “вынуждают” функцию 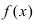 также приближаться к той же самой прямой (“куда идут два милиционера, ведущие арестованного, туда идет и сам арестованный”).
также приближаться к той же самой прямой (“куда идут два милиционера, ведущие арестованного, туда идет и сам арестованный”). 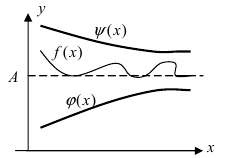
Рис. 62. Иллюстрация теоремы о “2-х милиционерах”.
Доказательство: Пусть 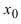 - точка сгущения для функций
- точка сгущения для функций 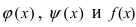 в общей области определения. Это означает, что в некоторой
в общей области определения. Это означает, что в некоторой 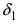 -окрестности точки
-окрестности точки 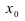 выполняется неравенство
выполняется неравенство 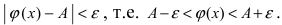 В
В 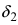 -окрестности точки
-окрестности точки 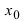 выполняется неравенство
выполняется неравенство 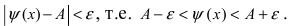 Так как значения функции
Так как значения функции 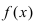 заключены между значениями функций
заключены между значениями функций 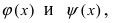 то в некоторой
то в некоторой 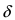 -окрестности точки
-окрестности точки 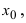 меньшей из
меньшей из 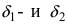 -окрестностей будет выполняться неравенство
-окрестностей будет выполняться неравенство 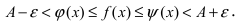 Отсюда следует, что выполняется неравенство
Отсюда следует, что выполняется неравенство 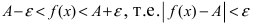 или
или 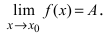
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 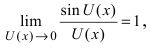 и называется первым замечательным пределом.
и называется первым замечательным пределом.
Пример:
Пределы являются первыми замечательными пределами 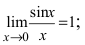
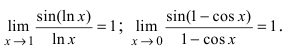
Доказательство: Для вывода этой формулы построим окружность с центром в точке О(0; 0) и радиусом R = 1. Выберем угол 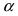 в первой координатной четверти и сравним площади трех фигур: треугольник АОВ, сектор АОВ и треугольник AOD (Рис. 63):
в первой координатной четверти и сравним площади трех фигур: треугольник АОВ, сектор АОВ и треугольник AOD (Рис. 63): 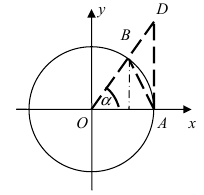
Рис. 63. Иллюстрация вывода формулы первого замечательного предела.
Из рисунка видно, что площади указанных фигу р связаны соотношением:
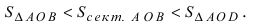
Вычислим эти площади 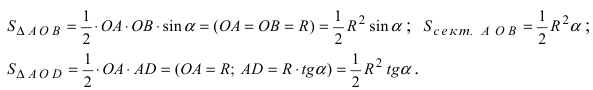
Следовательно, вышеприведенное неравенство приводится к виду 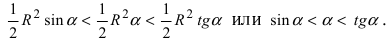 В силу того, что
В силу того, что 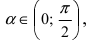 получаем
получаем 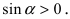 Разделим полученное неравенство на
Разделим полученное неравенство на 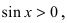 знак всех неравенств не изменится:
знак всех неравенств не изменится: 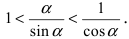 Переходя к обратным неравенствам,
Переходя к обратным неравенствам, 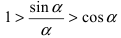 или в силу того, что
или в силу того, что  то по теореме о 2-х милиционерах
то по теореме о 2-х милиционерах 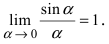
Аналогично проводится доказательство для любого значения угла 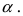
Таким образом, наличие в пределе, сводящемся к неопределенности 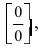 тригонометрических функции может указывать на первый замечательный предел.
тригонометрических функции может указывать на первый замечательный предел.
При вычислении первого замечательного предела используют следующие формулы:
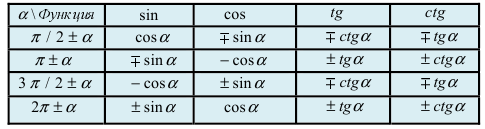
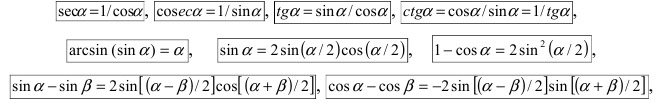 а также следующие таблицы:
а также следующие таблицы:
Табл. 1. Значения синуса и косинуса на интервале 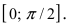

Табл. 2. Формулы приведения.
Пример:
Найти 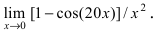
Решение:
При подстановке предельной величины переменной х имеем неопределенность 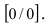 Воспользуемся формулой
Воспользуемся формулой 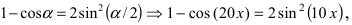 и преобразуем данный предел следующим образом:
и преобразуем данный предел следующим образом: 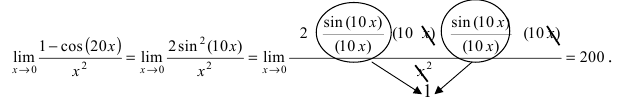
Пример:
Найти 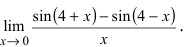
Решение:
При подстановке предельного значения переменной х имеем неопределённость 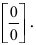 Воспользуемся формулой
Воспользуемся формулой 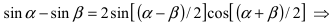
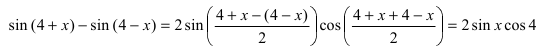 тогда данный предел равен:
тогда данный предел равен: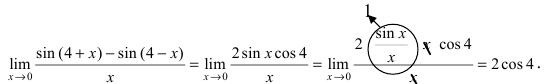
Пример:
Найти 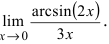
Решение:
При подстановке предельного значения переменной х имеем неопределённость 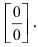 Введём замену
Введём замену 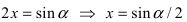 (при
(при 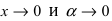 ) и воспользуемся следующей формулой
) и воспользуемся следующей формулой 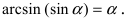 Предел преобразуется к виду:
Предел преобразуется к виду:
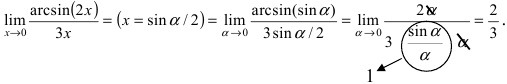
Пример:
Найти 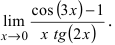
Решение:
При подстановке предельного значения переменной х имеем неопределённость 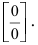 Воспользуемся формулами
Воспользуемся формулами 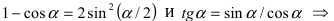
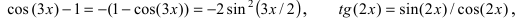 получим:
получим: 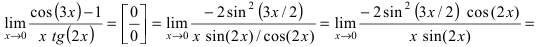
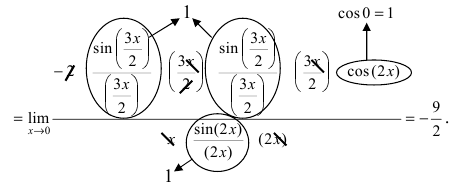
Число e и натуральные логарифмы. Второй замечательный предел
Рассмотрим логарифмическую функцию 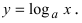 Выбирая различные значения основания, будем вычислять тангенсы угла наклона касательной к графику этой функции в точке
Выбирая различные значения основания, будем вычислять тангенсы угла наклона касательной к графику этой функции в точке 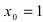 (см. график логарифмической функции в Лекции № 22).
(см. график логарифмической функции в Лекции № 22).
Определение: Натуральным логарифмом называется логарифм, для которого основание выбрано так, чтобы тангенс угла наклона касательной к положительному направлению оси абсцисс (Ох) был равен 1.
Основанием натурального логарифма является число 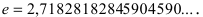 Это число трансцедентное, т.е. не является решением ни одного алгебраического уравнения. Установим связь между натуральными
Это число трансцедентное, т.е. не является решением ни одного алгебраического уравнения. Установим связь между натуральными 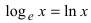 и десятичными
и десятичными 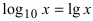 логарифмами:
логарифмами: 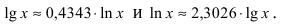
Определение: Вторым замечательным пределом называется предельное равенство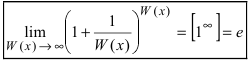 (первая форма)
(первая форма)
или
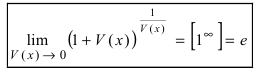 (вторая форма).
(вторая форма).
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 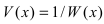 с учетом теоремы о связи бесконечно большой функции с бесконечно малой функцией.
с учетом теоремы о связи бесконечно большой функции с бесконечно малой функцией.
Замечание: Наличие неопределенности 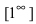 указывает на второй замечательный предел, т.е. если пределы функций
указывает на второй замечательный предел, т.е. если пределы функций 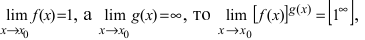 что указывает на второй замечательный предел.
что указывает на второй замечательный предел.
Пример:
Найти 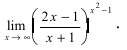
Решение:
При подстановке предельного значения переменной х не имеем неопределенности 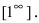
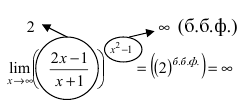 - не второй замечательный предел.
- не второй замечательный предел.
Пример:
Найти lim 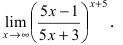
Решение:
При подстановке предельного значения переменной х имеем неопределенность 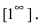 Проведём преобразование подлимитной функции:
Проведём преобразование подлимитной функции: 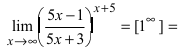 ( - первая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела)
( - первая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела) 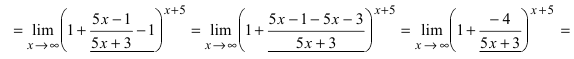
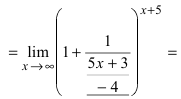 (роль функции
(роль функции 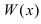 играет выражение
играет выражение 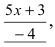 возведем круглую скобку в эту степень, а за квадратной скобкой возведем в обратную степень для тождественности проводимых преобразований, получим) =
возведем круглую скобку в эту степень, а за квадратной скобкой возведем в обратную степень для тождественности проводимых преобразований, получим) =
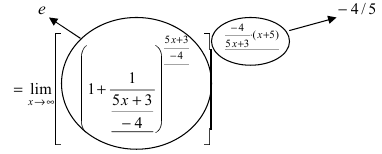 = (выражение в квадратных скобках стремится к числу е, а показатель степени - к числу -4/5 (см. раскрытие неопределённости
= (выражение в квадратных скобках стремится к числу е, а показатель степени - к числу -4/5 (см. раскрытие неопределённости 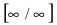 для полиномов примере из пункта Вычисление пределов и раскрытие неопределенностей поэтому окончательный ответ имеет вид)=
для полиномов примере из пункта Вычисление пределов и раскрытие неопределенностей поэтому окончательный ответ имеет вид)= 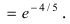
Пример:
Найти 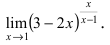
Решение:
При подстановке предельного значения переменной х имеем неопределенность 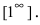 Проведём преобразование подлимитной функции:
Проведём преобразование подлимитной функции:
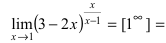 (вторая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела)=
(вторая форма второго замечательного предела, преобразуем данное выражение под вид второго замечательного предела)= 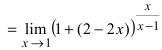 = (роль функции
= (роль функции 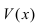 играет выражение (2-2х))=
играет выражение (2-2х))= 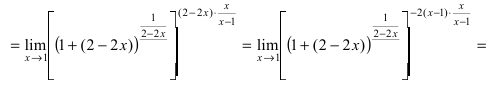
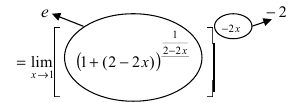 =(выражение в квадратных скобках стремится к числу е, а показатель степени - к числу -2 (подставить в показатель степени вместо переменной х ее предельное значение 1), поэтому окончательный ответ имеет вид)
=(выражение в квадратных скобках стремится к числу е, а показатель степени - к числу -2 (подставить в показатель степени вместо переменной х ее предельное значение 1), поэтому окончательный ответ имеет вид) 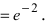
Сравнение бесконечно малых функций
Сравнить две бесконечно малые функции 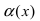 и
и 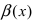 означает вычислить предел
означает вычислить предел 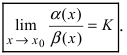
Определение: Если предел К не существует, то бесконечно малые функции 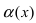 и
и 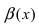 называются несравнимыми.
называются несравнимыми.
Пример:
Пусть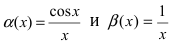 - две бесконечно малые функции при
- две бесконечно малые функции при 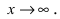 Доказать, что эти бесконечно малые функции несравнимые.
Доказать, что эти бесконечно малые функции несравнимые.
Решение:
Для доказательства вычислим предел 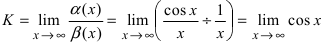 -данный предел не существует, так как нельзя указать предельное значение для подлимитной функции cosx на бесконечности.
-данный предел не существует, так как нельзя указать предельное значение для подлимитной функции cosx на бесконечности.
Определение: Если предел К равен нулю, то бесконечно малая функция 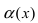 называется бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция
называется бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция 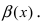
Пример:
Пусть 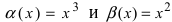 - две бесконечно малые функции при
- две бесконечно малые функции при 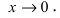 Доказать, что бесконечно малая функция
Доказать, что бесконечно малая функция 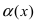 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция 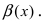
Решение:
Для доказательства вычислим предел 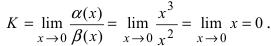 Следовательно, бесконечно малая функция
Следовательно, бесконечно малая функция 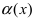 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малая функция 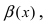 при
при 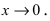
Определение: Если предел К равен 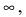 то бесконечно малая функция
то бесконечно малая функция 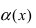 называется бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция
называется бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция 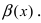
Пример:
Пусть 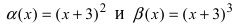 - две бесконечно малые функции при
- две бесконечно малые функции при 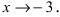 Доказать, что бесконечно малая функция
Доказать, что бесконечно малая функция 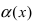 является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция
является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция 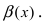
Решение:
Для доказательства вычислим предел 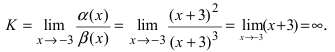
Следовательно, бесконечно малая функция 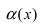 является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция
является бесконечно малой функцией более низкого порядка малости, чем бесконечно малая функция 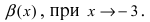
Определение: Если предел К равен конечному числу 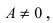 то бесконечно малые функции
то бесконечно малые функции 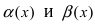 называются бесконечно малыми функциями одного порядка малости.
называются бесконечно малыми функциями одного порядка малости.
Пример:
Пусть 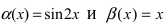 - две бесконечно малые функции при
- две бесконечно малые функции при 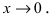 Доказать, что бесконечно малые функции
Доказать, что бесконечно малые функции 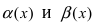 являются бесконечно малыми функциями одного порядка малости.
являются бесконечно малыми функциями одного порядка малости.
Решение:
Для доказательства вычислим предел 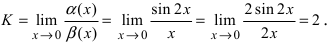
Следовательно, бесконечно малые функции 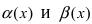 являются бесконечно малыми функциями одного порядка малости при
являются бесконечно малыми функциями одного порядка малости при 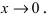
Определение: Если предел К равен 1, то бесконечно малые функции а(х) и Д(х) называются эквивалентными.
Пример:
Пусть 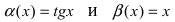 - две бесконечно малые функции при
- две бесконечно малые функции при 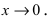 Доказать, что бесконечно малые функции
Доказать, что бесконечно малые функции 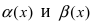 являются эквивалентными.
являются эквивалентными.
Решение:
Вычислим предел 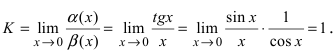 Следовательно, бесконечно малые функции
Следовательно, бесконечно малые функции  являются эквивалентными при
являются эквивалентными при  Рассмотрим признак эквивалентности бесконечно малых функций.
Рассмотрим признак эквивалентности бесконечно малых функций.
Теорема: Для того чтобы бесконечно малые функции  были эквивалентными, необходимо и достаточно, чтобы разность бесконечно малых функций
были эквивалентными, необходимо и достаточно, чтобы разность бесконечно малых функций 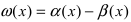 была бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции
была бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции  .
.
Доказательство:
1. Необходимость. Пусть бесконечно малая функция 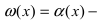
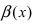 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции 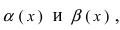 т.е. пределы
т.е. пределы 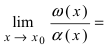
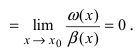 Докажем, что бесконечно малые функции
Докажем, что бесконечно малые функции 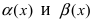 эквивалентны. Преобразуем первый из этих пределов:
эквивалентны. Преобразуем первый из этих пределов: 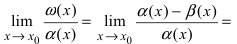
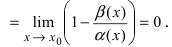 Отсюда следует, что
Отсюда следует, что 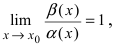 т.е. бесконечно малые функции
т.е. бесконечно малые функции 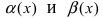 эквивалентны. Аналогично преобразуется второй пре- дел.
эквивалентны. Аналогично преобразуется второй пре- дел.
2. Достаточность. Пусть бесконечно малые функции 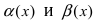 являются эквивалентными, т.е.
являются эквивалентными, т.е. 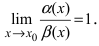 Докажем, что разность двух бесконечно малых функций
Докажем, что разность двух бесконечно малых функций 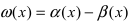 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции 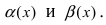 Преобразуем данный предел следующим образом:
Преобразуем данный предел следующим образом: 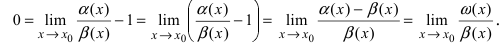 Отсюда следует, что функция
Отсюда следует, что функция 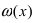 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции 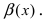 Аналогично доказывается, что функция
Аналогично доказывается, что функция 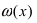 является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции
является бесконечно малой функцией более высокого порядка малости, чем бесконечно малые функции 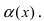
Замечание: При вычислениях одна бесконечно малая функция может быть заменена на эквивалентную бесконечно малую функцию. Например, функции 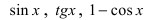 эквивалентны функции х при
эквивалентны функции х при 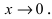
---вышмат
Замечательные пределы
Первый замечательный предел
Предел отношения синуса бесконечно малой дуги к самой дуге, выраженной в радианах, равен единице:
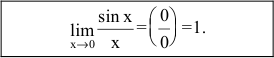 Следовательно,
Следовательно,
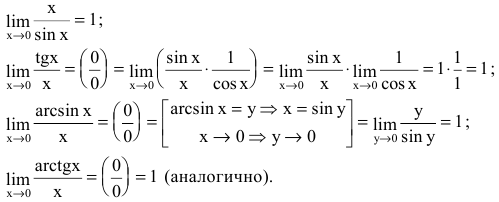
Пример №25
Найти 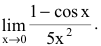
Решение:
Применим первый замечательный предел: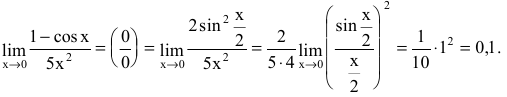
Второй замечательный предел
Числом е называется предел функции
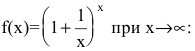
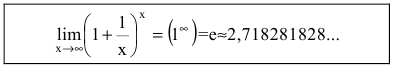
(Для запоминания: 2<е<3; 1828 - год рождения Л.Н. Толстого) Следовательно, 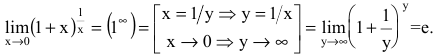
Задача о непрерывном начислении процентов
Первоначальный вклад в банк составил 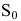 денежных единиц. Банк выплачивает ежегодно
денежных единиц. Банк выплачивает ежегодно 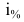 годовых. Необходимо найти размер вклада
годовых. Необходимо найти размер вклада 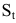 через t лет.
через t лет.
Решение:
Размер вклада будет увеличиваться ежегодно в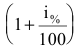 раз и
раз и
через t лет составит 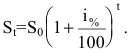 Если же начислять проценты n раз в году,
Если же начислять проценты n раз в году,
то будущая сумма составит 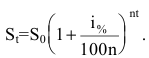 Предположим, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365), каждый час (n=8760) и, наконец, непрерывно (n
Предположим, что проценты по вкладу начисляются каждое полугодие (n=2), ежеквартально (n=4), ежемесячно (n=12), каждый день (n=365), каждый час (n=8760) и, наконец, непрерывно (n ). Тогда за год размер вклада составит:
). Тогда за год размер вклада составит: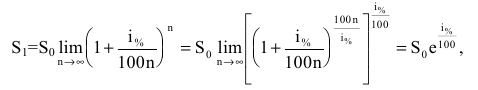
а за t лет: 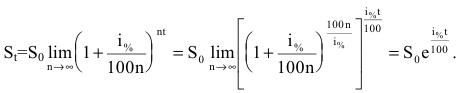
Пример №26
Найти 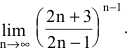
Решение:
Т.к. 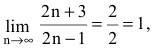 имеем неопределенность вида
имеем неопределенность вида 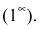 Для ее раскрытия воспользуемся вторым замечательным пределом, выделив предварительно у дроби целую часть:
Для ее раскрытия воспользуемся вторым замечательным пределом, выделив предварительно у дроби целую часть:
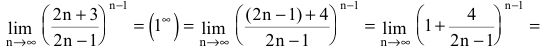
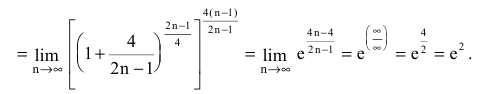
Пример №27
Найти 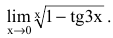
Решение:
Преобразуя выражение и используя непрерывность показательно-степенной функции, получим:
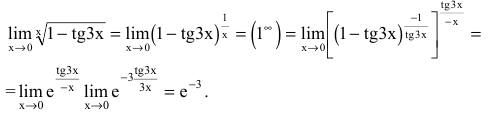
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Непрерывность функций и точки разрыва
- Точки разрыва и их классификация
- Дифференциальное исчисление
- Исследование функций с помощью производных
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Бесконечно малые и бесконечно большие функции