Законы и правила Кирхгофа для электрических цепей

Применение законов Кирхгофа для расчета сложных цепей:

В предыдущих главах рассматривались простейшие схемы электрических цепей — одноконтурные схемы, цепная схема с одним источником электрической энергии и схемы с двумя узлами. Были описаны методы преобразования схем, с помощью которых в ряде случаев удается упростить расчет разветвленной электрической цепи. При этом под расчетом цепи подразумевается вычисление значений электрических величин или их отношений при заданных схеме и параметрах цепи.

В случае, когда схема электрической цепи достаточно сложна и не приводится к схеме одноконтурной цепи или цепи с двумя узлами, пользуются более общими методами расчета.

Описываемые ниже методы и теоремы применимы для цепей постоянного и переменного тока; ради общности изложения они приводятся в комплексной форме.

В общем случае искомые значения электрических величин и их соотношения могут быть найдены в результате совместного решения системы уравнений, выражающих первый и второй законы Кирхгофа для заданной электрической цепи.

Положим, что в схеме, содержащей р ветвей и q-узлов, заданными являются источники э. д. с., а искомыми — токи в ветвях. Следовательно, число неизвестных равно числу ветвей.

По первому закону Кирхгофа, выражающему равенство нулю алгебраической суммы токов в узле, может быть записано q — 1 независимых уравнений; уравнение для последнего, q-го, узла является следствием предыдущих q — 1 уравнений. Действительно, ввиду того, что каждая ветвь связывает два узла, ток каждой ветви входит дважды с различными знаками в уравнения, записанные для q узлов. Поэтому если просуммировать q уравнений, то получится тождество вида 0 = 0. Следовательно, одно из этих уравнений является зависимым, т. е. вытекающим из всех остальных уравнений.

Узлы, для которых записываются независимые уравнения по первому закону Кирхгофа, можно назвать независимыми узлами. Из сказанного следует, что из общего числа q узлов любые q — 1 узлов являются независимыми, а оставшийся последний узел является зависимым.

По второму закону Кирхгофа, выражающему равенство алгебраической суммы э. д. с. в контуре алгебраической сумме падений напряжения в нем, может быть записано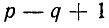

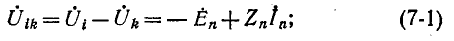
здесь 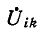— комплексное напряжение между узлами i и k; 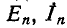— комплексные э. д. с. источника и Ток в n-й ветви, направленные от узла i к узлу 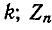— комплексное сопротивление той же ветви.

В систему уравнений вида (7-1) входят р неизвестных токов 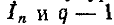неизвестных потенциалов 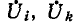и т. д. (потенциал одного из узлов принимается равным нулю). Если из имеющейся системы уравнений исключить эти неизвестные потенциалы, останется р — q + 1 уравнений, связывающих комплексные э. д. с. источников с напряжениями на комплексных сопротивлениях; полученные таким путем уравнения выражают второй закон Кирхгофа.

Итак, расчет электрической цепи с помощью первого и второго законов Кирхгофа сводится к решению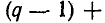 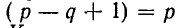уравнений — по числу ветвей.

Контуры, для которых уравнения, записанные по второму закону Кирхгофа, являются независимыми, называются независимыми контурами.

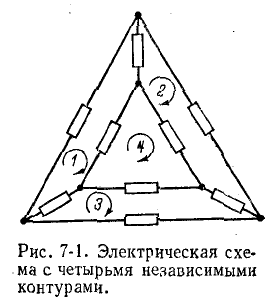
На рис, 7-1 в виде примера показана электрическая схема с числом ветвей р — 9 и числом узлов q — 6. Соответственно число уравнений по первому закону Кирхгофа равно 9 — 6 = 3 и по второму закону Кирхгофа 9 — 6  + 1 = 4. В схеме рис. 7-1 независимыми являются четыре контура. На рис. 7-1 показан один из многих возможных вариантов выбора независимых контуров.

Для того чтобы уравнения по второму закону Кирхгофа, а следовательно, и сами контуры были независимыми, достаточно, чтобы каждый последующий контур отличался от предыдущих хотя бы одной новой ветвью. Например, если в схеме рис. 7-1 обходить контур 4 не в последнюю очередь, то каждый последующий контур будет содержать новую ветвь.

Независимый контур в отдельных случаях может не содержать новой ветви схемы, например контур 4 в схеме рис. 7-1, если обходить контуры в порядке их нумерации. При выборе независимых контуров заданную схему цепи удобно изображать в виде г р а ф а, в котором ветви представляются отрезками линий; идеальный источник э. д. с. учитывается как короткозамкнутая ветвь, а идеальный источник тока — как разомкнутая ветвь. На рис. 7-2, а показан граф схемы рис. 7-1.

Граф содержит всю информацию, относящуюся к геометрической структуре соединения ветвей.

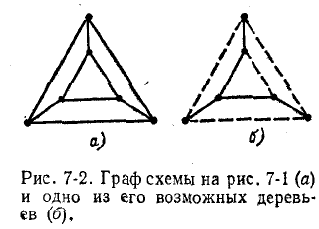
Часть графа, содержащая все узлы, но не содержащая ни одного замкнутого контура, называется деревом графа.

Легко показать, что число ветвей дерева на единицу меньше числа узлов схемы, г. е. равно q— 1.

Ветви графа, не входящие в состав дерева, называются главными ветвями дерева или хордами. Подключение к дереву каждой из главных ветвей создает по одному независимому контуру. Совокупность главных ветвей дерева называется дополнением дерева. Так как граф содержит р ветвей, а дерево q — I, то число главных ветвей дерева равно р — (q — I) = р — q + 1, т. е. числу независимых контуров.

На рис. 7-2, б сплошными линиями показано одно из возможных деревьев графа, а пунктиром — главные ветви дерева.

Из сказанного следует способ выбора независимых контуров: чертится дерево схемы и затем поочередно добавляются главные ветви. Любой контур, образуемый добавлением новой ветви, является независимым, так как он отличается от предыдущих контуров новой ветвью. Когда к дереву добавятся все главные ветви, получится граф схемы и число независимых контуров станет достаточным для расчета цепи.

Предлагаем читателям выбрать таким способом независимые контуры в схеме рис. 7-1.

Для получения независимых контуров, достаточных для расчета цепи, можно начать и не с построения дерева, а с самого графа схемы, а затем поочередным размыканием главных ветвей дойти до дерева. В этом случае руководствуются следующим правилом: в заданной схеме выбирается какой-либо контур, размыкается одна из ветвей этого контура и в оставшейся части схемы выбирается новый контур, затем размыкается одна ветвь этого нового контура и т. д. до тех пор, пока в схеме не останется ни одного контура.

Предлагаем читателям применить для выбора независимых контуров и это правило.

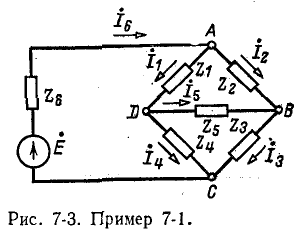
Пример 7-1.. В мостовой схеме, представленной на рис. 7-3, заданы все комплекс-, ные сопротивления и э. д. с. Е. Требуется определить ток 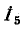в ветви 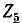(ток в диагонали мостовой схемы).

Схема содержит четыре узла и шесть ветвей. Следовательно, могут быть составлены три уравнения по первому закону Кирхгофа и три уравнения по второму закону Кирхгофа

: для узла А

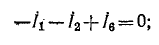
для узла В

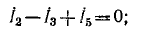
для узла С

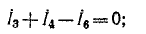
для контура ABDA

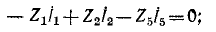
для контура BCDB

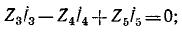
для контура АВС А

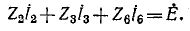
В полученной системе из шести уравнений неизвестными являются токи в ветвях. Решая систему уравнений относительно искомого тока, находим:

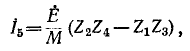
где

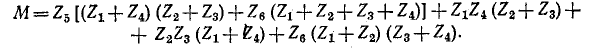
Полученное выражение показывает, что ток в диагонали равен нулю, если выполнено условие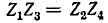 (условие равновесия мостовой схемы).

Применение законов Кирхгофа для разветвленных электрических цепей

Рассмотрим применимость данного метода на примере схемы, представленной на рис. 3.1.

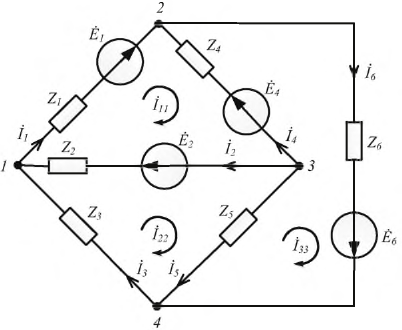
Рис. 3.1. Разветвленная цепь с источниками ЭДС

Для составления уравнений зададимся произвольно положительными направлениями токов в ветвях.

Уравнения по первому закону Кирхгофа:

1^ый узел: 

2^ой узел: 

4^ый узел: 

Если просуммировать уравнения 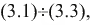то получим

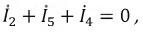
т.е. уравнение для третьего узла. Оно является избыточным, т.к. не содержит новых токов, следовательно, по первому закону Кирхгофа составляем уз. - 1 уравнений, где уз. - число узлов схемы.

Остальные 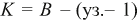 уравнения составляем по второму закону Кирхгофа, где  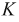— число независимых контуров,  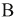- число ветвей. Направления обхода контуров произвольны:

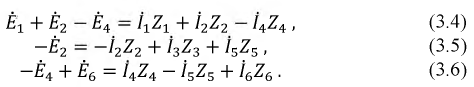
Для уменьшения объема работ по расчету схемы применяют искусственные методы расчета.