Закон сохранения механической энергии в теоретической механике

Закон сохранения механической энергии:

Для материальной точки теорему об изменении кинетической энергии можно выразить в следующем виде:

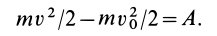
Если материальная точка движется в стационарном потенциальном силовом поле, то

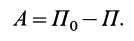
Следовательно,

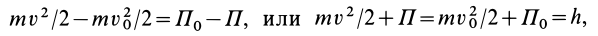
где 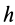 — постоянная величина.

Обозначая через 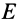полную механическую энергию точки, состоящую из ее кинетической и потенциальной энергий, получаем

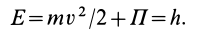
Таким образом, при движении точки в стационарном потенциальном силовом поле ее полная механическая энергия остается постоянной величиной, что является законом сохранения механической энергии для точки, который и есть первый интеграл дифференциальных уравнений движения точки.

Закон сохранения механической энергии системы

Теорему об изменении кинетической энергии для системы можно представить в виде

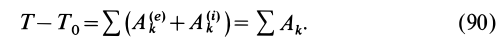
Если система движется в стационарном потенциальном силовом поле, то

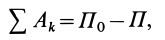
где 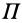—потенциальная энергия внутренних и внешних сил, действующих на систему. Следовательно,

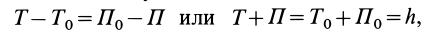
где 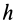— постоянная величина.

Обозначая через 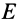полную механическую энергию системы, имеем

Формула (91) выражает закон сохранения механической энергии для системы: полная механическая энергия при движении системы в стационарном потенциальном силовом поле внешних и внутренних сил является постоянной величиной.

В случае абсолютно твердого тела работа всех внутренних сил равна нулю и, следовательно, потенциальная энергия внутренних сил является постоянной величиной, которую можно считать равной нулю. Тогда в (91) за потенциальную энергию следует принять только потенциальную энергию внешних сил, которая вместе с кинетической энергией является постоянной величиной. При движении изменяемой механической системы сумма кинетической энергии системы и потенциальной энергии внешних сил не является постоянной. Она становится постоянной только вместе с потенциальной энергией внутренних сил. Механические системы, для которых выполняется закон сохранения механической энергии, называют консервативными.

При движении точки или системы в непотенциальном силовом поле, встречающемся в действительности, когда непотенциальность связана с действием сил сопротивления, механическая энергия изменяется, причем она всегда уменьшается на работу сил сопротивления. Потерянная системой часть механической энергии обычно переходит в тепловую энергию. Полная энергия всех видов (механическая, тепловая, химическая и т. д.) не изменяется при движении точки или системы в любом силовом поле. При этом происходит только преобразование одного вида энергии в другой.

Рассмотрим теперь комплексный пример на основные виды движения твердого тела: поступательное, вращение вокруг неподвижной оси и плоское движение, а также вычисление количества движения, кинетического момента и кинетической энергии системы.

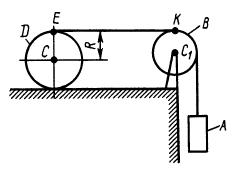
Рис. 78    

Пример:

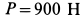Груз силой тяжести  опускается вниз, приводя в движение с помощью невесомой и нерастяжимой нит и однородный диск силой тяжести (рис. 78). Нить намотана на диск  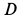и переброшена через блок  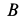силой тяжести 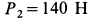. Нить по блоку не скользит. Диск 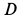имеет радиус 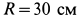. Он движется по горизонтальному рельсу. Коэффициент трения скольжения между диском и рельсом 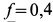; коэффициент трения качения 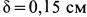. Блок считать однородным диском с радиусом 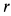. Трением на оси блока пренебречь. Система начинает движение из состояния покоя.

Определить уравнения движения диска 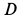, давления блока 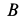на ось, количество движения и кинетическую энергию системы и кинетический момент катка 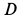относительно его точки соприкосновения с рельсом через 1 с после начала движения.

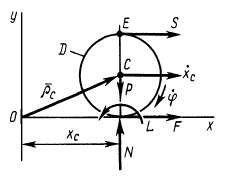
Рис. 79

Решение:

Составим уравнения движения отдельных тел под действием приложенных к ним сил.

Каток совершает плоское движение. К нему приложены внешние для него сила тяжести , натяжение нити и реакция рельса, состоящая из нормальной реакции N, силы трения 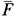и пары сил, препятствующей качению с моментом 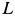(рис. 79). Силу трения предполагаем направленной в положительную сторону оси .

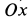При составлении уравнений моменты сил и угловые характеристики тел считаем положительными, если они направлены против часовой стрелки.

Для катка 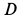 имеем следующие уравнения движения:

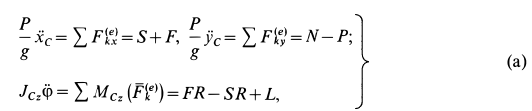
где 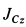— момент инерции катка относительно оси 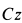, проходящей через центр масс перпендикулярно плоскости диска. При сделанном выборе осей координат 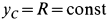и, следовательно, .

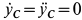Блок 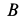вращается вокруг неподвижной оси 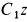, проходящей через его центр масс 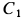(рис. 80). На блок действуют внешние силы тяжести 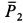, реакция оси с составляющими 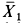,  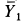 и силы натяжения нитей, числовые значения которых 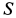и 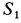. Дифференциальное уравнение вращения блока вокруг неподвижной оси

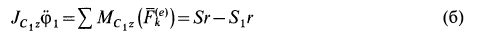
где 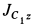— момент инерции блока относительно оси вращения .

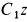Груз 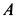совершает прямолинейное движение по оси 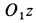(рис. 81). К нему приложены внешние силы тяжести 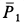и натяжения нити, числовое значение которой 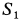. Уравнение движения груза

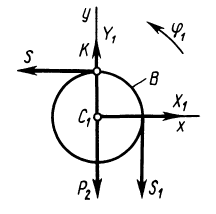
Рис. 80

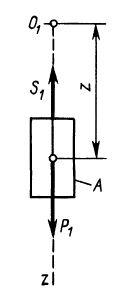
Рис. 81

Имеем систему пяти уравнений (а), (б), (в), в которую входят девять неизвестных: 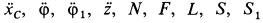. Так как 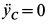, то его считаем известным.

К системе пяти уравнений движения следует добавить уравнения связи движений тел вследствие нерастяжимости нити и отсутствия ее скольжения по катку 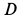и блоку .

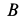Если переменные величины отсчитывать от начальных положений тел, то для момента времени 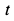для блока и груза (рис. 80, 81) получаем 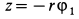и после дифференцирований по времени

Знак минус здесь и дальше ставится для того, чтобы при отрицательном значении 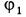(вращение блока происходит по часовой стрелке) получить положительное значение 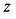(груз движется вниз в положительную сторону оси ).

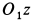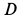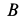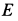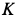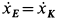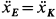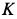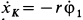Так как нить не скользит по катку и блоку , то скорости и касательные ускорения точек катка и блока (рис. 80, 81) одинаковы, т. е. и . Но для точки блока и 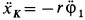. Для точки 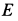катка, приняв за полюс точку 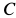, по формуле связи скоростей двух точек тела при плоском движении для произвольного момента времени с учетом знаков величин, имеем

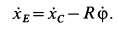
После дифференцирования по времени

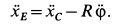
Таким образом, получаем дополнительное уравнение связи движений

Кроме того, считаем, что при движении груза 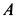вниз каток 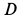катится по рельсу. Условие его качения для момента пары, препятствующей качению, выразится в форме

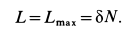
В тех случаях, когда направление качения катка заранее не известно, следует задаться направлением 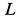и решить задачу. Если вращение катка получится при этом против принятого направления для 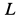, то предположение о направлении 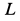правильно. Если вращение катка получится по направлению 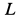, то следует изменить направление для 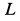на обратное и заново решать систему уравнений.

• Заказать решение задач по теоретической механике

Качение катка может быть как со скольжением, так и без скольжения. Поэтому сила трения остается неизвестной и по модулю, и по направлению.

Добавились два уравнения (г) и (д) и одно неизвестное 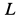выразилось через другое 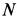. Для полной определенности задачи необходимо иметь еще одно уравнение и, кроме того, следует еще установить характер движения катка, т. е. будет ли он катиться со скольжением или без скольжения.

Предположим, что каток катится без скольжения, т. е. его мгновенный центр скоростей находится в точке соприкосновения катка с рельсом. Тогда скорость 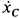точки 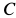, предполагаемой положительной, выражается через угловую скорость  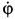зависимостью 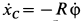, так как 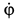при этом отрицательно. Эта зависимость справедлива для любого момента времени. Путем дифференцирования ее по времени получим дополнительное условие

После этого уравнение (д) примет вид

Уравнение (е) справедливо только при отсутствии скольжения катка в отличие от других уравнений, которые не зависят от характера движения катка.

Итак, имеем систему семи линейных уравнений с семью неизвестными, считая, что 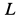 исключено из уравнений благодаря зависимости .

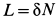Характер движения катка можно установить, если из полученной системы уравнений определить силу трения 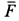и сравнить ее числовое значение с предельной силой трения 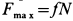. Если окажется 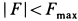, то система уравнений не приводит к противоречию с динамическим условием отсутствия скольжения. Предположение об отсутствии скольжения катка правильно. Если же 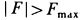, то предположение об отсутствии скольжения неверно, так как требует такой силы трения, которая возникнуть не может. В этом случае каток катится со скольжением и условие (е) не выполняется. Но при качении со скольжением 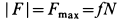, т.е. имеем дополнительное уравнение для одной из неизвестных вместо отбрасываемого уравнения (е). Число неизвестных оказывается равным числу неизвестных и задачу можно решить. Силу трения 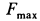следует подставить в уравнения вместо 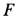с тем же знаком, с которым получилась из уравнений сила трения 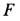, не соответствующая по модулю.

Для определения силы трения 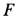с учетом условия (е) целесообразно свести систему семи линейных уравнений последовательным исключением неизвестных к двум линейным уравнениям для 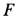и, например, 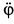, чтобы затем использовать правило Крамера.

Так как 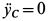, то из второго уравнения системы (а) следует 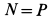и потому 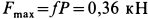, 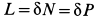. Определим предварительно силы натяжения 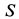и 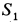, в общем случае не используя (е). Из уравнения (в) с учетом (г) и (д) имеем

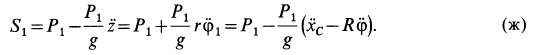
При отсутствии скольжения, т. е. при выполнении условия (е), из (ж) получаем

Из уравнения (б) с учетом (ж) и значения момента инерции 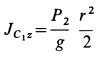 определяем силу натяжения:

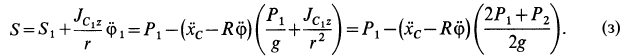
Таким образом, при выполнении условия (е), имеем

Определим силу трения, предположив отсутствие скольжения, т. е. когда для сил натяжения выполняются условия (ж') и (з'). Подставляя эти значения 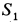 и 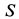 в оставшиеся два уравнения системы (а) с учетом (е), после несложных преобразований получаем следующую систему двух линейных уравнений:

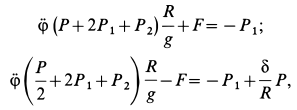
так как момент инерции катка 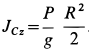. Эту систему уравнений кратко можно выразить в форме 

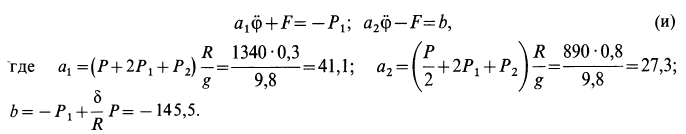
Из системы уравнений (и) определяем силу трения:

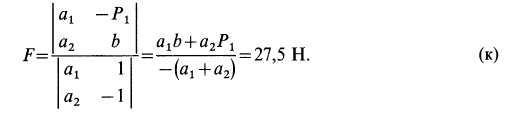
Сила трения из уравнений получается со знаком плюс; следовательно, предположение о ее направлении в положительную сторону оси оказалось правильным.

Сравнивая числовое значение полученной силы трения 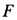с предельной силой трения 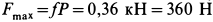, имеем 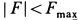. Предположение об отсутствии скольжения не привело к противоречию. Каток действительно катится без скольжения 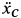и и 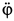удовлетворяют уравнению (е).

Подставляя значение полученной силы трения из (к) в первое уравнение (и), получаем

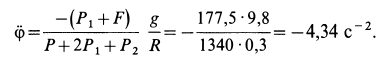
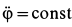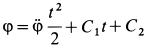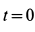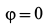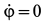Так как , то . В начальный момент ,  и . Поэтому .

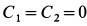Итак,

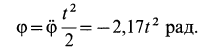
Из (е) находим

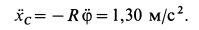
Так как 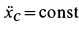, то 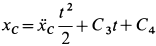. Из начальных условий  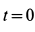, , 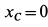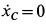получаем 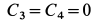. Следовательно,

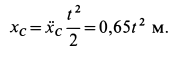
Получены следующие уравнения движения катка :

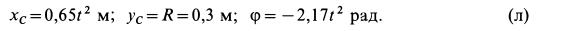
По известным значениям 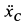 и , и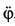спользуя (д'), (г) и условие (е), получаем

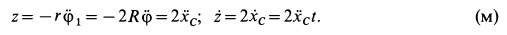
Реакцию оси блока определяем из условия, что центр масс блока 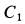неподвижен, и потому на основании теоремы о движении центра масс суммы проекций внешних для блока сил на оси координат 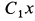и 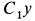равны нулю. Имеем

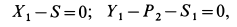
или

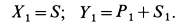
Определяем силы натяжения ните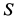й  и 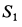из (ж') и (з'):

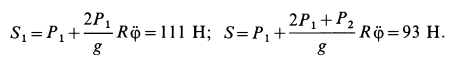
После этого для силы реакции оси блока имеем

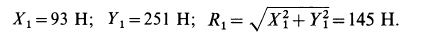
Давление блока на ось по числовой величине равно реакции оси блока 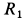. Количество движения, кинетическую энергию и кинетический момент определим из общих теорем динамики.

По теореме об изменении количества движения системы,

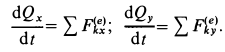
Система не движется в направлении оси 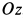, поэтому .

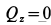Внешними силами системы являются силы тяжести 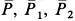, составляющие реакции оси блока 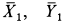и силы реакции рельса 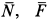, и пара сил с моментом 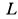. Все силы натяжения нити для всей системы являются внутренними силами. Для проекций, внешних сил на оси координат имеем

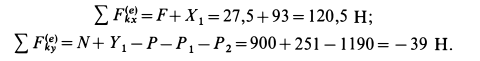
Таким образом,

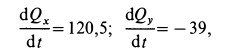
или

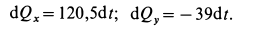
Интегрируя эти выражения в пределах от 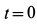 до 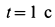 и учитывая, что при 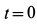, , 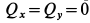получаем

.

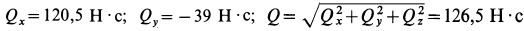По теореме об изменении кинетической энергии системы для промежутка времени от 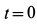  до 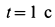 с имеем

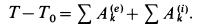
Здесь 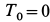. Кроме того,  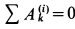так как силы натяжения нитей дают работу, равную нулю.

Работа внешних сил системы за рассматриваемый промежуток времени

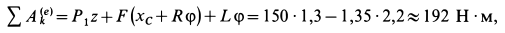
так как

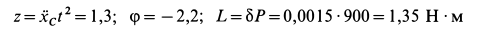
и путь точки соприкосновения катка 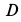с рельсом 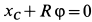при качении катка без скольжения. Другие внешние силы 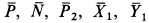не совершают работы, так как перпендикулярны перемещениям или приложены в неподвижных точках.

Таким образом,

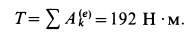
По теореме об изменении кинетического момента относительно неподвижной оси 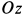для катка ,

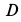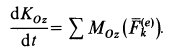
Внешними силами катка 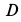являются силы 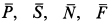и пара сил с моментом 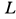. Имеем

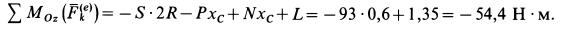
Так как 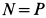, то

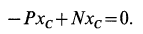
После этого

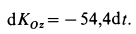
Интегрируя это соотношение от начального момента времени до момента, соответствующего 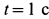, получаем

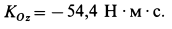
Проверим полученные значения количества движения, кинетической энергии и кинетического момента, вычислив их по формулам.

Количество движения системы 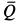состоит из векторной суммы количеств движения отдельных тел:

Так как центр масс блока 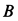неподвижен, то 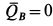. Для катка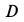

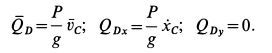
Груз движется в положительную сторону оси 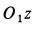(вниз); следовательно, .

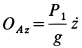Проецируя (н) на оси координат, причем 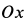направлена по горизонтали вправо, а — по вертикали вверх и используя (м), получаем

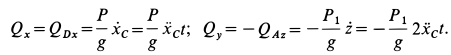
При 

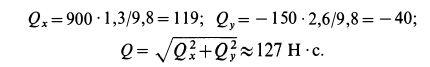
Кинетическая энергия системы состоит из кинетических энергий отдельных тел:

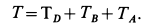
Каток совершает плоское движение. Его кинетическая энергия при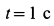 

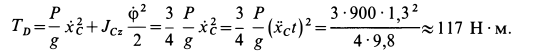
Блок вращается вокруг неподвижной оси; следовательно, при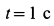

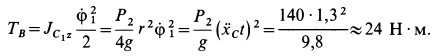
Груз движется поступательно, а потому при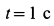 

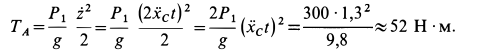
Кинетическая энергия системы через 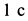после начала движения системы

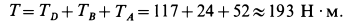
Кинетический момент катка 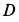относительно неподвижной точки 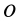рельса вычисляем по формуле

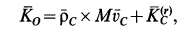
где

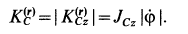
Для проекции 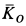на ось , учитывая, что кинетический момент в направлении часовой стрелки следует считать отрицательным, имеем

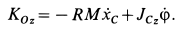
Так как плечо вектора 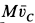, приложенного в точке 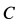относительно точки 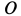, не зависит от ее выбора на рельсе, то и 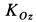не зависит от положения точки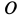. Точкой  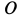может быть точка соприкосновения катка с рельсом. В рассматриваемом случае 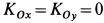, поэтому при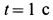

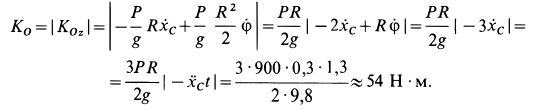
Полученные двумя способами величины 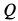, 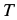и 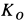почти совпадают. Небольшие расхождения связаны с округлениями величин при вычислениях.