Закон сохранения механической энергии в физике - формулы и определение с примерами

Содержание:

Закон сохранения механической энергии:

Любое тело может обладать одновременно и кинетической, и потенциальной энергией. Тело, падающее с определенной высоты, имеет потенциальную энергию в поле силы тяжести и кинетическую энергию, поскольку оно движется с определенной скоростью относительно Земли.

Сумму потенциальной и кинетической энергий тела называют полной механической энергией: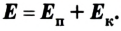

Кинетическая и потенциальная энергии тела могут изменяться, но в замкнутой системе их сумма остается постоянной. В этом состоит суть закона сохранения и превращения механической энергии: если в замкнутой системе действуют только силы упругости и тяжести, то полная механическая энергия системы остается неизменной - взаимные превращения происходят с кинетической и потенциальной энергией:

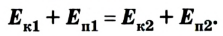
Если в замкнутой системе действуют только силы упругости и тяжести, то полная механическая энергия системы остается постоянной.

Действие силы трения приводит к увеличению внутренней энергии тела. Точные экспериментальные исследования показали, что все «потери» механической энергии равны увеличению внутренней энергии. Это говорит о том, что энергия не возникает из ничего и не исчезает бесследно.

Она только переходит из одного вида в другой.

Этот вывод отражает суть общего закона природы - закона сохранения и превращения энергии, открытого в 1840 г. Р. Майером. Несмотря на то что ученый совершил это открытие в процессе медицинских наблюдений над организмом человека, закон оказался всеобщим и был проверен и подтвержден в процессе многочисленных исследований.

Если в системе действует и сила трения то полная механическая энергия претерпевает изменения.

Определения и формулы

В механике различают и изучают силы упругости, трения, всемирного тяготения. Сила упругости возникает в результате взаимодействия микрочастиц, из которых состоят тела.

Сила трения также имеет электромагнитную природу.
Сила всемирного тяготения действует между всеми без исключения телами. Она пропорциональна произведению масс взаимодействующих тел и обратно пропорциональна квадрату расстояния между ними: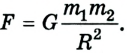

Первый закон динамики: любое тело сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока приложенные к нему силы не выведут его из этого состояния.

Второй закон динамики: ускорение, полученное телом в результате взаимодействия, прямо пропорционально силе, действующей на тело, обратно пропорционально его массе и имеет то же направление, что и сила: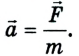

Третий закон динамики: любое действие порождает равное по величине и противоположное по направлению противодействие: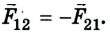

Равновесие - это состояние тела, при котором под действием приложенных к нему сил отсутствует перемещение любых его точек. При равновесии тел выполняются такие два условия:

1)    геометрическая сумма приложенных к телу сил равна нулю: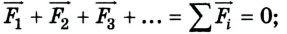

2)    алгебраическая сумма моментов сил, приложенных к телу относительно какой-либо неподвижной оси, равна нулю:

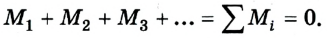
Каждое движущееся тело имеет импульс: 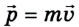и кинетическую энергию: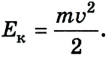

В замкнутой системе сумма импульсов тел при любых взаимодействиях между ними остается постоянной (закон сохранения импульса).

В общем случае механическая работа: 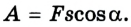Она характеризует изменение энергии тела.

Взаимодействующие тела имеют потенциальную энергию. В поле силы тяжести: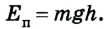

Полная механическая энергия замкнутой системы остается постоянной, если в ней действуют лишь силы тяжести или упругости: изменяются только кинетическая и потенциальная энергия (закон сохранения механической энергии):

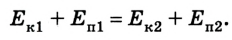
Закон сохранения механической энергии

В предыдущих параграфах мы познакомились с двумя видами механической энергии тел: кинетической и потенциальной. Кинетическая энергия — это энергия тела, движущегося с некоторой скоростью относительно выбранной системы отсчета. Потенциальная энергия — это энергия взаимодействия. Естественно, при движении некоторого тела могут изменяться и кинетическая, и потенциальная энергии. Рассмотрим этот вопрос более подробно на примере тела массой m, брошенного под углом к горизонту. На такое тело действуют две силы — сила тяжести 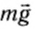и сила сопротивления воздуха 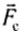. (рис. 145).

Равнодействующая этих сил: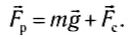

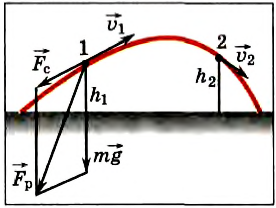
Рис. 145

Предположим, что в положении 1 тело имеет скорость 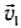и находится на высоте h₁, а в точке 2 имеет скорость 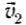и находится на высоте h₂ относительно некоторого уровня, принятого за нулевой. При движении тела из начального положения 1 в конечное положение 2, как уже было раньше показано, работа равнодействующей (результирующей) силы равна сумме работ всех сил, действующих на тело. В нашем случае

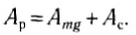     (1)

Работа результирующей силы равна изменению кинетической энергии тела:
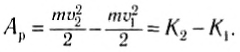     (2)

В тоже время, как мы знаем, работа силы тяжести равна убыли потенциальной энергии тела:

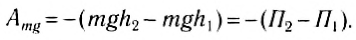     (3)

Поэтому выражение (1) с учетом (2) и (3) можно переписать в следующем

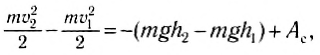
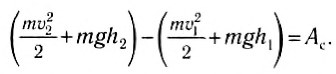   (4)

В полученном выражении в скобках стоит сумма кинетической и потенциальной энергии тела в конечном и начальном положениях тела. Эта величина называется полной механической энергией тела или просто механической энергией W:

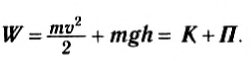
Используя понятие полной механической энергии, выражению (4) можно придать вид:
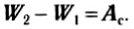   (5)

Сила трения не является потенциальной, поэтому из (5) следует, что изменение механической энергии тела равно работе непотенциальных сил. Если сил трения нет, то A_с = 0, мы приходим к закону сохранения механической энергии:

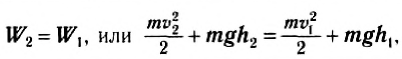
т. е. для тел, движущихся под действием силы тяжести в отсутствие сил сопротивления, полная механическая энергия сохраняется.

• Заказать решение задач по физике

При движении тела вверх его потенциальная энергия увеличивается, а кинетическая энергия уменьшается. И наоборот, при движении вниз его потенциальная энергия уменьшается, зато увеличивается кинетическая. Например, такое превращение энергии происходит при раскачивании на качелях (рис. 146). Причем изменение одной в точности равно изменению другой, если пренебречь сопротивлением воздуха и трением в подвесе качелей.
Это следует из формулы (6), которую можно переписать в виде:

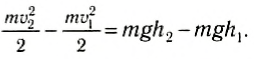
Рис. 146

Если на тело, кроме силы тяжести, действует еще и сила упругости пружины, то можно ввести полную механическую энергию системы в виде:
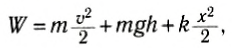    (7)

и она будет сохраняться при движении тела, если работа всех других сил, действующих на него, равна нулю.

Закон сохранения полной механической энергии является частным случаем общего закона сохранения и превращения энергии.

Если работа сил трения не равна нулю, то механическая энергия системы изменяется. Мы показали раньше, что работа этих сил идет на изменение внутренней энергии тел: тела нагреваются. Если все тщательно подсчитать, то сумма кинетической, потенциальной и внутренней энергии всех взаимодействующих тел остается неизменной. При движении тел происходит взаимное превращение одного вида энергии в другой. Но полная энергия остается постоянной.

Закон сохранения и превращения энергии является одним из важнейших законов не только физики, но и всех других наук о природе. На его основе строятся новые научные теории.
Любой теоретический вывод следует проверить «испытанием» на совместимость с этим законом. Если вывод не согласуется с законом сохранения и превращения энергии, то он неверен.

Главные выводы:

1. Полная механическая энергия равна сумме кинетической и потенциальной энергии тела.
2. Если на тело действуют сила тяжести и сила упругости, которые являются потенциальными силами, то изменение полной механической энергии, определенной равенством (7), равно работе непотенциальных сил, действующих на тело.
3. Если диссипативные силы не действуют или работой этих сил можно пренебречь, то выполняется закон сохранения энергии в виде W₁ = W₂, т. е. полная механическая энергия системы есть величина постоянная.
4. Закон сохранения полной механической энергии является частным случаем общего закона сохранения и превращения энергии.