Закон Паскаля - основные понятия, формулы и определения с примерами

Закон Паскаля:

В предыдущем параграфе установлено, что силы давления, действующие на стенку сосуда, перпендикулярны ей. Тоже относится и к любой площадке, мысленно выделенной внутри жидкости. Зависит ли давление от ориентации площадки? Для ответа на этот вопрос выделим мысленно внутри жидкости небольшой объем в виде треугольной призмы (рис. 165, а), одна из граней которой расположена горизонтально. Площади оснований призмы будем считать малыми по сравнению с площадями боковых граней. Малым будет и объем призмы, и, следовательно, силой тяжести, действующей на призму, можно пренебречь по сравнению с силами давления, действующими на грани призмы.

На рисунке 165, б изображено поперечное сечение призмы. На боковые грани призмы действуют силы давления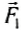

Поскольку призма покоится, то

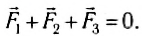
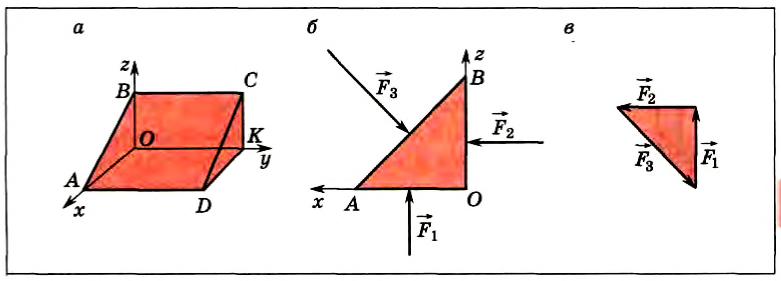
Рис. 165

Векторы этих сил образуют треугольник (рис. 165, в), подобный треугольнику основания призмы AOB (см. рис. 165, б), так как углы в этих двух треугольниках соответственно равны. Из подобия треугольников следует, что

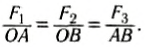
Умножим знаменатели этого равенства на высоту призмы BC = OK = AD. Из рисунка 165, а видно, что знаменатель каждой дроби станет равен площади соответствующей боковой грани. 

Обозначив площади этих граней призмы S₁,S₂, S₃, получим:
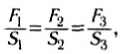 или 
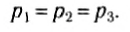  (1)

Таким образом, давление в неподвижной жидкости или газе не зависит от ориентации площадки внутри жидкости, т. е. давление — изотропно.

Вспомним, что по определению давление не зависит и от размеров площадки, на которую оно действует, оно всегда относится к единице площади поверхности. Таким образом, давление представляет собой такую характеристику состояния жидкости в данном месте, которая не зависит ни от ориентации, ни от размеров площадки, на которой давление измеряется. Давление зависит лишь от степени сжатия жидкости в данном месте.

Давление внутри жидкости на некоторой глубине согласно формуле (2) предыдущего параграфа создается внешними силами и гидростатическим давлением. Следовательно, давление, создаваемое внешними силами, передается без изменения в каждую точку жидкости. В этом и состоит суть закона Паскаля.

Если давление, создаваемое внешними силами, изменится на некоторую величину, то на столько же изменится и давление в каждой точке жидкости.

Закон Паскаля можно подтвердить экспериментально с помощью металлического шара с отверстиями и присоединенного к нему цилиндра с поршнем. Если заполнить эту систему водой (задымленным воздухом) и вдвигать поршень (рис. 166), то из отверстий брызнут радиально расходящиеся одинаковые струи воды.

Рис. 166

Закон Паскаля позволяет объяснить действие распространенного в технике устройства — гидравлического пресса. Гидравлический пресс состоит из двух цилиндров разных диаметров, снабженных поршнями и соединенных трубкой (рис. 167). Пространство под поршнями и трубка заполняются жидкостью (обычно машинным маслом). Обозначим площадь малого поршня через S₁ , а большого поршня — через S₂. Пусть к малому поршню приложена сила .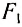

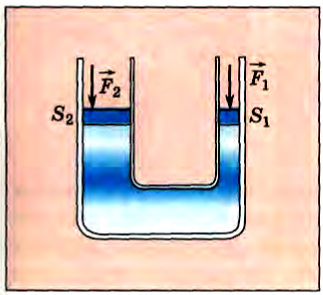
Рис. 167

Эта сила создает в жидкости давление 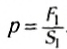, которое передается без изменения в большой цилиндр. Следовательно, для того чтобы жидкость не была вытеснена из первого цилиндра во второй, к нему нужно приложить силу:

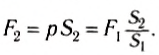
Сила F₂ во столько раз больше силы F₁ во сколько раз площадь второго поршня больше площади первого. Таким образом, при помощи гидравлического пресса малой силой можно уравновесить большую силу.

На принципе работы гидравлического пресса основано действие гидроусилителей руля и гидротормозов автомобилей, гидравлических домкратов рис. 168) для подъема тяжелых грузов.

Рис. 168

Главные выводы

1. Давление в жидкости и газе не зависит от ориентации площадки и ветчины ее площади. Оно характеризует степень сжатия жидкости или газа.
2. Давление, создаваемое внешними силами, передается во все точки жидкости (газа) одинаково.