
Закон больших чисел - определение и вычисление с примерами решения
Содержание:
Закон больших чисел:
Теория вероятностей изучает закономерности, свойственные массовым случайным явлениям. Как и любая другая наука, теория вероятностей предназначена для того, чтобы возможно точнее предсказать результат того или иного явления или эксперимента. Если явление носит единичный характер, то теория вероятностей способна предсказать лишь вероятность исхода в весьма широких пределах. Закономерности проявляются только при большом числе случайных явлений, происходящих в однородных условиях.
Группа теорем, устанавливающих соответствие между теоретическими и экспериментальными характеристиками случайных величин и случайных событий при большом числе испытаний над ними, а также касающихся предельных законов распределения, объединяются под общим названием предельных теорем теории вероятностей.
Есть два типа предельных теорем: закон больших чисел и центральная предельная теорема.
Закон больших чисел, занимающий важнейшее место в теории вероятностей, является связующим звеном между теорией вероятностей как математической наукой и закономерностями случайных явлений при массовых наблюдениях над ними.
Закон играет очень важную роль в практических применениях теории вероятностей к явлениям природы и техническим процессам, связанным с массовым производством.
Предельные законы распределения составляют предмет группы теорем - количественной формы закона больших чисел. Т.е. закон больших чисел - ряд теорем, в каждой из которых устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным, т.е. устанавливают факт сходимости по вероятности некоторых случайных величин к постоянным. Это теоремы Бернулли, Пуассона, Ляпунова, Маркова, Чебышева.
1. а) Теорема Бернулли - закон больших чисел (была сформулирована и доказана ранее в п. 3 § 6 при рассмотрении предельной интегральной теоремы Муавра-Лапласа.)
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте. Иначе, вероятность того, что отклонение относительной частоты 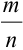
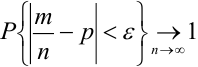
b) Теорема Чебышева.
При неограниченном увеличении числа независимых испытаний среднее арифметическое наблюдаемых значений случайной величины, имеющей конечную дисперсию, сходится по вероятности к ее математическому ожиданию иначе, если 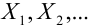 независимые одинаково распределенные случайные величины с математическим ожиданием
независимые одинаково распределенные случайные величины с математическим ожиданием 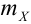 и ограниченной дисперсией
и ограниченной дисперсией 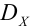 , то при любом
, то при любом 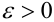 справедливо:
справедливо:
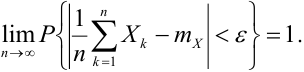
Теорема Чебышева (обобщенная). Если случайные величины в последовательности 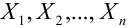 попарно независимы, а их дисперсии удовлетворяют условию
попарно независимы, а их дисперсии удовлетворяют условию 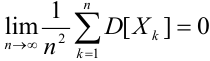 , то для любого положительного
, то для любого положительного 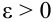 справедливо утверждение:
справедливо утверждение:
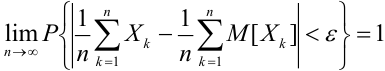 или, что то же
или, что то же
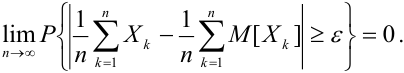
с) Теорема Маркова, (закон больших чисел в общей формулировке)
Если дисперсии произвольных случайных величин в последовательности
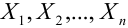 удовлетворяют условию:
удовлетворяют условию: 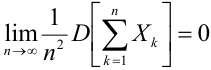 , то для любого положительного
, то для любого положительного 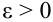 имеет место утверждение теоремы Чебышева:
имеет место утверждение теоремы Чебышева:
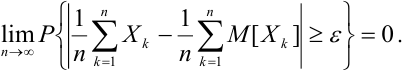
d) Теорема Пуассона.
При неограниченном увеличении числа независимых опытов в переменных условиях частота события А сходится по вероятности к среднему арифметическому его вероятностей 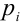 при данных испытаниях.
при данных испытаниях.
Замечание. Ни в одной из форм закона больших чисел мы не имеем дела с законами распределения случайных величин. Вопрос, связанный с отысканием предельного закона распределения суммы 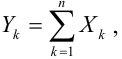 когда число слагаемых неограниченно возрастает, рассматривает центральная предельная теорема.
когда число слагаемых неограниченно возрастает, рассматривает центральная предельная теорема.
2. Теорема Ляпунова - центральная предельная теорема (устанавливает условия, при которых указанный предельный закон является нормальным.)
Теорема Ляпунова (простейшая форма, когда 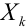 взаимно независимы и одинаково распределены)
взаимно независимы и одинаково распределены)
Если случайные величины 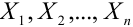 взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией D, причем существует третий абсолютный момент
взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией D, причем существует третий абсолютный момент 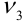 , то при неограниченном увеличении n закон распределения суммы неограниченно приближается к нормальному.
, то при неограниченном увеличении n закон распределения суммы неограниченно приближается к нормальному.
Замечание. Случайные величины 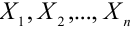 , фигурирующие в теореме, могут обладать произвольными распределениями вероятностей. Если считать, что все
, фигурирующие в теореме, могут обладать произвольными распределениями вероятностей. Если считать, что все 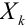 одинаково распределены, то придем к интегральной теореме Муавра-Лапласа, представляющей собой простейший частный случай центральной предельной теоремы.
одинаково распределены, то придем к интегральной теореме Муавра-Лапласа, представляющей собой простейший частный случай центральной предельной теоремы.
Определение закона больших чисел
Массовые явления и закон больших чисел:
Огромный опыт, накопленный человечеством, учит нас, что явления, имеющие вероятность, весьма близкую к единице, почти обязательно происходят. Точно так же события, вероятность наступления которых очень мала (иными словами, очень близка к нулю), наступают очень редко. Это обстоятельство играет основную роль для всех практических выводов из теории вероятностей, так как указанный опытный факт даёт право в практической деятельности считать мало вероятные события практически невозможными, а события, происходящие с вероятностями, весьма близкими к единице, практически достоверными. При этом на вполне естественный вопрос, какова должна быть вероятность, чтобы мы могли событие считать практически невозможным (практически достоверным), однозначного ответа дать нельзя. И это понятно, так как в практической деятельности необходимо учитывать важность тех событий, с которыми приходится
иметь дело.
Так, например, если бы при измерении расстояния между двумя пунктами оказалось, что оно равно 5340м и ошибка этого измерения с вероятностью 0,02 равна или больше (или меньше) 20м, то мы можем пренебречь возможностью такой ошибки и считать что расстояние действительно равно 5340м. Таким образом, в данном примере мы считаем событие с вероятностью 0,02 практически несущественным (практически невозможным) и в своей практической деятельности его не учитываем. В то же время в других случаях пренебрегать вероятностями 0,02 и даже ещё меньшими нельзя. Так, если при строительстве большой гидроэлектростанции, требующей огромных материальных затрат и человеческого труда, выяснилось, что вероятность катастрофического паводка в рассматриваемых условиях равна 0,02, то эта вероятность будет сочтена большой и при проектировании станции она должна быть обязательно учтена, а не отброшена, как
это было сделано в предыдущем примере.
Таким образом, только требования практики могут нам подсказать критерии, согласно которым мы будем считать те или иные события практически невозможными или практически достоверными.
В то же время необходимо заметить, что любое событие, имеющее положительную вероятность, пусть даже близкую к нулю, может произойти. И если число испытаний, в каждом из которых оно может произойти с одной и той же вероятностью, очень велико, то вероятность хотя бы однократного его появления может стать сколь угодно близкой к единице. Это обстоятельство постоянно следует иметь в виду. Из сказанного понятно, что в практической деятельности, да и в общетеоретических задачах, большое значении имеют события с вероятностями близкими к единице или нулю. Отсюда становится ясным, что одной из основных задач теории вероятностей должно быть установление закономерностей, происходящих с вероятностями, близкими к единице; при этом особую роль должны играть закономерности, возникающие в результате наложения большого числа независимых или слабо зависимых случайных фактов.
Действительно, нельзя заранее уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые мы не в состоянии. Казалось бы, что поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так.
Оказывается, что при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Наличие связи между теоретическими и экспериментальными характеристиками случайных величин, проявляемой в большом числе опытов, позволяет предугадывать результаты массовых случайных явлений долей уверенности. Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в ряде предельных теорем, одна группа которых объединена под общим названием «Закон больших чисел», другая же – под общим названием «Центральная предельная теорема».
Закон больших чисел состоит из теорем Чебышева и Бернулли (имеются и другие теоремы), в которых доказывается приближение при определённых условиях среднего арифметического случайных величин к некоторым случайным характеристикам. Теорема Чебышева является наиболее общим законом больших чисел, теорема Бернулли – простейшим.
В другой же группе предельных теорем, объединённых под общим названием «Центральная предельная теорема», устанавливается факт приближения при определённых условиях закона распределения суммы 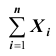 случайных величин к нормальному закону распределения. Математически это выражается в виде условий, которые должны выполняться для рассматриваемых случайных величин, то есть необходимо выполнение некоторых условий для случайных величин
случайных величин к нормальному закону распределения. Математически это выражается в виде условий, которые должны выполняться для рассматриваемых случайных величин, то есть необходимо выполнение некоторых условий для случайных величин 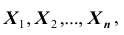 при которых суммарная случайная величина
при которых суммарная случайная величина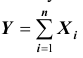 распределена
распределена
по нормальному закону.
Таким образом, закон больших чисел и центральная теорема составляют две группы предельных теорем теории вероятностей, которые в совокупности позволяют вполне обоснованно осуществлять прогнозы в области случайных явлений, давая при этом оценку точности производимых прогнозов.
Теорема Чебышева
Для доказательства теоремы Чебышева (да и других теорем, в том числе) воспользуемся одноимённым неравенством. Неравенство Чебышева (как впрочем и теорема) справедливо как для дискретных, так и для непрерывных случайных величин. Мы ограничимся, например, доказательством неравенства для непрерывной случайной величины.
НЕРАВЕНСТВО Чебышева :
:
Вероятность того, что отклонение случайной величины Х, имеющей конечную дисперсию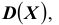 от её математического ожидания по абсолютной величине на меньше любого положительного числа
от её математического ожидания по абсолютной величине на меньше любого положительного числа 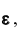 ограничена сверху величиной
ограничена сверху величиной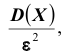 то есть, справедливо неравенство:
то есть, справедливо неравенство:
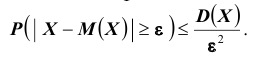
Доказательство: По определению дисперсии для непрерывной случайной величины можем записать 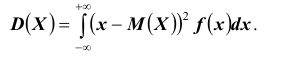
Выделим на числовой оси 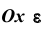 -окрестность точки
-окрестность точки 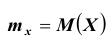 (см. рис.). Заменим теперь интегрирование по всей оси интегралом по переменной х на множестве
(см. рис.). Заменим теперь интегрирование по всей оси интегралом по переменной х на множестве 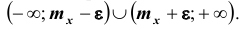

Так как под знаком интеграла стоит неотрицательная функция  , то результат интегрирования в результате может только уменьшиться, то есть
, то результат интегрирования в результате может только уменьшиться, то есть 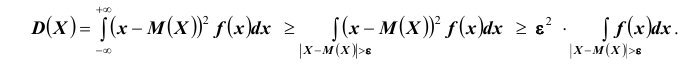
Интеграл в правой части полученного неравенства – это вероятность того, что случайная величина Х будет принимать значения вне интервала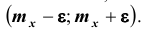 Значит
Значит
12 Есть и другая формулировка: Вероятность того, что отклонение случайной величины Х от её математического ожидания по абсолютной величине меньше положительного числа 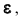 не меньше чем
не меньше чем 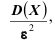 то есть справедливо неравенство
то есть справедливо неравенство 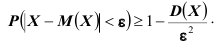
13 Напомним, что 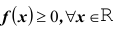
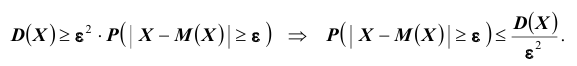 Неравенство доказано.
Неравенство доказано.
Замечание. Неравенство Чебышева имеет для практики ограниченное значение, поскольку часто даёт грубую, а иногда и тривиальную
(не представляющую интереса) оценку. Например, если 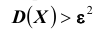 и, следовательно,
и, следовательно,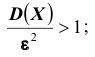 таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения находится в пределах от нуля до единицы, а это и без того очевидно, так как любая вероятность удовлетворяет этому условию.
таким образом, в этом случае неравенство Чебышева указывает лишь на то, что вероятность отклонения находится в пределах от нуля до единицы, а это и без того очевидно, так как любая вероятность удовлетворяет этому условию.
Теоретическое же значение неравенства Чебышева весьма велико. Оценка, полученная Чебышевым, является универсальной, она справедлива для любых случайных величин, имеющих 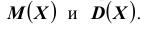
Пример №1
Найти вероятность выхода случайной величины Х, имеющей математическое ожидание 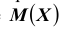 и дисперсию
и дисперсию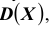 за трёхсигмовые границы.
за трёхсигмовые границы.
Решение. Воспользуемся неравенством Чебышева:
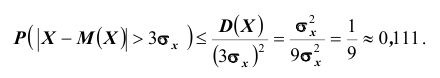
Сравним полученный результат с тем, который следует из правила трёх сигм
для нормального закона распределения: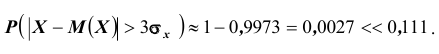
Нетрудно сделать ВЫВОД: случайные величины, встречающиеся на практике, чаще всего имеют значительно меньшую вероятность выхода за
трёхсигмовые границы, чем 1/9. Для них область 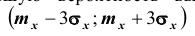 является областью практически возможных значений случайной величины.
является областью практически возможных значений случайной величины.
ТЕОРЕМА Чебышева (частный случай): Пусть 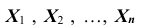 – попарно независимые случайные величины, имеющие одно и то же математическое ожидание М(Х), и пусть дисперсии этих величин равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к их математическому ожиданию, то есть имеет место равенство:
– попарно независимые случайные величины, имеющие одно и то же математическое ожидание М(Х), и пусть дисперсии этих величин равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к их математическому ожиданию, то есть имеет место равенство:
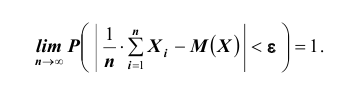
Доказательство. Применим к случайной величине 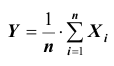 неравенство Чебышева:
неравенство Чебышева:
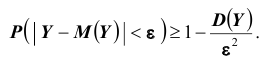 Заметим (по условиям теоремы), что для дисперсии
Заметим (по условиям теоремы), что для дисперсии 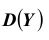 справедливы соотношения:
справедливы соотношения:
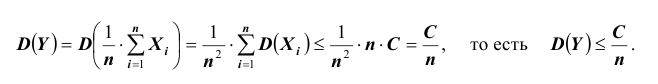 Тогда, согласно неравенству Чебышева
Тогда, согласно неравенству Чебышева
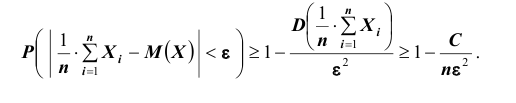 Переходя к пределу при
Переходя к пределу при  получаем
получаем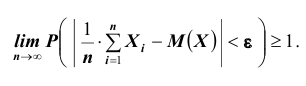
А так как вероятность не может быть больше единицы, то отсюда и следует
утверждение теоремы.
Теорема Чебышева была обобщена на более общий случай, доказательство которой проводится аналогично доказательству, предложенному выше.
ТЕОРЕМА Чебышева (общий случай): Пусть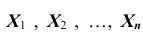 – попарно независимые случайные величины, и пусть дисперсии этих величин
– попарно независимые случайные величины, и пусть дисперсии этих величин
равномерно ограничены (то есть не превышают некоторого постоянного числа С). Тогда, при достаточно большом числе независимых опытов среднее арифметическое наблюдаемых значений случайных величин сходится по вероятности к среднему арифметическому их математических ожиданий, то есть имеет место равенство:
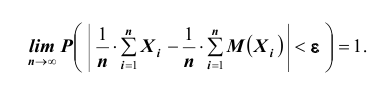
Сущность теоремы Чебышева
Сущность доказанной теоремы такова: хотя отдельные независимые случайные величины могут принимать значения далёкие от своих математических ожиданий, среднее арифметическое достаточно большого числа случайных величин с большой вероятностью принимает значения близкие к определённому постоянному числу, а имен к числу 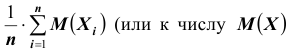 в частном случае). Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало. Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть какое значение примет
в частном случае). Другими словами, отдельные случайные величины могут иметь значительный разброс, а их среднее арифметическое рассеянно мало. Таким образом, нельзя уверенно предсказать, какое возможное значение примет каждая из случайных величин, но можно предвидеть какое значение примет
их среднее арифметическое. Итак, среднее арифметическое достаточно большого числа независимых случайных величин (дисперсии которых равномерно ограничены) утрачивает характер случайной величины. Объясняется это тем, что отклонения каждой из величин от своих математических ожиданий могут быть как положительными, так и отрицательными, а в среднем арифметическом они взаимно погашаются
Значение теоремы Чебышева для практики
Приведём примеры применения теоремы Чебышева к решению практических задач. Обычно для измерения некоторой физической величины производят несколько измерений и их среднее арифметическое принимают в качестве искомого размера. При каких условиях этот способ измерения можно считать правильным? Ответ на этот вопрос даёт теорема Чебышева (частный случай). Действительно, рассмотрим результаты каждого измерения как случайные величины  . К этим величинам может быть применена теорема Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены. Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных измерений.
. К этим величинам может быть применена теорема Чебышева, если: 1) они попарно независимы, 2) имеют одно и то же математическое ожидание, 3) дисперсии их равномерно ограничены. Первое требование выполняется, если результат каждого измерения не зависит от результатов остальных измерений.
Второе требование выполняется, если измерения произведены без систематических (одного знака) ошибок. В этом случае математические ожидания всех случайных величин одинаковы и равны истинному размеру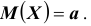 Третье требование выполняется, если прибор обеспечивает определённую точность измерений. Хотя при этом результаты отдельных измерений различны, но
Третье требование выполняется, если прибор обеспечивает определённую точность измерений. Хотя при этом результаты отдельных измерений различны, но
рассеяние их ограничено. Если все указанные требования выполнены, мы вправе применить к результатам измерений теорему Чебышева (частный случай): при достаточно большом n - числе измерений вероятность неравенства
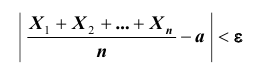
как угодно близка к единице. Другими словами, при достаточно большом числе измерений почти достоверно, что их среднее арифметическое сколь угодно мало отличается от истинного значения измеряемой величины. Итак, теорема Чебышева указывает условия, при которых описанный способ измерения может быть применим На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемых сотнями. В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зёрен малó сравнительно со всей массой зерна, но само по себе оно достаточно великó. Уже из приведённых примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
На теореме Чебышева основан широко применяемый в статистике выборочный метод, суть которого состоит в том, что по сравнительно небольшой случайной выборке судят обо всей совокупности (генеральной совокупности) исследуемых объектов. Например, о качестве кипы хлопка заключают по небольшому пучку, состоящему из волокон, наудачу отобранных из разных мест кипы. Хотя число волокон в пучке значительно меньше, чем в кипе, сам пучок содержит достаточно большое количество волокон, исчисляемых сотнями. В качестве другого примера можно указать на определение качества зерна по небольшой его пробе. И в этом случае число наудачу отобранных зёрен малó сравнительно со всей массой зерна, но само по себе оно достаточно великó. Уже из приведённых примеров можно заключить, что для практики теорема Чебышева имеет неоценимое значение.
Однако ошибочно думать, что увеличивая число измерений можно достичь сколь угодно большой точности. Дело в том, что сам прибор даёт показания лишь с точностью поэтому каждый из результатов измерений, а следовательно и их среднее арифметическое, будут получены лишь с точностью, не превышающей точности прибора.
Теорема Бернулли
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равна р. Другими словами, пусть имеет место схема Бернулли. Можно ли предвидеть какова будет примерно относительная частота появлений события? Положительный ответ на этот вопрос даёт теорема, доказанная Я.Бернулли , которая получила название «закона больших чисел» и
, которая получила название «закона больших чисел» и
положила начало теории вероятностей как науки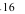 .
.
ТЕОРЕМА Бернулли: Если в каждом из n независимых испытаний, проводимых в одинаковых условиях, вероятность р появления события А
постоянна, то относительная частота появления события А сходится по вероятности к вероятности р – появления данного события в отдельном опыте, то есть
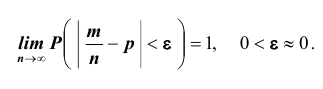
Доказательство. Итак, имеет место схема Бернулли,  . Обозначим через
. Обозначим через  дискретную случайную величину – число появлений события А в i -ом испытании. Ясно, что каждая из случайных величин может принимать лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие А не наступило) с вероятностью
дискретную случайную величину – число появлений события А в i -ом испытании. Ясно, что каждая из случайных величин может принимать лишь два значения: 1 (событие А наступило) с вероятностью р и 0 (событие А не наступило) с вероятностью 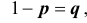 то есть
то есть
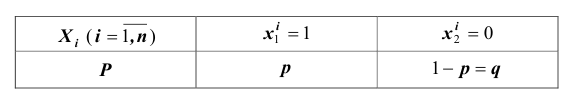
Нетрудно найти
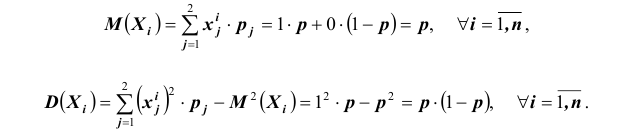
Доказательство впервые было опубликовано в 1713 году.
Доказательство, предложенное Я.Бернулли, было сложным; более простое доказательство было дано П.Чебышевым в 1846 году.
Можно ли применить к рассматриваемым величинам теорему Чебышева?
Можно, если случайные величины попарно независимы и дисперсии их равномерно ограничены. Оба условия выполняются. Действительно, попарная независимость величин 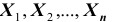 следует из того, что испытания независимы. Далее
следует из того, что испытания независимы. Далее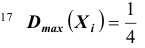 при
при 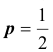 следовательно, дисперсии всех величин ограничены, например числом
следовательно, дисперсии всех величин ограничены, например числом 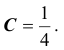
Кроме того, заметим, что каждая из случайных величин 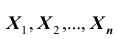 при появлении события А в соответствующем испытании принимает значение, равное единице. Следовательно, сумма
при появлении события А в соответствующем испытании принимает значение, равное единице. Следовательно, сумма 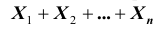 равна числу m - появлений события А в n испытаниях, а значит
равна числу m - появлений события А в n испытаниях, а значит
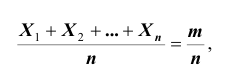 то есть дробь
то есть дробь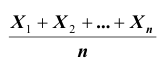 равна относительной частоте
равна относительной частоте 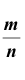 появлений события А в n испытаниях.
появлений события А в n испытаниях.
Тогда, применяя теорему Чебышева к рассматриваемым величинам, получим:
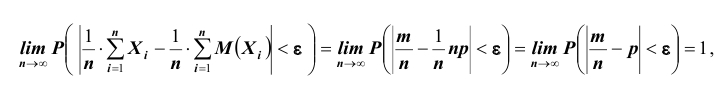 что и требовалось доказать.
что и требовалось доказать.
Замечание 1: Теорема Бернулли является простейшим частным случаем теоремы Чебышева.
Замечание 2: На практике часто неизвестные вероятности приходится приближённо определять из опыта, то для проверки согласия теоремы Бернулли с опытом было проведено большое число опытов. Так, например, французский естествоиспытатель XVIII века Бюффон бросил монету 4040 раз. Герб выпал при этом 2048 раз. Частота появления герба в опыте Бюффона приближённо равна 0,507. Английский статистик К.Пирсон бросал монету 12 000 раз и при этом наблюдал 6019 выпадений герба. Частота выпадения герба в этом опыте Пирсона равна 0,5016. В другой раз он бросил монету 24 000 раз, и герб при этом выпал 12 012 раз; частота выпадения герба при этом оказалась равной 0,5005. Как видим,
во всех приведённых опытах частота лишь немного уклонилась от вероятности 0,5 – появления герба в результате одного бросания монеты.
Известно, что произведение двух сомножителей, сумма которых есть величина постоянная, имеет наибольшее значение при равенстве сомножителей.
Замечание 3: Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство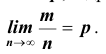 В теореме речь идёт лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Таким образом, сходимость относительной частоты
В теореме речь идёт лишь о вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании. Таким образом, сходимость относительной частоты 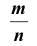 к вероятности
к вероятности
р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если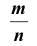 стремится при
стремится при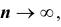 к р как пределу в смысле обычного анализа, то, начиная с некоторого
к р как пределу в смысле обычного анализа, то, начиная с некоторого 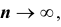 и для всех последующих значений n , неуклонно выполняется неравенство
и для всех последующих значений n , неуклонно выполняется неравенство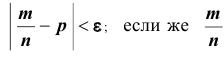
Теоремы Пуассона и Маркова
Замечено, если условия опыта меняются, то свойство устойчивости относительной частоты появления события А сохраняется. Это обстоятельство доказано Пуассоном.
ТЕОРЕМА Пуассона: При неограниченном увеличении числа независимых испытаний, проводимых в переменных условиях, относительная частота появления события А сходится по вероятности к среднему арифметическому вероятностей появления данного события в каждом из опытов, то есть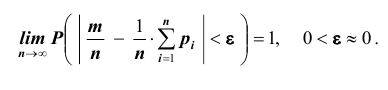
Замечание 4: Нетрудно убедиться, что теорема Пуассона является частным случаем теоремы Чебышева. Далее, закон больших чисел применительно к зависимым событиям был дан А.А.Марковым, который заметил, что рассуждения Чебышева позволяют получить
более общий результат.
ТЕОРЕМА Маркова: Если последовательность случайных величин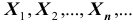 (как угодно зависимых) такова, что при
(как угодно зависимых) такова, что при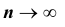
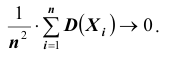 Отсюда видно, что теорема Чебышева является частным случаем теоремы Маркова.
Отсюда видно, что теорема Чебышева является частным случаем теоремы Маркова.
Центральная предельная теорема (Теорема Ляпунова)
Рассмотренные теоремы закона больших чисел касаются вопросов приближения некоторых случайных величин к определённым предельным значениям независимо от их закона распределения. В теории вероятностей, как уже отмечалось, существует другая группа теорем, касающихся предельных законов распределения суммы случайных величин. Общее название этой группы теорем – центральная предельная терема. Различные её формы различаются условиями, накладываемыми на сумму составляющих случайных величин. Впервые одна из форм центральной предельной теоремы была доказана выдающимся русским математиком А.М.Ляпуновым в 1900 году с использованием специально разработанного им метода характеристических функций.
ТЕОРЕМА Ляпунова: Закон распределения суммы независимых случайных величин 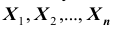 приближается к нормальному закону распределения при неограниченном увеличении n (то есть, при
приближается к нормальному закону распределения при неограниченном увеличении n (то есть, при 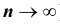 ), если выполняются следующие условия:
), если выполняются следующие условия:
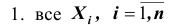 имеют конечные математические ожидания и дисперсии:
имеют конечные математические ожидания и дисперсии: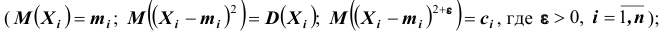
Ни одна из случайных величин по степени своего влияния на всю сумму случайных величин не отличается от остальных (то есть, влияние каждой из случайных величин на всю сумму ничтожно мало. Другими словами выполняется условие: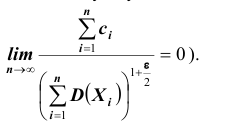 тогда
тогда 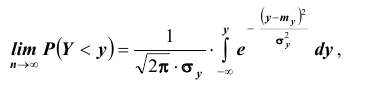
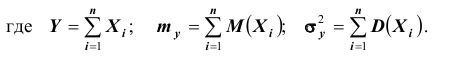
Следует отметить, что центральная предельная теорема справедлива не только для непрерывных, но и для дискретных случайных величин. Практическое значение теоремы Ляпунова огромно. Опыт показывает, что закон распределения суммы независимых случайных величин, сравнимых по своему рассеиванию, достаточно быстро приближается к нормальному. Уже при числе слагаемых порядка десяти закон распределения суммы можно заменить на нормальный (в частности, примером такой суммы может быть среднее арифметическое наблюдаемых значений случайных величин, то есть 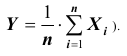
Частным случаем центральной предельной теоремы является теорема Лапласа. В ней, как вы помните, рассматривается случай, когда случайные величины  дискретны, одинаково распределены и принимают только два возможных значения: 0 и 1.
дискретны, одинаково распределены и принимают только два возможных значения: 0 и 1.
Далее, вероятность того, что Y заключено в интервале 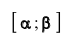 можно вычислить по формуле
можно вычислить по формуле 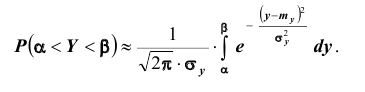
Используя функцию Лапласа, последнюю формулу можно записать в удобном для расчётов виде: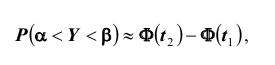 где
где 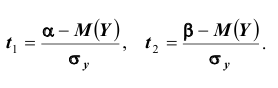
Пример №2
Пусть производится измерение некоторой физической величины. Любое измерение даёт лишь приближённое значение измеряемой величины, так как на результат измерения оказывают влияние очень многие независимые случайные факторы (температура, колебания прибора, влажность и др.). Каждый из этих факторов порождает ничтожную «частную ошибку». Однако, поскольку число этих факторов очень велико, совокупное их действие порождает уже заметную «суммарную ошибку». Рассматривая суммарную ошибку как сумму очень большого числа взаимно независимых частных ошибок, мы вправе заключить, что суммарная ошибка имеет распределение, близкое к нормальному. Опыт подтверждает справедливость такого заключения.
Понятие закона больших чисел
В материалах сегодняшней лекции мы рассмотрим закон больших чисел.
Что такое закон больших чисел
(Чебышев Пафнутий Львович (1821 - 1824) - русский математик)
На практике сложно сказать какое конкретное значение примет случайная величина, однако, при воздействии большого числа различных факторов поведение большого числа случайных величин практически утрачивает случайный характер и становится закономерным.
Этот факт очень важен на практике, т.к. позволяет предвидеть результат опыта при воздействии большого числа случайных факторов.
Однако, это возможно только при выполнении некоторых условий, которые определяются законом больших чисел. К законам больших чисел относятся теоремы Чебышева (наиболее общий случай) и теорема Бернулли (простейший случай), которые будут рассмотрены далее.
Рассмотрим дискретную случайную величину X (хотя все сказанное ниже будет справедливо и для непрерывных случайных величин), заданную таблицей распределения:

Требуется определить вероятность того, что отклонение значения случайной величины от ее математического ожидания будет не больше, чем заданное число £.
Теорема. (Неравенство Чебышева) Вероятность того, что отклонение случайной величины X от её математического ожидания по абсолютной величине меньше положительного числа 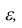 не меньше чем
не меньше чем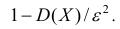
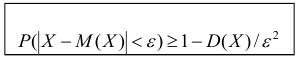
Доказательство этой теоремы приводить не будем, оно имеется в литературе.
Теорема Чебышева
Теорема. Если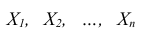 - попарно независимые случайные величины, причём дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число
- попарно независимые случайные величины, причём дисперсии их равномерно ограничены (не превышаю постоянного числа С), то, как бы мало не было положительное число 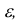 вероятность неравенства
вероятность неравенства
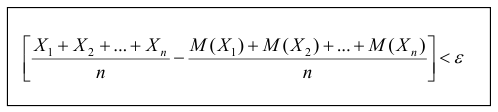
будет сколь угодно близка к единице, если число случайных величин дост а точно велико.
Т.е. можно записать:
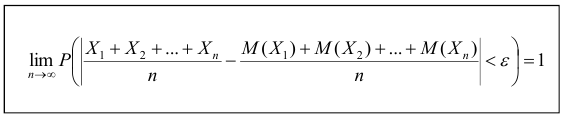
Часто бывает, что случайные величины имеют одно и то же математическое ожидание. В этом случае теорема Чебышева несколько упрощается:

Дробь, входящая в записанное выше выражение есть не что иное, как среднее арифметическое возможных значений случайной величины.
Теорема утверждает, что хотя каждое отдельное значение случайной величины может достаточно сильно отличаться от своего математического ожидания, но среднее арифметическое этих значений будет неограниченно приближаться к среднему арифметическому математических ожиданий.
Отклоняясь от математического ожидания, как в положительную, так и в отрицательную сторону, от своего математического ожидания, в среднем арифметическом отклонения взаимно сокращаются.
Таким образом, величина среднего арифметического значений случайной величины уже теряет характер случайности.
Теорема Бернулли
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А равно р.
Возможно определить примерно относительную частоту появления события А.
Теорема. Если в каждом из n независимых испытаний вероятность р появления события А постоянно, то сколь угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний р достаточно велико.
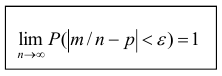
Здесь m - число появлений события А. Из всего сказанного выше не следует, что с увеличением число испытаний относительная частота неуклонно стремится к вероятности p, т.е. 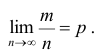 В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.
В теореме имеется в виду только вероятность приближения относительной частоты к вероятности появления события А в каждом испытании.
Теорема Пуассона
В случае, если вероятности появления события А в каждом опыте различны, то справедлива следующая теорема, известная как теорема Пуассона.
Теорема. Если производится п независимых опытов и вероятность появления события А в каждом опыте равна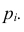 то при увеличении п частота события А сходится по вероятности к среднему арифметическому
то при увеличении п частота события А сходится по вероятности к среднему арифметическому
вероятностей 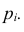
Предельные теоремы
Как уже говорилось, при достаточно большом количестве испытаний, поставленных в одинаковых условиях, характеристики случайных событий и случайных величин становятся почти неслучайными. Это позволяет использовать результаты наблюдений случайных событий для предсказания исхода того или иного опыта.
Предельные теоремы теории вероятностей устанавливают соответствие между теоретическими и экспериментальными характеристиками случайных величин при большом количестве испытаний.
В рассмотренном выше законе больших чисел нечего не говорилось о законе распределения случайных величин.
Поставим задачу нахождения предельного закона распределения суммы
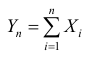
когда число слагаемых n неограниченно возрастает. Эту задачу решает Центральная предельная теорема Ляпунова.
В зависимости от условий распределения случайных величин 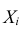 образующих сумму, возможны различные формулировки центральной предельной теоремы.
образующих сумму, возможны различные формулировки центральной предельной теоремы.
Допустим, что случайные величины 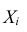 взаимно независимы и одинаково распределены.
взаимно независимы и одинаково распределены.
Теорема. Если случайные величины 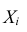 взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией
взаимно независимы и имеют один и тот же закон распределения с математическим ожиданием m и дисперсией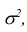 причём существует трет и й а бсолют н ы й мом ент
причём существует трет и й а бсолют н ы й мом ент , то при неограниченном увеличении числа испытаний п закон распределения суммы
, то при неограниченном увеличении числа испытаний п закон распределения суммы
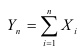 неограниченно приближается к нормальному.
неограниченно приближается к нормальному.
При доказательстве этой теоремы Ляпуновым использовались так называемые характеристические функции.
Определение. Характеристической функцией случайной величины X называется функция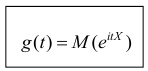
эта функция представляет собой математическое ожидание некоторой комплексной случайной величины 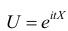 являющейся функцией от случайной величины X. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.
являющейся функцией от случайной величины X. При решении многих задач удобнее пользоваться характеристическими функциями, а не законами распределения.
Зная закон распределения, можно найти характеристическую функцию по формуле (для непрерывных случайных величин):
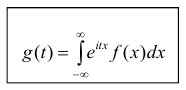
Как видим, данная формула представляет собой не что иное, как преобразование Фурье для функции плотности распределения. Очевидно, что с помощью обратного преобразования Фурье можно по характеристической функции найти закон распределения.
Введение характеристических функций позволяет упростить операции с числовыми характеристиками случайных величин.
В случае нормального распределения характеристическая функция имеет вид:
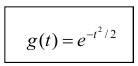
Сформулируем некоторые свойства характеристических функций:
1) Если случайные величины X и У связаны соотношением
Y = aX
где а - неслучайный множитель, то
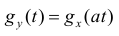
2) Характеристическая функция суммы независимых случайных величин равна произведению характеристических функций слагаемых.
Случайные величины 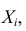 рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.
рассмотренные в центральной предельной теореме, могут обладать произвольными распределениями вероятностей.
Теорема Муавра - Лапласа
Если все эти случайные величины одинаково распределены, дискретны и принимают только два возможных значения 0 или 1, то получается простейший случай центральной предельной теоремы, известный как теорема Муавра - Лапласа.
Теорема. (Теорема Муавра - Лапласа) Если производится п независимых опытов, в каждом из которых событие Л появляется с вероятностью р, то для любого интервала 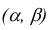 справедливо соотношение:
справедливо соотношение:
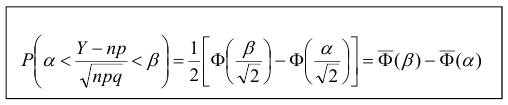
где Y - число появлений события А в п опытах, q = 1 - р, Ф(х) - функция Лапласа, 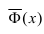 - нормированная функция Лапласа.
- нормированная функция Лапласа.
Теорема Муавра - Лапласа описывает поведение биноминального распределения при больших значениях n.
Данная теорема позволяет существенно упростить вычисление по формуле биноминального распределения.
Расчёт вероятности попадания значения случайной величины в заданный интервал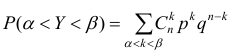 при больших значениях n
при больших значениях n
крайне затруднителен. Гораздо проще воспользоваться формулой:
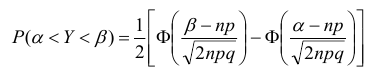
Теорема Муавра - Лапласа очень широко применяется при решении практических задач.
Примеры с решением
Пример №3
Пусть 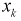 - результат
- результат 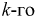 измерения длины, например комнаты.
измерения длины, например комнаты.
1. Случайные величины 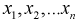 - независимы.
- независимы.
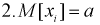 - т. к. длина комнаты - существует.
- т. к. длина комнаты - существует.
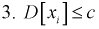 т. к. ошибка не накапливается.
т. к. ошибка не накапливается.
Тогда вероятность при 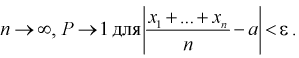
Пример №4
Пусть проводится эксперимент с броском монеты. Обозначим через событие  появление герба. Путь при
появление герба. Путь при  бросках герб появится
бросках герб появится 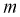 раз. Найдем относительную частоту появления герба:
раз. Найдем относительную частоту появления герба: 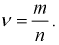 Повторяя такой опыт много раз, будем откладывать результаты на графике, (рис. 7.1).
Повторяя такой опыт много раз, будем откладывать результаты на графике, (рис. 7.1).
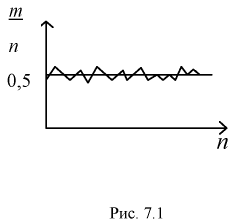
Мы увидим, что относительная частота будет колебаться около некоторого постоянного числа (в случае с симметричной монетой это 0,5). И это значение можно принимать за неизвестную вероятность события 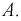 Но надо оговорить,
Но надо оговорить, 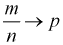 при
при 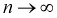 по вероятности, т. к. возможность отклонения всегда остается.
по вероятности, т. к. возможность отклонения всегда остается.
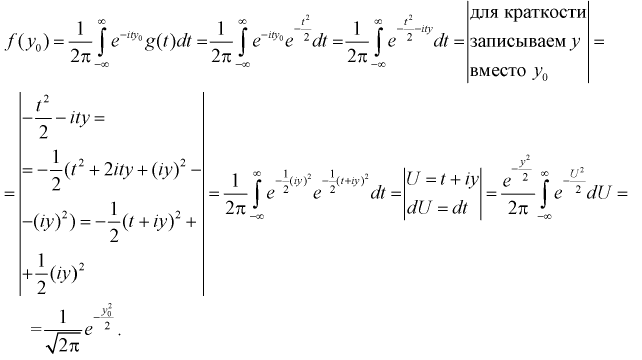
Пример №5
Показать, что характеристическая функция 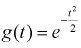 имеет плотность распределения нормированной нормальной случайной величины.
имеет плотность распределения нормированной нормальной случайной величины.
Решение.
Используем обратное преобразование Фурье:
Пример №6
Вероятность успешной работы телевизора после сборки равна 0,75. Найти вероятность того, что из 10 телевизоров 8 заработают. Используем локальную теорему Лапласа и получаем 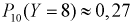 - по таблицам, а по формуле Бернулли-
- по таблицам, а по формуле Бернулли- 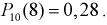
Заключение по лекции:
В лекции мы рассмотрели закон больших чисел.
222
Закон больших чисел
При статистической обработке опытных данных используют определения и правила, установленные теорией вероятностей.
Теория вероятностей—математическая наука, возникшая в середине XVII столетия. Первые работы, в которых зарождались основные понятия теории вероятностей, принадлежали Б. Паскалю, П. Ферма и X. Гюйгенсу. Дальнейшее развитие теории вероятностей связано с именем Я Бернулли, доказавшим теорему, впоследствии названную законом больших чисел. В XIX столетии теория вероятностей начала успешно применяться в страховом деле, статистике народонаселения, биологической статистике и в артиллерийской стрельбе. В этот период она обогатилась работами А. Муавра, П. Лапласа, К. Гаусса и С. Пуассона. »
Наиболее плодотворный для развития теории вероятностей период связан с именами П. Л. Чебышева и его учеников А. А. Маркова и А. М. Ляпунова, усилиями которых она была превращена в стройную математическую науку.
Велика заслуга русских и советских ученых С. Н. Бернштейна, В. И. Романовского, А. Н. Колмогорова, А. Я. Хинчина, Б. В. Гнеденко, Н. В. Смирнова, Б. С. Ястремского и др., своими исследованиями внесших крупный вклад в теорию вероятностей и сделавших важные открытия, приведшие к созданию новых ее ветвей.
В настоящее время теория вероятностей весьма плодотворно применяется в статистике производств, при анализе технологических процессов, статистическом предупредительном контроле качества продукции, в физике, биологии и т. д.
Объектом теории вероятностей является измерение степени возможности различных случайных, результатов. Знание выявленных с помощью теории вероятностей закономерностей позволяет предвидеть, как эти события будут протекать в дальнейшем.
Испытанием или опытом называют комплекс условий, в которых могут осуществиться или не осуществиться рассматриваемые события (результаты).
Случайное событие определяется как событие, которое может произойти или не произойти, в отличие от достоверного события, которое обязательно осуществляется (при данных условиях), и невозможного события, осуществление которого при данных условиях исключается. Для обозначения событий приняты буквы А, Б, В и т. д. При многократном повторении комплекса условий мы имеем серию испытаний.
Пусть, например, имеется совокупность, состоящая из деталей различных сортов. По жребию или другим аналогичным способам (наудачу) из совокупности отбирается одна деталь.
В этом случае испытанием является отбор одной детали. Появление при этом детали определенного сорта называется случайным событием. Если отбор одной детали из совокупности будет повторяться несколько раз, то это будет серией испытаний.
Несовместимые и совместимые события. События А, Б,
В... называются несовместимыми, если в условиях испытания возможно появление только одного из них, т. е. если они не могут появиться одновременно. Так, отобранная в результате испытания деталь не может быть одновременно первосортной и второсортной, так как эти события несовместимы. Если же появление одного события не исключает появления другого, то эти события называются совместимыми. Например, имеются две совокупности деталей, содержащих детали различных сортов. Из каждой совокупности отбирается по одной детали. В этом случае отборы первосортной детали из первой и из второй совокупностей будут событиями совместимыми.
Понятие о равновозможности
Если из совокупности, состоящей из N единиц, обладающих некоторыми признаками, отбирается одна единица и при этом никакой, из единиц, состав; ляющих данную совокупность, не отдается предпочтения по сравнению с другими, то говорят, что каждой единице обеспечена равная возможность быть отобранной (принцип равновозможности). О равновозможности событий можно судить либо исходя из общих свойств изучаемых явлений (выпадение каждой грани идеально правильной и материально однородной игральной кости считают равновозможным событием), либо по числу появлений событий в достаточно большой серии испытаний. Так, если при бросании игральной кости 600 раз каждая грань выпадает приблизительно по 100 раз, то мы считаем выпадение каждой грани равновозможными событиями.
В случае соблюдения принципа равновозможности выбор вполне определенной конкретной единицы имеет один шанс (случай) из числа N таких же шансов. Выбор же единицы, обладающей данным значением признака (например, первосортной детали, число которых во всей совокупности М) имеет М равновозможных шансов из N таких же шансов.
Математическая вероятность события
Измерение вероятностей основывается на подсчете шансов. Математическая вероятность того, что событие А произойдет, измеряется отношением числа шансов (равновозможных и несовместимых), благоприятствующих данному событию А (М), к общему числу благоприятствующих и неблагоприятствующих шансов (N):
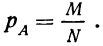
Такое определение вероятности называют классическим. При таком понимании вероятности мы ограничиваем сферу ее практического применения только такими событиями, которые допускают различение дискретных шансов.
Пример 1. Из партии в 200 деталей, среди которых 4 бракованные и 196 доброкачественных (соответствующих стандарту), производится выборка одной детали. Как велика вероятность того, что отобранная деталь окажется бракованной? Находим вероятность события А в соответствии с приведенным выше определением вероятности. Из возможных 200 случаев исхода данного отбора 4 случая благоприятствуют событию А, вероятность которого мы ищем. Поэтому:
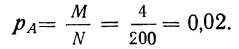
Повторный и бесповторный отбор
Отбор единиц из совокупности, при котором каждая отобранная и обследованная единица в совокупность не возвращается и в дальнейших испытаниях не участвует, называют бесповторным отбором, или отбором по схеме невозвращенного шара. Если же после обследования отобранной из совокупности единицы она мыслится возвращенной в совокупность и может быть повторно отобрана, то такой отбор называют повторным, или отбором по схеме возвращенного шара.
Зависимые и независимые событи
События А, Б, В... называют зависимыми друг от друга, если вероятность появления хотя бы одного из них изменяется в зависимости от появления или непоявления других событий. Примером зависимых событий являются события, происходящие при отборе единиц из совокупности по схеме невозвращенного шара, когда от появления годного или бракованного изделия при первом испытании зависит вероятность появления годного изделия при втором испытании.
Так, если из совокупности 30 деталей, содержащих 27 годных и 3 бракованные детали, отбирается при первом испытании одна деталь и не возвращается в совокупность, то вероятность отбора годной детали при втором испытании будет зависеть от того, какая деталь была отобрана при первом испытании: если при персом испытании была отобрана годная деталь, то вероятность отбора годной детали при втором испытании будет равна 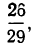 а если бракованная, то вероятность отбора годной детали будет равна
а если бракованная, то вероятность отбора годной детали будет равна 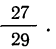
События называются независимыми, если вероятности появления каждого из них не зависят от появления или непоявления прочих из них.
Простые и сложные события
События, происходящие в результате совпадения или последовательного появления нескольких событий, называются сложными событиями, а события, их составляющие, — простыми. Так, если мы отбираем из совокупности, содержащей детали различных сортов, последовательно три детали первого сорта, то это событие будет сложным, состоящим из совпадения трех событий: отбор детали первого сорта в каждом из трех испытаний.
Статистическая вероятность
Кроме математической вероятности случайного события, определяемой непосредственным подсчетом равновозможных и несовместимых шансов, имеется статистическое понимание вероятности. Если в результате достаточно большого числа испытаний установлено, что частость случайного события 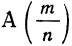 приближается к некоторой величине, то эту величину в силу закона больших чисел, содержание которого выяснится ниже, принимают за численное значение вероятности данного события
приближается к некоторой величине, то эту величину в силу закона больших чисел, содержание которого выяснится ниже, принимают за численное значение вероятности данного события 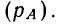 Ясно, что установление вероятности случайного события опытным путем носит несколько неопределенный характер.
Ясно, что установление вероятности случайного события опытным путем носит несколько неопределенный характер.
Если вероятность случайного события определяется до испытания, приведшего к определенному исходу, то численное значение этой вероятности называют априорным (доопытным).
Вероятность события после опыта, приведшего к определенному результату, в отличие от доопытной вероятности называют апостериорной вероятностью.
§ 9. Вероятность того, что событие А не произойдет 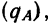 исчисляется в соответствии с определением вероятности как отношение числа шансов, не благоприятствующих событию А, к общему числу шансов. Если N — общее число шансов и событию А благоприятствует М шансов, то не благоприятствует ему N—М шансов. Тогда:
исчисляется в соответствии с определением вероятности как отношение числа шансов, не благоприятствующих событию А, к общему числу шансов. Если N — общее число шансов и событию А благоприятствует М шансов, то не благоприятствует ему N—М шансов. Тогда:
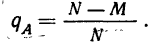
Полученную вероятность называют вероятностью противоположного события.
Пример 2. По данным примера 1 найти вероятность того что отобранная деталь не окажется бракованной, т. е. окажется доброкачественной.
Число случаев, благоприятствующих тому, что отобранная деталь не окажется бракованной, равно 200—4 = 196
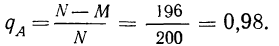
§ 10. Сумма вероятностей двух противоположных событий, т. е. таких, из которых в результате испытания может произойти либо одно, либо другое, равна единице:
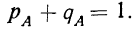
Отсюда вытекает, что, зная вероятность события А, можно вычитанием ее из единицы определить вероятность того, что А не произойдет
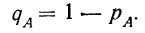
Пример 3. Используя результат, полученный в примере 1 по вероятности события А, найдем вероятность противоположного события.
Имеем:
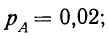
тогда:
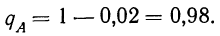
Достоверное событие
Если все N случаев благоприятствуют событию А (M = N), то вероятность события А равна единице. Такое событие называется достоверным
Пример 4. Если в партии из 200 деталей все 200 доброкачественны, то вероятность того, что отобранная наудачу деталь окажется доброкачественной, есть событие достоверное
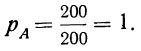
Невозможное событие
Если число случаев, благоприятствующих событию А, равно нулю (M = 0), то вероятность события А равна нулю. Такое событие называется невозможным
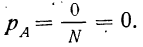
Пример 5. Если в партии из 200 деталей нет ни одной бракованной, то вероятность того, что отобранная деталь окажется бракованной, равна нулю. Это событие невозможно
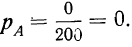
Пределы вероятностей
Вероятности событий находятся в пределах от нуля до единицы
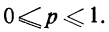
Чем ближе к единице вероятность события, тем оно достовернее.
При решении различных задач по исчислению вероятностей событий используются основные теоремы теории вероятностей.
Теорема сложения вероятностей
Если события А и Б несовместимы, то вероятность того, что произойдет — или событие А, или событие Б 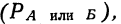 —равна сумме вероятностей наступления каждого события
—равна сумме вероятностей наступления каждого события
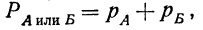
где 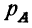 —вероятность события А;
—вероятность события А;
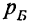 — вероятность события Б.
— вероятность события Б.
Теорема сложения вероятностей может быть распространена на три и более несовместимых событий.
Пример 6. Партия из 200 деталей состоит из 150 деталей I сорта, 30 деталей II сорта, 16 деталей III сорта и 4 бракованных деталей.
Как велика вероятность того, что отобранная наудачу деталь будет либо I сорта, либо II сорта?
Так как при данных условиях событие А (I сорт) и событие Б (II сорт) несовместимы (одно из них исключает возможность другого), то можно применить теорему сложения вероятностей.
Имеем:
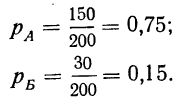
Следовательно:
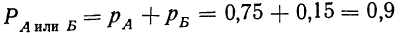
или
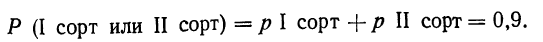
Следствие теоремы сложения вероятностей. Сумма вероятностей единственно . возможных и несовместимых событий равна единице
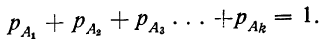
Такие несовместимые события, сумма вероятностей которых равна единице, составляют полную группу событий. Если полная группа состоит из двух событий, то эти события называются противоположными.
Пример 7. По данным примера 6. найти вероятность того, что отобранная наудачу деталь окажется либо I, либо II, либо III сорта, либо бракованной.
Имеем:
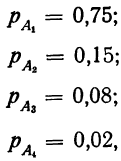
отсюда
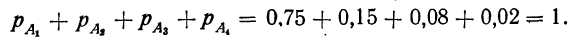
Первая теорема умножения вероятностей
Если имеется сложное событие, состоящее из совпадения двух независимых друг от друга событий (А и Б), то вероятность того, что произойдет это сложное событие (включающее в себя и событие А и событие Б), равна произведению вероятностей каждого события:
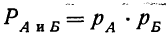
Указанная теорема может быть распространена и на сложные события, состоящие из нескольких (более двух) независимых событий.
Пример 8. Имеются две партии деталей: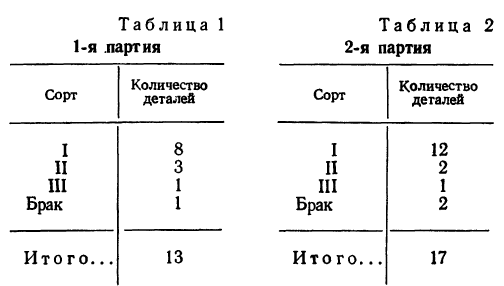
Из каждой партии наудачу отбирается по одной детали. Как велика вероятность того, что отобранные две детали окажутся I сорта?
Данное событие является сложным и состоит из двух простых: отбор детали I сорта из 1-й партии (событие А) и отбор детали I сорта из 2-й партии (событие Б). Оба простых события А и Б независимы, так как вероятность отбора детали I сорта из 2-й партии не зависит от того, окажется ли отобранная деталь I сорта из 1-й партии. Следовательно, можно применить. 1-ю теорему умножения вероятностей.
Имеем:
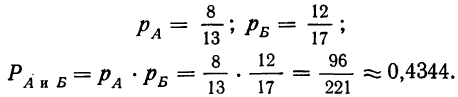
Пример 9. Сохраняя условие примера 8, произведем наудачу выборку двух деталей только из 1-й партии с возвратом 1-й отобранной детали после ее извлечения. Как велика вероятность, того, что 1-я деталь окажется I сорта, а 2-я—II сорта?
В данном случае налицо все условия применения 1-й теоремы умножения вероятностей.
Имеем:
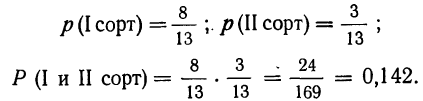
Следствие 1-й теоремы умножения вероятностей
Вероятность повторения события A k раз при k независимых испытаниях, в которых вероятность его остается одинаковой, равна вероятности события А при каждом испытании, возведенной в степень k:
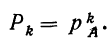
Пример 10. По данным примера 8. находим вероятность того, что при отборе наудачу трех деталей из 1-й партии (по одной с возвратом) все три детали окажутся I сорта. Вероятность появления детали I сорта при одном испытании:
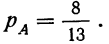
Находим вероятность того, что все три детали окажутся I сорта:
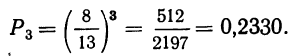
Условная вероятность
Условной вероятностью события Б 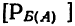 при осуществлении А называют такую вероятность этого события, которая вычислена при предположении, что-событие А состоялось. Если из совокупности 200 деталей, из которых I сорта — 150 деталей, II —30, III —16, бракованных — 4, отбирается последовательно две детали по схеме невозвращенного шара (т. е. без возврата), то вероятность того, что. первая отобранная деталь окажется первосортной, равна
при осуществлении А называют такую вероятность этого события, которая вычислена при предположении, что-событие А состоялось. Если из совокупности 200 деталей, из которых I сорта — 150 деталей, II —30, III —16, бракованных — 4, отбирается последовательно две детали по схеме невозвращенного шара (т. е. без возврата), то вероятность того, что. первая отобранная деталь окажется первосортной, равна 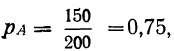 а условная вероятность того, что вторая отобранная деталь также окажется первосортной, будет равна
а условная вероятность того, что вторая отобранная деталь также окажется первосортной, будет равна
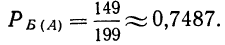
Как видно из примера, условная вероятность второго события вычислена при предположении, что первое событие состоялось, т. е. осталось всего 199 деталей, из них первосортных 149. Аналогично можно установить условные вероятности того, что -вторая отобранная деталь будет второсортной и бракованной
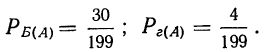
Вторая теорема умножения вероятностей
Вероятность сложного события, состоящего из двух простых зависимых событий, равна произведению вероятностей одного события на условную вероятность другого:
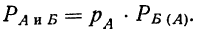
Пример 11. По данным примера 8 по выборке из 1-й партии определить вероятность того, что при отборе двух деталей (без возврата) первая отобранная деталь окажется I сорта, а вторая — II сорта.
Вероятность того, что первая деталь окажется I сорта:
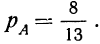
Предполагая, что данное событие условную вероятность второго события
осуществилось, находим
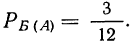
Вычисляем вероятность сложного события, состоящего из двух простых зависимых событий:

Полная вероятность события А
Если некоторое событие А может произойти только тогда, когда имеет место какая-нибудь из нескольких гипотез, то полная вероятность события А равна сумме произведений вероятностей гипотез на вероятности события А при условии осуществления каждой данной гипотезы:
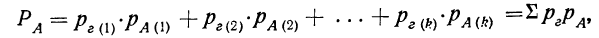
где 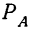 — полная вероятность события А;
— полная вероятность события А;
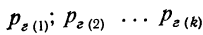 — вероятность гипотезы 1-й, 2-й и т.д. до k;
— вероятность гипотезы 1-й, 2-й и т.д. до k;
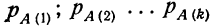 — вероятность события А по первой гипотезе, по второй гипотезе и т. д. до k-й. При подсчете полной вероятности мы пользуемся двумя теоремами: сложения и умножения вероятностей.
— вероятность события А по первой гипотезе, по второй гипотезе и т. д. до k-й. При подсчете полной вероятности мы пользуемся двумя теоремами: сложения и умножения вероятностей.
Пример 12. Имеется 6 ящиков, одинаковых по внешнему виду и по числу содержащихся в них деталей, но с разным количеством деталей I сорта.
Определить полную вероятность того, что при выборке наудачу одной детали она окажется первосортной.
Вероятность предположения, что отобранная деталь окажется взятой из ящиков, содержащих 8 деталей 1 сорта (ящики № 1, 2 и 3—гипотеза первая), может быть исчислена как отношение числа ящиков, благоприятствующих этому исходу, к общему числу ящиков:
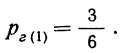
Вероятность второй гипотезы, т. е. того, что деталь окажется взятой из ящиков, содержащих 6 деталей I сорта (ящики № 4 и 5):
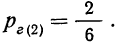
Вероятность третьей гипотезы (ящик № 6):
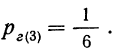
Определим вероятность событий А, т. е. отбора детали I сорта, по гипотезам.
Вероятность отбора детали I сорта по первой гипотезе:
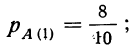
по второй гипотезе:
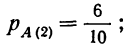
по третьей гипотезе:
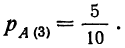
Определяем полную вероятность события А:
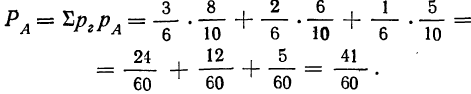
Здесь применена сначала теорема сложения вероятностей, затем теорема умножения вероятностей и, наконец, еще раз теорема сложения вероятностей. Когда мы определяли вероятность гипотезы, то считали, что вероятность первой гипотезы равна 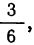 но ведь эта первая гипотеза осуществится, если деталь окажется взятой из ящика № 1
но ведь эта первая гипотеза осуществится, если деталь окажется взятой из ящика № 1
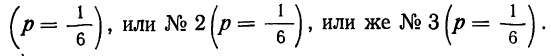
Следовательно, вероятность первых двух гипотез мы и получили, складывая вероятности каждого из событий, составляющих эту гипотезу:
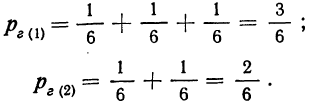
Вероятность того, что произойдет первое сложное событие, состоящее в том, что отобранная деталь окажется взятой по первой гипотезе из ящиков, содержащих 8 деталей I сорта, и будет первосортной, мы определяли по теореме умножения вероятности:
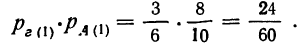
Вероятность второго сложного события, состоящего в том, что отобранная деталь окажется взятой по второй гипотезе из ящиков, содержащих 6 деталей I сорта, и будет первосортной:
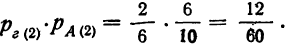
Так же получена и вероятность третьего сложного события:
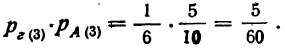
Для того чтобы отобранная деталь оказалась I сорта, должно иметь место либо первое сложное событие, либо второе, либо третье. Поэтому исчисленные вероятности этих событий мы складывали, применяя снова теорему сложения вероятностей:
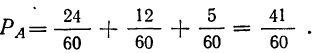
Теорема деления вероятностей
Из теоремы умножения вероятностей видно, что условная вероятность события Б при предположении, что событие А имело место, может быть определена как отношение вероятности совместного совершения обоих событий А и Б к вероятности события А:
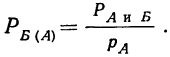
Теорема Байеса или теорема о вероятности гипотез дает возможность судить о величине вероятности какого-либо предположения после опыта, давшего определенный результат, и формулируется следующим образом: вероятность гипотезы i после испытания, приведшего к осуществлению события А, равна произведению вероятности этой гипотезы до испытания на вероятность события по этой гипотезе, деленному на полную вероятность события А, т. е. на сумму таких произведений для всех гипотез:
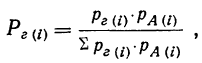
где 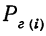 —вероятность i гипотезы после испытания;
—вероятность i гипотезы после испытания;
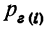 —вероятность i гипотезы до испытания;
—вероятность i гипотезы до испытания;
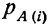 —вероятность события А при предположении, что
—вероятность события А при предположении, что
данная гипотеза осуществилась.
Применяя теорему Байеса, удобно пользоваться следующей схемой (см. табл. 4).
Пример 13. Используя данные примера 12, предположим, что мы выбрали наудачу один ящик и из него отобрали одну деталь, которая оказалась I сорта. Требуется определить вероятность того, что: 1) отобранный ящик содержал 8 деталей I сорта (т. е. оказался ящиком № 1, 2 или 3), 2) отобранный ящик содержал 6 деталей I сорта (т. е. оказался ящиком № 4 и 5) и 3) отобранный ящик содержал 5 деталей I сорта (т. е. оказался ящиком № 6).
Для исчисления искомых вероятностей расположим все исходные и расчетные показатели в таблицу (см. табл. 5).
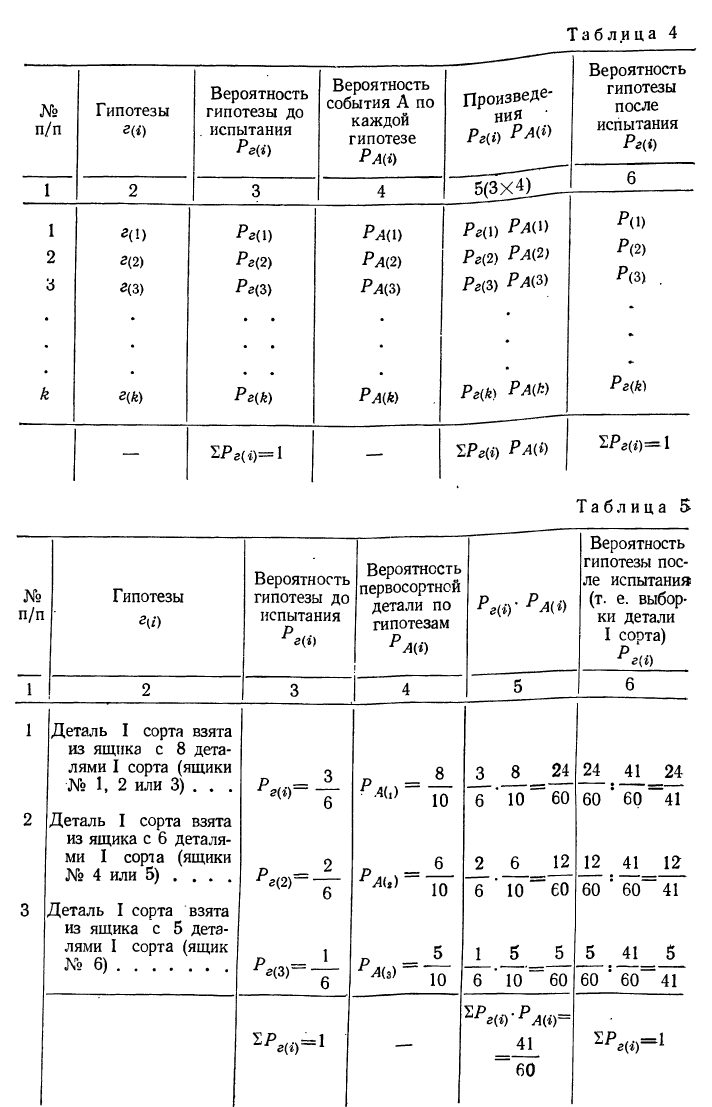
Окончательный расчет для ответа на все три вопроса дан в колонке 6. По теореме Байеса получаем:
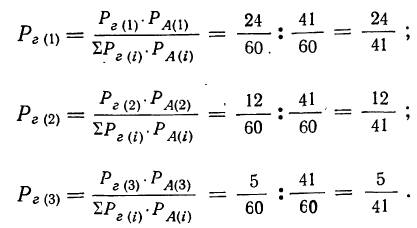
Сумма вероятностей гипотез до испытания и после испытания равна 1 (что видно из сумм колонок 3 и 6).
Биномиальный закон вероятностей при n повторных независимых испытаниях очень часто называют бернуллиевым распределением вероятностей.
При повторных независимых испытаниях, в каждом из которых может осуществиться некоторое событие А (с одной и той же вероятностью р), вероятности любого числа его появлений соответствуют членам разложения бинома Ньютона в степени равной числу испытаний
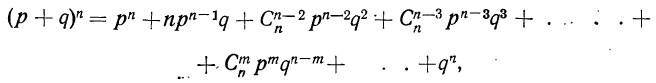
где 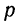 — вероятность события А;
— вероятность события А;
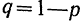 — вероятность того, что событие А не произойдет;
— вероятность того, что событие А не произойдет;
n — число испытаний;
m—число осуществлений события А или частота события А;
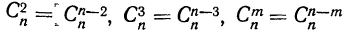 —числа сочетаний из n элементов по n—2; n—3; n—m элементов;
—числа сочетаний из n элементов по n—2; n—3; n—m элементов;
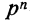 —первый член биномиальной строки; его величина соответствует вероятности такого исхода (комбинации), при котором событие А осуществляется n раз (см. следствие первой теоремы умножения вероятностей);
—первый член биномиальной строки; его величина соответствует вероятности такого исхода (комбинации), при котором событие А осуществляется n раз (см. следствие первой теоремы умножения вероятностей);
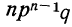 — второй член биномиальной строки; его величина соответствует вероятности такого исхода, при котором событие А осуществляется n—1 раз, а не осуществляется один раз и т. д. до
— второй член биномиальной строки; его величина соответствует вероятности такого исхода, при котором событие А осуществляется n—1 раз, а не осуществляется один раз и т. д. до 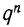 — последнего члена строки, дающего вероятность такого исхода, при котором событие А ни разу не осуществилось.
— последнего члена строки, дающего вероятность такого исхода, при котором событие А ни разу не осуществилось.
Таким образом, вероятность осуществления события А m раз в n независимых испытаниях с одинаковой вероятностью р можно рассчитать по формуле общего члена разложения бинома Ньютона:
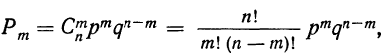
где 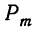 — вероятность того, что при т испытаниях событие А осуществится m раз;
— вероятность того, что при т испытаниях событие А осуществится m раз;
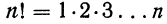 —произведение натурального ряда чисел от 1 до n — читается «n факториал»;
—произведение натурального ряда чисел от 1 до n — читается «n факториал»;
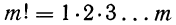 — читается «m факториал»;
— читается «m факториал»;
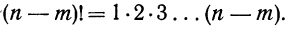
Примечание. 0! считается равным единице (см. гамму-функцию от n стр. 147.)
Пример 14. По данным примера 6 найти вероятность того, что при отборе наудачу 5 деталей:
1) все 5 деталей окажутся I сорта;
2) 4 детали — I сорта и 1 деталь—не I сорта;
3) 3 детали — I сорта и 2 детали — не I сорта;
4) 2 детали — I сортa и 3 детали—не I сорта;
5) 1 деталь —I сорта и 4 детали — не I сорта;
6) все 5 деталей окажутся не I сорта.
Вероятности отбора детали I сорта при единичном испытании:
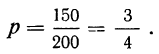
Вероятность отбора детали не I сорта при единичном испытании:
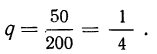
Рассчитываем по формуле 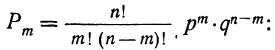
1) вероятность того, что все 5 деталей окажутся I сорта
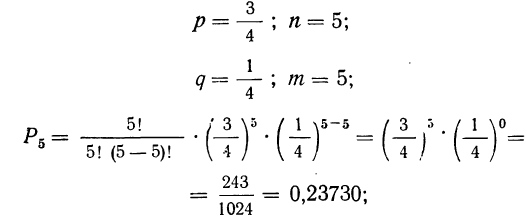
2) вероятность того, что 4 детали окажутся I сорта, а одна деталь не I сорта
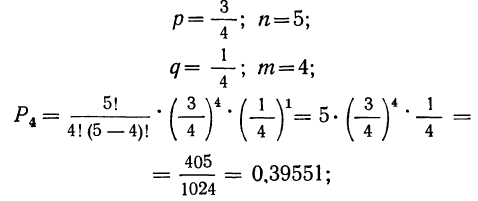
3) вероятность того, что 3 детали окажутся I сорта, а 2 детали не I сорта
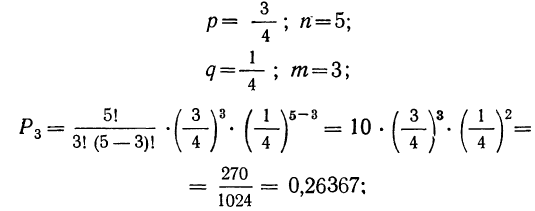
4) вероятность того, что 2 детали окажутся I сорта, а 3 детали не I сорта
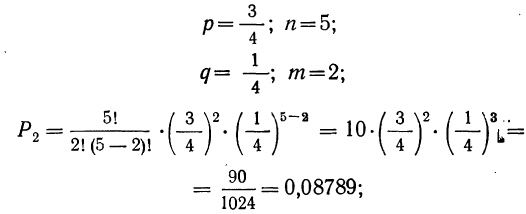
5) вероятность того, что 1 деталь окажется I сорта, а 4 детали не I сорта
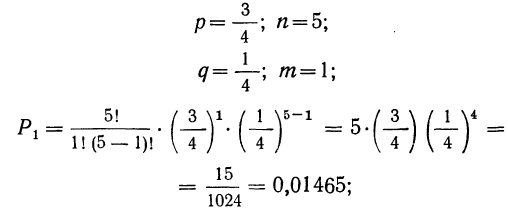
6) вероятность того, что все 5 деталей окажутся не I сорта
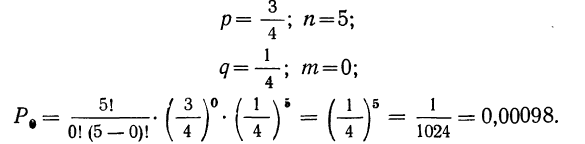
Сумма всех найденных вероятностей равна:
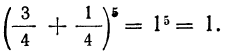
Формула Стирлинга
При расчете вероятностей бернуллиевого распределения  затруднения в громоздких вычислениях факториалов могут быть устранены использованием формулы Стирлинга (1730 г.):
затруднения в громоздких вычислениях факториалов могут быть устранены использованием формулы Стирлинга (1730 г.):
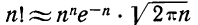
или более точной:
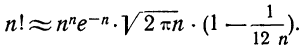
Точность данной формулы возрастает при увеличении числа n. Относительная погрешность составляет 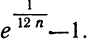
Пример 15. Найдем по формуле Стирлинга 10! и 20! и оценим допущенные при этом ошибки.
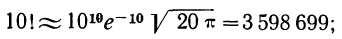 точное значение 10! 3 628 800 (ошибка составляет 0,83%)
точное значение 10! 3 628 800 (ошибка составляет 0,83%)
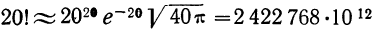 (ошибка составляет 0,41%,).
(ошибка составляет 0,41%,).
§ 22. Для определения коэффициентов при разложении вероятностей в биномиальную строку используют треугольник

Паскаля, в котором каждый коэффициент строки образуется сложением двух стоящих над ним (справа и слева) коэффициентов предыдущей строки.
Пример 16. В примере 14 нам необходимы были коэффициенты разложения бинома при n = 5, которые можно взять из треугольника Паскаля (см. 5-ю строку).
При n = 5 имеем коэффициенты: 1; 5; 10; 10; 5; 1.
Следовательно, искомые вероятности соответственно равны:
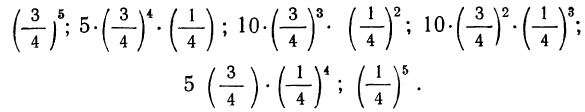
В качестве характеристик биномиального распределения признака (бернуллиево распределение) используют начальные, начальные относительно 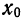 и центральные моменты (см. раздел I, § 39—42):
и центральные моменты (см. раздел I, § 39—42):
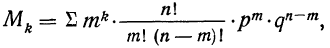
где m—число появлений события;
р — вероятность события;
n — число испытаний.
Начальные моменты:
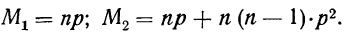
Центральные моменты получаются из начальных по общему правилу (см. раздел I, § 41).
Например:
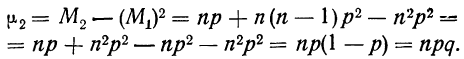
Биномиальный ряд может быть представлен следующими характеристиками:
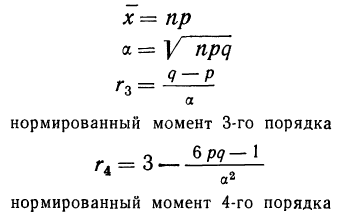
Пример 17. Пусть дан вариационный ряд, в котором числа появлений события будут рассматриваться как варианты (x), а вероятности данного исхода при n = 5; 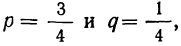
считанные по формуле разложения вероятностей в биномиальную строку, — как частоты (m). Вычислим характеристики данного ряда по указанным формулам:
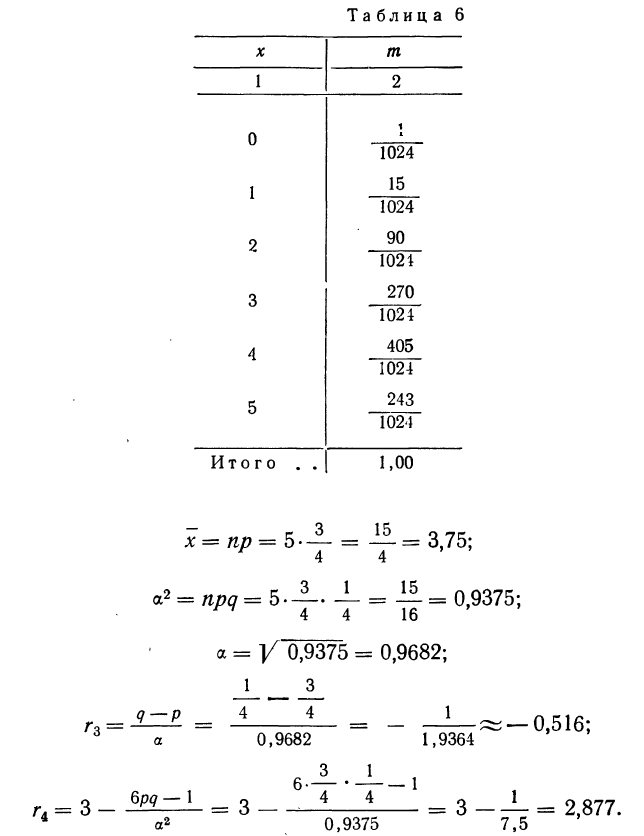
Полигон распределения вероятностей
Каждый возможный исход событий обладает определенной вероятностью.
Если на оси абсцисс наносить возможные исходы событий, а на оси ординат — вероятности этих исходов, то ломаная линия, характеризующая изменение вероятностей различных исходов событий при повторных испытаниях, называется полигоном (многоугольником) распределения вероятностей (см. раздел I, § 11).
Пример 18. По результатам разложения в биномиальную строку из примера 14 построить полигон распределения вероятностей.
В системе координат строим полигон.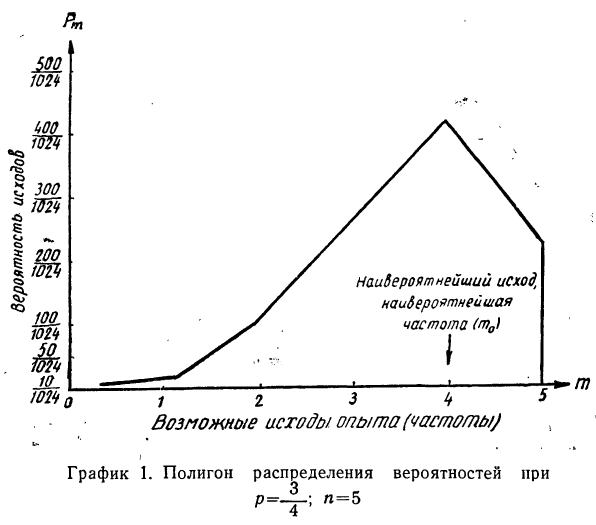
Обычно при построении полигона распределения вероятностей используют формулу общего члена (разложение бинома в строку). Придавая m различные значения от 0 до n, получают вероятности  которые наносятся на график.
которые наносятся на график.
Пример 19. Дано  построить многоугольник распределения вероятностей.
построить многоугольник распределения вероятностей.
Находим вероятности различных исходов (частот) по формуле 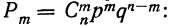
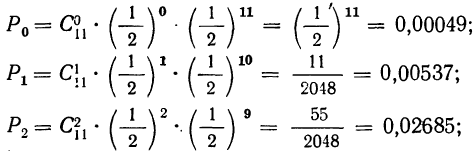
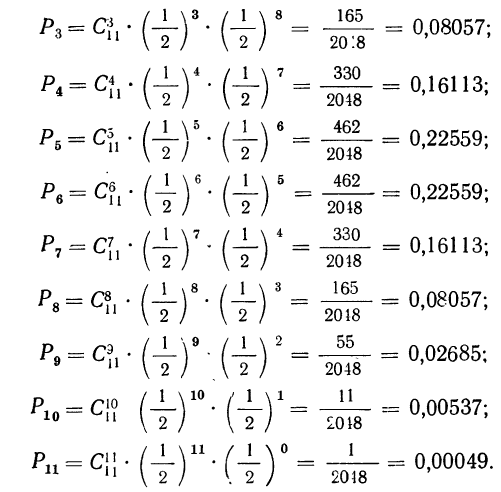
Наносим полученные данные на график (см. график 2).
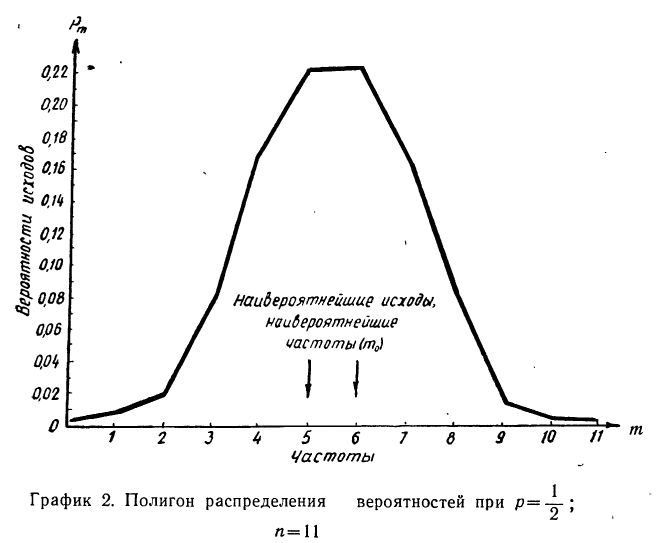
Наивероятнейшая частота
По полигонам распределения вероятностей наглядно видно, что частоты обладают различными вероятностями. Одни частоты менее вероятны, другие более вероятны. Имеется частота, обладающая наибольшей вероятностью (иногда две частоты с одинаковыми наибольшими вероятностями). Такая частота называется наивероятнейшей частотой, или наивероятнейшим исходом, обозначается 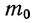 и определяется из следующего неравенства:
и определяется из следующего неравенства: 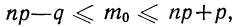
где п — число испытаний;
р — вероятность события А при одном испытании; 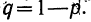
Примечания:
1. 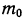 выражается в целых числах.
выражается в целых числах.
2. Если границы неравенства (левая и правая) — целые числа, то, следовательно, имеются две наивероятнейшие частоты.
3. Если границы неравенства (левая и правая) — дроби, то между ними выбирают целое число, которое и будет наивероятнейшей частотой. Таким образом, 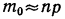 ближайшее к
ближайшее к 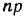 целое число.
целое число.
Пример 20. По данным примеров 14 и 6 при отборе 5 деталей определить наивероятнейший исход.
Имеем: 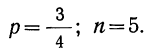
Следовательно: 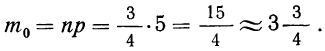
По формуле наивероятнейшей частоты получаем:
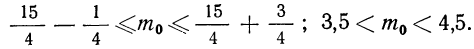
Границы (левая и правая) есть дроби 3,5 и 4,5.
Целым числом между ними является 4. Следовательно, 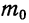 =4.
=4.
По графику 1, где частота (m), равная 4, обладает наибольшей вероятностью, убеждаемся в совпадении результатов.
Пример 21. По данным примера 19 определить наивероятнейшую частоту.
Имеем:
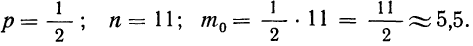
По рассматриваемой формуле получаем:
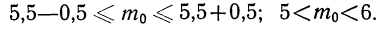
Границы (левая и права) — целые числа. Следовательно, имеем две наивероятнейшие частоты: 5 и 6. По графику 2, где частоты 5 и 6 обладают равными наибольшими вероятностями, убеждаемся в совпадении их вероятностей.
§ 26. Для расчета вероятностей всех исходов вместо разложения в биномиальную строку можно воспользоваться одной из следующих формул: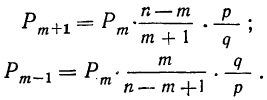
Пример 22. На основе данных примера 19 рассчитать вероятности всех частот по вышеприведенным формулам. Предварительно нужно найти вероятность какой-нибудь одной частоты. Пусть мы нашли вероятность частоты 5 по формуле:
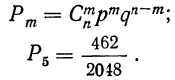
Используя формулу 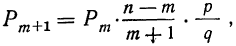 находим вероятности всех частот, больших 5:
находим вероятности всех частот, больших 5:
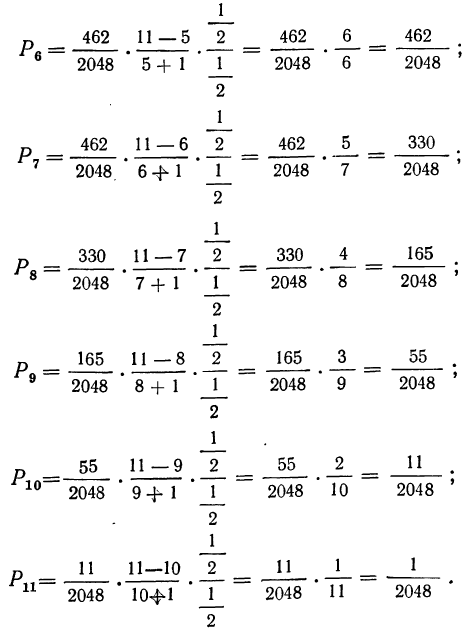
Используем формулу 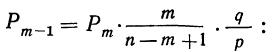

Как видим, вероятности всех частот совпадают с результатами, полученными в примере 19.
Вероятность наивероятнейшей частоты
Для расчета вероятности наивероятнейшей частоты используется формула,, дающая приближенный результат. Точность формулы зависит от числа испытаний (n) и по мере увеличения числа испытаний возрастает.
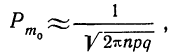
где 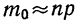 — наивероятнейшая частота;
— наивероятнейшая частота;
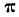 — число, равное 3,14159.
— число, равное 3,14159.
Доказательство. Возьмем выражение
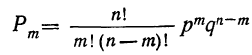
и найдем вероятность наивероятнейшей частоты, т. е. 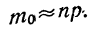
Тогда
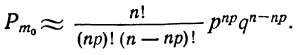
Зная, что 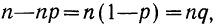 получим:
получим: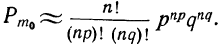
Используем формулу Стирлинга (см. § 21):
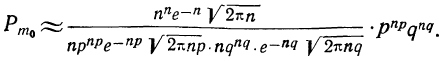
Произведя сокращения, получим:
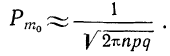
Для расчетов используют эту формулу в несколько измененном виде:
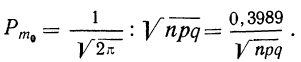
Пример 23. В примерах 20 и 21 найдены наивероятнейшие частоты. Вычислить приближенно их вероятности.
Из примера 20 имеем: 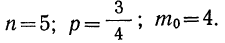
Подставляя эти значения в формулу 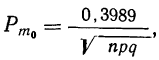 находим вероятность наивероятнейшей частоты:
находим вероятность наивероятнейшей частоты: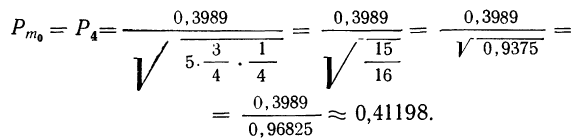
Из примера 21 имеем: 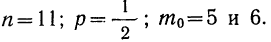
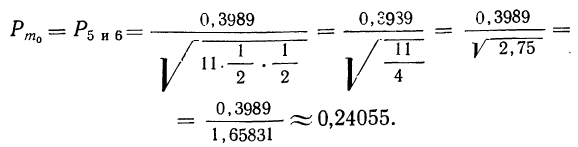
Сопоставляя приближенные результаты вероятностей наивероятнейших исходов, полученные в данном примере, с точными, полученными в примерах 14 и 19, видим их несомненную близость.
В примере 14 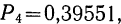 в данном примере
в данном примере 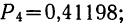 в примере 19
в примере 19 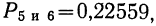 в данном примере
в данном примере 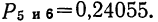 Погрешности не превышают 5%.
Погрешности не превышают 5%.
Локальная формула Лапласа
Для приближенного вычисления вероятностей биномиального распределения используется формула, которую часто называют локальной формулой Лапласа: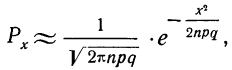
где х — отклонение частоты от наивероятнейшей частоты пр, т. е. х=m—nр;
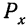 —вероятность такого события, при котором частота отклоняется от nр на величину х;
—вероятность такого события, при котором частота отклоняется от nр на величину х;
е—неперово число, основание натуральных логарифмов, приближенно равное 2,71828;
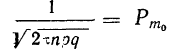 —вероятность наивероятнейшей частоты.
—вероятность наивероятнейшей частоты.
Доказательство.
Обозначая искомую функцию 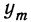 и полагая
и полагая 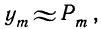 будем судить о
будем судить о 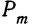 по отношению производной
по отношению производной 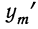 к функции
к функции 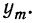
Найдем производную функции 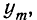 т. е.
т. е. 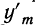 как отношение конечного приращения функции
как отношение конечного приращения функции 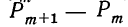 к приращению аргумента
к приращению аргумента 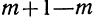
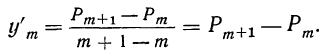
Тогда отношение
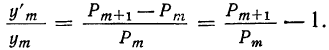
Подставляя формулу 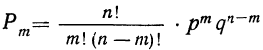 в правую часть полученного равенства, имеем:
в правую часть полученного равенства, имеем:
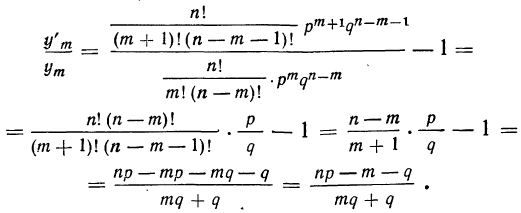
Вводим новую переменную х = m—nр, т. е. отклонение частоты от наивероятнейшей частоты, тогда
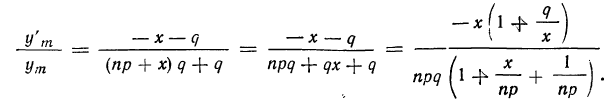
Полагая n величиной весьма большой, а р и q правильными дробями, заметно отличающимися от нуля, можнo положить равным нулю следующие величины:
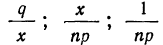
и пренебречь ими.
Тогда
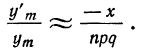
Решая дифференциальное уравнение, получаем:
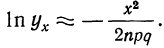
Откуда
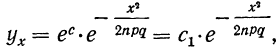
где постоянная величина 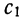 определяется из частного значения
определяется из частного значения 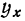 при x = 0 (или, что то же самое,
при x = 0 (или, что то же самое, 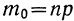 ). Следовательно, получим:
). Следовательно, получим:
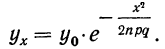
Заменяя
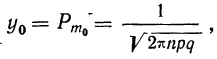
имеем:
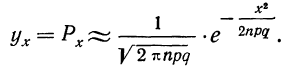
П р и м е р 24. Из партии, в которой доля деталей I сорта равна 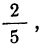 отобрано 50 единиц (с возвратом). Определить вероятность того, что среди отобранных единиц 25 окажутся I сорта.
отобрано 50 единиц (с возвратом). Определить вероятность того, что среди отобранных единиц 25 окажутся I сорта.
Дано: 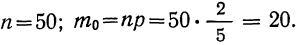
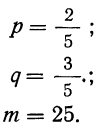
Мы должны найти вероятность частоты 25 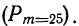 Находим отклонение искомой частоты от наивероятнейшей: х = 25—20 = 5.
Находим отклонение искомой частоты от наивероятнейшей: х = 25—20 = 5.
По формуле 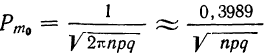 определяем вероятность наивероятнейшей частоты:
определяем вероятность наивероятнейшей частоты:
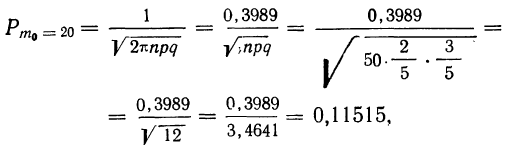
а по локальной формуле Лапласа получаем вероятность того, что частота отклонится от наивероятнейшей частоты на 5
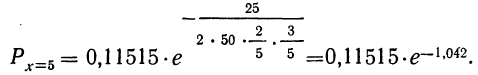
Для нахождения второго множителя обратимся к таблице (см. приложение X), из которой приближенно найдем:
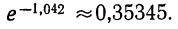
Тогда получаем:
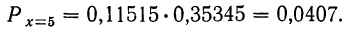
Характерно, что и вероятность частоты 15 будет такой же. В формулу Лапласа х входит возведенным в квадрат, а поэтому значения + х и —х приводят по этой формуле к одинаковой вероятности:
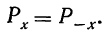
Так, если мы ищем вероятность частоты 15, то х = 15—20 =—5, а поэтому 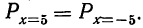
Для вычислений по локальной формуле Лапласа в ней производят замену: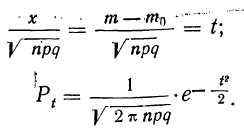
Имеются таблицы значений:
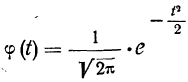
(см. приложение II). Следовательно:
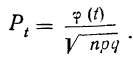
Придавая m различные значения, определяем сначала t по формуле 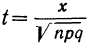 затем
затем 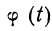 — по приложению II, найденные
— по приложению II, найденные 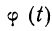 делим на
делим на 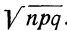
Пример 25. На основе данных примера 24 определить искомую вероятность, пользуясь указанной формулой.
Дано:
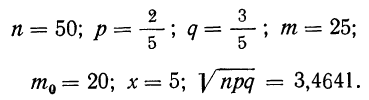
Находим t по формуле 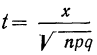 при m = 25
при m = 25
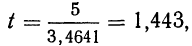 или приближенно t = 1,44.
или приближенно t = 1,44.
По приложению II определяем: 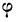 (1,44) =0,1415.
(1,44) =0,1415.
По формуле 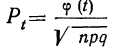 получаем:
получаем:
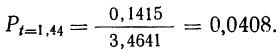
Расхождение с результатом в примере 24 в 0,0001 получилось за счет неточно взятого t.
Стандартизованное распределение вероятностей
Локальной формулы Лапласа можно получить формулу, выражающую стандартизованное распределение вероятностей.
Мы знаем, что множитель 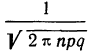 в формуле
в формуле
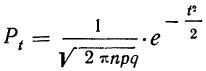
есть вероятность наивероятнейшей частоты 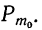 Тогда:
Тогда:
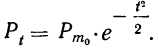
Используя приложение X, в котором даны значения е в различных степенях, можно по последней формуле построить таблицу стандартизованного распределения вероятностей (см. табл. 7).
По полученным в таблице показателям строят график стандартизованного распределения вероятностей. На оси абсцисс наносят значения t и х. На оси ординат откладывают найденные вероятности 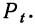
Графическое изображение стандартизованного распределения вероятностей называется нормальной кривой, или кривой Гаусса—Лапласа (способы ее построения см. раздел IV).
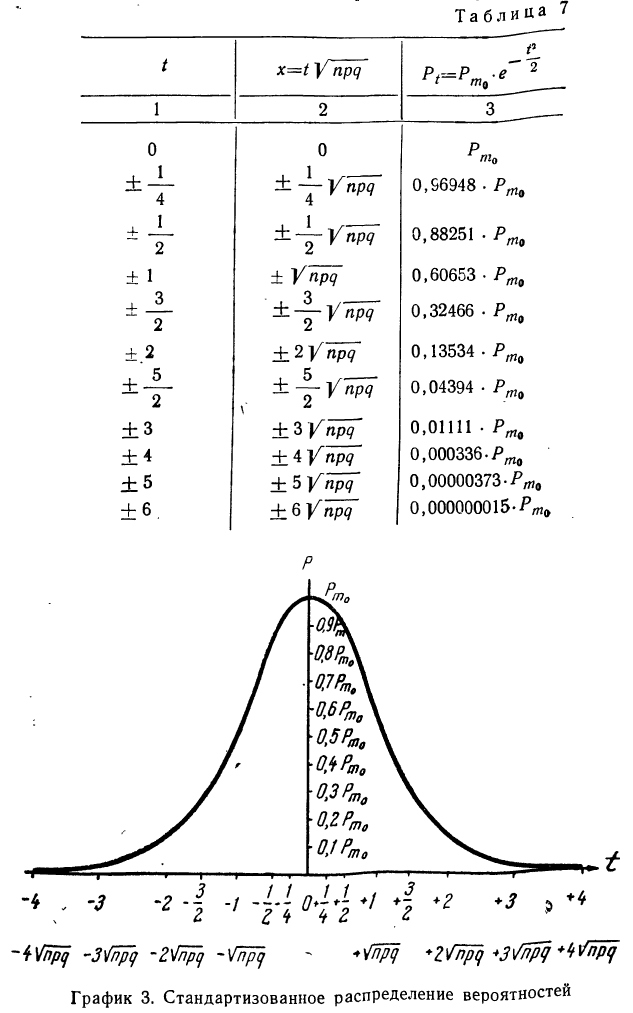
Особенности данной кривой:
- максимальная ордината равна вероятности наивероятнейшей частоты;
- кривая симметрична относительно оси ординат.
По мере удаления t от 0 в обе стороны вероятности уменьшаются. Это означает, что более вероятными являются частоты, примыкающие к наивероятнейшей частоте.
Для приближенного исчисления вероятностей по схеме «невозвращенного шара» (бесповторный отбор, при котором отобранная единица в совокупность не возвращается) можно воспользоваться несколько иной формулой:
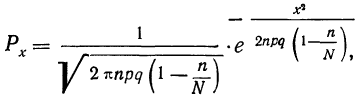
где N — численность совокупности, из которой производится отбор.
Если n по сравнению с N — величина незначительная, то эта формула сводится к локальной формуле Лапласа.
Интегральная формула Лапласа
Если необходимо рассчитать вероятность того, что при п испытаниях число осуществлений события А будет находиться в заданных границах а и b, используют интегральную формулу Лапласа:
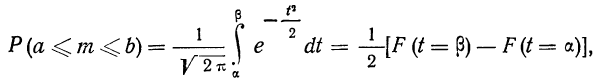
где а и b — заданные границы, числа осуществлений события А;
а и 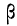 — пределы интегрирования (см. ниже);
— пределы интегрирования (см. ниже);
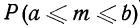 —вероятность того, что при п числе испытаний число появлений события А будет заключено между числами а и b.
—вероятность того, что при п числе испытаний число появлений события А будет заключено между числами а и b.
В приложении III даны значения F(t), по которым можно определять искомое значение вероятности.
Числа а и b связаны с границами интегрирования определенным соотношением:
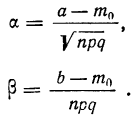
(Практическое применение этой связи см. в примере 26—второй вопрос.)
Если заданные границы числа осуществлений события А (а и b) отличаются от nр на одинаковую величину t, то интегральная формула Лапласа примет вид:
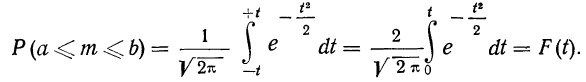
В этом случае
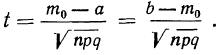
Пример 26. Из партии в 500 деталей, в которой первосортных 300, отбирается наудачу 150 деталей с возвратом. Какова вероятность того, что число деталей I сорта будет находиться в пределах: 1) от 78 до 102? 2) от 78 до 108?
Для первого вопроса дано: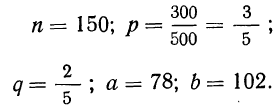
Находим:
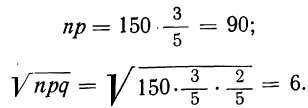
Границы а и b отличаются от 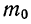 на одинаковую величину, равную 12:
на одинаковую величину, равную 12:
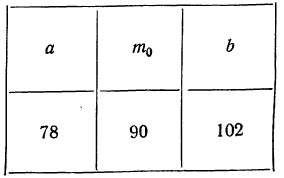
Находим t из соотношений
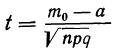 или
или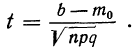
Получаем:
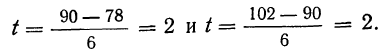
Для использования таблицы приложения III берем t = 2.
Следовательно:
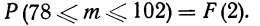
По таблице приложения III находим F(2) =0,9545.
Для второго вопроса ищем вероятность того, что частота лежит в границах от 78 до 108.
Имеем:
Находим  и
и  из соотношений:
из соотношений:
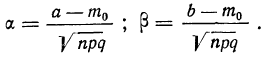
Получаем:
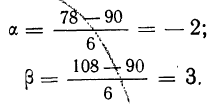
По интегральной формуле Лапласа: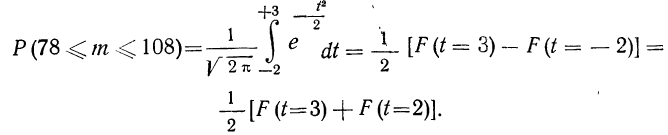
По приложению III находим:
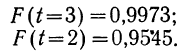
Тогда:
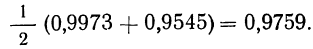
Значит, вероятность того, что число деталей I сорта находится в границах от 78 до 108, равна 0,9759.
Интеграл вероятностей
Использованный в предыдущем параграфе интеграл
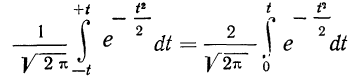
называется интегралом вероятностей от —t до +t и обозначается F(t).
Этот интеграл в общем виде не берется. Поэтому его можно вычислить путем разложения в ряд Маклорена:
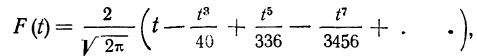
а затем подстановкой различных значений t получают F(t). Функция F(t) является нечетной, т. е. F(—t) =—F(t). При изменении t от 0 до  функция F(t) возрастает очень быстро от 0 до 1, так что уже F(4) =0,999937.
функция F(t) возрастает очень быстро от 0 до 1, так что уже F(4) =0,999937.
С геометрической точки зрения F(t) представляет площадь, заключенную между кривой вероятностей, осью абсцисс и соответствующими ординатами. Интеграл вероятностей широко используется в расчетах, связанных с применением выборочного метода, в следующих случаях: 1) при оценке результатов выборки с определенной вероятностью; 2) при определении наименьшей численности выборки, обеспечивающей необходимую точность; 3) при определении границ отклонений генеральной средней от выборочной.
Применяется несколько видов таблиц интеграла вероятностей:
1) Таблица Маркова дает значения интеграла вероятностей:
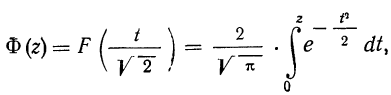
представляющего собой площадь, ограниченную кривой вероятностей, осью абсцисс и двумя ординатами, расположенными на расстоянии z, выраженном в единицах модуля вероятностей.
2) Таблица Шеппарда строится по формуле
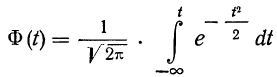
и дает значения интеграла вероятностей на протяжении от —  до t, выраженном в единицах среднего квадратического отклонения. Значения вероятностей в таблице Шеппарда могут быть получены из вероятностей таблицы Маркова при использовании следующей формулы:
до t, выраженном в единицах среднего квадратического отклонения. Значения вероятностей в таблице Шеппарда могут быть получены из вероятностей таблицы Маркова при использовании следующей формулы:
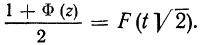
3) Из таблицы Шеппарда можно составить таблицу значений интеграла вероятностей F(t), используя формулу F(t) = = 2Ф(z) — 1.
Существуют и другие виды таблиц интеграла вероятностей.
Случайные величины
Величина х, принимающая в зависимости от некоторых случайных обстоятельств одно из значений 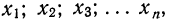 имеющих определенные вероятности
имеющих определенные вероятности 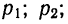
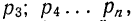 называется случайной величиной.
называется случайной величиной.
Случайные величины бывают дискретными (с дискретным рядом возможных значений) и непрерывными (имеющие сколь угодно близкие возможные значения). Совокупность значений случайных величин и соответствующих вероятностей называют распределением случайной величины.
Пример 27. Если производится отбор 11 деталей из партии, в которой вероятность первосортной детали равна 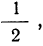 то частота (m) представляет собой дискретную случайную величину, вероятность значений которой можно рассчитать по соответствующим формулам (например, по формуле общего члена разложения в биномиальную строку).
то частота (m) представляет собой дискретную случайную величину, вероятность значений которой можно рассчитать по соответствующим формулам (например, по формуле общего члена разложения в биномиальную строку).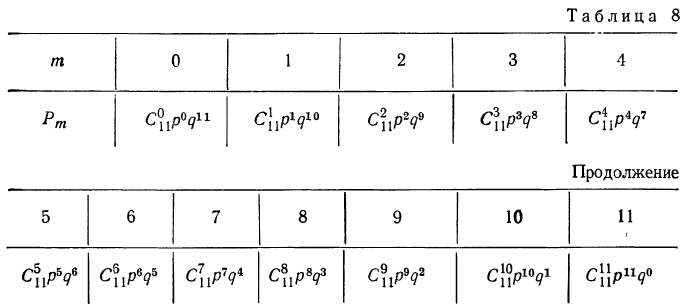
Здесь совокупность m и 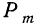 будет распределением случайной величины m. В данном примере приводится биномиальное распределение.
будет распределением случайной величины m. В данном примере приводится биномиальное распределение.
Математическое ожидание дискретной случайной величины равно сумме произведений каждого возможного значения этой величины на его вероятность
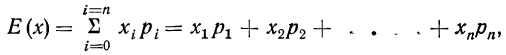
где Е— символ математического ожидания;
 —математическое ожидание случайной величины х, которое очень часто называют центром распределения или центром рассеивания. Математическое ожидание случайной величины равно средней ее значений, взвешенной по вероятностям:
—математическое ожидание случайной величины х, которое очень часто называют центром распределения или центром рассеивания. Математическое ожидание случайной величины равно средней ее значений, взвешенной по вероятностям: 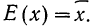
Такая средняя называется стохастической.
П р и м е р 28. На основе данных примера 19 ищем математическое ожидание случайной величины.
Дано:
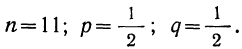
Применим формулу:
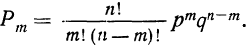
Располагаем полученные данные в таблицу и вычисляем произведения частот на их вероятности.
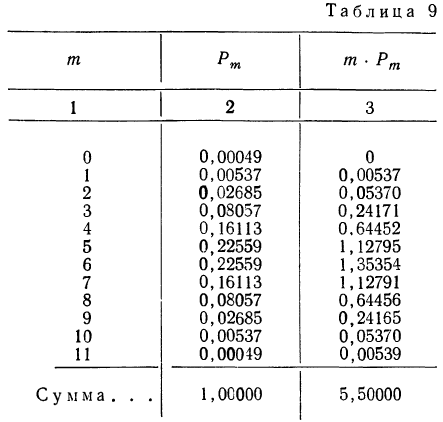
Получаем по формуле математического ожидания:
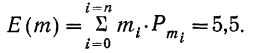
Математическое ожидание непрерывной случайной величины исчисляется по формуле:
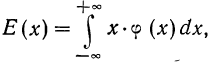
где  — функция плотности вероятностей.
— функция плотности вероятностей.
Свойства математического ожидания:
а) Математическое ожидание постоянной величины равно этой постоянной:
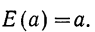
Доказательство. Постоянную величину а можно рассматривать как случайную величину, принимающую только одно значение а, с вероятностью, равной единице:
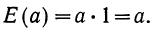
б) Постоянный множитель выносится за знак математического ожидания:
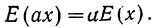
Доказательство.
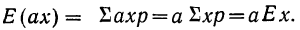
в) Математическое ожидание алгебраической суммы случайных величин равно алгебраической сумме их математических ожиданий:
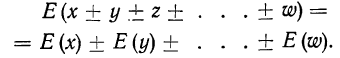
г) Математическое ожидание произведения независимых случайных величин равно произведению их математических ожиданий:
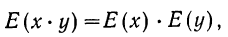 если х и у независимы.
если х и у независимы.
Доказательство. Имеются две независимые случайные величины х и у со значениями: 
 и вероятностями для
и вероятностями для  и для
и для 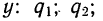
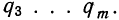 Определяем вероятности совместного осуществления
Определяем вероятности совместного осуществления 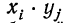 по теореме умножения вероятностей независимых событий.
по теореме умножения вероятностей независимых событий.
Получаем 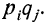 Следовательно, имеем произведения значений независимых случайных величин и вероятности этих произведений.
Следовательно, имеем произведения значений независимых случайных величин и вероятности этих произведений.
Найдем математическое ожидание произведения:
Сгруппируем члены, содержащие  и, выводя их за скобку, получим:
и, выводя их за скобку, получим:

Учитывая, что выражение, стоящее в скобках, есть 
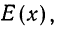 выносим его за скобку. Тогда:
выносим его за скобку. Тогда:
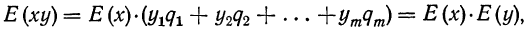 что и требовалось доказать.
что и требовалось доказать.
д) Математическое ожидание случайной величины, принимающей только два значения: 1 — при осуществлении некоторого события и 0 — при его неосуществлении, равно вероятности события:
Е(х)=р.
Пример 29. В партии 500 деталей, из них I сорта 300. Производится отбор одной детали. Найти математическое ожидание числа деталей I сорта.
Имеем два варианта: 1 и 0.
Найдем вероятности вариантов:
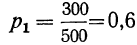 (вероятность варианта 1);
(вероятность варианта 1);
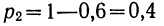 (вероятность варианта 0).
(вероятность варианта 0).
Получаем:
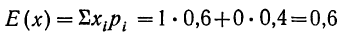
и видим, что математическое ожидание данной случайной величины равно вероятности первого варианта.
е) ^Математическое ожидание случайной величины всегда заключено между наименьшим и наибольшим ее значением:
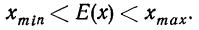
ж) Математическое ожидание частоты при биномиальном распределении равно произведению числа испытаний на вероятность события:
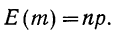
Математическое ожидание квадрата отклонения случайной величины от ее математического ожидания называется стохастической дисперсией (обозначается 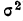 ) и вычисляется по формуле:
) и вычисляется по формуле:
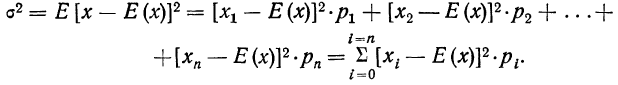
Если имеется несколько независимых случайных величин 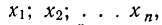 то математическое ожидание их средней равно средней их математических ожиданий:
то математическое ожидание их средней равно средней их математических ожиданий:
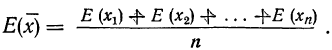
Найдем: 1) стохастическую дисперсию каждой случайной величины, измеряющую отклонения значений случайной величины ст ее математического ожидания.
Стохастическая дисперсия первой случайной величины: 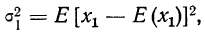
второй случайной величины:
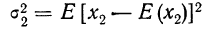
и т. д., а в общем виде 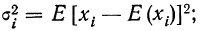
2) стохастическую дисперсию, измеряющую отклонения общей средней от своего математического ожидания:
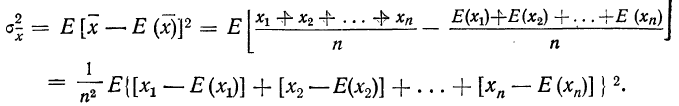
Возводим в квадрат отклонения и учитываем, что ввиду независимости случайных величин математическое ожидание произведения отклонений двух случайных величин равно нулю, т. е. 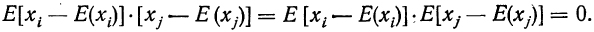
Поэтому, исключая удвоенные попарные произведения, получаем:
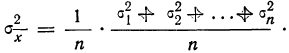
Полагая, что второй множитель равен средней из дисперсий случайных величин, записываем 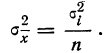 Если дисперсии всех случайных величин равны между собой, то имеем:
Если дисперсии всех случайных величин равны между собой, то имеем:
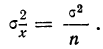
Следовательно, стохастическая дисперсия средней в п раз меньше стохастической дисперсии каждой случайной величины.
Среднее квадратическое отклонение  равно квадратному корню из стохастической дисперсии:
равно квадратному корню из стохастической дисперсии:
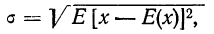
и следовательно:
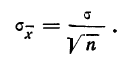
В качестве меры рассеяния может быть использован модуль вероятностей, обозначаемый М и вычисляемый по формуле:
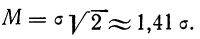
Иногда для характеристики рассеяния нормальной кривой применяют меру точности, обозначаемую h и представляющую собой величину, обратную модулю вероятностей:
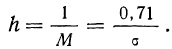
Лемма Маркова
Если имеем k вариантов случайной величины, могущей принять одно из положительных значений 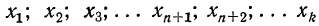 с соответствующими вероятностями
с соответствующими вероятностями 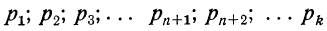 и
и 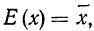 то вероятность того, что
то вероятность того, что 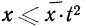 будет больше, чем
будет больше, чем 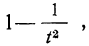 где число
где число  больше единицы.
больше единицы.
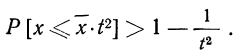
Можно лемму Маркова записать и так:
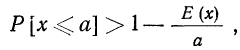
если принять 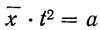 и учитывать, что
и учитывать, что 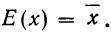
Следствие леммы Маркова.
Вероятность того, что  не больше
не больше  .
.
Отсюда:
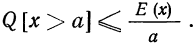
Первое неравенство Чебышева
Из леммы Маркова вытекает неравенство, называемое первым неравенством Чебышева. Если случайная величина u принимает положительные и отрицательные значения и если a — произвольная величина, то вероятность того, что случайная величина и будет находиться в границах между —а и +а, т. е. вероятность неравенства 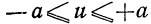 (или, что то же самое, неравенства
(или, что то же самое, неравенства 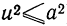 ), будет
), будет
больше 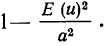
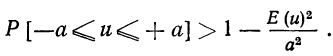
Следствие первого неравенства Чебышева
Возьмем вместо случайной величины и другую случайную величину х—Е(х), тогда первое неравенство Чебышева примет вид:
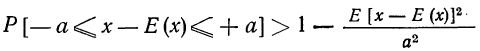
и, заменяя 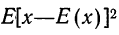 дисперсией
дисперсией 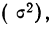 получим:
получим:
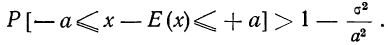
Второе неравенство Чебышева
Если вместо случайной величины u из первого неравенства Чебышева взять другую случайную величину 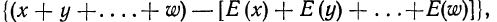 т. е. отклонение суммы случайных величин от суммы их математических ожиданий, и учесть следствие первого неравенства Чебышева, то получим второе неравенство Чебышева:
т. е. отклонение суммы случайных величин от суммы их математических ожиданий, и учесть следствие первого неравенства Чебышева, то получим второе неравенство Чебышева:
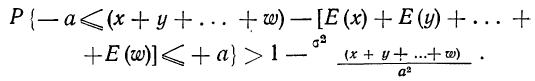
Если при этом величины  взаимно независимы, то
взаимно независимы, то
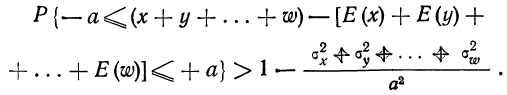
Теорема Чебышева
Второе неравенство Чебышева может быть записано иначе.
Если положить
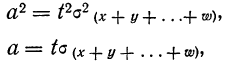
то в правой части заключительной формулы предыдущего параграфа получим: 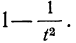 С другой стороны, слева тройное неравенство в скобках разделим на n. Тогда получим:
С другой стороны, слева тройное неравенство в скобках разделим на n. Тогда получим:
Но если все 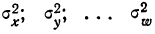 меньше некоторого числа L, то
меньше некоторого числа L, то 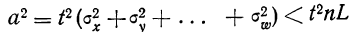 и
и 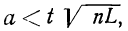 наконец,
наконец, 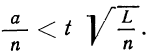 Правая часть неравенства при достаточном n может быть сделана сколь угодно малой величиной
Правая часть неравенства при достаточном n может быть сделана сколь угодно малой величиной  Иначе говоря:
Иначе говоря:
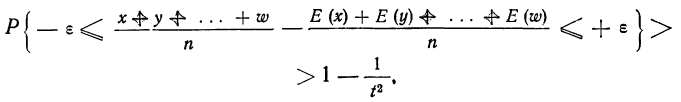
где 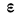 —сколь угодно малая величина.
—сколь угодно малая величина.
Эта формула выражает знаменитую теорему Чебышева и читается так: с вероятностью, сколь угодно близкой к единице (достоверности), можно утверждать, что если  суть независимые случайные величины, имеющие определенные математические ожидания и ограниченные дисперсии, то при достаточно большом числе случайных величин их средняя арифметическая будет как угодно мало отличаться от средней арифметической их математических ожиданий.
суть независимые случайные величины, имеющие определенные математические ожидания и ограниченные дисперсии, то при достаточно большом числе случайных величин их средняя арифметическая будет как угодно мало отличаться от средней арифметической их математических ожиданий.
Теорема Чебышева в весьма общем виде выражает закон больших чисел, суть которого состоит в том, что совокупные действия большого числа случайных факторов приводят к результату, почти не зависящему от случая.
Следствие теоремы Чебышева
Если 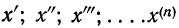 — случайные величины с одинаковыми возможными значениями:
— случайные величины с одинаковыми возможными значениями: 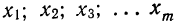 и одинаковыми их вероятностями:
и одинаковыми их вероятностями: 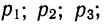
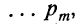 то при достаточно большом числе испытаний средняя арифметическая этих величин будет как угодно мало отличать ся от их математического ожидания Е(х)
то при достаточно большом числе испытаний средняя арифметическая этих величин будет как угодно мало отличать ся от их математического ожидания Е(х)
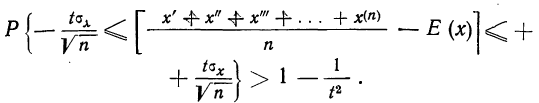
Чтобы убедиться в этом, достаточно учесть, что в этом случае
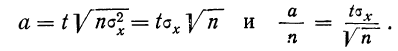
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |