Закон Архимеда - основные понятия, формулы и определения с примерами

Закон Архимеда:

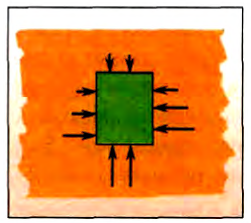
На поверхность тела, погруженного в жидкость, действуют силы давления. Так как давление увеличивается с глубиной погружения, то силы давления, действующие на нижнюю часть тела, всегда больше, что отражено на рисунке 169 длиной стрелок. Поэтому можно ожидать, что равнодействующая сил давления будет направлена вверх. Опыт подтверждает это предположение.

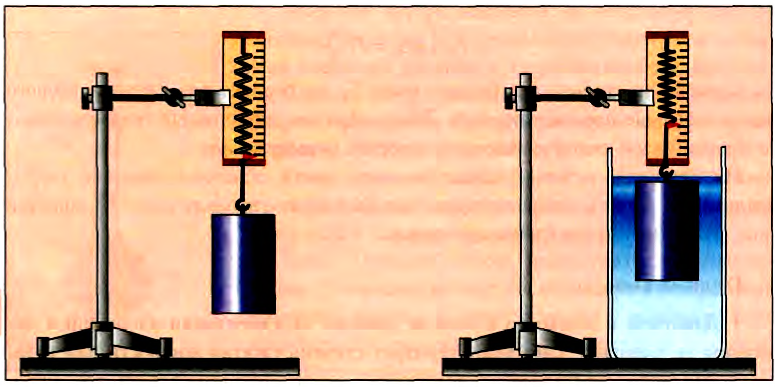
Если подвешенное к крючку динамометра тело опустить в воду, то показания динамометра уменьшатся (рис. 170).

Равнодействующая сил давления на тело, погруженное в жидкость, называется выталкивающей силой или силой Архимеда.

Рассмотрим тело, имеющее форму прямоугольного параллелепипеда, погруженное в жидкость так, что его основания расположены горизонтально (рис. 171). Силы давления, действующие на боковые грани тела, уравновешены. Они сжимают тело. Силы же, действующие на основания параллелепипеда, не одинаковы. Модуль силы давления, действующей на верхнее основание:

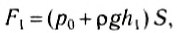
где p₀ — внешнее давление, h₁ — высота столба жидкости над верхним основанием, р — плотность жидкости, S — площадь основания.

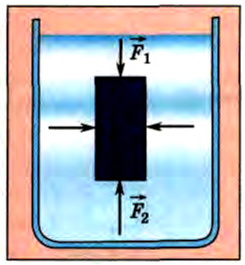
Рис. 171

Модуль силы давления жидкости, действующей на нижнее основание:

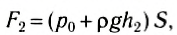
где h₂ — глубина, на которой находится нижнее основание. Поскольку h₂ > h₁ , то F₂> F₁, и, следовательно, равнодействующая будет направлена вверх и по модулю равна:

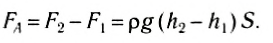
Так как ( h₂ - h₁ ) — высота параллелепипеда, то
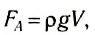,    (1)
где V=S( h₂ - h₁ ) — объем тела.

В векторном виде выражение для силы Архимеда примет вид:
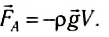    (2)

Мы получили выражение выталкивающей силы для прямоугольного параллелепипеда, погруженного в жидкость. Однако эта формула справедлива для тела любой формы. Действительно, выталкивающая сила, действующая на тело (рис. 172), есть равнодействующая сил давления жидкости на его поверхность. Представим себе, что тело удалено, и его место занято той же жидкостью (рис. 173). Давление на поверхность такого мысленно выделенного объема будет таким же, каким было давление на поверхность самого тела. Значит, и равнодействующая сила давления па тело (выталкивающая сила) равна равнодействующей силе давления на выделенный объем жидкости. Но этот объем жидкости находится в равновесии. Силы, действующие на него, — это сила тяжести 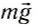и выталкивающая сила 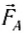(см. рис. 173). Значит, выталкивающая сила равна по модулю силе тяжести, действующей на выделенный объем жидкости, и приложена она в центре масс выделенного объема жидкости. Точку приложения выталкивающей силы называют также центром давления.

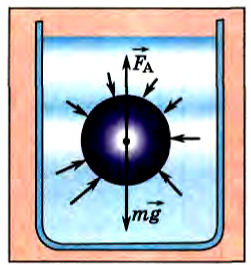Рис. 172

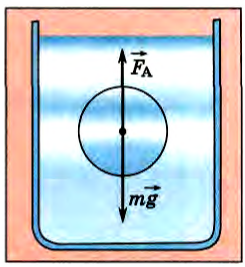Рис. 173

Таким образом,

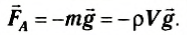
Итак, на тело, погруженное в жидкость, действует выталкивающая сила, равная по модулю весу жидкости в объеме, занимаемом телом (вытесненный объем), и приложенная в центре масс этого объема (центре давления).

Это и есть закон Архимеда, экспериментально установленный Архимедом более 2200 лет тому назад. Примерная схема опыта Архимеда изображена на рисунках 174, 175, 176. Пустой стакан А («ведерко Архимеда») и сплошной цилиндр В, имеющий объем, в точности равный вместимости стакана, подвесим к динамометру (см. рис. 174). Затем, подставив сосуд с водой, погрузим цилиндр в воду. Равновесие нарушится, и растяжение динамометра уменьшится (см. рис. 175). Разность показаний динамометра как раз равна выталкивающей силе, действующей на цилиндр. Если наполнить стакан водой, то пружина динамометра снова растянется до первоначальной длины (см. рис. 176). Таким образом, доказано, что выталкивающая сила, действующая на погруженное тело, равна силе тяжести жидкости в объеме тела.

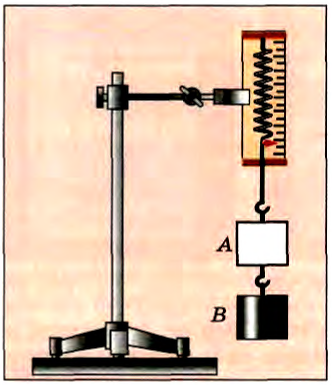Рис. 174

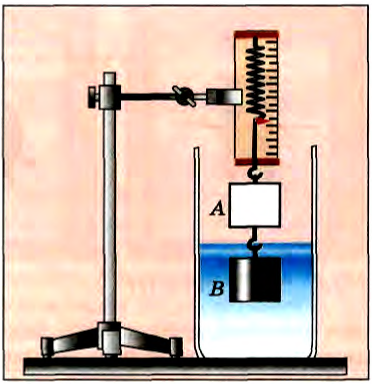Рис. 175

По третьему закону Ньютона если жидкость действует на погруженное тело, то и тело действует на жидкость. Эта сила направлена вертикально вниз и равна по модулю силе Архимеда. Это утверждение доказывается следующим опытом. Неполный стакан с водой уравновешивают на весах. Затем в стакан погружают тело, подвешенное на штативе. При этом чашка со стаканом опускается, и для восстановления равновесия приходится добавить на другую чашку гири, вес которых равен весу воды, вытесненной телом.

Сила Архимеда действует также на тела в воздухе. Однако плотность воздyxa мала, и действием выталкивающей силы в большинстве случаев можно пренебречь.

Выталкивающая сила действует на тела в жидкостях и газах, потому что они сжаты силой притяжения к Земле. В состоянии невесомости сила Архимеда не действует.

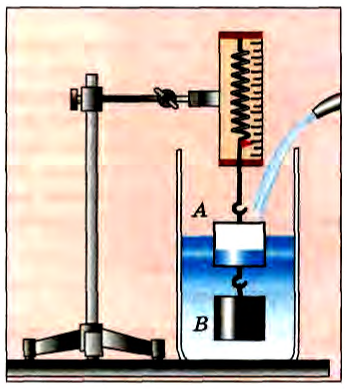
Рис. 176

Главные выводы:

1. Из-за того что давление увеличивается с глубиной погружения, на тело, погруженное в жидкость (газ), действует выталкивающая сила.
2. На тело, погруженное в жидкость или газ, действует выталкивающая :ила, равная по модулю весу жидкости в объеме, занимаемом телом. Эта :ила приложена в центре давления.
3. Тело, погруженное в жидкость, действует на жидкость с силой, равной по модулю выталкивающей силе и противоположно направленной.
4. В невесомости сила Архимеда отсутствует.

Плавание тел и воздухоплавание:

Закон Архимеда дает возможность объяснить все вопросы, связанные с плаванием тел. Погрузим полностью тело в жидкость и предоставим самому себе. Если сила тяжести больше силы Архимеда, то оно будет тонуть, пока не упадет на дно сосуда (рис. 177). Если сила тяжести меньше силы Архимеда, то оно будет всплывать, поднимаясь к поверхности жидкости (см. рис. 177). В том случае, когда сила тяжести в точности равна выталкивающей силе, оно будет находиться в равновесии и плавать внутри жидкости.

Рис. 177

Рассмотрим тела, которые тонут в жидкости. Если тело однородное, т. е. во всех точках имеет одну и ту же плотность, то нетрудно показать, что в этом случае плотность тела больше плотности жидкости. Действительно:

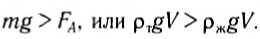
Отсюда следует, что р_т > р_ж.

Если тело неоднородное, т. е. плотность тела неодинакова в различных точках, например тело с пустотами внутри, то под плотностью тела необходимо понимать среднюю плотность: (р_т)>р_ж.

Для тонущих тел неправильной формы, объем которых трудно найти при помощи измерения размеров тела, закон Архимеда позволяет экспериментально определить плотность тела. Для этого тело необходимо дважды взвесить: один раз в воздухе, а другой раз — погружая его в жидкость, плотность которой известна. Первое взвешивание дает значение силы тяжести: P = p_TgV. Результат второго взвешивания F дает разность между силой тяжести mg и выталкивающей силой F_A:

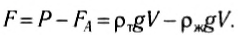
Заменив в этой формуле объем тела V на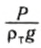, легко получить, что
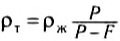∙    (1)

В случае неоднородного тела определяемая по этой формуле величина р_T даст среднюю плотность.
Если тело, погруженное в жидкость, находится в равновесии, то плотность тела (или его средняя плотность) равна плотности жидкости. Можно проделать следующий опыт. Куриное яйцо тонет в пресной воде, но плавает в соленой. При растворении соли плотность раствора увеличивается. При этом концентрация раствора постепенно уменьшается кверху, т. е. раствор является неоднородной жидкостью. Его плотность вверху меньше, чем внизу. Поэтому в таком растворе куриное яйцо вначале будет тонуть, а затем остановится, не достигнув дна, и будет плавать на такой глубине, где его плотность равна средней плотности раствора на данной глубине.

Другим примером плавания тел под водой является плавание подводных лодок (рис. 178). Они должны иметь возможность всплывать и погружаться в воду, а также плыть под поверхностью воды. Так как объем лодки остается во всех случаях неизменным, то для выполнения этих маневров на лодке должна быть предусмотрена возможность изменения ее массы. В лодке сделан ряд балластных отсеков, которые при помощи специальных устройств можно заполнить забортной водой (при этом масса лодки увеличивается, и она погружается) и освободить от воды (при этом масса лодки уменьшается, и она всплывает). Конечно, трудно подобрать такую массу воды, чтобы выталкивающая сила в точности была равна силе тяжести. Поэтому для сохранения заданной глубины нужно все время изменять количество балласта либо все время двигаться, маневрируя рулями глубины.
 

Рис. 178

Если сила тяжести тела, погруженного в жидкость, меньше силы Архимеда, то оно всплывает. Поднявшись на поверхность, оно плавает так, что часть его выступает из жидкости. В этом случае плотность тела меньше плотности жидкости. В самом деле, на тело, плавающее таким образом, действуют сила тяжести mg = p_TgV и выталкивающая сила F_A= p_TgV₁, где V₁ — объем погруженной в жидкость части тела:

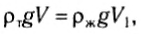
и так как V₁ < V, то из (2) следует, что р_T < р_ж. Из (2) также следует, что объем тела, погруженного в жидкость, зависит от отношения плотностей жидкости и тела. Так, для льдины, плавающей на воде, под водой находится примерно 92 % ее объема (плотность льда 920 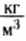, плотность воды 1000 ).

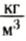На основании закона плавания тел сконструирован прибор — ареометр, с помощью которого измеряют плотности жидкостей. Ареометр представляет собой стеклянный сосуд с грузиком и длинным отростком, на котором нанесена шкала (рис. 179, а). При плавании в жидкости ареометр погружается на большую или меньшую глубину в зависимости от плотности жидкости (рис. 179, б). Чем больше плотность жидкости, тем меньше он погружается. На шкале непосредственно отмечаются значения плотности жидкости. Ареометр применяется обычно для точных измерений в жидкостях с близкими плотностями.

Рис. 179

Сплошные тела плавают в жидкости так, чтобы равновесие было устойчивым. Для доказательства этого утверждения рассмотрим плавание бревна в воде. Если бревно однородное, то оно плавает, так как показано на рисунке 180. Очевидно, что сила тяжести приложена в центре масс бревна С, а выталкивающая сила в центре масс вытесненной жидкости D (центре давления). Причем линии действия этих сил совпадают. В отклоненном положении (рис. 181) центр масс вытесненной жидкости смещается относительно бревна, и возникает момент сил, который возвращает бревно в исходное состояние.

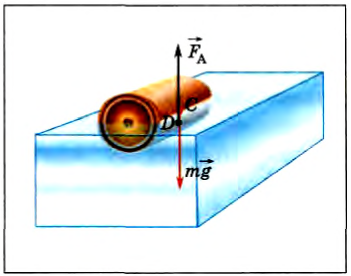Рис. 180

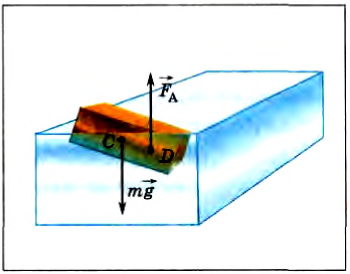Рис. 181

Тело, имеющее полости, куда жидкость не проникает при плавании, вытеснит такой же объем, что и сплошное тело. Поэтому и сила Архимеда для такого тела такая же, как и для сплошного. Но масса тела с полостями меньше массы сплошного тела. Поэтому при достаточно больших полостях такое тело может плавать, хотя плотность вещества тела больше плотности жидкости (например, корабли, лодки и т. п.). Объем вытесненной кораблем воды значительно больше объема стали, из которой сделан корпус судна, поэтому он может плавать, несмотря на то что плотность стали в 8 раз больше плотности воды.

Если пространство внутри судна заполнить водой, например, в случае течи, то вытесненный объем воды уменьшится и судно начнет тонуть.

Полет воздушного шара или дирижабля (рис. 182) в воздухе напоминает плавание подводной лодки под водой. Если масса всего летательного аппарата, в том числе и масса газа, заполняющего оболочку, меньше массы воздуха в объеме, вытесняемом аппаратом, то он поднимается вверх. Если эти массы равны- шар неподвижно висит в воздухе. Если масса аппарата с газом больше массы вытесняемого воздуха, то аппарат опускается.

Рис. 182

Главные выводы:

• Тело, погруженное в жидкость, тонет, плавает внутри жидкости или всплывает, если плотность тела (средняя плотность) больше, равна или меньше плотности жидкости соответственно.