Заказать решение задач по физике

Вам нужна помощь в решении задач по физике? Вы пытаетесь закончить задание, которое начали, но не можете закончить или хотите проверить свои мысли или научиться решать задачи по физике, тогда присылайте мне в чат ваши задания по физике.

Я, Анна Евкова и у меня своя команда преподавателей. Мы умеем всё, и делаем это каждый час, более 28 лет. В дополнение к решениям по физике вы можете воспользоваться любимы другими услугами так как я и моя команда делаем всё, что связано с учёбой. 

Вопросы и ответы:

Почему заказать физику или другой предмет нужно у вас?

Я и моя команда здесь уже 28 лет и за это время мы наработали репутацию и "знания" как оформлять работу и какой "стиль" решения любит каждый Универститет. У меня и моей команды преподавателей университетское образование в области фиики. Мы знаем, какое решение нужно именно вам!

Сколько стоит?

Вы получаете подробное решение, и уверенность в результате, любое задание присылайте мне в чат whatsapp и сразу вы получите правильную оценку именно вашего задания + скидку, если большой объём заданий.

Могу ли я понять ваше решение или сможете ли вы обяснить?

Вы получите готовую работу в виде файла Word или фото листа (рукописи), содержащего все условия заданий, полное решение с пояснениями, рисунки и диаграммы, таблицы и т.д. 

Выполните ли вы мою заказ в срок?

Все, что вам нужно сделать, это правильно указать дату и время, когда вы хотите, чтобы ваш заказ был доставлен в чат, и я отправлю его в срок или раньше указанной даты вам в чат.

Кто-нибудь уже сделал заказ?

Более 893 000 школьников и студентов уже заказали любые задания по разным предметам у меня. Вы можете прочитать мнения обо мне на странице отзывов.

А если есть ошибки?

Не ошибаются только те, кто ничего не делает. Я и мокая команда преподавателей работает качественно, наши расчеты проверяются (по возможности) с помощью программ, но бывают опечатки и даже ошибки, переделывается около 1% заказов. Я бесплатно вношу все изменения, связанные с неточностями по моей вине.

Физика

Физика — это область естествознания: наука о наиболее общих законах природы, о материи, её структуре, движении и правилах трансформации. Понятия физики и её законы лежат в основе всего естествознания и физика является точной наукой.

Содержание:

Учимся решать задачи по физике

Для чего нужно уметь решать задачи по физике? Что надо сделать для того, чтобы научиться их решать? Как именно решать задачи? Сегодня мы только начинаем отвечать на эти вопросы, учимся решать простейшие задачи, но пройдет время...

Для чего нужно решать задачи по физике? Попробуем ответить на этот вопрос вместе. С этой целью обратимся к простейшей конкретной задаче, с которой вы можете встретиться в реальной жизни.

Предположим, что вам нужно купить 3 кг растительного масла. У вас есть только пластиковый баллон вместимостью 3 литра. Поместится ли в него нужное количество масла?

Согласитесь, многие из нас сталкиваются с подобными задачами в жизни. Поэтому нам нужно уметь решать физические задачи прежде всего для того, чтобы, используя знание физики, отвечать на практические вопросы.

Очевидно, что, не зная необходимых физических величин, формул, физических законов, вы не сможете ответить на вопрос, поставленный в задаче. Таким образом, только хорошее знание физических законов, формул, условий хода физических процессов, описанных в задачах, дает возможность успешно решать задачи по физике. И наоборот: нам необходимо решать задачи по физике также для того, чтобы лучше знать и понимать физику в целом.

Этапы решения физических задач

В ходе решения большей части физических задач можно выделить несколько этапов.

1-й этап. Анализ физической проблемы

На этом этапе вам необходимо:

• а)    внимательно прочитать условие задачи;
• б)    выяснить, какие величины уже известны, какие нужно найти, значение каких величин можно отыскать в справочной литературе;
• в)    выполнить пояснительный рисунок (схему, график), если в этом есть необходимость;
• г)    кратко записать условие задачи;
• д)    определить, в каких единицах она будет решаться (если величины, использованные в задаче, даны не в единицах СИ или с приставками, такие величины преимущественно переводят в единицы СИ и без приставок).

2 й этап. Поиск математической модели

На этом этапе необходимо:

• а)    записать общие уравнения, связывающие физические величины, которые характеризуют рассмотренное в данной задаче физическое явление;
• б)    конкретизировать эти уравнения для данной задачи.
   

З-й этап. Решение и анализ результатов

На этом этапе следует:

• а)    решить уравнение относительно искомой величины;
• б)    проверить единицу искомой величины;
• в)    выполнить необходимые вычисления;
• г)    проанализировать результаты.

Решим задачу, предложенную в начале параграфа, проследив основные этапы ее решения.

Анализ физической проблемы. Выяснить, поместятся ли 3 кг растительного масла в пластиковый баллон вместимостью 3 л, мы можем двумя способами:

1. определить, сколько килограммов масла вмещается в баллон, и сравнить результат с массой необходимого нам масла;
2. определить, какой объем занимает масло массой 3 кг, и сравнить результат с вместимостью баллона.

При этом в любом случае нам необходимо знать плотность растительного масла — это значение можно найти по таблице. Перед этим следует определиться, в каких единицах лучше решать задачу. Эту задачу лучше решать в единицах СИ.

Завершив анализ, мы можем записать краткое условие задачи.

(Понятно, что в дальнейшем, записывая решение задачи, часть рассуждений вы будете проводить устно.)

Краткое условие задачи

Дано:

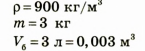
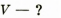
Поиск математической модели Воспользуемся определением плотности:

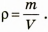
Решение и анализ результатов

Решим полученное уравнение относительно

неизвестной величины:

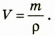
Проверим единицу искомой величины:

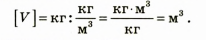
Определим числовое значение: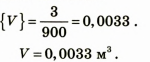

Проанализируем результат:

емкость баллона 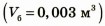меньше, чем объем 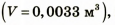, который занимает масло массой 3 кг. Ответ: масло в баллон не поместится.

Пример решения задачи:

Кубик с ребром, равным 2 см, имеет массу 20 г. Из какого материала изготовлен кубик?

Анализ физической проблемы. Чтобы ответить на поставленный вопрос, необходимо определить плотность вещества, из которого изготовлен кубик, а потом, воспользовавшись таблицей плотностей, выяснить, какому веществу соответствует найденное значение плотности. Эту задачу можно решать в заданных единицах.
Дано:

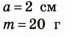
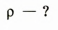
Поиск математической модели По определению плотности:

Из математики известно, что объем куба можно вычислить по формуле V = 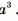.   (2)

Решение и анализ результатов

Подставив выражение (2) в выражение (1), получим формулу для расчета плотности материала, из которого изготовлен кубик:

-

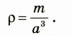Проверим единицу искомой величины:

г    г
см см см см Определим числовое значение:

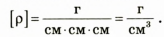
Определим число значение:

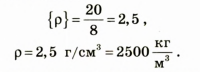
Проанализируем результат: воспользовавшись таблицей плотностей, выясним, какому веществу соответствует полученное значение плотности; плотность 2500 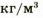имеет стекло. Ответ: кубик может быть изготовлен из стекла.

Задача №1

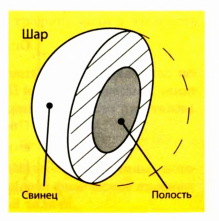
Свинцовый шар объемом имеет массу 0,565 кг. Определите, сплошной этот шар или полый. Если шар полый, то определите объем полости.

Анализ физической проблемы. Выполним пояснительный рисунок.

Если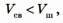то шар полый. Понятно, что объем полости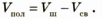

Чтобы найти объем полости, выясним, какой объем занимает в шаре свинец. Плотность свинца найдем по таблице. В этой

задаче следует массу выразить в граммах, объем — в сантиметрах кубических, плотность, соответственно,— в граммах на сантиметр кубический.

Дано:

Поиск математической модели

По определению плотности: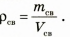

Решение и анализ результатов

Из формулы для определения плотности найдем формулу для определения объема: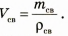

Проверим единицу искомой величины:

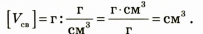
Определим числовое значение искомой величины:

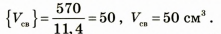
Проанализируем результат: поскольку объем свинца меньше, чем объем шара, то шар полый.

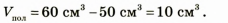
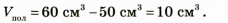шар имеет полость объемом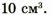

Задача №2

Канистру, вмещающую 20 кг воды, наполнили бензином. Определите массу бензина в канистре.

Анализ физической проблемы. Для определения массы бензина в канистре нам необходимо найти плотность бензина и емкость канистры, которая равна объему воды. Объем воды определим по ее массе и плотности. Плотность воды и плотность бензина найдем по таблице. Задачу лучше решать в единицах СИ.

Дано:

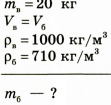
Поиск математической модели

По определению плотности: т    т

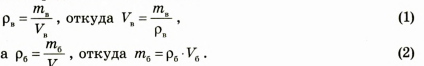
Решение и анализ результатов

Поскольку 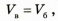, подставив формулу (1) в формулу (2), получим:  

 
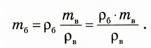
Проверим единицу искомой величины: 

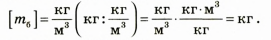
Определим числовое значение:

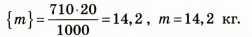
Проанализируем результат: полученное значение массы бензина в канистре достаточно реально.

Ответ: канистра содержит бензин массой 14,2 кг.

Задача №3

Сколько железнодорожных цистерн потребуется для перевозки 1080 т нефти, если объем каждой цистерны 25 м3?

Анализ физической проблемы. Чтобы найти количество цистерн, необходимо вычислить общий объем нефти, которую нужно перевезти. Общий объем нефти определим по ее массе и плотности. Разделив общий объем нефти на емкость каждой цистерны, мы легко найдем количество цистерн. Плотность нефти найдем по таблице. Задачу лучше решать в единицах СИ.
Дано:

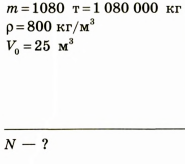
Поиск математической модели Количество цистерн N рассчитаем по формуле

где V — общий объем нефти, 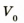— емкость

По определению плотности: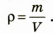

Отсюда 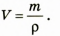 (2)

Решение и анализ результатов

Подставив формулу (2) в формулу (1), найдем

общее количество цистерн:

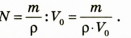
Проверим единицу искомой величины:

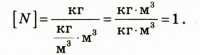
Найдем числовое значение:

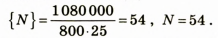
Проанализируем результат: количество цистерн, полученное нами в результате расчетов, достаточно реально.

Ответ: потребуется 54 цистерны.
 

Задача №4

В мензурку с водой (рисунок а) опустили сплошной металлический цилиндр массой 675 г (рисунок б). Определите плотность вещества, из которого изготовлен цилиндр. Что это за вещество?

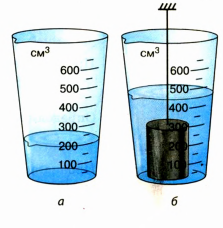
Дано:

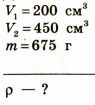
Анализ физической проблемы; поиск математической модели. Плотность вещества, из которого изготовлен цилиндр, равна плотности цилиндра.

По определению плотности р = — .

Масса цилиндра известна из условия задачи.

Объем цилиндра вычислим по формул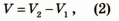е: где 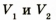— объемы воды в мензурке до и после погружения цилиндра соответственно.

Задачу лучше решать в данных единицах.

Решение и анализ результатов

Подставив выражение (2) в выражение (1), получим формулу для вычисления плотности цилиндра:

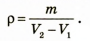
Проверим единицу искомой величины:

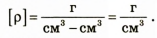
Найдем числовое значение:

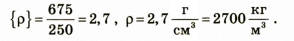
Проанализируем результат: воспользовавшись таблицей плотностей, выясним, какому веществу соответствует полученное значение плотности; плотность 2700 кг/м3 имеет алюминий.

Ответ: плотность вещества 2700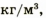 это алюминий.

Как решать задачи динамики

Типы задач. В динамике рассматривают два типа задач, решение которых основывается на законах Ньютона для материальной точки:

1. зная силы, действующие на тело, записать уравнение движения (например, вывести закон движения снаряда, в частности, время и дальность полета, траекторию, зная его массу, начальную скорость и силу сопротивления);
2. из уравнения движения тела найти действующие на него силы (например, определить силу трения шин по асфальту, если известны скорость движения и пройденный автомобилем путь до полной остановки).

Подчеркнем, что при поступательном движении тело можно считать материальной точкой, расположенной в центре масс.

Для решения задач первого типа необходимо знать начальные условия (координаты, скорости). Если известны силы, действующие на тело, и они считаются постоянными, то ускорение тела находят из уравнения 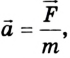т. е. уравнение его движения определяют по формулам кинематики.

Таким образом, решение задач первого типа можно разделить на следующие этапы:

Этапы решения задач первого типа

1. Зная силу F и массу тела т, по второму закону динамики находят ускорение а, а потом по формулам кинематики - мгновенную скорость тела v.
2. Зная скорость, находят перемещение тела s по формулам для равноускоренного движения.
3. Составляют уравнение (закон) движения тела, например, для координаты х в любой момент времени:

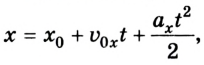
или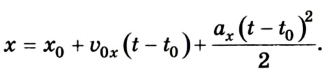

Задачи второго типа решаются аналогичным способом, только в обратной последовательности.

Этапы решения задач второго типа

1. Из заданного уравнения движения находят соответствующие кинематические величины.
2. Если ускорение тела не удалось установить из уравнения (или по условиям), определяют его по формулам кинематики.
3. Силу, действующую на тело, находят из уравнения

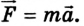
Особенности решения задач по динамике:

Рассмотрим особенности решения задач динамики и сформулируем общие рекомендации по применению законов механики Ньютона с учетом специфических проявлений сил различной природы (гравитационной силы, силы упругости, трения).

Первая рекомендация к решению задач

Решение задач по динамике начинают с подробного описания явлений, рассматриваемых в условиях задач. Затем выбирают систему отсчета, которую можно считать инерциальной для данного случая. Следует помнить, что правильно выбранная система отсчета может упростить решение задачи.

Учитывая, что в школьном курсе физики рассматривают лишь те движения, которые происходят в одной плоскости, достаточно выбрать декартову систему координат на плоскости, а направление осей - соответственно условиям конкретной задачи. Если действие всех сил происходит вдоль одной прямой, достаточно взять одну ось и направить ее по направлению движения тела (вдоль направления действия сил).

Вторая рекомендация к решению задач

При использовании второго закона Ньютона, его записывают сначала в векторной форме: 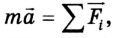а потом переходят к скалярным уравнениям проекции сил и ускорений на соответствующие координатные оси, учитывая их знаки. Для этого нужно все силы и ускорения разложить на составляющие по направлениям координатных осей и записать второй закон Ньютона в виде:

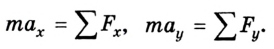
Если в задаче достаточно использовать одну координатную ось, то уравнение будет одно: 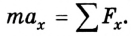Во время записи уравнений в проекциях следует учитывать следующее: если в данном направлении тело не перемещается или движется равномерно, то его ускорение равно нулю, поэтому сумма проекций всех сил на эту ось также равна нулю.

Если в задаче необходимо найти не только силы и ускорения, но и координаты, перемещения, скорости и другие величины, описывающие движение, то можно воспользоваться системой кинематических уравнений.

Если в данном направлении тело не смещается или движется равномерно, то его ускорение равно нулю, поэтому сумма проекции всех сил на эту ось также равна нулю.

Третья рекомендация к решению задач

В решениях задач динамики явно или неявно имеет место третий закон Ньютона, поскольку сила всегда является результатом взаимодействия тел. Следует обратить внимание, что силы взаимодействия приложены к разным телам и поэтому не могут складываться. При неправильном понимании этого иногда возникает вопрос, как может тело, например поезд, двигаться равноускоренно, ведь сила, с которой электровоз действует на состав, равна силе противодействия со стороны состава? Как правило, в таких случаях надо рассматривать взаимодействие всех тел: электровоз-состав, электровоз-рельсы, состав-рельсы. На соответствующих рисунках нужно показать все силы, действующие на тело, и учесть, что каждая из них действует независимо от других.    
Силы всегда являются результатом взаимодействия тел. Взаимодействие может происходить в случае непосредственного контакта или через поля.

Силы взаимодействия, приложенные к разным телам, не могут складываться.
Четвертая рекомендация к решению задач

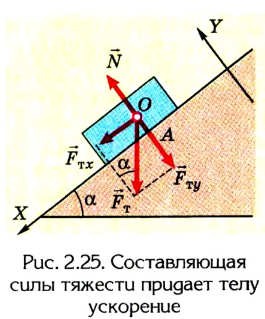
Следует помнить, что в механике рассматривают лишь три вида сил: гравитационную, упругости и трения (сопротивления). Нет так называемых «ускоряющих», «скатывающих» и т. п. сил. Это, как правило, результирующие действующих на тело сил или их составляющие.

Например, «скатывающая» сила -это составляющая силы тяжести в ее проекции на ось, направленную вдоль наклонной плоскости (рис. 2.25).

Не существует и особой «центростремительной» силы. Центростремительное ускорение сообщает телу не какая-нибудь особенная сила, а
равнодействующая, направленная к центру окружности перпендикулярно к скорости. В небесной механике, например, такой силой является гравитационная. Поэтому термин «центростремительная сила» употребляют, чтобы подчеркнуть, какая именно сила или равнодействующая каких сил сообщает телу центростремительное ускорение.

Типичная ошибка при составлении уравнений для таких случаев, когда на ось проектируют как действующие на тело силы, так и их результирующую.

Пятая рекомендация к решению задач

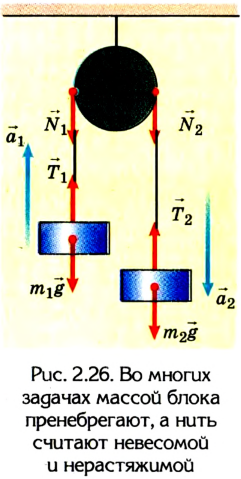
В задачах динамики на движение связанных тел (рис. 2.26), как правило, оговариваются нерастяжимость нити и невесомость блока. Поясним, с какой целью это делается.

Если два тела соединены нитью, то ее нерастяжимость означает, что дополнительной силы упругости в ней не возникает. На этом основании можно сделать вывод, что ускорения, которые получают тела, будут одинаковые:

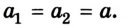
По условиям невесомости блока силу натяжения нити при переходе через блок можно считать не изменяющейся по модулю:

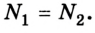
Алгоритм решения задач по динамике:

Решение задач динамики может быть подано в виде определенной последовательности действий - алгоритма, который построен с учетом рассмотренных выше этапов решения основной задачи
механики, а также логики познавательной деятельности при решении физических задач вообще. Основные шаги алгоритма могут быть сформулированы так.

1. Определить характер и направление движения тела. Установить, с какими телами взаимодействует тело, движение которого рассматривается.
2. Сделать рисунок. Показать все силы, действующие на тело. Выбрать тело отсчета и связанную с ним систему координат.
3. Записать в векторной форме уравнение второго закона динамики 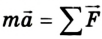для каждого из движущихся тел.
4. Спроектировать на координатные оси силы, скорости и ускорения. Записать уравнение второго закона динамики в проекциях на координатные оси, учитывая знаки проекций векторов. Если в полученной системе уравнений число неизвестных величин равно или меньше числа уравнений, то задача математически сформулирована верно и может быть решена. В ином случае придется записать дополнительные уравнения, например кинематические.
5. Решить уравнение или систему уравнений одним из известных способов. Найти значения искомых величин и оценить их реальность.
6. Проанализировать полученный ответ. Если он противоречит физической сущности задачи, найти новые способы ее решения.
7. Проанализировать другие возможные способы решения этой задачи. Решить ее одним из них и сравнить результаты. Оценить, какой из способов наиболее рациональный.

Примеры решения задач по динамике:

I. Сила тяжести и вес

Решение заказа №1

Шахтная клеть массой Ют начинает равноускоренно опускаться и проходит 75 м за 10 с. Определите силу натяжения троса, на котором закреплена клеть, и вес груза, находящегося в ней, если его масса 80 кг.
Дано:

М = 10 т = 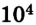кг,

m = 80 кг,

s = 75 м, t = 10 с.

T- ?Р- ?
Решение

1.    Неизвестны - натяжение троса, который держит шахтную клеть, и сила, с которой груз действует на днище клети. Движение клети и груза - равноускоренное вниз, без начальной скорости.
Клеть взаимодействует с Землей и тросом, груз в результате притяжения Земли давит на пол клети. Естественно, что клеть и груз имеют одинаковое ускорение.

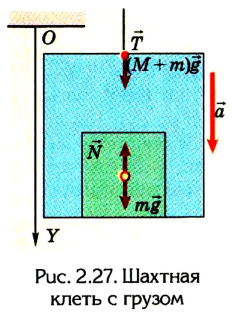
2.    Выполним рисунок. За тело отсчета возьмем Землю и свяжем с ней систему координат - ось OY, направив ее вниз (рис. 2.27). На клеть действует сила тяжести, направленная вертикально вниз, и сила натяжения троса, направленная вертикально вверх. На груз -сила тяжести и сила реакции опоры (пола клети). По определению вес тела: Р = N.
3.    Запишем в векторной форме второй закон Ньютона для каждого тела отдельно: для шахтной клети - уравнение (1), для веса - уравнение (2):

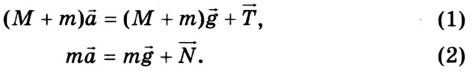
4.    Запишем эти уравнения в скалярной форме в проекциях на ось ОУ:

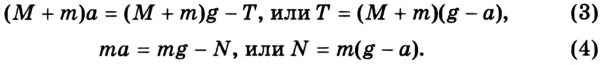
Учитывая, что m < М, этой величиной в уравнении (3) можно пренебречь. Поскольку в этих уравнениях две неизвестные величины -Т и а (3), N и а (4), запишем кинематическое уравнение для ускорения:

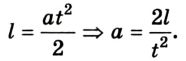
5.    Уравнения (3) и (4) легко решаются подстановкой значения ускорения а. Поэтому сначала вычислим а:

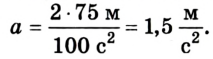
Подставляя его значение в (3) и (4), получим:

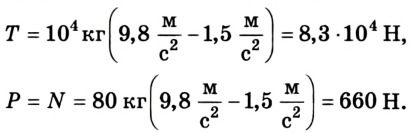
6.    Полученный ответ соответствует житейскому опыту человека, который чувствует снижение давления на пол, например, во время равноускоренного движения лифта вниз.

7.    Если воспользоваться формулой веса тела, которое равноускоренно движется вниз Р = m(g - а), то получим аналогичный результат веса груза.

Ответ: Т = 8,3 • 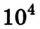Н, Р = 660 Н.

II. Действие силы упругости

Решение заказа №2

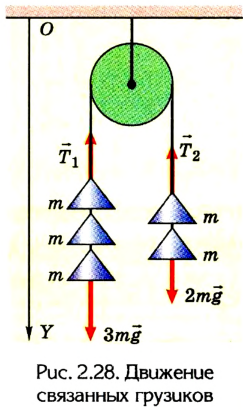
Какой путь проходит каждый из грузиков (рис. 2.28) за первую секунду от начала движения, если их массы одинаковы?

Решение

1-2. Поскольку в условии задачи не дано никакой информации о блоке и нити, естественно допустить, что нити невесомы и нерастяжимы, а трением в блоке и его массой можно пренебречь.
По условию задачи, предварительным уточнениям и рисунку понятно, что три грузика будут опускаться вниз. Поэтому координатную ось OY целесообразно направить также вниз.

3.    Запишем уравнение движения в векторной форме для всей системы тел:

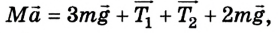
где М = 5m - масса всей системы.

4.    Спроектируем на ось OY силы с учетом направления их действия:

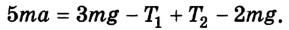
Соответственно условию задачи и принятым нами уточнениям силы натяжения нити 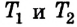одинаковы, поэтому

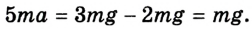
Отсюда находим ускорение движения системы: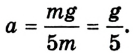

5. В общем случае равноускоренного движения путь, который проходит тело, будет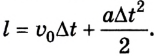
Если в момент начала
движения грузиков их скорость равна нулю 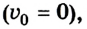уравнение приобретает вид 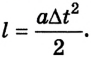Имея в виду, что 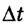= 1 с, а ускорение 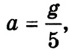находим путь, который проходит каждый из грузиков 5

за первую секунду движения: I = 1 м (если считать g = 10 ).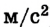

6-7. Эту задачу можно решить и другим способом. Запишем

систему скалярных уравнений отдельно для левых и правых грузиков:

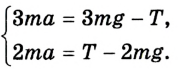
Решение этой системы путем сложения уравнений дает то же значение ускорения движения грузиков: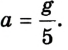

Ответ: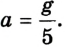

III. Торможение автомобиля

Решение заказа №3

Водитель отключил двигатель автомобиля и начал тормозить на горизонтальной дороге при скорости 72 км/ч.
Определить путь, который прошел автомобиль за 20 с, если коэффициент трения во время торможения равен 0,2.
Дано:

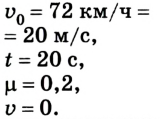
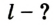
Решение

1-2. На горизонтальной дороге на автомобиль действует сила тяжести 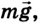направленная вертикально вниз, и сила реакции дороги  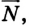направленная вертикально вверх. Если двигатель отключен, то на автомобиль действует лишь сила трения 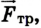направление которой противоположно направлению скорости движения. Выполним соответствующий рисунок (рис. 2.29).

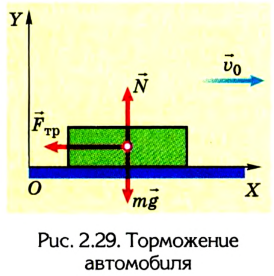
3.    Запишем второй закон динамики в векторной форме:

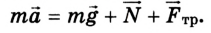
4.    Запишем уравнение в проекциях на координатные оси:
на ось ОХ: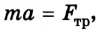
на ось ОУ: 0 = N - mg.

Сила трения 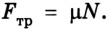Найдем значение ускорения а, с которым двигался автомобиль с учетом силы трения: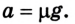
Направление ускорения противоположно направлению скорости, тогда уравнение для определения пройденного автомобилем пути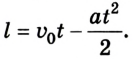  
5.    Рассчитаем путь, который прошел автомобиль за 20 с (по

условию задачи):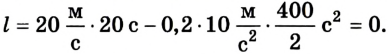

6.    Но этот результат неправильный. Автомобиль не мог остановиться мгновенно в момент начала торможения. Нужно искать ошибку.

Воспользуемся кинематическими уравнениями для скорости и найдем время движения автомобиля до его остановки:

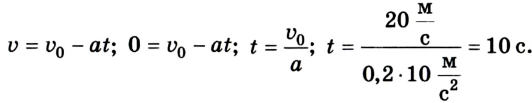
В задаче указано время 20 с, а автомобиль двигался во время торможения лишь 10 с. Теперь можно найти значение тормозного пути:

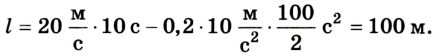
7. Решим эту задачу другим способом. Зная ускорение а, с которым двигался автомобиль во время торможения до полной остановки, пройденный им путь можно найти по формуле

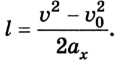
Учитывая, что v = 0 и 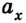= -а, получим

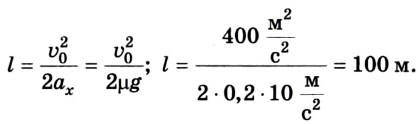
Ответ: l = 100 м.

IV. Движение тела, брошенного горизонтально

Решение заказа №4

На высоте 5 м над поверхностью земли бросили горизонтально шарик со скоростью 10 м/с. Определите положение шарика каждые 0,1 с и по полученным данным постройте траекторию его движения до падения на землю. Через сколько времени шарик упадет на землю? Какую скорость он будет иметь в момент касания земли? Какое расстояние преодолеет шарик в горизонтальном направлении и какое совершит перемещение от начала движения до момента падения?

С целью упрощения вычислений можно принять ускорение свободного падения равным 10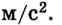

Решение

Данное движение можно представить как два независимых движения: равномерное и прямолинейное, совершаемое в горизонтальном направлении со скоростью кидка 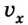= 10 м/с, и свободное падение шарика с высоты h = 5 м с ускорением g = 10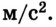

Для того чтобы описать движение, выберем прямоугольную систему координат XOY: направим ось ОХ в горизонтальном направлении, а ось ОУ вертикально вниз (рис. 2.30).

Уравнения движения шарика согласно выбранным координатным осям будут иметь такой вид:

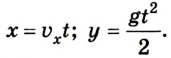
Скорость тела в любой точке траектории определяется по формул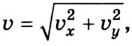е где 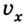остается во время движения постоянной, a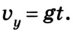
Для того чтобы построить траекторию движения шарика, необходимо найти ее координаты каждые 0,1 с. Полученные данные занесем в таблицу и на координатную плоскость, на которой построим траекторию шарика.

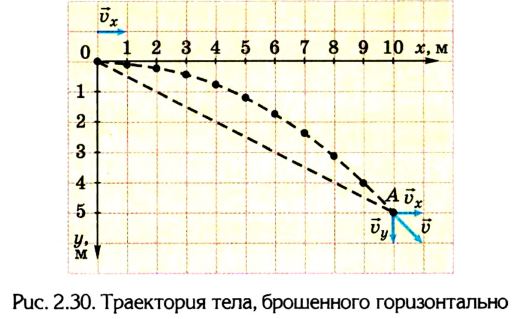
На основании выполненных вычислений и построенной траектории можно сделать вывод, что шарик упадет через 1 с после броска. В момент касания земли горизонтальная составляющая скорости 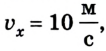а вертикальная 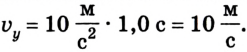Поскольку результирующая скорость шарика определяется по формуле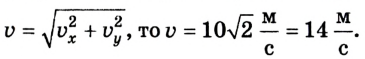

В горизонтальном направлении шарик преодолеет расстояние 10 м.

Значение перемещения измерим при помощи масштабной линейки: в данном случае оно будет приблизительно равно 11,2 м.

Кривая, описывающая движение шарика, является веткой параболы.

V. Грузики на блоке

Решение заказа №5

Через невесомый блок перекинута нитка с грузиками, массы которых 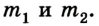Определить разницу сил, действующих на ось блока, если он закреплен жестко и если вращается свободно. Считать нитку невесомой, нерастяжимой и не скользящей на блоке.
Дано:

Решение

1.    Если блок закреплен жестко и не может вращаться, а нитка не скользит по нему (по условию задачи), то на ось блока действует сила

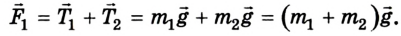
Если блок вращается свободно, натяжение нитки с обеих сторон одинаково и равно Т. В этом случае на ось блока действует сила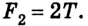

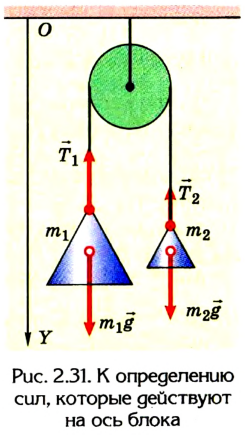
2.    Выполним рисунок (рис. 2.31). Направим ось OY вертикально вниз, предположив, что в этом направлении будет двигаться тело если его масса больше, чем

3.    Запишем второй закон механики Ньютона для обоих тел в векторной форме для случая, когда блок свободно вращается:

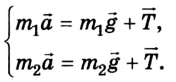
4.    В проекциях на ось OY система уравнений имеет следующий вид

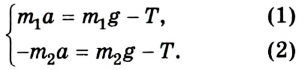
5.    Решив систему уравнений, найдем ускорение тел:

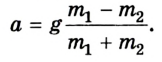
Из уравнения (1) можно найти силу натяжения:

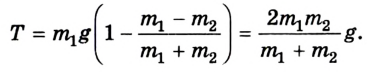
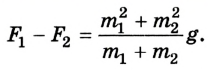
6. Силу натяжения Т можно найти также из уравнения (2):

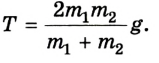
Результат будет одинаковым.

VI. Движение по окружности

Особенностью уравнения движения тела по окружности является то, что приложенные к телу силы могут вызвать как изменение направления скорости, так и изменение его модуля. В школьном курсе физики, как правило, рассматривается случай равномерного вращения, т. е. когда равнодействующая сил сообщает телу центростремительное ускорение.

Особенностью уравнения движения тела по окружности является то, что приложенные к телу силы могут вызвать как изменение направления скорости, так и ее значение.

Кроме того, следует помнить, что центростремительное ускорение сообщает телу не какая-то особенная «центростремительная сила», а одна из действующих на тело сил, которая изменяет направление его скорости. Поэтому, употребляя термин «центростремительная сила», подчеркивают не особую природу этой силы, а ее направление - к центру кривизны траектории в данной ее точке.

Решение заказа №6

Автомобиль массой 1 т движется по вогнутому мосту со скоростью 54 км/ч. Радиус кривизны моста 200 м. С какой силой давит автомобиль на мост в точке, в которой нормаль с вертикалью составляет угол 60°?
Дано:

m = 1 т = 1000 кг,

v = 54 км/год = 15 м/с,

R = 200 м,

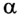= 60°.
F-?
Решение

1-2. Непосредственно силу давления автомобиля на мост найти невозможно, однако несложно найти силу реакции моста на автомобиль. По третьему закону Ньютона эти силы приложены к разным телам и противоположно направлены, но одинаковы по значениям: F=N.
Автомобиль движется по окружности радиуса R с постоянной по значению скоростью v.
Ускорение автомобиля направлено к центру кривизны моста и равно 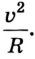 Направим ось координат к центру окружности (рис. 2.32).

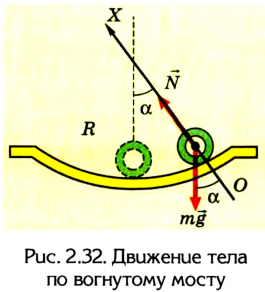
На автомобиль действуют сила тяжести 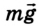и сила упругости 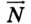деформированного моста, которая перпендикулярна к поверхности моста.

3.    Второй закон механики Ньютона в векторной форме имеет вид

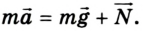
4.    Запишем уравнение в проекциях на выбранную ось ОХ:

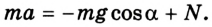
5. Найдем силу реакции N:

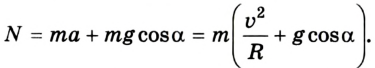
Если считать g = 10 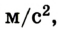то N = 61 250 Н, F 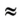60 кН.

6. Анализ результата решения задачи в общем виде показывает, что в разных точках автомобиль давит на поверхность моста по-разному: сила давления имеет наибольшее значение в точке, когда 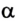= 0 и cos 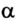= 1, т. е. в самой нижней его точке:

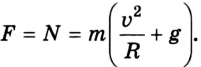
Решение заказа №7

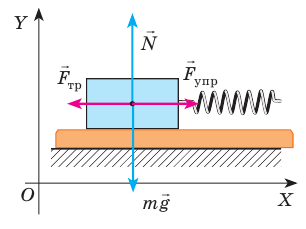
Деревянный брусок массой 200 г равномерно тянут по горизонтальной поверхности с помощью пружины жесткостью 40 Н/м. Определите удлинение пружины, если коэффициент трения скольжения 0,25.

Анализ физической проблемы. Чтобы вычислить удлинение пружины, нужно знать силу упругости — ее найдем, воспользовавшись вторым законом Ньютона. Следует учесть, что брусок тянут равномерно, поэтому ускорение его движения равно нулю.

Выполним пояснительный рисунок, на котором укажем силы, действующие на тело, и направления осей координат.

Дано:

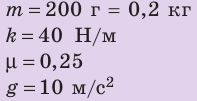
Найти:

Поиск математической модели, решение

Запишем второй закон Ньютона в векторном виде:

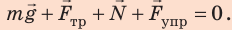
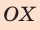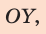Найдем проекции сил на оси и запишем формулы для вычисления силы упругости и силы трения скольжения:

Решив систему уравнений, найдем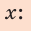

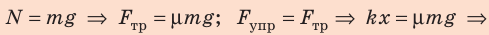
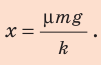
Проверим единицу, найдем значение искомой величины:

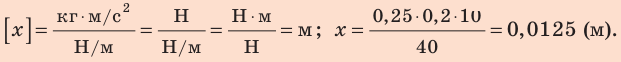
Ответ: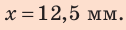

Решение заказа №8

Вычислите тормозной путь и время торможения автомобиля, если он двигался по прямому горизонтальному участку дороги и перед началом торможения имел скорость 54 км/ч. Коэффициент трения скольжения резины по бетону — 0,75.

Анализ физической проблемы. Чтобы определить тормозной путь и время торможения автомобиля, необходимо знать ускорение его движения. Ускорение найдем, воспользовавшись вторым законом Ньютона.

Выполним пояснительный рисунок, на котором укажем силы, действующие на автомобиль, оси координат, направления начальной скорости, перемещения и ускорения (автомобиль останавливается, поэтому 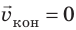и

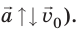
Дано:

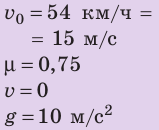
Найти:

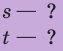
Поиск математической модели, решение

Согласно второму закону Ньютона:

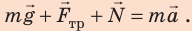
Найдем проекции сил и ускорения на оси и запишем формулу для вычисления силы трения скольжения:

Решив систему уравнений, найдем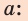

Тормозной путь и время движения определим, воспользовавшись формулами:

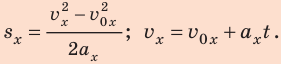
Учитывая, что 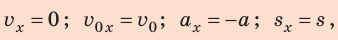имеем: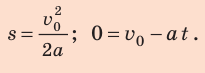

Следовательно, 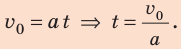Учитывая, что 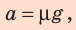получаем:

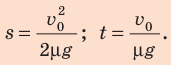
Проверим единицы, найдем значения искомых величин:

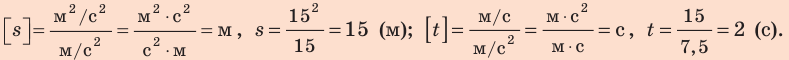
Анализ результатов. Получен реальный результат: тормозной путь автомобиля действительно достаточно велик. Помните об этом и никогда не нарушайте правила дорожного движения!

Ответ: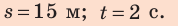

Решение заказа №9

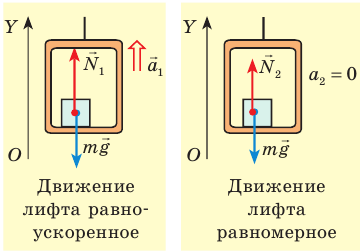
Человек массой 70 кг зашел в лифт. Лифт начинает движение с ускорением 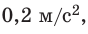направленным вверх, а затем поднимается с постоянной скоростью. На сколько изменяется вес человека во время этого движения?

Анализ физической проблемы

Вес тела — это сила, действующая на опору — лифт. По третьему закону Ньютона сила, с которой тело действует на опору, равна силе, с которой опора действует на тело: 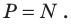Значит, нужно найти силу нормальной реакции опоры, действующую на человека при каждом виде движения лифта.

Выполним пояснительные рисунки, на которых укажем силы, действующие на человека, направление ускорения и направление оси

Дано:

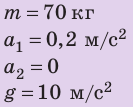
Найти:

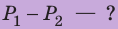
Поиск математической модели, решение

Запишем второй закон Ньютона для каждого случая и найдем проекции сил и ускорения на ось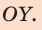

1. Движение равноускоренное: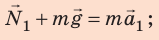

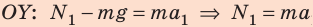
Значит,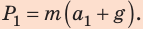

2. Движение равномерное: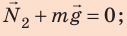

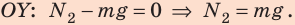Значит,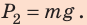

Найдем значения искомых величин:

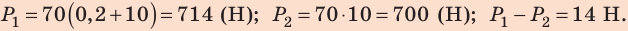
Ответ: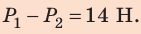

Решение заказа №10

Автомобиль массой 4 т поднимается в гору, замедляя движение. Определите силу тяги автомобиля, если уклон горы — 0,02, а коэффициент сопротивления движению — 0,04. Ускорение автомобиля — 0,15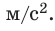

Обратите внимание!

Уклон дороги — синус угла 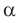наклона полотна дороги к горизонту. Если уклон невелик (меньше 0,1), то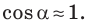

Коэффициент сопротивления движению 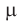учитывает все виды трения: качения, скольжения в осях и т. д. Сила сопротивления направлена противоположно движению тела и вычисляется по формуле: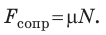

Анализ физической проблемы

На тело действуют четыре силы: сила тяжести 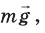сила 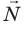нормальной реакции опоры, сила тяги 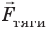и сила сопротивления 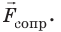Скорость тела уменьшается, поэтому ускорение направлено противоположно направлению движения тела.

Выполним пояснительный рисунок, указав силы, действующие на тело, направления осей координат и ускорения движения тела.

Дано:

Найти:

Поиск математической модели, решение

Запишем второй закон Ньютона в векторном виде:

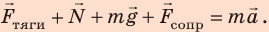
Спроектируем уравнение на оси координат (сила 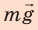не лежит на оси координат, поэтому для нахождения ее проекций опустим от конца вектора 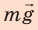перпендикуляры на оси и и 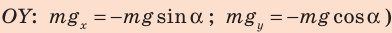запишем выражение для

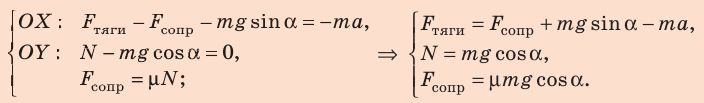
Подставив выражение для 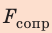в первое уравнение системы, найдем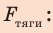

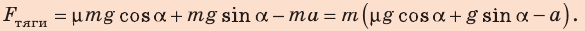
Проверим единицу, найдем значение искомой величины:

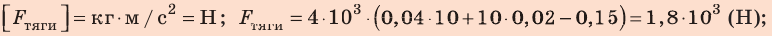
Ответ: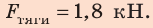

Вывод:

Вы ознакомились с решением некоторых задач на движение тел под действием нескольких сил. Конечно, рассмотреть в рамках учебника все типы таких задач невозможно, да и не нужно. Главное — у вас есть алгоритм решения и примеры работы по этому алгоритму. Остальное — за вами.

Итак, решая задачу по динамике, сначала выполните пояснительный рисунок, укажите силы, запишите уравнение второго закона Ньютона, выберите систему отсчета, найдите проекции. Нужно знать, как направлены силы, когда они возникают и по каким формулам их определяют. А дальше, даже если вы сразу не видите всего хода решения задачи, — ничего страшного. Вы обязательно найдете какую-то величину, знание которой поможет вам увидеть дальнейший ход решения. Можно даже сказать так: «Если не знаешь, как решать задачу, то начни ее решать». Не нужно бояться сделать ошибочный шаг. Тот не побеждает, кто не умеет проигрывать. Научиться решать задачи по физике может каждый, нужно только их решать!

Как решать задачи по кинематике

1. Прочитайте условие задачи. Выясните, какие тела участвуют в движении, каков характер движения тел, какие параметры движения известны.
2. Запишите краткое условие задачи. При необходимости представьте значения физических величин в единицах СИ.
3. Выполните пояснительный рисунок, на котором укажите ось координат, направления скорости движения, перемещения, начальной скорости и ускорения движения тела.
4. Из формул, описывающих прямолинейное равноускоренное движение, выберите наиболее соответствующие условию задачи.

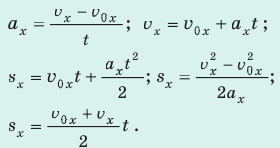
Выбранные формулы конкретизируйте для задачи. 5. Решите задачу в общем виде. 6. Проверьте единицу, найдите значение искомой величины. 7. Проанализируйте результат. 8. Запишите ответ.

Решение заказа №11

Тормоз легкового автомобиля исправен, если на сухом асфальте при скорости 28 м/с тормозной путь автомобиля равен 49 м. Определите время торможения и ускорение движения автомобиля.

Дано:

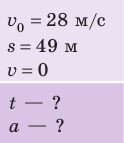
Решение:

Выполним пояснительный рисунок. Ось ОX направим в направлении движения автомобиля. Автомобиль тормозит, поэтому

Поскольку в задаче дано , v и s, то для определения времени торможения самой удобной является формула 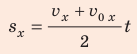(1), а для определения ускорения — формула 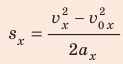(2). Конкретизируем данные формулы (перейдем от проекций к модулям):

• направление перемещения и направление начальной скорости совпадают с направлением оси ОX, поэтому ;
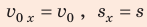• конечная скорость равна нулю: ;
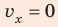• направление ускорения противоположно направлению оси ОХ, поэтому .

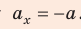Итак, из формулы (1): 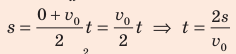; из формулы (2): 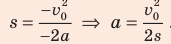. Проверим единицы, найдем значения искомых величин:

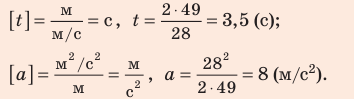
Ответ: t = 3 5, с; a = 8 м/с2.

Решение заказа №12

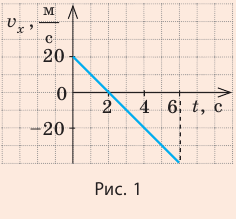
На рис. 1 представлен график зависимости 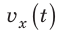для движения тела вдоль оси ОХ. 1) Опишите характер движения тела. 2) Запишите уравнение зависимости 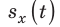. 3) Постройте график зависимости .

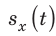Решение:

1) График зависимости 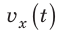— отрезок прямой, а тело все время двигалось вдоль оси ОХ, поэтому его движение равноускоренное прямолинейное. Первые 2 с скорость движения тела уменьшалась от 20 м/с до 0, затем тело развернулось и 4 с ускоряло свое движение, двигаясь в противоположном направлении.

2) Для равноускоренного прямолинейного движения:

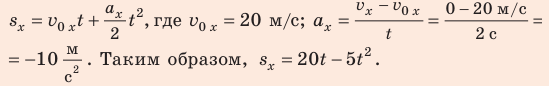
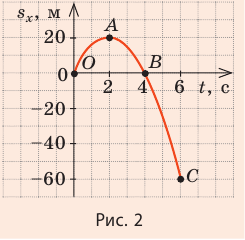
3) График зависимости 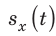— парабола, вершина которой соответствует точке разворота. Поэтому точка A с координатами 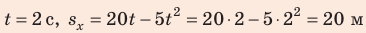— это вершина параболы. Данная парабола проходит через точку О с координатами (t = 0, 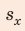= 0) и симметричную ей относительно прямой t = 2 с точку В с координатами (t = 4 с, 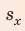= 0). В конце наблюдения: 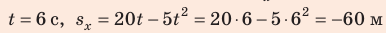(точка С). По четырем точкам (О, A, B, C) можем построить параболу (рис. 2).

Выводы:

• Равноускоренное прямолинейное движение — это движение, при котором тело движется по прямолинейной траектории с неизменным ускорением.
• Для равноускоренного прямолинейного движения тела: — ускорение тела не изменяется со временем, график проекции ускорения (график зависимости 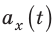) — прямая, параллельная оси времени; — скорость движения изменяется линейно: 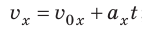; график зависимости 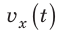— отрезок прямой, наклоненной к оси времени; — уравнение проекции перемещения: 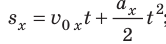; график зависимости 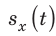— парабола, вершина которой соответствует точке разворота; — координату тела определяют из уравнения 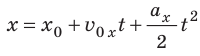; график координаты — парабола.