
Задачи на вращательное движение тела в теоретической механике
Задачи на вращательное движение тела:
Мерой инертности материальной точки, а также тела при поступательном движении является их масса.
Если же тело вращается, то мерой инертности служит его момент инерции —величина, зависящая от величины массы тела и от того, каким образом масса распределена относительно оси вращения тела.
Как известно, моментом инерции тела относительно некоторой оси называется величина, составленная из суммы произведений масс всех материальных точек тела на квадраты расстояний от этих точек до оси вращения.
В математической форме величину момента инерции тела можно представить такой формулой:
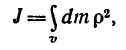
Этой формулой можно пользоваться для определения моментов инерции тел, имеющих геометрическую форму тел вращения.
Если тело составлено из нескольких частей, имеющих определенную геометрическую форму, удобно использовать еще формулу
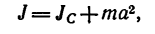
где Jc—момент инерции тела относительно центральной оси (т. е. относительно оси, проходящей через центр тяжести тела); J — момент инерции тела относительно оси, параллельной центральной оси; m—масса тела и а —расстояние между осями.
Если тело имеет очень сложную форму, то момент инерции определяется либо из опыта, либо по формулам, приведенным в различных технических справочниках.
Приведем несколько формул для определения моментов инерции тел (во всех формулах т—масса тела, а линейные размеры обозначены на рисунках).
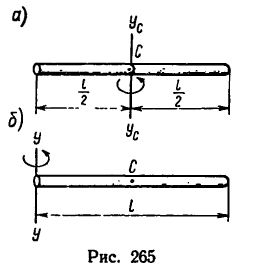
1. Момент инерции тонкого прямого
стержня относительно его центральной оси, перпендикулярной к стержню (рис. 265,а)
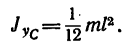
2. Момент инерции тонкого прямого стержня относительно оси, перпендикулярной к стержню и расположенной у одного из его концов (рис. 265, б):
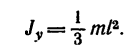
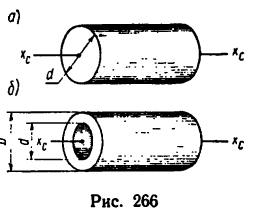
3. Момент инерции сплошного однородного цилиндра относительно его геометрической оси (рис. 266, а)
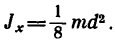
4. Mомент инерции полого однородного цилиндра относительно его геометрической оси (рис. 266, б)
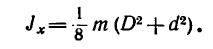
Сопоставляя между собой при помощи рисунков формулы (I) и (2), а также (3) и (4). необходимо учитывать то, что при одной и тон же массе стержней и одинаковой длине второй стержень обладает в четыре раза большим моментом инерции (см. рис. 265, б), а также при одинаковых внешних размерах цилиндров и одинаковой массе (если цилиндры изготовлены из различных материалов, например из алюминия и стали) полый цилиндр обладает большим моментом инерции.
Если в формуле (4) пренебречь толщиной стенки цилиндра, т. е считать, что D—d. (вся масса распределена по ободу цилиндра), то
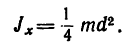
Единицей измерения момента инерции тела являются в СИ: 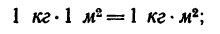
в системе МКГСС:
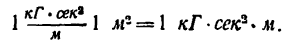
При вращательном движении (см. § 45-11) движущим фактором является вращающий момент (пара сил).
Если алгебраическая сумма моментов всех пар сил, приложенных к телу, имеющему ось вращения, не равна нулю, то тело приобретает угловое ускорение, числовое значение которого прямо пропорционально вращающему моменту 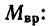
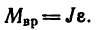
В этом уравнении, выражающем основной закон динамики для вращательного движения тела, множителем пропорциональности является момент инерции тела. Тело с большим моментом инерции труднее привести во вращение.
Кинетическая энергия вращающегося тела
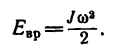
Если тело находится в плоскопараллельном движении, например катящееся колесо, то его кинетическая энергия складывается из двух слагаемых:
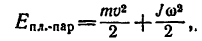
где 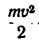 —кинетическая энергия, получающаяся от поступательной части этого сложного движения (см. § 37-8) при скорости
—кинетическая энергия, получающаяся от поступательной части этого сложного движения (см. § 37-8) при скорости 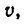 равной скорости центра тяжести тела, а
равной скорости центра тяжести тела, а 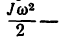 кинетическая энергия от вращательной части, причем J —момент инерции относительно оси, проходящей через центр тяжести тела.
кинетическая энергия от вращательной части, причем J —момент инерции относительно оси, проходящей через центр тяжести тела.
Задача №1
Два цилиндра, изготовленных из различных материалов (см. рис. 266), имеют одинаковую массу 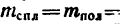 = 80 кг; их наружные диаметры
= 80 кг; их наружные диаметры 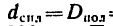 = 240 мм, а внутренний диаметр полого цилиндра
= 240 мм, а внутренний диаметр полого цилиндра 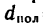 = 200 мм. Полый цилиндр вращается вокруг собственной оси с угловой скоростью
= 200 мм. Полый цилиндр вращается вокруг собственной оси с угловой скоростью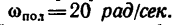 С какой скоростью должен вращаться сплошной цилиндр, чтобы оба цилиндра имели одинаковый запас кинетической энергии?
С какой скоростью должен вращаться сплошной цилиндр, чтобы оба цилиндра имели одинаковый запас кинетической энергии?
Решение.
1. Если кинетические энергии обоих цилиндров обозначить, соответственно,
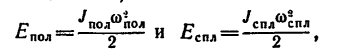
то по условию задачи
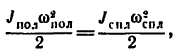
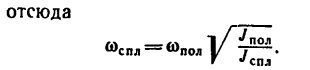
2. Если определять числовые значения моментов инерции обоих цилиндров, то
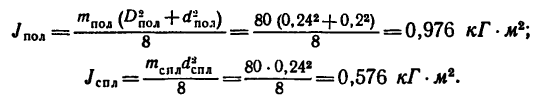
Определим скорость сплошного цилиндра
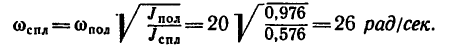
3. Если же числовые значения моментов инерции не определять, то
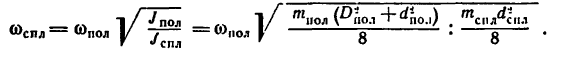
В полученную формулу
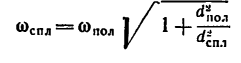
подставим числовые значения диаметров:
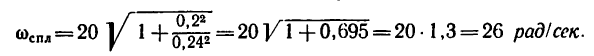
Для второго варианта решения, как видно, массу цилиндров можно и не задавать.
Задача №2
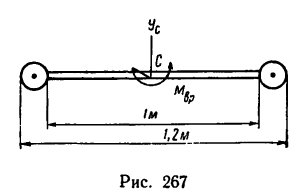
Стержень длиной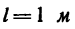 и массой 3 кг имеет на концах шарообразные массы по 2 кг каждая (диаметры шариков d—10 см). Какой вращающий момент нужно приложить к стержню, чтобы привести его во вращение с угловым ускорением
и массой 3 кг имеет на концах шарообразные массы по 2 кг каждая (диаметры шариков d—10 см). Какой вращающий момент нужно приложить к стержню, чтобы привести его во вращение с угловым ускорением 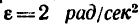 вокруг оси, перпендикулярной к стержню и
вокруг оси, перпендикулярной к стержню и
проходящей через центр тяжести системы (рис. 267)?
Решение.
1. Чтобы определить необходимый вращающий момент, нужно воспользоваться уравнением основного закона динамики для вращательного движения тела
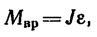
но предварительно надо определить момент инерции системы стержня и шариков.
2. Находим момент инерции этой системы 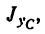 который складывается из момента инерции стержня
который складывается из момента инерции стержня 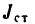 и двух моментов инерции шариков
и двух моментов инерции шариков 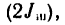 которые считаем материальными точками, т. е. при определении моментов инерции шариков принимаем, что их массы сосредоточены в центрах шариков на расстоянии
которые считаем материальными точками, т. е. при определении моментов инерции шариков принимаем, что их массы сосредоточены в центрах шариков на расстоянии
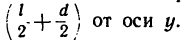
Следовательно,
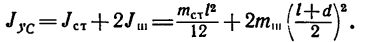
Подставим числовые значения:
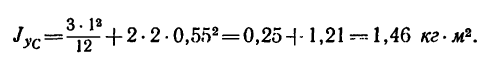
3. И теперь определим вращающий момент, необходимый для сообщения стержню ускорения 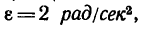
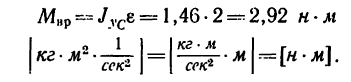
Задача №3
Тормозной шкив, масса которого m— 2 кг, диаметр d—0,8 м, имеет форму сплошного диска и вращается но инерции с угловой скоростью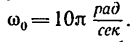 Для остановки вала
Для остановки вала
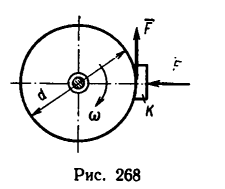
к шкиву прижимают тормозную колодку k с силой Q—5 н. Через сколько секунд вал остановится и сколько оборотов он сделает до остановки, если коэффициент трения колодки о шкив f — 0,4? Трением в подшипниках вала, на котором насажен шкив, пренебречь; массу вала не учитывать.
Решение 1 - при помощи основного закона для вращающегося тела.
1. Изобразим шкив на рис. 268. Прижатая к шкиву колодка создает силу трения F=fQ, направленную в сторону, противоположную вращению колеса. Таким образом, на шкив с момента прижатия колодки начинает действовать тормозной момент, направленный в сторону, противоположную его
вращению,
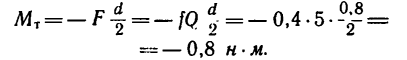
2. Шкив имеет форму сплошного диска, его момент инерции определяется но формуле
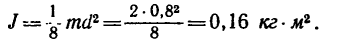
3. Из основного уравнения динамики для вращательного движения 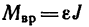 находим угловое ускорение е:
находим угловое ускорение е:
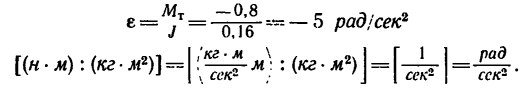
4. Из формулы для углового ускорения равнопеременного вращения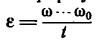 находим время торможения:
находим время торможения:
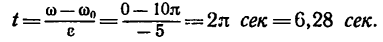
5. По уравнению равнопеременного вращения определяем угол поворота шкива (вала) за это время:
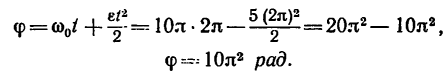
6. Находим число оборотов вала, сделанное им с момента начала торможения до остановки:
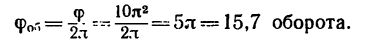
Эту задачу можно решить и другим способом (используя закон кинетической энергии для вращающегося тела).
Решение 2.
1. Закон кинетической энергии вращающегося тела выражается уравнением
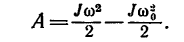
2. В данном случае тормозной момент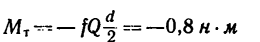 производит при остановке шкива (вала) работу
производит при остановке шкива (вала) работу
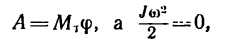
так как конечная угловая скорость 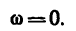 энергии шкива имеет вид
энергии шкива имеет вид
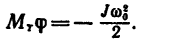
Отсюда (значение J —найдено в первом решении)
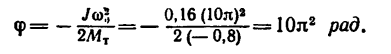
Число оборотов вала
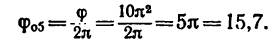
4. Время торможения можно найти из формулы 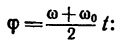
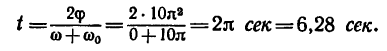
Задача №4
Цилиндр 1, масса которого 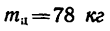 и диаметр d=24 сж, может свободно вращаться около горизонтальной оси. На цилиндр намотана гибкая нить, имеющая на конце груз 2
и диаметр d=24 сж, может свободно вращаться около горизонтальной оси. На цилиндр намотана гибкая нить, имеющая на конце груз 2
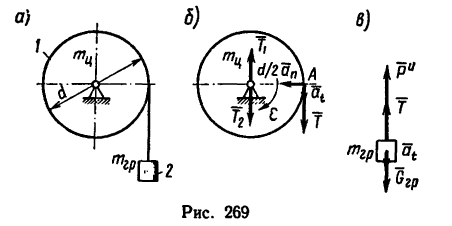
массой 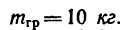 Падая, груз разматывает нить и вращает цилиндр (рис. 269, а).
Падая, груз разматывает нить и вращает цилиндр (рис. 269, а).
Определить угловое ускорение цилиндра, натяжение нити, кинетическую энергию груза А и цилиндра через t = 4 сек после начала движения.
Массой нити и трением в оси цилиндра пренебречь.
Решение — при помощи метода кинетостатики и уравнения основного закона динамики для вращающегося тела.
1. В задаче рассматриваются два связанных между собой тела: вращающийся цилиндр и поступательно двигающийся груз. Мысленно разрежем нить и изобразим оба тела с действующими на них силами отдельно друг от друга.
2. На рис. 269, б показан цилиндр, на который действует вращающий момент нары сил 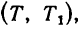 созданной натяжением нити (сила
созданной натяжением нити (сила 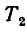 приложена к подшипнику цилиндра, см. § 45-11):
приложена к подшипнику цилиндра, см. § 45-11):
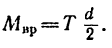
3. Вращение цилиндра определяется уравнением:
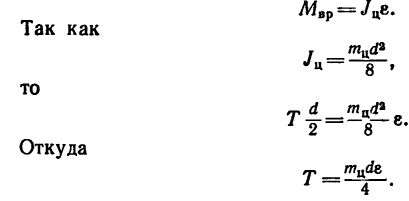 (а)
(а)
В полученное выражение для Т входит вторая неизвестная величина е. Чтобы облегчить дальнейшие вычисления, подставим сюда те величины, которые известны (в единицах СИ: 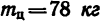 и d = 0,24 м):
и d = 0,24 м):
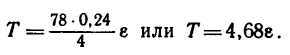 (а')
(а')
4. Изобразим теперь (рис. 269, в) груз, на который действуют его вес 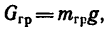 реакция нити Т, равная ее натяжению. Так как цилиндр падает с ускорением
реакция нити Т, равная ее натяжению. Так как цилиндр падает с ускорением 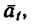 то силы
то силы 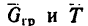 не уравновешивают друг друга. Добавим к ним силу инерции
не уравновешивают друг друга. Добавим к ним силу инерции 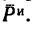 Тогда уравнение равновесия сил примет вид
Тогда уравнение равновесия сил примет вид
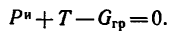
Заменим в последнем уравнении силу инерции и вес груза их значениями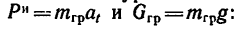
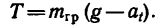
5. Считая нить нерастяжимой, получаем, что ускорение а, груза равно ускорению любой точки нити, а следовательно, и точки А на ободе цилиндра (см. рис. 269, б). Но точка А принадлежит телу, вращающемуся с угловым ускорением е, поэтому
и теперь
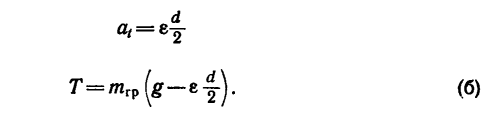
Получено второе уравнение с теми же неизвестными Т и е.
Подставив в (б) числовые значения 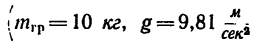 и d=0,24 м), получаем
и d=0,24 м), получаем
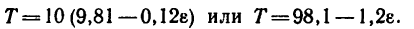 (б')
(б')
6. Решим систему уравнений (а') и (б'). Правые части обоих уравнений равны 7, значит
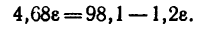
Отсюда
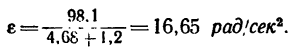
Подставим найденное значение е в любое из уравнений, например в (а'):
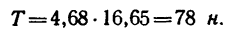
7. Определим кинетическую энергию цилиндра и груза через t = 4 сек после начала движения системы:
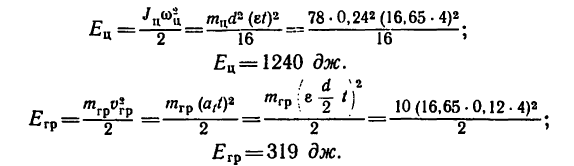
8. Таким образом, общий запас кинетической энергии обоих тел
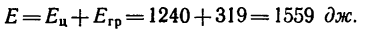
Решение 2 —при помощи закона кинетической энергии.
1. Второе решение начинается с того, чем заканчивается первое.
Через t — 4 сек оба тела приобретают кинетическую энергию благодаря работе, произведенной грузом 2 при падении с высоты h (рис.70)
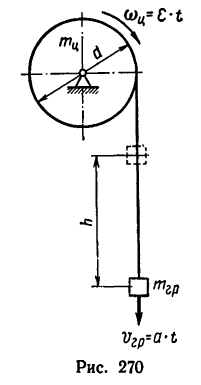
2. Работа груза
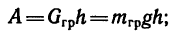
кинетическая энергия цилиндра
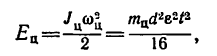
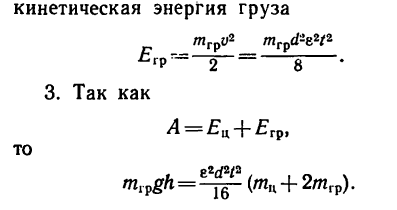
Здесь h —путь, пройденный грузом за t = 4 сек с ускорением 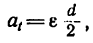 поэтому
поэтому
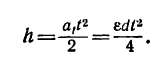
4. Подставим в левую часть равенства (а) значение h и сократим обе части равенства на общие множители:
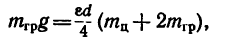
откуда
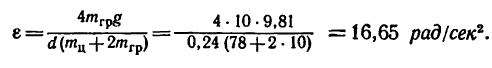
5. Натяжение Т нити найдем при помощи уравнения основного
закона динамики
Здесь 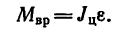
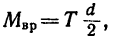
поэтому
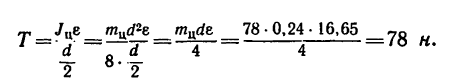
6. Так как значение углового ускорения е известно, легко найти величины кинетических энергий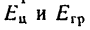 (см. п. 2 решения).
(см. п. 2 решения).
Вращательное движение тела
При изучении темы ВРАЩАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛА вы научитесь решать простые задачи кинематики тела. В таких задачах вводятся векторные величины — угловая скорость 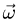 и угловое ускорение
и угловое ускорение 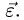 Важно понять, что для вращательного движения тела эти векторы постоянно направлены по оси вращения. При сферическом движении (§ 10.1) векторы угловой скорости и углового ускорения могут лежать на разных прямых, и направления их в общем случае зависят от времени.
Важно понять, что для вращательного движения тела эти векторы постоянно направлены по оси вращения. При сферическом движении (§ 10.1) векторы угловой скорости и углового ускорения могут лежать на разных прямых, и направления их в общем случае зависят от времени.
ПОСТАНОВКА ЗАДАЧИ. Твердое тело вращается вокруг неподвижной оси. Заданы некоторые кинематические характеристики движения тела и (или) кинематические характеристики движения точки этого тела. Найти остальные кинематические характеристики движения тела или точки.
План решения:
Пусть тело вращается вокруг оси z. Кинематические характеристики движения тела:
- — угол поворота
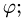
- — угловая скорость
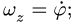
- — угловое ускорение
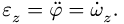
Кинематические характеристики точки на теле:
- — радиус траектории (расстояние до оси вращения) R:
- — скорость
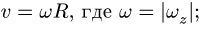
- — ускорение
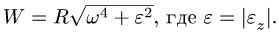
1. Записываем систему уравнений для всех величин, входящих в условие задачи. В зависимости от условия возможны три основных варианта решения.
Гл.7.Вращательное движение тела
— Неизвестный закон вращения. Записываем систему двух уравнений для скорости 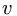 точки, лежащей на расстоянии R от оси вращения, и ее ускорения W:
точки, лежащей на расстоянии R от оси вращения, и ее ускорения W:
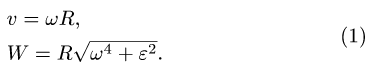
Для решения задачи необходимо, чтобы три из пяти величин 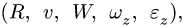 входящих в (1), были заданы в условии.
входящих в (1), были заданы в условии.
— Вращение с постоянной угловой скоростью. Интегрируя уравнение 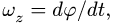 ,при
,при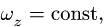 получаем
получаем

Как правило, отсчет ведется от 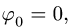 поэтому в системе трех уравнений (1-2) содержатся семь величин
поэтому в системе трех уравнений (1-2) содержатся семь величин 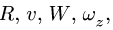
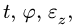 четыре из которых должны быть заданы в условии задачи.
четыре из которых должны быть заданы в условии задачи.
— Вращение с постоянным угловым ускорением. Дважды интегрируя уравнение
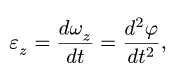
получаем, при 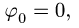
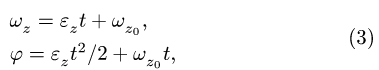
где 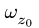 — начальная угловая скорость. Совместно с (1) получаем систему четырех уравнений для восьми величин
— начальная угловая скорость. Совместно с (1) получаем систему четырех уравнений для восьми величин 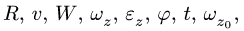 четыре из которых должны быть заданы в условии задачи.
четыре из которых должны быть заданы в условии задачи.
2. Решаем систему. Находим искомые величины.
Замечание. Ряд величин задан в тексте задач неявно. Например, угол поворота 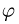 может быть задан числом оборотов
может быть задан числом оборотов 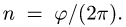 Слова "покой" и "остановка" соответствуют математической записи
Слова "покой" и "остановка" соответствуют математической записи 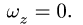
Задача №5
Диск вращается вокруг неподвижной оси с постоянным угловым ускорением 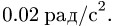 Найти ускорение точки, лежащей на расстоянии 4 см от оси вращения, через 7 с после начала движения из состояния покоя.
Найти ускорение точки, лежащей на расстоянии 4 см от оси вращения, через 7 с после начала движения из состояния покоя.
Решение
1. В задаче задано постоянное угловое ускорение. Записываем систему уравнений для величин, входящих в условие задачи:

По условию задачи диск в начальный момент находился в покое, следовательно, 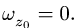 Кроме того, при t = 7 с, даны значения R = 4 см,
Кроме того, при t = 7 с, даны значения R = 4 см,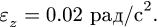 Решая систему двух уравнений (4) с двумя неизвестными
Решая систему двух уравнений (4) с двумя неизвестными 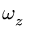 и W, находим
и W, находим
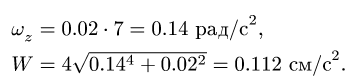
Ответ. 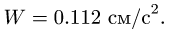
Передача вращения
Постановка Задачи. Механизм состоит из вращающихся на неподвижных осях блоков и поступательно движущихся элементов. Все элементы находятся во фрикционном, зубчатом или ременном зацеплениях. Задана какая-либо кинематическая характеристика одного из тел. Найти кинематические характеристики других тел.
План решения:
1. Определяем кинематические характеристики тела, с заданным законом движения. Если это тело движется прямолинейно поступательно, то скорость и ускорение любой его точки имеет вид
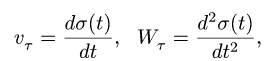
где 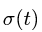 — закон движения тела. При заданном вращательном движении находим угловую скорость и угловое ускорение:
— закон движения тела. При заданном вращательном движении находим угловую скорость и угловое ускорение:
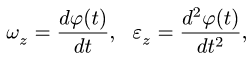
где 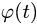 — закон вращения тела (зависимость угла поворота в радианах от времени).
— закон вращения тела (зависимость угла поворота в радианах от времени).
2. Определяем угловую скорость тела, связанного нерастяжимой нитью (ремнем, тросом), фрикционно или зубчатым зацеплением с телом, угловая скорость которого известна:

где 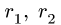 — радиусы ободов колес (блоков) 1, 2, на которые надет ремень в случае ременной передачи, или радиусы колес, находящихся в зацеплении;
— радиусы ободов колес (блоков) 1, 2, на которые надет ремень в случае ременной передачи, или радиусы колес, находящихся в зацеплении; 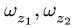 — проекции угловых скоростей колес на ось, параллельную осям вращения. Знак минус берем при внешнем зацеплении, или крестообразной ременной передаче, когда вращение колес происходит в разные стороны. При внутреннем зацеплении (рис. 83) или простой ременной передаче (рис. 84) берем знак плюс. Отношение
— проекции угловых скоростей колес на ось, параллельную осям вращения. Знак минус берем при внешнем зацеплении, или крестообразной ременной передаче, когда вращение колес происходит в разные стороны. При внутреннем зацеплении (рис. 83) или простой ременной передаче (рис. 84) берем знак плюс. Отношение 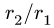 называется передаточным числом от тела 1 к телу 2. Для зубчатых соединений аналогом (1) является соотношение угловых скоростей
называется передаточным числом от тела 1 к телу 2. Для зубчатых соединений аналогом (1) является соотношение угловых скоростей
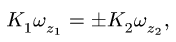
в которое вместо радиусов 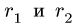 входят числа зубцов
входят числа зубцов 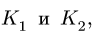 пропорциональные длинам окружностей шестеренок.
пропорциональные длинам окружностей шестеренок.
Если поступательное движение тела 1 передается вращательному движению тела 2 (или наоборот), то связь линейной и угловой скоростей имеет вид

где 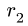 — радиус обода, находящегося в контакте с поступательно движущимся телом.
— радиус обода, находящегося в контакте с поступательно движущимся телом.
3. Повторяя п.2 для всех пар кинематически связанных тел, составляем и решаем систему уравнений для неизвестных линейных и угловых скоростей.
4. Дифференцируя уравнения полученной системы, получаем аналогичную систему для угловых и линейных ускорений. Например, из уравнения (1) следует, что 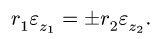
Аналогично, из (2) следует связь линейного ускорения поступательно движущегося тела и углового ускорения связанного с ним вращающегося тела:
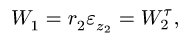
где 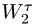 — тангенциальная составляющая ускорения точки вращающегося тела в месте контакта. Было бы ошибкой считать
— тангенциальная составляющая ускорения точки вращающегося тела в месте контакта. Было бы ошибкой считать 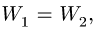 так как полное ускорение точки на вращающемся теле включает в себя и нормальную составляющую
так как полное ускорение точки на вращающемся теле включает в себя и нормальную составляющую 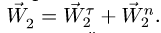 Решаем систему уравнений для ускорений.
Решаем систему уравнений для ускорений.
Задача №6
Механизм состоит из двух колес 1, 3 и блока 2, вращающихся на неподвижных осях. Ведущее колесо 1 механизма соединено ремнем с внутренним ободом блока 2. Внешний обод блока находится во фрикционном зацеплении с колесом 3 (рис. 84). Проскальзывание в точке зацепления отсутствует, ремень считать нерастяжимым.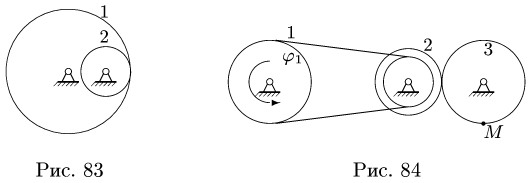
Задан закон движения ведущего колеса: 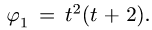 Стрелкой указано положительное направление изменения угла
Стрелкой указано положительное направление изменения угла 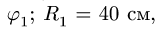
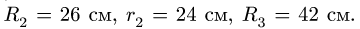 При t = 0.5 с найти ускорение точки М, лежащей на ободе колеса 3.
При t = 0.5 с найти ускорение точки М, лежащей на ободе колеса 3.
Решение
1. Находим угловую скорость ведущего колеса 1:
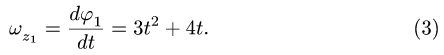
7.2.Передача вращения
2. Определяем угловую скорость блока 2, связанного нерастяжимым ремнем с колесом 1:

где 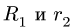 — радиусы ободов, огибаемые ремнем.
— радиусы ободов, огибаемые ремнем.
3. Колеса 2 и 3 находятся во внешнем зацеплении и вращаются в разные стороны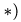 , следовательно
, следовательно

Уравнения (3-5) образуют систему, решая которую, при t = 0.5 с, получаем
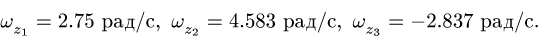
4. Дифференцируя уравнения системы (3-5), получаем аналогичную систему для угловых ускорений:
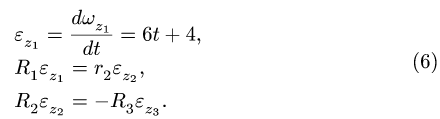
Решаем систему уравнений для ускорений (6) и получаем
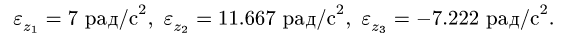
Вычисляем ускорение точки М:
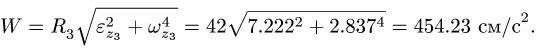
Ответ. 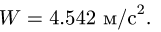
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |