
Задачи на поступательное движение тела в теоретической механике
Задачи на поступательное движение тела:
Если точка массой m, находясь под действием постоянной силы Р в течение t сек, двигается прямолинейно, то теорема об изменении количества движения выражается формулой
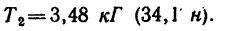
где разность 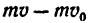
В СИ количество движения и импульс силы измеряются в ньютон-секундах (н-сек); в системе МКГСС— соответственно в килограмм-секундах в (кГ сек).
Если, рассматривая действие силы Р на материальную точку массой т, учитывать не продолжительность ее действия, а протяженность, т. е. то расстояние, на котором действует сила, то получим теорему об изменении кинетической энергии точки:

где А — работа всех сил, приложенных к точке, а 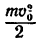 и
и
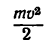 кинетическая энергия точки соответственно в начале и
кинетическая энергия точки соответственно в начале и
конце действия сил.
Кинетическая энергия измеряется единицами работы, т. е. в СИ — в джоулях (дж), в системе МКГСС—в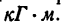
Необходимость введения двух динамических характеристик объясняется тем, что одна характеристика не отражает все особенности движения точки. Например, зная количество движения автомобиля (т. е. величину 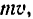 а не величины
а не величины 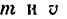 отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормозной путь, но по этим данным нельзя найти время торможения.
отдельности) и действующую на него при торможении силу, можно определить, через сколько секунд автомобиль остановится, но по этим данным нельзя найти пройденный за время торможения путь. Наоборот, зная начальную кинетическую энергию автомобиля и тормозящую силу, можно определить тормозной путь, но по этим данным нельзя найти время торможения.
Если же в задаче заданы и масса точки, и ее скорость, то в принципе можно использовать для решения любую из теорем, но при этом необходимо иметь в виду, что для определения времени движения целесообразно использовать теорему об изменении количества движения, а для определения пройденного пути — теорему об изменении кинетической энергии.
Уравнения (1) и (2) применимы также и при рассмотрении поступательно движущихся тел. В этом случае любое твердое тело отождествляется с материальной точкой, имеющей массу всего тела и расположенной в его центре массы или в точке, совпадающей с центром тяжести тела.
Задача №1
Машинист тепловоза отключает двигатель и начинает тормозить в момент, когда тепловоз имеет скорость 90 км/ч. Через сколько времени и пройдя какой путь тепловоз остановится, если сила торможения постоянна н составляет 0,12 его веса, а движение происходит по горизонтальному и прямолинейному участку дороги?
Решение.
1. Тепловоз движется поступательно, поэтому рассмотрим движение его центра тяжести С (центра массы), считая, что к нему приложены все внешние силы (рис. 262).
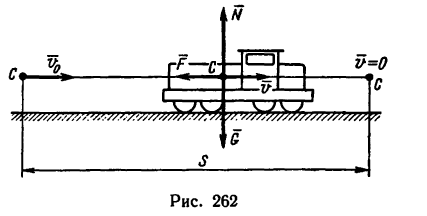
2. После того как отключается двигатель и включается тормозное устройство, на тепловоз действуют три силы: сила тяжести G, нормальная реакция рельсов Лг и сила торможения F. В начале торможения скорость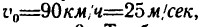 в конце
в конце 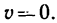 Требуется определить путь s и время t, за которое этот путь пройден (см. рис. 262).
Требуется определить путь s и время t, за которое этот путь пройден (см. рис. 262).
3. Для определения времени торможения применим теорему об изменении количества движения.
Спроектировав векторы на горизонтальную ось
(ось х), увидим, что проекции сил G и N равны нулю, а проекция силы F получается равной ее модулю, но со знаком минус; проекция скорости 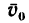 также равна ее модулю, поэтому уравнение (1) в данном случае примет вид
также равна ее модулю, поэтому уравнение (1) в данном случае примет вид
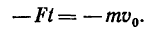
4. Решаем это уравнение относительно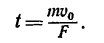
Так как сила торможения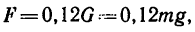 то окончательно
то окончательно
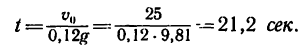
5. Для определения тормозного пути s применим теорему об изменении кинетической энергии. В данном случае 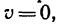 А =
А =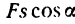 (угол а между направлением силы F и направлением перемещения равен 180° и, следовательно, cos 0 = cos 180° = — 1, а работы сил G и N равны нулю (эти силы действуют перпендикулярно к направлению перемещения) поэтому уравнение (2) принимает вид
(угол а между направлением силы F и направлением перемещения равен 180° и, следовательно, cos 0 = cos 180° = — 1, а работы сил G и N равны нулю (эти силы действуют перпендикулярно к направлению перемещения) поэтому уравнение (2) принимает вид
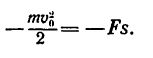
6. Решаем это уравнение относительно s:
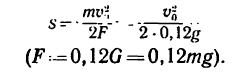
После подстановки в эту формулу числовых значений
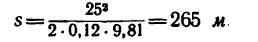
Таким образом, тепловоз остановится через 21,2 сек, пройдя 265 м.
Задача №2
Каков коэффициент трения колес заторможенного автомобиля о дорогу (считать, что заторможены все четыре колеса), если в момент выключения двигателя и нажатия тормоза скорость движения автомобиля 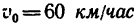 и автомобиль останавливается через 5 сек после начала торможения.
и автомобиль останавливается через 5 сек после начала торможения.
Решение.
1. В задаче известно время движения заторможенного автомобиля, т. е. имеется в виду импульс силы, поэтому для ее решения применим формулу (1)—закон количества движения.
2. На заторможенный автомобиль действуют девять сил (рис. 263, а): С —вес автомобиля, четыре реакции поверхности дороги, приложенные к каждому колесу, и четыре силы трения, также приложенные к колесам.
Принимая автомобиль за материальную точку, считаем, что все эти силы приложены в центре тяжести автомобиля, и тогда, заменив четыре реакции поверхности их суммой R и четыре силы трения их суммой F, получим только три силы G, N и F(pnc. 263, б).
3. Силы G и N численно равны друг другу и взаимно уравновешиваются. Следовательно, импульс создается силой трения F.
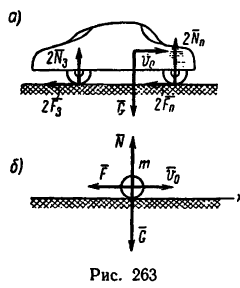
4. Импульс силы трения в данном случае действует в сторону, противоположную движению, поэтому уравнение (1) для данной задачи примет вид
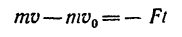
Но автомобиль через t = 5 сек останавливается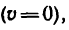 , поэтому
, поэтому
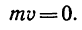
Следовательно,
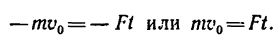
5. Подставим сюда значения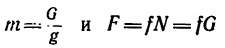 (так как N = G):
(так как N = G):
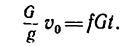
Откуда, имея в виду, что 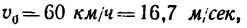
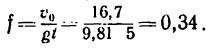
Эту задачу можно решить, используя теорему об изменении кинетической энергии. Рекомендуем этот вариант решения выполнить самостоятельно.
Задача №3
За 500 м до станции, стоящей на пригорке высотой 2 м, машинист поезда, идущего со скоростью 12 м/сек, закрывает пар и начинает тормозить Как велико должно быть сопротивление от торможения, считаемое постоянным, чтобы поезд остановился у станции, если масса поезда равна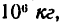 сопротивление трения 2000
сопротивление трения 2000 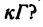
Решение.
1. Решаем задачу, используя теорему об изменении кинетической энергии, так как в условии задачи задано уже не время торможения, а тормозной путь s = 500 м.
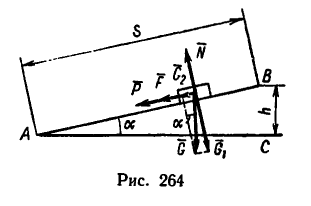
2. Поезд двигается поступательно, поэтому достаточно рассмотреть движение его центра тяжecYи О. Приложим к точке О все действующие силы (рис. 264). Вес поезда G разлагаем на две составляющие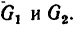
На поезд в сторону, противоположную его движению, действуют три силы: составляющая веса 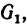 сила трения F и искомая сила торможения Р.
сила трения F и искомая сила торможения Р.
3. Равнодействующая этих сил, равная их сумме 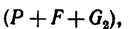 действуя на расстоянии s, производит работу
действуя на расстоянии s, производит работу 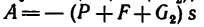 (работа сил сопротивления отрицательна).
(работа сил сопротивления отрицательна).
4. Работа А равна изменению кинетической энергии поезда [уравнение (2)]:
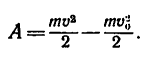
Но так как конечная скорость поезда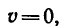 то
то
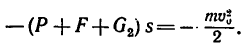
Из последнего уравнения можно найти силу торможения Р:
5. Но предварительно нужно определить составляющую веса 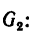
А так как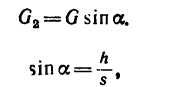
то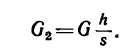
Затем вычисляем величину силы Р в системе МКГСС, учитывая, что
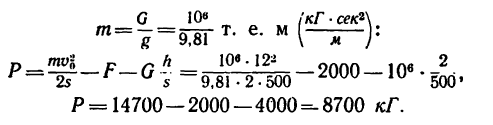
6. Если решить задачу в единицах СИ, то все предварительные рассуждения не изменятся, но в окончательную расчетную формулу
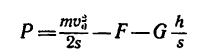
нужно подставить числовое значение силы F в ньютонах (F = = 2000 кГ = 19600 я), а вес G выразить через массу (G—mg):
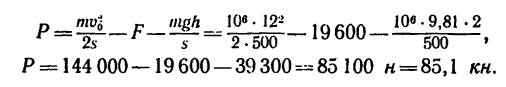
Легко заметить, что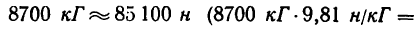
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |