Задачи на построение циркулем и линейкой с примерами решения

Содержание:

Основные задачи на построение циркулем и линейкой:

В данном параграфе рассмотрим вопрос о построении геометрических фигур. Вы уже знаете, что геометрические построения можно осуществлять с помощью масштабной линейки, циркуля, транспортира и чертежного угольника. В то же время оказывается, что многие геометрические фигуры можно построить, пользуясь только циркулем и линейкой без масштабных делений.

При построении геометрических фигур с помощью циркуля и линейки без масштабных делений учитывается, что:

1. с помощью линейки можно провести произвольную прямую, а также построить прямую, проходящую через две точки;
2. с помощью циркуля можно провести окружность произвольного радиуса, а также построить окружность с центром в данной точке и радиусом, равным данному отрезку.

Теперь рассмотрим основные задачи на построение циркулем и линейкой: построение угла, равного данному, построение серединного перпендикуляра к отрезку, построение биссектрисы угла.

Задача 1 (построение угла, равного данному)

От данного луча OF отложите угол, равный данному углу ABC.

Поиск решения.

Предположим, что угол DOF, удовлетворяющий условию задачи, построен (рис. 130, а).

Пусть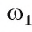

Построение.

1) Строим окружность 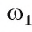(В, R) , где R — произвольный радиус, и отмечаем точки А₁ и С₁ пересечения ее со сторонами угла ABC.

2) Строим окружность 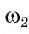(0, R) с центром в точке О того же радиуса R и отмечаем ее точку пересечения F₁ с лучом OF.

3) Строим окружность (F₁, A₁C₁).

4) Пусть D₁ — одна из точек пересечения окружностей (0, R) и (F₁, A₁C₁) (рис. 130, б). Тогда угол D₁OF — искомый. Докажем, что D₁OF =ABC.

Доказательство.

Равенство D₁OF =ABC следует из равенства треугольников А₁ВС₁ и D₁OF₁. Действительно, по построению А₁В = D₁O = С₁В = F₁O. Кроме того, по построению F₁D₁ = А₁С₁, следовательно, треугольники А₁ВС₁ и D₁OF₁  равны по трем сторонам. Отсюда следует, что D₁OF =А₁ВС₁, т. е. построенный угол D₁OF  равен данному углу ABC.

Задача 2 (построение серединного перпендикуляра к отрезку)

Постройте серединный перпендикуляр к данному отрезку АВ.

Поиск решения.

Проведем рассуждения, которые помогут осуществить необходимое построение. Предположим, что серединный перпендикуляр а к отрезку АВ построен (рис. 131, а). Пусть точки F и D лежат на серединном перпендикуляре так, что OF = OD. Прямоугольные треугольники FOB и DOB равны по двум катетам, следовательно, BF = BD. Иначе говоря, точки F и D лежат на окружности (B, BF) и BF > ОВ. Аналогично AF =AD, так как треугольник FOA равен треугольнику DOA. Кроме того, легко увидеть, что AF = BF. Таким образом, точки F и D лежат также и на окружности (A, BF).

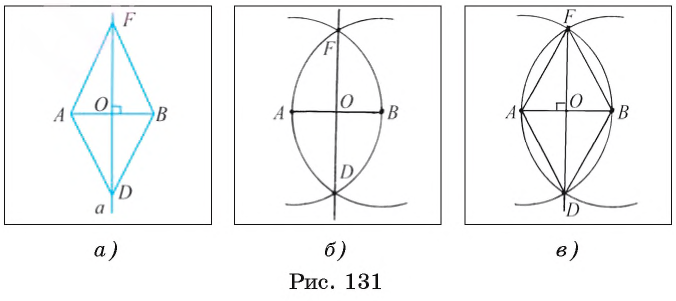
Построение.

1) Строим окружности (A, R) и (B, R) , где R 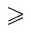AВ. Пусть, например, R = AB: (A, AB) и (B, AB) (рис. 131, б).

2) Отмечаем точки F и D пересечения окружностей (A, AB) и (B, AB).

3) Тогда прямая FD — серединный перпендикуляр к отрезку АВ. Докажем это.

Доказательство.

Рассмотрим треугольники FAD и FBD (рис. 131, в). Указанные треугольники равны по трем сторонам. Следовательно, AFD = BFD. Отсюда следует, что в равнобедренном треугольнике AFD отрезок FO является биссектрисой, а значит, и высотой и медианой, т. е. прямая FO — серединный перпендикуляр к отрезку АВ.

Задача 3 (построение биссектрисы угла)

Постройте биссектрису данного угла ABC.

Поиск решения.

Допустим, что биссектриса BE данного угла ABC построена (рис. 132, а). Пусть точки F и D лежат на сторонах угла так, что BF = BD, О = FD BE, а точка Т лежит на луче, противоположном лучу ОВ. Из равенства прямоугольных треугольников FOT и DOT (FO = OD, катет ОТ — общий) следует, что FT = DT, т. е. точка Т принадлежит окружностям равных радиусов с центрами в точках F и D. Построив точку Т, мы построим биссектрису ВТ данного угла.

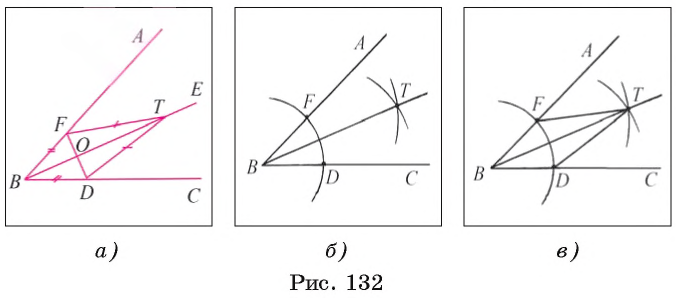
Построение.

1) Строим окружность (B, R₁) произвольного радиуса R₁  с центром в вершине В данного угла (рис. 132, б).

2) Отмечаем точки F и D, в которых окружность (B, R) пересекает соответственно стороны ВА и ВС данного угла.

3) Строим окружности (F, R₂) и (D, R₂), где R2 > FD. Отмечаем точку Т их пересечения, которая лежит внутри данного угла.

4) Проводим луч ВТ. Луч ВТ — искомый. Докажем это.

Доказательство.

Рассмотрим треугольники BFT и BDT (рис. 132, в). Эти треугольники равны по трем сторонам (BF = BD и FT = DT — по построению, ВТ — общая сторона). Из равенства этих треугольников следует, что FBT = DBT, т. е. луч ВТ — биссектриса угла ABC.

Построение треугольника по трем элементам

В данном пункте рассмотрим задачи на построение треугольника по: а) двум сторонам, и углу между ними; б) стороне и двум прилежащим к ней углам; в) трем сторонам.

Задача 4 (построение треугольника по двум сторонам и углу между ними)

Постройте треугольник, две стороны которого равны двум данным отрезкам а и b, а угол между этими сторонами равен данному углу hk.

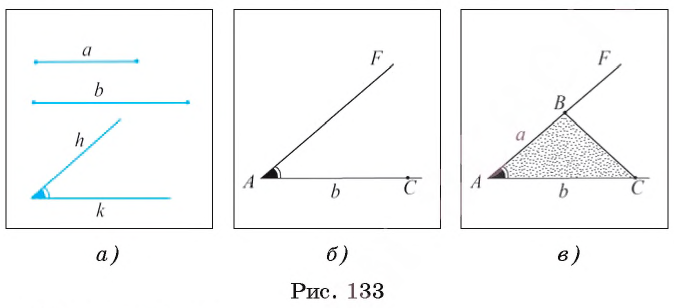
Даны два отрезка а, b и угол hk (рис. 133, а). Требуется с помощью циркуля и линейки построить треугольник ABC, две стороны которого, например, АВ и АС, равны соответственно отрезкам а и b, а угол ВАС равен углу hk.

Построение.

1) Проведем прямую, на ней отложим отрезок АС, равный отрезку b (рис. 133, б).

2) Строим угол CAF, равный углу hk.

3) На луче AF отложим отрезок АВ, равный отрезку а, и проведем отрезок ВС. Треугольник ABC — искомый (рис. 133, в).

Доказательство.

По построению имеем, что АС = b, АВ = а и BAC = hk.

Исследование.

При любых данных отрезках а и b и неразвернутом угле hk каждое из построений 1) — 3) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по двум сторонам и углу между ними, поэтому говорят, что данная за дача имеет единственное решение.

Задача 5 (построение треугольника по стороне и двум прилежащим к ней углам)

Постройте треугольник, сторона которого равна данному отрезку а, а углы, прилежащие к этой стороне, равны данным углам hk и mq.

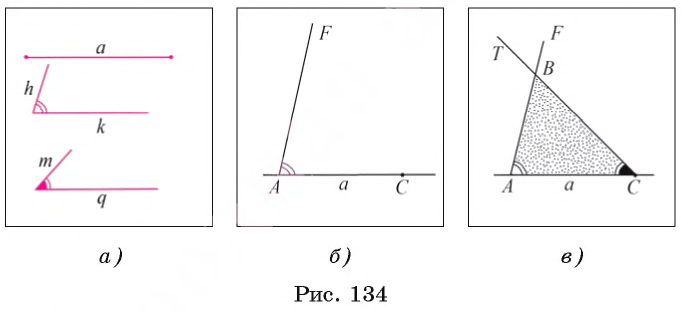
Дан отрезок а и два угла hk и mq (рис. 134, а). Требуется с помощью циркуля и линейки построить треугольник ABC, сторона которого, например АС, равна отрезку а, а углы ВАС и ВСА равны соответственно углам hk и mq.

Построение.

1) Проведем прямую и на ней отложим с помощью циркуля отрезок АС, равный отрезку а (рис. 134, б).

2) Строим угол CAF, равный углу hk.

3) Строим угол ACT, равный углу mq.

4) Отмечаем точку В пересечения лучей AF и СТ. Треугольник ABC — искомый (рис. 134, в).

Доказательство.

По построению имеем, что АС = a, BAC = hk и ACB = mq.

Исследование.

Для любого данного отрезка а и неразвернутых углов hk и mq каждое из построений 1) — 4) выполнимо, т. е. искомый треугольник можно построить. Треугольники, которые удовлетворяют условию задачи и строятся при различном выборе прямой и отрезка АС, равны между собой по стороне и двум прилежащим к ней углам, поэтому говорят, что данная задача имеет единственное решение.

Задача 6 (построение треугольника по трем сторонам)

Постройте треугольник, стороны которого равны данным отрезкам а, b, с.

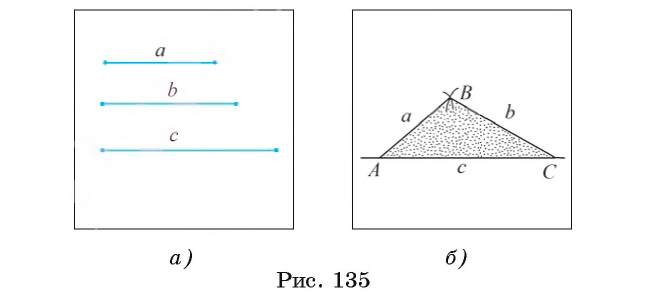
Даны отрезки а, b, с (рис. 135, а). Требуется с помощью циркуля и линейки построить треугольник ABC, стороны которого АВ, ВС и АС равны соответственно отрезкам a, b и с.

Построение.

1) Проведем прямую и на ней с помощью циркуля отложим отрезок АС, равный отрезку с (рис. 135, б).

2) Строим окружность (A, a).

3) Строим окружность (C, b).

4) Пусть В — одна из точек пересечения окружностей (A, a) и (C, b). Тогда треугольник ABC — искомый.

Доказательство.

По построению АС = с, АВ = а, ВС = b.

Исследование.

Данная задача не всегда имеет решение. Известно, что в любом треугольнике длина каждой стороны меньше суммы длин двух других его сторон. Таким образом, если длина какого-либо из данных отрезков больше суммы длин двух других, то нельзя построить треугольник, стороны которого равны данным отрезкам.