
Задачи на построение по геометрии с примерами решения
Содержание:
Ранее мы выполняли построения на плоскости при помощи линейки с делениями, чертежного треугольника, транспортира и циркуля.
Математиков всегда интересовали построения геометрических фигур, которые можно выполнить только при помощи циркуля и линейки. В геометрии специально выделяют задачи на построение, которые могут быть решены с помощью этих двух инструментов.
Например, при помощи циркуля и линейки можно построить треугольник, стороны которого равны трем данным отрезкам. Или построить угол, равный данному углу.
Рассмотрим одну из таких задач на построение. На прямой 
Найти точку — это значит построить ее при помощи циркуля и линейки. Если перемещать некоторую точку по прямой  (положения К1 К2, К3), то расстояния от этой точки до точек А и В будут меняться. Когда эти расстояния станут равными, точка на прямой будет равноудалена от концов отрезка АВ. Значит, она будет лежать на серединном перпендикуляре к отрезку АВ. Это и есть идея построения: нужно построить серединный перпендикуляр к отрезку АВ и найти точку его пересечения с прямой
(положения К1 К2, К3), то расстояния от этой точки до точек А и В будут меняться. Когда эти расстояния станут равными, точка на прямой будет равноудалена от концов отрезка АВ. Значит, она будет лежать на серединном перпендикуляре к отрезку АВ. Это и есть идея построения: нужно построить серединный перпендикуляр к отрезку АВ и найти точку его пересечения с прямой  .
.
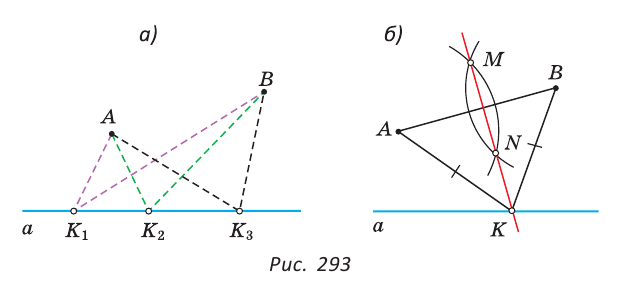
Чтобы построить серединный перпендикуляр, нужно построить две пересекающиеся окружности равных радиусов с центрами в точках А к В (рис. 293, б). Затем провести прямую MN через точки пересечения этих окружностей (ниже мы обоснуем это построение). В пересечении серединного перпендикуляра MN к отрезку АВ и прямой 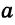 получим искомую точку К.
получим искомую точку К.
Рассмотренная задача может иметь и практический смысл. Допустим, есть два населенных пункта и шоссе рядом с ними. На шоссе нужно найти место для остановки, чтобы путь для жителей обоих населенных пунктов до остановки был одинаковым. Все построения будут сделаны на карте населенного пункта.
При решении задач на построение линейка считается односторонней и без делений. При помощи такой линейки нельзя построить две параллельные прямые, проведя линии по краям линейки, нельзя измерять и откладывать отрезки, нельзя строить перпендикуляры, используя прямоугольную форму линейки. Рассмотрим, какие операции можно выполнять линейкой, а какие циркулем.
Операции с линейкой
При помощи линейки можно провести (построить):
а) произвольную прямую;
б) прямую, проходящую через две точки (рис. 294).
Операции с циркулем
При помощи циркуля можно:
а) построить произвольную окружность и окружность (дугу окружности) с данным центром и радиусом, равным данному отрезку (рис. 295);
б) отложить отрезок, равный данному отрезку, на некоторой прямой.

Откладывание отрезка
Для откладывания отрезка, равного данному отрезку 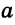 (рис. 296, а) на прямой
(рис. 296, а) на прямой 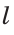 (рис. 296, б), следует: 1) отметить на прямой
(рис. 296, б), следует: 1) отметить на прямой 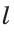 точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой
точку М; 2) радиусом, равным а, провести дугу окружности с центром в точке М (сделать засечку на прямой 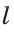 ).
).
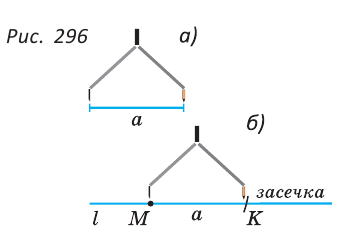
В пересечении дуги и прямой  получим точку К и отрезок МК, равный
получим точку К и отрезок МК, равный  .
.
Операция откладывания отрезка на прямой позволяет построить сумму и разность двух отрезков (рис. 297): в первом случае на произвольной прямой откладывают последовательно два отрезка, во втором — на большем отрезке от любого его конца откладывают меньший отрезок.
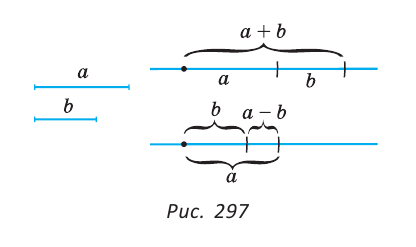
В дальнейшем при решении задач на построение мы не будем описывать процедуру откладывания отрезка на прямой, считая ее элементарной операцией.
Перечислим 5 основных задач на построение, к которым сводятся другие задачи. Решая сложные задачи, будем ссылаться на эти основные, не описывая ту часть решения, которая связана с одной из основных задач.
- Задача I. Построение треугольника по трем сторонам.
- Задача II. Построение угла, равного данному.
- Задача III. Построение биссектрисы угла.
- Задача IV. Построение середины отрезка.
- Задача V. Построение прямой, перпендикулярной данной.
В некотором смысле «линейка» и «циркуль» — это два идеальных робота, которые могут выполнять определенный набор операций. И наша задача — составить алгоритм из последовательности таких операций — команд для этих роботов, который приведет к построению необходимой фигуры. Фактически нужно написать программу для «циркуля» и «линейки».
Замечание. В треугольнике ABC стороны, противолежащие углам А, В и С, будем соответственно обозначать 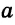 ,
, 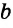 и
и 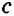 , а сами эти углы —
, а сами эти углы — 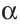 ,
, 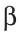 и
и 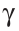 (рис. 298). Медианы, проведенные к сторонам
(рис. 298). Медианы, проведенные к сторонам 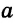 ,
, 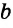 и
и 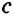 , —
, — 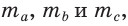 высоты —
высоты — 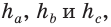 биссектрисы —
биссектрисы — 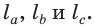
Построение треугольника по трем сторонам. Построение угла, равного данному
Задача №1
Построить треугольник со сторонами  ,
,  и
и  .
.
Решение:
Пусть даны отрезки  ,
,  и
и  . На произвольной прямой откладываем отрезок АВ =
. На произвольной прямой откладываем отрезок АВ =  (рис.300).
(рис.300).
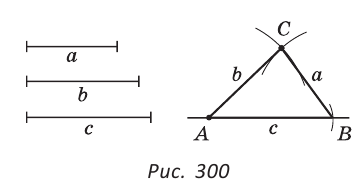
Строим окружность с центром в точке А радиусом  . Строим окружность с центром в точке В радиусом
. Строим окружность с центром в точке В радиусом  . Находим точку С пересечения этих окружностей. Проведем отрезки АС и ВС.
. Находим точку С пересечения этих окружностей. Проведем отрезки АС и ВС.
Треугольник ABC — искомый, так как у него ВС =  , АС =
, АС =  , АВ =
, АВ =  по построению.
по построению.
Задача имеет решение, если для данных отрезков  ,
,  и
и  выполняется неравенство треугольника:
выполняется неравенство треугольника:  <
<  +
+  ,
,  <
<  +
+  ,
,  <
<  +
+  . Если решение существует, то оно единственное, так как все построенные треугольники будут равны по 3-му признаку равенства треугольников.
. Если решение существует, то оно единственное, так как все построенные треугольники будут равны по 3-му признаку равенства треугольников.
Следствие.
Если для чисел  ,
,  и
и  выполняется неравенство треугольника, то существует, и причем единственный, треугольник со сторонами, равными
выполняется неравенство треугольника, то существует, и причем единственный, треугольник со сторонами, равными  ,
,  и
и  .
.
Замечание. При решении задач на построение под числом решений понимается число фигур разной формы, удовлетворяющих условию. В данном случае решение одно.
Задача №2
Построить угол, равный
Решение:
Пусть дан угол А (рис. 301, а).
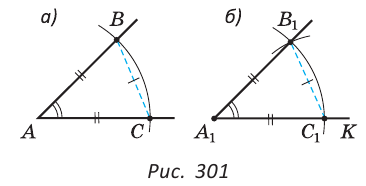
Нужно построить угол А1, равный углу А. Идея решения состоит в том, чтобы построить некоторый треугольник ABC с углом А и равный ему треугольник A1B1C1.
Строим произвольный луч А1К (рис. 301, б). Произвольным, но одним и тем же радиусом строим дуги с центрами в точках А и А1. Получаем АВ =АС =А1С1. Строим дугу окружности с центром в точке C1 радиусом, равным СВ, до пересечения ее с уже построенной дугой в точке В1. Строим луч А1В1. Угол A1 — искомый. Действительно, так как  АВС и
АВС и  А1В1С1 равны по трем сторонам (АВ = А1В1, АС=А1С1, ВС = В1С1 по построению), то
А1В1С1 равны по трем сторонам (АВ = А1В1, АС=А1С1, ВС = В1С1 по построению), то 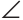 A1 =
A1 =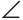 A как соответствующие в двух равных треугольниках.
A как соответствующие в двух равных треугольниках.
Замечания. Построение угла, равного данному, дает возможность строить сумму и разность двух углов.
Задача №3
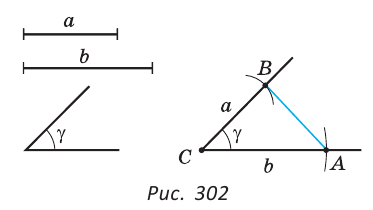
Построить треугольник по двум сторонам и углу между ними.
Решение:
Пусть даны отрезки 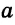 и
и 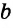 и угол
и угол 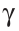 (рис. 302).
(рис. 302).
Нужно построить треугольник со сторонами 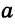 и
и 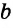 и углом
и углом 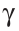 между ними. Вначале строим угол С, равный данному углу
между ними. Вначале строим угол С, равный данному углу 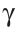 (основная задача). На сторонах угла С откладываем отрезки СВ =
(основная задача). На сторонах угла С откладываем отрезки СВ = 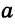 и СА =
и СА = 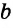 и проводим отрезок АВ. Треугольник ABC — искомый, так как удовлетворяет условию задачи: СВ =
и проводим отрезок АВ. Треугольник ABC — искомый, так как удовлетворяет условию задачи: СВ = 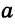 , CA =
, CA = 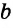 ,
,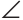 C =
C = 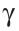 по построению.
по построению.
Заметим, что решение существует, если 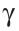 < 180°, и оно единственное, так как все построенные треугольники будут равны по 1-му признаку равенства треугольников.
< 180°, и оно единственное, так как все построенные треугольники будут равны по 1-му признаку равенства треугольников.
Задача №4
Построить треугольник по стороне и двум прилежащим к ней углам.
Решение:
Пусть дана сторона 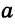 и углы
и углы 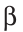 и
и 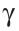 (рис. 303).
(рис. 303).
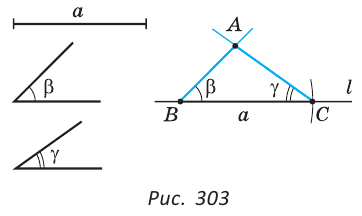
Нужно построить треугольник со стороной 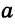 и прилежащими к ней углами
и прилежащими к ней углами 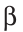 и
и 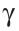 .
.
На произвольной прямой 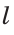 откладываем отрезок ВС =
откладываем отрезок ВС = 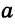 .
.
От лучей ВС и СВ в одну полуплоскость откладываем углы, равные углу 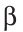 и углу
и углу 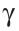 (основная задача). Отмечаем точку А, в которой пересекаются стороны углов В и С. Треугольник ABC — искомый.
(основная задача). Отмечаем точку А, в которой пересекаются стороны углов В и С. Треугольник ABC — искомый.
Решение существует, если 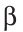 +
+ 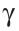 < 180°, и оно единственное, так как все построенные треугольники будут равны по 2-му признаку равенства треугольников.
< 180°, и оно единственное, так как все построенные треугольники будут равны по 2-му признаку равенства треугольников.
Построение биссектрисы угла. Построение середины отрезка
Задача:
Построить биссектрису данного угла.
Решение:
Пусть дан угол А (рис. 305).
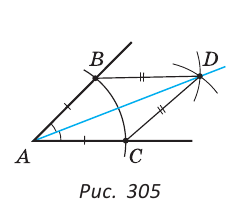
Нужно построить его биссектрису. Произвольным радиусом строим дугу окружности с центром в точке А, которая пересекает стороны угла А в точках В и С. Далее одинаковым радиусом строим две дуги с центрами в точках В и С до их пересечения в точке D. Строим луч AD, который является искомой биссектрисой. Доказательство следует из того, что  ABD =
ABD = ACD по трем сторонам (АВ = АС, BD = CD как радиусы, сторона AD — общая), откуда
ACD по трем сторонам (АВ = АС, BD = CD как радиусы, сторона AD — общая), откуда 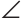 BAD =
BAD =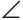 CAD.
CAD.
Задача №5
Построить середину отрезка (разделить данный отрезок пополам).
Решение:
Пусть АВ — данный отрезок. Произвольным, но одним и тем же радиусом (большим половины отрезка АВ) проводим две дуги с центрами в точках А и В до их пересечения в точках С и D (рис. 306).
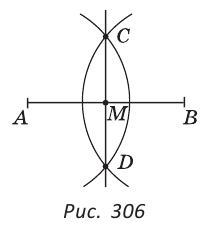
Через точки С и D проводим прямую. В пересечении прямых CD и АВ получаем точку М — середину отрезка АВ. Докажем это. Так как точки С и D равноудалены от концов отрезка АВ (СА = СВ = DA = DB как радиусы), то они лежат на серединном перпендикуляре к этому отрезку. Поскольку две точки задают единственную прямую, то CD — серединный перпендикуляр к отрезку АВ.
Следовательно, AM = MB.
Замечание. Указанный способ построения середины отрезка также является и способом построения серединного перпендикуляра к отрезку.
Задача №6
Построить треугольник по стороне 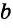 , прилежащему углу
, прилежащему углу 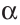 и биссектрисе
и биссектрисе 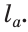
Решение:
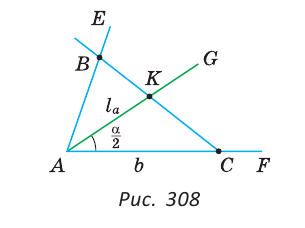
Предположим, что задача решена, и сделаем чертеж искомого треугольника АВС (рис. 307).
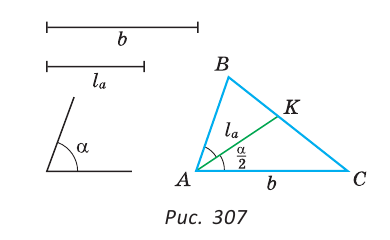
Пусть AC = 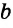 ,
, 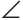 A =
A = 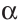 , биссектриса АК =
, биссектриса АК = 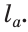 Так как АК — биссектриса, то
Так как АК — биссектриса, то 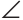 KAC =
KAC = 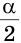 . Треугольник АКС можно построить по двум сторонам и углу между ними:
. Треугольник АКС можно построить по двум сторонам и углу между ними:
AC = 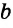 , AK =
, AK = 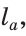
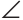 KAC=
KAC=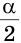 . Далее треугольник АКС легко достроить до искомого треугольника ABC. Опишем построение (рис. 308).
. Далее треугольник АКС легко достроить до искомого треугольника ABC. Опишем построение (рис. 308).
1) Строим 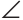 EAF =
EAF = 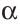 (основная задача).
(основная задача).
2) Строим биссектрису AG угла EAF (основная задача). Получаем 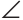 GAF =
GAF =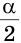
3) Строим треугольник АКС по двум сторонам и углу между ними: на луче AF откладываем отрезок AC = 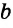 , на луче AG — отрезок АК =
, на луче AG — отрезок АК = 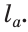
4) Находим точку В пересечения луча СК и луча АЕ. Треугольник ABC — искомый.
Задача №7
Построить центр данной окружности.
Решение:
Мы знаем, что серединный перпендикуляр к хорде проходит через центр окружности. Серединные перпендикуляры к двум хордам окружности будут пересекаться в ее центре. Отсюда построение.
Строим хорду АВ (рис. 309) и к ней серединный перпендикуляр МК (основная задача).
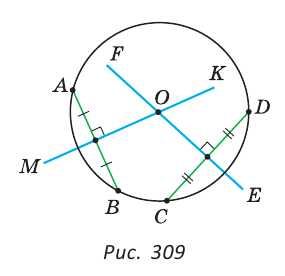
Строим хорду CD (не параллельную АВ) и к ней серединный перпендикуляр EF. Точка О пересечения прямых МК и EF — центр окружности.
Замечание. Вторым способом решения будет построение одного серединного перпендикуляра МК к хорде АВ, нахождение точек Т и Р пересечения МК с окружностью и построение середины О диаметра ТР.
Построение прямой, перпендикулярной данной
Задача:
Построить прямую, перпендикулярную прямой 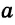 и проходящую через данную точку А.
и проходящую через данную точку А.
Решение:
Алгоритм построения одинаков для случая, когда точка А не принадлежит прямой 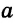 (рис. 310, а) и когда точка А принадлежит прямой
(рис. 310, а) и когда точка А принадлежит прямой 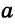 (рис. 310, б).
(рис. 310, б).
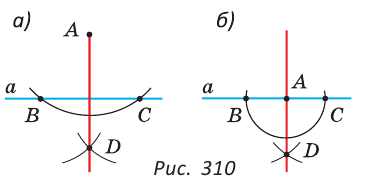
Построение.
Проводим дугу с центром в точке А, которая пересекает прямую 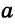 в точках В и С. Из точек В и С как из центров одним и тем же радиусом проводим дуги до пересечения их в точке D. Строим прямую AD. Получаем AD
в точках В и С. Из точек В и С как из центров одним и тем же радиусом проводим дуги до пересечения их в точке D. Строим прямую AD. Получаем AD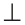
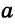 .
.
Доказательство:
Так как точки А и D равноудалены от концов отрезка ВС (АВ=АС, BD = CD как радиусы), то AD — серединный перпендикуляр к отрезку ВС.
Следовательно, AD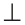
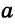 .
.
Этапы решения задачи на построение
При решении задачи на построение выделяют 4 этапа.
1. Анализ.
На этом этапе предполагают, что задача решена, делают чертеж с изображением искомой фигуры и указывают идею решения задачи.
2. Построение.
На этом этапе дают описание последовательности шагов, приводящих к построению искомой фигуры, то есть алгоритм построения. Иногда на этом этапе проводят и сами операции построения на произвольно взятых отрезках, углах и других фигурах. В сложных задачах обычно указывают лишь шаги построения, ссылаясь на основные и ключевые задачи.
3. Доказательство.
На этом этапе доказывают, что построенная фигура удовлетворяет требованию задачи. Иногда это следует непосредственно из построения.
4. Исследование.
На данном этапе определяют, при какой величине заданных в условии отрезков и углов существует решение и число решений.
При записи решения задачи на построение этапы анализа и исследования в школе необязательны, если в условии задачи нет специальных указаний.
Задача №8
Построить прямоугольный треугольник по катету и прилежащему острому углу.
Решение:
Пусть дан катет 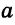 и прилежащий к нему острый угол
и прилежащий к нему острый угол 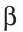 . Нужно построить прямоугольный треугольник с катетом
. Нужно построить прямоугольный треугольник с катетом 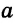 и углом (рис. 311).
и углом (рис. 311).
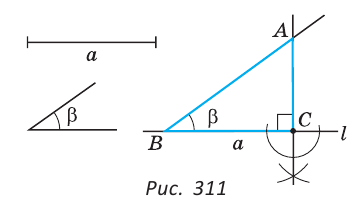
Построение.
1) Строим прямой угол. Для этого проводим произвольную прямую 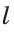 и строим перпендикулярную ей прямую, проходящую через произвольно взятую на прямой
и строим перпендикулярную ей прямую, проходящую через произвольно взятую на прямой 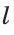 точку С (основная задача). Получаем прямой угол С.
точку С (основная задача). Получаем прямой угол С.
2) На одной стороне прямого угла С от его вершины откладываем отрезок СВ = 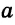 .
.
3) Строим 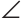 B =
B = 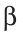 (основная задача).
(основная задача).
4) В пересечении стороны угла В со стороной прямого угла получим точку А.
Доказательство:
Треугольник АВС — искомый, так как по построению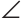 C=90°, ВС=
C=90°, ВС=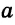 — катет,
— катет,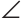 B=
B=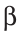 — прилежащий острый угол.
— прилежащий острый угол.
Замечание. Мы не описываем построение прямой, перпендикулярной данной, и построение угла, равного данному, так как это основные задачи. На рисунке 311 построение прямого угла С показано для наглядности.
Задача №9
Построить прямую, параллельную данной прямой, если расстояние между этими прямыми равно заданному отрезку.
Решение:
Пусть дана прямая 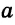 и отрезок
и отрезок 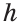 , равный расстоянию между параллельными прямыми
, равный расстоянию между параллельными прямыми  и
и  (рис. 312).
(рис. 312).
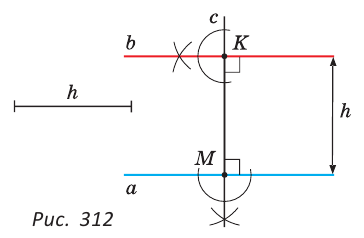
Нужно построить прямую  , параллельную прямой
, параллельную прямой 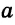 и находящуюся от прямой
и находящуюся от прямой 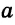 на расстоянии
на расстоянии 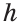 . Воспользуемся теоремой о том, что на плоскости две прямые, перпендикулярные третьей, параллельны между собой.
. Воспользуемся теоремой о том, что на плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Построение.
1) Отмечаем на прямой 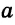 точку М и строим прямую с, перпендикулярную прямой
точку М и строим прямую с, перпендикулярную прямой 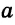 и проходящую через точку М (основная задача).
и проходящую через точку М (основная задача).
2) Откладываем на прямой 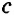 перпендикуляр MK =
перпендикуляр MK = 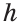 .
.
3) Строим прямую 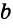 , перпендикулярную прямой
, перпендикулярную прямой 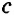 и проходящую через точку К (основная задача). Получаем
и проходящую через точку К (основная задача). Получаем 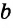 ||
|| 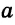 .
.
Доказательство:
Так как 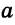
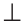
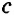 ,
, 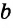
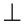
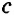 и на плоскости две прямые, перпендикулярные третьей, параллельны между собой, то
и на плоскости две прямые, перпендикулярные третьей, параллельны между собой, то 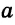 ||
|| 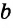 . Расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из любой точки одной из прямых на другую прямую: KM
. Расстояние между параллельными прямыми равно длине перпендикуляра, опущенного из любой точки одной из прямых на другую прямую: KM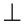 a, KM=
a, KM=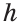 .
.
Задача №10
Построить треугольник по основанию 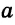 , высоте
, высоте 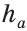 и медиане
и медиане 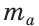 , проведенным к этому основанию.
, проведенным к этому основанию.
Решение:
Анализ. Пусть у треугольника ABC ВС = 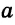 , высота АН =
, высота АН = 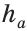 и медиана AM =
и медиана AM = 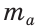 (рис. 313).
(рис. 313).
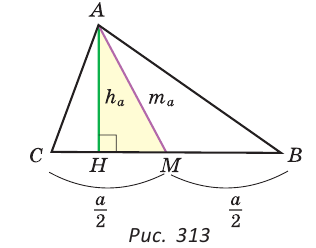
Заметим, что треугольник АНМ может быть построен по катету и гипотенузе, а затем достроен до искомого треугольника ABC путем откладывания от точки М влево и вправо отрезков МС = MB = 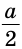 .
.
Построение.
1) Строим прямой угол Н (рис. 314).
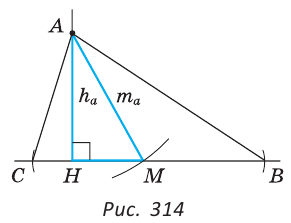
На одной его стороне откладываем отрезок АН = 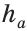 , из точки А как из центра делаем засечку на второй стороне угла радиусом
, из точки А как из центра делаем засечку на второй стороне угла радиусом 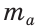 — получаем точку М.
— получаем точку М.
2) Делим отрезок 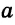 пополам (основная задача) и на прямой НМ откладываем по разные стороны от точки М отрезки МВ=
пополам (основная задача) и на прямой НМ откладываем по разные стороны от точки М отрезки МВ= 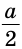 и МС=
и МС= 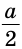 . Проводим отрезки СА и ВА.
. Проводим отрезки СА и ВА.
Доказательство:
 ABC — искомый, так как у него высота АН=
ABC — искомый, так как у него высота АН=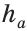 , медиана АМ=
, медиана АМ=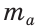 , сторона ВС=
, сторона ВС=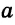 по построению.
по построению.
Исследование*. Так как катет меньше гипотенузы, то высота 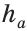 должна быть меньше или равна медиане
должна быть меньше или равна медиане 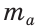 . Поэтому решение существует, если
. Поэтому решение существует, если 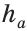 <
< 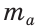 , и оно единственное. Если
, и оно единственное. Если 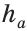 =
= 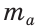 , получим равнобедренный треугольник.
, получим равнобедренный треугольник.
Геометрическое место точек
Определение. Геометрическим местом точек (ГМТ) называется множество всех точек, обладающих общим свойством.
Примеры геометрических мест точек на плоскости
1. Окружность — это геометрическое место точек плоскости, равноудаленных от данной точки.
2. Серединный перпендикуляр — это геометрическое место точек плоскости, равноудаленных от концов отрезка.
3. Биссектриса — геометрическое место точек внутри угла, равноудаленных от сторон угла.
4. Геометрическое место точек, находящихся на заданном расстоянии 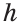 от данной прямой
от данной прямой 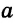 , — две прямые
, — две прямые 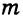 и
и 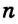 , параллельные данной, находящиеся в разных полуплоскостях от этой прямой на заданном расстоянии от нее (рис. 316).
, параллельные данной, находящиеся в разных полуплоскостях от этой прямой на заданном расстоянии от нее (рис. 316).
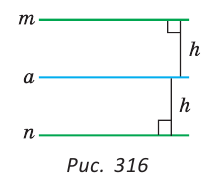
5. Геометрическое место точек, равноудаленных от двух данных параллельных прямых  и
и  , есть параллельная им прямая
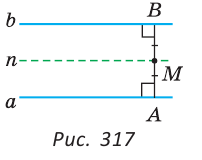
, есть параллельная им прямая  , проходящая через середину М их общего перпендикуляра АВ (рис. 317).
, проходящая через середину М их общего перпендикуляра АВ (рис. 317).
В пространстве геометрическим местом точек, равноудаленных от данной точки, является сфера.
Метод геометрических мест точек
Одним из методов решения задач на построение является метод пересечения двух геометрических мест точек. Суть его состоит в следующем. Пусть искомая точка удовлетворяет, например, некоторым двум условиям: геометрическое место точек, удовлетворяющих первому условию, — это некоторая фигура F1 (окружность, биссектриса угла, серединный перпендикуляр и т. д.), а геометрическое место точек, удовлетворяющих другому условию, — это фигура F2. Искомая точка, принадлежащая и фигуре F1, и фигуре F2, является точкой их пересечения. В частности, методом пересечения двух геометрических мест точек решена основная задача о построении треугольника по трем сторонам.
Задача №11
Построить внутри данного угла точку, которая равноудалена от сторон угла на данное расстояние  .
.
Решение:
Анализ. Пусть дан угол ВАС и отрезок длиной  (рис. 318).
(рис. 318).
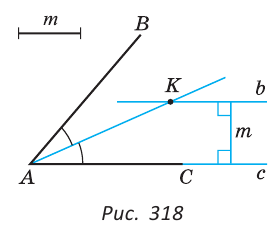
Все точки, равноудаленные от сторон угла, лежат на биссектрисе угла. Поэтому искомая точка лежит на биссектрисе угла. С другой стороны, все точки, удаленные от стороны угла на расстояние 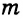 , лежат на двух прямых, параллельных стороне угла и находящихся от нее на расстоянии
, лежат на двух прямых, параллельных стороне угла и находящихся от нее на расстоянии 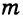 . Искомая точка будет находиться на пересечении указанных двух геометрических мест точек.
. Искомая точка будет находиться на пересечении указанных двух геометрических мест точек.
Построение.
1) Строим прямую 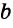 , параллельную прямой АС, с их общим перпендикуляром, равным
, параллельную прямой АС, с их общим перпендикуляром, равным 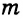 (ключевая задача 2 § 30).
(ключевая задача 2 § 30).
2) Строим биссектрису угла ВАС (основная задача).
3) В пересечении биссектрисы и прямой 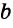 получаем искомую точку К.
получаем искомую точку К.
Доказательство:
Расстояние между параллельными прямыми 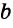 и АС равно
и АС равно 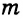 . Значит, и расстояние от точки К до стороны АС угла ВАС равно
. Значит, и расстояние от точки К до стороны АС угла ВАС равно 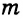 . Все точки биссектрисы равноудалены от сторон угла, в том числе и точка К. Точка К удовлетворяет требованию задачи.
. Все точки биссектрисы равноудалены от сторон угла, в том числе и точка К. Точка К удовлетворяет требованию задачи.
Задача №12
Построить треугольник по двум сторонам 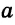 и
и 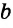 и высоте
и высоте 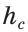 , опущенной на сторону
, опущенной на сторону 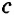 .
.
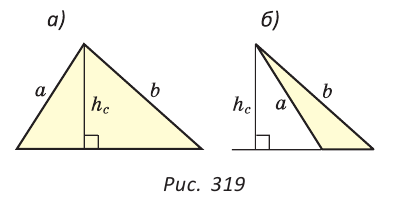
Решение:
Заметим, что в общем случае существует два треугольника со сторонами 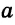 ,
, 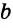 и высотой
и высотой 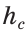 , (рис. 319, а, б).
, (рис. 319, а, б).
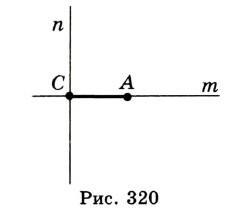
Построение (рис. 320).
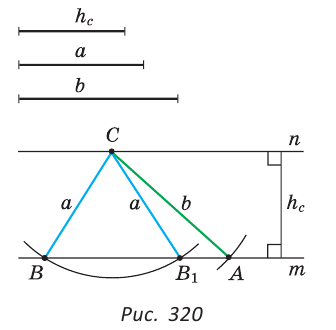
1) Строим две параллельные прямые  и
и  с расстоянием между ними (ключевая задача 2 § 30).
с расстоянием между ними (ключевая задача 2 § 30).
2) Строим дугу с центром в точке С и радиусом  , которая пересекает прямую
, которая пересекает прямую 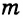 в точках В и В1.
в точках В и В1.
3) Строим дугу с центром в точке С радиусом 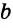 , которая пересечет прямую
, которая пересечет прямую 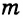 в точке А. Треугольники ABC и АВ1С — искомые.
в точке А. Треугольники ABC и АВ1С — искомые.
Доказательство:
Следует из построения и теоремы о расстоянии между параллельными прямыми.
Исследование. Так как перпендикуляр меньше наклонной, проведенной из той же точки к одной прямой, то задача может иметь решение, только если 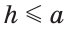 и
и 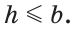 Если
Если 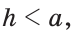
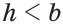 и
и 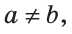 то задача имеет два решения. Если
то задача имеет два решения. Если 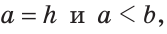 то треугольник прямоугольный, и задача имеет одно решение. Если
то треугольник прямоугольный, и задача имеет одно решение. Если 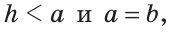 то задача имеет одно решение — равнобедренный треугольник. Если
то задача имеет одно решение — равнобедренный треугольник. Если 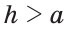 или
или 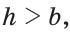 задача не имеет решения.
задача не имеет решения.
Задачи на построение с решением
С помощью линейки с делениями, циркуля, угольника, транспортира, шаблонов (рис. 312) вам не раз приходилось проводить различные геометрические построения.

А можно ли обходиться меньшим количеством чертежных инструментов? Оказывается, что во многих случаях достаточно использовать только циркуль и линейку без делений. Например, чтобы провести биссектрису угла, совсем не обязательно иметь транспортир, а разделить отрезок пополам можно и тогда, когда на линейку не нанесена шкала.
А стоит ли в наше время, когда созданы точнейшие приборы и совершенные компьютерные программы, позволяющие выполнять сложнейшие измерения и построения, обходиться такими «скудными» средствами, как циркуль и линейка? На практике, конечно, нет. Поэтому, например, конструкторы, строители, архитекторы, дизайнеры не ограничивают себя в выборе инструментов.
Однако при изучении геометрии очень полезно принять участие в игре по таким правилам:
- все построения выполняются только с помощью циркуля и линейки без делений;
- с помощью линейки можно через заданную точку
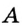 провести прямую, а также через заданные две точки
провести прямую, а также через заданные две точки 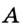 и
и 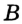 провести прямую
провести прямую 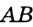 ;
; - с помощью циркуля можно построить окружность с данным центром и радиусом, равным заданному отрезку
 .
.
Итак, договоримся, что если в задаче требуется построить какую-то фигуру, то построение выполняется по описанным выше правилам.
Решить задачу на построение — это значит составить план (алгоритм) построения фигуры; реализовать план, выполнив построение; доказать, что полученная фигура является искомой.
Рассмотрим основные задачи на построение.
Задача №13
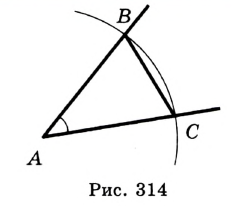
Постройте угол, равный данному, одна из сторон которого является данным лучом.
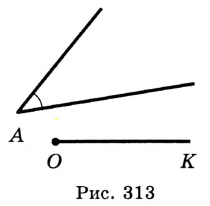
Решение:
На рисунке 313 изображены угол  и луч
и луч  . Надо построить угол, равный углу
. Надо построить угол, равный углу 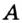 , одной из сторон которого является луч
, одной из сторон которого является луч  . Проведем окружность произвольного радиуса с центром в точке
. Проведем окружность произвольного радиуса с центром в точке 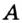 . Точки пересечения этой окружности со сторонами угла
. Точки пересечения этой окружности со сторонами угла 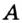 обозначим
обозначим  и
и  (рис. 314).
(рис. 314).
Пусть 
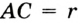 .
.
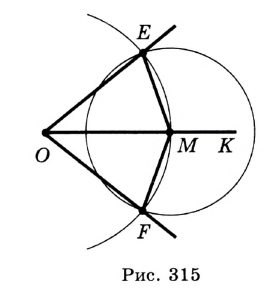
Проведем окружность радиуса 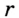 с центром в точке
с центром в точке 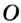 (рис. 315). Она пересекает луч
(рис. 315). Она пересекает луч 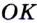 в точке
в точке 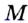 . Затем с центром в точке
. Затем с центром в точке 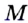 проведем окружность, радиус которой равен
проведем окружность, радиус которой равен 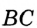 . Пусть
. Пусть 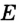 и
и 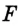 — точки пересечения окружностей с центрами
— точки пересечения окружностей с центрами 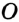 и
и 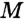 .
.
Покажем, что каждый из углов 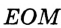 и
и 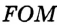 — искомый. Докажем, например, что
— искомый. Докажем, например, что 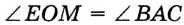 . Рассмотрим треугольники
. Рассмотрим треугольники 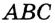 и
и 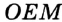 . Имеем:
. Имеем: 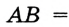
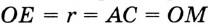 . Кроме того, по построению
. Кроме того, по построению 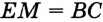 . Следовательно,
. Следовательно, 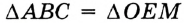 по третьему признаку равенства треугольников. Отсюда
по третьему признаку равенства треугольников. Отсюда 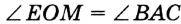 . Аналогично можно показать, что
. Аналогично можно показать, что 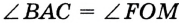 .
.
Задача №14
Постройте серединный перпендикуляр данного отрезка.
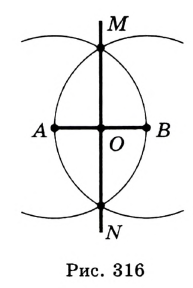
Решение:
Пусть 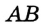 — данный отрезок. Проведем две окружности с центрами
— данный отрезок. Проведем две окружности с центрами 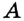 и
и 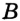 радиуса
радиуса 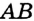 (рис. 316). Точки пересечения этих окружностей обозначим
(рис. 316). Точки пересечения этих окружностей обозначим 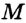 и
и 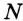 . Из построения следует, что
. Из построения следует, что 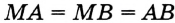 и
и 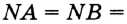
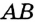 . Следовательно, точки
. Следовательно, точки 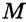 и
и 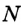 принадлежат серединному перпендикуляру отрезка
принадлежат серединному перпендикуляру отрезка 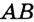 . Прямая
. Прямая 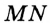 и является серединным перпендикуляром отрезка
и является серединным перпендикуляром отрезка 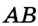 .
.
Замечание. Поскольку прямая 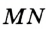 пересекает отрезок
пересекает отрезок 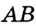 в его середине, точке
в его середине, точке 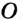 , то тем самым решена
, то тем самым решена
Задача №15
Даны прямая и не принадлежащая ей точка. Через эту точку проведите прямую, перпендикулярную данной.
Решение:
Пусть 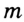 — данная прямая,
— данная прямая, 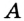 — не принадлежащая ей точка. Проведем окружность с центром в точке
— не принадлежащая ей точка. Проведем окружность с центром в точке 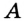 так, чтобы она пересекла прямую
так, чтобы она пересекла прямую 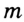 в двух точках. Обозначим эти точки
в двух точках. Обозначим эти точки  и
и  (рис. 317).
(рис. 317).
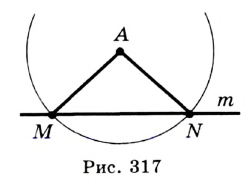
Поскольку 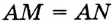 , то точка
, то точка 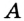 принадлежит серединному перпендикуляру отрезка
принадлежит серединному перпендикуляру отрезка 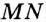 . Построив этот серединный перпендикуляр (см. задачу 2), мы тем самым решим задачу.
. Построив этот серединный перпендикуляр (см. задачу 2), мы тем самым решим задачу.
Задача №16
Даны прямая и принадлежащая ей точка. Через эту точку проведите прямую, перпендикулярную данной.
Решение:
Пусть 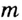 — данная прямая,
— данная прямая, 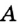 — принадлежащая ей точка. Проведем окружность произвольного радиуса с центром в точке
— принадлежащая ей точка. Проведем окружность произвольного радиуса с центром в точке 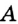 . Она пересекает прямую
. Она пересекает прямую 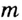 в точках
в точках 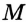 и
и 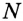 (рис. 318).
(рис. 318).
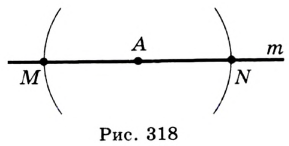
Поскольку 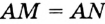 , то задача опять-таки свелась к построению серединного перпендикуляра отрезка
, то задача опять-таки свелась к построению серединного перпендикуляра отрезка 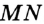 .
.
Задача №17
Постройте биссектрису данного угла.
Решение:
Пусть 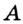 — данный угол. Проведем окружность произвольного радиуса с центром в точке
— данный угол. Проведем окружность произвольного радиуса с центром в точке 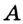 . Эта окружность пересекает стороны угла в точках
. Эта окружность пересекает стороны угла в точках 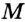 и
и 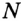 (рис. 319). Тем же радиусом проведем окружности с центрами
(рис. 319). Тем же радиусом проведем окружности с центрами  и
и  .
.
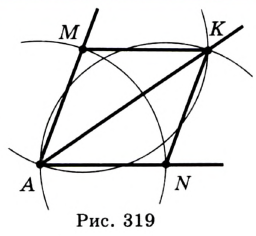
Эти окружности пересекаются в точках  и
и 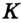 . Докажем, что луч
. Докажем, что луч 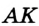 — искомая биссектриса. Действительно,
— искомая биссектриса. Действительно, 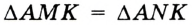 по трем сторонам. Следовательно,
по трем сторонам. Следовательно, 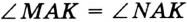 .
.
Задача №18
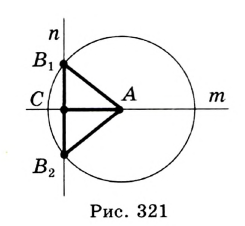
Постройте прямоугольный треугольник по гипотенузе и катету.
Решение:
Проведем две перпендикулярные прямые  и
и  ,
,  — точка их пересечения (рис. 320). На прямой отложим отрезок
— точка их пересечения (рис. 320). На прямой отложим отрезок 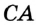 , равный данному катету. С центром в точке
, равный данному катету. С центром в точке 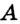 проведем окружность радиусом, равным данной гипотенузе. Эта окружность пересечет прямую
проведем окружность радиусом, равным данной гипотенузе. Эта окружность пересечет прямую 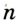 в двух точках
в двух точках 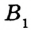 и
и  (рис. 321). Каждый из треугольников
(рис. 321). Каждый из треугольников  и
и  — искомый.
— искомый.
Задача №19
Постройте треугольник по стороне и высотам, проведенным к двум другим сторонам.
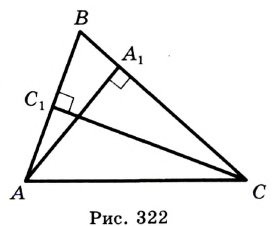
Решение:
На рисунке 322 изображен треугольник  ,
,  и
и  — его высоты. Если известны отрезки
— его высоты. Если известны отрезки 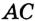 ,
, 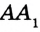 и
и 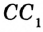 то можно построить прямоугольные треугольники
то можно построить прямоугольные треугольники 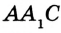 и
и 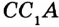 по гипотенузе и катету. Проведенный анализ подсказывает план построения.
по гипотенузе и катету. Проведенный анализ подсказывает план построения.
Построим прямоугольный треугольник  , в котором гипотенуза
, в котором гипотенуза  равна данной стороне, а катет
равна данной стороне, а катет 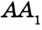 — одной из данных высот (рис. 323). В построенном треугольнике угол
— одной из данных высот (рис. 323). В построенном треугольнике угол  равен одному из углов, прилежащих к заданной стороне искомого треугольника. С помощью аналогичного построения можно получить другой прилежащий к данной стороне угол (рис. 324).
равен одному из углов, прилежащих к заданной стороне искомого треугольника. С помощью аналогичного построения можно получить другой прилежащий к данной стороне угол (рис. 324).
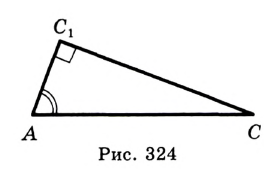
Теперь осталось построить треугольник по стороне и двум прилежащим к ней углам. Выполните это построение самостоятельно.
Задача №20
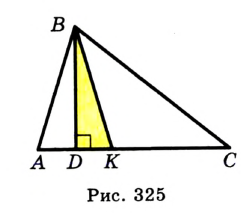
Постройте треугольник по углу, высоте и биссектрисе, проведенным из вершины этого угла.
Решение:
На рисунке 325 изображен треугольник 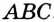 , в котором отрезок
, в котором отрезок 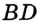 — высота, отрезок
— высота, отрезок 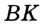 — биссектриса.
— биссектриса.
Если известны длины отрезков 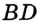 и
и 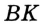 , то прямоугольный треугольник
, то прямоугольный треугольник 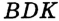 можно построить по гипотенузе и катету. Также отметим, что если известен угол
можно построить по гипотенузе и катету. Также отметим, что если известен угол  , то можно построить углы
, то можно построить углы  и
и 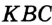 , каждый из которых равен
, каждый из которых равен 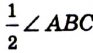 . Отсюда получаем план построения.
. Отсюда получаем план построения.
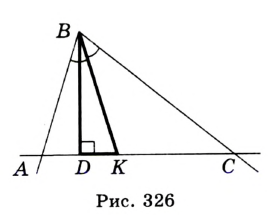
Строим прямоугольный треугольник  , в котором гипотенуза
, в котором гипотенуза 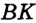 равна данной биссектрисе, а катет
равна данной биссектрисе, а катет 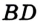 — данной высоте (рис. 326). Строим два угла, каждый из которых равен половине данного, так, чтобы луч
— данной высоте (рис. 326). Строим два угла, каждый из которых равен половине данного, так, чтобы луч 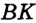 был их общей стороной. На рисунке 326 это углы
был их общей стороной. На рисунке 326 это углы 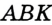 и
и 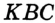 . Треугольник
. Треугольник 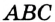 — искомый.
— искомый.
Метод геометрических мест точек в задачах на построение
Известно, что если смешать синий и желтый цвета, то получим зеленый. Пусть на плоскости надо найти точки, обладающие какими-то двумя свойствами одновременно. Если синим цветом покрасить точки, обладающие первым свойством, а желтым — обладающие вторым свойством, то понятно, что «зеленые» точки будут обладать сразу двумя свойствами. В этом и состоит идея метода ГМТ, которую проиллюстрируем следующими задачами.
Задача №21
Постройте треугольник по трем данным его сторонам.
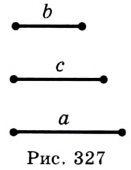
Решение:
Пусть даны три отрезка, длины которых равны 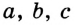 (рис. 327). Надо построить треугольник
(рис. 327). Надо построить треугольник 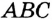 , в котором
, в котором 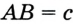 ,
, 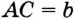 ,
, 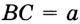 . Проведем произвольную прямую. С помощью циркуля отложим на ней отрезок
. Проведем произвольную прямую. С помощью циркуля отложим на ней отрезок  , равный
, равный  (рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки
(рис. 328). Понятно, что задача свелась к построению третьей вершины треугольника, точки  .
.
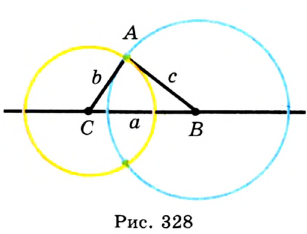
Воспользуемся тем, что точка 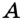 обладает сразу двумя свойствами:
обладает сразу двумя свойствами:
- принадлежит геометрическому месту точек, равноудаленных от точки
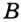 на расстояние
на расстояние 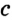 с, т. е. «синей» окружности (рис. 328);
с, т. е. «синей» окружности (рис. 328); - принадлежит геометрическому месту точек, равноудаленных от точки
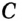 на расстояние
на расстояние 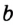 , т. е. «желтой» окружности (рис. 328).
, т. е. «желтой» окружности (рис. 328).
В качестве точки 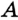 можно выбрать любую из двух образовавшихся «зеленых» точек. Полученный треугольник
можно выбрать любую из двух образовавшихся «зеленых» точек. Полученный треугольник 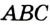 является искомым, так как в нем
является искомым, так как в нем 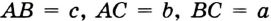 .
.
Из описанного построения следует, что если каждый из трех данных отрезков меньше суммы двух других, то эти отрезки могут служить сторонами треугольника.
Задача №22
Постройте фигуру, все точки которой принадлежат данному углу, равноудалены от его сторон и находятся на заданном расстоянии а от его вершины.
Решение:
Искомые точки принадлежат сразу двум геометрическим местам точек: биссектрисе данного угла и окружности с центром в его вершине и радиусом, равным 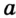 а. Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка
а. Построим биссектрису угла и указанную окружность (рис. 329). Их пересечением является искомая точка 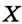 .
.
Задача №23
Постройте центр окружности радиуса 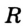 , проходящей через данную точку
, проходящей через данную точку 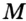 и касающуюся данной прямой
и касающуюся данной прямой 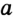 .
.
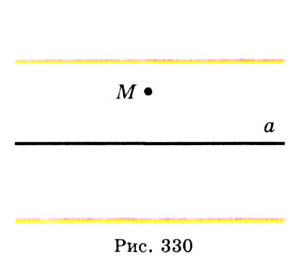
Решение:
Поскольку окружность касается прямой 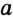 , то ее центр находится на расстоянии
, то ее центр находится на расстоянии 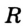 от нее. Геометрическим местом точек, удаленных от данной прямой на данное расстояние, являются две параллельные прямые (см. задачу 500). Следовательно, центр окружности надо искать на «желтых» прямых (рис. 330).
от нее. Геометрическим местом точек, удаленных от данной прямой на данное расстояние, являются две параллельные прямые (см. задачу 500). Следовательно, центр окружности надо искать на «желтых» прямых (рис. 330).
Геометрическое место точек, являющихся центрами окружностей радиуса 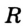 , проходящих через точку
, проходящих через точку 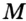 , — это окружность данного радиуса с центром в точке
, — это окружность данного радиуса с центром в точке 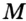 . Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения «синей» окружности с одной из «желтых» прямых (рис. 331).
. Поэтому в качестве центра искомой окружности можно выбрать любую из точек пересечения «синей» окружности с одной из «желтых» прямых (рис. 331).
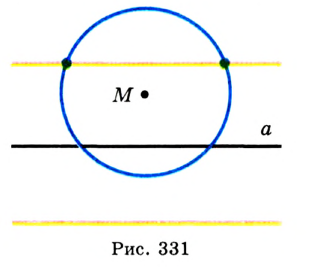
Построение для случая, когда данная точка принадлежит данной прямой, рассмотрите самостоятельно.
Задача №24
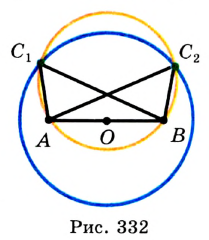
Постройте треугольник по стороне, медиане, проведенной к этой стороне, и радиусу описанной окружности.
Решение:
Построим окружность данного радиуса и проведем хорду 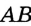 , равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности («желтая» окружность) и окружности Рис 332 с центром в точке
, равную стороне искомого треугольника. Тогда концы хорды являются двумя вершинами искомого треугольника. Понятно, что третья вершина принадлежит одновременно построенной окружности («желтая» окружность) и окружности Рис 332 с центром в точке 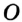 , являющейся серединой хорды
, являющейся серединой хорды 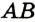 , и радиусом, равным данной медиане («синяя» окружность). Каждый из треугольников
, и радиусом, равным данной медиане («синяя» окружность). Каждый из треугольников 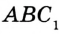 и
и 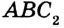 (рис. 332) является искомым.
(рис. 332) является искомым.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Угол - определение, виды, как обозначают с примерами
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Неравенство треугольника - определение и вычисление
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой