Явление самоиндукции - основные понятия, формулы и определение с примерами

Явление самоиндукции:

Масса — мера инертности тела. Основной закон динамики (второй закон Ньютона):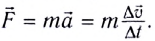

Согласно закону Фарадея явление электромагнитной индукции наблюдается во всех случаях, когда изменяется магнитный поток, пронизывающий рассматриваемый контур. Важным частным случаем этого явления служит явление самоиндукции, когда изменяющийся магнитный поток через проводящий контур создается изменяющимся в нем током. Такой магнитный поток называется собственным магнитным потоком. ЭДС индукции согласно закону Фарадея пропорциональна скорости изменения магнитного потока. Магнитный поток Ф, пронизывающий проводящий контур, в свою очередь, пропорционален модулю индукции магнитного поля В внутри контура, т. е. Ф~В, а модуль магнитной индукции пропорционален силе тока I в контуре, т. е. В ~ l.

Следовательно, при неизменных форме и размерах неподвижного контура собственный магнитный поток через контур может изменяться только при изменении силы тока в нем. Таким образом, собственный магнитный поток прямо пропорционален силе тока в контуре:

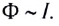
Эту зависимость математически можно представить в виде
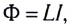где L — коэффициент пропорциональности, который называют индуктивностью контура или его коэффициентом самоиндукции.
 

Индуктивность — скалярная физическая величина, численно равная собственному магнитному потоку, пронизывающему контур, при силе тока в контуре 1 А:  

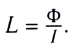
В СИ единицей индуктивности является генри: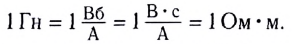
1 Гн — это индуктивность контура, магнитный поток через который равен 1 Вб при силе тока в контуре, равной 1 А.

Индуктивность контура зависит от его формы и размеров, а также от магнитных свойств окружающей среды и не зависит от силы тока в контуре.
Так, индуктивность соленоида длиной l и площадью поперечного сечения S, содержащего N витков, в вакууме определяется по формуле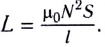 

Используя закон электромагнитной индукции для контура индуктивностью L, получаем выражение для ЭДС самоиндукции:

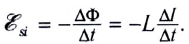
Отсюда следует, что индуктивность контура численно равна ЭДС самоиндукции, возникающей в нем при изменении силы тока на 1 А в течение 1 с. Это означает также, что катушка имеет индуктивность 1 Гн, если при изменении в ней силы тока на 1 А в течение 1 с в ней возникает ЭДС самоиндукции в 1 В:

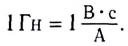
Таким образом, под явлением самоиндукции понимают возникновение в контуре ЭДС индукции, создаваемой вследствие изменения силы тока в самом контуре.

Рассмотрим этот процесс подробнее. При изменении (увеличении или уменьшении) силы тока в контуре изменяется и индукция собственного магнитного поля в пространстве, окружающем проводник. Это изменение магнитного поля вызывает возникновение вихревого электрического поля. Его энергетической характеристикой является появляющаяся в проводнике ЭДС самоиндукции, которая согласно правилу Ленца стремится противодействовать вызвавшей ее причине. Вследствие этого сила тока в проводнике не может мгновенно увеличиться или уменьшиться, т. е. электромагнитным процессам в электрических цепях присуще свойство инертности. Таким образом, индуктивность является мерой инертности электромагнитных процессов, происходящих в контуре по отношению к изменению тока.

Свойство инертности впервые обсуждалось в механике при изучении законов Ньютона, где мерой инертности являлась масса тела. Напомним, что, благодаря наличию массы, скорость тела не может мгновенно увеличиться или уменьшиться.

Рассмотрим тело массой m, поступательно движущееся под действием силы 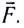Согласно второму закону Ньютона  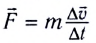для изменения скорости тела на 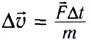необходимо время 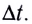Сравнивая модули силы и ЭДС самоиндукции, видим, что аналогом массы m является индуктивность L, аналогом модуля скорости v — сила тока I, аналогом модуля силы 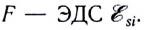Таким образом, как для изменения скорости тела на некоторую величину требуется конечный промежуток времени 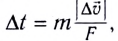так и для изменения силы тока в контуре на требуется некоторый конечный промежуток времени 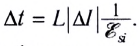Из последнего соотношения видно, что промежуток времени тем больше, чем больше индуктивность контура.

Явление самоиндукции можно наблюдать при замыкании и размыкании электрических цепей, содержащих элементы значительной индуктивности.

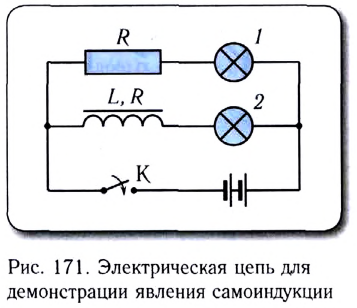
На рисунке 171 изображена схема электрической цепи, содержащей две одинаковые лампочки 1 и 2, подключенные параллельно к источнику тока. Первая лампочка подключена к источнику через резистор сопротивлением R, а вторая — через катушку с железным сердечником индуктивностью L, имеющую такое же сопротивление R.

При замыкании ключа К первая лампочка вспыхивает практически сразу, а вторая — с заметным опозданием. Причиной этой задержки является действие ЭДС самоиндукции, препятствующей нарастанию тока в цепи лампочки 2. Действительно, после замыкания ключа К сила тока в цепи лампочки 2 увеличивается, что приводит к увеличению магнитного потока через катушку. В соответствии с правилом Ленца в катушке при этом возникает ЭДС самоиндукции, препятствующая нарастанию тока. График зависимости силы тока от времени в цепи лампочки 2 после замыкания цепи представлен на рисунке 172.

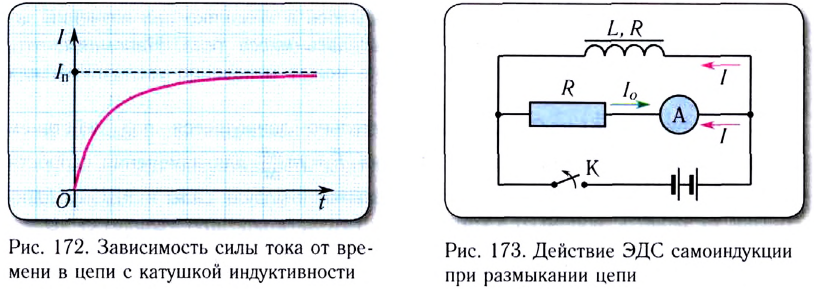
ЭДС самоиндукции в катушке существует до тех пор, пока происходит увеличение силы тока. Как видно из графика на рисунке 172, скорость увеличения силы тока с течением времени замедляется. Это приводит к постепенному уменьшению ЭДС самоиндукции в цепи катушки вплоть до полного исчезновения в момент установления режима постоянного тока.
Поскольку катушка индуктивности в цепи лампочки 1 отсутствует, то и сила тока нарастает в ней гораздо быстрее, в результате чего она и вспыхивает первой.

Проявление действия ЭДС самоиндукции при размыкании цепи можно наблюдать в цепи, изображенной на рисунке 173.

При размыкании ключа в катушке индуктивности L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в этот момент через гальванометр идет ток обратного направления.

Заметим, что при размыкании цепи изменение тока происходит более резко, чем при замыкании. Поэтому ЭДС самоиндукции, возникающая при размыкании цепи, гораздо больше, чем при замыкании. Более того, величина ЭДС самоиндукции при размыкании цепи может превысить ЭДС источника. Вследствие этого размыкание электрической цепи всегда сопровождается искрой, возникающей в месте разрыва цепи (рис. 174). Это обстоятельство является причиной перегорания некоторых электрических лампочек при их выключении.