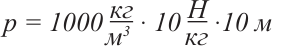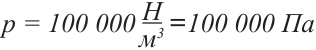Взаимодействие тел в физике - виды, формулы и определения с примерами
Содержание:
Взаимодействие тел:
В окружающем мире мы наблюдаем самые разнообразные взаимодействия тел. Если выпустить из рук какой-нибудь предмет, то он будет падать вниз с увеличивающейся скоростью, потому что его притягивает Земля. Вследствие трения шайба, скользящая по льду, останавливается (рис. 18.1).
Наэлектризованная трением расческа притягивает мелкие бумажки. При ударе пластилинового шарика о стену он изменяет свою форму (деформируется).
Таким образом, взаимодействием двух тел называют явление, при котором тела изменяют характер своего движения (величину или направление скорости) или деформируются (изменяют форму).

Инертность:
Опыт:
Положим на гладкую поверхность стола массивную книгу – например, энциклопедию. Привяжем к ней сложенную вдвое швейную нить, оставив свободным конец длиной 30–40 см (рис. 18.2). Натянем конец нити и плавно приведем книгу в движение, медленно передвигая ее по столу. Убедимся, что нить достаточно крепкая, чтобы преодолевать трение. Теперь повторим опыт, но отпустим нить, а потом резко дернем за ее конец. В этом случае нить разорвется, даже если ее сложить втрое или вчетверо, а книга практически не сдвинется с места.

В этом простом опыте мы сталкиваемся с двумя эффектами: 1) при взаимодействии тел их скорость начинает изменяться, и 2) свойством тел «противиться» изменению скорости, которую называют инертностью. Инертность – это свойство тела не изменять свою скорость мгновенно.
Книга не смогла сразу набрать скорость, которую мы придали нити, в результате чего нить удлинилась и разорвалась. Мы специально предложили взять массивную книгу, чтобы опыт легко удался.
В случае изменения телом его скорости, масса тела является количественной мерой его инертности, то есть чем больше масса тела, тем тяжелее увеличить или уменьшить его скорость. По этой причине очень опасно перебегать дорогу перед движущимся транспортом. Как бы ни были эффективны-ми тормоза автомобиля, он не может остановиться мгновенно и проезжает до полной остановки определенный тормозной путь.
Движение по инерции:
Инерцией называется явление сохранения телом своей скорости (как по направлению, так и по величине) при отсутствии взаимодействия с другими телами.
Для того, чтобы перемещать тяжелый ящик по полу, надо приложить значительное усилие. Однако, если хорошо подумать, то становится понятно, что усилие в этом случае нужно только для компенсации трения.
Галилео Галилей был первым, кто заметил, что равномерное прямолинейное движение может происходить без взаимодействия с другими телами. Он предложил опыт, который подтверждает эту мысль.
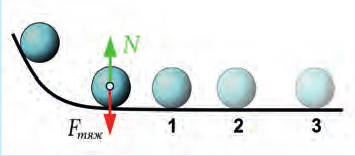 Рис. 18.3. Чем меньше сила трения, тем дальше катится шар. В случае компенсации сил или их отсутствия тело никогда не остановится |
 Рис. 18.4. Даже брошенный с небольшой скоростью, шар боулинга достигает цели |
Пустим массивный шар катиться с небольшой горки, которая плавно пере-ходит в горизонтальную плоскость (рис. 18.3). Сначала горизонтальная поверхность была глиняной, и шар остановился в точке 1. По деревянному настилу шар прокатился дальше и остановился в точке 2. Наиболее далеко (точка 3) шар катился по гладкому мраморному полу. Если представить, что трение и сопротивление воздуха вообще отсутствуют, то логично допустить, что шар никогда не остановится. Опыт Галилея демонстрирует игра в боулинг. Гладкий пол позволяет массивному шару достигать цели, даже если его бросить с не-большой скоростью (рис. 18.4).
Реально взаимодействие тел полностью устранить невозможно, потому опыт Галилея можно назвать мысленным. Если на тело действуют силы, но они взаимно уравновешены, то движение по инерции возможно. Об этом идет речь в первом законе Ньютона.
Первый закон Ньютона: существуют такие системы отсчета, относительно которых тело сохраняет состояние покоя или равномерного прямолинейного движения, если на это тело не действуют другие тела или их действие скомпенсировано. Такие системы называют инерциальными.
Первый закон Ньютона не может быть доказан теоретически, но его справедливость подтверждается некоторыми экспериментальными фактами, а также справедливостью следствий данного закона, поэтому, аналогично аксиомам в геометрии, этот закон называют постулатом о существовании инерциальных систем отсчета.
Итоги
- Взаимодействием двух тел называют явление, при котором тела изменяют характер своего движения (величину или направление скорости) или деформируются (изменяют форму).
- Инертностью называется свойство тела не изменять свою скорость мгновенно.
- Инерцией называется явление сохранения телом своей скорости (как по направлению, так и по величине) при отсутствии взаимодействия с другими телами или в случае компенсации действия внешних сил.
Масса тела и плотность вещества
Все материальные тела притягиваются к Земле. Тела одинаковой массы одинаково притягиваются к Земле, потому это свойство используют при измерении массы.
Определение массы тела
Массу тела обозначают буквой m и определяют с помощью рычажных весов. Весы (рис. 19.2) состоят из коромысла, которое может свободно вращаться вокруг оси, находящейся посредине и закрепленной на вертикально размещенной опоре. К концам коромысла подвешены две чаши весов, которые перед взвешиванием должны занимать горизонтальное положение, то есть находиться в равновесии.
 Рис. 19.1. Эталон 1 кг |
 Рис. 19.2. Массу тела определяют с помощью рычажных весов |
 Рис. 19.3. Набор разновесов для взвешивания |
На одну чашу весов кладут тело, массу которого хотят определить, а на другую – разновесы (рис. 19.3), масса которых известна. Разновесы подбирают так, чтобы возобновилось равновесие весов. Суммарная масса всех разновесов равняется искомой массе тела.
В качестве эталона массы сначала взяли массу 1 литра (1 л) дистиллирован-ной воды при температуре 4°С. Это вода, очищенная от солей и пылинок, ее используют в аптеках при изготовлении лекарств, доливают в автомобильный аккумулятор. Сейчас эталоном массы является цилиндр (высота 39 мм, диаметр 39 мм) из платиново-иридиевого сплава (90% платины, 10% иридия). Это – 1 кг (килограмм) – основная единица массы в СИ. Разновесы, которые используют-ся при определении массы, – копии эталона. Используют как большие, так и меньшие, чем 1 кг, единицы массы (табл. 19.1).
Таблица 19.1 Соотношение между единицами массы
| 1 т (тонна) = 1 000 кг | 1 кг = 0,001 т |
| 1 кг = 1 000 г (грамм) | 1 г = 0,001 кг |
| 1 г = 1 000 мг (миллиграмм) | 1 мг = 0,001 г |
| 1 мг = 1 000 мкг (микрограмм) | 1 мкг = 0,000 001 г |
Таблица 19.2 Массы некоторых тел
| Тело | Масса |
| Крылышко мухи | 50 мкг |
| Мячик для настольного тенниса | 2,5 г |
| Футбольный мяч | 400 г |
| Велосипед | 12–14 кг |
| Человек (в среднем) | 70 кг |
| Легковой автомобиль | 1 500 кг |
| Слон | 4 т |
| Трактор | 10 т |
| Пассажирский вагон | 50 т |
| Кит | 100 т |
Атомная единица массы
В атомной физике используют атомную единицу массы (а. е. м.). 1 а. е. м. равняется 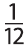 части массы атома Карбона. Обозначение химического элемента Карбона – С (Carbon).
части массы атома Карбона. Обозначение химического элемента Карбона – С (Carbon).
Массы протона и нейтрона приблизительно равняются 1 а. е. м. Масса атома Гидрогена – 1 а. е. м., Карбона – 12 а. е. м., Урана – 238 а. е. м. Масса электрона в 1836 раз меньше, чем масса протона.
Плотность вещества
Плотность вещества – это масса единицы объема этого вещества. Обозначим объем буквой V, а массу некоторого количества однородного вещества – m. Их отношение назовем плотностью и обозначим греческой буквой ρ (читается «ро»). Тогда формула плотности будет такой:
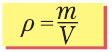
Чаще всего используют такие единицы плотности: кг/м3 та г/см3.
Пример №1
Масса одного литра воды приблизительно равняется 1 кг, это значит, что плотность воды равняется 1кг/л. Поскольку литр – это 1000 см3, а 1 кг = 1000 г, то 1кг/л = 1 г/см3 = 1000 кг/м3.
Зная плотность вещества, из которого состоит тело, и объем этого тела, можно найти его массу:
m = ρ · V (19.2)
Плотность тела
Тело может иметь полости, то есть не быть сплошным, или состоять из веществ разной плотности. В этом случае можно определить среднюю плотность тела, разделив всю массу тела на весь объем. Так плотность корабля, корпус которого сделан из стали, меньше плотности воды (иначе он бы не плавал), по-тому что внутри много пустот.
Чтобы получить плотности веществ в кг/м3, нужно данные, приведенные в та-блице 19.3, умножить на 1000. Например, плотность льда: 0,9 г/см3 = 900 кг/м3..
Таблица 19.3 Плотности некоторых веществ в твердом, жидком и газообразном состояниях (кг/дм3 или г/см3)
| ТВЕРДЫЕ ТЕЛА | ||
| Рыхлый снег 0,1 | Пробка 0,24 | Пенобетон 0,5-0,9 |
| Дерево 0,8 | Лед 0,9 | Резина 0,92 |
| Бумага 0,7–1,2 | Плексиглас 1,2 | Песок 1,7 |
| Алюминий 2,7 | Алмаз 3,5 | Стекло 2,4–2,6 |
| Медь 8,9 | Сталь 7,85 | Серебро 10,49 |
| Свинец 11,34 | Уран 19,0 | Золото 19,29 |
| Платина 21,45 | Иридий 22,42 | Осмий 22,6 |
| Тело человека ≈ 1 г/см3 | ||
| ЖИДКОСТИ | ||
| Вода (4°) 0,999973 | Вода (10°) 0,99970 | Вода (20°) 0,99820 |
| Вода (50°) 0,9981 | Вода (100°) 0,95835 | Тяжелая вода 1,105 |
| Морськая вода 1,03 | Спирт 0,83 | Бензин 0,78 |
| Керосин 0,8 | Ртуть 13,546 | Нефть 0,8 |
| ГАЗЫ (0°С, 760 мм рт. ст.) | ||
| Водород 0,09 | Гелий 0,18 | Азот 1,25 |
| Воздух 1,29 | Кислород 1,43 | |
| ПРОДУКТЫ | ||
| Сахар 1,61 | Соль 2,17 | Мука 0,4–0,55 |
| Картошка 1,06 | Раст. масло 0,91 | |
Кстати:
Твердые тела и жидкости очень трудно сжать, потому их плотность мало изменяется. Плотность же газов в значительной степени зависит от давления и температуры. В XIX в. некоторые газы удалось превратить в жидкости с помощью сжатия. А вот водород и гелий никак не поддавались сжижению, хотя их сжимали до плотности, превышающей плотность воды.
Итоги
- Массу тела определяют на рычажных весах и измеряют в СИ в кг.
- Массу единицы объема вещества называют плотностью. Плотность определяют по формуле
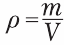 .
.
Силы в природе
Мы ежедневно наблюдаем действие разных сил. Когда мы несем чемодан, то хорошо чувствуем, как он тянет руку вниз, растягивая мышцы. Именно деформация (растяжение) и напряжение наших мышц дает нам ощущение силы.
Чемодан действует на руку, потому что его притягивает вниз Земля, а не падает он толь-ко потому, что действие на него со стороны руки направлено вверх и компенсирует (уравновешивает) действие силы тяжести.
Силой называется количественная мера взаимодействия тел. Ее обычно обозначают буквой F (от англ. force - сила), но в некоторых случаях используют индексы и другие буквы. Сила является векторной физической величиной и на рисунках ее изображают стрелкой, которая указывает направление действия силы. Напомним, что векторные величины помечают полужирными буквами или буквами со стрелками над ними.
Равнодействующая двух одинаковых по вели-чине и противоположных по направлению сил, которые действуют на одно и то же тело и лежат на одной прямой, равняется нулю, то есть они компенсируют друг друга. Это значит, что эти силы, действуя вместе, не нарушат состояние по-коя тела, а только деформируют его.
Прямую, которая совпадает с вектором силы, называют линией действия силы. Точку на теле, где размещено начало вектора силы, принято называть точкой приложения силы (рис. 20.1).

Рис. 20.1. Три характеристики вектора силы
Силы тяжести, трения и упругости
В повседневной жизни мы чаще всего сталкиваемся с действием сил тяжести, трения и упругости. Величину силы в СИ измеряют в ньютонах (Н). Так почтен выдающийся английский физик Исаак Ньютон, который впервые детально исследовал силу притяжения.
На рис. 20.2 изображен груз, подвешенный на тросе к потолку. На груз действует сила тяжести (Fтяж), направленная вертикально вниз. Не падает груз потому, что на него со стороны троса действует вверх сила упругости, которая возникла в результате растяжения троса. Эту силу называют силой натяжения и обозначают буквой T. Силу упругости легко почувствовать, сжимая или растягивая пружину (рис. 20.3).
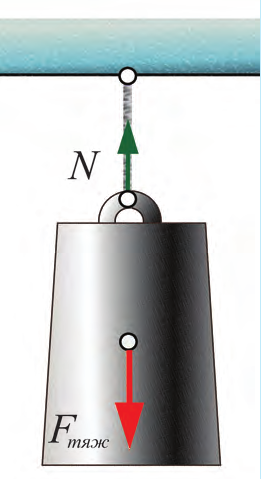
Рис. 20.2. Груз, подвешенный на тросе

Рис. 20.3. При сжатии или растяжении пружины возникает сила упругости
Равновесие сил
В нашем примере (рис. 20.2) сила тяжести и сила натяжения равны по величине и противоположны по направлению. В сумме эти векторы сил дают ноль, и тело находится в состоянии покоя (не падает). Сила натяжения T возникла в тросе потому, что груз его растягивает. Характерным признаком действия на тело силы является его деформация. Деформацией называют изменение размеров и формы тела.
Если положить чемодан на диван, то легко заметить, что диван прогибается (рис. 20.4). Пружины дивана сжимаются до тех пор, пока сила N, которая действует на чемодан со стороны опоры (дивана), не уравновесит силу тяжести Fтяж. С это-го момента чемодан будет находиться в равновесии. Силу N называют реакцией опоры (слово «реакция» означает «обратное действие»).
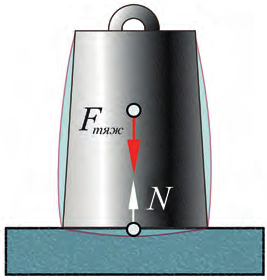
Рис. 20.4. Сила тяжести и сила реакции опоры компенсируют друг друга
Случай, когда на тело действуют две равные по величине и противоположные по направлению силы, является самым простым примером компенсации сил. Следует заметить, что в приведенном примере чемодан также деформируется.
Например, под действием сил Fтяж и N (рис. 20.4) чемодан немного сплющивается по вертикали и становится толще по горизонтали.
Следовательно, под действием сил, которые компенсируются, тело находится в состоянии покоя и только деформируется.
Виды деформаций
Деформацией называют изменение формы и размеров тела. Перечислим виды деформации. Деформация растяжения-сжатия возникает, например, если мы растягиваем или сжимаем пружину (рис. 20.5, случай 1, 2). Если концы линейки поворачивать в разные стороны – получим деформацию кручения (случай 3). Согнув линейку дугой, вы произведете деформацию изгиба (случай 4). Строгая ножом деревянную палочку, мы осуществляем деформацию сдвига (случай 5).
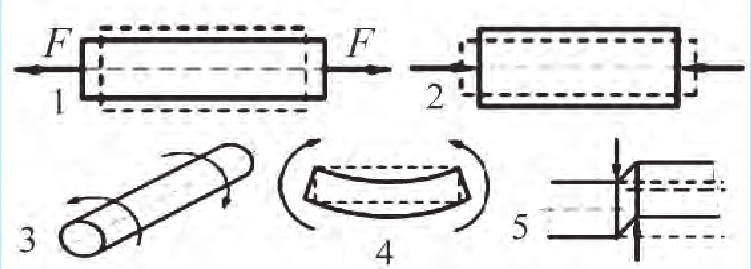
Рис. 20.5. Виды деформаций
Подвесим легкую пружину так, чтобы она мога свободно занять вертикальное положение (рис. 20.6). Длину пружины в недеформированном состоянии обозначим l0. Потянем свободный конец пружины с некоторой силой F вниз. Длину пружины после удлинения обозначим через l. Разность l – l0 называют удлинением и обозначают буквой «x».
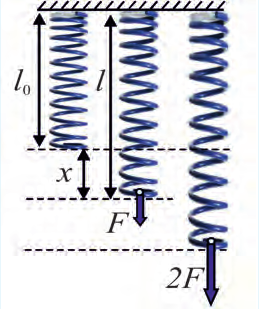
Рис. 20.6. l0 – длина недеформированной пружины, l – длина деформированной пружины.
Удлинение x = l – l0
Упругая деформация
Деформация называется упругой, если после прекращения действия повлекших деформацию сил тело восстанавливает свою форму и размеры.
Сила, приложенная к пружине, будет растягивать ее до тех пор, пока направленная вверх сила упругости не уравновесит эту силу. Если прекратить действие внешней силы, то сила упругости возвращает пружине форму и раз-мер, которые она имела до начала опыта.
Приложим к пружине вдвое большую силу и убедимся, что удлинение стало вдвое больше. Втрое большая сила даст втрое большее удлинение.
Закон Гука
До тех пор, пока пружина сохраняет упругие свойства, удлинение пружины прямо пропорционально величине силы, которая ее деформирует, и направлено в противоположную направлению силы сторону. Этот простой закон поведения упругих тел, открытый английским физиком Робертом Гуком, назван в его честь – законом Гука. В математической форме его можно записать так:
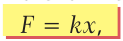 (20.1)
(20.1)
где F – это растягивающая пружину сила, а x – удлинение пружины. Коэффициент пропорциональности «k» называют жесткостью пружины, и его можно определить из формулы (20.1) как:
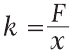
Жесткость измеряют в Н/м, если «x» измерять в метрах; или Н/см, если «x» измеряли в сантиметрах. Жесткость показывает, какую силу надо приложить к пружине, чтобы она удлинилась на единицу длины.
Пример №2
Жесткость пружины k = 0,5 Н/см. а) Какой физический смысл указанного значения жесткости? б) Составьте таблицу зависимости силы F и жесткости k от удлинения х этой пружины. в) Начертите график зависимости силы от удлинения.
Решение. а) Жесткость 0,5 Н/см значит, что сила 0,5 Н растягивает пру-жину на 1 см. Чем больше жесткость, тем тяжелее пружину растягивать или сжимать.
б)
| х, см | 2 | 4 | 6 | 8 | 10 |
| F, H | 1 | 2 | 3 | 4 | 5 |
| k, Н/см | 0,5 | 0,5 | 0,5 | 0,5 | 0,5 |
в) См. рис. 20.7.
Замечание. Жесткость не зависит от приложенной силы и от величины удлинения, то есть является постоянной величиной для данной пружины. Это означает также, что графиком F(x) при упругих деформациях является прямая.
Задание. Постройте на том же рисунке (рис. 20.4) график зависимости величины деформирующей силы от удлинения пружины, жесткость которой 1 Н/см.
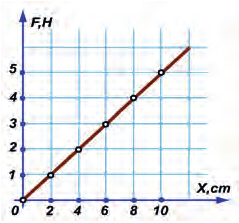
Рис. 20.7. График F(x)
Динамометр измеряет силу:
Прямо пропорциональная зависимость между деформацией «x» и деформирующей силой «F» позволяет использовать пружину для измерения силы. Прибор, с помощью которого измеряют величину силы, называют динамометром. Этот тер-мин происходит от двух греческих слов: динос – сила и метрон – измерять.
Основной деталью динамометра является стальная пружина. Сталь выбрана потому, что это достаточно упругий материал. К свободному концу пружины прикреплена стрелка, которая двигается вдоль шкалы с делениями, напротив которых указана величина силы (рис. 20.8). Динамометр имеет ограничитель, который не позволяет пружине удлиняться за пределы прямой пропорциональности
Пример №3
а) Какая жесткость пружины динамометра (рис. 20.8), если расстояние между нулевой и первой отметкой шкалы составляет 2,5 см? б) С какой силой действует на пружину батарейка?
Решение.
а) Согласно формуле (20.2)
k = 1H / 2,5 см = 0,4 H/см. б) Цена деления шкалы динамометра составляет 0,1 Н. Следовательно, он показывает силу 1,9 Н. Стандартная запись результата измерения силы:
F = (1,90 ± 0,05)H
Замечание. Начальное положение стрелки динамометра не совсем точно совпадает с нулем шкалы, потому груз действует на пружину с несколько меньшей силой, чем указывает стрелка. Можно попробовать оценить поправку.
Практическая ценность научного исследования
При строительстве кораблей, самолетов, домов, мостов, башен используют балки, которые служат опорами или же перекрытием. Проведем простой опыт, идея которого совершила революцию в строительной индустрии.
Опыт:
Возьмем длинный резиновый ластик и воткнем в него несколько иголок так, чтобы они выступали из обеих сторон (рис. 20.9). Согнем ластик, моделируя прогиб балки. Видно, что с одной стороны концы иголок сблизились, а с другой – разошлись. Это свидетельствует о том, что нижняя сторона нашей «балки» сжимается, а верхняя – растягивается.

Рис. 20.9. Деформация изгиба показывает, что внутренняя часть ластика не деформируется
А что происходит с серединой балки? Очевидно, что она деформируется мало. Это значит, что внутренняя часть балки может быть пустой без существенного вреда для прочности балки. Круглую сплошную балку можно заменить трубой, прямоугольную –П-образной, Т-образной, волнистой (как шифер) или же похожей на рельсы, из которых монтируют железнодорожные пути.
Вы наверняка видели, что железобетонные плиты, которыми перекрываются этажи многоэтажных домов, имеют внутри трубоподобные пустоты (рис. 20.10). Эти «хитрости» дают следующие выгоды: а) уменьшение затрат матери-ала; б) уменьшение веса конструкции; в) улучшение тепло- и звукоизоляции.
Второй идеей, которая существенно изменила способ строительства, стало использование армированного железными прутьями бетона. Дело в том, что железо хорошо выдерживает деформацию растяжения, а бетон крепок «на сжимание». Таким образом, железобетон выдерживает любые деформации
Итоги
- Силой называется количественная мера взаимодействия тел.
- Деформацией называют изменение размеров или формы тел. Существуют деформации растяжения-сжатия, изгиба, сдвига, кручения.
- Закон Гука позволяет описать все виды деформации.
- Формула закона Гука для упругой деформации растяжения-сжатия: F = kx.
- Силу измеряют динамометром. Основная деталь прибора – стальная пружина.
- Знание физики деформаций привело к революции в строительной индустрии
Роберт Гук (Robert Hooke, 1635–1703) родился в 1635 г. на острове Уайт в семье церковного служителя. После окончания школы учился в Оксфордском университете. Начинал работать как ассистент известного физика Ро-берта Бойля, помогая ему конструировать воздушный насос. Гук построил большой зеркальный телескоп и открыл звездное скопление в созвездии Ориона – так называемую Трапецию Ориона, а также впервые заметил, что Юпитер вращается вокруг собственной оси. Кроме того, Гук усовершенствовал микроскоп и изучал строение кристаллов, в частности снежинок; ввел понятие «клетка» в биологии; рассматривал возможность создания искусственных волокон; в 1672 году открыл дифракцию света и, чтобы объяснить это явление, предложил волновую теорию света.

Гук оказался первым, кто доказал, что тела при нагревании расширяются, и изложил гипотезу, что воздух состоит из маленьких частиц, расположенных на относительно больших расстояниях. Он также догадался, что планеты движутся вокруг Солнца по эллипсам и притягиваются к нему с силой, обратно пропорциональной квадрату расстояния от планеты до Солнца (но не сумел этого доказать). Гук предложил использовать для исследования силы тяжести маятник. В 1660 году ученый открыл закон упругих де-формаций, то есть доказал, что упругое удлинение твердых тел пропорционально прилагаемой силе. Он даже сделал попытку теоретически объяснить свой закон взаимодействием атомов, из которых состоят тела, и показал, что жесткость пружины зависит не только от материала пружины, но и от ее длины и площади сечения. Гук применил закон упругих деформаций для исследования часовых пружин.
Ускорение
Когда футболист бьет ногой по мячу, то мяч резко увеличивает свою скорость, в то время как скорость ноги при ударе несколько уменьшается (рис. 21.1). При этом выполняется важный закон природы, который еще называют третьим законом Ньютона: в инерциальной системе отсчета силы, с которыми тела действуют друг на друга, одинаковы по величине и противоположны по направлению. Это можно коротко записать так:
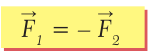 (21.1)
(21.1)

Рис. 21.1. Сила F1 действует на мяч, сила F2 – на ногу
Знак «–» указывает на то, что силы противоположны. Кроме того, силы взаимного действия направлены вдоль одной прямой и приложены к разным те-лам. В нашем примере сила F1 действует на мяч вперед, а сила F2 – на ногу футболиста назад. Линии действия этих сил совпадают. Ньютон сформулировал ІІІ-й закон очень просто: действие равняется противодействию.
Равнодействующая сил
Равнодействующей называется сила, результат действия которой на тело со-впадает с результатом одновременного действия всех приложенных к телу сил.
Графическое изображение сил
Рассмотрим силы, которые действуют вдоль одной прямой.
а) Когда силы направлены в одну сторону, то величина их равнодействующей равняется сумме величин этих сил и направлена в ту же сторону.
б) Если силы противоположно направлены, то величина их равнодействующей равняется разности величин этих сил и направлена в сторону большей силы.
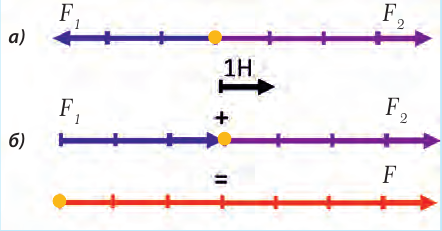
Рис. 21.2.
а) Силы вычитаются, когда они направлены в противоположные стороны.
б) Силы слагаются, когда они действуют в одном направлении
На рис. 21.2 выбран масштаб, при котором 1 см отвечает силе 1 Н. Тогда сила F1 = 4h будет изображена вектором, длина которого составляет 4 см, а сила F2 = 3h – вектором, длина которого составляет 3 см.
Равнодействующую сил F1 и F2 обозначим как F, это записывают так: F = F1 + F2. В случае а) результат общего действия сил F1 и F2 на данное тело будет та-кой же, как у силы F величиной 1 H, направленной вправо. В случае б), когда силы F1 и F2 действуют в одном направлении, их равнодействующая равняется сумме этих сил, то есть 7 H, и направлена так же, как и векторы этих сил.
Сложение сил, направленных произвольным образом
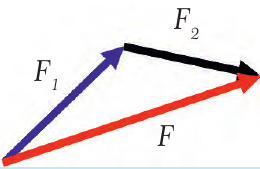
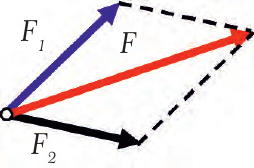
Силы складываются как векторы, то есть так же, как перемещение и скорости (рис. 21.3). При сложении сил принято проводить их из одной точки (точки приложения), как на рис. 21.4. Очевидно, что результаты сложения сил по правилу треугольника и правилу параллелограмма одинаковы. На рис. 21.5. изображен частный случай, когда силы направлены под прямым углом. В любом случае равнодействующая сила F = F1 + F2. Как уже говорилось в предыдущих параграфах, получить численное значение суммы сил, направленных произвольным образом, можно, выбрав длину стрелок в определенном масштабе.
 |
 |
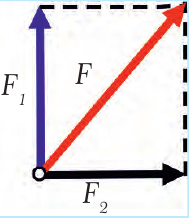 |
| Рис. 21.3. Сложение сил по правилу треугольника | Рис. 21.4. Сложение сил по правилу параллелограмма | Рис. 21.5. Сложение сил, направленных под прямым углом |
Пример №4
На тело в точке А (рис. 21.6) действуют три силы, пронумерованы как 1, 2 и 3. Каким будет результат действия этих сил на тело?
Решение. Найдем равнодействующую сил 1 и 3. Из рис. 21.7 видно, что равнодействующая этих сил есть вектор силы 4, который компенсирует силу 2. Следовательно, равно-действующая сил в точке А равняется нулю и тело не изменит своего состояния движения.
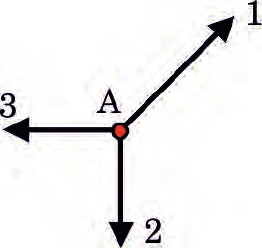
Рис. 21.6. На тело в точке А действуют три силы
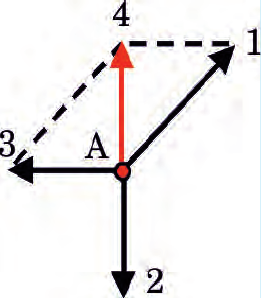
Рис. 21.7. Заменим силы 1 и 3 равнодействующей 5
Что нужно знать о ускорение
В случае, когда действующие на тело силы не компенсируются, его скорость изменяется и оно двигается неравномерно. Для полного описания неравномерного движения необходимая величина, которая бы показывала, как быстро изменяется скорость во времени. Эту величину называют ускорением и обозначают буквой «a» (от англ. аcceleration – ускорение).
Пусть тело, двигаясь прямолинейно, имело в некоторый начальный момент времени «t0» скорость «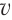 0», а в более поздний момент времени «t» его скорость стала равна «
0», а в более поздний момент времени «t» его скорость стала равна «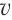 ». За промежуток времени (t – t0) скорость тела изменилась на величину (
». За промежуток времени (t – t0) скорость тела изменилась на величину (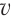 –
– 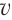 0). Ускорение – это векторная физическая величина, которая равняется отношению изменения скорости тела к промежутку времени, за который состоялось это изменение:
0). Ускорение – это векторная физическая величина, которая равняется отношению изменения скорости тела к промежутку времени, за который состоялось это изменение:
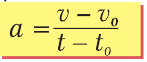 (21.2)
(21.2)
Ускорение показывает, на сколько изменяется (увеличивается или уменьшается) скорость тела за единицу времени.
Пример №5
Скорость тела за 5 с равномерно увеличилась от 6 м/с до 21 м/с. Чему равно ускорение тела?
Дано: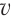 0 = 6 м/с 0 = 6 м/с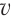 = 21 м/с = 21 м/сt = 5 c |
Решение: |
| a – ? |
Ответ. Ускорение тела 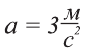 (читают: три метра за секунду в квадрате или, как говорят пилоты, три метра в секунду за секунду).
(читают: три метра за секунду в квадрате или, как говорят пилоты, три метра в секунду за секунду).
Именно в профессии военного летчика и космонавта учитывать ускорение очень важно, поскольку самолет (рис. 21.8) и ракета (рис. 21.9) могут двигаться с большими ускорениями, что, в свою очередь, приводит к значительным перегрузкам (увеличению веса тела). Почти предельные перегрузки чувствует летчик при катапультировании, когда кресло покидает кабину под действием пороховых зарядов, действующих подобно ракетам. Значительные ускорения и, соответственно, перегрузки, чувствуют на крутых виражах бобслеисты, горнолыжники и пилоты гоночных машин Формулы-1 (рис. 21.10).
 Рис. 21.8. Ускорение самолету придают мощные двигатели |
 Рис. 21.9. Ракета стартует с большим ускорением |
 Рис. 21.10. Сила тяги ускоряет автомобиль, а силы трения и сопротивления воздуха уменьшают его скорость |
Пример №6
Скорость тела за 3 с равномерно уменьшилась с 12 м/с до 6 м/с. Чему равно ускорение тела?
Дано: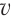 0 = 12 м/с 0 = 12 м/с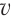 = 6 м/с = 6 м/сt = 3 c |
Решение: |
| a – ? |
Ответ. Ускорение тела: 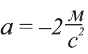
Сила и ускорение
Если силы, которые действуют на тело, не компенсируются, то тело одно-временно и деформируется, и изменяет свою скорость (то есть двигается с ускорением). Уточним определение силы: сила – это векторная физическая величина, которая является следствием действия на тело других тел и вызывает деформацию и ускорение.
Пример №7
Когда автомобиль трогается с места, сила тяги должна превысить силы, которые мешают движению (надо сильно жать на педаль акселератора).
Когда же автомобиль набрал нужную скорость, водитель жмет на акселератор только в той мере, чтобы сила тяги, действующая на автомобиль вперед, компенсировала силу трения и силу сопротивления воздуха, которая на большой скорости становится существенной.
При таких условиях ускорение становится равным нулю (то есть скорость не изменяется), и автомобиль двигается равномерно. (На рис. 21.10 силы, мешающие движению, изображенные зеленой стрелкой, а сила тяги – красной).
Сила, масса и ускорение
Ускорение тела зависит от величины равнодействующей тех сил, которые на него действуют, и от массы тела. Чем больше, например, масса автомобиля, тем медленнее он будет набирать скорость при данной силе тяги, то есть меньшим будет его ускорение. Масса тела является мерой инертности этого тела, и чем больше масса, тем большее усилие нужно приложить, чтобы изменить скорость тела, то есть придать ему ускорение. Этот факт отображен во втором законе Ньютона: в инерциальной системе отсчета тело двигается с ускорением, прямо пропорциональным равнодействующей сил, которые действуют на тело, и обратно пропорциональным массе тела. Направление ускорения совпадает с направлением равнодействующей.
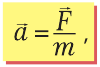
где m – масса тела, 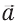 – его ускорение,
– его ускорение, 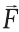 – равнодействующая сил тяги и сил трения, то есть их разность (потому что они противоположны).
– равнодействующая сил тяги и сил трения, то есть их разность (потому что они противоположны).
Формула (21.3) показывает, что ускорение «a» тела будет тем большим, чем больше равнодействующая сил, которые на него действуют (при неизменной массе), и ускорение «a» будет тем меньше, чем больше масса тела (при неизменной равнодействующей силе).
В зависимости от того, направлена равнодействующая сила вперед или на-зад, тело будет увеличивать или уменьшать свою скорость.
Силу измеряют в ньютонах (Н), массу в килограммах (кг), а ускорение в м/с2. Согласно формуле F = m · a: H = кг · м/с2 – это значит, что равнодействующая сила 1 Н придает телу массой 1 кг ускорение 1 м/с2 в направлении, совпадающем с направлением равнодействующей силы.
Пример №8
Сила тяги автомобиля составляет Fтяги = 4800 Н, а сила сопротивления Fсопр = 1800 Н. Масса автомобиля 1500 кг. а) Какое ускорение развивает автомобиль? б) Каким станет ускорение автомобиля, когда сила сопротивления вырастет до 4800 Н?
| Дано: Fтяги = 4800 Н а) Fсопр1 = 1800 Н б) Fсопр2 = 4800 Н m = 1500 кг |
Решение: Вычисления дают: б) Когда сила сопротивления вырастет до 4800 Н, |
| a – ? |
Ответ. а) Ускорение автомобиля: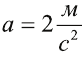 . б) а = 0, движение равномерное.
. б) а = 0, движение равномерное.
Столкновение тел
При столкновении (рис. 21.11), согласно ІІІ-му закону Ньютона, тела действуют друг на друга с одинаковыми по модулю и противоположно направленными силами независимо от их массы (формула 21.1). Если учесть также ІІ закон Ньютона (формула 21.3), то выходит, что при столкновении ускорение тела большей массы будет меньшим. В результате математических преобразований получаем:
m1 · a1 = – m2 · a2
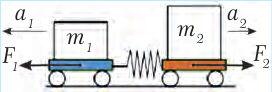
Рис. 21.11. F1 = F2 ; m2 > m1 , поэтому a2 < a1
Это соотношение справедливо при любом взаимодействии.
Рассмотрим простой случай, когда начальные скорости взаимодействующих тел равны нулю.
Пример №9
Две тележки массой m1 и m2, находящиеся на горизонтальной поверхности (рис. 21.12), скреплены пружиной, которая в начале опыта удерживается в сжатом состоянии нитью. После того, как нить пережгли, пружина растолкнула тележки, придав им некоторые скорости 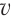 1 и
1 и 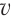 2.
2.
Во сколько раз будут отличаться скорости тележек?
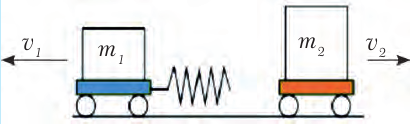
Рис. 21.12. m2 > m1 , тому 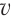 2 <
2 < 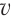 1
1
Решение. В этом упрощенном случае формула (21.2) дает такие результаты: 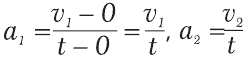 - взаимодействия одинаково. Тогда с помощью формулы (21.4) получаем: m1 ·
- взаимодействия одинаково. Тогда с помощью формулы (21.4) получаем: m1 · 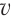 1 = – m2 ·
1 = – m2 · 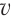 2, где знак «–» указывает на то, что тележки разъехались в разные стороны. Следовательно,
2, где знак «–» указывает на то, что тележки разъехались в разные стороны. Следовательно, 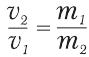 .Знак «–» в этом соотношении не ставится.
.Знак «–» в этом соотношении не ставится.
Ответ: 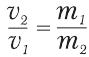 – скорость второй тележки во столько же раз больше скорости первой тележки, во сколько раз масса первой тележки больше, чем масса второй тележки. Или коротко: отношение скоростей обратно пропорционально отношению масс.
– скорость второй тележки во столько же раз больше скорости первой тележки, во сколько раз масса первой тележки больше, чем масса второй тележки. Или коротко: отношение скоростей обратно пропорционально отношению масс.
Итоги
- Сила – это векторная физическая величина, которая является следствием действия на тело других тел и вызывает деформацию и ускорение.
- Ускорение показывает изменение скорости тела в единицу времени.
- Второй закон Ньютона: ускорение, которое получает тело, прямо пропорционально равнодействующей сил, которые действуют на него, и обратно пропорционально массе тела.
- Третий закон Ньютона: силы, с которыми тела действуют друг на друга, одинаковы по величине и противоположны по направлению.
- При взаимодействии тел их ускорения противоположно направлены и обратно пропорциональны их массам.
Сила тяжести и вес тела
Где бы мы ни находились – высоко в горах, на равнине или в глубокой шахте – везде на нас действует сила тяжести. Интересно, почему же мы не проваливаемся «сквозь землю»?
Сила, с которой тело действует на опору
Рассмотрим тело 1 (рис. 22.1), которое находится в равновесии на горизонтально расположенной подставке 2. Подставкой в реальной жизни может быть дорога, пол или кресло.
На тело действует вертикально вниз со стороны Земли сила тяжести Fтяж, в результате чего со стороны тела на подставку перпендикулярно к поверхности действует сила давления FN. Обратное действие подставки на тело (реакция опоры N) является силой упругости и возникает в результате деформации тела и подставки.
Сила тяжести Fтяж и сила реакции опоры N в случае равновесия тела уравновешивают друг друга, то есть они равны по величине и противоположны по направлению.
Сила FN (действие тела на подставку) и сила N (противодействие подставки) всегда равны по величине и противоположны по направлению. Этот факт хорошо проверен на опытах и является следствием третьего закона Ньютона. Таким образом, тело, уравновешенное на горизонтальной подставке, действует на опору с силой FN, которая по величине и направлению равняется силе тяжести Fтяж.
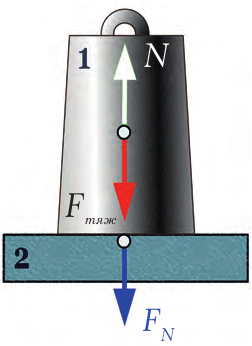
Рис. 22.1. Тeло 1 на подставке 2
Сила, с которой тело действует на подвес
Рассмотрим тело, подвешенное на тросе (рис. 22.2). На тело действует со стороны Земли сила притяжения Fтяж, в результате чего оно тянет трос вниз. Трос деформируется (растягивается) и действует на тело с силой натяжения, которую принято обозначать буквой T. Если тело уравновешено, то силы Fтяж и T должны компенсировать друг друга (то есть они равны по величине и противоположны по направлению). Силы T и T1 которые действуют на тело и потолок также равны, если пренебречь массой троса.
Силу FN и T1 обычно обозначают буквой P и называют весом. Вес – это сила, с которой тело действует на горизонтальную опору или растягивает вертикальный подвес в результате действия силы тяжести и движения опоры или подвеса с ускорением.
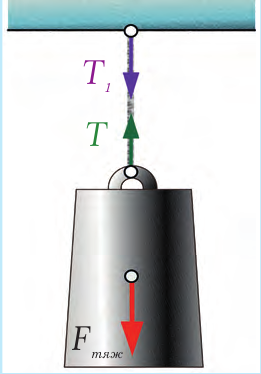
Рис. 22.2. Груз, подвешенный на тросе
Процедура взвешивания
Когда нужно взвесить тело, его кладут на чашу пружинных весов или подвешивают к пружине динамометра. Взвешивание требует соблюдения определенной процедуры. В частности, поверхность чашки должна быть горизонтальной, а пружина динамометра – размещенной вдоль вертикали. Кроме того, весы или динамометр должны быть неподвижными относительно тела отсчета (помещение, в котором происходит взвешивание).
Уточним понятие «вертикаль». Вертикаль – это линия, которая совпадает с нитью отвеса (рис. 22.3). Отвес легко изготовить, подвесив на нитке гайку.
Плоскость, перпендикулярную к вертикали, называют горизонтальной. Горизонтальность поверхности проверяют с помощью уровня – устройства, которое содержит несколько выгну-тую кверху трубку с водой, в которой находится пузырек воздуха. Поверхность воды в не слишком большом водоеме также горизонтальна.


Рис. 22.3.
а) Горизонтальность поверхности проверяют уровнем.
б) Нить отвеса определяет вертикаль
Свободное падение
В природе можно наблюдать движение, которое происходит с постоянным по величине ускорением. Это движение тела, когда никакие другие силы, кроме тяжести Земли, на него не действуют. Такое движение называют свободным падением, и его можно реализовать, на-пример, в вакууме. Движение парашютистов в затяжном прыжке лишь напоминает свободное падение (рис. 22.4).

Рис. 22.4. Под действием силы тяжести скорость парашютистов увеличивается
Если тело свободно падает, то есть двигается только под воздействием силы тяжести (например, в вертикальной трубе, из которой выкачали воздух), его скорость равномерно возрастает на 9,8 м/с за каждую секунду (ускорение составляет 9,8 м/с2). Ускорение свободного падения обозначают буквой «g». Если тело подбросить вверх, то его скорость будет уменьшаться на 9,8 м/с за каждую секунду (то есть его ускорение – 9,8 м/с2).
На рис. 22.5 изображен опыт с трубкой Ньютона. При наличии воздуха в трубке дробинка опережает перышко из-за сопротивления воздуха. Если откачать из трубки воздух, то перышко и дробинка падают одинаково (случай «а» и «б»). Рядом (случай «в») – фотография демонстрационного прибора, с помощью которого этот опыт можно показать. Удивительным в нем является то, что тела разной массы падают в вакууме с одинаковым ускорением.
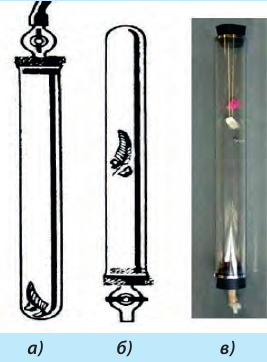
Рис. 22.5. Трубка Ньютона
Пример №10
Камешек выпустили из рук на высоте 25 м. а) Какова будет его скорость через 1 с и 2 с? б) Какое расстояние камешек пролетит за первую секунду и за две секунды? Считайте, что камешек свободно падает с ускорением g = 10 м/с2.
Решение.
а) Поскольку скорость тела при движении вниз растет на 10 м/с за каждую секунду, то в конце первой секунды скорость камешка будет составлять 10 м/с, а через две секунды – 20 м/с. б) Поскольку скорость камешка за первую секунду падения равномерно возрастет до 10 м/с, то его средняя скорость равняется среднему арифметическому от начальной и конечной скоростей, то есть 5 м/с. Следовательно, пройденное им за первую секунду расстояние равняется 5 м.
Аналогично, за две секунды средняя скорость составляет 10 м/с и пройденное расстояние равняется 20 м.
Пример №11
Стрела при выстреле из лука вертикально вверх вылетает со скоростью 30 м/с. Какими будут скорость стрелы (v) и ее высота (h) через 1, 2, 3, …, 6 с? Считайте, что стрела двигается с постоянным по величине ускорением g = – 10 м/с2.
Решение.
В данном случае ускорение стрелы отрицательно, то есть ее скорость каждую секунду уменьшается на 10 м/с. Через секунду скорость станет 20 м/с, через две секунды 10 м/с, и так далее. Будет удобно записать результаты расчетов в таблицу:
| t, c | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 , м/с , м/с |
30 | 20 | 10 | 0 | -10 | |||
| h, м | 0 | 25 | 40 |
Через три секунды скорость стрелы равняется нулю, то есть она достигла наивысшей точки своей траектории и дальше будет падать вниз. Через четыре секунды скорость стрелы составляет –10 м/с, знак «–» показывает, что стрела изменила направление движения. Средняя скорость стрелы за первую секунду равняется: (30 + 20)/2 = 25 м/с, следовательно, она достигнет высоты 25 м/с · 1 с = 25 м.
Задание. Остальные клеточки таблицы заполните самостоятельно.
Сила тяжести и масса
Поскольку при свободном падении сила тяжести придает телу ускорения g, то согласно формуле 21.3 второго закона Ньютона можно записать, что:
Fтяж = mg (22.1)
Таким образом, зная массу тела, по формуле (22.1) можно вычислить силу тяжести, которая на него действует.
Пример №12
Ясли ваша масса равняется 50 кг, то сила тяжести, которая действует на вас, составляет Fтяж = 50 кг · 9,8 м/с2 = 490 Н. В случае, когда опора, на которой вы стоите, горизонтальная и не двигается с ускорением, ваш вес P также будет составлять 490 Н (P = 490 H).
Нужно только помнить, что вес – это сила, которая действует на опору либо подвес, а сила тяжести действует на тело.
Если нужно по данной массе тела найти силу тяжести, которая действует на это тело,
то пишут: Fтяж = m · 9,8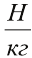 . В таком случае g используют как коэффициент пропорциональности для перехода от единиц массы к единицам силы. Но если хотят подчеркнуть, что сила тяжести придает свободно падающему телу ускорение
. В таком случае g используют как коэффициент пропорциональности для перехода от единиц массы к единицам силы. Но если хотят подчеркнуть, что сила тяжести придает свободно падающему телу ускорение 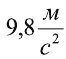 , то пишут
, то пишут 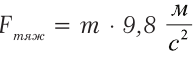 .
.
При не очень точных расчетах g округляют до 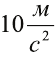 .
.
Пример №13
С какой силой действует на подставку тело массой 1 кг?
Решение: по формуле Fтяж = mg, Fтяж = 1 кг · 9,8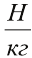 = 9,8Н. Следовательно, P = Fтяж
= 9,8Н. Следовательно, P = Fтяж 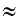 10 H.
10 H.
Кстати:
Если человека массой, скажем, 60 кг спросить, сколько он весит, то ответ, скорее всего, будет 60 кг, хотя правильно было бы сказать: приблизительно 600 Н. Такая путаница возникает из-за того, что когда-то массу и вес измеряли в одинаковых единицах – килограммах.
Невесомость
Если телу 1 и подставке 2 (рис. 22.1) предоставить возможность вместе свободно падать, то деформации, вызванные взаимодействием этих тел, исчезают, то есть силы FN и N становятся равными нулю. Такое состояние называют невесомостью. Невесомость наступает потому, что подставка и тело падают с одинаковым ускорением, независимо от того, какова их масса.
Невесомость одинаково наступает при свобод-ном падении вниз или вертикальном движении. То есть если подбросить тело, то его вес равняется нулю как на стадии подъема, так и на спуске.
Когда космический корабль выходит на околоземную орбиту и выключает двигатели, на-ступает невесомость. Человек довольно плохо переносит это состояние, и в будущем планируют делать космические станции в виде вращающейся «баранки», внутри которой будет создан искусственный вес (рис. 22.7).

Рис. 22.7. Будущие космические станции будут вращаться
Кстати:
Вес можно искусственно увеличить, как это де-лается в центрифуге стиральной машины. В научных лабораториях используют ультрацентрифуги (рис. 22.8), где вес предметов может возрастать в полмиллиона раз по сравнению с нормальным, который численно всегда равняется mg.

Рис. 22.8. Вес тела в ультрацентрифуге может превышать нормальный в 70 000 раз
Итоги
- Силу, с которой тело действует на горизонтальную опору или вертикально размещенный подвес, называют весом.
- Сила тяжести, которая действует на тело со стороны Земли, пропорциональна массе тела и рассчитывается по формуле Fтяж = mg.
- В системе отсчета, которая не ускоряется, вес тела: P = mg. При свободном падении тел наступает невесомость.
- Тело, которое находится в состоянии свободного падения, двигается около поверхности Земли с ускорением: а) +9,8 м/с2, когда летит вниз; б) –9,8 м/с2, когда летит вверх.
Силы трения
Трение в природе и технике:
Явление трения играет важную роль в нашей повседневной жизни, в природе и технике. Обратите внимание, как трудно идти или ехать на автомобиле в гололед, когда сила трения незначительна. Если бы исчезло трение, мы не могли бы усидеть на стуле, а гвозди не держались бы в стене. Увеличение силы трения бывает жизнен-но необходимым (рис. 23.1).
Так же важно во многих случаях уменьшить трение. Шариковые подшипники уменьшают трение в осях многих деталей машин и механизмов (рис. 23.2). А как чудесно скользят лыжи и коньки!

Рис. 23.1. Надежность торможения зависит от силы трения

Рис. 23.2. Шариковый подшипник
Опыт:
Положим на книгу, которая лежит на сто-ле, коробку спичек. Начнем поднимать один конец книги, увеличивая угол наклона (рис. 23.3). Некоторое время коробка будет не-подвижной, но при определенном угле на-клона она начнет соскальзывать вниз.
Приведенный опыт вызывает по край-ней мере два вопроса: а) почему коробка не скользит при малых углах и б) почему короб-ка при больших углах начинает скользить?
Одна из причин возникновения силы трения – это шершавость обеих соприкасающихся поверхностей (рис. 23.4). Маленькие неровности, которые обуславливают шершавость поверхностей, цепляются друг за друга при движении тела или при попытке сдвинуть его с места.
Трение скольжения
Трение, которое возникает при скольжении тела, называют трением скольжения. Несложные опыты показывают, что сила трения скольжения Fтр прямо пропорциональна величине силы реакции опоры N. Вектор силы трения скольжения направлен параллельно плоскости соприкосновения в сторону, противоположную направлению движения
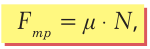 (23.1)
(23.1)
где μ (мю) – коэффициент пропорциональности, который зависит от материала поверхностей (табл. 23.1) и качества их обработки и называется коэффициентом трения.
Коэффициент трения скольжения μ можно определить как отношение силы трения скольжения к величине силы реакции опоры:
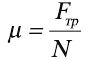 (23.2)
(23.2)
Вели чина коэффициента трения зависит от материала скользящих поверхностей и рельефа поверхности. Коэффициент трения является безразмерной величиной.
Сила трения скольжения очень слабо зависит от площади прикосновения скользящих поверхностей тел и скорости движения. Когда тело двигают по горизонтальной поверхности, сила реакции опоры численно равняется силе тяжести Fтяж и весу тела P. В этом случае можно записать формулу для расчета силы трения скольжения так:
Fтр = μ · P = μ · m · g (23.3)
Таблица 23.1 Коэффициенты трения
| Материалы | |
| Дерево по дереву | 0,25 |
| Сталь по стали | 0,20 |
| Резина по бетону | 0,75 |
| Сталь по льду | 0,05 |
| Сталь по стали, смазанные маслом | 0,05 |
Трение покоя
Когда некая параллельная к поверхности сила тяги F безрезультатно пытается сдвинуть тело с места (рис. 23.5), то понятно, что эта сила уравновешена какой-то другой силой, которая точно равняется прилагаемой силе по величине и противоположна ей по направлению. Эту силу называют силой трения покоя.
 |
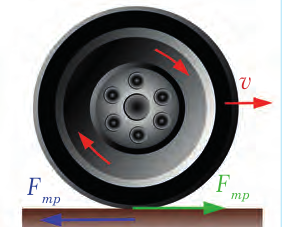 |
| Рис. 23.5. Сила трения покоя равна силе, питающейся двигать тела | Рис. 23.6. Трение покоя толкает ведущее колесо |
Сила трения покоя заставляет автомобиль двигаться и поворачивать. Она удерживает в покое тело, которое находится на наклонной плоскости. Благодаря этой силе мы ходим. Сила, с которой шина ведущего колеса автомобиля в месте соприкосновения с дорогой действует на поверхность дороги, направлена назад. Эта сила вызывает появление силы трения покоя, которая действует на колесо вперед, создавая силу тяги автомобиля (рис. 23.6).
Подобное явление отмечаем и при ходьбе.
Трение качения
Трение, которое действует на катящееся колесо, называют трением качения. Оно гораздо меньше трения скольжения, поэтому почти все виды наземного транспорта имеют колеса, а оси механизмов установлены на шариковые подшипники. Трение качения тем меньше, чем больший радиус колеса и чем тверже поверхности колеса и дороги. Оно также пропорционально силе реакции поверхности и зависит от материала обеих поверхностей.
Вязкое трение
Во время движения в жидкости или в газе возникает вязкое трение, которое гораздо меньше даже трения качения. Существуют специальные транспортные средства на «воздушной подушке», которые «летают» над землей или поверхностью воды. Примером могут быть скоростные паромы и некоторые виды военных десантных катеров. Проходят испытания поезда на «магнит-ной подушке», которые удерживаются в воздухе силами магнитного поля (рис. 23.8). По своей быстроходности они приближаются к самолетам. Важная особенность, которая существенно выделяет вязкое трение, заключается в том, что у него а) нет трения покоя, б) величина вязкого трения растет с увеличением скорости движения.
Трущиеся детали машин смазывают маслами, чтобы сделать трение вязким и уменьшить потери энергии.

Рис. 23.8. Сила вязкого трения возникает при движении в жидкости или в газе
Итоги:
- Сила трения скольжения прямо пропорциональна величине силы реакции опоры Fтр = μ · N.
- Вектор силы трения скольжения направлен параллельно плоскости соприкосновения в сторону, противоположную направлению движения.
- Сила трения покоя равняется и противоположна той силе, которая не может сдвинуть тело с места.
- Трение качения намного меньше трения скольжения.
- Вязкое трение возникает при движении в жидкости или газе. Не существует вязкого трения покоя.
Сила давления и давление твердых тел на поверхность
Об атмосферном давлении часто сообщают синоптики в прогнозах погоды, артериальное давление измеряет врач. В физике давлением называют физическую величину, которая численно равняется силе давления на единицу площади поверхности (рис. 24.1). Давление обозначают буквой «Р» (от англ, pressure - давление).
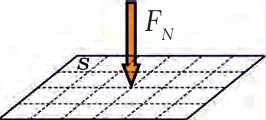
Рис. 24.1. Давление численно равняется силе, которая действует на единицу площади
Вычисление давления
Чтобы вычислить давление, нужно величину перпендикулярной поверхности силы давления FN разделить на площадь этой поверхности S:
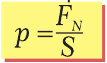
В отличие от силы, давление – скаляр. В СИ, где силу измеряют в H (ньютоне), а площадь – в м2, давление измеряется в 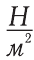 .
.
Сила давления величиной в 1 Н, которая действует на площадь в 1 м2, создает давление величиной в 1 Паскаль, то есть Па = H/м2. Единица давления на-звана в честь французского физика и математика, изобретателя первой механической вычислительной машины, гидравлического пресса и медицинского шприца, философа и писателя Блеза Паскаля.
Один Паскаль – очень маленькое давление (сравним с нормальным атмосферным давлением 760 мм рт. ст., которое составляет 101 325 Па, или приблизительно 100 000 Па = 105 Па).
В технике часто применяют более удобную единицу давления: одна физическая атмосфера (атм), 1 атм = 101 325 Па точно, или ≈100 000 Па. Например, давление в камере автомобильного колеса составляет приблизительно 2 атм.
От чего зависит давление
Если идти пешком по глубокому снегу – ноги проваливаются, а если на лыжах – нет. Сила давления на снег одна и та же. В чем же разница? А в том, что давление, которое создают на снег лыжи, намного меньше, поскольку их площадь значительно больше площади подошв. Следовательно, такая величина, как давление, в данном случае лучше объясняет явление, чем сила давления.
Увеличить давление, как видно из формулы (24.1), можно: или увеличивая силу давления, или уменьшая площадь поверхности, на которую действует сила. Например, пчела (рис. 24.2) при укусе создает большое давление, по-скольку площадь жала очень мала. Трактор (рис. 24.3) или даже танк давят на поверхность более слабо, чем мы при ходьбе, из-за большой площади гусениц.
 Рис. 24.2. Тонкое жало пчелы проникает сквозь кожу |
 Рис. 24.3. Трактор оказывает меньшее давление, чем нога человека |
Пример №14
Сравним давление, которое создают каблуки девушки и нога слона (рис. 24.4).
| g ≈ 10 H/кг | Девочка | Слон |
| Масса (m) | 50 кг | 4 000 кг |
| Сила тяжести (mg) | 500 Н | 40 000 Н |
| Сила давления (FN) | 500 Н | 40 000 Н |
| Площадь опори (S) | 2 см2 | 1 000 см2 |
| Давление (p = FN /S) | 250 Н/см2 | 40 Н/см2 |

Рис. 24.4. Кто «сильнее»?
Массы девушки и слона, а также площади каблучка и ступни слона взяты приблизительно (как это делают в оценочных задачах).
Пример №15
Пусть острый конец иглы имеет линейные размеры 0,1 мм (не очень острая игла). Тогда площадь острия будет составлять приблизительно 0,01 мм2. Если иглу придавить гирей 10 кг, то давление, с которым она будет давить на стол, будет в 100 000 раз больше атмосферного. Под таким давлением и при температуре 2300°С в 1955 году впервые получили искусственные алмазы.
Кстати:
Очень большое давление – 400 000 атм с помощью гидравлического пресса впервые получил американский инженер Бриджмен. Сверхсильные давления на больших площадях получают с помощью взрыва. Во время взрыва атомной бомбы создается давление в 10 000 миллиардов атм.
Пример №16
Оцените ваше давление на пол. Напомним, что площадь подошвы, получив ее отпечаток на листе бумаги в клеточку, можно подсчитать способом, указанным на рис. 24.6. Для этого нужно к числу целых клеточек прибавить половину числа нецелых клеточек и полученное число умно-жить на площадь одной клеточки. Сторона клеточки составляет 0,5 см.
 Рис. 24.5. Перси Бриджмен Рис. 24.5. Перси Бриджмен |
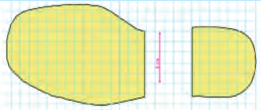 Рис. 24.6. Способ приблизительного вычисления площади подошвы Рис. 24.6. Способ приблизительного вычисления площади подошвы |
Итоги:
- Давление численно равно силе давления на единицу площади поверхности.
- Давление равняется отношению величины силы давления к площади поверхности:
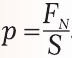
- Нормальное атмосферное давление составляет 760 мм рт. ст., что равняется 101 325 Па, то есть приблизительно 100 000 Па = 105 Па.
- Одна физическая атмосфера (атм): 1 атм = 101 325 Па.
Давление жидкостей и газов
Закон Паскаля:
Сила давления в жидкостях и газах действует во всех направлениях. Это можно продемонстрировать на простом опыте (рис. 25.1). Нужно крепко насадить на шприц мячик от настольного тенниса и сделать в нем иглой ряд симметрично находящихся отверстий. Потом наполнить цилиндр шприца и мячик водой. Если нажать на поршень вниз, то вода брызнет из отверстий во все стороны.
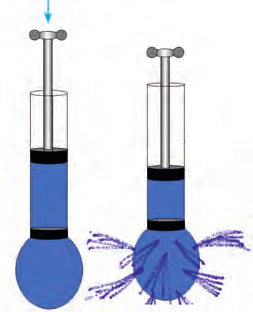
Рис. 25.1. Сила давления действует во всех направлениях
Объясним детальнее: сначала давление выросло около поршня, затем давление выросло и во всех других точках воды. Сила давления около отверстий направлена перпендикулярно поверхности мячика, а ее величина пропорциональна давлению:
FN = p ∙ S (25.1)
Закон Паскаля: давление в жидкостях и газах передается во все точки и во всех направлениях одинаково.
Давление жидкости
Вычислим давление в некоторой точке A, которая находится на глубине h в жидкости, плотность которой – ρ. Мысленно выделим прямоугольный столб жидкости высотой h, который опирается на поверхность площадью S (рис. 25.2). Объем выделенной геометрической фигуры можно вычислить по формуле V = S ∙ h. Сила давления столба жидкости FN равняется силе тяжести, которая действует на всю массу m жидкости выделенного объема и может быть вычислена как mg. Массу жидкости вычислим по формуле m = ρ · V. Тогда сила давления вы-деленного столба жидкости будет представлять:
FN = ρ · S · h · g. Давление жидкости на глубине h согласно формуле (26.1) будет составлять:
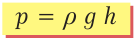 (25.2)
(25.2)
Это формула гидростатического давления (гидро-, лат. – вода, статикос, греч. – неподвижный). Чтобы получить по этой формуле давление в паскалях (то есть в H/м2), надо плотность выразить в кг/м3, а глубину – в метрах.
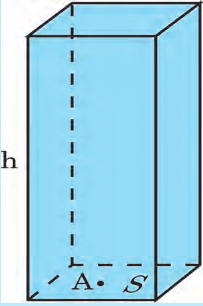
Мал. 26.2. Чем выше столб жидкости h, тем больше давление в точке А
Пример №17
Найдите давление столба воды высотой 10 м. Примем 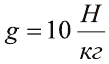 .
.
| Дано: h = 10 м ρ = 1000 кг/м3 g = 10 H/кг |
Решение: Окончательно |
| p – ? |
Ответ: давление столба воды высотой 10 м составляет приблизительно 100 000 Па.
Гидростатический парадокс
Обратите внимание, что давление, которое создается столбом жидкости, зависит только от плотности жидкости и высоты столба, и не зависит от площади, которая сокращается при математических преобразованиях. Этот результат на первый взгляд кажется неожиданным, поэтому его называют гидростатическим парадоксом (парадокс – утверждение, которое кажется неправильным или невозможным).
Давление жидкости не зависит от формы сосуда, в которой она находится, а только от высоты столба жидкости и ее плотности. Это утверждение можно продемонстрировать с помощью сообщающихся сосудов – прибора, состоящего из трубок разной формы и сечения, соединенных между собой и размещенных в вертикальной плоскости (рис. 25.3). Если жидкость неподвижна (статична), то она во всех сосудах устанавливается на одинаковом горизонтальном уровне. Водопроводная система или чайник – примеры сообщающихся сосудов.
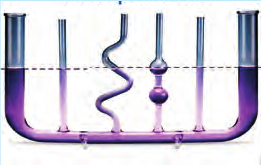
Рис. 25.3. Уровень жидкости в сообщающихся сосудах одинаковый
Таблица 25.1 Плотность некоторых жидкостей
| Жидкость | ρ, кг/м3 | ρ, г/см3 |
| Вода | 1000 | 1,00 |
| Растит., машинное масло | 900 | 0,90 |
| Спирт | 800 | 0,80 |
| Ртуть | 13 600 | 13,60 |
| Жидкий воздух (при -194ºC) | 860 | 0,86 |
История:
Паскаль в свое время поразил своих сограждан таким опытом, проведенным при всеобщем обозрении (рис. 25.4). Ученый заявил, что нарушит герметичность самой проч-ной бочки одной кружкой воды. Бочка должна была иметь герметичную крышку с латунной вставкой, в которой сделано отверстие с нарезанной резьбой определенного диаметра. Перед началом опыта бочку нужно было доверху наполнить водой. Цех бондарей (так называют мастеров, изготавливающих бочки) принял вызов. В определенный день бочка наивысшего качества была наполнена водой, и в нее вкрутили трубу высотой несколько метров. Внутренний диаметр трубы был таков, что туда помещалась как раз одна кружка воды. На втором этаже здания, вблизи которого проводился опыт, в трубку вставили лейку и влили всю воду, которая была в кружке. К удивлению присутствующих, бочка треснула по швам, и из нее брызнула вода!
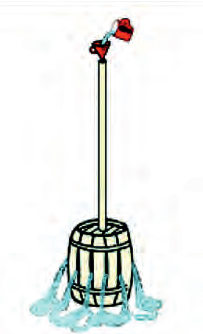
Рис. 25.4. Опыт Паскаля
Пример №18
Давайте выясним, что произошло в опыте с бочкой. Допустим, что она имела форму цилиндра (для упрощения расчетов) высотой H = 1 м и диаметром немного меньше 70 см (для того, чтобы длина периметра крышки составляла приблизительно 2 м: L = πd). При высоте трубки 3,5 м давление столба воды в центре бочки (добавляем еще 0,5 м) равнялось:
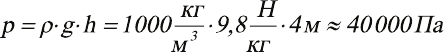 .
.
Около дна давление немного больше, около крышки – меньше, средняя сила давления, действующая на боковую поверхность бочки (площадь которой равняется 2 м2) будет равняться:
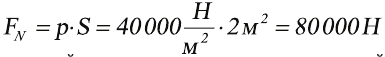 .
.
С такой силой будет действовать на опору груз массой приблизительно 8 000 кг, то есть 8 тонн! Действие такой значительной силы ни одна деревянная бочка не выдержит.
Глубинные аппараты
Впервые погружения на значительную глубину осуществил швейцарский физик и инженер Огюст Пикар. Еще с детства он увлекался книгами о морских путешествиях. Батискаф, построенный Пикаром, опустился в 1948 году на глубину 1 400 м, выдержав огромное давление воды. В 1953 году батискаф «Триест» достиг глубины 3 150 м. В 1957 году советский аппарат «Витязь» опустился на глубину 10 022 м. В 1960 году «Триест», в котором находился сын Огюста Пикара Жак, опустился в Марианскую впадину в Тихом океане на глубину 10 916 м. Аппараты Пикара были автономными и не нуждались в росе, который связывал бы их с кораблем. Дело в том, что трос такой длины не может выдержать даже собственного веса. Строительство глубинных аппаратов требует решения очень сложных инженерно-технических проблем, актуальных и в наше время.
Итоги:
- Давление в жидкостях и газах передается во все точки и во всех направлениях одинаково (закон Паскаля).
- Давление жидкости вычисляется по формуле p = ρgh.
- Давление жидкости не зависит от формы сосуда (гидростатический парадокс).
Блез Паскаль (Blaise Pascal, 1623–1662) – французский математик, механик, физик, философ и писатель. Он сформулировал закон передачи давления, известный в настоящее время как закон Паскаля, доказал, что давление жидкости на дно сосуда не зависит от формы сосуда, а только от уровня жидкости.

Паскаль создал первую механическую вычислительную машину (один из распространенных языков программирования – Pascal - назван в его честь именно по этой причине). Было изготовлено около 50 экземпляров такой машины, даже налажено их серийное производство.
Паскаль изобрел гидравлический пресс, медицинский шприц, предложил идею регулярного городского транспорта, который курсирует улицами городов по установленным маршрутам.
Паскаль изучал проблемы вакуума и равновесия жидкостей, определил плотность воздуха, повторил и усовершенствовал опыты с ртутным барометром, установил, что атмосферное давление зависит от высоты. У своего дома Паскаль установил водяной барометр, который позволял всем желающим наблюдать за изменением атмосферного давления.
Атмосферное давление
Атмосфера:
Мы находимся на дне воздушного океана, который называется атмосферой (рис. 26.1), а над нами – примерно стокилометровый слой воздуха. Столб воздуха создает давление благодаря тому, что воздух притягивается к Земле. Для расчета этого давления формулу p = ρ · h · g можно применить только приближенно для не слишком больших h, поскольку воздух легко сжимается.

Рис. 26.1. Воздушная оболочка Земли – атмосфера
Существует простое приближенное правило: около поверхности Земли давление уменьшается на 1 мм рт. ст. при поднятии вверх на каждые 12 метров.
Мы не замечаем давления атмосферы только потому, что воздух внутри наших легких имеет такое же давление – таким образом, силы давления снаружи и внутри уравновешивают друг друга.
Совсем другое дело, когда вы нырнули глубоко в воду. Давление воды настолько большое, что вашу грудную клетку сожмет сила, которая не даст вам вдохнуть, даже если у вас есть акваланг. Поэтому аквалангист дышит сжатым воздухом, давление которого нужно регулировать так, чтобы он равнялся внешнему давлению воды на тело (рис. 26.2).

Рис. 26.2. Аквалангист дышит сжатым воздухом
Опыт Торричелли
Воздух кажется невесомым, и поэтому опыт итальянского физика и математика Эванджелиста Торричелли (ученика Галилея) поразил современников. Он заполнил запаянную с одного конца стеклянную трубку длиной около метра ртутью. Потом закрыл отверстие пальцем и, перевернув трубку, поместил открытый конец на небольшую глубину в чашку со ртутью, придерживая трубку в вертикальном положении. После того, как он от-крыл отверстие, часть ртути вылилась, но столб ртути высотой приблизительно 76 см все равно остался в трубке (рис. 26.4). В пространстве над столбиком ртути ничего не осталось, там был вакуум, или, как это в то время называли, торричеллиева пустота. Торричелли догадался, что столб ртути удерживается силой давления атмосферы. Следовательно, столб ртути высотой 76 см уравновешивает, словно на чаше весов, вес столба воздуха высотой в сто километров.

Рис. 26.4. Опыт Торричелли
Магдебургские полушария
Чтобы продемонстрировать землякам силу атмосферного давления, бургомистр города Магдебург Отто фон Герике провел эффектный опыт (рис. 26.6). Это было в 1654 году, в присутствии императора Фердинанда III. По заказу Герике были изготовлены два хорошо подогнанных друг к другу полых внутри медных полушария, из которых можно было сложить герметичный шар диаметром 14 дюймов (35,5 см). В одном из полушарий была трубка для откачивания воздуха, и каждое из полушарий имело на поверхности крепкое кольцо. Полушария совместили и откачали воздух из шара, который при этом образовался. Для этого использовали вакуумный воздушный насос, изобретенный тем же Герике. Давление атмосферы настолько сильно сжало полушария, что две упряжки по восемь коней в каждой не смогли их разорвать!

Рис. 26.6. Опыт с магдебургскими полушариями
Ртутный барометр
Прикрепив рядом с трубкой линейку (рис. 26.7), Торричелли заметил, что уровень ртути ежедневно изменяется. Следовательно, изменяется давление атмосферы. Фактически, Торричелли изготовил первый прибор для измерения атмосферного давления – ртутный барометр. Сегодня прогноз погоды не может обойтись без сообщения о величине атмосферного давления, значительное уменьшение которого может предугадать сильный ветер или даже ураган.
Паскаль повторил опыт Торричелли и установил, что атмосферное давление уменьшается в зависимости от высоты. Возле своего дома он смонтировал водяной барометр с трубой, высота которой достигала почти 11 м. Вода была подкрашена красным вином для удобства наблюдений за изменением уровня.
Поскольку испарения ртути ядовиты, ртутный барометр требует особо осторожного обращения с ним. Кроме того, он громоздок. Поэтому барометр Торричелли используется только в лабораториях. Величину атмосферного давления традиционно измеряют в миллиметрах ртутно-го столба (мм рт. ст.). Давление атмосферы, при котором высота столбика ртути в барометре составляет 760 мм, принято называть нормальным. Пишут: p0 = 760 мм рт. ст. (или 760 мм Hg). Чтобы выяснить, сколько «паскаль» составляет нормальное атмосферное давление, нужно воспользоваться формулой гидростатического давления (26.2), подставив туда плотность ртути и высоту ртутного столбика, выраженную в метрах:
p = ρ·g·h = 13 600 кг/м3·9,8 м/с2·0,76 м ≈ 100 000 Н/м2 = 100 000 Па

Рис. 26.7. Ртутный барометр
Барометр-Анероид
Для измерения атмосферного давления в быту преимущественно пользуются барометром-анероидом («анероид» значит «безжидкостный»). Вполне возможно, что он есть и у вас дома (рис. 26.8). Чувствительным элементом в этом барометре является металлическая герметичная коробочка, в которой давление воздуха несколько меньше атмосферного. Одна стенка крепится к корпусу, а другая посредством системы рычагов и зубчатых колес двигает стрелку прибора.
Чувствительность анероида достаточно большая – стрелка заметно смещается, если его поднять или опустить на несколько метров. Можно проградуировать шкалу анероида непосредственно в единицах высоты и получим высотомер – альтиметр. Такими приборами пользуются пилоты и альпинисты.
Если к стрелке барометра прикрепить перо, касающееся поверхности барабана, который вращается и на который натянута специальная бумага в клеточку, то получим барограф (рис. 26.9). Барабан вращается с помощью часового механизма и делает один оборот за сутки. Прибор позволяет получить график изменения давления со временем.
 |
Рис. 26.8. Барометр-анероид. Принцип действия |
 Рис. 26.9. Барограф |
Пример №19
Вычислите давление столбика ртути высотой 1 мм (то есть 0,001 м). Примите g = 10 H /кг .
| Дано: h = 1 мм =0,001 м ρ = 13 600 кг/м3 g = 10 H/кг |
Решение: Согласно формуле p = ρ g h, 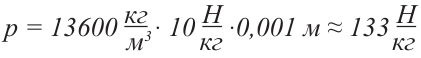 |
| p – ? |
Ответ: давление столбика ртути высотой 1 мм приблизительно равно 133 Па.
Пример №20
Столбик ртутного барометра установился на высоте H над уровнем ртути в чашке (рис. 26.10). Какое давление в ртути в точке А, находящейся на высоте h над уровнем ртути в чашке?
Решение.
Очевидно, что давление ртути на уровне поверхности в чашке составляет ρ·g·H. При поднятии вверх высота столба ртути уменьшается – следовательно, уменьшается и давление. В точке А давление станет меньше давления внизу на ρ·g·h. Следовательно, давление ртути в точке А составляет:
PA = ρ·g·H – ρ·g·h = ρ·g·(H – h).

Рис. 26.10
Итоги
- Столбик ртути в барометре Торричелли удерживается силой атмосферного давления.
- Столб атмосферы высотой 100 км оказывает такое же давление, как столб ртути высотой 760 мм
- Нормальное атмосферное давление составляет p0 = 760 мм рт. ст., или приблизительно 100 000 Па.
- Одна атмосфера (внесистемная единица измерения давления, как и ÂÂмм рт. ст.) : 1 атм = 101 325 Па (точно).
Отто фон Герике (1602–1686, Otto von Guericke). Родился в г. Магдебург. Немецкий физик, инженер и политический деятель. Изучал естественные науки в университете города Лейпцига, право в университете города Йена, математику и механику в городе Лейдене. С 1631 года служил инженером в армии шведского короля Густава ІІ. С 1646 по 1681 год избирался бургомистром города Магдебурга и членом магистрата города Бранденбурга.

В 1650 году Отто Герике сконструировал вакуумный насос. Опыты с вакуумом поразили современников, поскольку в те времена ученые утверждали, что пустого места в пространстве в принципе не может существовать. Он выяснил, что свет распространяется и в пустоте, а звук – нет. Колокольчик в вакууме не звонил, животные погибали, свеча гасла, рыба раздувалась. Выяснилось, что кислород необходим для дыхания и горения.
Когда Герике откачал насосом воздух из жестяной коробки, она была смята атмосферным давлением. Герике организовал показ знаменитого опыта с «Магдебургскими полушариями», демонстрируя соотечественникам давление атмосферы, в которое тогда также никто не верил.
Отто фон Герике изобрел электростатическую машину и выяснил, что сера светится при сильной электризации, то есть открыл явление люминесценции.
Герике также изучал астрономию и предложил гипотезу о том, что кометы прилетают к нам из окраин Солнечной системы. Это предположение позднее подтвердили астрономы-профессионалы.
Манометры, насосы и гидравлический пресс
Металлический манометр:
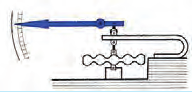
Манометром называют прибор, предназначенный для измерения давлений, которые значительно больше или меньше атмосферного. Металлический манометр состоит из согнутой в виде дуги эластичной металлической трубки, один конец которой запаян, а другой – соединен с резервуаром, в котором измеряется давление. Когда воздух или другой газ под большим давлением входит в трубку, она немного распрямляется и посредством системы рычагов и зубчатых колес вращает стрелку прибора по часовой стрелке (рис. 27.1). Если давление в трубке меньше атмосферного, то трубка свертывается и вращает стрелку прибора в направлении против часовой стрелки. Таким манометром, например, измеряют давление в камерах автомобильных колес.

Рис. 27.1. Металлический манометр
Жидкостные манометры
Жидкостные манометры позволяют измерять давление с большей точностью, чем металлические. Они состоят из выгнутой в виде буквы U стеклянной трубки, две стороны которой называют соответственно левым и правым коленами манометра. В трубку наливают жидкость. Как правило, это ртуть, но используются и водяные манометры. Одно колено манометра соединяют труб-кой с резервуаром, в котором надо измерить давление, а другое открыто, и на поверхность жидкости в трубке действует давление атмосферы (это так называемый открытый манометр).
Рассмотрим случай, когда уровень жидкости в правом колене манометра выше, чем в левом (рис. 27.2). Это значит, что давление «p» в баллоне больше атмосферного на величину ρ ∙ g ∙ h, то есть p = pa + ρ ∙ g ∙ h , где pa – атмосферное давление, а ρ – плотность жидкости в манометре. Если уровень жидкости в правом колене ниже, то давление в баллоне меньше атмосферного на величину ρ ∙ g ∙ h.
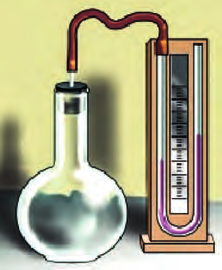 Рис. 27.2. Открытый жидкостный манометр Рис. 27.2. Открытый жидкостный манометр |
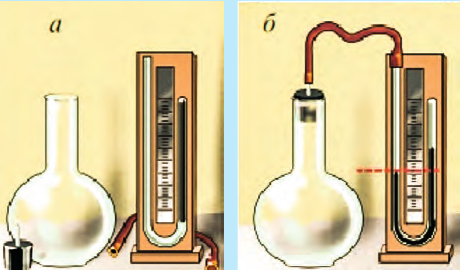 Рис. 27.3. Закрытый манометр измеряет малые давления |
У манометра, который предназначен для измерения очень малых давлений, правое колено запаяно и полностью заполнено жидкостью перед началом измерений (рис. 27.3а) – это так называемый укороченный манометр. На рис. 27.3б над ртутью в правом колене – вакуум, поэтому давление в колбе равняется избыточному давлению столбика ртути над линией равновесия (пунктир), то есть ρ ∙ g ∙ h.
Почему вода следует за поршнем
Набирайте в шприц воду, следя за тем, как вода поднимается за поршнем (рис. 27.4). Люди несколько тысячелетий не могли понять этого явления! Древнегреческий ученый Аристотель объяснял его так: когда поршень двигается вверх по трубке насоса, под ним образуется пустота, которую вода вынуждена заполнить. Люди тогда просто не могли представить себе возможность существования ничем не заполненного пространства, то есть вакуума. Как выяснилось после опытов Торричелли, Паскаля и Герике, воду «вдавливает» под поршень сила атмосферного давления, действующая на свободную поверхность воды в сосуде и передающаяся во все точки и во всех направлениях, в частности – вверх. Когда начали закачивать воду на большую высоту, оказалось, что природа «боится» пустоты только до высоты, которая приблизительно составляет 10,5 м, а дальше «отказывается» следовать за поршнем, поскольку сила давления столба воды уравновешивает силу атмосферного давления.
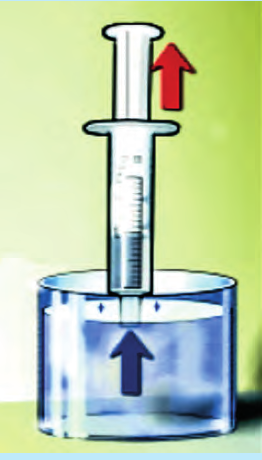
Рис. 27.4. Вода двигается за поршнем насоса, потому что ее туда «втискивает» сила атмосферного давления
Поршневые насосы
Рассмотрим конструкцию и принцип действия водяного насоса – обычной ручной водяной помпы. Она состоит из цилиндра с поршнем и двух клапанов (рис. 27.5). Входной клапан находится в верхней части трубы, соединяющей насос с водоносным слоем почвы, и впускает воду вверх по ходу поршня, но не выпускает на-зад при движении поршня вниз. Второй клапан находится в поршне и пропускает воду вверх, когда поршень двигается вниз. При следующем ходе поршня вверх верхний клапан закрывается и часть воды, которая находится над ним, выливается в ведро.
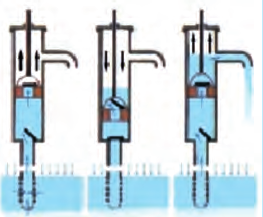
Рис. 27.5. Клапаны водяной помпы пропускают воду вверх и не дают ей «убежать» вниз
Кстати
Интересную конструкцию насоса изобрел Архимед (рис. 27.6). «Винт Архимеда» находится в трубе, один конец которой надо опустить в воду. При вращении винта в определенном направлении вода начинает подниматься вверх по трубе. Подобная конструкция применяется в домашней ручной мясорубке.
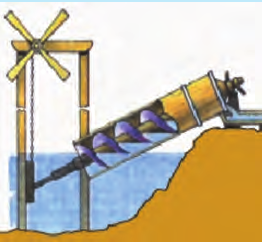
Рис. 27.6. Винт Архимеда позволяет перекачивать пульпу (смесь глины и воды)
Воздушные насосы и компрессоры
Чтобы накачать воздух в футбольный мяч, камеру велосипеда или автомобиля, используют воздушные насосы (рис. 27.7). Задание состоит в том, чтобы накачать в камеру воздух до определенного давления и сделать так, чтобы назад из камеры он не выходил. Поршень насоса сделан
из кожи так, что его распирает при нагнетании воздуха. В этом случае края поршня крепко прижимаются к стенкам цилиндра и не дают воздуху «убежать». При обратном ходе поршня давление в цилиндре уменьшается, потому что клапан не выпускает воздух из камеры. Края кожи сминаются, и воздух опять заполняет пространство под поршнем. Для лучшей герметизации поршень и стенки цилиндра должны быть смазаны специальным маслом. Пространство под поршнем через систему вентилей и трубочек соединено со штуцером (трубка, к которой присоединяют шланг насоса при накачке камеры).
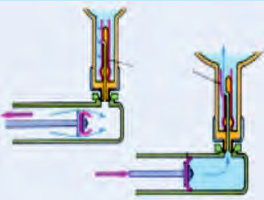
Рис. 27.7. Велосипедный насос
Поршневой компрессор (от латинского com-pressus – сжатый) – это нагнетательный воздушный насос, поршень которого приводится в действие двигателем. Он используется для подачи сжатого воздуха в пневматические инструменты. Вы, наверное, видели (и слышали!) как работают пневматический молоток или отвертка. С помощью компрессора накачивают автомобильные шины, перегоняют природный газ в газопроводах, распыляют краску пульверизатором. Специальный кривошипно-шатунный механизм двигает поршень компрессора «туда-сюда», а два клапана – впускной и выпускной – вынуждают воздух двигаться в нужном направлении (рис. 27.8).

Рис. 27.8. Поршневой компрессор
Гидравлический пресс
Гидравлические устройства, например гидроусилитель руля в автомобиле, широко при-меняются в современной технике. Из названия понятно, что речь идет об устройствах, которые используют жидкость и многократно усиливают начальное действие. Легко нажав на гидравлический тормоз (рис. 27.9), можно остановить грузовой автомобиль или поезд. Гидравлический подъемник поднимает и удерживает автомобиль (рис. 27.10). Гидравлический пресс штампует ка-кой угодно профиль, даже из толстого стального листа.
Все эти машины и механизмы действуют по единому принципу – принципу гидравлического пресса, изобретенного Паскалем. Гидравлический пресс состоит из двух цилиндров разных диаметров (рис. 27.11). Внутри цилиндров двигаются поршни. Цилиндры герметически соединены между собой и заполнены жидкостью (как правило, минеральным маслом).
Пусть на меньший поршень площадью S1 действует сила F1. Поршень давит на жидкость, создавая в ней давление p = F1/S1.
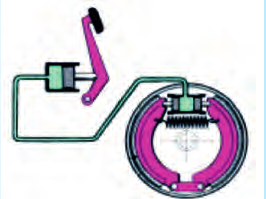 Рис. 27.9. Гидравлический тормоз автомобиля |
 Рис. 27.10. Гидравлический подъемник |
По закону Паскаля, это давление передается во все точки жидкости. Тогда на второй поршень, площадь которого больше и равняется S2, будет действовать сила F2 = p ∙ S2 = F1 ∙ S2/S1.
Следовательно, усилие, которое развивает второй поршень, во столько же раз больше начального, во сколько раз площадь большего поршня больше площади меньшего поршня:
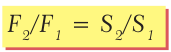 (27.1)
(27.1)
В мощных гидравлических машинах малый поршень является частью насоса, который быстро накачивает жидкость в цилиндр с большим поршнем. Если заменить в прессе жидкость воздухом, он тоже будет работать. Такие устройства называют пневматическими. Поскольку воздух легко сжимается, то пневматические тормоза действуют «мягче».
В общественном транспорте двери открываются и закрываются пневматическими устройствами, потому вы не пострадаете, даже если окажетесь в их плену.
Сервоскелет – довольно экзотическое устройство, которое состоит из гидравлических трубок с поршнями и имеет вид скелета. Вы одеваете эту конструкцию на себя – и каждое ваше движение повторяется и усиливается многократно. Можно, например, подойти к многотонной грузовой машине и поднять ее «руками».
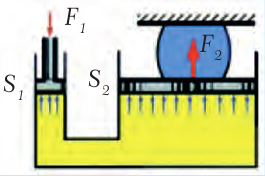
Рис. 27.11. Схема строения гидравлического пресса
Итоги
- Манометры используют для измерения давлений значительно больше или меньше атмосферного.
- Вода следует в трубе за поршнем насоса, потому что ее туда «вгоняет» атмосферное давление.
- Гидравлический пресс усиливает действие во столько раз, во сколько площадь большого поршня больше площади малого поршня: F2/F1 = S2/S1.
Выталкивающая сила в жидкостях и газах
Выталкивающая сила:
Попробуйте погрузить мяч в воду. Вы почувствуете довольно значительное противодействие силы, пытающейся его оттуда вытолкнуть. Оказывается, что и на тела, которые тонут, также действует выталкивающая сила. На воздушные шары, наполненные горячим воздухом или гелием, действует выталкивающая сила окружающего воздуха, благодаря которой они летают.
Опыт:
Подвесьте к динамометру тело, которое тонет, например, большую батарейку или наполненную монетами коробочку от фотопленки, и запомните показания прибора. Потом опустите тело в воду (рис. 28.1). Стрелка динамометра покажет меньшую силу. Разница показаний динамометра равняется выталкивающей силе, которую называют силой Архимеда и обозначают FA.

Рис. 28.1. Вес погруженного в жидкость тела уменьшается
Закон Архимеда: на тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости, которая вытеснена этим телом.
Для тел, «погруженных» в газ, выталкивающая сила значительно меньше, чем в жидкости.
Закон Архимеда можно выразить формулой. Если плотность жидкости обозначить ρж, а объем тела – буквой V, и считать, что тело погрузилось полностью, то объем вытесненной жидкости равняется объему тела. Найдем массу вытесненной жидкости: mж = ρж· V. Вес вытесненной жидкости будет равняться P = ρж· V · g . Следовательно, силу Архимеда можно вычислить по формуле:
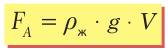
Почему возникает выталкивающая сила
Сначала объясним возникновение выталкивающей силы для случая, когда тело имеет форму параллелепипеда или цилиндра (рис. 28.2 а), площадь верхней и нижней грани которых обозначим буквой S, а высоту – буквой Н. На рис. 28.2б изображено только вертикальное сечение тела, погруженного в жидкость. Силы давления, которые действу-ют на поверхность тела со стороны жидкости, изображены черными стрелками.
Приведем основные логические шаги наших рассуждений:
- Силы давления действуют перпендикулярно поверхности.
- Чем глубже, тем сильнее жидкость давит на поверхность тела.
- Силы давления на боковую поверхность тела уравновешенны, и ими можно пренебречь (при условии, что тело не сжимается).
- Силы давления, которые действуют на нижнюю часть тела, направлены вверх, и они больше сил давления, которые действуют вниз, на верхнюю часть тела. Разность этих сил действует вверх – это и является причиной возникновения выталкивающей силы.
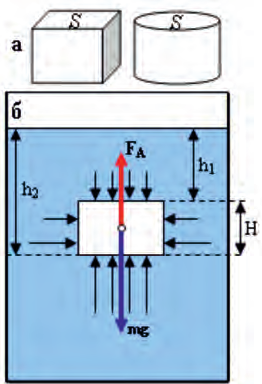
Рис. 28.2. Утворення виштовхувальнойсили
Вычисление выталкивающей силы
- Сила давления на нижнюю грань равняется произведению давления столба жидкости высотой h2 на площадь грани S: F2 = pжgh2S и направлена вертикально вверх.
- Сила давления на верхнюю грань равняется произведению давления столба жидкости высотой h1 на площадь грани S: F1 = pжgh1S и направлена вертикально вниз.
- Равнодействующая двух противоположных сил F1 и F9 равняется их разности и направлена в сторону большей силы, то есть вертикально вверх - это и есть сила Архимеда: FА = F2-F1.
- Подставляем значение сил: FА = pжgh2.S - pжgh1.S. Одинаковые величины можно вынести за скобки: FА = pжg.S.(h1 -h2). Заметим, что h1 -h2 = Н. Следовательно: FА = pжgh.Н
- Произведение S.H- это объем тела, и в то же время объем вытесненной жидкости: V = S.Н,то естьFА = pжg.V.-мы получили формулу (29.1).
- Произведение плотности жидкости на объем вытесненной жидкости - это ее масса: mp = pжV, а произведение массы жидкости на g равняется ее весу. Таким образом, величина выталкивающей силы равняется весу вытесненной жидкости: FА = mжg.
Логическое доказательство формулы (28.1). Представим, что мы оставили только невесомую поверхность-оболочку данного тела (пунктирная линия), и заполнили ее той же жидкостью, в которой оно плавает (рис. 28.3). Но определенный объем жидкости, находящийся в той же жидкости, пребывает в равновесии. Это значит, что сила тяжести, действующая на жидкость внутри оболочки, уравновешивается выталкивающей силой, возникшей за счет сил давления со стороны жидкости на поверхность тела.
Следовательно, выталкивающая сила равняется весу жидкости в объеме тела и направлена противоположно ему, то есть вертикально вверх.
Рис. 28.3
Парадокс Архимеда
Сила Архимеда, действующая на корабль, равна весу вытесненной им воды. Но количество воды, в которой корабль плавает, может быть значительно меньше количества воды, которое он должен вытеснить, чтобы плавать. Опыт, объясняющий этот парадокс, изображен на рис. 28.4. Подобная ситуация случается, когда корабль находится в шлюзе (рис. 28.5).
Гидростатическое взвешивание
Гидростатическим называют взвешивание тела, погруженного в жидкость. Выталкивающая сила (рис. 28.6) равняется разности веса тела в воздухе (F1) и в жидкости (F2):
FA = F1 – F2. (28.2)
С другой стороны, FA = ρ · V · g, а вес тела в воздухе равняется силе тяжести, которая действует на тело, то есть: F1 = mT g = ρTVg. Подставив два последних выражения в формулу (28.2), получаем:
ρжVg = ρTVg – F2 (28.3)
Формула (28.3) позволяет вычислить плотность тела, если известны плотность жидкости и объем тела. Гидростатическое взвешивание позволяет также определить плотность жидкости при известной плотности тела.
Замечание. Мы не учитывали при получении формул выталкивающую силу воздуха, которая в таких опытах намного меньше сил F1 и F2.
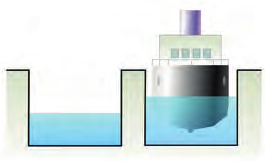 Рис. 28.4. Парадокс Архимеда: корабль может плавать в малом количестве воды |
 Рис. 28.5. Корабль в шлюзе |
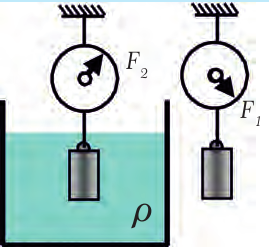 Рис. 28.6. Гидростатическое взвешивание |
Особые случаи:
- Случалось, что подводная лодка опускалась на глинистое дно и больше не могла подняться, в результате чего погибал экипаж. Это происходило из-за того, что при отсутствии действия силы давления воды на дно тела выталкивающая сила не возникает. Наоборот, силы давления в таком случае прижимают тело ко дну (рис. 28.7).
- Если тело прилипло к стенке сосуда, то выталкивающая сила уже не действует вертикально вверх (в такой ситуации находятся улитки, которые ползают по стенке аквариума).
Рис. 28.7. Особые случаи
Итоги:
- На тело, погруженное в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и численно равная весу жидкости, которая вытеснена этим телом.
- Сила Архимеда возникает из-за действия на поверхность тела сил давления со стороны жидкости или газа. Эта сила не зависит от того, что находится внутри тела.
Условия плавания тел
По рекам, озерами, морям и океанам плавают катера, яхты, торговые и пассажирские корабли, танкеры, крейсеры, ледоколы, авианосцы... Все они должны быть сконструированы так, чтобы держаться на поверхности воды, и при этом выдерживать непогоду и даже шторм. Подводные лодки должны плавать как на поверхности, так и под водой. Следовательно, рассмотрим условия плавания тел.
Условия плавания
Когда корабль плавает на поверхности воды, его вес точно уравновешен выталкивающей силой, которая равняется весу воды, вытеснен-ной погруженной частью корабля, находящейся ниже ватерлинии (верхняя граница красной полосы, рис. 29.1). Масса вытесненной кораблем воды называется его тоннажностью.
У тела, которое плавает на поверхности, в воду погружена только некоторая часть его объема. Независимо от того, погружено это тело незначительно или сильно – выталкивающая сила равняется силе тяжести (рис. 29.2), то есть обе силы, действующие на тело, уравновешиваются. Если надавить на плавающее тело, оно погрузится глубже, но выталкивающая сила вырастет, и после того, как мы перестанем на него давить, оно опять всплывет. Следовательно, тело будет плавать (или всплывать), если выталкивающая сила больше или по крайней мере равняется силе тяжести:
FA ≥ mTg, (29.1)
где mT – масса тела.
Рассмотрим предельный случай, когда тело полностью погрузилось в жидкость, но находится в зависшем состоянии, то есть не тонет и не всплывает. Поскольку теперь FA = mPg, можно записать, что ρж · V · g = ρT VTg, или, после сокращения одинаковых величин:
ρж = ρT (29.2)
Оказывается, все зависит только от соотношения между плотностью тела ρm и плотностью жидкости ρж: тело тонет, если его плотность больше плотности жидкости, в которую оно погружено.
Аналогично: тело плавает, если его плотность меньше плотности жидкости.

Рис. 29.1. Ватерлиния корабля
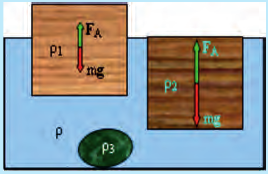
Рис. 29.2. Если тело плавает, сила Архимеда уравновешена силой тяжести
Если плотность тела равняется плотности жидкости, то оно может находиться на произвольной глубине в зависшем состоянии.
Пример №21
Тело массой 200 г плавает в воде. Какую массу воды вытесняет тело?
Решение. Поскольку тело плавает, его вес равен весу вытесненной воды. Таким образом, масса тела и масса вытесненной жидкости также равны.
Ответ: плавающее тело вытесняет массу воды, которая равна массе тела.
Пример №22
Тело плавает в воде, погрузившись 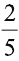 своего объема в воду. Какова плотность тела?
своего объема в воду. Какова плотность тела?
Решение.
Из таблиц известно, что плотность воды равняется 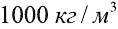 . Обозначим объем тела V, плотность тела ρm, плотность воды ρВ . Тогда объем вытесненной воды составляет V. Масса тела mT = ρm·V должна быть такой же, как масса вытесненной воды mB = ρВ·
. Обозначим объем тела V, плотность тела ρm, плотность воды ρВ . Тогда объем вытесненной воды составляет V. Масса тела mT = ρm·V должна быть такой же, как масса вытесненной воды mB = ρВ· 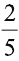 V, поскольку тело плавает.
V, поскольку тело плавает.
Следовательно: ρт·V = ρВ· 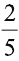 V, откуда следует, что ρт =
V, откуда следует, что ρт =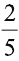 ρВ.
ρВ.
Опыт: «КАРТЕЗИАНСКИЙ ВОДОЛАЗ»
Этот опыт придумал французский физик, математик и философ Рене Декарт (фамилия Декарта на латыни звучит как Картезиус). Возьмите пипетку и наберите в нее столько воды, чтобы она едва плавала (рис. 29.3). Потом поместите пипетку в пластиковую бутылку, заполненную на три четверти своего объема водой, и плотно закрутите крышку. Если вы сожмете бутылку, пипетка начнет тонуть, и вы можете, изменяя давление на бутылку, двигать пипетку вниз или вверх, или держать ее неподвижной на определенной глубине.
Обратите внимание, что при сжатии бутылки (увеличение давления воздуха) уровень воды в пипетке повышается, то есть в пипетку заходит вода, а при уменьшении давления в бутылке вода из пипетки выходит.

Рис. 29.3. «Картезианский водолаз», сделанный из пипетки и пластиковой бутылки
Научитесь опускать и поднимать «водолаза», а также удерживать его в зависшем состоянии между дном и поверхностью воды.
Подводная лодка:
Подводная лодка (рис. 29.4) может менять свою плотность. Внутри лодки есть балластные цистерны; если туда набрать воду, то плотность лодки становится больше плотности воды, и она начинает погружаться. Для того, чтобы лодка начала всплывать, надо «продуть балласт», то есть вытеснить с помощью сжатого воздуха воду из цистерн за пределы лодки. Тогда плотность лодки опять становится меньше плотности воды. Двигаясь под водой, лодка маневрирует с помощью руля глубины и руля поворотов, которые действуют подобно крыльям самолета

Рис. 29.4. Если тело плавает, сила Архимеда уравновешена силой тяжести
Воздухоплавание
Воздушные шары (рис. 29.5) летают, потому что в воздухе также действует выталкивающая сила. Поскольку плотность воздуха невелика, то и сила Архимеда мала. Для человека среднего роста и телосложения (масса 70 кг, вес – приблизительно 700 Н) выталкивающая сила составляет около 1 Н, что в 700 раз меньше его веса.
Чтобы воздушный шар мог подняться, он должен иметь большой объем, а также его нужно заполнить газом, плотность которого меньше плотности воздуха (водяной пар, горячий воздух, водород или гелий). Подъемная сила, действующая на шар, должна быть больше веса газа, которым он заполнен, а также оболочки и поднимаемого груза

Рис. 29.5. Монгольфьер заполняют горячим воздухом
Пример №23
Воздушный шар объемом V, заполненный газом плотностью ρ, вытесняет такой же объем воздуха плотностью ρ0. Найдем величину подъемной силы воздушного шара. Массой оболочки можно пренебречь.
Подъемная сила равняется разности силы Архимеда FA = ρ0 · g · V и веса газа ρV g, которым заполнен шар:
F = ρ0 ·g·V – ρ·g·V = (ρ0 – ρ)·g·V (29.3)
Из формулы (29.3) видно, что чем меньше плотность газа, которым заполняют шар, и чем больший объем шара, тем большей будет подъемная сила.
Итоги:
- Если тело плавает, то выталкивающая сила равняется силе тяжести, которое действует на тело.
- Тело тонет, если его плотность больше плотности жидкости, в которую оно погружено, и плавает, если его плотность меньше плотности жидкости.
История:
Братья Монгольфье
С давних времен люди мечтали о возможности летать, как птицы, и придумывали для этого замысловатые устройства и машины, которые махали крыльями. Но случилось так, что впервые человек оторвался от Земли и поднялся в воздух с помощью воздушного шара, который изобрели братья Монгольфье.

Люди мечтали летать, как птицы
В конце ХVIIІ века двое французских мальчиков, братья Жозеф и Жак Монгольфье, занимались опытами, наполняя бумажные пакеты горячим воздухом и паром из кипящего чайника. Они решили, что, поскольку пар поднимается вверх, образовывая тучи, то и легкий мешок, наполненный паром, также должен летать. Летать ребята мечтали с детства. Жак в девять лет спрыгнул с зонтиком с крыши сарая и получил синяки.

Опыты длились несколько лет, и наконец был проведен полет шара на открытом воздухе в присутствии мэра и жителей городка. Мешок, пошитый из старой юбки, подвесили отверстием вниз над очагом, разожженным из влажной соломы. Мешок раздулся, взлетел высоко в воздух и опустился за несколько километров от села. Братья были в восторге, но не понимали, почему их шар через некоторое время после начала полета падает.
В действительности же горячий воздух расширяется, и его часть, которая остается в шаре, весит меньше, чем воздух снаружи. В итоге выталкивающая сила становится больше веса шара. В полете воздух остывает, и подъемная сила постепенно уменьшается.
Известный французский физик Шарль в декабре 1783 года осуществил двух-часовой полет на шаре, наполненном водородом. Такой воздушный шар хорошо летает, потому что водород очень легкий, но при контакте с воздухом он легко воспламеняется, потому такие шары огнеопасны. Позже шары начали заполнять безопасным гелием. В наше время огромные шары, изготовленные из новейших легких материалов и наполненные горячим воздухом, нагревающимся с помощью газовых горелок, – монгольфьеры, участвуют в спортивных соревнованиях.
Карта взаимодействие тел и силы
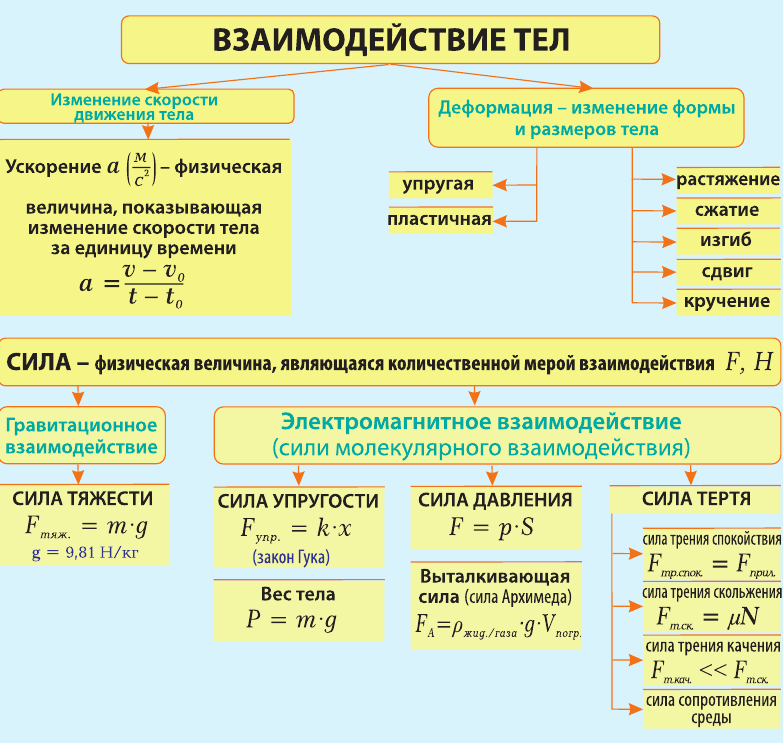
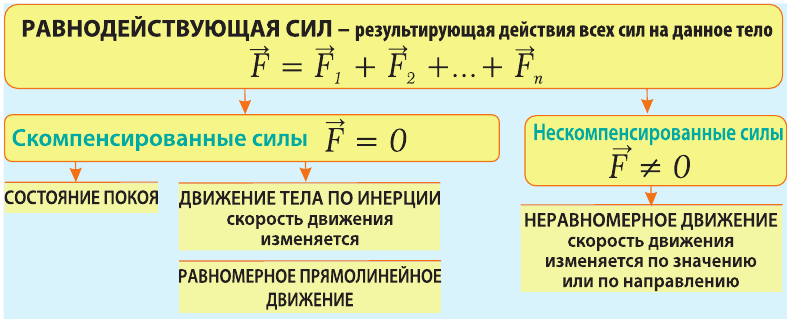
| ОСНОВНЫЕ ЗАКОНЫ НЬЮТОНА | ||
| I ЗАКОН | II ЗАКОН | II ЗАКОН |
| Существуют такие системы отсчета, относительно которых тело хранит состояние спокойствия или равномерного прямолинейного движения, если на него не действуют другие тела или действие других телскомпенсировано. Такие системы отсчета называются инерциальными | ПУскорение, которое приобретает тело, прямо пропорционально равнодействующей силе и обратно пропорционально массе тела: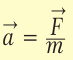 |
В инерциальной системе отсчета силы, с которыми тела действуют друг на друга, одинаковы по величине и противоположны по направлению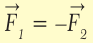 |
| ЗАКОН ПАСКАЛЯ | ЗАКОН АРХИМЕДА |
| Давление в жидкостях и газах передается во все точки и во всех направлениях одинаково | На тело, погруженное в жидкость или газ, действует выталкивающая сила, которая направлена вертикально вверх и равняется весу жидкости/газа, вытесненного этим телом FA = ρжид./газа · g · V |
| Сообщающиеся сосуды S1 = h1 S2 = h2 |
Плавание судов ρтела˂ ρжид |
| Гидравлические машины F1 = S1 F2 = S2 |
Воздухоплавание ρжид˂ρтела |
Нормальное атмосферное давление pa = 760 мм рт. ст. = 101 кПа 1 атм = 101 325 Па
Всё о взаимодействие тел
Почему Луна движется вокруг Земли, а не улетает в космическое пространство? Какое тело называется заряженным? Как взаимодействуют друг с другом заряженные тела? Часто ли мы сталкиваемся с электромагнитным взаимодействием?
Это только часть вопросов, с которыми нам предстоит разобраться в этом параграфе. Приступим!
В повседневной жизни мы постоянно встречаемся с различными видами воздействий одних тел на другие. Чтобы открыть дверь, нужно «подействовать* на нее рукой, от воздействия ноги мяч летит в ворота, даже присаживаясь на стул, вы действуете на него (рис. 1.35).
В то же время, открывая дверь, мы ощущаем ее воздействие на нашу руку, действие мяча на ногу особенно ощутимо, если вы играете в футбол босиком, а действие стула не позволяет нам упасть на пол. То есть действие всегда является взаимодействием: если од hi тело действует на другое, то и другое тел( действует на первое.

Можно наглядно убедиться в том, что действие не бывает односторонним. Проведите не сложный эксперимент: стоя на коньках, слегка толкните своего товарища. В результате начнет двигаться не только ваш товарищ, но и вы сами Эти примеры подтверждают вывод учены? о том, что в природе мы всегда имеем дело с взаимодействием, а не с односторонним действием Рассмотрим более подробно некоторые видь взаимодействий.
Гравитационное взаимодействие
Почему любой предмет, будь то карандаш выпущенный из руки, лист дерева или капля дождя, падает, двигается вниз (рис. 1.36)? Почему стрела, выпущенная из лука, не летит прямо а в конце концов падает на землю? Почему Луш движется вокруг Земли? Причина всех этих явлений заключается в том, что Земля притягиваем к себе другие тела, а эти тела также пригягивают к себе Землю. Например, притяжение Лунь вызывает на Земле приливы (рис. 1.37). Наш* планета и все другие планеты Солнечной системы притягиваются к Солнцу и друг к другу.
В 1687 году выдающийся английский физик Исаак Ньютон (рис. 1.38) сформулировал закон, согласно которому между всем! телами во Вселенной существует взаимное притяжение.

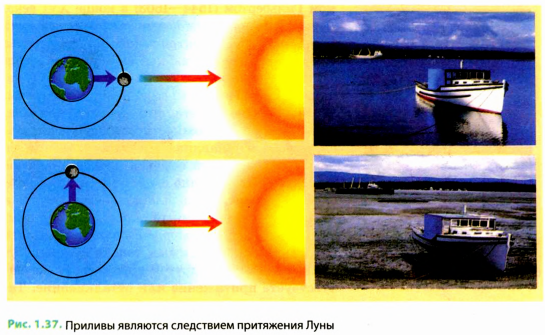
Такое взаимное притяжение материальных объектов называют гравитационным взаимодействием. Опираясь на опыты и математические расчеты, Ньютон установил, что интенсивность гравитационного взаимодействия увеличивается с увеличением масс взаимодействующих тел. Именно поэтому легко убедиться в том, что нас с вами притягивает Земля, но мы совершенно не чувствуем притяжения нашего соседа по парте.

Электромагнитное взаимодействие

Существуют и другие виды взаимодействий. Например, если потереть воздушный шарик кусочком шелка, он начнет притягивать к себе различные легкие предметы: ворсинки, зернышки риса, листочки бумаги (рис. 1.39). Про такой шарик говорят, что он наэлектризован, или заряжен.
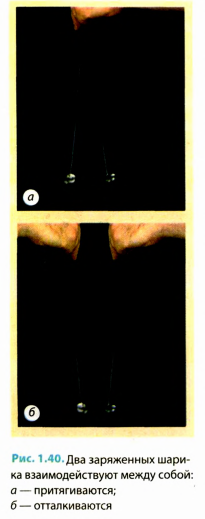
Заряженные тела взаимодействуют между собой, но характер их взаимодействия может быть разным: они либо притягиваются, либо отталкиваются друг от друга (рис. 1.40). Впервые серьезные исследования этого явления были проведены английским ученым Уильямом Гильбертом (1544—1603) в конце XVI века. Взаимодействие между заряженными телами Гильберт назвал электрическим (от греч. слова elektron — янтарь), так как еще древние греки заметили, что янтарь, если его потереть, начинает притягивать к себе мелкие предметы.
Вы хорошо знаете, что стрелка компаса, если дать ей возможность свободно вращаться, всегда останавливается так, что один ее конец указывает на север, а другой — на юг (рис. 1.41). Это связано с тем, что стрелка компаса — магнит, наша планета Земля — тоже магнит, причем огромный, а два магнита всегда взаимодействуют друг с другом. Возьмите два любых магнита, и как только вы попробуете приблизить их друг к другу, сразу же почувствуете притяжение или отталкивание. Такое взаимодействие называется магнитным.
Физики установили, что законы, описывающие электрические и магнитные взаимодействия, едины. Поэтому в науке принято говорить о едином электромагнитном взаимодействии.
С электромагнитными взаимодействиями мы встречаемся буквально на каждом шагу — ведь при ходьбе мы взаимодействуем с покрытием дороги (отталкиваемся), и природа этого взаимодействия электромагнитная. Благодаря электромагнитным взаимодействиям мы двигаемся, сидим, пишем. Видим, слышим, обоняем и осязаем мы также с помощью электромагнитного взаимодействия (рис. 1.42). Действие большинства современных приборов и бытовой техники основано на электромагнитном взаимодействии.
Скажем больше: существование физических тел, в том числе и нас с вами, было бы невозможно без электромагнитного взаимодействия. Но как со всем этим связано взаимодействие заряженных шариков и магнитов? — спросите вы. Не спешите: изучая физику, вы обязательно убедитесь, что эта связь существует.
Сталкиваемся с нерешенными проблемами:
Наше описание окажется неполным если мы не упомянем еще два вида взаимодействий, которые были открыты только в середине прошлого века.

Они называются сильное и слабое взаимодействия и действуют только в пределах микромира. Таким образом, существуют четыре различных вида взаимодействии. Не много ли? Конечно, было бы гораздо удобнее иметь дело с единым универсальным видом взаимодействия. Тем более, что пример объединения различных взаимодействий — электрического и магнитного — в единое электромагнитное уже имеется.
На протяжении многих десятилетий ученые пытаются создать теорию такого объединения. Некоторые шаги уже сделаны. В 60-х годах XX века удалось создать теорию так называемого электро-слабого взаимодействия, в рамках которой были объединены электромагнитное и слабое взаимодействия. Но до полного («великого») объединения всех видов взаимодействия еще далеко. Поэтому у каждого из вас есть шанс совершить научное открытие мирового значения!
Итоги:
Взаимодействием в физике называется действие тел или частиц друг на друга. Мы коротко охарактеризовали два вида взаимодействия из четырех, известных науке: гравитационное и электромагнитное.
Притяжение тел к Земле, планет к Солнцу и наоборот — это примеры проявления гравитационного взаимодействия.
Примером электрического взаимодействия является взаимодействие наэлектризованного воздушного шарика с листочками бумаги. Примером магнитного взаимодействия служит взаимодействие стрелки компаса с Землей, которая также является магнитом, в результате чего один конец стрелки всегда указывает на север, а второй — на юг.
Электрическое и магнитное взаимодействия — это проявления единого электромагнитного взаимодействия.
Сила и энергия
Первоначальный смысл слова «сила» и образованных от него поня тий «силач», «сильный» был связан с возможностями человека, с его мускульными усилиями. Согласно древнегреческому мифу, герои Тесей для доказательства своей силы должен был сдвинуть громадную каменную глыбу и достать из-под нее отцовский меч. А какое содержание вкладывают физики в понятие «сила»?
Понятие «сила»
Понятие «сила* неразрывно связано со взаимодействием физических тел. Чтобы сдвинуть каменную глыбу, Тесею пришлось взаимодействовать с ней. Наши руки взаимодействуют со стулом, который необходимо передвинуть. В момент прыжка наши ноги взаимодействуют с землей.

Обратите внимание на то, что в каждом из приведенных примеров результат будет различным в зависимости от того, насколько сильным было то или иное взаимодействие. Так, семикласснику ничего не стоит передвинуть стул, а для малыша-дошкольника эта задача может оказаться непосильной. Подъемный кран играючи поднял бы глыбу, которую Тесей едва сдвинул с места. Чем выше вы стремитесь прыгнуть, тем сильнее надо оттолкнуться. Из этих примеров становится очевидным, что взаимодействие тел следует определить количественно.
Физическая величина, с помощью которой количественно определяют взаимодействие тел, называется силой.
Иными словами, сила — это количественная мера взаимодействия тел. Силу обозначают символом F. Единицей силы в СИ является ньютон (1 Н).
Чтобы охарактеризовать силу, необходимо указать не только численное значение этой силы, но также направление силы и точку ее приложения. Одна и та же по значению сила может привести к совершенно разным результатам в зависимости от направления ее действия (рис. 1.43). Каким бы ни был силачом легендарный Тесей, он не смог бы сдвинуть глыбу с места, если бы давил на нее сверху вниз. Вероятно, ему не хватило бы сил и для того, чтобы поднять камень (направление силы снизу вверх). Но той же силы, приложенной в горизонтальном направлении, оказалось достаточно, чтобы извлечь из тайника отцовский меч.
Что означают понятия «работа» и «энергия» для физиков
Тесно связана с силой еще одна физическая величина, которая называется работой. В широком значении понятие «работа* включает многие виды человеческой деятельности, например расчеты на компьютере, которые практически не требуют мышечных усилий. В естествознании же понятие «работа» употребляют в том случае, когда происходит перемещение тела под действием силы. Кран на стройке совершает работу, поднимая кирпичи, причем чем больший груз требуется поднять, тем большую работу
совершает кран. Работа также возрастает с увеличением расстояния, на которое перемещают тело. Попробуйте переместить стул по комнате сначала один раз, потом десять, а затем раз пятьдесят или сто, и вы немедленно убедитесь в правильности этого вывода.
Здесь вам предстоит познакомиться с еще одной очень важной физической величиной, которая носит название «энергия*. Общее определение этой физической величины звучит следующим образом: энергия — это общая количественная мера движения и взаимодействия различных видов материи.
В отношении физических тел мы с вами будем пользоваться такой формулировкой:
- I Физическая величина, характеризующая способность тела совершать работу, называется энергией тела.
Обычно энергию обозначают символом W и измеряют в джоулях (1 Дж).
Способность тел совершать работу можно продемонстрировать на следующем примере. Поместим маленький шарик на край стола, а на полу под ним поставим небольшую емкость с водой (рис. 1.44). Если столкнуть шарик с края стола, то он полетит вниз, упадет в воду и разбрызгает часть жидкости. Появление брызг означает, что шарик совершил определенную работу. Если же шарик не трогать, он останется неподвижно лежать на столе. Таким образом, энергия шарика может быть реализована путем совершения работы при его падении или сохранится «до лучших времен*.
Превращение одних видов энергии в другие
Вы, безусловно, знакомы с понятиями тепловая энергия' и «электрическая энергия». Но, оказывается, существуют еще и «механическая энергия», «химическая энергия*, «энергия света* и другие формы энергии.
*В этом разделе мы употребили понятие «тепловая энергия* вместо обычно используемого физиками «внутренняя энергия*. Это сделано осознанно, чтобы подчеркнуть связь внутренней энергии с температурой.

Различные формы энергии могут превращаться одна в другую (рис. 1.44). Так, механическая энергия падающего шарика превратилась в механическую энергию разлетающихся брызг воды. Однако точные измерения температуры установят, что вода в емкости при падении в нее шарика немного нагрелась. Значит, механическая энергия шарика частично-превратилась в механическую энергию брызг, а частично — в тепловую энергию воды.
Превращения энергии вы осуществляете ежедневно, часто даже не подозревая об этом (рис. 1.46). Так, при включении магнитофона часть электрической энергии преобразуется в звуковую энергию. Включая лампочку, мы даем возможность электрической энергии превратиться в световую и тепловую. В этом случае преобразование в световую энергию очевидно, а для проверки того, что электрическая энергия превратилась в тепловую, достаточно приблизить ладонь к лампочке — и вы сразу же почувствуете тепло.
Превращение электрической энергии в тепловую в лампочке — «побочный* и даже вредный эффект. Однако нередко электрическую энергию преобразуют в тепловую целенаправленно, создавая для этого специальные устройства. Это всем известный электрический чайник, утюг, электрокамин, нагревательный элемент автоматической стиральной машины и другие бытовые устройства. Превращение электрической энергии в тепловую используется и в промышленности — например, для плавки металлов.
Чтобы у вас не возникло ошибочное впечатление, что только электрическая энергия может превращаться в другие формы энергии, укажем и на противоположные процессы. Например, на гидроэлектростанциях механическая энергия падающей воды превращается в электрическую (рис. 1.45).
Итоги:
Сила — это количественная мера взаимодействия тел. Сила характеризуется численным значением, направлением, точкой приложения. Символ силы — F.
Физическая величина, характеризующая способность тела совершать работу, называется энергией тела (W).
Существует много форм энергии — механическая, тепловая, химическая, звуковая, электрическая и ряд других. В ходе различных физических процессов и взаимодействий энергия может из одной формы превращаться в другие.
Начинаем изучать физику:
Что изучает физика?
Методы физических исследований
Физические величины
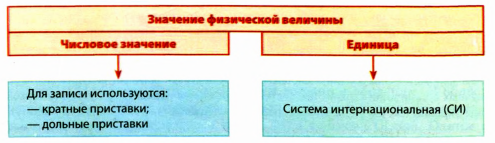
Структурные уровни физического мира
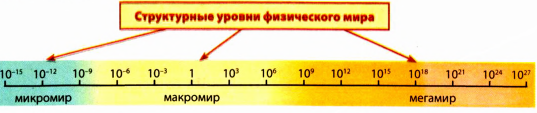
Вселенная существует в пространстве и во времени
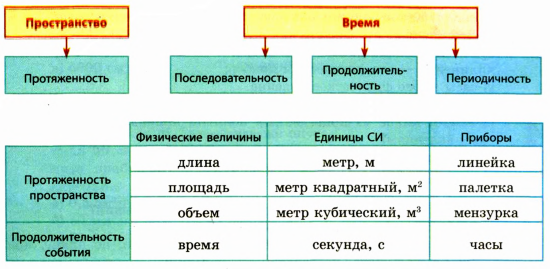
Виды взаимодействий, а также физические величины, которые характеризуют взаимодействие.
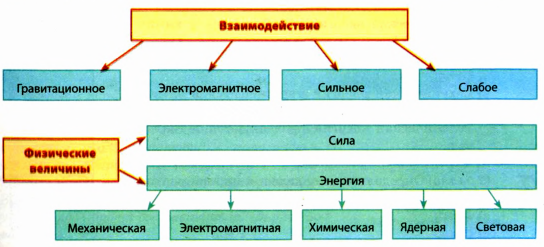
Справочник по взаимодействие тел
Автомобиль мчится по шоссе, в небе летит птица, шар для боулинга катится по дорожке. Благодаря чему происходит каждое из этих движений? Существует ли причина их возникновения? Нужно ли вообще что-то, чтобы поддерживать движение? Почему скорость движения одних тел изменяется, а других — остается неизменной? Попробуем разобраться.
В повседневной жизни мы постоянно имеем дело с различными видами действия одних тел на другие. Чтобы открыть дверь, мы действуем на нее рукой; мяч летит в ворота благодаря действию ноги; садясь на стул, мы действуем на него своим телом. В то же время, открывая дверь, мы чувствуем и ее действие на руку; действие мяча на ногу особенно ощутимо, если играть в футбол босиком; действие стула не дает нам упасть на пол. То есть действие всегда является взаимным: если одно тело действует на другое, то и другое тело действует на первое — тела взаимодействуют (рис. 14.1).

Проведите опыт. Стоя с товарищем на скейтах, потяните за шнур, который он держит в руках. Кто из вас начнет двигаться? Прокомментируйте результат опыта, опираясь на рис. 14.2.

При каких условиях тело находиться в состоянии покоя
Мяч, лежащий на полу, находится в состоянии покоя. Но стоит толкнуть мяч рукой — и состояние покоя нарушится: в результате взаимодействия с рукой мяч начнет движение. А взаимодействовал ли мяч с чем-то до этого? Конечно, да. Вы хорошо знаете, что все тела, находящиеся вблизи Земли, взаимодействуют с ней. И если «убрать» пол, то под действием притяжения Земли мяч сразу придет в движение. А находится он в состоянии покоя потому, что действие Земли на мяч скомпенсировано (уравновешено) действием пола. Тело находится в состоянии покоя, если действия на него других тел скомпенсированы (рис. 14.3, 14.4).

При каких условиях тело движется равномерно прямолинейно
Более 2500 лет назад Аристотель, размышляя о причинах движения тел, пришел вроде бы к правильному с точки зрения жизненного опыта, но ошибочному с точки зрения физики выводу: для поддержания движения тела требуется постоянное действие на него других тел (рис. 14.5). И только в конце ХVІ в. Галилео Галилей, проведя опыты со скатыванием шариков по наклонному желобу и осуществив мысленный эксперимент* (рис. 14.6), выяснил, что идеи Аристотеля не могут правильно объяснить причины движения тел.
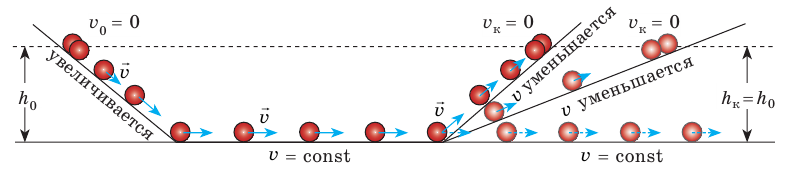

Проведем мысленный эксперимент и мы. Представьте: мальчик мчится по очень длинной горизонтальной ледовой дорожке (рис. 14.7). Если его никто не толкает и не тянет, то, как подсказывает наш опыт, в конце концов мальчик остановится. При этом время его движения будет зависеть от внешних условий. Если, например, на льду есть намерзший снег, то мальчик проедет только 2–3 м; если лед гладкий, не будут пределом и 20 м; а если мальчик наденет коньки, он может «пролететь» и сотню метров. Рассуждаем дальше. Представьте, что «торможения» нет совсем, а мальчик не испытывает никакого действия извне. В этом случае воображаемый мальчик будет скользить с постоянной скоростью по воображаемой ледовой дорожке сколь угодно долго. При этом действие дорожки, которое не дает мальчику «провалиться», и действие Земли будут уравновешивать (компенсировать) друг друга. Условие движения тела с постоянной скоростью известно в механике как закон инерции: Тело движется равномерно прямолинейно или находится в состоянии покоя лишь тогда, когда на него не действуют другие тела или действия других тел скомпенсированы.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
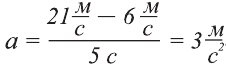 . Этот результат значит,
. Этот результат значит, 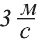
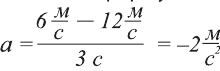 . Этот результат значит,
. Этот результат значит, 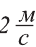
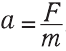 .
.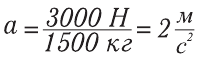
 а = 0. То есть автомобиль нач-
а = 0. То есть автомобиль нач-