Взаимное расположение точек и прямых - определение и вычисление с примерами решения

На уроках математики в предыдущих классах и в главе 1 вы уже познакомились со свойствами некоторых геометрических фигур. Теперь вы приступаете к систематическому изучению геометрии.

Как уже отмечалось ранее, основными геометрическими фигурами являются точка, прямая, плоскость. Представление об этих фигурах вы уже имеете.

Например, туго натянутая нить дает представление о части прямой, страница книги или грань прямоугольного параллелепипеда — о части плоскости (рис. 22, а, б, в).

Точки обозначаются заглавными буквами латинского алфавита А, В, С, ..., а прямые — строчными буквами а, b, с, ... или двумя заглавными буквами АВ, СD и т. д.

Если точка А принадлежит прямой b, то говорят, что прямая b проходит через точку А. Это записывают так: А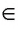

Если точка А не принадлежит прямой b, то говорят, что прямая b не проходит через точку А. В этом случае используется запись А 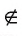 b (читают: «Точка А не принадлежит прямой b», «Точка А не лежит на прямой b» или «Прямая b не проходит через точку А»).

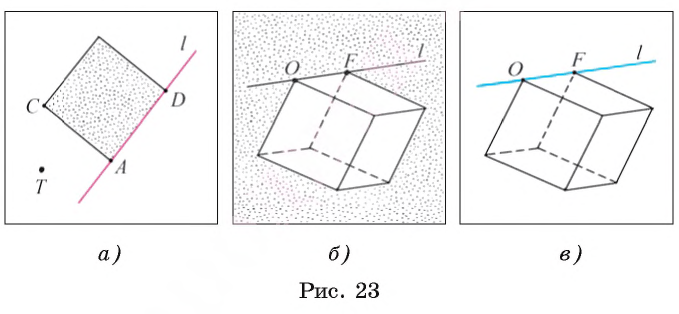
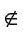Например, на рисунке 23, а изображены точка С — вершина квадрата и точка Т, не лежащие на прямой l (С  l, Т  l), проходящей через вершины А и D квадрата (А  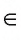l, D 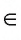 l). На рисунке 23, б, в изображена прямая l, проходящая через вершины О и F куба (O  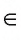l, F  l).

В курсе геометрии понятия « точка», « прямая» и «плоскость» относятся к основным понятиям и принимаются без определений, другие геометрические понятия определяются через основные. К основным понятиям относятся также понятия «принадлежать» и «лежать между». Свойства геометрических фигур устанавливаются путем логических рассуждений на основе некоторых утверждений (аксиом), которые принимаются без доказательств. Аксиомы выражают основные свойства геометрических фигур, которые соответствуют формам и отношениям, наблюдаемым в окружающем пространстве.

Утверждение, которое обосновывается путем логических рассуждений, называется теоремой, а само обоснование — доказательством. Доказать теорему — это значит путем рассуждений обосновать, что она следует из некоторых аксиом или ранее доказанных теорем.

Взаимное расположение точек и прямых на плоскости характеризуют следующие основные свойства (аксиомы):

• А1. Каждой прямой принадлежат по крайней мере две точки.
• А2. Существуют по крайней мере три точки, не принадлежащие одной прямой.
• АЗ. Через любые две точки плоскости проходит единственная прямая, каждая точка которой принадлежит плоскости¹.

Прямая, которая проходит через точки А и В, обозначается АВ или ВА.

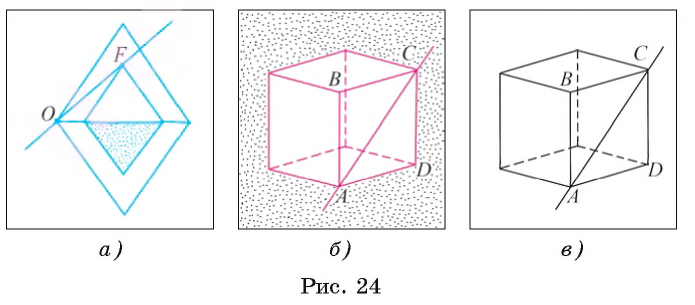
Например, на рисунке 24, а изображена прямая ОF, которая проходит через точки О и F, а на рисунке 24, б, в показана прямая АС, которая проходит через вершины А и С куба и лежит в той же плоскости, что и грань АВСD куба.

¹ Здесь и в дальнейшем, говоря «две точки», «две прямые» и т. д., будем считать, что эти точки, прямые и т. д. различны.

Пересекающиеся и параллельные прямые

Рассмотрим понятия пересекающихся и параллельных прямых.

Определение. Две прямые называются пересекающимися, если они имеют одну общую точку.

Если прямые а и b пересекаются в точке О, то это обозначается так: О = а  b (читают: «Прямые а и b пересекаются в точке О»).

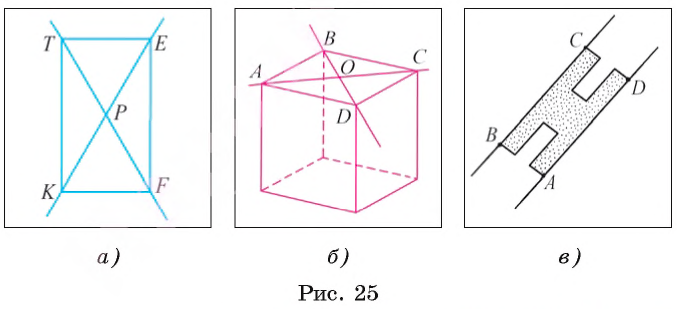
Например, на рисунке 25, а изображены прямые КЕ и TF, которые проходят через вершины прямоугольника и пересекаются в точке Р (Р =TF  КЕ).

На рисунке 25, B изображены прямые АС и BD, которые проходят через вершины куба и пересекаются в точке О (О = АС 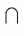ВD).

Определение. Две прямые называются параллельными, если они лежат в одной плоскости и не пересекаются.

Параллельные прямые l₁ и l₂ обозначаются так: l₁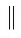 l₂ (читают: «Прямая l₁ параллельна прямой l₂ »).

Например, на рисунке 25, в изображены параллельные прямые ВС и АD (ВС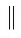АD).

Теорема. Если две прямые плоскости имеют общую точку, то она единственная.

Доказательство.

Пусть две прямые а и b имеют общую точку О. Докажем, что других общих точек эти прямые не имеют. Допустим, что прямые а и b имеют еще одну общую точку O₁. Тогда получается, что через точки O и O₁ проходят две прямые а и b. Но этого быть не может, так как по аксиоме А3 через две точки проходит единственная прямая. Таким образом, наше предположение неверно, и прямые а и b имеют единственную общую точку.

Теорема доказана.