Взаимное расположение геометрических образов и фигур с примерами (Начертательная геометрия)

Содержание:

Показать на чертеже точку (или прямую), принадлежащую плоскости, занимающей общее положение в системе плоскостей проекций, произвольно, не связывая ее с другими элементами плоскости, невозможно. Поэтому точка в плоскости выбирается из условия, что она находится на прямой линии этой плоскости.

Прямая же линия принадлежит плоскости, если она проходит:

• - через две точки этой плоскости;
• - через одну точку плоскости и параллельно какой-нибудь прямой этой плоскости.

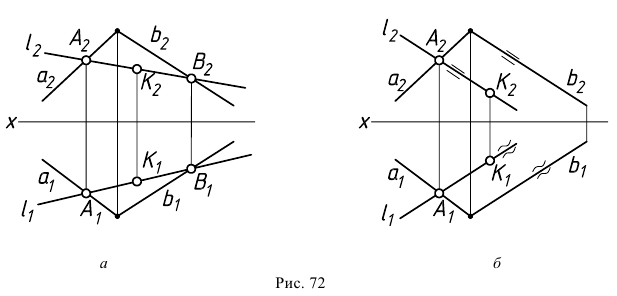
Рис. 72 иллюстрирует вышеизложенные условия принадлежности прямой плоскости на чертеже.

Прямая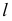

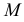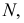Случай принадлежности прямой и точки плоскости, заданной следами, представлен на рис. 73. Здесь общими точками прямой и плоскости являются следы прямой  и принадлежащие соответствующим следам плоскости.

Принадлежность точек и прямых линий плоскостям, занимающим частное положение, определяется собирательным свойством их проекций. Так, ниже приведены фронтально-проецирующая плоскость 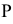 (рис. 74, а) и горизонтальная плоскость уровня 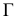(рис. 74, 6), а также показаны точка 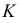и линия  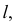лежащие в этих плоскостях.

Главные линии плоскости

Главными называют следующие линии плоскости:

• - прямые, принадлежащие плоскости и параллельные какой-либо плоскости проекций, - линии уровня;
• - прямые, принадлежащие плоскости и перпендикулярные какой-нибудь из линий уровня, - линии наибольшего наклона плоскости к плоскостям проекций.

Линии уровня в плоскости

В заданной плоскости, как и в пространстве, можно выделить три типа линий уровня:

• - горизонталь плоскости, линию параллельную 
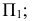
• - фронталь плоскости, линию параллельную
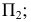
• - профильную прямую плоскости, линию параллельную

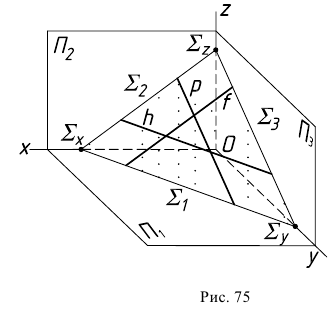
На рис.75 показаны горизонталь 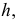фронталь 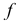и профильная прямая 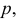принадлежащие плоскости  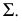Из рис. 75 видно также, что каждая из линий уровня всегда параллельна соответствующему следу плоскости :

• - горизонталь 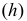- горизонтальному следу плоскости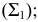
• - фронталь 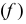- фронтальному следу плоскости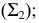
• - профильная прямая 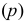- профильному следу плоскости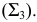

Исходя из этого, следы плоскостей называют еще линиями нулевого уровня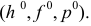

Рис. 76 иллюстрирует задание линий уровня плоскости на чертеже.

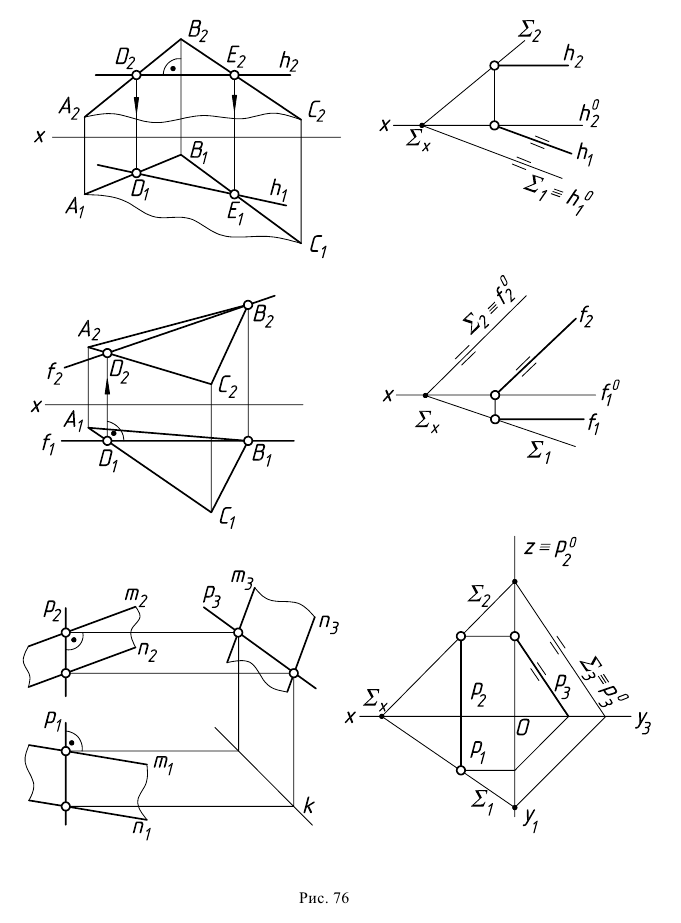
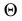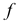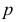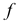В плоскостях частного положения некоторые из линий уровня становятся проецирующими прямыми. Так (рис. 77, а), в горизонтально-проецирующей плоскости фронталь и профильная прямая  займут горизонтально-проецирующее положение, а в горизонтальной плоскости уровня (рис. 77, 6) фронталь станет профильно-проецирующей прямой, а профильная прямая  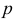- фронтально-проецирующей прямой.

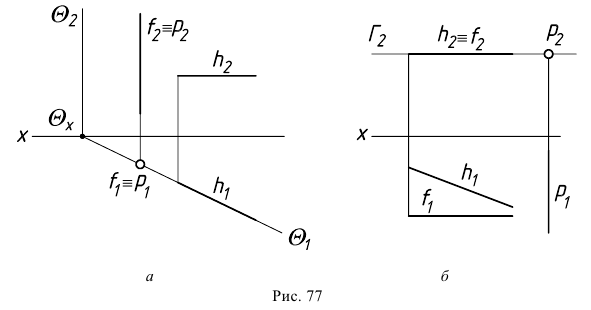
Линии наибольшего наклони плоскости

Другой разновидностью главных линий плоскости являются линии наибольшего наклона плоскости к плоскостям проекций. Для плоскостей общего положения это всегда прямые общего положения.

На рис. 78 показана линия 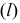наибольшего наклона плоскости 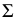к горизонтальной плоскости проекций  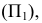которую иногда называют линией наибольшего ската плоскости. Отличительной особенностью этой линии является перпендикулярность ее к горизонтали (или горизонтальному следу) плоскости.

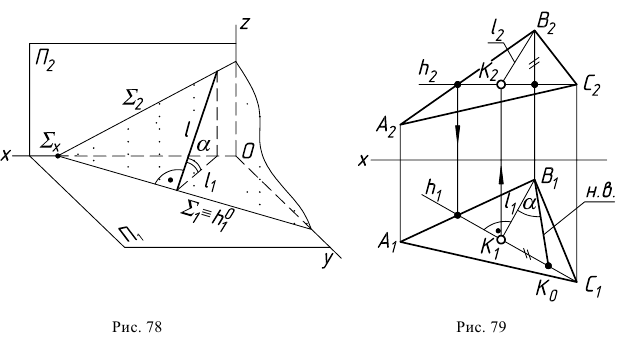
Аналогично на эпюре (рис. 79) горизонтальная проекция линии наибольшего ската 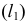перпендикулярна горизонтальной проекции горизонтали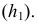 

Для линии наибольшего наклона плоскости к 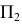характерно, что ее фронтальная проекция перпендикулярна к фронтальной проекции фронта-ли (или фронтальному следу). И, наконец, профильная проекция линии наибольшего наклона к  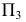займет положение, перпендикулярное к профильной проекции профильной прямой плоскости.

Из рис. 79 видно, что линиями наибольшего наклона можно пользоваться для определения угла наклона заданной плоскости к плоскостям проекций. Здесь с помощью способа прямоугольного треугольника определены натуральная величина линии наибольшего наклона 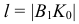и угол ее наклона к плоскости 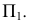Этот же угол определяет наклон и самой плоскости 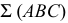к 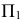(см. рис.78).

Параллельность прямой и плоскости, параллельность плоскостей

Прямая параллельна плоскости, если она параллельна какой-либо прямой, лежащей в этой плоскости. Через заданную точку в пространстве можно провести бесчисленное множество прямых линий, параллельных заданной плоскости. Для получения единственного решения требуется задать дополнительное условие - определить прямую, принадлежащую плоскости. Так, на рис. 80 показана прямая 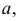 которая параллельна плоскости  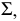так как она параллельна прямой  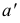этой плоскости.

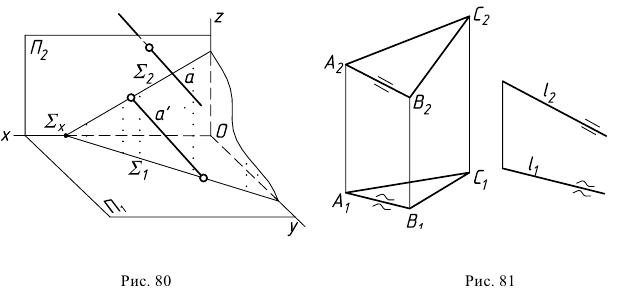
Условие параллельности прямой и плоскости на эпюре иллюстрирует рис. 81. Здесь прямая 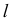параллельна плоскости 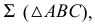так как выдержано условие параллельности ее одной из сторон треугольника - 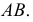Параллельность лини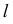и и 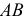подтверждается параллельностью их одноименных проекций на эпюре.

Случай параллельности прямой плоскости при задании плоскости следами показан для плоскости общего положения (рис. 82, а) и частного положения (рис. 82, б).

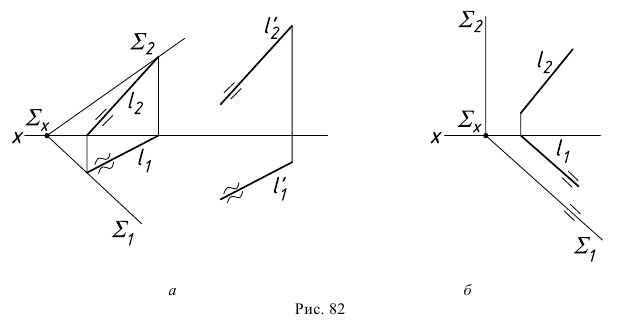
Плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Такими пересекающимися прямыми могут быть:

• - произвольные прямые плоскости (рис. 83, а);
• - следы плоскостей (рис. 83, б).

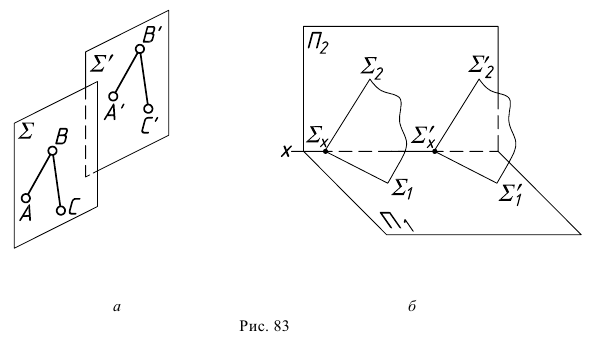
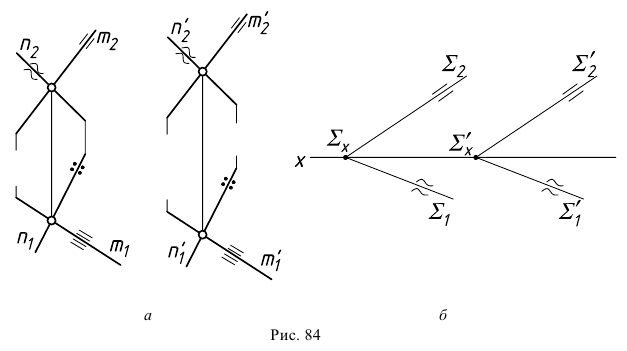
На рис. 84,а показаны две параллельные плоскост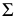и и 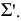Их параллельность определяется на эпюре параллельностью соответствующих проекций пересекающихся прямых: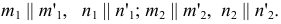 

На рис. 84,б показан случай параллельности двух плоскостей при задании их следами. Здесь параллельность плоскостей обеспечивает параллельность их одноименных следов: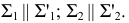

Перпендикулярность прямой и плоскости, перпендикулярность плоскостей

Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым этой плоскости (рис. 85, а).

Перпендикуляр к плоскости общего положения - это всегда прямая общего положения, поэтому для подтверждения перпендикулярности этой прямой и плоскости на чертеже в качестве двух пересекающихся прямых плоскости выбираются линии уровня. В соответствии с вышеизложенным прямой угол проецируется в натуральную величину на 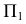 между прямой и горизонталью, а на  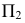- между прямой и фронталью плоскости.

Следовательно, на чертеже: (рис. 85, б) горизонтальная проекция перпендикуляра к плоскости перпендикулярна горизонтальной проекции горизонтали плоскости, а фронтальная - перпендикулярна фронтальной проекции фронтали плоскости.

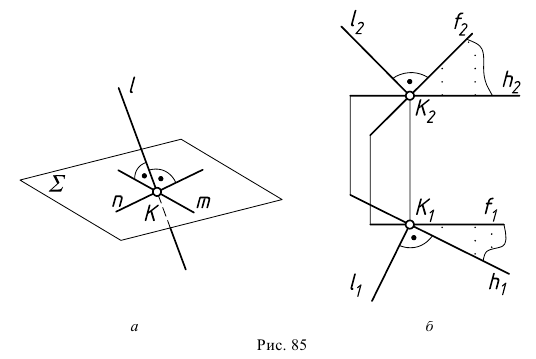
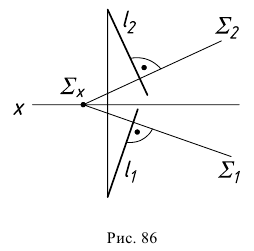
На рис. 86 показан случай перпендикулярности прямой к плоскости общего положения при задании плоскости следами. Здесь прямая 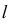 перпендикулярна плоскости 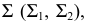так как она перпендикулярна следам плоскости, которые являются горизонталью и фронталью нулевого уровня.

Перпендикулярность двух плоскостей

Две плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

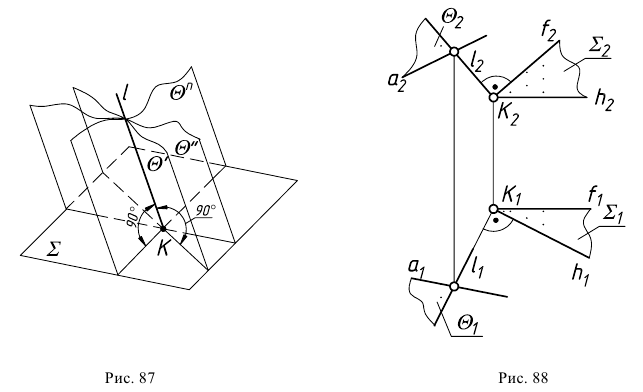
Как видно из рис. 87, через перпендикуляр к плоскости можно провести бесчисленное множество плоскостей, перпендикулярных данной. Поэтому для однозначного решения требуется задать дополнительные условия. Так, на рис. 88 для построения на чертеже плоскости, перпендикулярной заданной 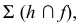 введена прямая  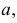пересекающая перпендикуляр к плоскости  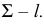Новая плоскость 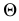здесь будет задана проекциями пересекающихся прямых 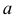и 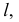и она перпендикулярна 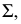так как проходит через перпендикуляр  к ней.

На рис. 89 показан случай перпендикулярности двух плоскостей  и общего положения при задании их следами. Здесь перпендикулярность плоскостей определяется прямой 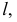 принадлежащей плоскости  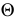и перпендикулярной плоскости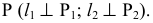

Следует запомнить: две плоскости общего положения не перпендикулярны между собой, если они заданы взаимно перпендикулярными, одноименными следами, так как в плоскости нет прямой, перпендикулярной другой плоскости.

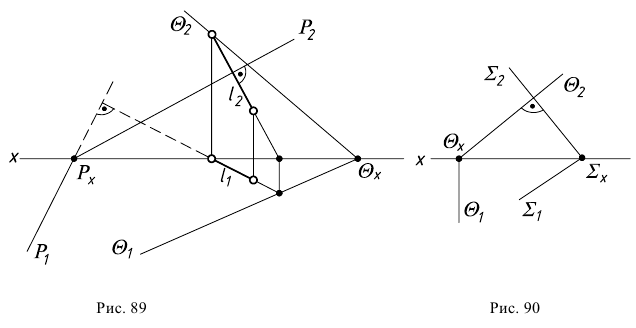
Рис. 90 иллюстрирует перпендикулярность плоскости общего положения 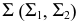 и фронтально-проецирующей плоскости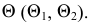

Пересечение прямой и плоскости, пересечение плоскостей

Аналитическое решение задачи о прямой, пересекающей плоскость, сводится к решению системы уравнений с тремя неизвестными. Допустим, что плоскость 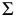задана уравнением

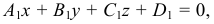
а прямая 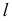задана совокупностью двух уравнени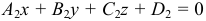й

 и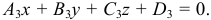

Координаты точки пересечения прямой 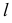с плоскостью  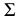определяются в результате совместного решения этих трех уравнений.

При аналитическом решении задачи о пересечении двух плоскостей, заданных общими уравнениями, получают общее уравнение прямой линии

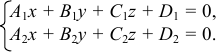
Вопрос может состоять только лишь в переводе этой совокупности общих уравнений в каноническое уравнение прямой.

Графическое решение позиционных задач на пересечение простейших геометрических образов в общем случае включает в себя построение либо точки встречи прямой с плоскостью, либо линии пересечения двух плоскостей. При этом линия пересечения плоскостей однозначно определяется двумя точками. Таким образом, в конечном итоге задачи на пересечение сводятся к нахождению точек (одной или двух), общих для обоих пересекающихся геометрических образов, и выявлению видимости этих образов относительно друг друга.

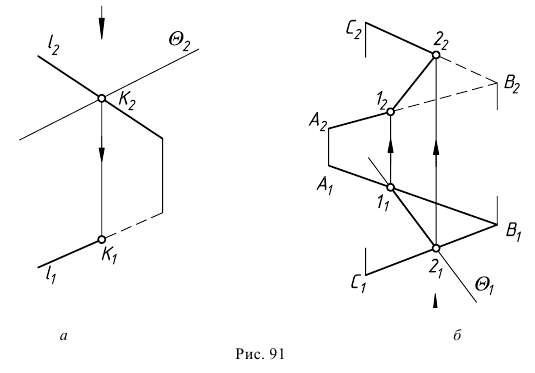
При построении таких общих точек важную роль играет расположение геометрических образов относительно плоскостей проекций. Так, если плоскость, с которой пересекается либо прямая, либо другая плоскость, занимает частное положение, то общая точка (линия) легко находится в чертеже без дополнительных построений (рис. 91, а, б).

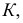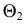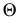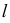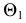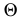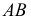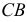Здесь искомыми являются точка фронтальная проекция которой определяется при пересечении следа плоскости с фронтальной проекцией прямой  (см. рис. 91, а), и линия 12, горизонтальная проекция которой определяется точками пересечения следа плоскости с горизонтальными проекциями прямых и (см. рис. 91, б).

При определении видимости условно считается, что заданная проецирующая плоскость непрозрачна, поэтому видимым будет то, что находится перед ней (см. рис. 91, б) и над ней (см. рис. 91, а). Стрелкой на чертеже показано направление взгляда на ту плоскость проекций, видимость на которой определяется. На плоскости проекций, которой заданная плоскость перпендикулярна, видимость уже определена, так как плоскость проецируется в прямую и ничего от наблюдателя не закрывает.

В случае, когда пересекающиеся геометрические образы (в частности, плоскости) занимают общее положение относительно плоскостей проекций, нахождение точек (линий) пересечения без дополнительных построений невозможно.

При решении таких задач применяют один из наиболее распространенных в начертательной геометрии способов - способ вспомогательных секущих плоскостей. Этот способ является частным случаем общего способа вспомогательных секущих поверхностей, так как плоскость можно рассматривать как простейшую поверхность. Способ вспомогательных секущих поверхностей более полно будет рассмотрен далее.

Сущность способа вспомогательных секущих плоскостей заключается в том, что в системе плоскостей проекций с заданными геометрическими образами вводятся вспомогательные секущие плоскости. Такие плоскости пересекают заданные г.о. и позволяют с помощью ряда построений выявить общие для обоих образов точки. В качестве секущих удобно использовать плоскости частного положения, пересечение с которыми определить, как было показано ранее, достаточно просто.

Рассмотрим алгоритм применения способа вспомогательных секущих плоскостей на примере решения следующих задач:

• - пересечения прямой линии с плоскостью общего положения;
• - пересечения двух плоскостей общего положения;
• - анализа взаимного положения прямой и плоскости, двух плоскостей.

Пересечение прямой линии с плоскостью общего положения

При решении этой задачи необходимо построить точку, одновременно принадлежащую прямой и плоскости, и определить видимость прямой относительно плоскости.

Алгоритм решения задачи следующий:

1. через заданную прямую проводят вспомогательную секущую плоскость;
2. строят линию пересечения двух плоскостей - секущей и заданной;
3. находят общую точку построенной линии пересечения с заданной прямой;
4. определяют видимость прямой относительно плоскости.

На рис. 92 проиллюстрирован алгоритм решения задачи. Здесь 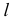- заданная прямая,  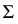- заданная плоскость, 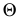- секущая плоскость, 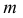- линия пересечения секущей плоскости с заданной, 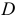- искомая точка пересечения прямой с плоскостью.

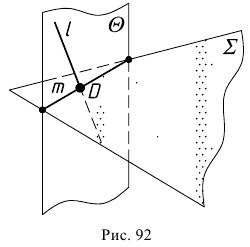
Приведенный алгоритм решения задачи справедлив и при выполнении построений на эпюре. Однако следует обратить внимание на то, что вспомогательную секущую плоскость можно вводить как на 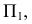так и на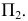

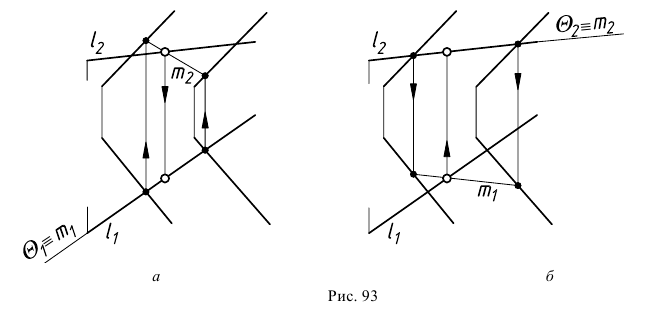
На рис. 93,а через прямую 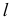проведена горизонтально-проецирующая вспомогательная секущая плоскость  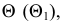а на рис. 93,б через прямую 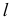проведена фронтально-проецирующая вспомогательная секущая плоскость  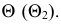Результат решения не будет зависеть от того, какой секущей плоскости отдано предпочтение. На рис. 93 видимость прямой не рассматривается.

Примеры построения точки пересечения прямой линии с плоскостью общего положения

На рис. 94 задана прямая 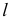и плоскость общего положения  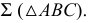В качестве секущей выбрана горизонтально-проецирующая плоскость 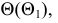проходящая через прямую 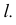Вспомогательная секущая плоскость  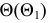пересекает данную плоскость 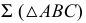по линии 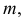горизонтальная проекция которой находится на следе секущей плоскости 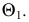Фронтальная проекция линии пересечения строится по точкам, принадлежащим соответственно фронтальным проекциям сторон треугольника 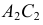и 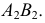На фронтальной плоскости проекций определится проекция 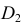искомой точки пересечения. Это есть точка пересечения линии  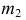с фронтальной проекцией заданной прямой 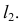Горизонтальная проекция 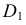лежит на горизонтальной проекции прямой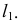

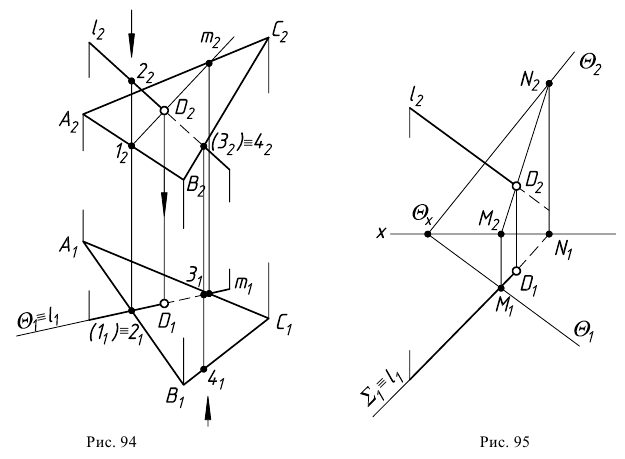
Для определения видимости используют пары конкурирующих точек, принадлежащих прямой 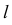 и скрещивающейся с ней стороной треугольника. Видимость на горизонтальной плоскости проекций определяется по паре горизонтально-конкурирующих точек 1, 2, на фронтальной плоскости проекций - по паре фронтально-конкурирующих точек 3, 4.

В точке 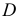 пересечения прямой с плоскостью видимость прямой будет меняться на противоположную.

На рис. 95 представлено построение точки пересечения прямой с плоскостью, заданной следами. Заданы прямая общего положения 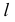 и плоскость 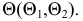Через прямую 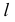проведена горизонтально-проецирующая плоскость 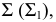которая пересекает заданную плоскость 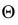по прямой 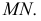Горизонтальная проекция линии пересечения 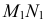совпадает со следом секущей плоскости 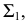а фронтальная проекция 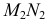определяется по линиям проекционной связи. Фронтальная проекция заданной прямой 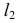пересекает линию 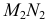в точке 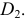Горизонтальная проекция точки 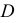принадлежит горизонтальной проекции данной прямой 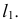Точка 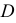принадлежит как прямой, так и заданной плоскости и является искомой точкой встречи прямой  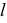с плоскостью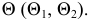 

Пересечение двух плоскостей общего положения

При решении этой задачи необходимо построить линию пересечения плоскостей, которая определяется двумя точками, и показать видимость плоскостей относительно друг друга. Алгоритм решения задачи способом вспомогательных секущих плоскостей следующий:

1. Определяется первая точка искомой линии пересечения:

• - вводится вспомогательная секущая плоскость, рассекающая обе заданные;
• - строятся линии пересечения секущей плоскости с каждой из заданных плоскостей;
• - находится точка пересечения построенных линий.

2. Аналогично определяется вторая точка искомой линии пересечения.

3. Показывается видимость плоскостей относительно друг друга.

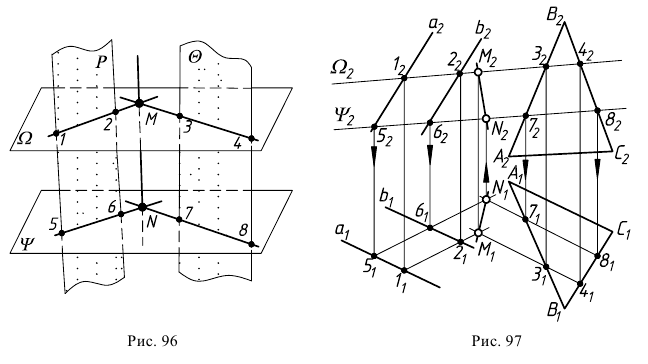
Алгоритм решения задачи проиллюстрирован на рис. 96. Здесь 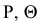-заданные плоскости общего положения, 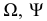- вспомогательные секущие плоскости; 12, 34 - линии пересечения секущей плоскости  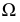с заданными плоскостями; 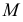- первая искомая точка линии пересечения, 56, 78 - линии пересечения секущей плоскости 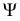с заданными плоскостями; 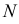- вторая искомая точка линии пересечения; 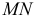-искомая линия пересечения.

Следует напомнить, что в качестве вспомогательных удобнее использовать секущие плоскости частного положения. Для построения линии пересечения, как правило, достаточно двух секущих плоскостей (при анализе взаимного положения плоскостей вспомогательных секущих плоскостей может быть больше двух).

Приведенный алгоритм решения задачи в пространстве справедлив и при выполнении построения на эпюре.

Пример построения на эпюре задачи нахождения линии пересечения двух плоскостей общего положения приведен на рис. 97.

Заданы плоскости общего положения 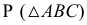и 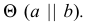Для решения задачи выбираются две секущие фронтально-проецирующие плоскост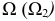и  и 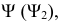пересекающие каждую из заданных плоскостей.

При пересечении плоскосте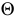й и 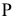плоскостью 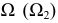получаются линии пересечения с проекциям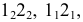и и 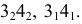Эти прямые, расположенные в секущей плоскости 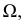в своем взаимном пересечении определяют горизонтальную проекцию первой искомой точки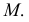

Вторая секущая плоскость 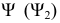 при пересечениями с заданными плоскостям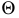и и 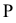 дает прямые с проекциями  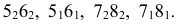Эти прямые, расположенные в плоскости 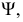в своем пересечении определяют горизонтальную проекцию второй точки 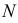искомой линии пересечения.

Фронтальные проекции точек 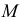и 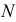находятся на следах соответствующих секущих плоскостей. Таким образом определяются проекци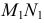и

и 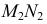искомой линии пересечения плоскосте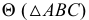й  и 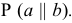 Вопрос видимости г.о. в данном примере не рассматривается.

В рассмотренном построении были взяты в качестве вспомогательных две фронтально-проецирующие плоскости. Результат построений не изменится, если будут взяты иные секущие плоскости частного положения.

При выполнении построений рекомендуется использовать особенности задания плоскостей и проводить вспомогательные секущие плоскости в соответствии с этим. Например, иногда удобно проводить вспомогательные секущие плоскости через прямые, которыми задана одна из плоскостей. В этом случае построения сводятся к двум последовательным решениям задачи на пересечение прямой с плоскостью.

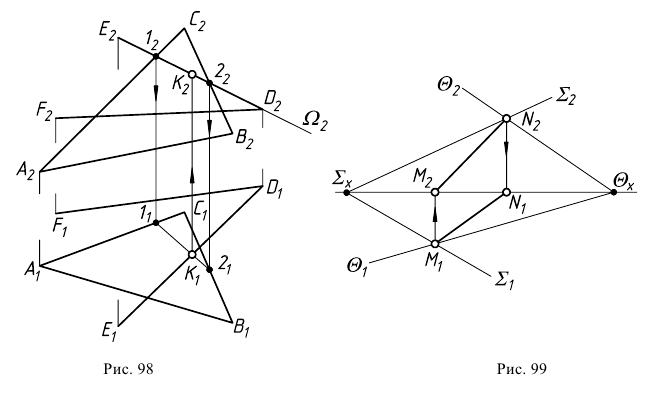
На рис. 98 показан вариант введения секущих плоскостей для случая, когда проекции заданных плоскостей накладываются.

Заданы две плоскости общего положения 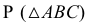и 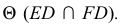Фронтально-проецирующая секущая плоскость  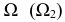проведена через прямую 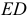плоскости  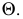Секущая плоскость  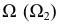пересекает плоскость

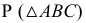 по линии 12, а плоскость  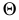о заданной прямой  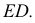На горизонтальной плоскости проекций определится проекция первой точки  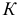искомой линии пересечения. В то же время точку 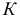можно рассматривать как точку встречи прямой  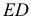с плоскостью  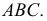Для определения второй точки искомой линии пересечения плоскостей можно провести секущую плоскость через любую из сторон треугольника или через прямую  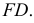Полное решение аналогичной задачи приведено ниже.

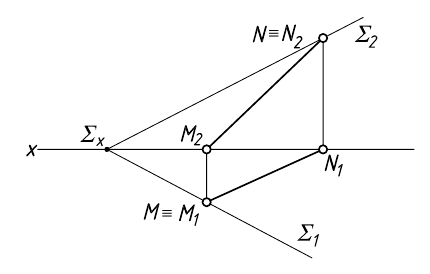
Построение линии пересечения для случая, когда плоскости заданы следами, приведено на рис. 99. Заданы следами плоскост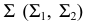и и 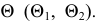Здесь роль секущих плоскостей выполняют сами плоскости проекций. Точки пересечения одноименных следов плоскостей являются следами линии пересечения этих плоскостей. Поэтому сначала определяются проекция точки 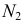в пересечении фронтальных следов 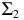и 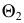и проекция точки 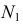в пересечении горизонтальных следов  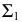и 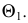 Потом строятся недостающие проекци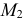и  и 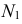и проекции искомой линии пересечения  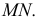Таким образом, если плоскости задают следами, то линия пересечения данных плоскостей проходит через точки пересечения одноименных следов плоскостей.

Анализ взаимного положения прямой и плоскости, двух плоскостей

Способ вспомогательных секущих плоскостей удобно использовать для анализа взаимного положения прямой и плоскости, двух плоскостей.

Для прямой и плоскости возможны три варианта их взаимного расположения: прямая пересекает плоскость, параллельна или принадлежит

Анализ сводится к решению задачи на пересечение прямой с плоскостью общего положения. Взаимное расположение прямой и линии пересечения секущей плоскости с заданной может быть следующим:

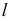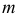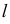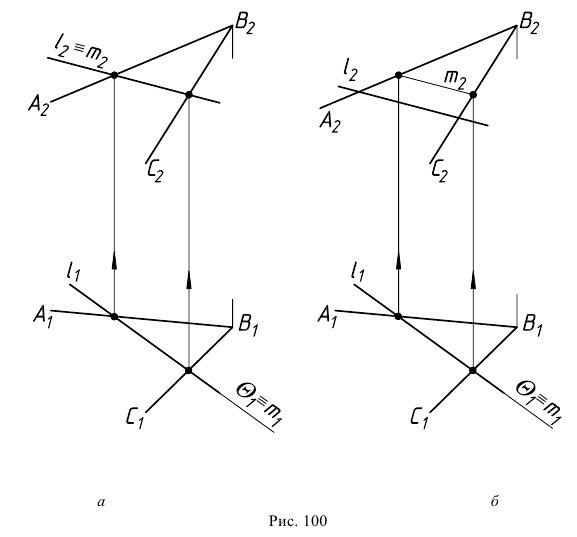
• -  прямая совпадает с прямой  т.е. данная прямая  будет принадлежать плоскости 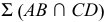(рис. 100, а);
• -    прямая 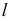параллельна прямой 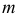, т.е. данная прямая 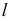параллельна плоскости 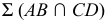(рис. 100, б)
• -    прямая 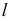пересекает прямую 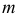, значит, данная прямая 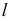пересекает плоскость 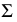(см. рис. 94).

Анализ задачи о взаимном расположении двух плоскостей состоит в том, чтобы выяснить, пересекаются или параллельны между собой данные плоскости. Анализ проводится при решении задачи на пересечение двух плоскостей общего положения. При этом в ходе решения задачи расположение линий пересечения вспомогательной секущей плоскости с каждой из заданных может оказаться следующим:

• - линии пересечения, получаемые от одной секущей плоскости, будут параллельны: 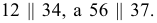В этом случае данные плоскости параллельны между собой (рис. 101);
• - линии пересечения, получаемые от каждой секущей плоскости, будут соответственно пересекаться: 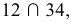а 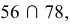следовательно, заданные плоскост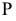и и 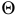пересекаются между собой (см. рис. 97).

Наряду с рассмотренным выше способом анализ задач о взаимном пересечении прямой и плоскости, двух плоскостей иногда проще провести, используя способы преобразования эпюра, которые будут рассмотрены далее.

Примеры решения задач

Задача 1. Определить расстояние от точки до прямой общего положения.

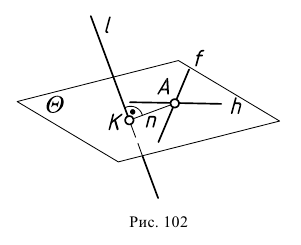
Расстояние от точки до прямой определяется длиной отрезка перпендикуляра, опущенного из точки на прямую. На рис. 102 для выявления этого перпендикуляра воспользуемся плоскостью 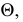проведенной через точку 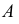перпендикулярно прямой 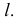Именно в этой плоскости будет лежать искомый

перпендикуляр 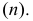 На эпюре такую плоскость необходимо задать горизонталью  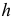и фронталью  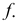Пример решения задачи на эпюре приведен на рис. 103. Через точку 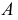проведена 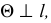заданная горизонталью 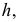у которой 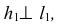и фронталью  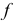с фронтальной проекцией  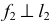(рис. 103, а).

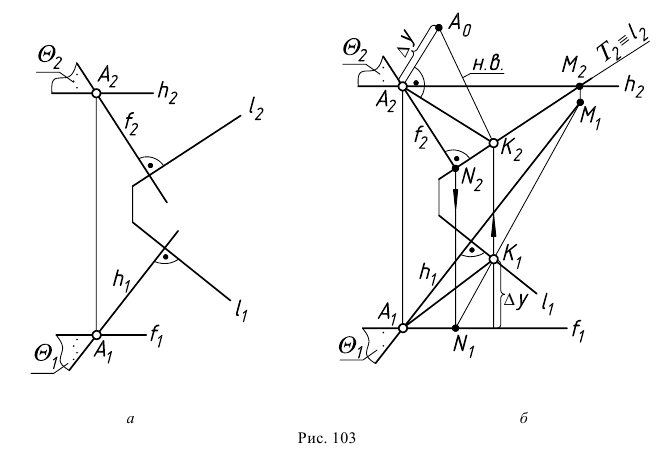
Для построения основания перпендикуляра точки 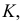как точки пересечения прямой  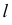и плоскости 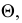через прямую вводится вспомогательная фронтально-проецирующая плоскость  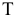(на рис. 103, б она задана следом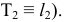 

Плоскост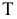и  и 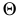пересекаются по линии 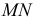с проекциям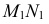и и 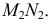На пересечении построенной линии 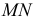и заданной 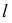определяется точка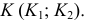 

Прямая 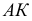- искомый перпендикуляр к прямой 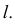Далее определяется натуральная величина отрезка 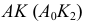способом прямоугольного треугольника.

Задача 1,а. Определить расстояние от точки до прямой частного положения.

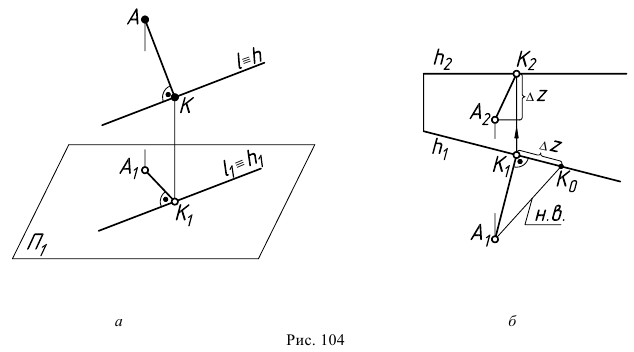
Если заданная прямая занимает частное положение, то алгоритм решения задачи значительно упрощается (рис. 104, а). Здесь опустить перпендикуляр из т. 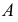на прямую  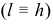можно сразу, без введения дополнительной плоскости, так как в этом случае прямой угол 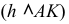спроецируется на плоскость  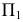в натуральную величину.

На рис. 104, б показано решение задачи на эпюре. Сначала строится горизонтальная проекция прямой 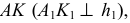затем с помощью линии связи фронтальная проекция  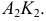Способом прямоугольного треугольника определяем натуральную величину перпендикуляра (искомого расстояния) -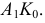

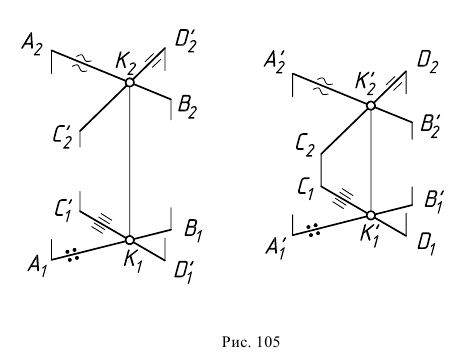
Задача 2. Через скрещивающиеся прямые провести параллельные плоскости (рис. 105).

Пусть заданы две скрещивающиеся прямые 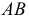и 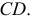 Через эти прямые можно провести только одну пару параллельных плоскостей (плоскостей параллелизма). Используя признак параллельности, такие плоскости следует определить парой пересекающихся прямых, взаимно параллельных между собой. Таким образом, для построения искомых плоскостей необходимо выполнить следующие построения.

Через произвольную точку 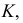выбранную на прямой  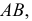проводим прямую, параллельную прямой  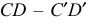с проекциям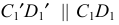и  и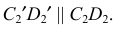 

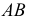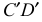Прямые  и определяют первую искомую плоскость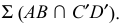

Аналогично через произвольную точку 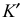 прямой 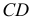проведем линию, параллельную прямой  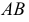(на эпюре 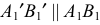и

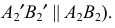
Пересекающиеся прямые 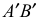 и 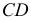 определяют вторую искомую плоскость  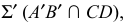параллельную плоскости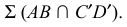

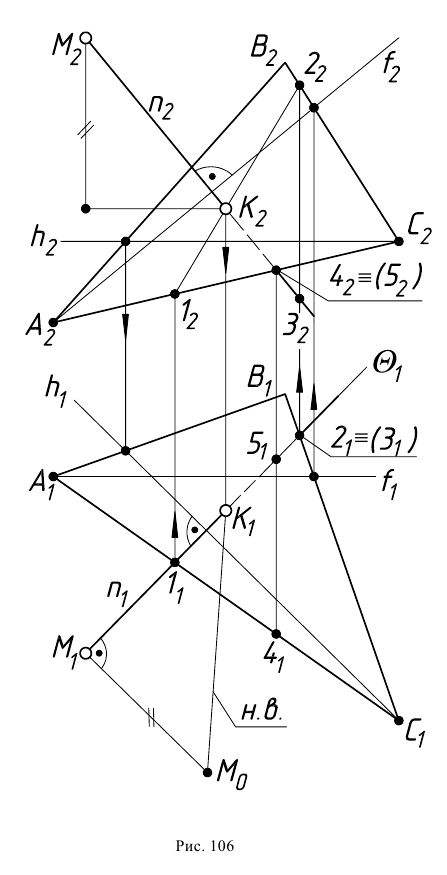
Задача 3. Определить расстояние от точки до плоскости общего положения (рис. 106).

Кратчайшим расстоянием от точки до плоскости является перпендикуляр, опущенный из заданной точки на плоскость. Для нахождения этого расстояния необходимо последовательно выполнить следующие три этапа построения:

1) задать направление прямой, перпендикулярной к заданной плоскости;

2) определить точку пересечения этой прямой с плоскостью (основание перпендикуляра);

3) найти натуральную величину перпендикуляра.

В соответствии с признаком перпендикулярности прямой и плоскости горизонтальная проекция прямой перпендикулярна горизонтальной проекции горизонтали плоскости, а ее фронтальная проекция - перпендикулярна фронтальной проекции фронтали этой плоскости. Поэтому для выполнения первого этапа построений проводим в плоскости 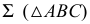горизонталь 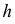и фронталь  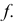Затем через точку  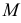проводим прямую 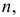перпендикулярную горизонтали и фронтали плоскости, т.е. выполняем условие: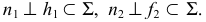 

На втором этапе решения задачи определяем основание перпендикуляра на плоскости - точку 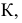 как точку пересечения прямой  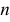с плоскостью  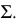Для этого используем способ вспомогательных секущих плоскостей. В качестве секущей выбрана плоскость  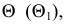которая является горизонтально-проецирующей и проходит через прямую  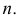На линии 12 пересечения секущей плоскости с заданной 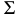определится общая точка с прямой 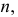которая и будет являться основанием перпендикуляра на заданной плоскости - точка 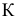(на эпюре: 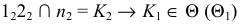и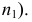 

По конкурирующим точкам 4, 5, и 2, 3 определяется видимость перпендикуляра относительно плоскости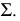

Перпендикуляр 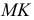 есть прямая общего положения. Его натуральную величину найдем способом прямоугольного треугольника (на эпюре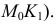 

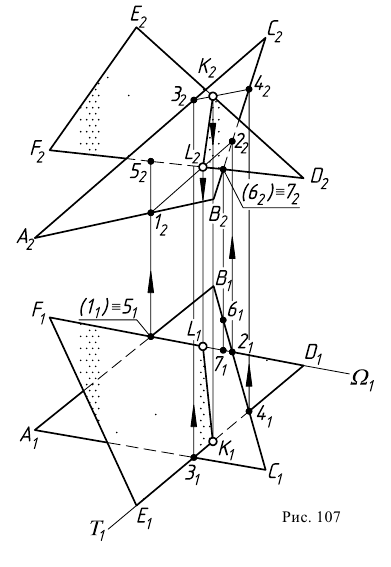
Задача 4. Построить линию пересечения двух плоскостей общего положения (рис. 107).

Для определения линии пересечения плоскостей используется способ вспомогательных секущих плоскостей. Для решения задачи достаточно двух вспомогательных плоскостей. Первая секущая плоскость 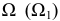является горизонтально-проецирующей и проходит через сторону 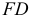треугольника  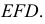Эта плоскость пересекает  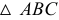по прямой 12, которая имеет общую точку 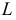со стороной  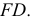Точка 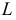будет первой искомой точкой линии пересечения (на эпюре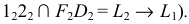

Вторая вспомогательная горизонтально-проецирующая секущая плоскость 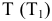 проходит через сторону 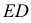треугольника  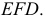Она пересекает этот треугольник по стороне  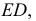а другой 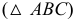- по прямой 34. На фронтальной плоскости проекций строится фронтальная проекция второй искомой точки пересечения 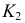как точка пересечения прямых 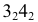и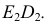 

Прямая 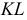- искомая линия двух плоскосте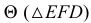й и 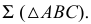 Видимость плоскостей определяется с использованием двух пар конкурирующих точек (1, 5 и 6, 7).

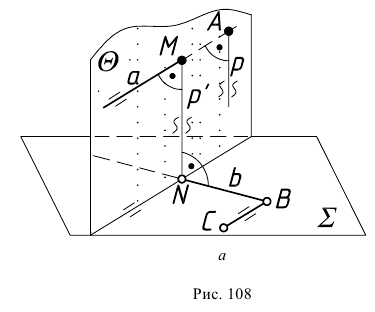
Задача 5. На скрещивающихся прямых построить точки, находящиеся на кратчайшем расстоянии друг от друга.

Кратчайшим расстоянием между скрещивающимися прямыми является перпендикуляр к ним, основания которого (точк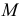и и 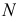) расположены на заданных прямых  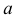и 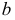 (рис. 108, а). Если одну из заданных прямых 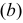заключить в плоскость 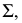параллельную другой прямой 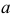(параллельность плоскости 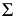прямой а определена на рисунке вспомогательной прямой 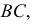лежащей в плоскости  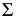и параллельной прямой 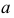), то расстояние между плоскостью и прямой будет величиной постоянной. Отсюда перпендикуляр опущенный из любой точки прямой 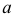к плоскости 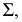определит искомое расстояние между заданными скрещивающимися прямыми. Перпендикуляр 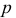и прямая 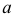образуют плоскость 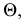перпендикулярную построенной плоскости 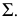Там, где плоскость  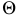пересечет прямую 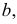определится первая искомая точка 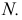Перпендикуляр  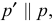восстановленный из точки 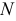до пересечения с прямой 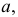даст вторую искомую точку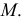

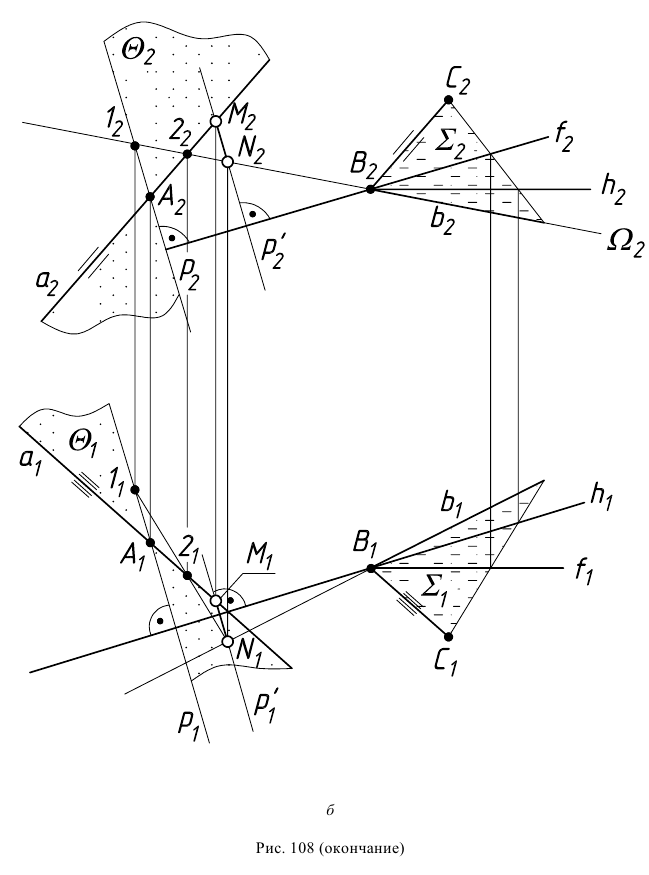
На рис. 108, б приведено решение задачи на эпюре. Через прямую 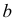проведена пересекающаяся с ней прямая 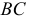параллельно данной прямой а, образуя таким образом плоскость 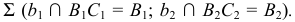Из произвольной точки 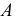на заданной прямой 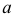опущен перпендикуляр 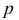к плоскости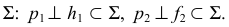

Прямая 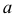 и перпендикуляр 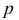образуют плоскость 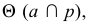перпендикулярную плоскости 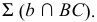Для определения точки встречи прямой  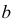с плоскостью 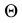введена вспомогательная секущая плоскость  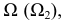которая пересекает плоскость 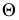по прямой 12. Пересечение прямых 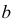и 12 даст искомую точку  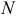- основание перпендикуляра на прямой 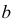. Восстановив из точки 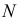искомый перпендикуляр  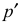параллельно построенному 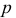, до пересечения 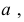получают вторую точку 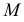- основание перпендикуляра на прямой  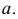Таким образом, 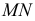- кратчайшее расстояние между скрещивающимися прямым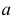и и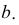

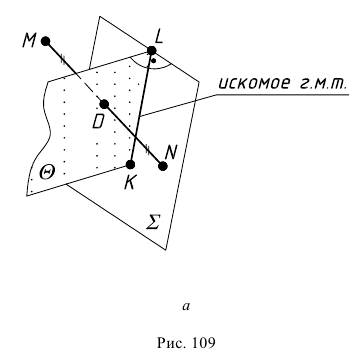
Задача 6. В заданной плоскости построить г.м.т., равноудаленных от двух точек пространства.

Геометрическим местом точек, равноудаленных от заданных точек 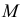и 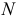(рис. 109, а), является, как известно, плоскость 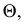проходящая через середину отрезка  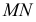(точка  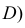и перпендикулярная ему. Искомое же г.м. точек, по условию задачи расположенных в заданной плоскости  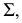будет находиться на линии пересечения  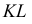этой плоскости  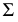и построенной плоскости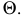

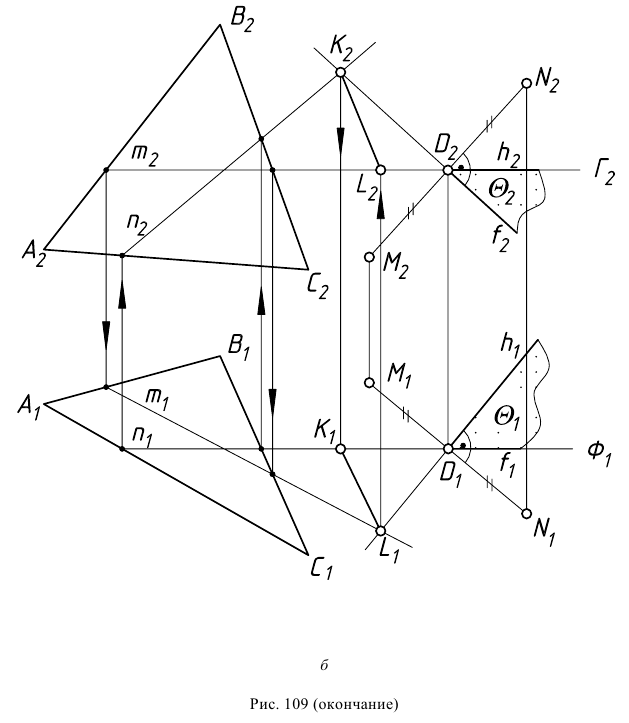
На эпюре (рис. 109, б) через середину отрезка 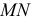и перпендикулярно ему проведена плоскость 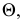заданная фронталью  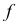и горизонталью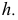 

Линия пересечения 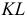плоскости  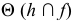и заданной плоскости 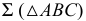определена способом вспомогательных секущих плоскостей. Первая секущая плоскость 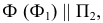проведенная через фронталь  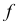плоскости  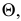пересекает плоскость 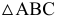по линии  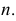На фронтальной плоскости проекций при пересечении фронтальной проекции 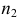и фронтальной проекции 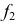получается проекция 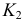первой искомой точки  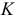линии пересечения.

Вторая секущая плоскость 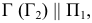проведенная через горизонталь плоскости 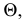пересекает плоскость треугольника  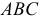по линии 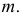На горизонтальной плоскости проекций при пересечении соответствующих проекций горизонтали и линии 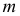находится проекция 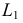второй искомой точки  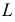линии пересечения.

Соединив полученные одноименные проекции точек 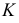 и 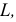 определяем проекции линии  - искомого г.м.т.