Вынужденные колебания в физике - формулы и определения с примерами

Содержание:

Вынужденные колебания:

Происходящие в какой-либо среде свободные колебания являются затухающими (рис. 5.5), потому что колеблющееся тело в период колебания встречает сопротивление со стороны среды в результате трения. 

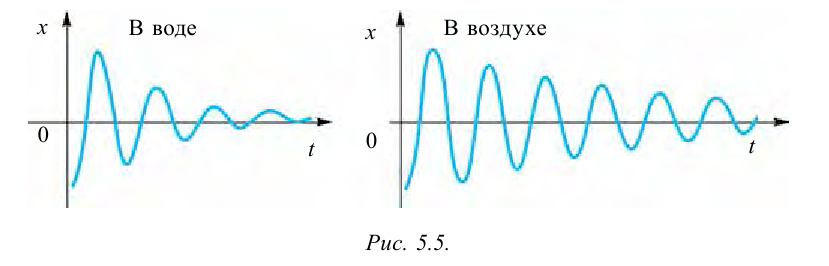
По этой причине свободными колебаниями на практике не пользуются.

Чтобы колебания не затухали, требуется периодически пополнять использованную энергию. Для этого на колеблющую систему нужно периодически воздействовать с помощью внешних сил. Простой макет такого оборудования, где со стороны действует внешняя сила, приводится на рисунке 5.6. Если груз, подвешенный на пружине, потянуть и отпустить, то он будет колебаться. Если в это время крутить ручку железной оси, к которой подвешена пружина, то колебания не угаснут. Колебания системы, которые происходят под периодическим воздействием внешних сил, называются вынужденными колебаниями. 

Периодически меняющаяся внешняя сила, которая создает эти вынужденные колебания, называется вынуждающей силой. 

Можно привести множество примеров вынужденных колебаний из повседневной жизни. Мембраны радиодинамиков ваших любимых радиоприемников, магнитофонов, телевизоров колеблются под воздействием проходящего через них вынуждающего тока. Когда рядом с домом или классом проезжают большегрузные автомобили, то вы слышите, как дребезжат стекла. Пневматические молотки (отбойные молотки), с помощью которых ломают бетонные конструкции (фундамент, столбы), рушат горные породы, тоже работают под воздействием периодических внешних сил.

Чтобы воспользоваться вынужденными колебаниями или избавиться от них, нужно изучить это явление. С помощью оборудования, приведенного на рисунке 5.6, рассмотрим воздействие внешних вынуждающих сил на колебания, происходящие в колебательной системе.

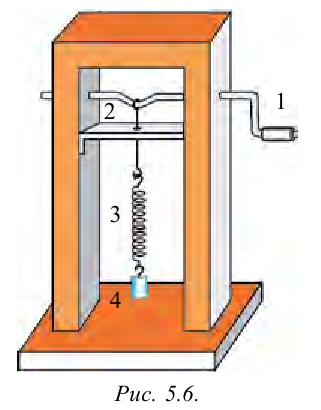
Пружина (3) с подвешенным грузом (4) висит на крючке (2). Кончик крючка имеет форму кольца, и может скользить по металлической оси (1), согнутой в виде дуги. Когда ось начинает вращаться под воздействием внешней силы, колебания груза сначала немножко отстают, а затем совпадают с вращением оси. Колебание становится устойчивым.
Сколько раз за единицу времени будет вращаться ось, столько же раз будет колебаться пружина с грузом.

Значит, частота вынужденных колебаний, происходящих в колебательных системах, равна частоте вынуждающих сил. 

Вынужденные колебания – это колебания, которые не затухают.

Явление резонанса

Теперь посмотрим, каким образом влияет амплитуда колебаний, происходящих в колебательной системе, на вынуждающую силу. Для этого проведем простой опыт. Веревку длиной 4–5 метров протянем из одного конца комнаты в другой с небольшим провисанием.

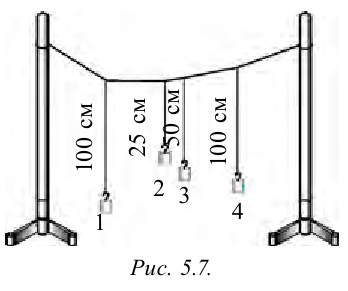
К этой веревке подвесим 3–4 груза на лентах разной длины (рис. 5.7).
Выберем для первого и четвертого груза ленты одинаковой длины. Если первый маятник вывести из равновесного состояния и отпустить, то он начинает колебаться. Его колебания, передаваясь по общей веревке, приводят в движение остальные маятники. После установления устойчивых колебаний второго, третьего и четвертого маятников, можно убедиться, что амплитуда четвертого маятника окажется самой большой. Из-за того, что длина четвертого и первого маятников одинаковы, их периоды свободного колебания (частота) получаются
взаимно равными.

Значит, в вынужденных колебаниях в случае, когда частота вынуждающей силы равна частоте собственного колебания колебательной системы, амплитуда колебаний будет самой большой, т.е. происходит резонанс.

Явление резкого увеличения амплитуды колебания в случае, когда частота внешней вынуждающей силы равняется собственной частоте колебательной системы, называется резонансом.

Причиной резкого увеличения амплитуды во время резонанса является взаимное совпадение направления вынуждающей силы и направления движения колеблющегося тела.

Резонанс широко используется в технике и в быту. В часах, во всех видах звонков, сиренах, пневматических молотках используют явление резонанса.
Однако явления резонанса не всегда полезны.

Например, когда человек проходит по висячему мосту через реку, он качается. В зависимости от скорости, с которой человек проходит по мосту (быстро или медленно), колебания моста могут увеличиваться или уменьшаться. Если частота шага совпадает с собственной частотой моста, его опоры могут не выдержать и трос или канат может оборваться.

В тех случаях, когда резонанс наносит вред, в целях уменьшения воздействия предпринимают соответствующие меры. Фундаменты производственных помещений строят тяжелыми и большими, чтобы в результате вращения деталей оборудования не возникал резонанс. Для быстрого погашения колебаний в автомобилях устанавливаются амортизаторы.

Автоколебания

Для того, чтобы вынужденные колебания не затухали, нужна внешняя периодическая сила. Но колебания системы могут быть негаснущими и без воздействия внешних периодических сил. Если внутри свободно колеблющейся системы будет иметься источник энергии, и система сможет направлять необходимую энергию из этого источника к колеблющемуся телу, чтобы восполнять затраченную энергию, то в такой системе появляются негаснущие колебания.

Самым простым примером системы такого типа являются обычные часы с маятником. Эта система имеет определенный запас энергии, т.е. потенциальную энергию поднятого на определенную высоту груза или энергию сжатой пружины.

Системы, которые создают негаснущие колебания за счет снабжения из источника энергии, называются автоколебательными системами. Электрический звонок, сердце и легкие человека тоже можно рассматривать как автоколебательные системы.

Негаснущие колебания, которые могут осуществляться в системе под воздействием внутреннего источника и без воздействия внешней периодической силы, называются автоколебаниями.

Частота вынужденного колебания будет совпадать с частотой внешних сил. Частота и амплитуда автоколебаний определяются собственными особенностями системы. Амплитуда автоколебаний не зависит от величины кратковременного воздействия (удара), которое привело к этим колебаниям.

Вынужденные колебания, резонанс

Под действием изменяющейся по гармоническому закону внешней силы (например, 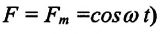 в колебательной системе создаются вынужденные колебания.

Частота вынужденных колебаний всегда совпадает с частотой изменения вынуждающей силы — с какой частотой изменяется внешняя сила, с такой же частотой колеблется система.

Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы. При приближении значения частоты вынуждающей силы к значению частоты свободных колебаний системы амплитуда колебаний увеличивается (d). При равенстве этих частот 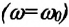наблюдается:

Резонанс - резкое возрастание амплитуды вынужденных колебаний системы.  

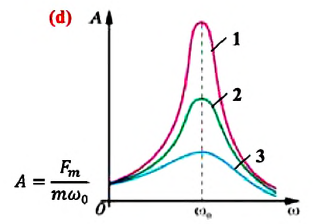
Форма резонансной кривой зависит от значения силы трения в системе. Так, при малых значениях силы трения резонансная кривая выше (1-я кривая), а при больших значениях силы трения, наоборот, резонансная кривая ниже (3-я кривая).

Исследуем это теоретически с помощью горизонтального пружинного маятника: предположим, что шарик массой 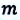совершает вынужденные колебания под действием внешней силы, изменяющейся по закону

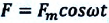(е).

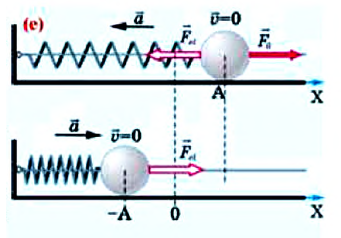
Уравнение вынужденных колебаний маятника с учетом II закона Ньютона можно записать так:

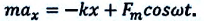
Если в этом уравнении принять во внимание формулы смещения и ускорения, изменяющихся по периодическому закону 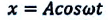и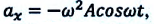 

то: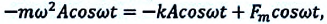    

или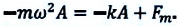    

Если же принять во внимание

то: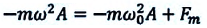  

Или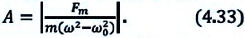 

Где 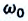— циклическая частота свободных колебаний колебательной системы, 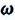— циклическая частота вынужденных колебаний, 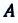— амплитуда вынужденных колебаний.

Из формулы (4.33) зависимости амплитуды колебаний от циклической частоты видно, что при явлении резонанса, если 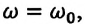амплитуда колебания увеличивается до бесконечности: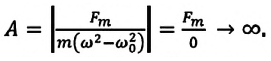

Резонанс вынужденных колебаний колебательной системы создает большую разрушительную силу, которая может быть причиной катастрофы. Например, если частота действия вынуждающей силы, создаваемая марширующей через мост войсковой частью, совпадает с частотой свободных колебаний моста, то амплитуда вынужденных колебаний моста резко увеличивается, что может привести к его разрушению. По этой причине при переходе через мосты солдатам приказывают идти вольным шагом.

Распространение колебаний в упругой среде: механическая волна

Как вы знаете, во время землетрясения скорость распространения продольных волн Р-типа, возникающих внутри Земли, больше скорости распространения поперечных волн L-типа, возникающих на поверхности Земли. На основании разности между этими скоростями ученые-сейсмологи определяют расстояние от точки расположения сейсмографа до эпицентра землетрясения.

Волна

Механические колебания были изучены в разных замкнутых колебательных системах - пружинном и математическом маятниках. Однако в природе наиболее часто встречающимися колебаниями являются колебания в связных колебательных системах. В связанных колебательных системах колебания передаются от одной части системы к другой. Например, при падении камня на поверхность стоячей воды наблюдается возникновение концентрических водяных кругов, которые расходятся из точки падения камня во все стороны. Кажется, что вода перемещается в пространстве в форме чередования выпуклостей и впадин. Однако, если расположить около точки падения камня поплавок или теннисный мячик, то наблюдается только его колебательное движение вверх-вниз на одном месте. Таким образом, возникающие в определенной точке колебательные движения частичек воды, передаваясь соседним частичкам воды вызывают колебательные движения все новых и новых частичек воды, и создают распространяющиеся во все стороны, колебательные движения системы связанных частичек. При таком распространении, называемом волной, перенос воды не происходит, а переносится только форма ее. движения

Волна — это процесс распространения колебаний в пространстве с течением времени.

В это время в среде происходят следующие явления: а) колебательные движения частичек среды, в которой распространяется волна — частички среды совершают колебательные движения только вокруг положения своего равновесия, и в волне не происходит перенос вещества; b) взаимодействия частичек среды с соседними частичками - в результате взаимодействия между частичками происходит перенос энергии. По этой причине волне можно дать следующее определение:

Волна — это процесс переноса энергии без переноса вещества.

Механическая волна

В природе наиболее часто встречается механическая волна.

Механическая волна — это процесс распространения механических колебаний в среде (механическая волна в вакууме не распространяется). Механические волны распространяются только в упругих средах (твердых телах, жидкостях и газах).

Упругие волны - это процесс распространения механических колебаний в упругой среде. Этот процесс происходит с частотой, соответствующей частоте колебания источника, создающего эту волну. За пределами среды упругие волны не существуют. Волны бывают двух видов: поперечные и продольные.

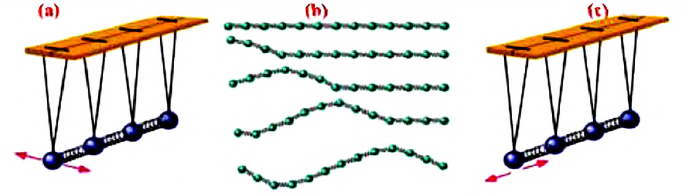
Поперечная волна — это волна, распространяющаяся перпендикулярно направлению колебательного движения частиц среды. Поперечные волны могут распространяться только в твердых телах и по поверхности жидкостей. Поперечные волны распространяются в среде в форме сменяющих друг друга выпуклостей и впадин (d).

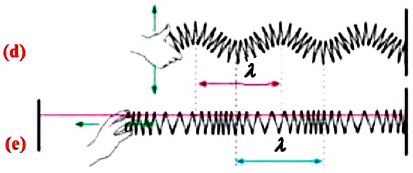
Продольная волна — это волна, распространяющаяся вдоль направления колебательного движения частиц среды. Продольные волны могут распространяться во всех средах (твердых телах, жидкостях и газах). Продольные волны распространяются в среде в форме сменяющих друг друга зон сгущения и разрежения среды. Например, пропустив через длинную пружину пластмассовую нить, закрепите горизонтально оба конца нити и один из концов пружины к опорам, затем, периодически двигая свободный конец пружины вправо-влево, можно наблюдать чередование зон сгущения и рассеивания колец пружины (е).

Характеристика волны

Колебания, происходящие в какой-либо точке среды, передаются в другие точки не мгновенно, а с определенной конечной скоростью, которая определяет скорость волны.

Скорость волны — это скорость распространения колебаний в среде.

Так как волна в однородной среде распространяется равномерно, скорость волны будет равна:

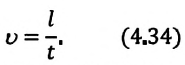
Где 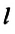- расстояние, на которое распространяется волна за время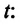 

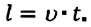
Другими характеристиками волны являются частота, период и длина волны.

Частота волны (период)—это частота (период) колебаний источника, создающего волну.

Длина волны - это расстояние 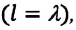 на которое волна распространяется за время, равное одному периоду колебания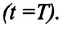 

Приняв во внимание это определение в (4.34), получим выражение для скорости распространения волны:

или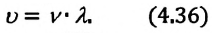    

Где 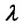(лямбда) — длина волны, в СИ единица ее измерения — метр. Из последних двух формул можно определить длину волны:

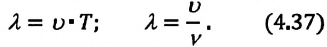
Скорость волны не зависит от ее частоты и периода. Скорость волны зависит от свойств и агрегатного состояния среды. Длина волны в однородной среде 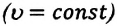 прямо пропорциональна периоду колебаний и обратно пропорциональна частоте колебаний.

При переходе из одной среды в другую частота и период волны не меняются, однако так как скорость волны в разных средах разная, то длина волны меняется.

Длина волны —это расстояние между двумя ближайшими точками, колеблющимися в одинаковых фазах. Длина волны в поперечных волнах равна расстоянию между двумя соседними точками вершин выпуклостей (или впадин) (cм: d), в продольных же волнах, - расстоянию между двумя соседними точками зон сгущения (или разрежения) (см: е).

Уравнение волны

Предположим, что источник волны колеблется по гармоническому закону колебательное движение распространяется со скоростью 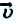в окружающей источник среде, тогда в результате возникает волна, которая через определенный промежуток времени достигнет точки, находящейся на расстоянии 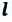 от источника:

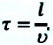
Это значит, что колебания в точке, находящейся на расстоянии 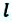от источника, происходят по тому же закону и возникнут с опозданием на 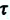секунд. Поэтому уравнение волны, достигшей произвольной точки на расстоянии 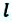от источника колебания, можно записать так:

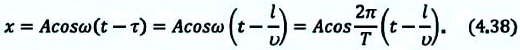
График волны по форме схож с графиком гармонических колебаний, однако это не одно и то же. Так, если график гармонических колебаний показывает изменение по гармоническому закону одной из характеристик колеблющейся точки, например, смещения от времени (f), то график волны—это картина расположения связанных точек среды в данный момент времени, то есть гармоничность этой волны в среде (g).