
Вычисление площадей плоских фигур с примерами решения
Вычисление площадей плоских фигур:
Определение 1. Пусть Ф – фигура на плоскости. Рассмотрим множество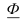
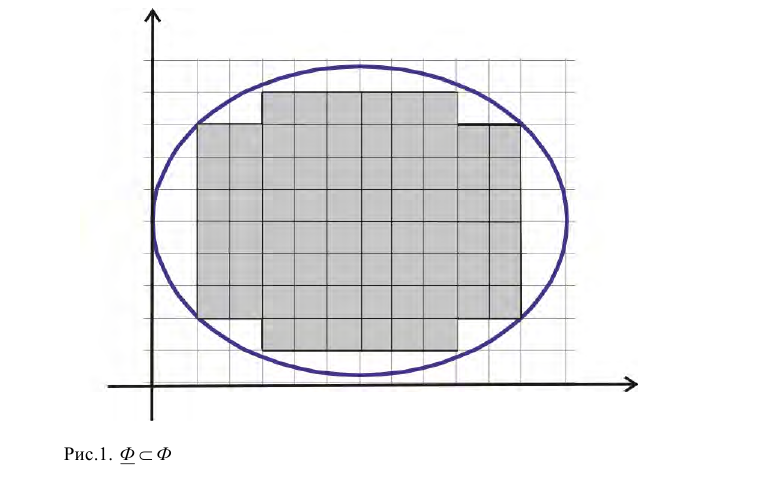
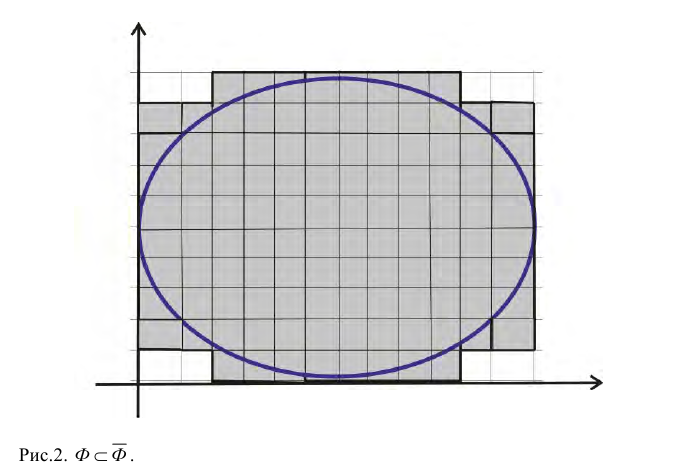
Пусть 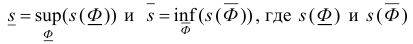 - площади фигур
- площади фигур 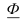 и
и 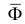 . Фигура Ф называется квадрируемой, если
. Фигура Ф называется квадрируемой, если 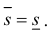 При этом число
При этом число 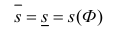 (1) называется площадью фигуры Φ (по Жордану).
(1) называется площадью фигуры Φ (по Жордану).
Замечание. Для квадрируемости фигуры Ф необходимо и достаточно,
чтобы 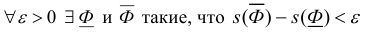
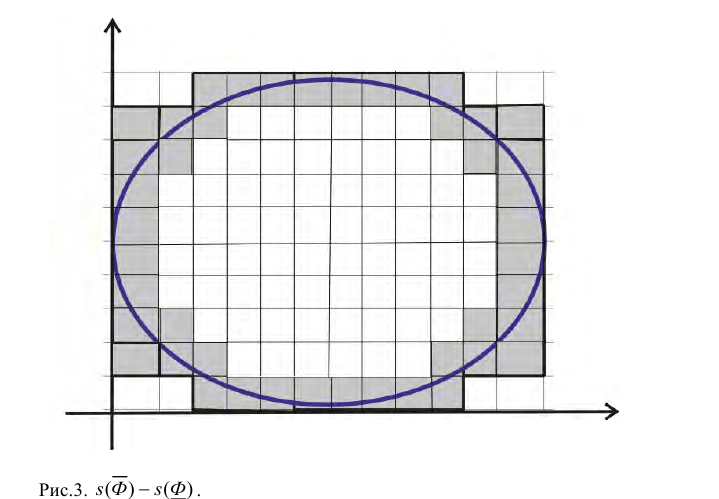
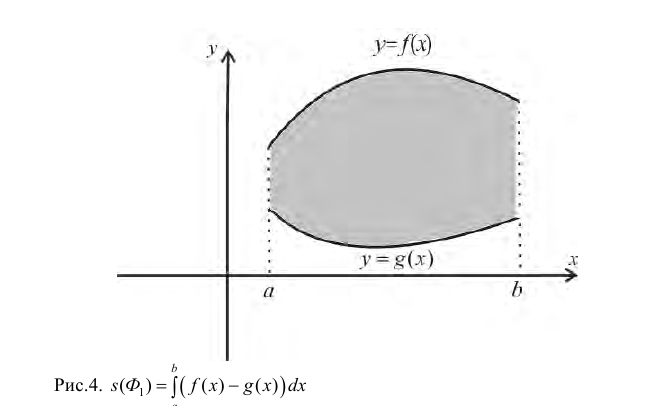
В частности, для криволинейной трапеции 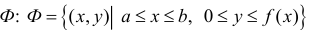 (см. § 24) в качестве
(см. § 24) в качестве 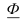 и
и 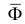 можно рассматривать нижние и верхние суммы Дарбу (см. рис. 3, 4, 5 из § 24). И тогда, с учетом § 24, из (1) следует, что
можно рассматривать нижние и верхние суммы Дарбу (см. рис. 3, 4, 5 из § 24). И тогда, с учетом § 24, из (1) следует, что 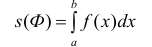 (2)
(2)
Пусть 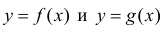 - непрерывны на
- непрерывны на 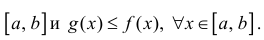 Тогда из (2) следует, что для фигуры
Тогда из (2) следует, что для фигуры 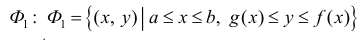
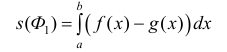 (3)
(3)
Пример 1.
Найти площадь фигуры Ф, ограниченной линиями 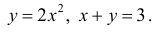
Решение.
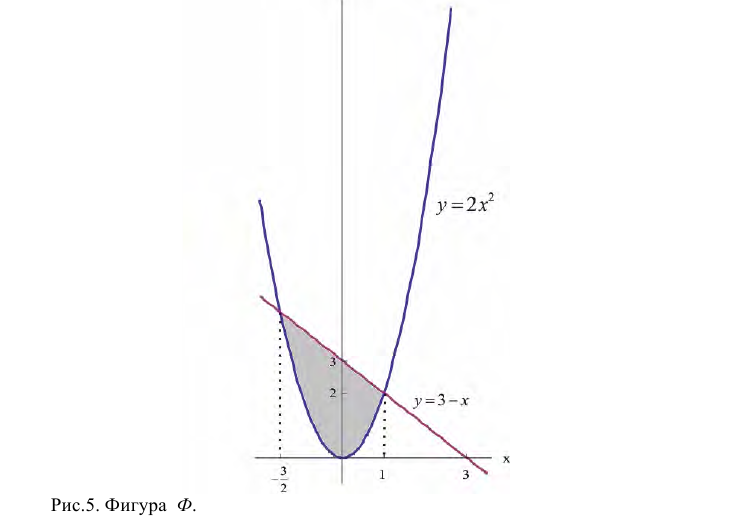
Точки пересечения линий 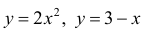 − найдем, решив систему:
− найдем, решив систему:
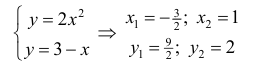
Сверху фигура ограничена прямой y=3-x, снизу – параболой 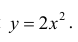 . Поэтому
. Поэтому
по формуле (3): 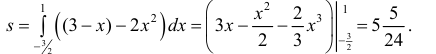
Пример 2.
Найти площадь фигуры Ф, ограниченной линиями 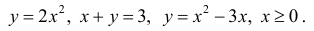
Решение.
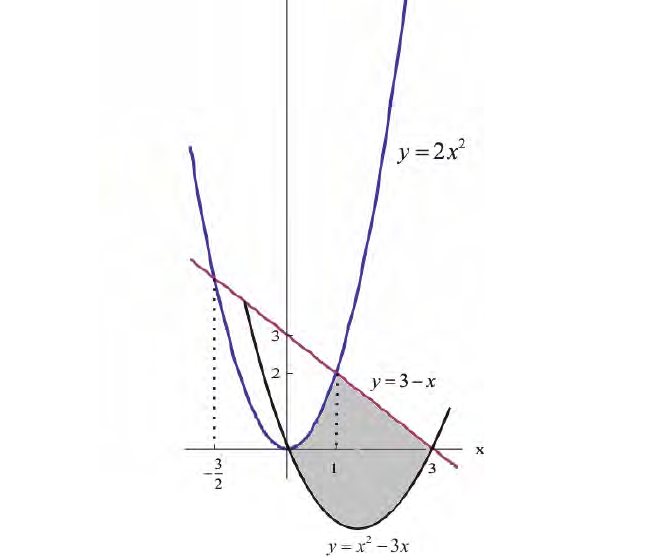
Рис.6. Фигура Ф.
Снизу фигура ограничена параболой 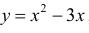 , сверху – кривой
, сверху – кривой 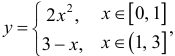 заданной двумя аналитическими выражениями.
заданной двумя аналитическими выражениями.
Поэтому разобьем отрезок интегрирования [0, 3] на два: [0,1] и [1, 3] , и
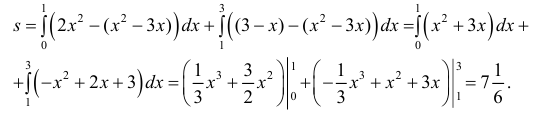
Пример 3.
Найти площадь фигуры Ф, ограниченной линиями 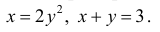
Решение.
Точки пресечения линий 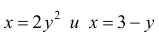 − найдем, решив систему:
− найдем, решив систему:
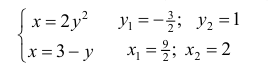
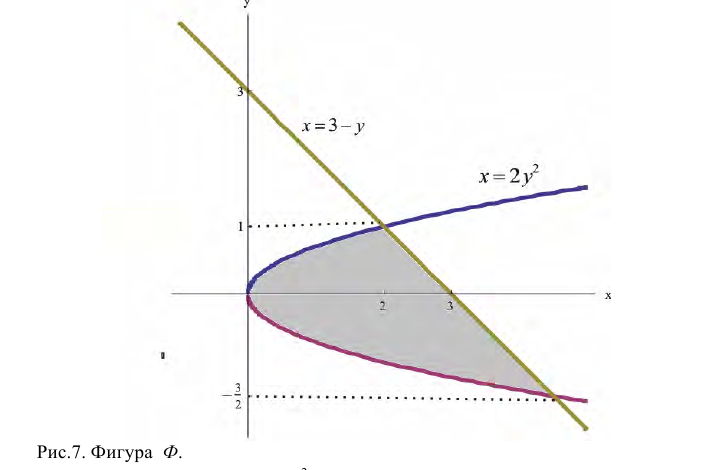
За независимую переменную в данном случае удобно считать у , а х – функцией от у.
Справа фигура ограничена прямой x=3- y, слева – параболой 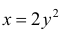 . По формуле (3):
. По формуле (3): 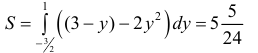 (см. пример 1).
(см. пример 1).
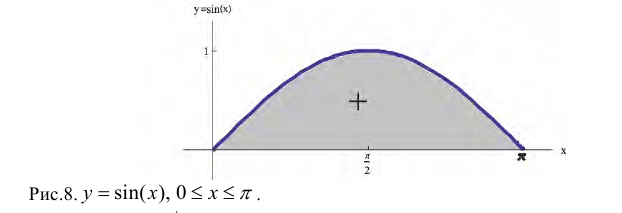
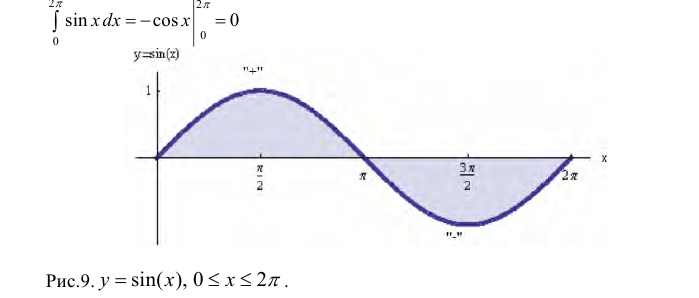
Замечание. Необходимо помнить, что 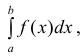 когда функция y=f(x) не является знакопостоянной, равен алгебраической сумме площадей криволинейных трапеций, расположенных выше оси Ох (со знаком «+») и ниже оси Ох (со знаком «-»).
когда функция y=f(x) не является знакопостоянной, равен алгебраической сумме площадей криволинейных трапеций, расположенных выше оси Ох (со знаком «+») и ниже оси Ох (со знаком «-»).
Пример 4.
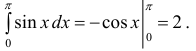
Рассмотрим кривую на плоскости, заданную параметрически в виде
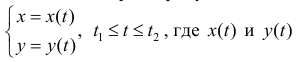 - непрерывны при
- непрерывны при 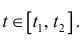 Предположим вначале, что кривая не имеет точек самопересечения ( простая кривая ) или образует петлю (если - простая замкнутая кривая ).
Предположим вначале, что кривая не имеет точек самопересечения ( простая кривая ) или образует петлю (если - простая замкнутая кривая ).
Пример 5.
а) График любой непрерывной функции 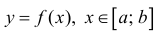 − простая кривая:
− простая кривая: 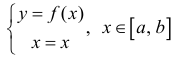 (в качестве параметра берем х).
(в качестве параметра берем х).
б) График любой непрерывной функции 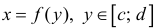 − простая кривая:
− простая кривая: 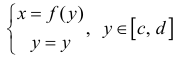 (в качестве параметра берем у).
(в качестве параметра берем у).
в) Эллипс 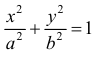 − простая замкнутая кривая:
− простая замкнутая кривая:
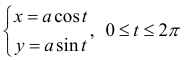 (см. пример 8 § 17).
(см. пример 8 § 17).
г) Кривая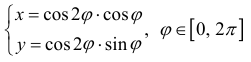 (см. пример 10 §17) не является простой (имеет точки самопересечения при
(см. пример 10 §17) не является простой (имеет точки самопересечения при 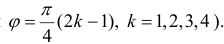
Рассмотрим криволинейную трапецию 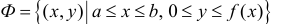
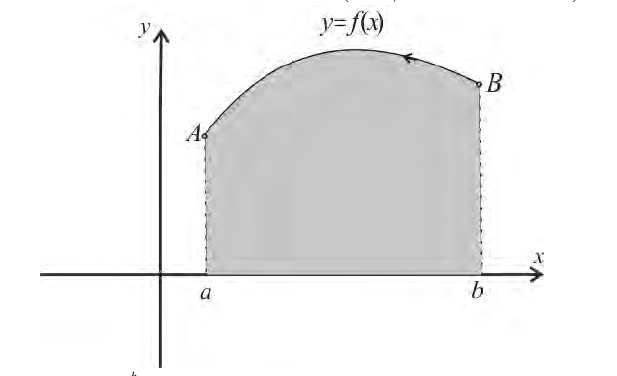
Площадь трапеции 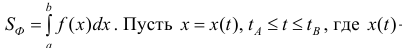 − непрерывно-
− непрерывно-
дифференцируема на промежутке 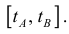 Тогда по формуле (1) § 26:
Тогда по формуле (1) § 26:
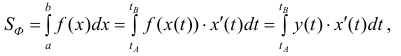 (4) где
(4) где 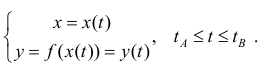
Таким образом 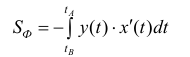 (5) (кривую удобно обходить так, чтобы область Ф оставалась слева).
(5) (кривую удобно обходить так, чтобы область Ф оставалась слева).
Аналогично, для криволинейной трапеции 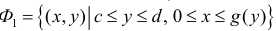
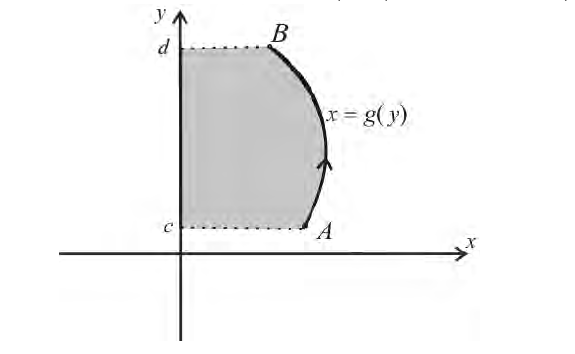
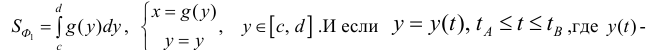 непрерывно-дифференцируемая на промежутке
непрерывно-дифференцируемая на промежутке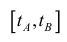 функция, то
функция, то
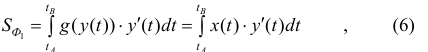 где
где 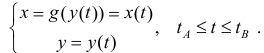
При движении от А к В область остается слева.
Рассмотрим простую замкнутую кривую
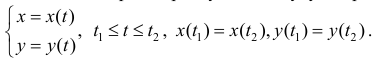 Площадь Ф, которую она ограничивает можно находить как по формуле (5), так и по формуле (6):
Площадь Ф, которую она ограничивает можно находить как по формуле (5), так и по формуле (6):
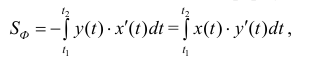 а также по формуле:
а также по формуле: 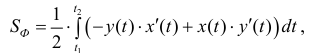 (7) и при изменении параметра t от
(7) и при изменении параметра t от 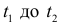 полный обход контура проходит против часовой стрелки (область остается слева).
полный обход контура проходит против часовой стрелки (область остается слева).
Пример 6.
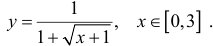
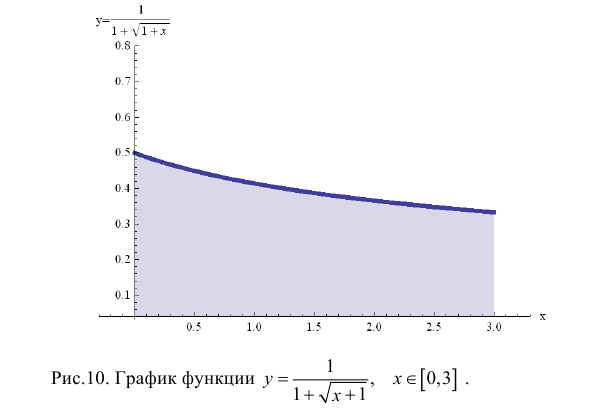
Найдем площадь криволинейной трапеции, ограниченной графиком функции и прямыми х = 0 и х = 3.
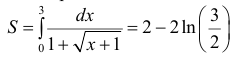 (см. пример 1 § 26).
(см. пример 1 § 26).
С другой стороны кривая задается параметрически в виде:
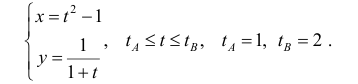
Поэтому, по формуле (5)
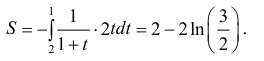
Пример 7.
Найдем площадь ограниченную эллипсом 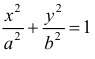
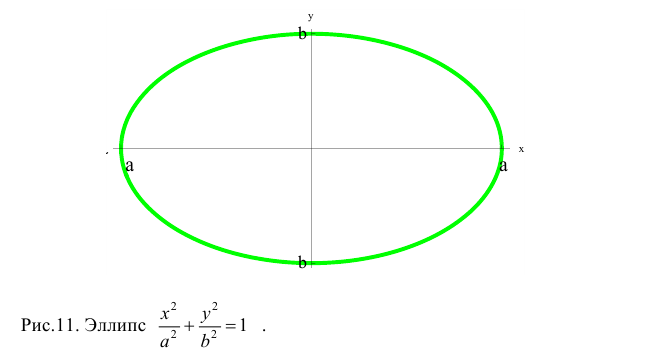
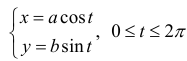 - параметрическое уравнение эллипса.
- параметрическое уравнение эллипса.
Решение.
Найдем площадь по формуле (7)
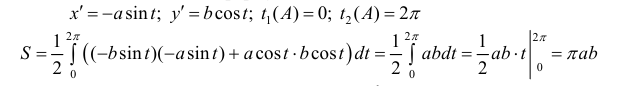
Пример 8.
Найти площадь петли кривой: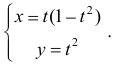
Решение:
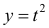 − четная относительно t функция,
− четная относительно t функция, 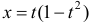 − нечетная, поэтому кривая симметрична относительно оси Оу .
− нечетная, поэтому кривая симметрична относительно оси Оу .
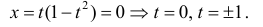
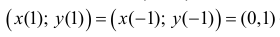 − точка самопересечения кривой.
− точка самопересечения кривой.
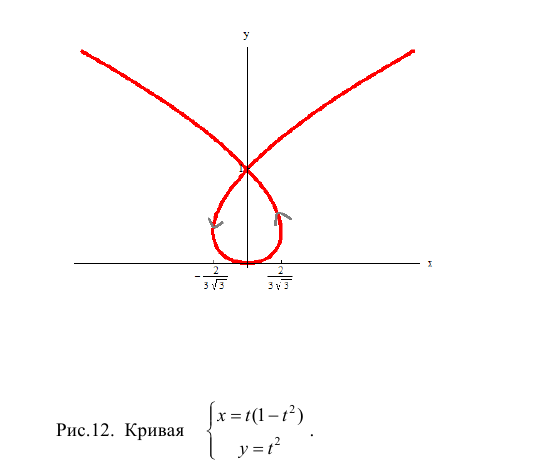
При изменении t от -1 до 1 обход контура проходит против часовой стрелки.
По формуле (6):
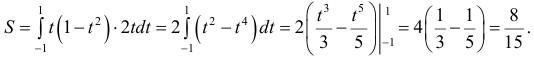
Рассмотрим замкнутую кривую, имеющую точки самопересечения. В этом случае, проинтегрировав по всему контуру в формулах (5) – (7), мы получим алгебраическую сумму площадей фигур, ограниченных каждой пройденной петлей взятых со знаком «+», если петля проходится против часовой стрелки, и со знаком «-», если петля проходится по часовой стрелке.
Пример 9.
Рассмотрим кривую 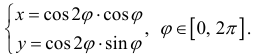
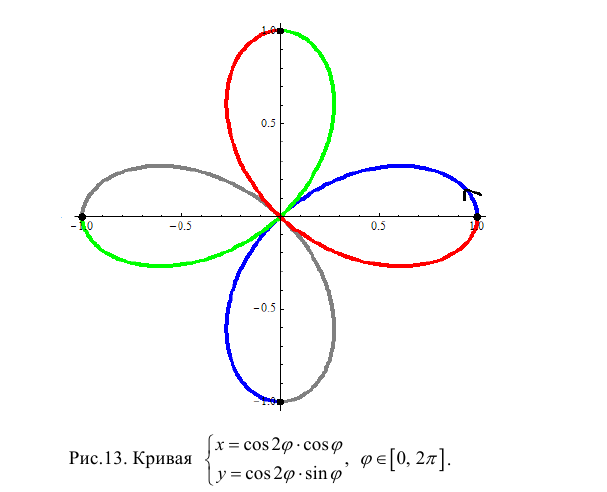
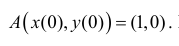 При изменении ϕ от 0 до 2π каждый лепесток кривой проходится против часовой стрелки, поэтому
При изменении ϕ от 0 до 2π каждый лепесток кривой проходится против часовой стрелки, поэтому 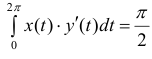 - площадь
- площадь
ограниченная четырьмя лепестками.
Площадь одного лепестка:
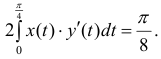
Вычисления проводим в пакете
Mathematica:
Ячейка Input:
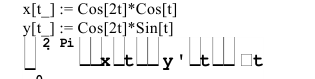
Ячейка Output: 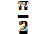
Иногда удобнее найти площадь одного лепестка и результат умножить на
количество лепестков.
Пример 10.
Рассмотрим кривую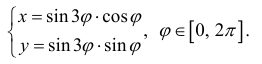
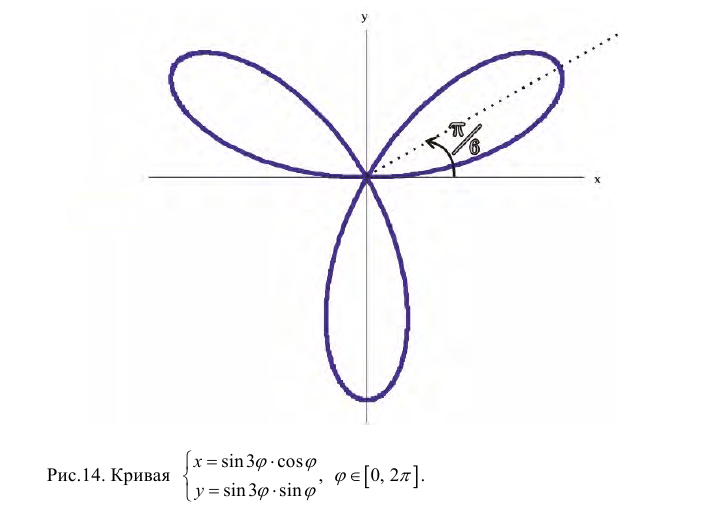
При изменении ϕ от 0 до 2π каждый лепесток проходится дважды (и оба раза против часовой стрелки); 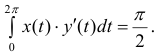 Площадь одного лепестка :
Площадь одного лепестка : 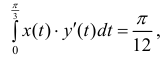 площадь всей фигуры равна
площадь всей фигуры равна 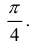
Пример 11.
Рассмотрим кривую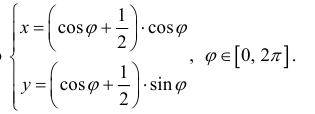
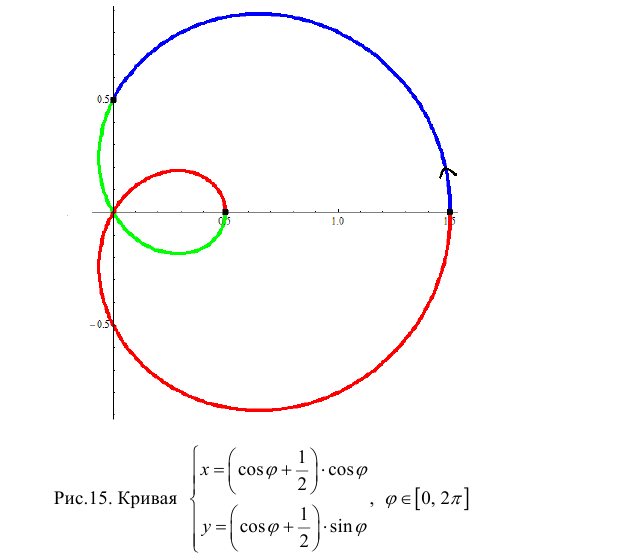
Фигура, ограниченная малой петлей обходится дважды (и оба раза против часовой стрелки). Площадь, ограниченная внешним контуром:
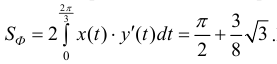 Площадь ограниченная внутренним контуром:
Площадь ограниченная внутренним контуром:
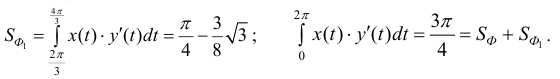
Пример 12.
Рассмотрим кривую 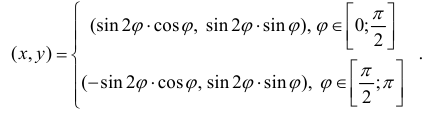
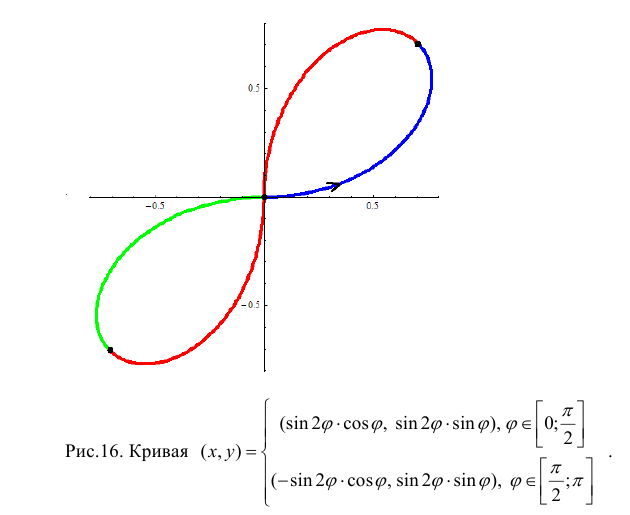
Один лепесток проходится по часовой стрелке, второй – против:
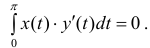 Площадь одного лепестка:
Площадь одного лепестка: 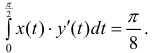
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |