Второй и третий признаки равенства треугольников - определение и вычисление с примерами решения

Второй и третий признаки равенства треугольников:

Рассмотрим еще два признака, позволяющих доказать равенство треугольников по равенству их соответствующих элементов.

Теорема 1 (второй признак равенства треугольников). Если, сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Доказательство.

1) Пусть AВС и A₁В₁С₁ — два треугольника, у которых АС = A₁С₁ , А = А₁ и С = C₁ (рис. 78, а, б). Докажем, что треугольники АBС и A₁В₁С₁  равны.

2) Отложим угол В₁A₁С₁  в той полуплоскости с границей АС, в которой лежит угол ВАС. Так как А = А₁, то на основании аксиомы откладывания угла в полуплоскость лучи A₁В₁ и АВ совпадут, а поскольку АС=A₁С₁, то по аксиоме откладывания отрезка на луче точка С₁, совпадет с точкой С. Угол В₁C₁A₁ будет отложен в ту же полуплоскость от луча СА и, согласно аксиоме откладывания угла в полуплоскость, лучи C₁B₁ и СВ совпадут (рис. 78, в).

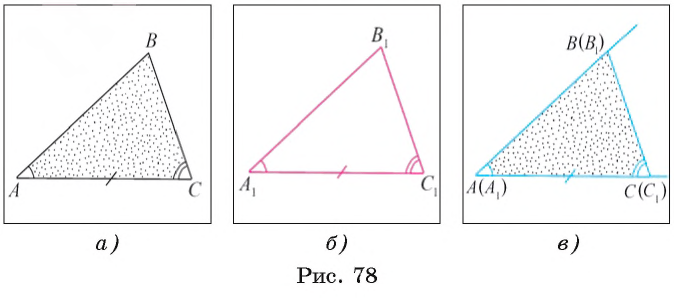
3) Так как лучи A₁В₁ и C₁В₁  совпали соответственно с лучами AB и СВ, то точка их пересечения В₁ совпадет с точкой В. Следовательно, стороны и углы треугольника A₁В₁C₁  совпадут со сторонами и углами треугольника ABC, а, значит, АВС = A₁В₁C₁.

Теорема доказана.

Теорема 2 (третий признак равенства треугольников). Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Доказательство.

1) Пусть ABC и A₁В₁C₁ — два треугольника, у которых АВ=A₁В₁, ВС = B₁C₁, и СА = C₁A₁. Докажем, что

АВС = A₁В₁C₁.

2) Отложим угол B₁A₁C₁ в ту полуплоскость с границей АС, в которой не лежит ВАС, так, чтобы луч A₁C₁  совпал с лучом АС. Так как CA = C₁A₁, то на основании аксиомы откладывания отрезка на луче точки C₁ и С совпадут (рис. 79, а). Пусть F — точка пересечения отрезка ВB₁ и прямой АС. При этом возможны три случая: а) точка F лежит между точками А и С; б) точка С лежит между точками А и F (рис. 79, б); в) точка F совпадает с точкой С (рис. 79, в).

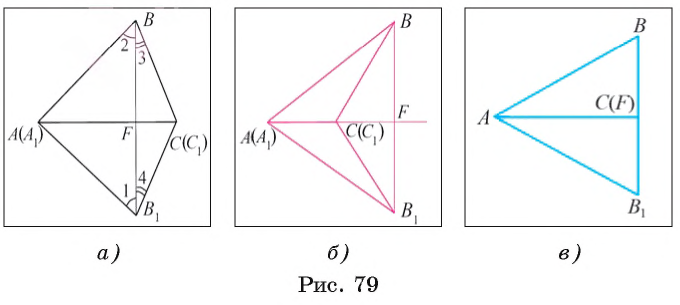
3) Проведем доказательство, когда точка F лежит между точками А и С (два других случая рассмотрите самостоятельно). По условию теоремы АВ=A₁В₁ и ВС = B₁C₁, следовательно, треугольники ВАВ₁ и ВCВ₁  равнобедренные. Тогда по свойству углов при основании равнобедренного треугольника 1 = 2 и З = 4. Отсюда следует, что АВС = A₁В₁C₁. Таким образом, АВ=A₁В₁, ВС = В₁C₁  и ABC = A₁В₁C₁,  а, значит, по первому признаку равенства треугольников АВС = A₁В₁C₁.

Теорема доказана.

Пример:

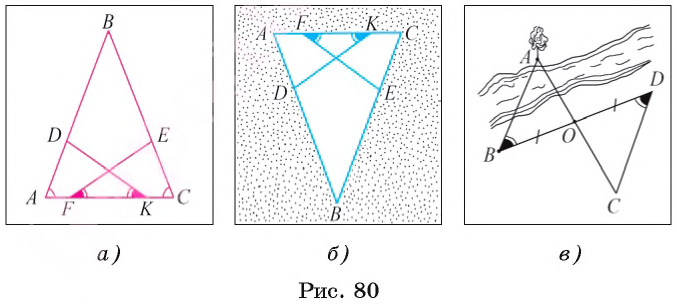
В равнобедренном треугольнике АВС точки F и К лежат на основании АС так, что АF = КС (рис. 80, а, б), а точки D и Е лежат соответственно на сторонах АВ и СВ так, что АКD = EFC . Докажите, что АD = СЕ.

Решение.

1) Так как треугольник ABC равнобедренный и AB = ВС, то его углы при основании равны, т. е. A = C.

2) Рассмотрим треугольники ADK и CEF. Прежде всего, заметим, что АК=АС - КС и CF = АС - AF, а так как по условию АF = КС, то АК = СF. Кроме того, AКD = ЕFС.

3) Таким образом, сторона АК и два прилежащих к ней угла треугольника АDК равны соответственно стороне СF и двум прилежащим к ней углам треугольника СЕF. На основании второго признака равенства треугольников получим, что ADК = СЕF. Отсюда следует, что АD = СЕ, что и требовалось доказать.

Второй признак равенства треугольников можно применять при решении задач практического характера. Рассмотрим пример решения такой задачи.

Пример:

Найдите расстояние от точки В до дерева, расположенного на противоположном берегу реки (рис. 80, в).

Решение.

1) Отметим на местности точки О, D и С так, чтобы точка О была серединой отрезка ВD, а ВDС был равен ABO. Тогда искомое расстояние равно расстоянию между точками С и D.

2) Действительно, АОВ = СОD по стороне и двум прилежащим к ней углам, так как ВО = ОD и D = B по построению, а углы АОВ и СОD равны, т. к. являются вертикальными. Из равенства треугольников следует, что АВ = СD. Таким образом, для нахождения расстояния АВ достаточно измерить расстояние СD.