Вписанные и описанные многоугольники - формулы, свойства и примеры с решением

Содержание:

Рассмотрим вопрос о взаимном расположении прямой и окружности. Ранее уже отмечалось, что возможны три случая взаимного расположения прямой и окружности:

1. прямая имеет только две общие точки с окружностью;
2. прямая имеет только одну общую точку с окружностью;
3. прямая не имеет общих точек с окружностью.

Если прямая имеет две общие точки с окружностью, то она называется секущей.

Понятие о вписанных и описанных многоугольниках

Взаимное расположение окружности со (О, R) с центром в точке О радиуса R и прямой I характеризуется соотношением между расстоянием d(0, I) от центра О окружности до прямой I и радиусом R окружности. Докажем это.

1) Прямая I имеет только две общие точки с окружностью, если расстояние от центра окружности до прямой I меньше радиуса окружности, т. е.

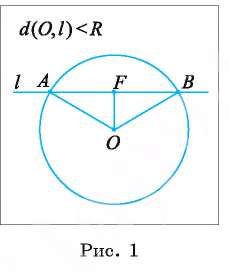
Пусть прямая I не проходит через центр О окружности и расстояние 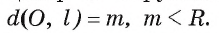. Обозначим OF 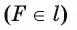— перпендикуляр, проведенный из точки О к прямой I, тогда OF = m. Пусть точки А и В лежат на прямой I

так, что 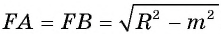. Докажем, что точки А и В принадлежат окружности.

Действительно, так как по теореме Пифагора

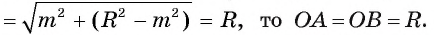
 Таким образом, точки А и В — общие точки прямой и окружности. Докажем, что других общих точек прямая I и окружность не имеют.

Предположим, что существует еще одна точка X — общая для окружности и прямой. Тогда центр окружности О равноудален от точек А, В, и X, а значит, он лежит на серединных перпендикулярах к отрезкам АВ и ВХ, т. е. О — точка перессечения серединных перпендикуляров. Но так как,. Получили противоречие. Значит, наше предположение не верно и других общих точек прямой и окружности нет.

Если прямая I проходит через центр О окружности, т. е. d(0, Z) = 0, то она пересекает окружность в двух точках, которые являются концами диаметра, лежащего на этой прямой.

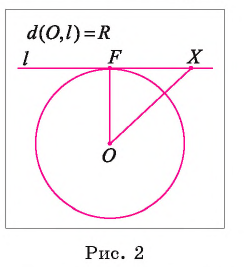
2) Прямая I имеет только одну общую точку с окружностью, если расстояние от центра окружности до прямой I равно радиусу окружности, т. е. если d(0, I) = R.

Пусть расстояние от центра окружности до прямой I равно радиусу окружности, а точка F — основание перпендикуляра, проведенного из центра окружности к прямой I (рис. 2). Тогда OF = R, а значит, точка F лежит на окружности. Других общих точек прямая и окружность не имеют. Действительно, для любой точки X прямой I, не совпадающей с точкой F, выполняется условие ОХ > OF, OF = R, так; как наклонная ОХ больше перпендикуляра OF.

Следовательно, точка X не лежит на окружности.

3) Прямая I не имеет общих точек с окружностью, если расстояние от центра О окружности до прямой I больше радиуса окружности, т. е. если d(0, I) > R.

Пусть расстояние от центра О окружности до прямой I больше радиуса R. Обозначим буквой F основание перпендикуляра, проведенного из центра О окружности к прямой I (рис. 3). Тогда OF = d(0, I), d(0, I) > R.
 

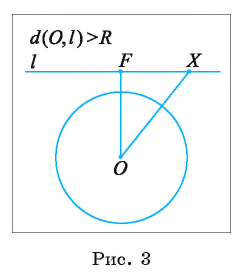
Для любой точки X прямой выполняется условие 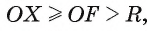, следовательно, точка X не лежит на окружности. Таким образом, в случае 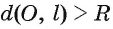прямая и окружность не имеют общих точек.

Касательная к окружности

Рассмотрим случай, когда прямая и окружность имеют единственную общую точку. Прямая, имеющая единственную общую точку с окружностью, имеет специальное название — касательная.

Определение. Касательной к окружности называется прямая, которая имеет с окружностью только одну общую точку.

Единственная общая точка прямой и окружности называется точкой касания прямой и окружности.

Если прямая I имеет единственную общую точку А с окружностью, то говорят, что прямая I касается окружности в точке А.

Теорема 1 (о свойстве касательной). Касательная к окружности перпендикулярна радиусу этой окружности, проведенному в точку касания.

Доказательство.

1) Пусть прямая I касается окружности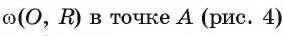 Докажем, что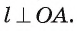

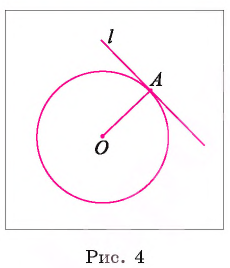
2) Предположим, что это не так. Тогда радиус ОА является наклонной к прямой I. Перпендикуляр, проведенный из точки О к прямой I, меньше наклонной ОА, следовательно, расстояние от центра окружности до прямой

меньше радиуса. Значит, прямая и окружность имеют две общие точки, что противоречит условию. Таким образом, прямая I перпендикулярна радиусу ОА.

Теорема доказана.

Рассмотрим следствия из данной теоремы.

Пусть через точку А проведены две прямые, касающиеся окружности Тогда отрезки АВ и АС называются отрезками касательных, проведенными из точки А (рис. 5).

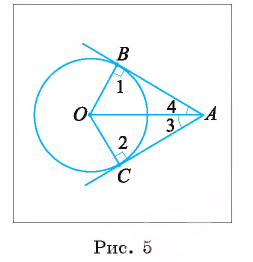
Следствие 1. Отрезки касательных к окружности, проведенные из одной точки, равны.

Доказательство.

1) Пусть АВ и АС — отрезки касательных, проведенные из точки А (рис. 5). Для доказательства равенства АВ = АС рассмотрим треугольники АВО и АСО.

2) По свойству касательной и 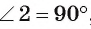, т. е. треугольники АВО и АСО — прямоугольные.

3)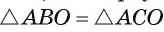, так как АО — общая гипотенуза, а катеты О В и ОС равны как радиусы окружности. Отсюда следует, что АВ =АС.

Следствие 1 доказано.

Из равенства треугольников АВО и АСО вытекает также, что 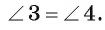. Таким образом, получим еще одно следствие.

Следствие 2. Отрезки касательных к окружности, проведенные из одной точки, составляют равные углы с прямой, проходящей через эту точку и центр окружности.

Теперь докажем признак, который позволяет устанавливать, в каком случае прямая касается окружности. Оказывается, для этого достаточно установить, что прямая перпендикулярна радиусу и проходит через его конец, лежащий на окружности.

Теорема 2 (признак касательной). Если прямая перпендикулярна радиусу окружности и проходит через его конец, лежащий на окружности, то она касается этой окружности.

Доказательство.

1) Пусть прямая I проходит через точку А окружности и перпендикулярна радиусу О А (рис. 6). Для доказательства того, что прямая I касается окружности, достаточно доказать, что она имеет с этой окружностью единственную общую точку.

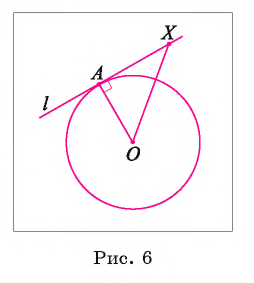
2) Так как точка А лежит на окружности и прямая I проходит через точку А, то А — общая точка прямой I и окружности.

3) Других общих точек прямая I и окружность не имеют. Действительно, для любой точки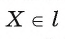 отрезок ОХ является наклонной, так как по условию 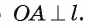Следовательно, ОХ > ОА, т. е. точка X не принадлежит окружности.

Таким образом, точка А — единственная общая точка прямой I и окружности, а, значит, прямая I — касательная к окружности.

Теорема доказана.

Пример №1

Через точку А, находящуюся от центра О окружности на расстоянии 10 см, проведены две касательные АВ и АС, где Б и С — точки касания. Вычислите площадь 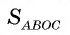четырехугольника АВОС, если АВ + АС = = 16 см ( рис. 7).

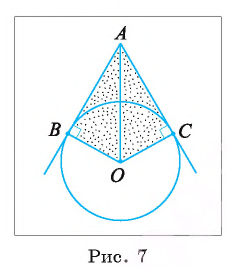
Решение:

1) Площадь четырехугольника АВОС равна сумме площадей треугольников АВО и АСО.

2) По свойству касательной 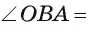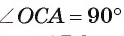. Прямоугольные треугольники АВО и АСО равны по гипотенузе и катету (АО — общая, ОВ = ОС). Значит,

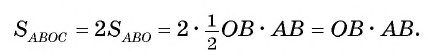
3) Отрезки касательных к окружности, проведенные из одной точки, равны. Следовательно, АВ=АС = 8 см. Теперь, применив теорему Пифагора, вычислим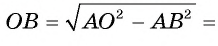

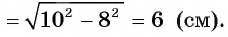
Таким образом,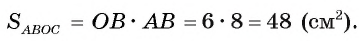

Ответ: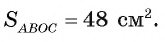

Пример №2

Точка F — середина основания ВС равнобедренного треугольника АБС. Докажите, что прямая ВС является касательной к окружности 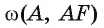 (рис. 8, а, б).

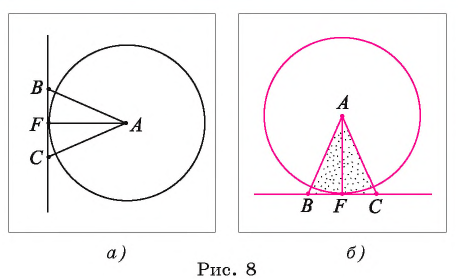
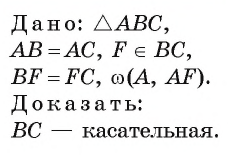
Доказательство.

1) Прямая ВС проходит через конец F радиуса окружности 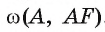. Для доказательства того, что ВС является касательной, достаточно доказать, что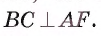

2) В равнобедренном треугольнике AВС отрезок AF — медиана, проведенная к его основанию. Следовательно, 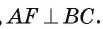Таким образом, по признаку касательной прямая ВС касается окружности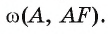

Что и требовалось доказать.

Пример №3

Точка А лежит вне окружности 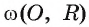Постройте прямую, которая касается окружности и проходит через точку А.

Поиск решения.

1) Пусть прямая I, проходящая через точку А и касающаяся окружности 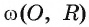, построена. Точка В — точка касания. Тогда по свойству касательной OB LAB (рис. 9, а). Следовательно, для построения искомой касательной необходимо построить точку В на окружности 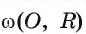так, что .

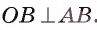2) Рассмотрим окружность coj, диаметром которой является отрезок АО, т. е. 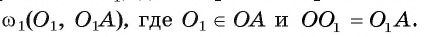Пусть В и С — точки пересечения окружностей и 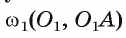(рис. 9, б). Заметим, что 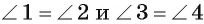, как углы при основании равнобедренных треугольников ВО,О и ВО,А соответственно. Так как 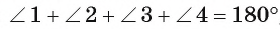, то 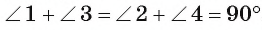Значит, 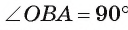, т. е.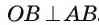. Аналогично доказывается, что. Отсюда по признаку

касательной к окружности следует, что прямые АВ и АС являются касательными. Теперь понятна последовательность необходимых построений.

Построение.

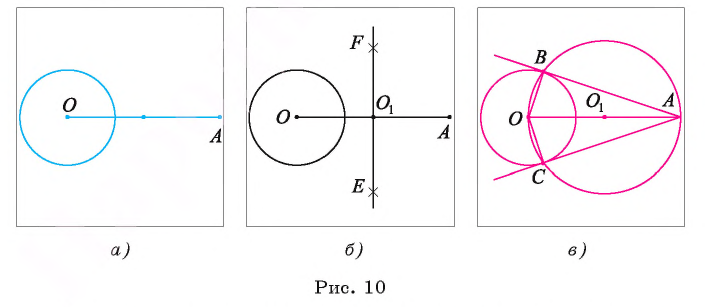
1) Проводим отрезок О А, соединяющий центр О данной окружности и точку А (рис. 10, а).

2) Строим середину 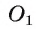 отрезка ОА: 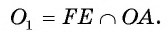Точки F и Е — точки пересечения окружностей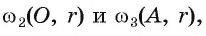

где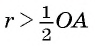(рис. 10, б).

3) Строим окружность 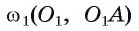 (рис. 10, в) и точки Б, С — точки пересечения данной и построенной окружностей.

4) Прямые АВ и АС — искомые касательные к данной окружности.

Доказательство. По построению 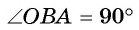 и 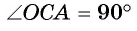(см. задачу № 251 учебного пособия «Геометрия, 7»), т. е. АВ1ОВ и АС 1ОВ. Следовательно, по признаку касательной АВ и АС — касательные.

Взаимное расположение двух окружностей

Рассмотрим вопрос о взаимном расположении двух окружностей в плоскости. Возможны следующие случаи взаимного расположения двух различных окружностей:

1) окружности не имеют общих точек (в этом случае говорят, что они не пересекаются (рис. 11, а ));

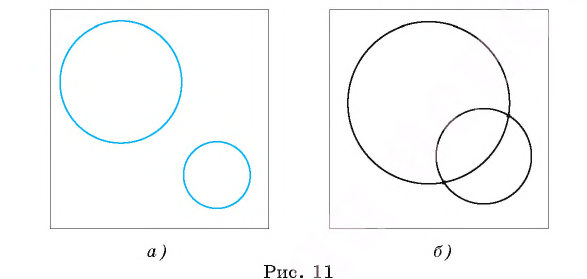
2) окружности имеют две общие точки (в этом случае говорят, что окружности пересекаются (рис. 11, б));

3) окружности имеют только одну общую точку, и одна из окружностей лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внутренним образом (рис. 12, а ));

4) окружности имеют только одну общую точку, и ни одна из окружностей не лежит внутри круга, ограниченного другой окружностью (в этом случае говорят, что они касаются внешним образом, (рис. 12, б)).

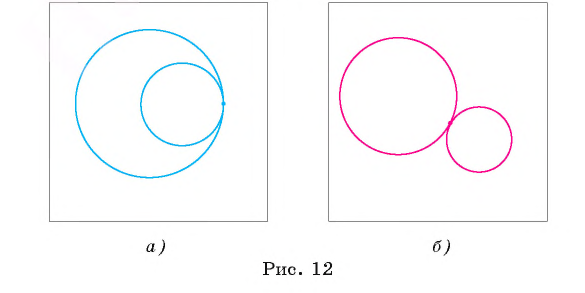
Пример №4

Докажите, что если две окружност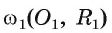и и 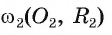касаются внешним образом, то расстояние между их центрами равно сумме их радиусов, т. е.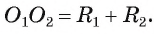

Доказательство.

1) Пусть окружности 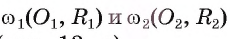касаются внешним образом в точке А (рис. 13, а).

2) Докажем, что точка А лежит на отрезке 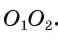Допустим, что точка А не лежит на отрезке 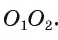Заметим, что в случае внешнего касания точка А не может лежать на продолжении отрезка 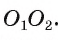Пусть точка касания А не лежит на отрезке 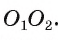(рис. 13, б). Тогда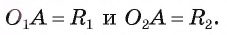

3) Пусть F — точка, симметричная точке А относительно прямой 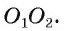. Тогда 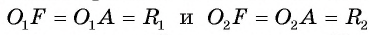, а значит, точка F принадлежит каждой окружности. Таким образом, окружности 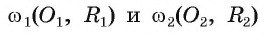имеют две общие точки А и F, что противоречит условию их касания. Следовательно, точка касания А лежит на отрезке

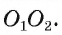
4) Докажем, что 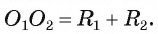Точка А лежит на отрезке 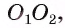значит,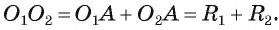

Теорема доказана.

Справедливо и обратное утверждение.

Пример №5

Докажите, если расстояние между центрами двух окружностей, лежащих в плоскости, равно сумме их радиусов, то такие окружности касаются внешним образом.

Доказательство.

1) Пусть даны две окружности 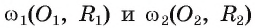и известно, что 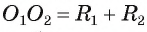Докажем, что окружности касаются внешним образом.

2) На отрезке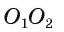рассмотрим точку А такую, что 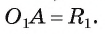Тогда 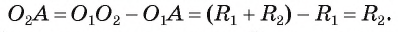. Таким образом, точка А принадлежит каждой из данных окружностей.

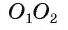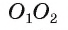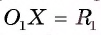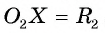3) Докажем, что окружности не имеют других общих точек. Действительно, на прямой таких точек нет. Предположим, что существует точка X вне прямой принадлежащая каждой окружности. Тогда и В треугольнике 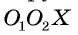длина стороны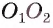равна сумме длин сторон 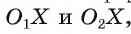, что невозможно.

4) Таким образом, предположение о существовании еще одной точки, принадлежащей окружностям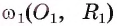 и 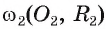, приводит к противоречию. Следовательно, других общих точек, кроме точки А, не существует, т. е. окружности касаются.

5) Докажем, что окружности касаются внешним образом. Для любой точки F окружности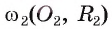выполняется условие 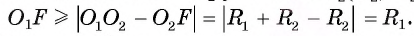Таким образом, либо точка F лежит вне окружности 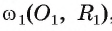когда 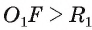, либо эта точка принадлежит обеим окружностям, если 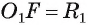Но в этом случае точка F есть точка А касания окружностей. Следовательно, окружность 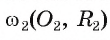расположена вне части плоскости, ограниченной окружностью 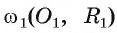. Аналогично можно доказать, что окружность 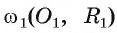расположена вне части плоскости, ограниченной окружностью 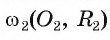. Теперь доказано, что окружност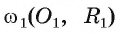и  и 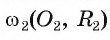касаются внешним образом.

Пример №6

Докажите, что две окружности касаются внутренним образом тогда и только тогда, когда расстояние между их центрами равно модулю разности их радиусов.

Другими словами, если окружности 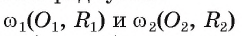касаются внутренним образом, то 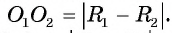И наоборот, если выполняется равенство 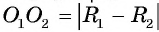, то окружности касаются внутренним образом.

Пример №7

Две окружности с центрами в точках О и К, радиусы которых равны 16 см и 9 см соответственно, касаются внешним образом в точке С. К окружностям проведена общая касательная АВ, где точки А и В — точки касания.

Общая касательная, проведенная через точку С, пересекает касательную АВ в точке Т (рис. 14, а). Вычислите длину отрезка СТ.
 

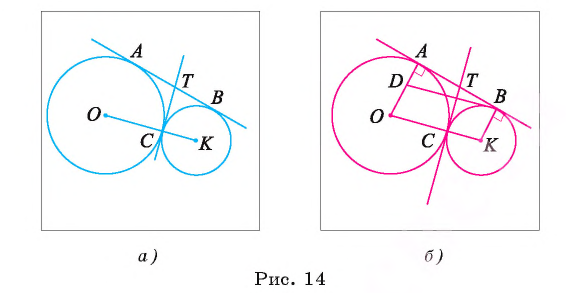
Решение:

Для решения задачи воспользуемся тем, что отрезки касательных, проведенные к окружности из одной точки, равны, а радиусы, проведенные в точку касания, перпендикулярны касательной. Учтем также, что окружности касаются внешним образом, а значит, расстояние между их центрами равно сумме их радиусов.

1) Так как отрезки касательных к окружности, проведенные из одной точки, равны, то ТС = ТА = ТВ, т. е. 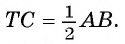. Значит, нам необходимо вычислить длину отрезка АВ.

2) Так как окружности касаются внешним образом, то ОК = ОС + СК = 16 + 9 = 25 (см).

3) Рассмотрим четырехугольник ODBK. Пусть 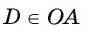и 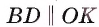(рис. 14, б). Так как радиус, проведенный в точку касания, перпендикулярен касательной, то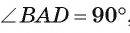, т. е. треугольник BAD — прямоугольный. Следовательно,

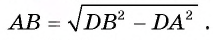
4) Четырехугольник ODBK — параллелограмм, так как его противолежащие стороны параллельны, значит, DB = ОК = = 25 см. Кроме того, DA = ОА - OD = ОА - КВ =16-9 = 7 (см).

Тогда 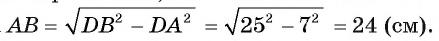Следовательно,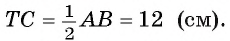

Ответ: ТС = 12 см.

Центральные и вписанные углы

В данном параграфе изучим понятия центрального и вписанного углов.

Определение. Центральным углом окружности называется угол с вершиной в центре этой окружности.

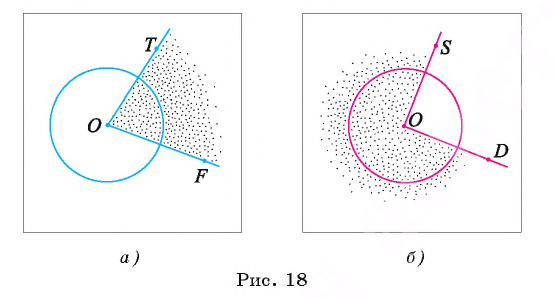
Например, на рисунке 18, а изображен центральный угол TOF, который меньше развернутого угла, а на рисунке 18, б — центральный угол SOD — больше развернутого угла.

Любые две различные точки А и В окружности служат концами двух дуг. Для различия этих дуг на каждой из них отмечается некоторая промежуточная точка. Например, если на дугах отмечены точки F и Т, то в этом случае дуги обозначаются 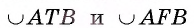и данная запись читается так: «дуга АТВ и дуга AFB» (рис. 19, а). Если понятно, о какой из двух дуг идет речь, употребляется также обозначение

Дуга АВ окружности называется полуокружностью, если ее концы служат концами диаметра этой окружности.

Например, на рисунке 19, б изображены полуокружности ALB и АС В.

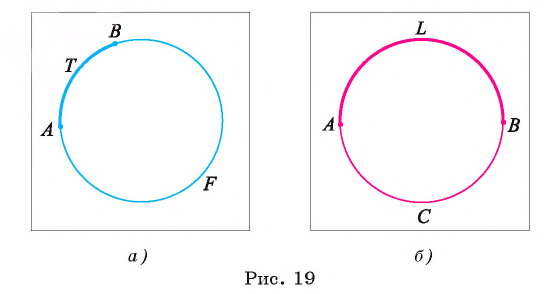
Пусть точки А и Б не являются концами диаметра окружности с центром в точке О. Тогда лучи ОА и ОБ служат сторонами двух центральных углов, один из которых меньше, а другой больше развернутого угла (рис. 20, а).

Дуга АВ окружности и центральный угол АОВ, внутри которого лежит эта дуга, называются соответствующими.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который меньше развернутого угла, то говорят, что эта дуга меньше полуокружности.

Если дуга окружности лежит внутри соответствующего ей центрального угла, который больше развернутого угла, то говорят, что дуга больше полуокружности.

Например, на рисунке 20, а изображены дуга AFB, которая меньше полуокружности, и дуга АТВ — больше полуокружности.

Для сравнения дуг окружности вводится понятие градусной меры дуги окружности.

Дадим определение градусной меры дуги окружности.

Определение. Градусной мерой дуги окружности называется градусная мера соответствующего ей центрального угла.

Градусная мера дуги АВ, как и сама дуга, обозначается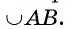

Таким образом, если дуга АВ окружности меньше полуокружности, a 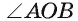— соответствующий ей центральный угол, то 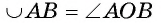(см. рис. 20, а).

Если дуга АВ является полуокружностью, то ее градусная мера равна 180° (рис. 20, б).

Градусная мера дуги АТВ, которая больше полуокружности и дополняет дугу АВ, меньшую полуокружности, до окружности, равна 360° 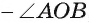, где угол АОВ соответствует дуге АВ (рис. 20, в).

Понятие градусной меры дуги позволяет определить понятие равенства дуг окружности.

Две дуги одной и той же окружности называются равными, если равны их градусные меры.

Если градусная мера дуги АВ равна 33°, то пишут 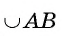= 33°. Читают: «Градусная мера дуги АВ равна 33°», или кратко «Дуга АВ равна 33°».

Рассмотрим примеры. Пусть диагонали квадрата ABCD пересекаются в точке О. Окружность 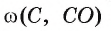пересекает стороны ВС и CD квадрата в точках F и L соответственно. Тогда 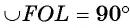, а градусная мера дуги FO, которая меньше полуокружности, равна 45°. Градусная мера дуги FLO, которая больше полуокружности, равна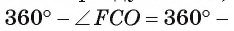 (рис. 21, а).

Рассмотрим еще один пример. Пусть точка О — центр окружности, отрезок АВ — хорда окружности, равная ее радиусу, а отрезок АС — диаметр окружности (рис. 21, б).

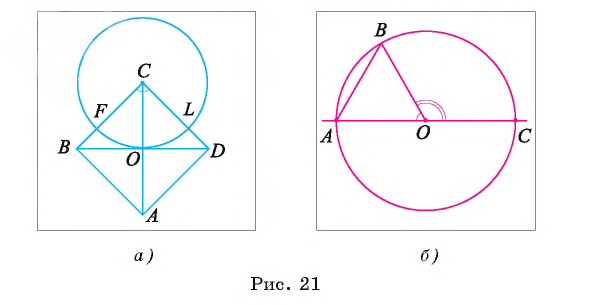
Тогда градусная мера дуги АВ, которая меньше полуокружности, равна 60°, так как треугольник АОВ — равносторонний, а значит, градусная мера соответствующего ей центрального угла АОВ равна 60°. Градусная мера дуги ВС, которая меньше полуокружности, равна 120°, так как градусная мера соответствующего ей центрального угла ВОС равна 120°.

Можем вычислить градусную меру дуги ВАС, которая больше полуокружности:   = 240°.

Вписанные углы. Рассмотрим понятие вписанного угла

Определение. Угол называется вписанным в окружность, если он меньше развернутого угла, вершина его лежит на окружности, а стороны пересекают эту окружность.

Например, на рисунке 22, а изображен вписанный угол TOF. Если точки А, В и С лежат на окружности, то каждый из угол ABC, ВСА, САВ является вписанным (рис. 22, б).

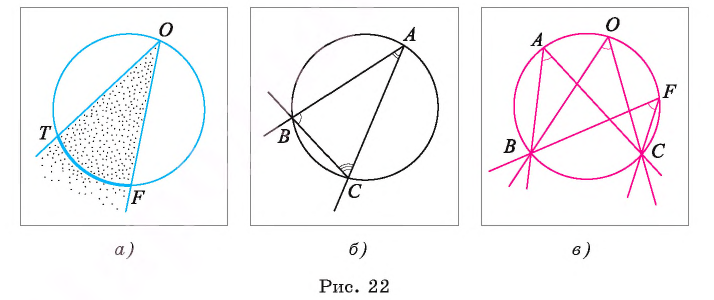
Пусть 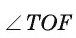— вписанный угол, при этом Г и В — точки пересечения его сторон с окружностью, a TF — дуга, которая лежит внутри этого вписанного угла. В этом случае говорят, что вписанный угол TOF опирается на дугу TF (см. рис. 22, а).

Например, на рисунке 22, в изображены вписанные углы ВАС, ВОС и BFC, которые опираются на одну и ту же дугу ВС.

Теперь докажем теорему о вписанном угле.

Теорема 1(о вписанном угле). Градусная мера вписанного угла равна половине градусной меры, дуги, на которую он опирается.

Доказательство.

Пусть вписанный в окружность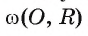угол ABC опирается на дугу АС.

Докажем, что Рассмотрим три возможных случая. Центр О окружности лежит: 1) на одной из сторон угла; 2) во внутренней области угла; 3) во внешней области угла.

Первый случай. Центр О окружности лежит на одной из сторон угла ABC, например на стороне ВС (рис. 23).

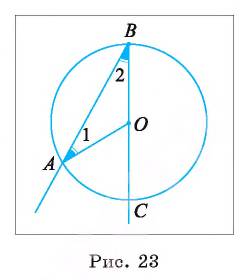
1) Дуга АС меньше полуокружности, следовательно,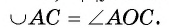

2) Угол АОС — внешний угол равнобедренного треугольника АОВ, значит,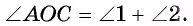

3) Так как углы при основании равнобедренного треугольника АОВ равны, то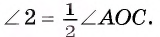

4) Так как 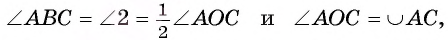, то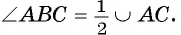

Второй случай. Центр О окружности лежит во внутренней области угла.

1) Пусть D — точка пересечения луча ВО и дуги АС (рис. 24). Тогда по доказанному в первом случае

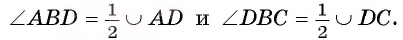
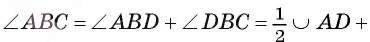
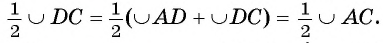
Таким образом,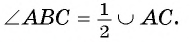

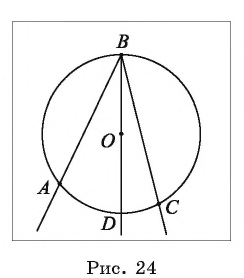
Третий случай. Центр О окружности лежит во внешней области угла ABC.

1) Пусть D — точка пересечения луча ВО с окружностью (рис. 25). Тогда согласно доказанному в первом случае

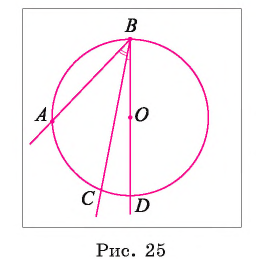
Таким образом, 

Теорема доказана.

Из данной теоремы получим следующие следствия.

Следствие 1. Вписанные углы, опирающиеся на одну и ту же дугу, равны (рис. 26, а).

Следствие 2. Вписанный угол, опирающийся на полуокружность, прямой (рис. 26, б).

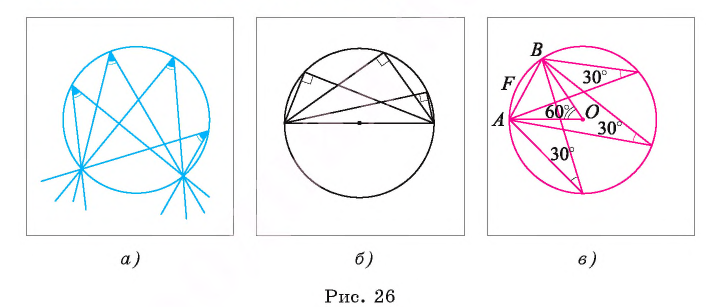
Рассмотрим пример. Пусть хорда АВ соединяет концы дуги AFB и равна радиусу окружности со (О, R). Тогда градусная мера каждого из вписанных углов, опирающихся на дугу AFB, равна 30° (рис. 26, в). Действительно, градусная мера центрального угла АОВ равна 60°, значит, . Каждый из указанных углов опирается на дугу AFB, следовательно, градусная мера каждого из них равна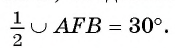

Теорема 2 (об угле между хордой и касательной).

Градусная мера угла, сторонами которого служат касательная и хорда, равна половине градусной меры дуги, расположенной внутри этого угла.
 

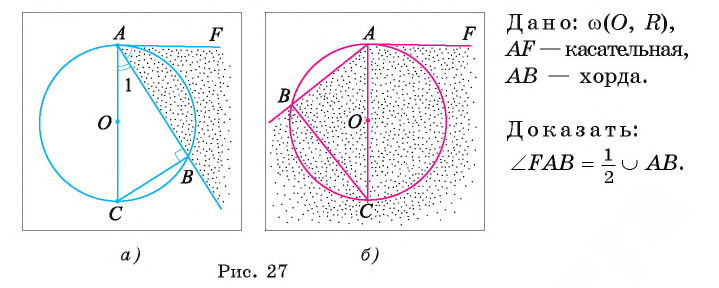
Доказательство.

Первый случай. Пусть угол FAB — острый (рис. 27, о.).

1) Проведем диаметр АС. Тогда вписанный угол СВ А опирается на полуокружность, значит, по следствию 2 он прямой, т. е.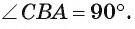

2) Треугольник СВА — прямоугольный, следовательно,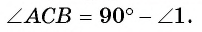

3) Так как диаметр АС перпендикулярен касательной FA, то 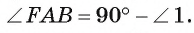Таким образом, 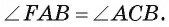Так как вписанный угол АСВ опирается на дугу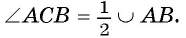

Следовательно,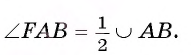

Второй случай. Пусть угол FAB — тупой (рис. 27, б). Проведем диаметр СА. Тогда

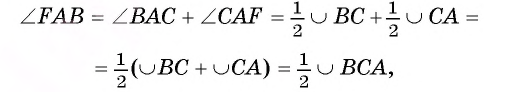
но дуга ВСА лежит внутри тупого угла FAB.

Теорема доказана.

Свойство пересекающихся хорд. Теорема о касательной и секущей

Теорема 3 (об отрезках пересекающихся хорд). Если две хорды окружности пересекаются, то произведение длин отрезков одной хорды равно произведению длин отрезков другой хорды.

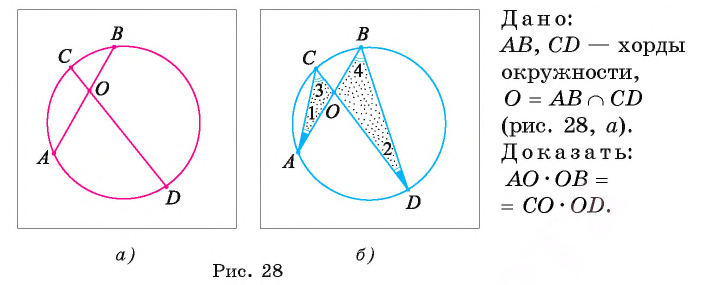
Доказательство.

1) Проведем хорды АС и BD (рис. 28, б). Рассмотрим треугольники АОСи DOB.

2) Заметим, что 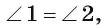так как они вписанные и опираются на одну и ту же дугу СВ. Кроме того, 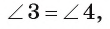, так как они вписанные и опираются на одну и ту же дугу AD.

3) Треугольник АОС подобен треугольнику DOB по первому признаку подобия треугольников, так как 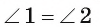и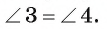

4) Из подобия треугольников АОС и DOB следует, что

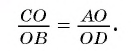
Значит,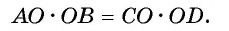  

Теорема доказана.

Пусть через точку S, лежащую вне окружности, проведена секущая, которая пересекает окружность в точках С и Б, и SC < SB.

Тогда отрезок SB называется отрезком секущей, а отрезок SC — ее внешней частью.

Теорема 4 (об отрезках секущей и касательной). Если через точку, лежащую вне круга, ограниченного окружностью, провести к этой окружности касательную и секущую, то квадрат длины отрезка касательной равен произведению длин отрезков секущей и ее внешней части.

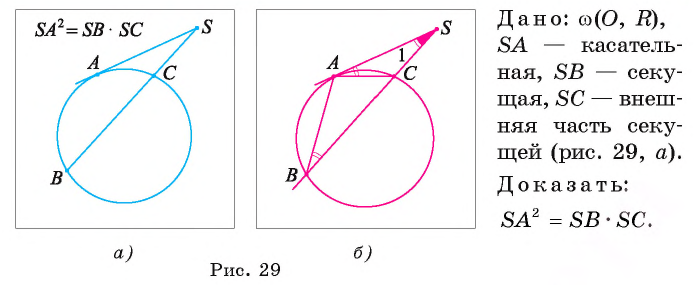
Доказательство.

1) Проведем хорды АС и АВ (рис. 29, б).

2) По теореме о вписанном угле 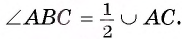. Кроме того, в силу теоремы 2 имеем 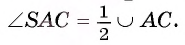. Значит,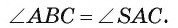

3) Так как 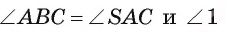— общий угол треугольников ASB и CSA, то эти треугольники подобны.

4) Из подобия треугольников АЗ В и CSA следует, что выполняется равенство

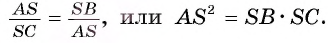
Теорема доказана.

Из данной теоремы получим следствие.

Следствие. Если через точку S, лежащую вне круга, ограниченного окружностью, проведены две секущие, пересекающие окружность соответственно в точках 

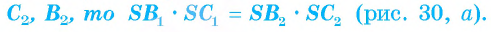
Пример №8

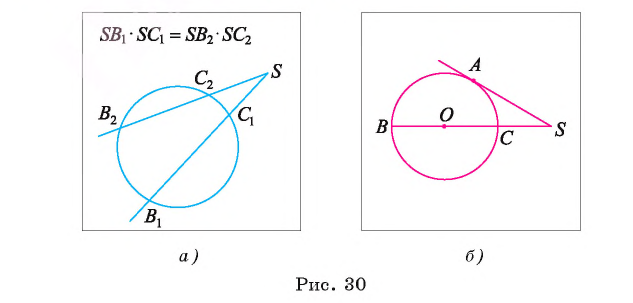
Через точку S проведена секущая, которая проходит через центр О окружности 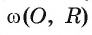и пересекает ее в точках С и Б, SC: СВ = 1-2. Найдите длину отрезка SA касательной (рис. 30, б).

Решение:

По теореме об отрезках секущей и касательной имеем 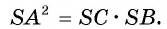. Так как SC : СВ = 1: 2, а СВ = 2R, то SC = R и SB = SC + СВ = 3R. Тогда 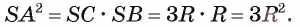Отсюда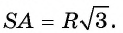

Ответ: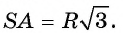

Пример №9

Радиус круга равен 7,5 см. Точка Р лежит внутри круга на расстоянии 6,5 см от его центра О. Через точку Р проведена хорда АВ, длина которой равна 9 см. Вычислите длины отрезков, на которые точка Р делит хорду АВ.

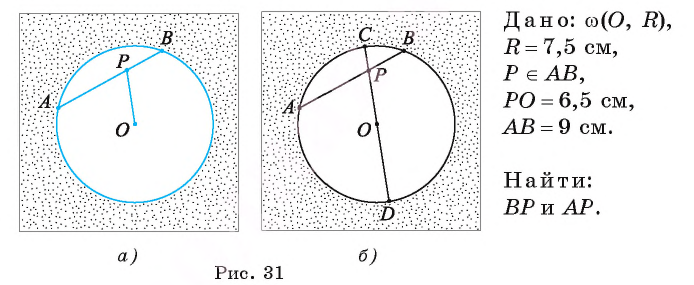
Решение:

Воспользуемся теоремой об отрезках пересекающихся хорд.

1) Пусть С и D — точки пересечения прямой ОР с границей круга (рис. 31, б). Тогда CO = OD = 7,5 см.

2) По теореме об отрезках пересекающихся хорд имеем АР • РВ = СР • PD, или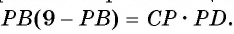

3) Заметим, что СР = СО-РО= 7,5-6,5=1 (см). Кроме того, PD = PO + OD= 7,5 + 6,5=14 (см). Таким образом, 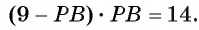Отсюда найдем: РВ = 2 см или РВ = 7 см. Следовательно, РВ = 2 см и АР = 7 см или РВ = 7 см и АР = = 2 см.

Ответ: 2 см, 7 см.

Замечательные точки треугольника

Ранее мы уже отмечали следующие свойства: медианы треугольника пересекаются в одной точке', биссектрисы треугольника пересекаются в одной точке', высоты треугольника, или прямые, их содержащие, пересекаются в одной точке.

Теорема о свойстве медиан треугольника была доказана в восьмом классе. Сейчас докажем теоремы о свойствах биссектрис и высот треугольника.

1. Теорема о точке пересечения биссектрис треугольника.

Предварительно докажем одно свойство биссектрисы угла.

Теорема 1 (о свойстве биссектрисы угла). Каждая точка биссектрисы угла, который меньше развернутого, равноудалена от его сторон. Каждая точка указанного угла, равноудаленная от его сторон, лежит на биссектрисе этого угла.

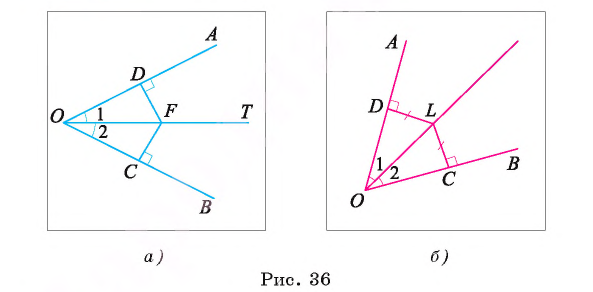
Доказательство.

I. Докажем, что каждая точка биссектрисы угла, который меньше развернутого угла, равноудалена от его сторон.

1) Пусть луч ОТ — биссектриса угла, а F — произвольная точка биссектрисы ОТ. Проведем перпендикуляры FC и FD к прямым ВО и АО соответственно и докажем, что FC = FD (рис. 36, а).

2) Рассмотрим прямоугольные треугольники OFD и OFC. Эти треугольники равны по гипотенузе и острому углу (отрезок OF — общая гипотенуза, ).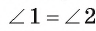

3) Из равенства треугольников OFD и OFC следует, что FC = FD.

Что и требовалось доказать.

II. Докажем, что если точка равноудалена от сторон угла, который меньше развернутого угла, то она лежит на его биссектрисе.

1) Пусть точка L равноудалена от сторон угла АОВ, т. е. перпендикуляры LD и LC, проведенные к сторонам угла, равны. Докажем, что луч OL — биссектриса угла АОВ (рис. 36, б).

2) Рассмотрим прямоугольные треугольники ODL и ОСЬ. Эти треугольники равны по гипотенузе и катету (отрезок OL — общая гипотенуза, LD = LC).

3) Из равенства треугольников ODL и ОСЬ следует, что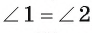, т. е. луч OL — биссектриса угла АОВ.

Что и требовалось доказать.

Теорема 2 (о точке пересечения биссектрис). Биссектрисы треугольника пересекаются в одной точке.

Доказательство.

1) Пусть отрезки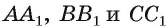— биссектрисы треугольника ABC. Докажем, что они пересекаются в одной точке (рис. 37).

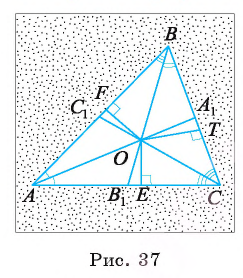
Пусть О — точка пересечения биссектрис АА, и ВВ,, отрезки OF, ОТ и ОЕ — перпендикуляры, проведенные из точки О к прямым АВ, ВС и АС соответственно.

2) Так как лун АО является биссектрисой угла ВАС, то по теореме о свойстве биссектрисы утла выполняется равенство ОЕ = OF. Так как луч ВО — биссектриса угла ABC, то OF = ОТ также по теореме о свойстве биссектрисы угла. Отсюда следует, что ОЕ = ОТ.

3) Равенство ОЕ = ОТ означает, что точка О равноудалена от сторон угла АСВ. Следовательно, по теореме о свойстве биссектрисы угла получим, что точка О лежит на биссектрисе угла АСВ. Иначе говоря, биссектриса 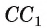, проходит через точку О. Таким образом, все три биссектрисы 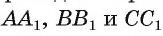треугольника ABC пересекаются в точке О.

Теорема доказана.

2. Теорема о точке пересечения прямых, содержащих высоты треугольника. Ранее было введено понятие серединного перпендикуляра к отрезку и доказана теорема о серединном перпендикуляре: каждая точка серединного перпендикуляра к отрезку равноудалена от его концов. И обратно', если точка равноудалена от концов отрезка, то она лежит на серединном, перпендикуляре к этому отрезку.

Воспользуемся этими свойствами для доказательства следующей теоремы.

Теорема 3(о точке пересечения серединных перпендикуляров к сторонам треугольника). Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке.

Доказательство.

Пусть 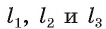— серединные перпендикуляры к сторонам АВ, ВС и АС треугольника ABC соответственно (рис. 38). Докажем, что серединные перпендикуляры пересекаются в одной точке.

1) Пусть О — точка пересечения серединных перпендикуляров

Тогда по теореме о серединном перпендикуляре справедливы равенства ОА = ОВ (так как прямая 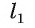— серединный перпендикуляр к отрезку АВ) и ОВ = ОС (так как прямая 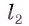— серединный перпендикуляр к отрезку ВС). Отсюда следует, что ОА = ОС.

2) Равенство ОА = ОС означает, что точка О равноудалена от вершин А и С. Значит, по теореме о серединном перпендикуляре точка О лежит на серединном перпендикуляре к стороне АС. Таким образом, все три серединных перпендикуляра 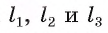пересекаются в одной точке.

Теорема доказана.

Воспользуемся теоремой 3 для доказательства свойства высот треугольника.

Теорема 4 (о точке пересечения прямых, на которых лежат высоты треугольника). Прямые, на которых лежат высоты треугольника, пересекаются в одной точке.

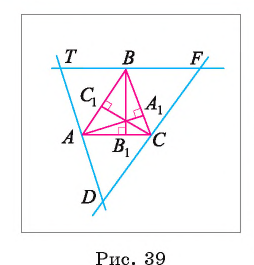
Доказательство.

1) Пусть отрезки 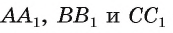— высоты произвольного треугольника ABC (рис. 39). Докажем, что прямые, содержащие высоты треугольника, пересекаются в одной точке.

2) Проведем через вершины А, В и С прямые, параллельные сторонам ВС, АС и АВ соответственно. Пусть Т, F и D — точки их пересечения.

3) Докажем, что точки А, В и С являются соответственно серединами сторон TD, TF и FD треугольника TFD. Например, докажем, что точка С — середина стороны DF. Так как четырехугольник ABCD — параллелограмм, то АВ = DC. Так как AJBFC — параллелограмм, то АВ = CF. Таким образом, DC = CF.

4) Аналогично доказывается, что AT=AD и ТВ = BF. По условию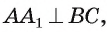, а по построению TD || ВС, следовательно, 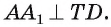. Аналогично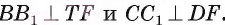. Значит, прямые 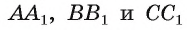, являются серединными перпендикулярами к сторонам треугольника TFD. Следовательно, они пересекаются в одной точке.

Теорема доказана.

Точка пересечения медиан, точка пересечения биссектрис и точка пересечения прямых, содержащих высоты треугольника, называются замечательными точками треугольника.

Заметим, что если треугольник остроугольный, то пересекаются в одной точке сами его высоты, а если треугольник тупоугольный, то пересекаются в одной точке прямые, содержащие высоты.

Вписанные и описанные треугольники

1. Окружность, вписанная в треугольник. Рассмотрим понятие окружности, вписанной в треугольник.

Определение. Окружность называется вписанной в треугольник, если она касается всех сторон треугольника. В этом случае треугольник называется описанным около окружности.

Например, на рисунке 44, а изображена окружность, вписанная в треугольник ABC. Окружность, которая изображена на рисунке 44, б не является вписанной в треугольник ABC, так как она не касается стороны ВС.

Круг называется вписанным в треугольник, если его граница вписана в этот треугольник.

Следующая теорема дает ответ на вопрос о существовании окружности, вписанной в треугольник.

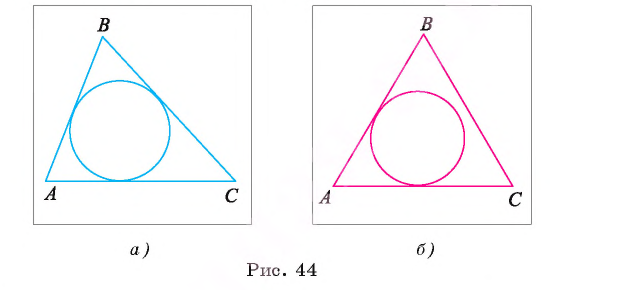
Теорема 1 (о существовании окружности, вписанной в треугольник). В любой треугольник можно вписать единственную окружность.

Доказательство.

I. Докажем, что в треугольник можно вписать окружность.

1) Пусть О — точка пересечения биссектрис произвольного треугольника ABC (рис. 45).

2) Отрезки OK, ОЕ и ОТ — перпендикуляры, проведенные из точки О к сторонам АВ, ВС и АС соответственно

3) По теореме о биссектрисе угла точка О равноудалена от сторон треугольника, следовательно, OK = ОЕ = ОТ. Таким образом, окружность с центром в точке О и радиусом, равным отрезку ОК, проходит через точки К, Е и Т.

4) Стороны АВ, ВС и АС треугольника касаются этой окружности в точках К, Е и Т, так как они перпендикулярны радиусам OK, ОЕ и ОТ соответственно. Следовательно, окружность с центром в точке О и радиусом ОК является вписанной в треугольник АБС. Существование вписанной окружности доказано.

II. Докажем, что такая окружность единственная.

Допустим, что в треугольник можно вписать две окружности. Тогда центр каждой из окружностей равноудален от сторон треугольника, а следовательно, совпадает с точкой О пересечения биссектрис треугольника; ее радиус равен расстоянию от точки О до сторон треугольника. Таким образом, эти окружности совпадают. Теорема доказана.

Окружность, описанная около треугольника

Рассмотрим понятие окружности, описанной около треугольника.

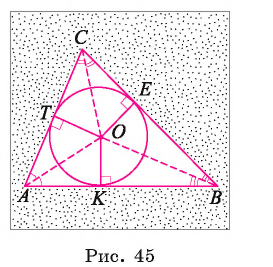
Определение. Окружность называется описанной около треугольника, если все его вершины лежат на этой окружности. В этом случае треугольник называется вписанным в окружность.

Например, на рисунке 46, а. изображена окружность, которая является описанной около треугольника TFE. Окружность, которая изображена на рисунке 46, б, не является описанной около треугольника АБС, так как вершина С не лежит на окружности.

Круг называется описанным около треугольника, если его граница описана около этого треугольника.
 

Докажем теорему о существовании описанной около треугольника окружности.

Теорема 2 (о существовании окружности, описанной около треугольника). Около любого треугольника можно описать единственную окружность.

Доказательство.

I. Докажем, что около треугольника можно описать окружность.

1) Пусть О — точка пересечения серединных перпендикуляров к сторонам произвольного треугольника ABC (рис. 47).

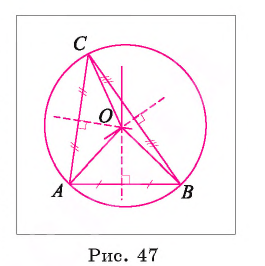
2) Так как точки серединного перпендикуляра к отрезку равноудалены от его концов, то О А = О В = ОС. Таким образом, окружность с центром в точке О и радиусом, равным отрезку ОА, проходит через все вершины треугольника ABC, а значит, является описанной около этого треугольника.

II. Докажем, что такая окружность единственная.

Предположим, что около треугольника можно описать еще одну окружность. Тогда ее центр равноудален от вершин треугольника, а следовательно, совпадает с точкой О пересечения серединных перпендикуляров к сторонам треугольника; ее радиус равен расстоянию от точки О до вершин треугольника. Таким образом, окружности совпадают. Теорема доказана.

Пример №10

Докажите, что радиус г вписанной в прямоугольный треугольник окружности можно найти по формуле г=р-с, где р — полупериметр прямоугольного треугольника, с — длина его гипотенузы.

Доказательство.

1) Пусть К, Т, F — точки касания вписанной окружности соответственно со сторонами АС, АВ и ВС треугольника ABC, точка О — центр этой окружности (рис. 48, а, б).

Четырехугольник CKOF — квадрат 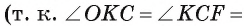, 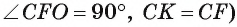значит, CF = CK = OK = OF = г.

2) Отрезки касательных, проведенные из одной точки, равны, следовательно, АТ = АК =АС -г и ВТ = BF = ВС - г.

3) Так как АТ + ВТ = с, то (АС - г) + (ВС - г) = с. Таким

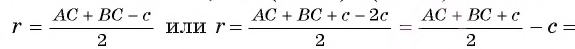
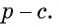
Что и требовалось доказать.

Пример №11

Докажите, что для произвольного треугольника ABC выполняется равенство 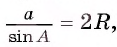стороны, лежащей против угла A, R окружности.

Доказательство.

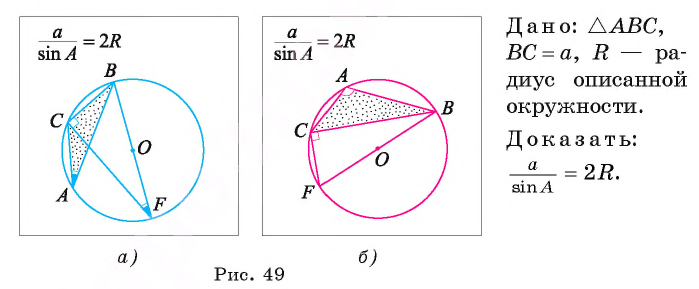
Пусть около треугольника ABC описана окружность. Проведем диаметр BF этой окружности. Возможны три случая.

Первый случай. Углы А и F опираются на одну дугу (рис. 49, а). Тогда 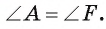. В прямоугольном треугольнике , 

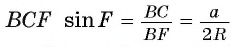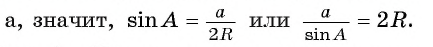
Второй случай. Углы А и F опираются на дуги, дополняющие друг друга до окружности, т. е. 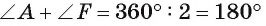(рис. 49, б). Тогда 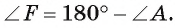. В прямоугольном треугольнике  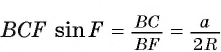Но так как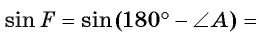 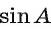 то в этом случае также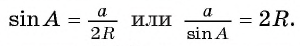

Третий случай. Если треугольник ВАС прямоугольный с прямым углом при вершине А, то формула верна, так как в этом случае sinA= 1 и сторона, лежащая против угла А, является диаметром окружности, т. е. а = 2R.

Что и требовалось доказать.

Окружность, вписанная в четырехугольник

Определим понятие окружности, вписанной в четырехугольник.

Определение. Окружность называется вписанной в четырехугольник, если она касается всех сторон четырехугольника. В этом случае четырехугольник называется описанным около окружности.

Например, на рисунке 53, а изображены квадрат AJ3CD и вписанная в него окружность. Окружность, изображенная на рисунке 53, б, не является вписанной в четырехугольник AFDC, так как она не касается его стороны DC.

Заметим, что не в любой четырехугольник можно вписать окружность. Например, в прямоугольник, не являющийся квадратом, нельзя вписать окружность. Существует окружность, которая касается трех сторон такого прямоугольника, и не существует окружности, касающейся всех его четырех сторон (рис. 53, в).

Круг называется вписанным, в четырехугольник, если его граница вписана в четырехугольник.
 

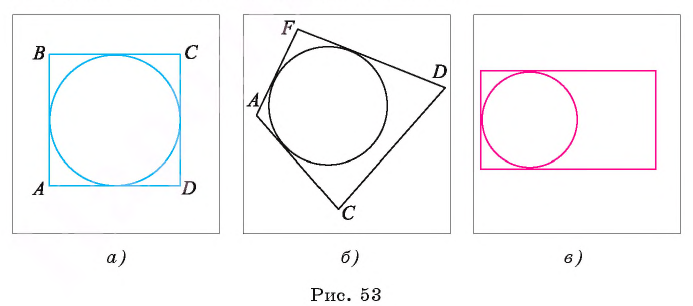
Следующая теорема характеризует свойство четырехугольника, в который можно вписать окружность.

Теорема 1(о свойстве четырехугольника, в который можно вписать окружность). Если в четырехугольник можно вписать окружность, то суммы длин его противолежащих сторон равны.

Доказательство.

1) Пусть в четырехугольник ABCD вписана окружность, которая касается его сторон в точках F, О, Т  и Е (рис. 54).

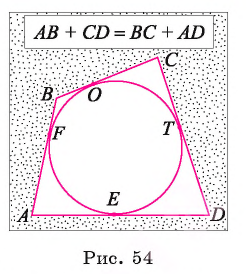
Докажем, что АВ + CD = ВС +AD.

2) Так как отрезки касательных к окружности, проведенные из одной точки, равны, то AF = АЕ = a, BF = ВО = b,

СО = СТ = m, DT = DE = с.

3) Таким образом, АВ+CD=(AF+FB)+

+ (СТ + DT) = a + b + c + m и ВС + AD = (ВО + ОС) + (АЕ + ED) = = а + b + с + т. Отсюда следует, что АВ + CD = ВС + AD.

Теорема доказана.

Справедливо и обратное утверждение, которое отвечает на вопрос, при каком условии в четырехугольник можно вписать окружность.

Теорема 2 (условие, при котором в четырехугольник можно вписать окружность). Если в выпуклом четырехугольнике суммы длин противолежащих сторон равны, то в этот четырехугольник можно вписать окружность.
 

Доказательство.

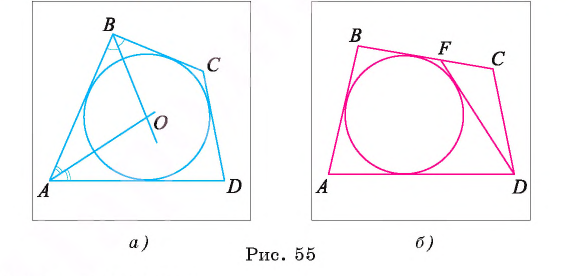
1) Пусть ABCD — выпуклый четырехугольник, в котором АВ + CD = ВС + AD. Докажем, что в этот четырехугольник можно вписать окружность.

2) Рассмотрим окружность, которая касается трех сторон: АВ, ВС и AD. Центр О этой окружности есть точка пересечения биссектрис углов СВА и BAD (рис. 55, а).

3) Докажем, что эта окружность вписана в четырехугольник, т. е. что она касается также и стороны CD. Предположим,
 

что это не так. Тогда либо сторона CD не пересекает окружность, либо является секущей.

4) Пусть сторона CD не пересекает окружность (рис. 55, б). Проведем касательную DF, где F е ВС. Так как ABFD — описанный четырехугольник, то верно равенство АВ + DF = = AD + BF. Кроме того, по условию АВ + CD = BF + FC + AD. Отсюда следует, что АВ + CD =АВ + DF + FC или CD = DF + FC, что невозможно, так как в треугольнике DFC длина стороны CD должна быть меньше суммы длин двух других сторон. Аналогично приводит к противоречию и предположение о том, что сторона CD является секущей.

5) Таким образом, предположение о том, что сторона CD не касается рассматриваемой окружности, неверно. Следовательно, сторона CD касается этой окружности, и, значит, окружность вписана в четырехугольник ABCD. Теорема доказана.

Окружность, описанная около четырехугольника

Определим понятие окружности, описанной около четырехугольника.

Определение. Окружность называется описанной около четырехугольника, если все его вершины лежат на окружности. В этом случае четырехугольник называется вписанным в окружность.

Круг называется описанным около четырехугольника, если его граница описана около четырехугольника.

Теперь рассмотрим свойство четырехугольника, вписанного в окружность.

Теорема 3 (о свойстве четырехугольника, вписанного в окружность). Если около четырехугольника описана окружность, то суммы градусных мер его противолежащих углов равны 180°.

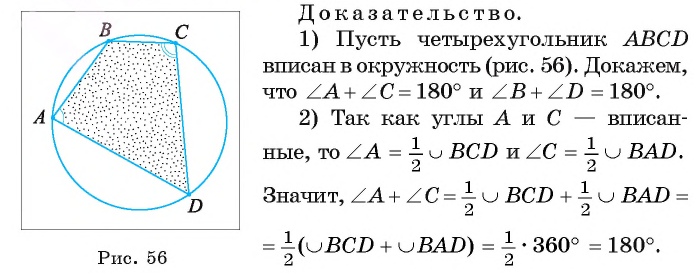
Так как сумма градусных мер углов четырехугольника ABCD равна 360° и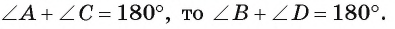

Теорема доказана.

Справедливо и обратное утверждение, которое характеризует условие, при котором около четырехугольника можно описать окружность.

Теорема 4 (условие, при котором, около четырехугольника можно описать окружность). Если в четырехугольнике суммы градусных мер противолежащих углов равны 180°, то около такого четырехугольника можно описать окружность.
 

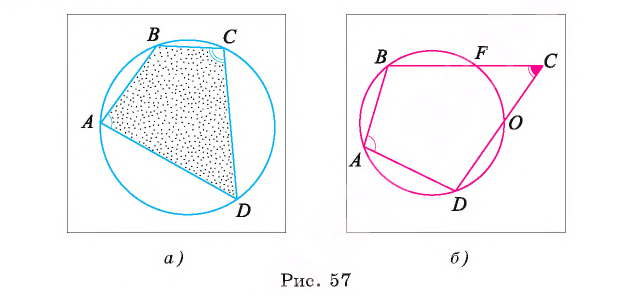
Доказательство.

1) Пусть в четырехугольнике ABCD выполняется равенство 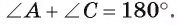. Докажем, что около четырехугольника ABCD можно описать окружность (рис. 57, а).

2) Рассмотрим окружность, описанную около треугольника ABD, и докажем, что эта окружность проходит также через вершину С. Предположим, что окружность не проходит через вершину С. Тогда либо вершина С лежит вне круга, границей которого служит рассматриваемая окружность, либо внутри этого круга.

3) Пусть вершина С лежит вне круга (рис. 57, б). Обозначим буквами F и О точки пересечения сторон ВС и DC с окружностью. Тогда 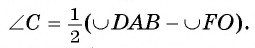Следовательно,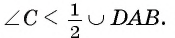Так как угол А является вписанным, то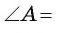

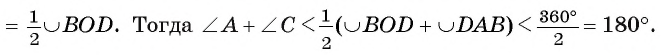
Это противоречит условию, значит, наше предположение неверно, т. е. окружность проходит через вершину С. Аналогично можно доказать, что вершина С не может лежать внутри круга. Теорема доказана.

Из доказанной теоремы следует, что около любого прямоугольника можно описать окружность.

Рассмотрим некоторые задачи, при решении которых используются доказанные теоремы.

Пример №12

Около окружности описана равнобедренная трапеция ABCD, длина ее боковой стороны равна 10 см, а градусная мера одного из ее углов равна 60°. Вычислите площадь трапеции.

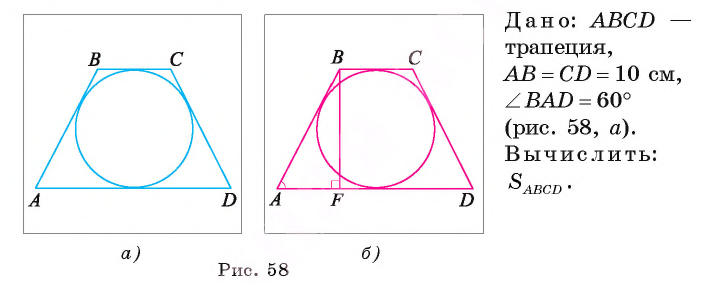
Решение:

Для нахождения площади трапеции воспользуемся формулой 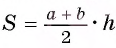, где а и b — длины ее оснований, h — высота.

1) Пусть отрезок BF — высота трапеции. Тогда 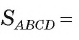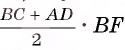(рис. 58, б).

2) Так как в трапецию ABCD вписана окружность, то ВС + AD = АВ + CD. Но так как трапеция равнобедренная, то ВС + AD = 2АВ = 20 см.

3) В прямоугольном треугольнике AFB длина катета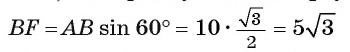 (см). Теперь вычислим площадь трапеции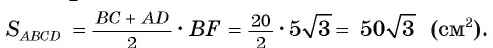 

Пример №13

Основанием прямоугольного параллелепипеда является квадрат. Вычислите площадь боковой грани параллелепипеда, если диаметр окружности, описанной около основания параллелепипеда, равен 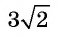см, а боковое ребро в два раза больше стороны основания.

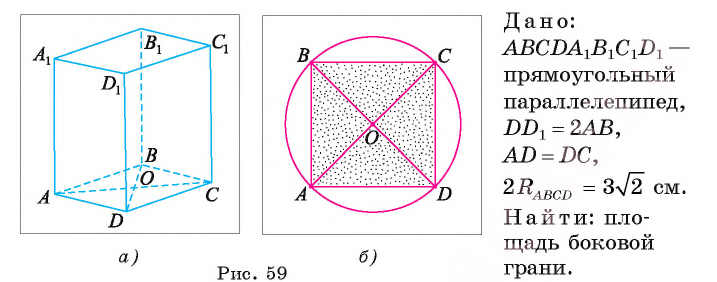
Решение:

Каждая грань прямоугольного параллелепипеда является прямоугольником. Так как основания параллелепипеда — квадраты, то боковые грани — равные прямоугольники. Площадь прямоугольника равна произведению длин его сторон, следовательно, достаточно вычислить, например, длины отрезков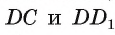 тогда площадь грани 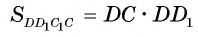(рис. 59, а).

1) Диагональ квадрата, вписанного в окружность, равна диаметру окружности, значит, 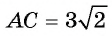(рис. 59, б).

2) В равнобедренном прямоугольном треугольнике ADC имеем 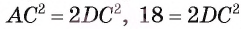. Значит, DC = 3 см.

3) По условию боковое ребро параллелепипеда в два раза больше стороны основания. Значит,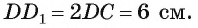

4) Теперь вычислим площадь боковой грани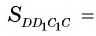

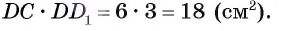
Ответ: 18 см2.