
Внешний угол треугольника - определение и вычисление с доказательствами и примерами решения
Внешний угол треугольника:
Углы треугольника называются еще его внутренними углами. Помимо внутренних углов, у треугольника есть и внешние углы.
Определение. Внешним углом треугольника называется угол, смежный с его внутренним углом.
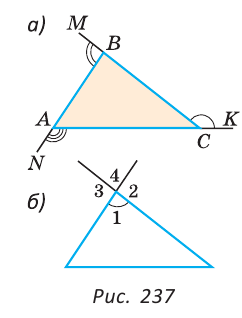
На рисунке 237, а углы ВСК, ABM, CAN — внешние, так как каждый из них является смежным с одним из внутренних углов треугольника. При каждой вершине треугольника один угол внутренний и два внешних. На рисунке 237, б угол 1 — внутренний, углы 2 и 3 — равные внешние углы. Угол 4 не является внешним, так как он не является смежным с внутренним углом 1.
Дано: 
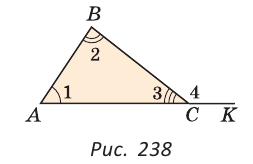
Доказать: 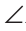 4 =
4 =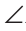 1 +
1 +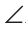 2.
2.
Доказательство:
Так как сумма углов треугольника равна 180°, то
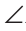 l +
l +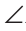 2 +
2 +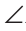 3 = 180°.
3 = 180°.
Так как сумма смежных углов равна 180°, то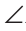 3 +
3 +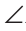 4 = 180°.
4 = 180°.
Тогда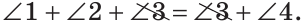 Отняв от обеих частей равенства
Отняв от обеих частей равенства 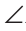 3, получим
3, получим 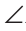 1 +
1 +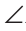 2 =
2 =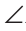 4. Теорема доказана.
4. Теорема доказана.
Следствие.
Внешний угол треугольника больше любого внутреннего угла, не смежного с ним.
Пример:
Доказать, что биссектриса внешнего угла при вершине равнобедренного треугольника параллельна основанию.
Доказательство:
Пусть в  АВС АВ=ВС, ВМ — биссектриса внешнего угла КВС,
АВС АВ=ВС, ВМ — биссектриса внешнего угла КВС, 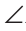 1 =
1 =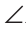 2 =
2 = 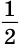
 KBC (рис. 239).
KBC (рис. 239).
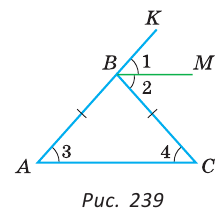
По свойству внешнего угла треугольника  KBC =
KBC = 3 +
3 + 4. Так как
4. Так как  АВС равнобедренный, то
АВС равнобедренный, то 3=
3= 4=
4=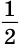
 KBC. Поэтому
KBC. Поэтому  2 =
2 = 4. Поскольку внутренние накрест лежащие углы 2 и 4 равны (при прямых ВМ и АС и секущей ВС), то прямые ВМ и АС параллельны.
4. Поскольку внутренние накрест лежащие углы 2 и 4 равны (при прямых ВМ и АС и секущей ВС), то прямые ВМ и АС параллельны.
Пример:
Доказать, что сумма углов А, В, С, D и Е «звездочки» равна 180° (рис. 240).
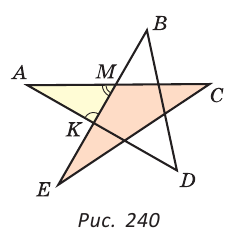
Решение:
Рассмотрим  АМК. Сумма его углов равна 180°. Угол АМЕ — внешний для
АМК. Сумма его углов равна 180°. Угол АМЕ — внешний для  ЕМС, поэтому
ЕМС, поэтому  AME =
AME = C +
C + E.
E.
Аналогично, угол АКВ — внешний для  KBD, поэтому
KBD, поэтому AKB =
AKB = B +
B + D.
D.
Так как A +
A + AMK +
AMK + AKM = 180°, то
AKM = 180°, то A + (
A + ( C +
C + E) + (
E) + ( B +
B + D) = 180°.
D) = 180°.
Геометрия 3D
Пример:
DABC — правильная треугольная пирамида, точка К — середина ребра DC, 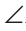 AKB = 50°. Найдите
AKB = 50°. Найдите 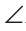 KAB (рис. 244).
KAB (рис. 244).
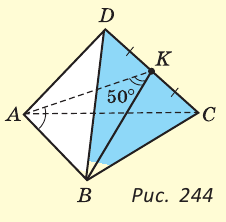
Решение:
Так как пирамида правильная, то треугольники ADC и BDC — равные равнобедренные, AD = BD, BD = CD, 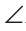 ADC =
ADC = 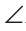 BDC. Тогда
BDC. Тогда  ADK =
ADK =  BDK по двум сторонам и углу между ними. Отсюда АК = ВК,
BDK по двум сторонам и углу между ними. Отсюда АК = ВК,  АКВ — равнобедренный,
АКВ — равнобедренный,
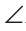 KAB = 65°.
KAB = 65°.
Ответ: 65°.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |
- Свойство точек биссектрисы угла
- Свойство катета прямоугольного треугольника, лежащего против угла в 30°
- Четырехугольник и его элементы
- Четырехугольники и окружность
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Сумма углов треугольника