Винтовые поверхности в начертательной геометрии с примером

Винтовые поверхности:

Винтовой поверхностью называется поверхность, которая описывается какой-либо линией (образующей) при ее винтовом движении.

Если образующей винтовой поверхности является прямая линия, то поверхность называется линейчатой винтовой поверхностью или ге­ликоидом (от франц, helic - спираль, винтовая линия). Геликоид назы­вается прямым или наклонным в зависимости от того, перпендикулярна образующая оси геликоида или наклонна.

Рассмотрим некоторые виды линейчатых винтовых поверхностей.

1.Прямой геликоид образуется движением прямолинейной образующей

2. Наклонный геликоид отличается от прямого геликоида тем, что его образующая 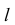пересекает ось геликоида под постоянным углом 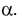Этот угол не равен прямому углу. Образующая 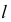наклонного геликоида движется по двум направляющим. Одна из направляющих является цилиндрической винтовой линией 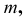а другая - ее осью 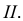Причем во всех своих положениях образующая 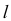параллельна образующим некоторого конуса вращения. У этого конуса угол между образующей и осью, параллельной оси геликоида, равен 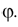Он называется направляющим кону­сом наклонного геликоида.

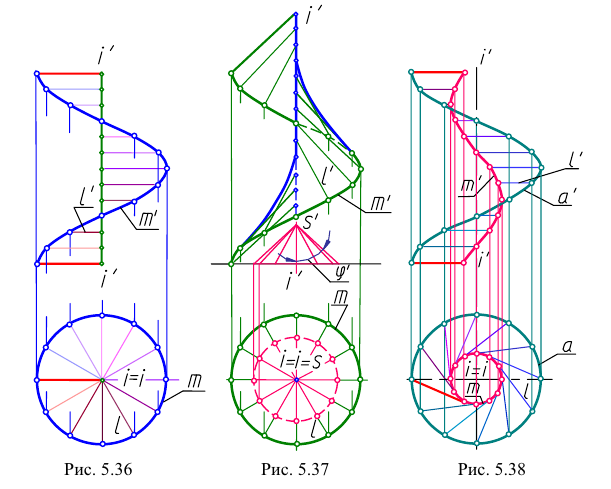
На рис. 5.37 показано построение проекций наклонного геликоида. Его направляющими являются цилиндрическая винтовая линия т и ее ось 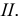Образующие геликоида параллельны соответствующим образующим направляющего конуса.

3. Развертывающийся геликоид образуется движением прямоли­нейной образующей 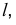касающейся во всех свих положениях цилиндри­ ческой винтовой линии 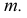Она является ребром возврата геликоида (рис. 5.38).

Развертывающийся геликоид, как линейчатая поверхность с ребром возврата, относится к числу торсов.

На рис. 5.38 поверхность развертывающегося геликоида ограни­чена ребром возврата 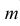и линией 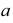от пересечения геликоида с поверхностью соосного цилиндра большего диаметра, чем диаметр винтовой линии 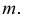Если образующая 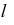пересекается с осью поверхности, геликоид называется закрытым (рис. 5.36 и 5.37). Если образующая 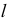не пересекается с осью поверхности, геликоид называется открытым (рис. 5.38).