
Векторное исчислени
Основы векторного исчисления:
Существуют две категории физических величин: скалярные и
векторные.
Скалярные и векторные величины
Скалярные величины характеризуются при выбранной единице меры одним числом. Сюда относятся, например, масса, объем тела, время, температура и т. п.
Векторные величины в отличие от скалярных характехарактеризуются, помимо численного значения, еще своим направлением в пространстве; к векторным величинам относятся сила, перемещение, скорость и ускорение точки, напряжение и т. п.
Условимся .в дальнейшем в тексте и на рисунках обозначать векторы жирными буквам латинского или греческого алфавита:
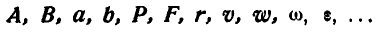
Скаляры и численные значения векторов условимся обозначать светлым
шрифтом латинского или греческого алфавита:
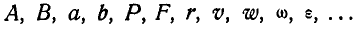
Так, например, если величина А вектора А (рис. 1) равна 5 кГ, а выбранный ними масштаб таков, что 1 см соответствует 1 кГ, то длина А изобразится отрезком в 5 см.
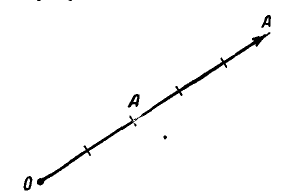
Рис. 1.
Иногда вектор обозначают двумя буквами, стоящими в начале и в конце вектора с чертой наверху, а его модуль обозначается теми же буквами, но без черты.
Так, например, вектор А (рис. 1) можно обозначать через 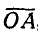 , а его модуль — через
, а его модуль — через 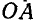 .
.
Типы векторов
Имеются три типа векторов — свободные, скользящие (или передвижные) и определенные.
Вектор называется свободным, если по смыслу выражаемой им величины начало вектора может быть взято в любой точке пространства. Начало передвижного вектора может быть передвинуто вдоль линии действия вектора, и, наконец, начало определенного вектора всегда скреплено с определенной точкой пространства.
Два свободных вектора А и В называются равными, если они имеют одинаковую численную величину и одинаковое направление. Два передвижных вектора равны один другому, когда они, помимо одинаковой численной величины и одинакового направления, лежат на одной прямой. Для равенства определенных векторов дополнительным условием является общая точка их приложения. Равенство двух векторов А и В записывается в виде: А = В.
Те операции, которые можно производить над свободными векторами. Эти операции могут быть распространены на передвижные и определенные векторы с некоторыми ограничениями, которые будут рассмотрены ниже в специальных отделах теоретической механики.
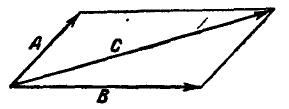
Рис. 2.
Суммой двух векторов.А и В или их результирующей (рис. 2) называется вектор С, равный по величине и направлению диагонали параллелограмма, построенного на слагаемых векторах.
Сложение векторов записывается в виде:
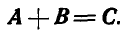
Разностью двух векторов А и В называется такой вектор, который в сумме с вычитаемым вектором В дает уменьшаемый вектор А.
Вычитание векторов обозначается равенством:
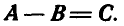
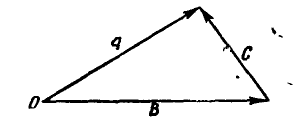
Рис. 3.
Отсюда следует, что для нахождения разности С надо оба вектора А и В отложить из общего начала О (рис. 3) и соединить их концы; отрезок, направленный от конца вычитаемого к концу уменьшаемого вектора, даст искомую разность С.
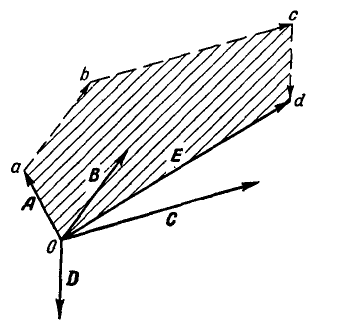
Рис. 4.
Несколько векторов А, В, С и D складывают по правилу многоугольника векторов, для чего из конца , вектора А (рис. 4) проводят вектор 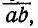 равный вектору В, далее из точки b — вектор
равный вектору В, далее из точки b — вектор 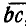 , равный С, и из точки с — вектор
, равный С, и из точки с — вектор 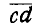 , равный D. Соединяя начало О первого вектора с концом d последнего вектора
, равный D. Соединяя начало О первого вектора с концом d последнего вектора 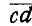 , получим результирующий вектор Е, имеющий направление, обратное направлению составляющих векторов:
, получим результирующий вектор Е, имеющий направление, обратное направлению составляющих векторов:
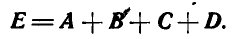
Вектор Е называется также геометрической суммой векторов, или замыкающей многоугольника векторов.
Если три вектора А, В и С не лежат в одной плоскости, то их результирующая D выразится диагональю построенного на слагаемых векторах (рис. 5).
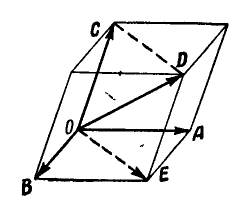
Рис. 5.
Это следует из того, что любые два вектора, найример В и А, можно заменить одним вектором Е = А + В. В свою очередь, векторы Е и С можно заменить вектором D, равным D = Е + С = А + В + С, что и доказывает изложенное правило.
При сложении данного вектора с противоположным сумма обращается в нуль. Противоположным вектором называется вектор, численно равный данному, но имеющий противоположное направление.
Не трудно показать обратно, что вектор можно разложить по любым двум направлениям на два составляющих вектора по правилу параллелограмма и по любым трем направлениям, не лежащим в одной плоскости, по правилу параллелепипеда.
Из сложения векторов следует, что вектор А можно умножить на любую скалярную величину 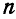 ; при этом получается новый вектор В, определяемый равенством
; при этом получается новый вектор В, определяемый равенством 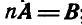 ; при
; при 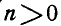 вектор В имеет то же направление, что и А; при
вектор В имеет то же направление, что и А; при 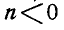 вектор В направлен противоположно А.
вектор В направлен противоположно А.
Деление вектора А на скалярную величину 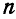 сводится к умножению его на
сводится к умножению его на 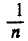 .
.
Если два вектора А и В дают в сумме вектор С, то при их умножении на скалярную величину 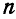 и геометрическом сложении получим новый вектор, который найдем из рассмотрения подобных угольников (рис. 6):
и геометрическом сложении получим новый вектор, который найдем из рассмотрения подобных угольников (рис. 6):
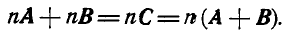
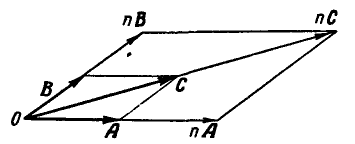
Рис. 6.
Вообще:
Вектор называется единичным, если его модуль равен единице. Единичные векторы мы будем обозначать малыми буквами, например  и т. д.
и т. д.
Любой вектор А можно представить как произведение его модуля, т. е. численной величины А на единичный вектор а, имеющий направление вектора А. Найдем проекцию вектора 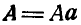 на ось L, при этом рассмотрим случай, когда вектор А и ось L не лежат в одной плоскости (рис. 7).
на ось L, при этом рассмотрим случай, когда вектор А и ось L не лежат в одной плоскости (рис. 7).
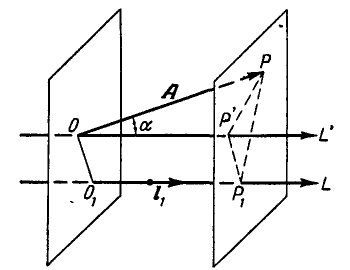
Рис. 7.
Для нахождения проекции проведем через начало О и конец Р вектора А две плоскости, перпендикулярные к оси проекций L, и тогда отрезок  на оси L, заключенный между плоскостями, и будет искомой проекцией
на оси L, заключенный между плоскостями, и будет искомой проекцией  . Проекцию вектора А на ось L можно найти иначе. Для этого перенесем мысленно ось L параллельно самой себе в начало вектора О (положение
. Проекцию вектора А на ось L можно найти иначе. Для этого перенесем мысленно ось L параллельно самой себе в начало вектора О (положение  ) и из конца Р вектора А опустим на перенесенную ось перпендикуляр
) и из конца Р вектора А опустим на перенесенную ось перпендикуляр 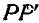 , тогда отрезок
, тогда отрезок 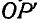 будет проекцией вектора А на ось L, так как
будет проекцией вектора А на ось L, так как 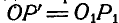 . Проекция вектора А на ось L является величиной скалярной и может быть найдена из прямоугольного треугольника
. Проекция вектора А на ось L является величиной скалярной и может быть найдена из прямоугольного треугольника 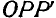 по формуле:
по формуле:

Знак для 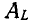 берется плюс, если направление проекции вектора совпадает с направлением оси L, как в нашем случае, и — минус, если направление проекции вектора обратно направлению оси L. Введя в рассмотрение единичный вектор оси
берется плюс, если направление проекции вектора совпадает с направлением оси L, как в нашем случае, и — минус, если направление проекции вектора обратно направлению оси L. Введя в рассмотрение единичный вектор оси 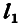 ; мы можем выразить вектор
; мы можем выразить вектор 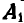 , равный проекции вектора А на ось L, в виде:
, равный проекции вектора А на ось L, в виде:
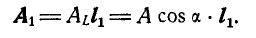
Спроектируем теперь результирующую С и составляющие векторы А, В и С на ось L (рис. 8).
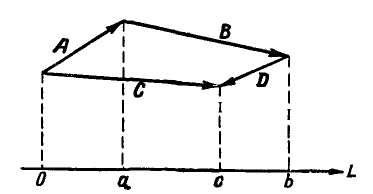
Рис. 8.
Имеем:
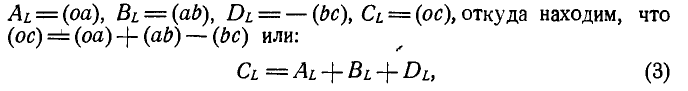
т. e. проекция замыкающей равна алгебраической сумме проекций составляющих.
Введем в рассмотрение прямоугольную систему координат. Имеются две системы прямоугольных координатных осей — левая и правая (рис. 9); при этом одна является зеркальным отображением другой.
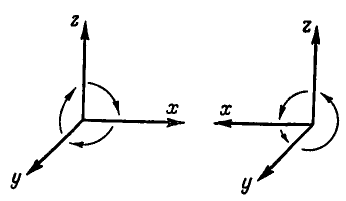
Рис. 9.
Если мы захотим последовательно совместить координатные оси, т. е. ось  и
и 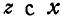 , то для левой системы осей это совмещение будет происходить по направлению движения часовой стрелки, для правой же — против движения стрелки часов.
, то для левой системы осей это совмещение будет происходить по направлению движения часовой стрелки, для правой же — против движения стрелки часов.
В дальнейшем в качестве основной системы координат примем правую. Если-имеется вектор А, отнесенный к правой системе координат, и если 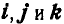 — единичные векторы (орты) координатных осей х, у и z (рис. 10), то вектор А может быть выражен через составляющие его векторы по координатным осям (компоненты)
— единичные векторы (орты) координатных осей х, у и z (рис. 10), то вектор А может быть выражен через составляющие его векторы по координатным осям (компоненты) 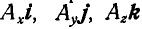 следующим образом:
следующим образом:
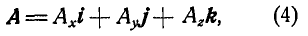
где
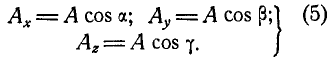
Из равенств (5) находим косинусы углов, которые составляет вектор А с координатными осями:
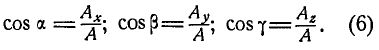
выразится фор-
Так как квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений, то
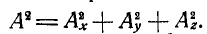
Отсюда модуль вектора А через его проекции выразится формулой:
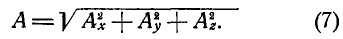
Возводя в квадрат и складывая равенства (6), получаем:
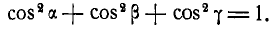
Перейдем теперь к умножению векторов. При умножении векторов различают два вида их произведения — скалярное и векторное.
Скалярное произведение векторов
Скалярным произведением двух векторов А и В (рис. 11) называется скалярная величина, равная произведению модулей перемножаемых векторов на косинус угла между ними.
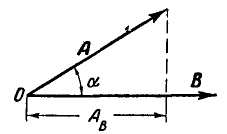
Рис. 11.
Скалярное произведение векторов обозначается символом 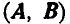 или
или 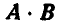 и определяется:
и определяется:
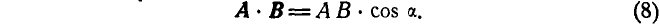
Примером скалярного произведения двух векторов из области механики является работа, где одним вектором является сила, другим — перемещение. Скалярное произведение двух векторов обладает следующими свойствами.
1. От порядка расположения перемножаемых векторов результат не меняется (свойство коммутативности), т. е, 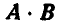
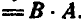 . Это свойство вытекает из определения скалярного произведения.
. Это свойство вытекает из определения скалярного произведения.
2. Скалярное произведение параллельных векторов равно произведению их модулей:
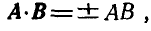
где знак плюс соответствует одинаково направленным, а знак минус — противоположно направленным векторам. В частности
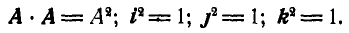
3. Скалярное произведение перпендикулярных векторов равно нулю, т. е. 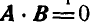 , и, следовательно:
, и, следовательно:
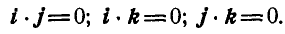
4. Скалярное произведение можно рассматривать как произведение проекции одного вектора на другой, умноженной на модуль другого вектора (рис. 11):
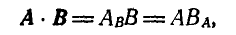
что следует из определения скалярного произведения. Отсюда проекция вектора на ось есть скалярное произведение вектора на единичный вектор оси проекций.
5. Скалярное произведение обладает свойством дистрибутивности (раскрытия скобок), например:
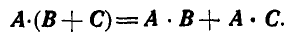
6. Чтобы умножить скалярное произведение на скалярный множитель 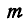 , достаточно умножить на него один из векторов:
, достаточно умножить на него один из векторов:
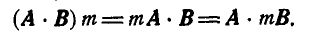
7. Скалярное произведение равно алгебраической сумме произведений одноименных проекций:
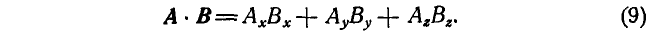
Равенство (9) получится, если векторы А и В выразить через их компоненты по равенству (4) и раскрыть скобки.
Остановимся на рассмотрении векторного произведения векторов.
Рассмотрим площадку в виде параллелограмма, построенного из векторов А и В (рис. 12).
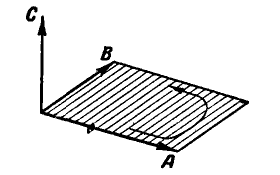
Рис. 12.
Этой площадке соответствует вектор С, направленный нормально к площадке и численно равный ее величине; такой вектор мы назовем вектором площадки, а откладывать его будем сообразно обходу контура площадки. Операцию, в результате которой получают вектор площадки, называют векторным произведением векторов А и В и обозначают символом 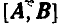 или
или  .
.
Таким образом, векторным произведением двух векторов А и В называется вектор С, модуль которого равен площади параллелограмма, построенного на этих векторах. Вектор С направлен перпендикулярно к плоскости этого параллелограмма в такую сторону, чтобы, смотря с острого конца этого вектора, направление обхода, задаваемое первым вектором, стоящим в векторном произведении, происходило против часовой стрелки при выбранной нами правой системе:
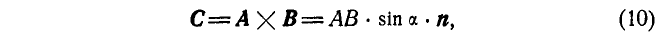
где 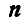 — единичный вектор нормали к площадке.
— единичный вектор нормали к площадке.
Векторное произведение двух векторов обладает следующими свойствами:
1. При перемене порядка перемножаемых векторов векторное произведение меняет знак:
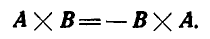
Это следует из того, что вектор С меняет свое направление.
2. Векторное произведение параллельных векторов равно нулю, т. е. 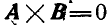 , так как при
, так как при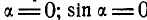 . В частности
. В частности
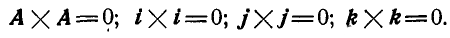
3. Численное значение векторного произведения перпендикулярных векторов равно произведению их численных зйачений, т. е. 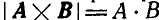 . В частности
. В частности
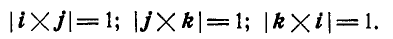
Векторы же 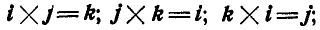
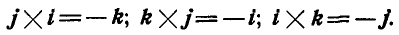
4. Векторное произведение обладает свойством дистрибутивности:
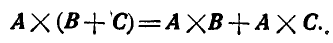
Это свойство не трудно доказать.
5. При умножении векторного произведения на скалярный множитель достаточно умножить на него один из сомножителей:
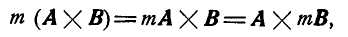
что следует из определения векторного произведения.
6. Векторное произведение может быть выражено через проекции перемножаемых векторов следующим образом:
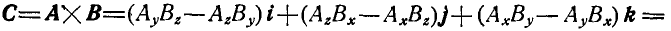
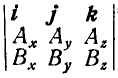
Эта более сокращенная запись называется детерминантом, или определителем. Наиболее часто встречаются детерминант второго порядка
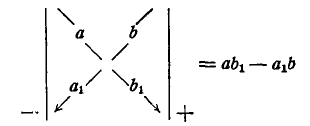
и детерминант третьего порядка
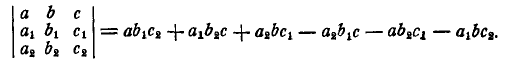
В справедливости последнего равенства можно легко убедиться, если вместо А и В подставить их компоненты по равенству (4) и произвести преобразования.
Коэффициенты, стоящие при ортах  и
и  , суть величины проекций векторного произведения на координатные оси х, у и z, выпишем их отдельно:
, суть величины проекций векторного произведения на координатные оси х, у и z, выпишем их отдельно:
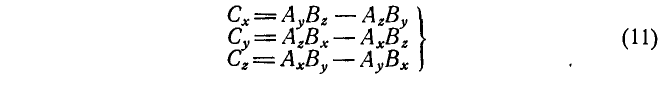
Формулы (11) легко запомнить, так как индексы у С, А и В меняются по закону круговой подстановки  минус произведение А на В с обратно переставленными индексами.
минус произведение А на В с обратно переставленными индексами.
Перейдем теперь к рассмотрению скалярно-векторного, или смешанного произведения векторов, обозначаемого 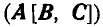 или
или 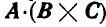 . Это произведение имеет простой геометрический смысл.
. Это произведение имеет простой геометрический смысл.
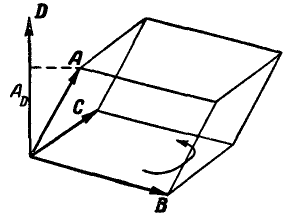
Рис. 13.
Построим на перемножаемых векторах А, В и С параллелепипед (рис. 13) и обозначим  через D, тогда имеем
через D, тогда имеем
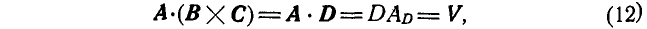
где 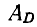 — проекция вектора А на направление D, выражает высоту параллелепипеда, a D по величине равен основанию параллелепипеда. Следовательно,
— проекция вектора А на направление D, выражает высоту параллелепипеда, a D по величине равен основанию параллелепипеда. Следовательно, 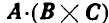 выражает объем параллелепипеда V.
выражает объем параллелепипеда V.
Не трудно видеть, что смешанное произведение не меняется при. циклической перестановке множителей, т. е.
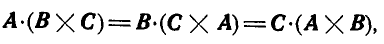
и обращается в нуль, если перемножаемые векторы комплонарны или если два из перемножаемых векторов коллинеарны, так как объем параллелепипеда, построенного на таких векторах, обращается в нуль.
Векторы, расположенные в одной плоскости, называются комплонарными.
Векторы называются коллинеарными, если они параллельны.
Смешанное произведение можно выразить через проекции перемножаемых векторов в виде:
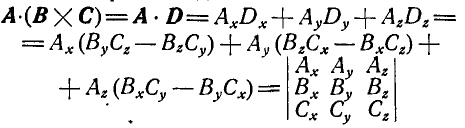
Рассмотрим,наконец, двойное векторное произведение 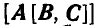 или
или 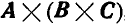 , которое дает некоторый вектор, комплонарный с векторами В и С. Действительно, векторное произведение
, которое дает некоторый вектор, комплонарный с векторами В и С. Действительно, векторное произведение  дает вектор Р, перпендикулярный к плоскости параллелограмма векторов В и С (рис. 14), а вектор
дает вектор Р, перпендикулярный к плоскости параллелограмма векторов В и С (рис. 14), а вектор 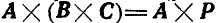 должен быть перпендикулярен к плоскости параллелограмма векторов А и Р, а следовательно, лежать в плоскости параллелограмма векторов В и С. Далее имеем:
должен быть перпендикулярен к плоскости параллелограмма векторов А и Р, а следовательно, лежать в плоскости параллелограмма векторов В и С. Далее имеем:
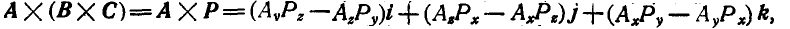
что после преобразования дает:
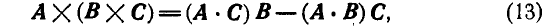
т. е. двойное векторное произведение равно среднему - вектору с коэффициентом, равным скалярному произведению двух оставшихся векторов минус второй вектор, во внутренний скобках, с коэффициентом, равным скалярному произведению оставшихся векторов.
Задача:
Найти величину и направление результирующей D трех передвижных векторов, линии действия которых пересекаются в одной точке:
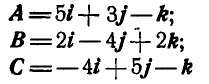
Решение. По формуле (3) находим результирующую D заданных векторов: 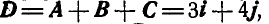 которая будет рас-положена в плоскости ху. Величина результирующей
которая будет рас-положена в плоскости ху. Величина результирующей 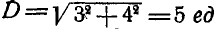 , а направление ее определится косинусами углов
, а направление ее определится косинусами углов  и
и  , которые результирующая составляет с осями координат х и у:
, которые результирующая составляет с осями координат х и у:
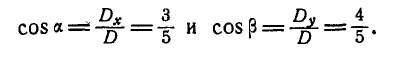
Краткие сведения из векторного анализа
Выше мы ограничились рассмотрением постоянных которые не меняли ни величины, ни направления с течением времени. Представим себе теперь движущуюся в пространстве точку М (рис. 15).
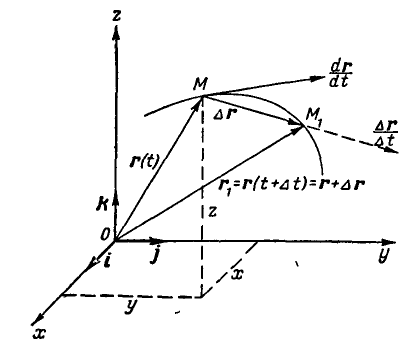
Рис. 15.
Положение ее в пространстве в данный момент времени определяется тремя координатами х, у и z или концом радиуса вектора r, проведенного из начала координат. За малый промежуток времени  точка М перейдет в положение
точка М перейдет в положение  , тогда ее положение в пространстве будет определяться уже другими координатами
, тогда ее положение в пространстве будет определяться уже другими координатами 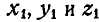 , а следовательно, и другим радиусом-вектором
, а следовательно, и другим радиусом-вектором 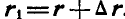 Здесь мы имеем дело с переменным радиусом-вектором, который является функцией скалярного аргумента времени t.
Здесь мы имеем дело с переменным радиусом-вектором, который является функцией скалярного аргумента времени t.
Вообще переменные векторы, зависящие от различных скалярных аргументов, принято обозначать через 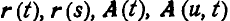 и т. д.
и т. д.
За время 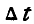 радиус-вектор движущейся точки получит приращение
радиус-вектор движущейся точки получит приращение 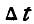 , которое называется геометрическим приращением вектора
, которое называется геометрическим приращением вектора 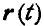 и найдется как геометрическая разность:
и найдется как геометрическая разность:
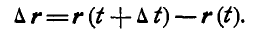
Вектор 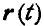 называется непрерывным, если при значении аргумента
называется непрерывным, если при значении аргумента 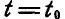 будет выполнено условие:
будет выполнено условие:
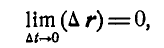
или
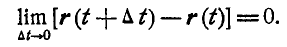
При дальнейших операциях мы будем рассматривать только непрерывные векторные функции. Если для ряда малых промежутков времени 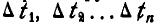 нам известен ряд последовательных положений
нам известен ряд последовательных положений 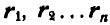 переменного вектора г, то, перенося все векторы
переменного вектора г, то, перенося все векторы 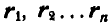 в общее начало О и переходя к пределу при
в общее начало О и переходя к пределу при 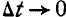 , мы получим плавную кривую, соединяющую концы перенесенных векторов. Эта кривая, будучи непрерывной при непрерывности г, называется годографом вектора г и играет по отношению к вектору г ту же роль, что и график скалярной функции по отношению к координатам х, у и z.
, мы получим плавную кривую, соединяющую концы перенесенных векторов. Эта кривая, будучи непрерывной при непрерывности г, называется годографом вектора г и играет по отношению к вектору г ту же роль, что и график скалярной функции по отношению к координатам х, у и z.
Для движущейся точки М (рис. 15) годографом радиуса-вектора г, определяющего положение точки М, является та кривая, которую описывает точка М при своем движении.
При движении точки М быстрота изменения вектора г будет определяться отношением 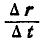 , которое представляет вектор, направленный по
, которое представляет вектор, направленный по 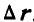 .
.
Переходя к пределу, получим:
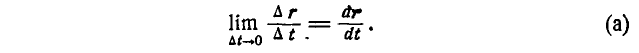
Последнее равенство выражает производную вектора г по скалярному аргументу t. Эта производная является вектором, направленным по касательной к кривой в точке М.
В самом деле, так как вектор г непрерывный, то при 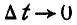 и
и 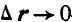 , а поэтому
, а поэтому 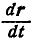 в пределе совпадает с направлением касательной к кривой в данной точке. Если г = const, то
в пределе совпадает с направлением касательной к кривой в данной точке. Если г = const, то 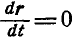 .
.
Рассмотрим теперь основные свойства производных от векторных функций.
Выводы математического анализа, известные для скалярных переменных, могут быть распространены на область переменных векторов, зависящих от скалярных аргументов. Эти выводы, хорошо известные из курса анализа, мы здесь не приводим.
1. Производная суммы векторов равна сумме производных от каждого слагаемого:
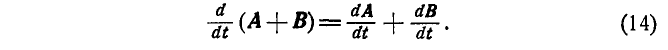
2. Производная от скалярного произведения двух векторов равна произведению первого вектора на производную второго плюс произведение второго вектора на производную первого:
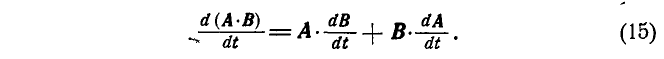
3. Производная от векторного произведения двух векторов находится аналогично предыдущему:
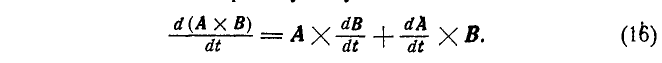
4. Производная от произведения скаляра на вектор находится аналогично (15):
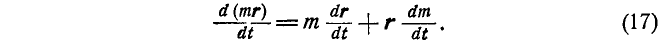
5. Постоянный множитель можно выносить за знак производной:
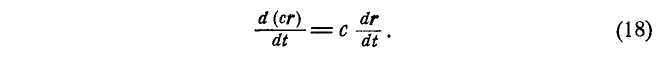
6. Скалярное произведение вектора на его производную равно произведению модуля вектора на производную его модуля:
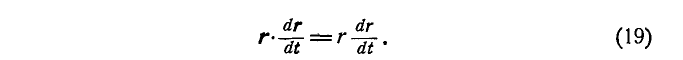
Действительно:
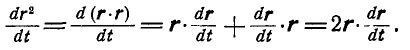
С другой стороны, 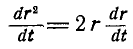 ; но так как
; но так как 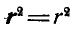 ,
,
то: 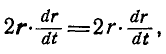
или 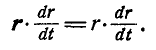
7. Производная вектора, имеющего постоянную величину, равна его модулю, умноженному на производную по скалярному аргументу от угла поворота, и представляет вектор, направленный перпендикулярно данному вектору в сторону его вращения:
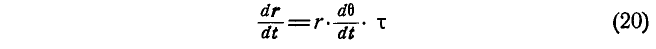
17
гдеτ— единичный вектор, направленный перпендикулярно к вектору г в сторону его вращения.
В самом деле, если модуль вектора вижном начале О вектора г его конец будет описывать окружность с центром в точке О (рис. 16).
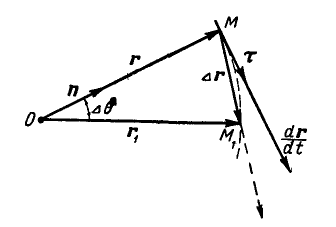
Рис. 16.
При повороте вектора на угол Δθ его конец опишет дугу 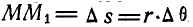 . Производная же вектора г по скалярному аргументу t согласно (а) найдется по выражению:
. Производная же вектора г по скалярному аргументу t согласно (а) найдется по выражению:
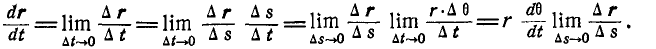
Так как предел отношения длины хорды к длине дуги равен единице, то предел отношения Δг к Δs представляет вектор, численно равный единице и направленный перпендикулярно к вектору г; обозначим его τ. Отсюда получаем равенство (20). В частности производная от единичного вектора n радиуса-вектора г, изменяющего только свое направление, будет равна:
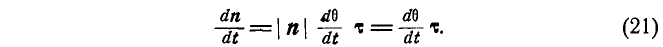
Аналогично находим:
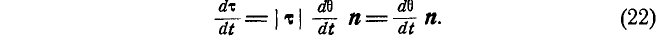
8. Производная вектора г, зависящего от скаляра s, который в свою очередь, зависит от скалярного аргумента t, находится по тем же правилам, что и для сложных скалярных функций:
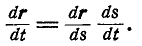
9. Все свойства нахождения производных от векторных функций можно распространить на случай их дифференцирования. Например:
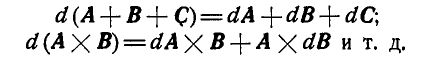
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |