
Векторное и смешанное произведения векторов с примерами решения
Содержание:
Векторное и смешанное произведения векторов в векторной алгебре
Векторное произведение
Определение: Тройка векторов 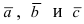
Пример:
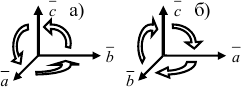
Рис. 13. Правая (а) и левая (б) тройки векторов.
Определение: Векторным произведением векторов 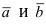 называется вектор
называется вектор 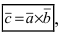 который:
который:
- по модулю численно равен площади параллелограмма, построенного на векторах
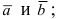
- перпендикулярен плоскости, в которой лежат вектора
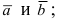
- тройка векторов
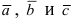 является правой.
является правой.
Замечание: Из определения векторного произведения следует, что направление вектора 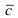 определяется по правилу правого винта: при вращении вектора
определяется по правилу правого винта: при вращении вектора 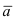 к вектору
к вектору 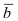 правый винт движется в направлении вектора
правый винт движется в направлении вектора 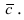 Вычислим площадь параллелограмма, построенного на векторах
Вычислим площадь параллелограмма, построенного на векторах 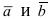 (Рис. 14):
(Рис. 14): 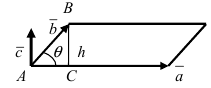
Рис. 14. Площадь параллелограмма, определяющего длину вектора 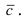 из треугольника АВС высота
из треугольника АВС высота 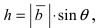 тогда
тогда 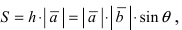 следовательно, длина вектора
следовательно, длина вектора 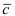 равна
равна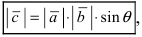 где
где 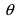 -угол между векторами
-угол между векторами 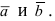
Векторное произведение векторов обладает следующими свойствами:
- 1.
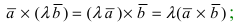
- 2.
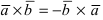 ;
; - 3.
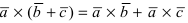 ;
; - 4. Если вектор
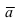 коллинеарен вектору
коллинеарен вектору 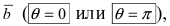 то их векторное произведение равно нулю:
то их векторное произведение равно нулю: 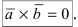
Замечание: Свойство 4. определяет второе условие коллинеарности векторов.
Формула для векторного произведения векторов через проекции перемножаемых векторов
Теорема: Пусть 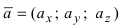 и
и 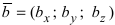 . Тогда
. Тогда 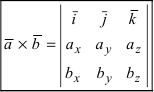
Доказательство: Запишем вектора 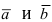 в декартовом базисе:
в декартовом базисе: 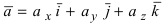 и
и 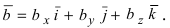 Для доказательства формулы теоремы составим таблицу векторных произведений ортов осей:
Для доказательства формулы теоремы составим таблицу векторных произведений ортов осей:
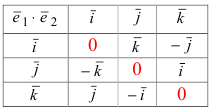
Используя эту таблицу, вычислим векторное произведение векторов 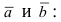
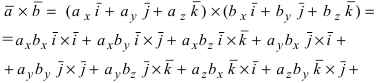
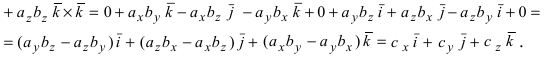
Отсюда следует, что 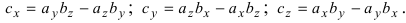 Для запоминания этих формул существует мнемоническое правило: надо запомнить переход проекций от одной к другой (Рис. 15):
Для запоминания этих формул существует мнемоническое правило: надо запомнить переход проекций от одной к другой (Рис. 15):
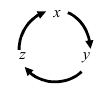
Рис. 15. Циклический переход от одной координаты к другой.
Для нахождения, например проекции 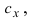 надо взять компонент у первого вектора и умножить на компоненту z второго вектора, а затем вычесть их произведение, обменяв местами обозначение компонент. Аналогично поступают при нахождении двух других проекций вектора
надо взять компонент у первого вектора и умножить на компоненту z второго вектора, а затем вычесть их произведение, обменяв местами обозначение компонент. Аналогично поступают при нахождении двух других проекций вектора 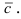 С другой стороны, полученную формулу можно записать в виде
С другой стороны, полученную формулу можно записать в виде
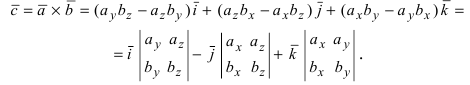
Полученное выражение представляет собой раскрытие определителя III порядка по элементам первой строки, то есть окончательно можно записать, что 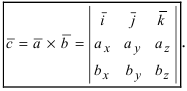
Пример:
Найти, при каком значении параметра m вектор 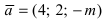 коллинеарен вектору
коллинеарен вектору 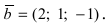
Решение:
Согласно свойству 4. для векторного произведения (пункт 1 Лекция № 6) найдем векторное произведение заданных векторов 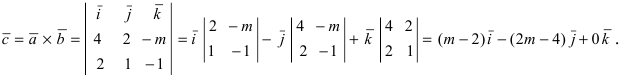
Так как вектор 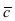 должен быть нулевым, то все его проекции должны быть равными нулю, следовательно, m = 2.
должен быть нулевым, то все его проекции должны быть равными нулю, следовательно, m = 2.
Пример:
Найти векторное произведение векторов 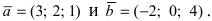
Решение:
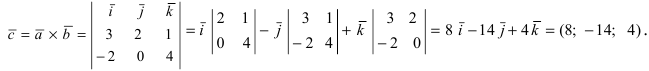
Пример:
Найти векторное произведение векторов 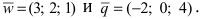
Решение:
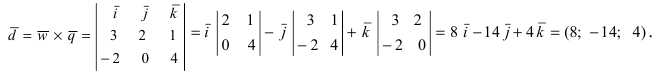
Приложения векторного произведения
1. Физика. Пусть точка начала вектора 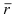 закреплена, а к его концу приложена сила
закреплена, а к его концу приложена сила 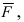 тогда момент этой силы будет равен
тогда момент этой силы будет равен 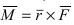 (Рис. 16).
(Рис. 16). 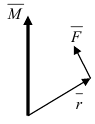 Рис. 16. Момент силы
Рис. 16. Момент силы 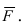
2. Геометрия. Пусть даны три разные точки 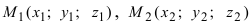 и
и 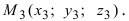 Требуется вычислить площадь треугольника
Требуется вычислить площадь треугольника 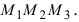
Введем в рассмотрение вектора 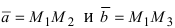 (Рис. 17).
(Рис. 17).
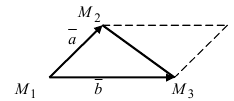
Рис. 17. Площадь треугольника 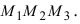
Проекции этих векторов равны:
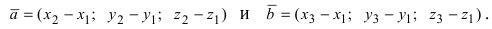
Так как площадь треугольника составляет половину от площади параллелограмма, площадь которого равна модулю векторного произведения векторов 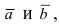 то
то 
Пример:
Даны три точки 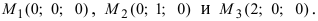 Вычислить площадь треугольника
Вычислить площадь треугольника 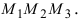
Решение:
Введем в рассмотрение вектора 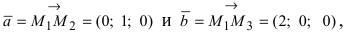 вычислим их векторное произведение
вычислим их векторное произведение 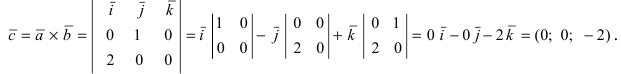 Следовательно, площадь треугольника равна
Следовательно, площадь треугольника равна 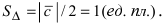
3. Тригонометрия. Выведем формулу для 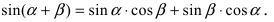
Пусть в плоской декартовой системе координат даны векторы 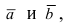 которые образуют с положительным направлением оси Ох углы
которые образуют с положительным направлением оси Ох углы 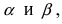 соответственно (Рис. 18):
соответственно (Рис. 18):
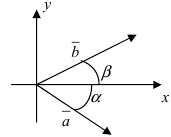
Рис. 18. Синус суммы двух углов.
Проекции векторов равны 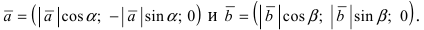 Используя формулу для векторного произведения векторов и свойство 4. для определителей (см. Лекция № 7), получим
Используя формулу для векторного произведения векторов и свойство 4. для определителей (см. Лекция № 7), получим 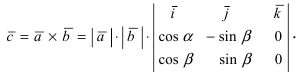 Раскрыв этот определитель по элементам третьего столбца, имеем
Раскрыв этот определитель по элементам третьего столбца, имеем 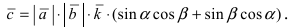
Длина этого вектора равна 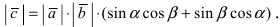 По определению векторного произведения его длина равна
По определению векторного произведения его длина равна 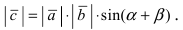 Сравнивая две полученные формулы, получаем формулу для синуса суммы двух углов. В частности, при
Сравнивая две полученные формулы, получаем формулу для синуса суммы двух углов. В частности, при 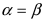 получаем, что синус удвоенного угла равен
получаем, что синус удвоенного угла равен 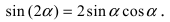
Смешанное произведение векторов
Определение: Смешанным произведением векторов 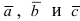 называется число равное векторному произведению
называется число равное векторному произведению 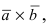 умноженному скалярно на вектор
умноженному скалярно на вектор 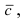 т.е.
т.е. 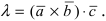
Получим формулу для вычисления смешанного произведения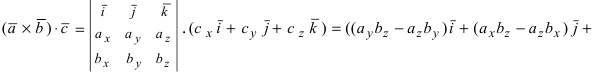
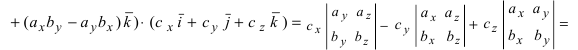
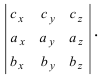
Обменяв местами первую строку со второй, а затем и с третьей, получим окончательную формулу 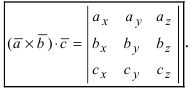
Таким образом, смешанное произведение векторов представляет собой определитель III порядка, откуда следуют его свойства:
1. 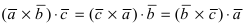 , т.е. вектора, входящие в смешанное произведение, можно циклически перестав.!ять местами, поэтому зачастую смешанное произведение пишут без знаков abc.
, т.е. вектора, входящие в смешанное произведение, можно циклически перестав.!ять местами, поэтому зачастую смешанное произведение пишут без знаков abc.
2. Смешанное произведение векторов 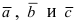 равно объему параллелепипеда, построенного на этих векторах, взятого со знаком «+», если тройка векторов правая, и со знаком «-», если тройка векторов левая (Рис. 19):
равно объему параллелепипеда, построенного на этих векторах, взятого со знаком «+», если тройка векторов правая, и со знаком «-», если тройка векторов левая (Рис. 19):
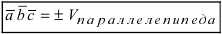
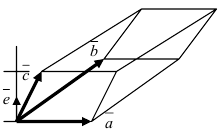
Рис. 19. Объем параллелепипеда, построенного на векторах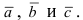
Так как 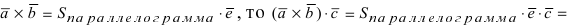
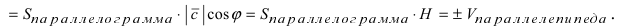
3. Если вектора 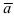 ,
, 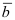 и
и 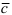 компланарны (лежат в одной плоскости или параллельных плоскостях), то их смешанное произведение равно нулю, т.е.
компланарны (лежат в одной плоскости или параллельных плоскостях), то их смешанное произведение равно нулю, т.е. 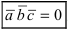 .
.
Замечание: Свойство 3. определяет условие компланарности трех векторов, т.е. если 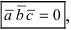 то вектора
то вектора 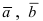 и
и 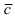 лежат в одной плоскости или параллельных плоскостях.
лежат в одной плоскости или параллельных плоскостях.
Пример:
Доказать, что вектора 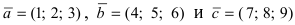 компланарны.
компланарны.
Решение:
Согласно формуле, определяющей смешанное произведение векторов, имеем 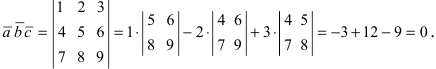
Пример:
Даны 4 точки 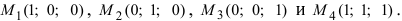 Вычислить объем параллелепипеда.
Вычислить объем параллелепипеда.
Решение:
Составим векторы 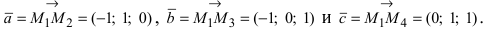 Вычислим объем параллелепипеда
Вычислим объем параллелепипеда 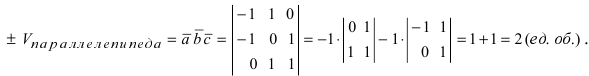 Положительность вычисленного объема указывает на то, что вектора
Положительность вычисленного объема указывает на то, что вектора 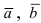 и
и 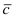 образуют правую тройку.
образуют правую тройку.
Пример:
Чему равен объём пирамиды с вершинами А, В, С и D (координаты точек А, В, С и D взять из VIII.). Найти длину высоту, которая опущена из точки А на основание BCD.
Решение:
Объём пирамиды равен 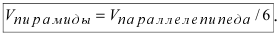 Используя векторы
Используя векторы 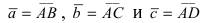 из VIII., которые имеют координаты
из VIII., которые имеют координаты 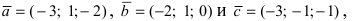 вычислим объём параллелепипеда
вычислим объём параллелепипеда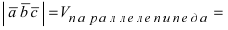
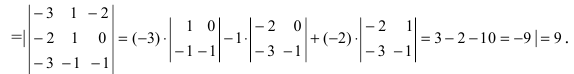 Следовательно, объём пирамиды с вершинами А, В, С и D равен
Следовательно, объём пирамиды с вершинами А, В, С и D равен
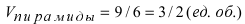
С другой стороны, её объём по формуле из средней школы равен
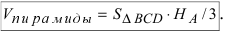
Вычислим площадь треугольника BCD, лежащего в основании пирамиды:  Вычислим векторное произведение этих векторов
Вычислим векторное произведение этих векторов 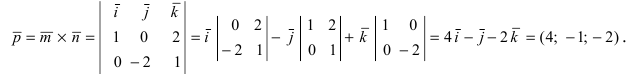 Найдём длину этого вектора
Найдём длину этого вектора 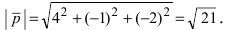 Следовательно, площадь треугольника BCD равна
Следовательно, площадь треугольника BCD равна 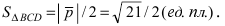 Тогда длина высоты, опущенной из точки А на основание BCD, равна
Тогда длина высоты, опущенной из точки А на основание BCD, равна
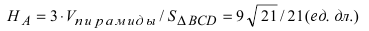
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |