Установившиеся процессы в линейных электрических цепях

Содержание:

Комплексный метод анализа установившихся процессов в линейных электрических цепях:

Анализ (расчет) электрической цепи состоит в определении отклика цепи (реакции) на входящие воздействия. Под воздействием в данном случае понимается включение в цепь источников напряжения и тока. Откликом в общем случае называют все токи в ветвях и все напряжения на пассивных элементах. Следовательно, рассчитать электрическую цепь — значит, найти все токи и все напряжения в этой цепи.

Для упрощения расчет цепи при гармоническом воздействии производится комплексным методом. Он состоит в том, что при расчете все гармонические функции (оригиналы токов, напряжений, источников) заменяют их комплексными изображениями (символами), а все пассивные элементы представляют их комплексными сопротивлениями. После определения комплексных токов и напряжений (изображений откликов) находят их оригиналы (вещественные мгновенные значения) по формуле Эйлера.

Алгебраические действия с комплексными числами

Любое комплексное число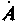

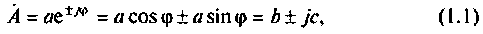
где 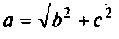— модуль комплексного числа;  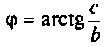— аргумент комплексного числа; 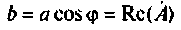— действительная

часть комплексного числа; 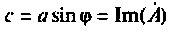— мнимая часть комплексного числа.

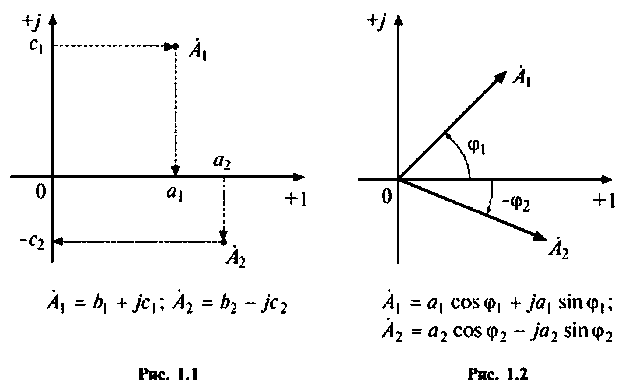
Алгебраическая форма соответствует изображению числа 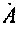 в виде точки на комплексной плоскости в декартовых координатах (рис. 1.1).

Тригонометрическая форма числа 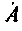соответствует полярной системе координат на комплексной плоскости (рис. 1.2).

Показательная форма записи получается ю тригонометрической по формуле Эйлера

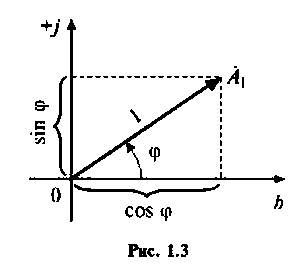
Комплексное число 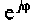изображают на комплексной плоскости вектором (рис. 1.3) с модулем, численно равным единице и составляющим угол 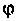с осью вещественных значений (осью 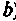). Угол откладывается от вещественной оси против часовой стрелки в случае положительных значений угла 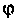и по часовой стрелке при отрицательных значениях .

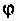При расчетах с помощью комплексных чисел обычно приходится переходить oт одной формы записи к другой. Например, для сложения (вычитания) комплексных чисел применяют алгебраическую форму записи. При этом отдельно складывают (вычитают) действительные и мнимые части чисел.

Показательная форма комплексного числа наиболее удобна для умножения и деления чисел. В этом случае модули чисел перемножают (делят), а аргументы складывают (вычитают).

Пример 1.1.

Даны два комплексных числа: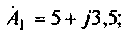

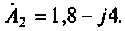
Найти сумму, разность, произведение и частное этих чисел.

Решение 

При сложении чисел получим

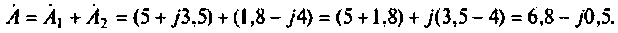
Разность этих чисел определяется по выражению

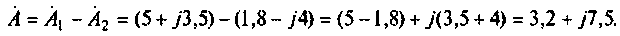
Для умножения и деления числа запишем в показательной форме:

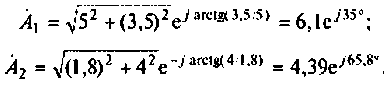
Тогда при умножении

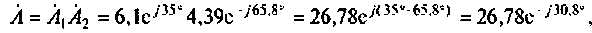
а при делении

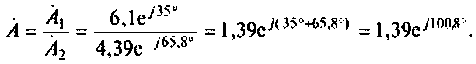
Оригиналы, значения и изображения синусоидальных токов и напряжений

Синусоидальные ток и напряжение а вещественной форме (оригиналы) записываются в виде

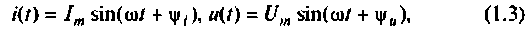
где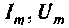 — амплитуды колебаний; 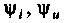— начальные фазы колебаний.

Среднее и действующее значения синусоидально изменяющейся величины. За среднее значение тока и напряжения принимают их среднее значение за полпериода. Среднее значение тока

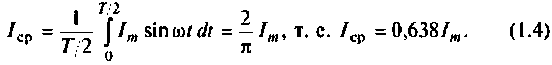
Аналогично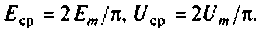

Действующее значение тока

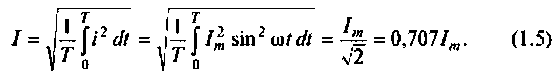
Аналогично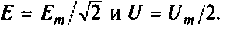

Мгновенные комплексные значения (изображения, символы) синусоидальных тока и напряжения:

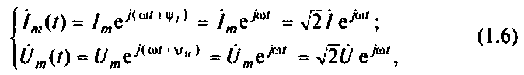
где 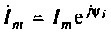— комплексная амплитуда тока; 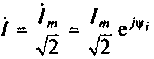— комплексный ток (комплексное действующее значение тока): 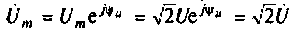— комплексная амплитуда напряжения; 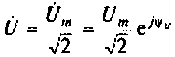—комплексное напряжение (комплексное действующее значение напряжения).
 

Комплексное сопротивление и проводимость цепи

При расчете цели комплексным метолом вводится понятие комплексного сопротивления (проводимости).

Комплексным сопротивлением Z называется отношение комплексного напряжения к комплексному току, вызванному этим напряжением:

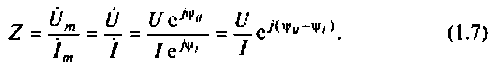
Применяют три формы записи комплексное сопротивления: 

 

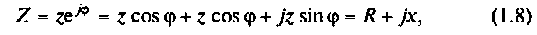
где 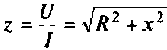— полное сопротивление току; 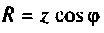— активное сопротивление; 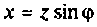— реактивное сопротивление; 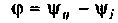— разность фаз напряжения и тока.

Комплексной проводимостью 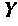 называется отношение комплексного тока к комплексному напряжению

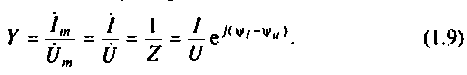
На основании выражения (1.9)

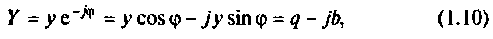
где 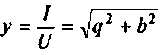—полная проводимость; 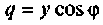—активная проводимость;  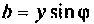— реактивная проводимость.

Составляющие сопротивления и проводимости связаны между собой следующими соотношениями:

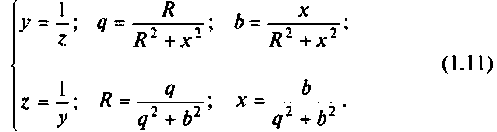
Примечание. Понятия комплексное сопротивление и комплексная проводимость могут относиться ко всей цепи, к части цепи или к ее отдельным элементам.

Основные законы токопрохождения в линейных электрических цепях

Закон Ома: Определяет связь между током, напряжением и сопротивлением пассивного элемента (ветви, участка цепи, цепи). Вещественная форма закона применима только для сопротивления:

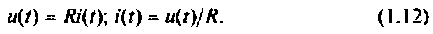
Закон Ома в комплексной форме справедлив для любого пассивного элемента:

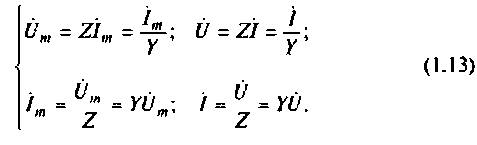
Первый закон Кирхгофа: Определяет баланс токов в любом узле электрической цепи. Его можно представить о вещественной

или в комплексной форме

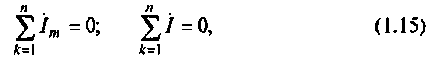
где 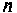— число ветвей, соединенных в данном узле.

Второй закон Кирхгофа. Определяет баланс напряжений в любом замкнутом контуре цепи:

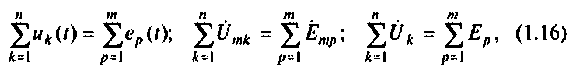
где 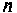— число пассивных элементов в замкнутом контуре: 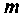—число источников, включенных в данный контур.

Связь между синусоидальными током и напряжением в пассивных элементах

В сопротивлении вещественная форма записи связи между током и напряжением определяется по закону Ома:

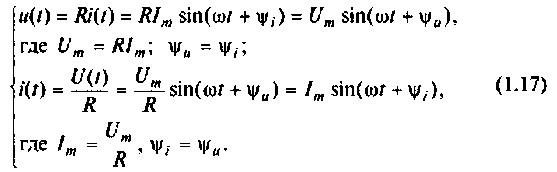
В комплексной форме (изображения) определяются выражениями:

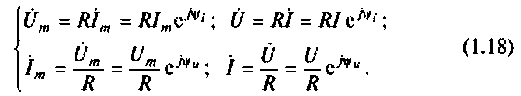
В сопротивлении ток и напряжение всегда синфазны, т. е.

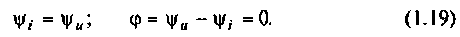
В индуктивности напряжение и ток связаны соотношениями:

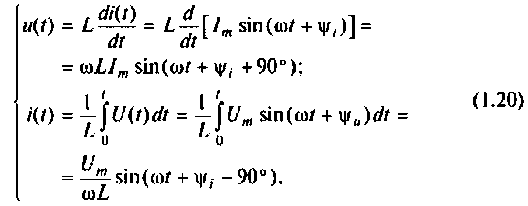
Запишем эти выражения в комплексной форме:

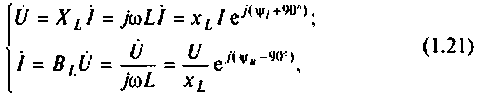
где 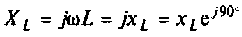— комплексное сопротивление индуктивности; 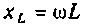— индуктивное сопротивление;

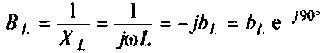— комплексная проводимость индуктивности;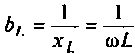— индуктивная проводимость.

Из формул (1.20) и (1.21) видно, что ток в индуктивности отстает по фазе от приложенного напряжения на угол .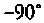

В емкости напряжение и ток связаны соотношениями:

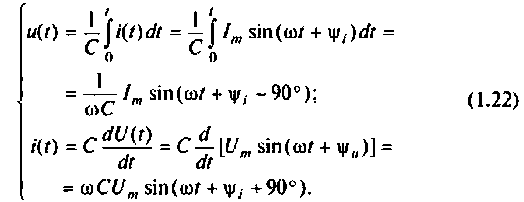
В комплексной форме выражения (1.22) принимают вид:

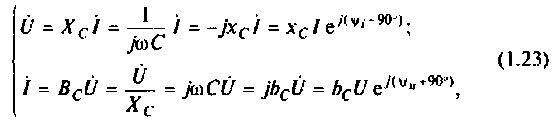
где 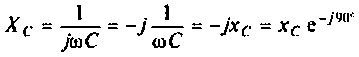— комплексное сопротивление емкости; 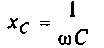— емкостное сопротивление; 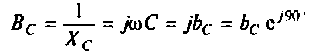— комплексная проводимость емкости; 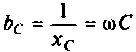— емкостная проводимость.

Из формул (1.22) и (1.23) видно, что ток в емкости опережает по фазе приложенное напряжение на угол .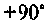

Диаграммы токов и напряжений

Для большей наглядности при анализе процессов и расчете пеней используют временные и векторные диаграммы.
    

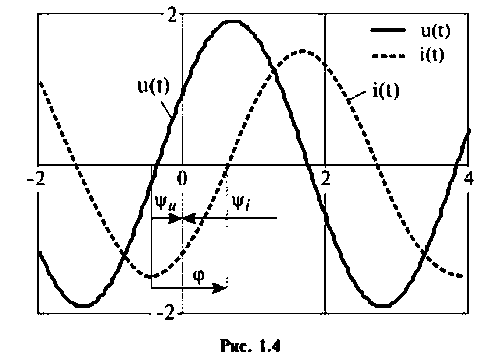
Временной диаграммой называют графики мгновенных значений токов и напряжений на координатной плоскости вдоль вещественной оси времени (рис. 1.4). Начальная фаза отчитывается ох нуля синусоиды (или от максимума косинусоиды) к началу координат. Начальная фаза положительная, если направление отсчета совпадает с направлением оси времени.

Фазовый сдвиг напряжения и тока отсчитывается по направлению от нуля напряжения к нулю тока. Если это направление совпадает с направлением оси времени, то фазовый сдвиг положительный.

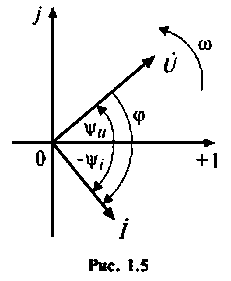
Векторной диаграммой называют совокупность векторов, построенных на комплексной плоскости с соблюдением взаимной ориентации по фазе. Длина вектора пропорциональна aмплетуде колебания.

Все векторы во времени вращаются против часовой стрелки со скоростью 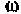. На рис.1.5 показана векторная диаграмма, соответствующая временной диаграмме, приведенной на рис. 1.4.

Начальная фаза отсчитывается от вещественной оси к вектору. Фазовый сдвиг отсчитывается от вектора тока к вектору напряжения. Начальная фаза и фазовый сдвиг положительны, если направление их отсчета совпадает с направлением вращения вектора (против часовой стрелки).

Мощность в цепи синусоидального тока

Произведение p(t) мгновенного значения приложенного к цепи напряжения u(t) на мгновенное значение протекающего по ней тока i(t) называется мгновенной мощностью [14].

Для напряжений и токов, изменяющихся по синусоидальному закону, получаем

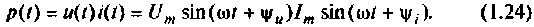
После выполнения тригонометрических преобразований получим

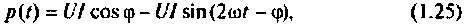
где 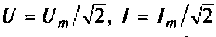— действующие значения напряжения и тока; 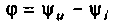— фазовый сдвиг между мгновенными значениями напряжения и тока.

Из выражения (1.25) видно, что мгновенная мощность в цепи синусоидального тока имеет постоянную и переменную составляющую, изменяющуюся во времени с удвоенной частотой.

Среднее значение мгновенной мощности за период

называют активной мощностью.

Для цепи синусоидального тока

т.е. активная мощность в цепи с синусоидальным током и напряжением равна произведению действующих напряжений, тока и косинуса угла фазового сдвига между напряжением и током. Она характеризует энергию, которая передается от источника к нагрузке, где она превращается в другие виды энергии. Активная мощность измеряется в ваттах (Вт). Множитель 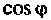называют коэффициентом мощности. Чем больше 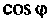, тем больше активная мощность при заданных значениях U и I. Для определения активной мощности применяются соотношения

где R и q — активное сопротивление и активная проводимость цепи.

Величину, равную при синусоидальном токе и напряжении произведению действующих значении напряжения, тока и синуса угла фазового сдвига между напряжением и током, называют реактивной мощностью

Реактивная мощность характеризует энергию, которая периодически циркулирует между источником и нагрузкой. Она измеряется в вольт-амперах реактивных (вар). При 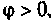 т.е. при индуктивной нагрузке, реактивная мощность положительна, а при 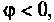т.е. при емкостной нагрузке, — отрицательна. Для определения реактивной мощности применяются соотношения

где х и b — реактивное сопротивление и реактивная проводимость цепи.

Величину, равную произведению действующих значений напряжения U и тока I называют полной мощностью

Полная мощность измеряется в вольт-амперах 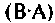и характеризует предельную активную мощность источника при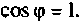

Учитывая, что 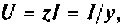 получаем

где z и у — полное сопротивление и полная проводимость цели.

Сложив квадраты активной (1.27) и реактивной (1,29) мощностей, получим

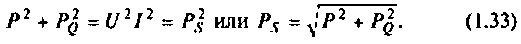
Из выражений (1.27) и (1.29) получим

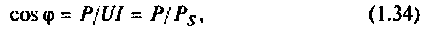
т.е. коэффициент мощности 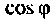показывает, какую часть от полной мощности составляет активная мощность.

Произведение комплексного напряжения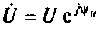 комплексный сопряженный ток 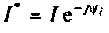называют комплексной мощностью

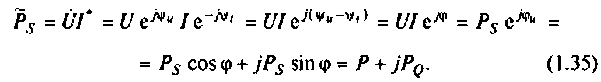
Из этого выражения видно» что вещественная часть комплексной мощности является активной, а мнимая — реактивной мощностью.

Особое обозначение комплексной мощности 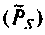выбрано для того чтобы подчеркнуть условный характер этой комплексной величины, так как от комплексной мощности нельзя перейти к ее мгновенному значению таким образом, как это делается для токов и напряжений. Эта величина вводится только для облегчения решения задачи [14].

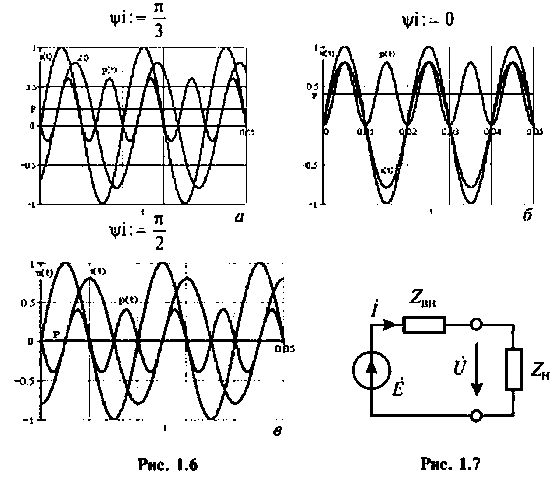
Графики мгновенной мощности, напряжения и тока для трех различных значений фазового сдвига между напряжением и током, выполненные в среде Mathcad, приведены на рис. 1.6.

При 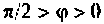(рис.1.6,а) мгновенная мощность p(t) изменяется по синусоидальному закону относительно прямой 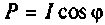с частотой, вдвое большей частоты тока и напряжения, имея положительные и отрицательные участки. Положительные значения мощности соответствуют поступлению энергии в цепь, где она частично запасается в электрических полях конденсаторов и магнитных полях индуктивных катушек и частично расходуется в цепи, выделяясь в виде тепла в активных сопротивлениях или преобразуясь в другие виды энергии (механическую, химическую и т.д.). Отрицательные значения мощности соответствуют возвращению энергии, запасенной в цепи, в источник. В рассмотренном случае энергия, поступающая от источника в цепь, больше энергии, возвращаемой из цепи к источнику, так как часть ее расходуется в цепи.

Программа построения графиков к рис. 1.6:

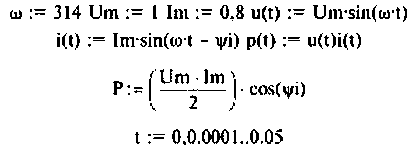
При 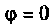(рис.1.6,б) мгновенная мощности изменяется по синусоидальному закону относительно прямой 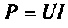также с удвоенной частотой, являясь нее время положительной. Энергия в этом случае только поступает в цепь. Такая цепь по отношению к ее входным зажимам эквивалентна цепи, содержащей только активные сопротивления. Если же в цепи фазовый сдвиг 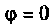и имеются конденсаторы и индуктивные катушки, например при резонансе напряжений, то между ними происходит взаимный обмен энергией без возвращения к источнику.

При 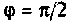(рис.1.6,в) 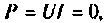а мгновенная мощность изменяется по гармоническому закону относительно оси времени и 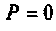также с удвоенной частотой. Положительные и отрицательные участки мощности равны между собой. Следовательно, в этом случае вся энергия, поступившая и цепь, обращается обратно в источник. Такая цепь содержит лишь идеальные L- и С-элементы.

Определим условия передачи максимальной активной мощности от источника в нагрузку. Для этого рассмотрим цепь синусоидального тока (рис.1.7), состоящую из источника ЭДС Е с внутренним сопротивлением 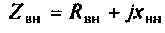и нагрузки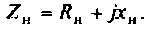 

Действующий ток в рассматриваемой цепи

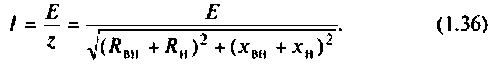
Активная мощность в нагрузке

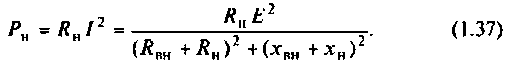
Из этого выражение видно, что первым условием передачи максимальной активной мощности от источника в нагрузку является 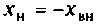, т. е. равенство по величине и противоположность знаков реактивных сопротивлении источника и нагрузки. При выполнении этого условия из выражения (1.37) получим

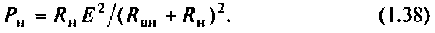
Взяв производную от лого выражения по 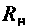и приравняв сс к нулю, получим второе условие: 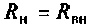, т, е. активное сопротивление нагрузки должно быть равно активному сопротивлению источника.

Таким образом, для получения максимальной активной мощности на нагрузке при заданных параметрах источника необходимо, чтобы сопротивление нагрузки было комплексно-сопряженным с внутренним сопротивлением источника, т.е. активное сопротивление нагрузки 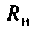должно быть равно активному сопротивлению источника а реактивные сопротивления должны быть равны по величине и иметь противоположные знаки. Активная мощность на нагрузке в этом случае будет максимальной и равной 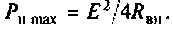При этом коэффициент полезного действия будет равен

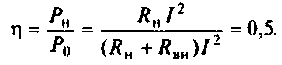
Сопротивление нагрузки, при котором на ней получается максимальная активная мощность, называется согласованным. Режим в цепи в этом случае также называют согласованным.

Пример 1.2.1. 

Электрическая цепь образована последовательным соединением двух участков из пассивных элементов. Определить напряжение на входе цепи, ее сопротивление и проводимость, если ток в цепи 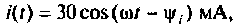а напряжения на элементах равны: 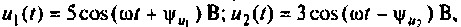где 

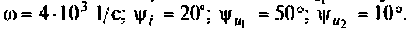
Построить векторную диаграмму токов и напряжений, составить схему электрической цепи.

Решение

1. Рассчитаем входное напряжение.

При последовательном соединении элементов общее (входное) напряжение равно сумме напряжений на элементах. В данном случае

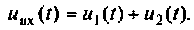
Воспользуемся комплексным методом и найдем изображения мгновенных напряжений:

Отсюда получим комплексные амплитуды напряжений:

Тогда комплексная амплитуда напряжения на входе электрической цепи

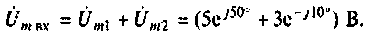
Запишем слагаемые в алгебраической форме:

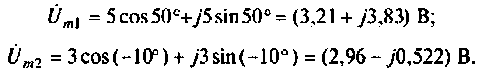
После суммирования 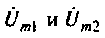получим

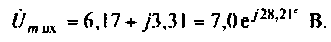
Найдем оригинал (мгновенное значение) напряжении. Для этого умножим 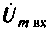на оператор вращения  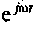и по формуле Эйлера определим реальную часть (так как исходное напряжение есть функции косинуса) комплексного числа.

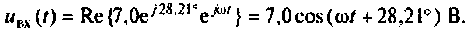
Примечание. Сравнивая напряжения 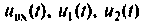или их комплексные амплитуды, легко увидеть, что второй закон Кирхгофа так же, как и первый, справедлив для мгновенных значений и не выполняется для амплитудных значений.

2. Определим сопротивление и проводимость цепи и ее элементов.

Комплексная амплитуда тока

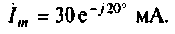
Тогда по закону Ома получим

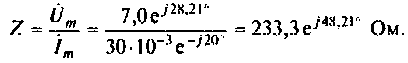
Следовательно, полное сопротивление току z=233,3 Ом. Соответственно активное и реактивное сопротивления:

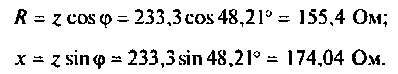
Найдем сопротивление элементов. В последовательной цепи в каждом элементе течет один и тот же ток, поэтому:

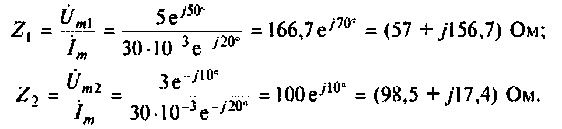
Найдем проводимости в цепи:

комплексная проводимость

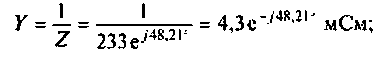
полная проводимость

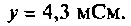
Активная и реактивная проводимости соответственно:

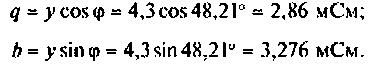
Аналогично найдем комплексные проводимости элементов:

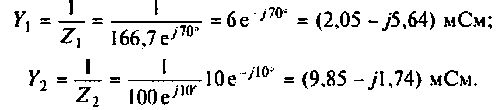
3. Построим векторную диаграмму тока и напряжений (рис. 1.8).

        
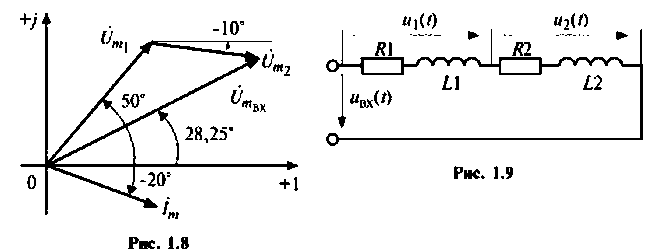
4. Составим схему электрической цепи (рис. 1.9).

Пример 1.2.2.

На вход электрической цепи подано напряжение 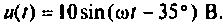 Рассчитать ток на входе и мощности в цепи, если ее комплексное сопротивление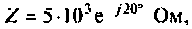

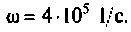
Решение

1. Рассчитаем ток в цепи.

Запишем комплексную амплитуду (изображение) напряжения в виде

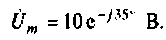
По закону Ома рассчитаем комплексную амплитуду тока и цепи

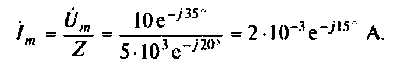
Умножим комплексную амплитуду тока на оператор вращения, и по формуле Эйлера (1.2) найдем оригинал тока (мгновенное значение)

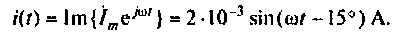
2. Рассчитаем мощность в цепи.

Найдем составляющие комплексною сопротивления:

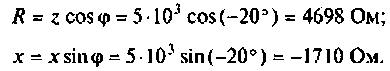
Следовательно, потребляемая активная мощность в цепи 

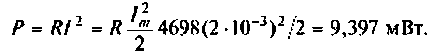
Реактивная мощность и цепи

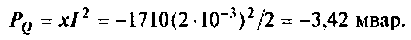
Полная мощность цепи

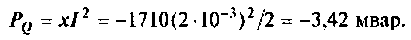
Примечание. Мощность в цепи можно рассчитать другим путем:

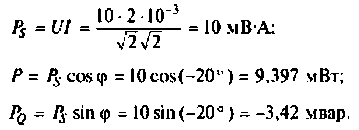
Пример 1.2.3.

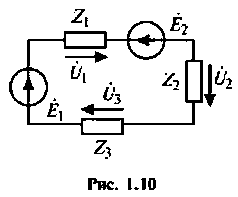
Рассчитать ток в электрической цепи (рис. 1.10), напряжение 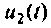и построить векторную диаграмму токов и напряжений.

Дано: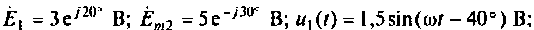

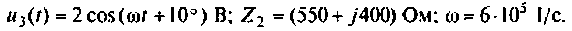
Решение

1. Рассчитаем напряжение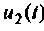 Запишем напряжение  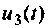как функцию синуса

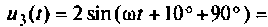
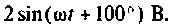
Перейдем к комплексным изображениям амплитуд напряжений:

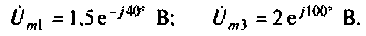
Запишем второй закон Кирхгофа  для замкнутого контура

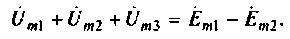
Отсюда получаем

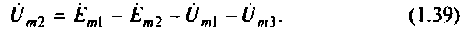
Комплексные величины вычитаются и складываются и алгебраической форме. Поэтому все комплексные амплитуды запишем в алгебраической форме:

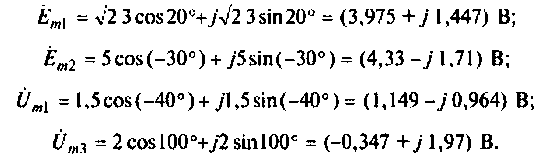
Подставим эти значения в (1.24) и после суммирования получим

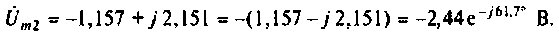
Отрицательная амплитуда свидетельствует о том, что направление напряжения необходимо изменить на противоположное. Поэтому изменим начальную фазу на 180° и тогда

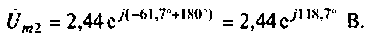
Такой же результат можно получить формальным преобразованием но формуле Эйлера

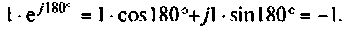
Перейдем к оригиналу напряжения

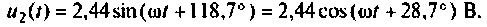
2. Рассчитаем ток в цепи.

При последовательном соединении во всех элементах цепи течет один и тот же ток. Известно сопротивление 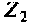и найдено напряжение на нем. Поэтому по закону Ома

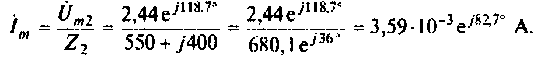
Следовательно

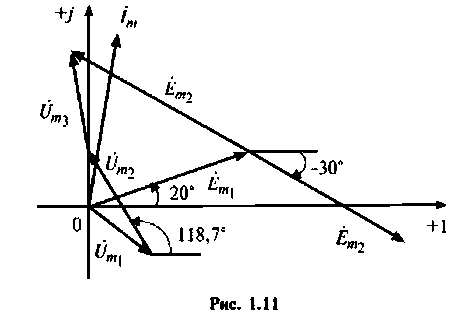
Векторная диаграмма показана на рис. 1.11. При построении векторной диаграммы учтено, что второй источник направлен противоположно первому. Поэтому начальная фаза 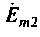изменена на 180°.