Условия равновесия системы сил в теоретической механике

Содержание:

Условия равновесия системы сил:

Условия равновесия системы сил в векторной форме

Из теоремы о приведении системы сил к силе и паре сил можно вывести условия равновесия системы сил, действующих на твердое тело. Очевидно, что если система сил находится в равновесии, то в равновесии находится и эквивалентная ей система, состоящая из силы и пары сил. Чтобы такая система сил была эквивалентна _ нулю, необходимо и достаточно равенства нулю как силы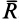

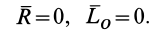
Условия (11) являются векторными условиями равновесия для любой системы сил.

Условия равновесия пространственной системы сил в аналитической форме

Если при равновесии системы сил, приложенных к твердому телу, главный вектор 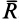равен нулю, то его проекция на каждую координатную ось также равна нулю. Это справедливо и для главного момента 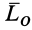. Таким образом, из векторных условий равновесия пространственной системы сил следует шесть условий:

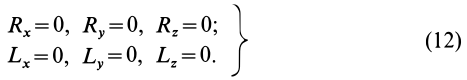
Учитывая формулы (5) и (7), эти шесть условий через силы системы выражают в форме

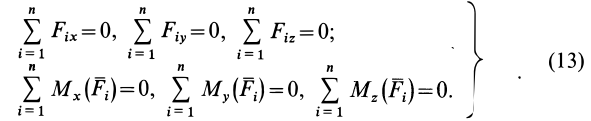
Таким образом, для равновесия пространственной системы сил, приложенных к твердому телу, необходимо и достаточно, чтобы три суммы проекций всех сил на оси декартовых координат были равны нулю и три суммы моментов всех сил относительно трех осей координат также были равны нулю.

Из общих условий равновесия для произвольной пространственной системы сил получаются условия равновесия для частных систем сил, приложенных к твердому телу.

Условия равновесия пространственной системы параллельных сил

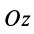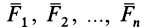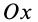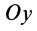Направим ось параллельно силам (рис. 37). Тогда проекции параллельных сил на перпендикулярные им оси и будут равны нулю и условия

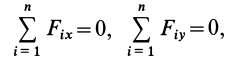
окажутся справедливыми для всех систем параллельных сил, т. е. превратятся в тождества. Момент относительно оси 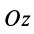каждой из параллельных сил равен нулю, и условие 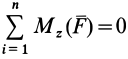тоже выполняется для всех систем параллельных сил. Отбрасывая

условия равновесия, которые выполняются тождественно при выбранном направлении оси 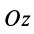, и учитывая, что сумма проекций сил на эту ось является алгебраической суммой сил, из (13) получаем следующие три условия равновесия пространственной системы параллельных сил:

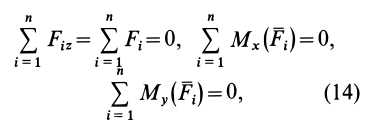
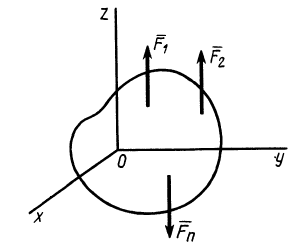
Рис. 37

т. е. для равновесия пространственной системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма этих сил была равна нулю и суммы моментов сил относительно двух координатных осей, перпендикулярных силам, также были равны нулю.

• Заказать решение задач по теоретической механике

Условия равновесия плоской системы сил

Расположим ос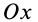и и 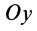в плоскости действия сил (рис. 38). Так как ось  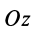перпендикулярна силам, то  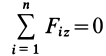выполняется для всех плоских систем сил, т. е. является тождеством. Каждая из сил расположена в одной плоскости с осями координат 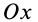и 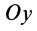, и поэтому ее моменты относительно этих осей равны нулю. Таким образом, условия равновесия

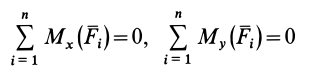
становятся тождествами. Моменты сил относительно оси 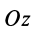, перпендикулярной силам, равны алгебраическим моментам этих сил относительно точки 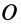. Таким образом,

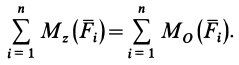
Из (13) для плоской системы сил после отбрасывания тождеств имеем следующие три условия равновесия:

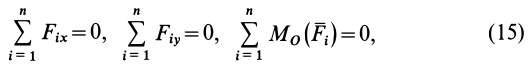
т. е. для равновесия плоской системы сил, действующих на твердое тело, необходимо и достаточно, чтобы суммы проекций этих сил на каждую из двух прямоугольных осей координат, расположенных в плоскости действия сил, были равны нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости действия сил, также была равна нулю.

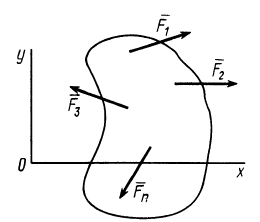
Рис. 38

Для плоской системы параллельных сил (рис. 39) одну из осей координат, например 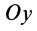, можно выбрать параллельной силам. Тогда сумма проекций параллельных сил на эту ось превратится в алгебраическую сумму сил. Проекция каждой из сил на ось 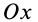равна нулю; следовательно, сумма проекций сил на ось 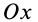равна нулю, даже если система сил не находится в равновесии. Это условие выполняется тождественно, и его следует отбросить.

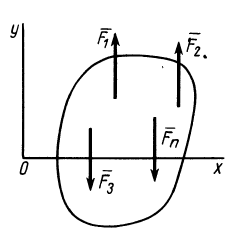
Рис. 39

Итак, для плоской системы параллельных сил из (15) имеем следующие условия равновесия:

т. е. для равновесия плоской системы параллельных сил, приложенных к твердому телу, необходимо и достаточно, чтобы алгебраическая сумма сил была равна нулю и сумма алгебраических моментов сил относительно любой точки, находящейся в плоскости сил, также была равна нулю.

Из условий равновесия плоской системы сил (15) можно получить и условия равновесия плоской системы сходящихся сил, для чего за моментную точку надо взять точку пересечения линий действия сходящихся сил. Тогда последнее из условий станет тождеством и в качестве условий равновесия для плоской системы сходящихся сил останутся только два первых условия из (15).