
Условие равновесия системы сходящихся сил в геометрической форме в теоретической механике
Условие равновесия системы сходящихся сил в геометрической форме:
Систему сил, линии действия которых пересекаются в одной точке, называют системой сходящихся сил, или пучком сил
Метод последовательного сложения сил
Изучение статики начнем с простейшего случая, а именно с системы сходящихся сил, т. е. таких сил, приложенных к твердому телу, линии действия которых пересекаются в одной точке. Всякую силу можно переносить вдоль линии действия. Мы имеем право перенести все эти силы в точку пересечения их линий действия и рассматривать систему сходящихся сил как пучок сил, приложенных к одной материальной частице. Если все силы расположены в одной плоскости, то пучок называют плоским пучком сил, или плоской системой сходящихся сил, в противном случае пучок, называют пространственным.
Одной из задач статики является преобразование систем сил в системы, им эквивалентные. Неуравновешенная система сходящихся сил может быть заменена одной силой, эквивалентной данной системе сходящихся сил и называемой равнодействующей пучка сил. Определить величину и направление равнодействующей, или, как говорят, привести систему сходящихся сил к равнодействующей, можно различными способами.
Познакомимся сначала со способом последовательного сложения сил пучка по правилу параллелограмма.
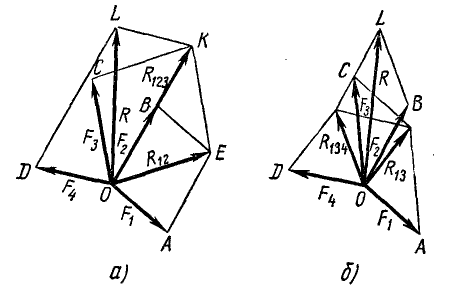
Пусть дана система нескольких сил (например, четырех сил), линии действия которых пересекаются в точке О. Перенеся все силы κ этой точке, изобразим их (рис. 7, а) в некотором масштабе векторами: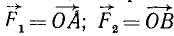
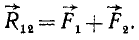
Мы имеем теперь систему трех сил 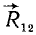 ,
, 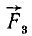 и
и 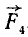 , эквивалентную системе четырех сил
, эквивалентную системе четырех сил 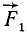 ,
, 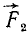 ,
,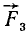 и
и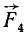 .
.
Складывая по правилу параллелограмма силу 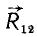 с какой-либо из оставшихся сил пучка, например с силой
с какой-либо из оставшихся сил пучка, например с силой 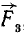 , и заменяя обе эти силы одной силой
, и заменяя обе эти силы одной силой 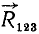 изображаемой диагональю
изображаемой диагональю 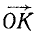 параллелограмма OCKE, мы получим систему двух сил
параллелограмма OCKE, мы получим систему двух сил 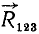 и
и 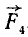 , причем
, причем
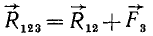
или, имея в виду предыдущее равенство,
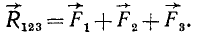
Складывая по закону параллелограмма 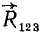 и
и 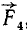 , найдем равнодействующую всей системы четырех сходящихся сил:
, найдем равнодействующую всей системы четырех сходящихся сил:
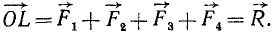
Этим методом последовательного сложения можно найти равнодействующую любого количества сходящихся сил, в частности пространственной системы сходящихся сил, поскольку всякие две силы пространственного пучка обязательно лежат в какой-либо плоскости (две пересекающиеся прямые всегда лежат в одной плоскости), а равнодействующая двух этих сил лежит в какой-либо плоскости со всякой другой силой пучка. Символически это записывают так:
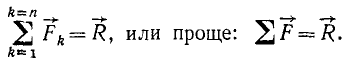
Как видно из хода нашего доказательства, последовательность, в которой силы пучка складывают по правилу параллелограмма, не влияет на результат, т. е. от перемены мест слагаемых геометрическая сумма не изменяется (рис. 7, а и б).
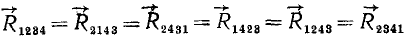 и т. д.
и т. д.
При построении силового многоугольника складываемые силы чертят последовательно одну за другой так, чтобы начало каждого вектора совладало с концом предыдущего. Начало вектора равнодействующей совпадает с центром пучка, а конец — с концом последнего приложенного вектора
Метод силового многоугольника. Взглянув на чертеж (рис. 7, а), нетрудно заметить, что, складывая силы пучка по методу последовательного применения правила параллелограмма, мы провели на этом чертеже много лишних линий. Для нахождения равнодействующей OL можно было не чертить линии BE, OE, СК, OK, DL.
Равнодействующую OL можно найти значительно проще. Для этого нужно от конца одного из слагаемых векторов, например от точки А (рис. 8), отложить вектор, равный и параллельный вектору какой-либо другой из слагаемых сил, например 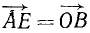 . Этим положение точки E вполне определено и нет надобности чертить линии BE и OE предыдущего чертежа. Если складывать силы в той же последовательности, какой мы только что придерживались (см. рис. 7, а), то для нахождения точки К надо отложить от точки E вектор
. Этим положение точки E вполне определено и нет надобности чертить линии BE и OE предыдущего чертежа. Если складывать силы в той же последовательности, какой мы только что придерживались (см. рис. 7, а), то для нахождения точки К надо отложить от точки E вектор 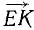 , равный вектору
, равный вектору 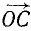 , а для нахождения точки L нужно лишь отложить от точки К вектор
, а для нахождения точки L нужно лишь отложить от точки К вектор 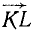 , равный вектору
, равный вектору 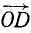 . Но коль скоро точка L найдена, то для нахождения равнодействующей остается только провести вектор
. Но коль скоро точка L найдена, то для нахождения равнодействующей остается только провести вектор 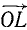 .
.
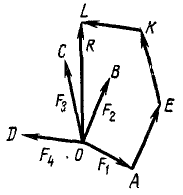
Рис. 8
Таким образом, для приведения системы сходящихся сил к равнодействующей нужно от конца вектора одной из сил пучка отложить вектор, равный вектору какой-либо другой силы пучка, от его конца отложить вектор, равный вектору какой-либо третьей силы пучка, и т. д., пока не будут таким образом отложены все силы системы. Для нахождения равнодействующей системы сил нужно соединить центр пучка с концом последнего отложенного вектора.
Ломаную OAEKL называют силовым многоугольником.
Последовательность, в которой прикладывают эти векторы друг к другу, не имеет значения, так как геометрическая сумма подчиняется закону переместительности, т. е. не зависит от перемены мест слагаемых. Но нужно твердо помнить, что векторы прикладывают так, чтобы начало каждого последующего приложенного вектора совпадало с концом предыдущего. Тогда, обходя последовательно вершины силового многоугольника OAEKL, будем все время передвигаться в направлении, указанном стрелками, и только равнодействующая 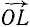 направлена иначе: в точке L она соединяется с вектором
направлена иначе: в точке L она соединяется с вектором 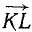 концами, а в точке 0 (в центре пучка)—с вектором
концами, а в точке 0 (в центре пучка)—с вектором  началами.
началами.
Способ силового многоугольника справедлив для всякой системы векторов, приложенных к одной точке, однако он удобнее в применении к плоским пучкам, так как плоские графические построения просты и наглядны.
Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут
Условие равновесия пучка сил в геометрической форме
Система сходящихся сил всегда может быть приведена к равнодействующей R, за исключением одного случая: R = O. Этот случай имеет особое значение для статики и на нем необходимо остановиться подробнее. Если равнодействующая пучка сил равна нулю, то, следовательно, эквивалентна нулю и вся система сходящихся сил, т. е. наличие системы эквивалентно ее отсутствию. Такие системы мы назвали уравновешенными. Следовательно, если равнодействующая системы сходящихся сил равна нулю, то система находится в равновесии. Очевидно, что справедливо и обратное заключение: если система сил находится в равновесии, то равнодействующая системы равна нулю.
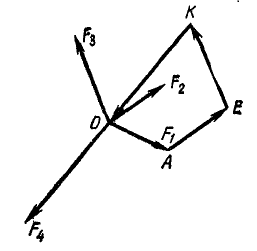
Рис. 9
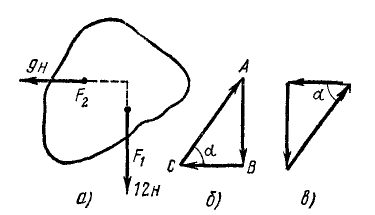
Рис. 10
В силовом многоугольнике равенство нулю равнодействующей выражается в том, что конец вектора последней силы совпадает с началом вектора первой силы, т. е. многоугольник является замкнутым. Замкнутость силового многоугольника является необходимым и достаточным условием равновесия пучка сил в геометрической форме. Такой случай изображен на рис. 9 и может быть записан так:
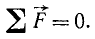 (2)
(2)
Задача №1
Тело находится в покое под действием трех сил, одна из которых F1 = 12 н и направлена вертикально вниз, другая F2 = 9 н и направлена горизонтально влево. Определить величину и направление третьей силы (рис. 10, а).
Решение. Приступая к решению какой бы то ни было задачи, нужно внимательно прочитать условие, обязательно уяснить, что именно требуется определить, наметить ход решения и уже после этого приступать к вычислениям.
В данной задаче тело находится под действием трех сил, две из которых даны, а третью требуется найти Тело покоится, следовательно, система действующих на него сил находится в равновесии. Так как сил только три и они непараллельны и взаимно уравновешены, то линии действия их пересекаются в одной точке, т. е. мы имеем пучок сил.
Теперь нетрудно наметить ход решения: рассмотреть равновесие пучка трех сил, действующих на тело, составить силовой многоугольник (треугольник), из которого определить неизвестную силу.
Последовательность, в которой расположены силы многоугольника, не имеет принципиального значения, однако начинать построение следует всегда с известных сил. Чертим вектор силы АВ= 12 н и от его конца—вектор силы BC = 9 н, причем желательно соблюдать масштаб (рис. 10, б). Но на тело действует еще одна (неизвестная) сила, и силовой многоугольник должен быть замкнутым. Следовательно, эта сила должна изображаться отрезком CA.
Треугольник ABC прямоугольный, а потому
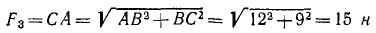
и
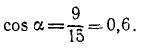
Ответ. F3 = 15 н (1,53 кГ), направлена вправо и вверх под углом а — arccos 0,6 к горизонтали и проходит через точку пересечения линий действия двух данных сил.
Тот же результат мы получили бы, если бы раньше начертили силу ВС, а от ее конца провели бы силу AB (рис. 10, в).
Задача №2
К вертикальной гладкой стене AB подвешен однородный шар О на веревке АС. Веревка составляет со стеной угол а, вес шара Р. Определить натяжение веревки T и давление Q шapa на стену (рис. 11, а).
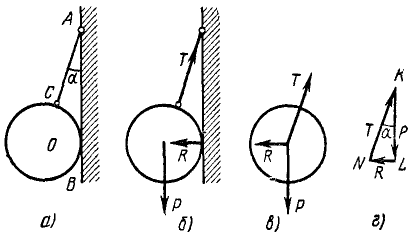
Рис. 11
Решение. Первый вопрос, который, решая задачу по статике, следует перед собой поставить, почти всегда бывает один и тот же:
1) равновесие какого объекта (точки, тела) нужно рассмотреть?
Ответить на этот вопрос не всегда бывает просто. В данной задаче обе искомые силы (Q и Т) действуют на стену: шар давит на стену с силой Q, а натяжение веревки, прикрепленной в точке А стены, действует на стену по направлению веревки вниз. Между тем за отсутствием всех необходимых данных (вес и размеры стены, реакции фундамента и т. п.) мы не имеем возможности рассматривать равновесие стены, а потому будем рассматривать равновесие шара, так как в условии задачи относительно него приведены необходимые данные; вес ею известен, на него действуют натяжение T веревки и давление (реакция) стены, равное и противоположное давлению шара Q на стену. Итак, на первый вопрос отвечаем: рассматриваем равновесие шара.
Второй вопрос, который нужно поставить при решении задачи по статике, тоже является почти трафаретным:
2) какие силы действуют на этот объект?
Отвечая на этот вопрос, нужно перечислить все силы, действующие на тело, и по возможности указать их точки приложения, направления и величины. На шар действуют (рис. 11, б):
- а) вес P шара. Эта сила приложена к центру шара и направлена по вертикали вниз;
- б) реакция стены, т. е. сила, с которой действует на шар тело, осуществляющее связь (стена). Эта реакция (обозначим ее R) приложена в той точке шара, в которой осуществляется связь, т. е. в точке касания, и направлена от стены к шару перпендикулярно плоскости виртуальных перемещений шара. Виртуальными перемещениями шара (воображаемыми малыми перемещениями шара, не нарушающими его связи со стеной) являются перемещения шара вдоль вертикальной стены, а потому реакция R стены направлена горизонтально от стены к центру шара;
- в) натяжение T веревки, соединяющей точку C на шаре и точку А на стене. Натяжение веревки, действующее на шар, приложено к шару в точке C и направлено вдоль веревки от C по направлению к А.
Шар О находится в равновесии под действием трех сил, следовательно, линии действия всех трех сил должны пересекаться в одной точке (рис. 11, в). Этой точкой является центр О шара.
Силовой многоугольник системы сил, пересекающихся в центре О, должен быть замкнут. Построение силового многоугольника начнем с известной силы Р, отложив вертикальный отрезок KL, изображающий вес шара (Рис. 11, г). Остальные силы пучка известны нам только по направлению. Отложим от точки L в направлении другой силы, например в направлении реакции R (горизонтально влево), отрезок неопределенной длины, так как мы не знаем величины силы R. Мы знаем только, что в вершине силового многоугольника, где заканчивается вектор, равный силе R, начинается вектор, представляющий силу Т. Он направлен параллельно веревке, на которой висит шар (см. рис. 11, а), и замыкает силовой многоугольник, т. е. заканчивается в точке К силового многоугольника. Поэтому от точки К проводим прямую, параллельную силе Г, под углом а к вертикали. Точка N пересечения этой прямой с направлением силы R в силовом многоугольнике позволит определить величины искомых сил:
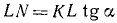 или
или 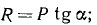
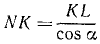 или
или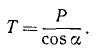
Найденная нами реакция R стены на шар по закону равенства действия и противодействия равна и противоположна давлению шара на стену.
Ответ:
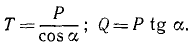
Задача №3
Чтобы вытянуть автомобиль, застрявший на плохой дороге, шофер натянул канат AB между автомобилем и деревом, привязав конец В к дереву на 2 м выше, чем конец А к автомобилю. Затем шофер встал на канат возле автомобиля, оттянув канат книзу собственным весом G = 770 н=78,5 кГ, после чего перемещался вдоль каната к дереву. Определить силу (натяжение каната), действующую на автомобиль в положении, когда шофер стоял на канате в точке C на расстоянии от дерева: 1) CD= 10 м и 2) CD = 2 м, считая, что канат нерастяжим, а CA горизонтальна.
Решение. Требуется определить силу, с которой канат тянет автомобиль вперед. Эта сила (натяжение каната между точками C и А) приложена к точке А автомобиля. По принципу равенства действия и противодействия на точку C действует сила TА, равная и противоположная искомой силе, действующей на автомобиль. Следовательно, для определения искомой силы мы можем рассмотреть равновесие точки А или равновесие точки C каната. Но нам неизвестны другие силы, действующие на точку А, зато известна сила (вес G шофера), приложенная к точке С. Поэтому на первый вопрос, задаваемый при решении задач по статике (равновесие какого тела изучается?), надо ответить: равновесие точки С
На второй обычный вопрос —какая система сил действует на это тело (или на эту точку)? — отвечаем: на точку C действуют три взаимно уравновешенные силы: 1) вес С шофера, 2) неизвестная по величине искомая сила TА и 3) сила TВ натяжения части СВ каната, направленная под углом 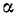 к горизонтали
к горизонтали 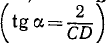 и тоже неизвестная по величине (рис. 12, а).
и тоже неизвестная по величине (рис. 12, а).
Силовой многоугольник (в данном случае треугольник) должен быть замкут, так как система находится в равновесии. Построение силового многоугольника начинаем всегда с известных сил. В данной задаче известна только одна сила — вес шофера. Начертив эту силу (рис. 12, б), от конца ее построим вектор силы TА.
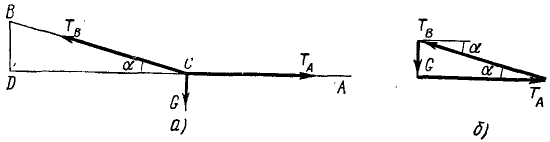
Рис. 12
Нам неизвестна величина силы. Однако мы знаем, что там, где заканчивается этот вектор, начинается вектор TВ , направленный под углом а параллельно ветви CB каната, и заканчивается TВ в той точке силового многоугольника, где начинается вектор силы G, так как силовой многоугольник должен быть замнут. Под углом а к горизонтали проведем от этой точки прямую до пересечения с горизонтальной прямой, по которой направлен вектор TА в силовом многоугольнике. Эта точка пересечения определит нам весь треугольник, а следовательно, и искомую силу TА.
Построив силовой многоугольник, переходим к вычислению:
TА = G ctg a = G∙CD: 2.
Ответ: 1) TА = 3850 н= 392,5 κΓ; 2) TB = 770 н = 78,5 кГ.
Данную силу можно разложить по двум заданным направлениям на плоскости или по трем заданным направлениям в пространстве
Составляющие силы
Займемся обратной задачей—разложением силы на составляющие. Сходящимися составляющими силами называют такие силы, которые, будучи приложены в одной точке с данной силой, в своей совокупности эквивалентны данной силе.
Эта задача — разложение силы на сходящиеся составляющие — не имеет однозначного решения, так как существует бесчисленное множество систем сходящихся сил, для которых данная сила является равнодействующей. Но в некоторых частных случаях она имеет вполне определенное решение. К таким случаям относится разложение силы на две составляющие, имеющие заданные направления в одной с ней плоскости.
Пусть, например, силу 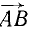 надо разложить на две составляющие: вертикальную и горизонтальную (рис. 13, а). Проведя заданные направления из начала и конца вектора силы, мы получим параллелограмм (прямоугольник) ACBD, диагональ которого AB является равнодействующей, а стороны AC и AD—искомыми составляющими силы.
надо разложить на две составляющие: вертикальную и горизонтальную (рис. 13, а). Проведя заданные направления из начала и конца вектора силы, мы получим параллелограмм (прямоугольник) ACBD, диагональ которого AB является равнодействующей, а стороны AC и AD—искомыми составляющими силы.
Пусть теперь силу 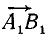 нужно разложить по двум каким-либо другим направлениям в плоскости чертежа, например по направлениям A1O и A1O'. Проводя прямые с заданным направлением из начала A1 вектора и параллельные им прямые из конца B1 вектора силы, получим параллелограмм A1KB1M, стороны A1K и A1M которого выражают искомые составляющие (рис. 13, б).
нужно разложить по двум каким-либо другим направлениям в плоскости чертежа, например по направлениям A1O и A1O'. Проводя прямые с заданным направлением из начала A1 вектора и параллельные им прямые из конца B1 вектора силы, получим параллелограмм A1KB1M, стороны A1K и A1M которого выражают искомые составляющие (рис. 13, б).
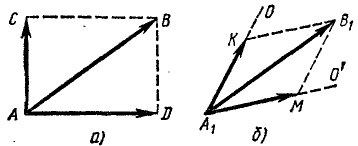
Рис. 13
Решение останется единственным, если силу 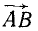 нужно разложить на две составляющие, одна из которых задана по величине и по направлению, а другая является искомой.
нужно разложить на две составляющие, одна из которых задана по величине и по направлению, а другая является искомой.
Разложить силу на две составляющие, не лежащие с ней в какой-либо одной плоскости, разумеется, невозможно. В трехмерном пространстве силу можно разложить на три составляющие, имеющие заданные направления. На практике часто встречается разложение силы на три взаимно перпендикулярные составляющие, направленные параллельно осям координат.
Составляющие данной силы, иначе называемые компонентами данной силы, являются векторными величинами и их складывают по правилам геометрического сложения. Так, обозначая составляющие силы 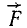 большими буквами
большими буквами 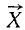 ,
, 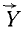 и
и 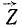 со стрелками сверху, чтобы подчеркнуть их векторную природу, мы можем написать геометрическое равенство
со стрелками сверху, чтобы подчеркнуть их векторную природу, мы можем написать геометрическое равенство
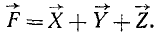
| Рекомендую подробно изучить предмет: |
| Ещё лекции с примерами решения и объяснением: |
- Условия равновесия системы сходящихся сил в аналитической форме
- Приведение двух параллельных сил к равнодействующей
- Пара сил в теоретической механике
- Приведение системы сил к данной точке
- Теорема о движении центра инерции
- Теорема количества движения
- Теорема моментов количества движения
- Теорема кинетической энергии