Ускорение точки при ее движении по окружности в физике - формулы и определения с примерами

Ускорение точки при ее движении по окружности:

При равномерном прямолинейном движении ускорение равно нулю. А почему ускорение возникает при движении по окружности? Как оно направлено? Чему равен его модуль?

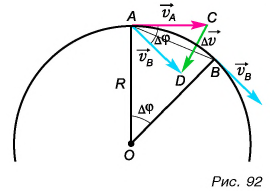
Пусть тело (рассматриваемое как материальная точка) движется по окружности радиусом R со скоростью, модуль которой не изменяется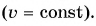

Найдем ускорение тела в точке А. Перенесем вектор 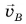в эту точку и построим вектор 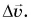Получились подобные равнобедренные треугольники ACD и ОАВ. Из их подобия следует:

где 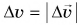— модуль изменения скорости, 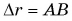— модуль перемещения. Разделим обе части равенства (2) на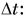

При малых 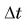отношение 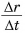практически равно модулю скорости тела 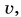а отношение 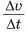— модулю его ускорения а в той же точке. В результате равенство (3) примет вид  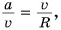откуда

Формула (4) определяет модуль ускорения 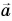в случае движения тела по окружности при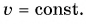

А каково направление ускорения 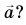Оно совпадает с направлением вектора 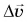при малых 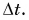Из рисунка 92 видно, что чем меньше 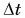и вместе с ним угол 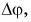тем направление вектора  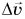ближе к направлению на центр окружности.

Значит, ускорение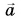 направлено по радиусу к центру окружности. Поэтому его называют центростремительным. В то же время вектор 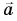перпендикулярен скорости 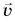(т. е. направлен по нормали к ней). Поэтому ускорение 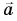называют также и нормальным ускорением.

А как связано центростремительное ускорение с угловой скоростью? Подставляя в формулу (4) выражение 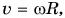находим:

Отсюда, учитывая, что 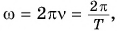получим еще две полезные формулы:

Выведите самостоятельно выражение для центростремительного ускорения через угловую и линейную скорости:

Для любознательных:

А как направлено ускорение тела, движущегося по окружности, если модуль его скорости

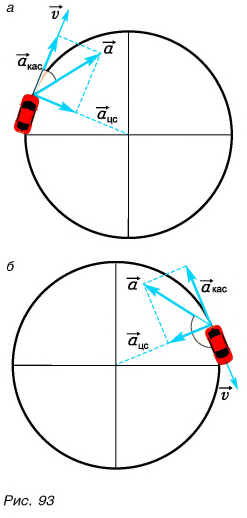
На рисунке 93, а (вид сверху) мчащийся по кольцевой трассе автомобиль набирает скорость. Ускорение автомобиля 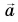равно сумме двух составляющих: 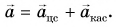Центростремительное ускорение 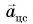обусловлено изменением направления скорости. А касательное к траектории ускорение 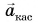возникает из-за изменения модуля скорости. При наборе скорости вектор 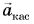направлен так же, как 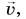а вектор 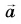составляет с 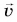острый угол.

На рисунке 93, б автомобиль тормозит. Модуль скорости уменьшается, составляющая 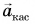направлена противоположно вектору 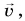а угол между ускорением 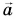и скоростью  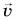— тупой. В обоих случаях модуль ускорения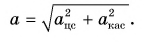
 

Главные выводы:

1. Тело, движущееся по окружности со скоростью, модуль которой 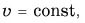обладает центростремительным ускорением.
2. Центростремительное ускорение перпендикулярно скорости и направлено к центру окружности.
3. Модуль центростремительного ускорения

• Заказать решение задач по физике

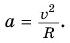
Пример решения задачи:

Период вращения 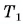первого колеса в 4 раза больше периода вращения 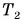второго колеса, а его радиус 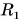в 2 раза меньше радиуса 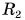второго колеса. У какого колеса больше центростремительное ускорение точек на его ободе? Во сколько раз?

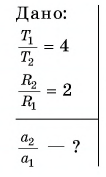
Решение

Согласно формуле (6) отношение модулей центростремительных ускорений точек на ободе второго и первого колеса:

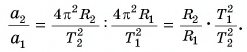
По условию задачи:

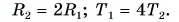
Тогда

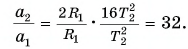
Ответ: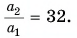

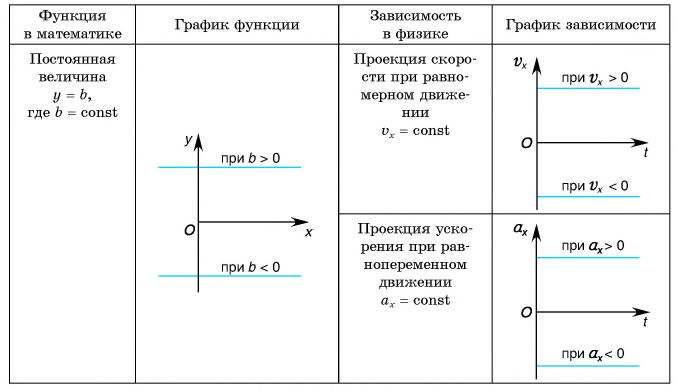
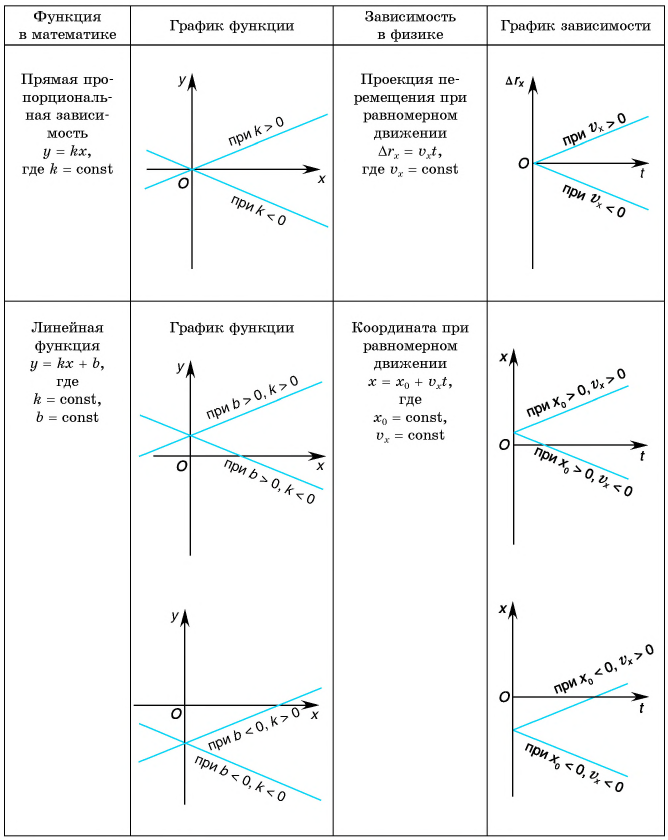
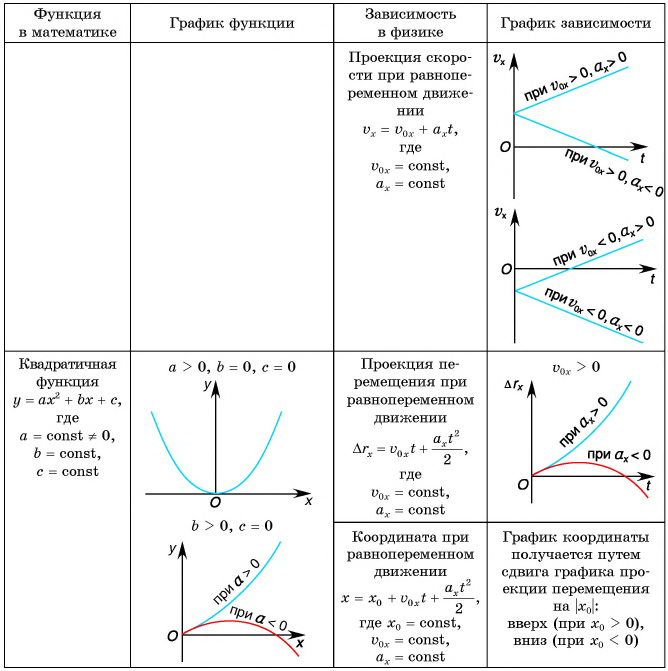
Основные кинематические величины и их графики: