
Уравнения прямых и кривых на плоскости с примерами решения
Содержание:
Уравнения прямых и кривых на плоскости
Уравнения кривых в большом количестве встречаются при чтении экономической литературы. Укажем некоторые из этих кривых.
Кривая безразличия - кривая, показывающая различные комбинации двух продуктов, имеющих одинаковое потребительское значение, или полезность, для потребителя.
Кривая потребительского бюджета - кривая, показывающая различные комбинации количеств двух товаров, которые потребитель может купить при данном уровне его денежного дохода.
Кривая производственных возможностей - кривая, показывающая различные комбинации двух товаров или услуг, которые могут быть произведены в условиях полной занятости и полного объема производства в экономике с постоянными запасами ресурсов и неизменной технологией.
Кривая инвестиционного спроса - кривая, показывающая динамику процентной ставки и объем инвестиций при разных процентных ставках.
Кривая Филлипса - кривая, показывающая существование устойчивой связи между уровнем безработицы и уровнем инфляции.
Кривая Лаффера - кривая, показывающая связь между ставками налогов и налоговыми поступлениями, выявляющая такую налоговую ставку, при которой налоговые поступления достигают максимума.
Уже простое перечисление терминов показывает, как важно для экономистов умение строить графики и анализировать уравнения кривых, каковыми являются прямые линии и кривые второго порядка - окружность, эллипс, гипербола, парабола. Кроме того, при решении большого класса задач требуется выделить на плоскости область, ограниченную какими-либо кривыми, уравнения которых заданы. Чаще всего эти задачи формулируются так: найти наилучший план производства при заданных ресурсах. Задание ресурсов имеет обычно вид неравенств, уравнения которых даны. Поэтому приходится искать наибольшее или наименьшее значения, принимаемые некоторой функцией в области, заданной уравнениями системы неравенств.
В аналитической геометрии линия на плоскости определяется как множество точек, координаты которых удовлетворяют уравнению 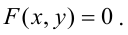
Пусть на плоскости задана прямоугольная декартова система координат. Прямая на плоскости может быть задана одним из уравнений:
1. Общее уравнение прямой:

Вектор 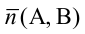 ортогонален прямой, числа А и В одновременно не равны нулю.
ортогонален прямой, числа А и В одновременно не равны нулю.
2. Уравнение прямой с угловым коэффициентом:

где 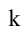 - угловой коэффициент прямой, то есть
- угловой коэффициент прямой, то есть 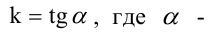 величина угла, образованного прямой с осью
величина угла, образованного прямой с осью 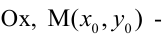 некоторая точка, принадлежащая прямой.
некоторая точка, принадлежащая прямой.
Уравнение (2.2) принимает вид 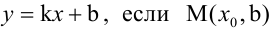 есть точка пересечения прямой с осью
есть точка пересечения прямой с осью 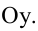
3. Уравнение прямой в отрезках:

где а и b - величины отрезков, отсекаемых прямой на осях координат.
4. Уравнение прямой, проходящей через две данные точки - 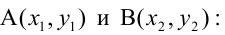

5. Уравнение прямой, проходящей через данную точку 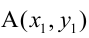 параллельно данному вектору
параллельно данному вектору 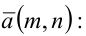

6. Нормальное уравнение прямой:

где 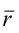 - радиус-вектор произвольной точки
- радиус-вектор произвольной точки 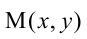 этой прямой,
этой прямой, 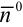 - единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой;
- единичный вектор, ортогональный этой прямой и направленный от начала координат к прямой; 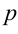 - расстояние от начала координат до прямой.
- расстояние от начала координат до прямой.
Нормальное уравнение прямой в координатной форме имеет вид:
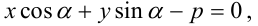 где
где 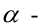 величина угла, образованного прямой с осью Ох.
величина угла, образованного прямой с осью Ох.
Уравнение пучка прямых с центром в точке 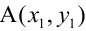 имеет вид:
имеет вид: 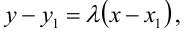
где 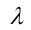 - параметр пучка. Если пучок задается двумя пересекающимися прямыми
- параметр пучка. Если пучок задается двумя пересекающимися прямыми 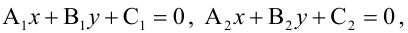 то его уравнение имеет вид:
то его уравнение имеет вид:
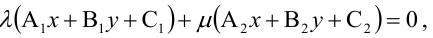 где
где 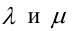 - параметры пучка, не обращающиеся в 0 одновременно.
- параметры пучка, не обращающиеся в 0 одновременно.
Величина угла между прямыми 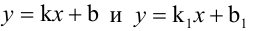 задается формулой:
задается формулой:
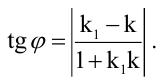
Равенство 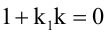 есть необходимое и достаточное условие перпендикулярности прямых.
есть необходимое и достаточное условие перпендикулярности прямых.
Для того, чтобы два уравнения
 задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:
задавали одну и ту же прямую, необходимо и достаточно, чтобы их коэффициенты были пропорциональны:
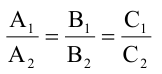
Уравнения (2.7), (2.8) задают две различные параллельные прямые, если 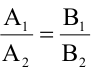 и
и 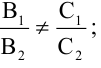 прямые пересекаются, если
прямые пересекаются, если 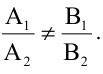 Расстояние d от точки
Расстояние d от точки 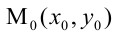 до прямой есть длина перпендикуляра, проведенного из точки
до прямой есть длина перпендикуляра, проведенного из точки 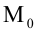 к прямой. Если прямая задана нормальным уравнением, то
к прямой. Если прямая задана нормальным уравнением, то 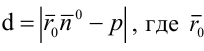 - радиус-вектор точки
- радиус-вектор точки 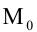 или, в координатной форме,
или, в координатной форме, 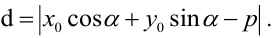
Общее уравнение кривой второго порядка имеет вид:
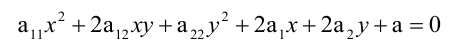
Предполагается, что среди коэффициентов уравнения 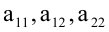 есть отличные от нуля.
есть отличные от нуля.
Уравнение окружности с центром в точке 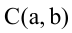 и радиусом, равным R:
и радиусом, равным R:  Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек
Эллипсом называется геометрическое место точек, сумма расстояний которых от двух данных точек 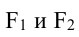 (фокусов) есть величина постоянная, равная 2а. Каноническое (простейшее) уравнение эллипса:
(фокусов) есть величина постоянная, равная 2а. Каноническое (простейшее) уравнение эллипса: 
Эллипс, заданный уравнением (2.10), симметричен относительно осей координат.
Параметры а и b называются полуосями эллипса.
Пусть 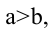 тогда фокусы
тогда фокусы 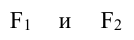 и находятся на оси Ох на расстоянии
и находятся на оси Ох на расстоянии 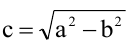 от начала координат. Отношение
от начала координат. Отношение 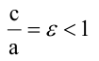 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса.
Расстояния от точки 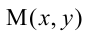 эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:
эллипса до его фокусов (фокальные радиусы-векторы) определяются формулами:
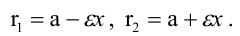
Если же 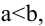 то фокусы находятся на оси
то фокусы находятся на оси 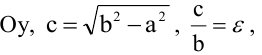
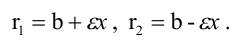
Если а=b, то эллипс является окружностью с центром в начале координат радиуса а.
Гиперболой называется геометрическое место точек, разность расстояний которых от двух данных точек 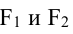 (фокусов) равна по абсолютной величине данному числу 2а.
(фокусов) равна по абсолютной величине данному числу 2а.
Каноническое уравнение гиперболы: 
Гипербола, заданная уравнением (2.11), симметрична относительно осей координат. Она пересекает ось 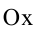 в точках
в точках 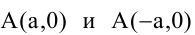 - вершинах гиперболы и не пересекает ось
- вершинах гиперболы и не пересекает ось 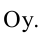 Параметр а называется вещественной полуосью, b - мнимой полуосью. Параметр
Параметр а называется вещественной полуосью, b - мнимой полуосью. Параметр 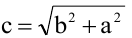 есть, расстояние от фокуса до начала координат. Отношение
есть, расстояние от фокуса до начала координат. Отношение 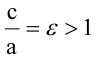 называется эксцентриситетом гиперболы. Прямые, уравнения которых
называется эксцентриситетом гиперболы. Прямые, уравнения которых 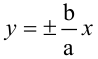 называются асимптотами гиперболы.
называются асимптотами гиперболы.
Расстояния от точки 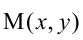 гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами:
гиперболы до ее фокусов (фокальные радиусы-векторы) определяются формулами: 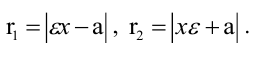
Гипербола, у которой а=b, называется равносторонней, ее уравнение 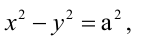 а уравнение асимптот
а уравнение асимптот 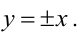
Гиперболы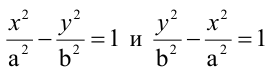 называются сопряженными. Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
называются сопряженными. Параболой называется геометрическое место точек, одинаково удаленных от данной точки (фокуса) и данной прямой (директрисы).
Каноническое уравнение параболы имеет два вида:
1. 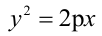 - парабола симметрична относительно оси Ох. 2.
- парабола симметрична относительно оси Ох. 2. 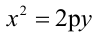 - парабола симметрична относительно оси Оy. В обоих случаях
- парабола симметрична относительно оси Оy. В обоих случаях 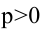 и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.
и вершина параболы, то есть точка, лежащая на оси симметрии, находится в начале координат.
Парабола, уравнение которой 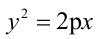 имеет фокус
имеет фокус 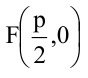 и директрису
и директрису 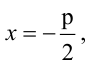 фокальный радиус-вектор точки
фокальный радиус-вектор точки 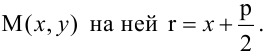 Парабола, уравнение которой
Парабола, уравнение которой 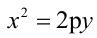 имеет фокус
имеет фокус 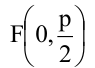 и директрису
и директрису 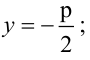 фокальный радиус-вектор точки
фокальный радиус-вектор точки 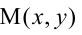 параболы равен
параболы равен 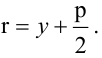
Уравнение 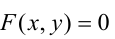 задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство
задает линию, разбивающую плоскость на две или несколько частей. В одних из этих частей выполняется неравенство 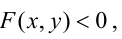 а в других - неравенство
а в других - неравенство 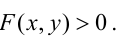 Иными словами, линия
Иными словами, линия 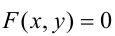 отделяет часть плоскости, где
отделяет часть плоскости, где 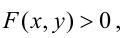 от части плоскости, где
от части плоскости, где 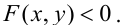
Прямая, уравнение которой 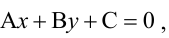 разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем
разбивает плоскость на две полуплоскости. На практике для выяснения того, в какой полуплоскости мы имеем 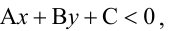 а в какой
а в какой 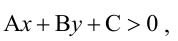 применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой, уравнение которой
применяют метод контрольных точек. Для этого берут контрольную точку (разумеется, не лежащую на прямой, уравнение которой 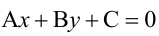 ) и проверяют, какой знак имеет в этой точке выражение
) и проверяют, какой знак имеет в этой точке выражение 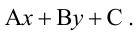 Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости
Тот же знак имеет указанное выражение и во всей полуплоскости, где лежит контрольная точка. Во второй полуплоскости 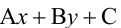 имеет противоположный знак.
имеет противоположный знак.
Точно так же решаются и нелинейные неравенства с двумя неизвестными.
Например, решим неравенство 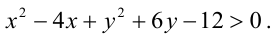 Его можно переписать в виде
Его можно переписать в виде 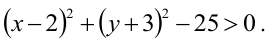
Уравнение 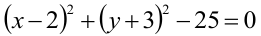 задает окружность с центром в точке С(2,-3) и радиусом 5. Окружность разбивает плоскость на две части - внутреннюю и внешнюю. Чтобы узнать, в какой из них имеет место данное неравенство, возьмем контрольную точку во внутренней области, например, центр С(2,-3) нашей окружности. Подставляя координаты точки С в левую часть неравенства, получаем отрицательное число -25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство
задает окружность с центром в точке С(2,-3) и радиусом 5. Окружность разбивает плоскость на две части - внутреннюю и внешнюю. Чтобы узнать, в какой из них имеет место данное неравенство, возьмем контрольную точку во внутренней области, например, центр С(2,-3) нашей окружности. Подставляя координаты точки С в левую часть неравенства, получаем отрицательное число -25. Значит, и во всех точках, лежащих внутри окружности, выполняется неравенство 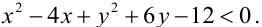 Отсюда следует, что данное неравенство имеет место во внешней для окружности области.
Отсюда следует, что данное неравенство имеет место во внешней для окружности области.
Пример:
Составьте уравнения прямых, проходящих через точку А(3,1) и наклоненных к прямой 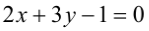 под углом 45°.
под углом 45°.
Решение:
Будем искать уравнение прямой в виде 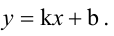 Поскольку прямая проходит через точку А, то ее координаты удовлетворяют уравнению прямой, т.е.
Поскольку прямая проходит через точку А, то ее координаты удовлетворяют уравнению прямой, т.е. 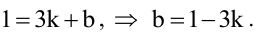
Величина угла между прямыми 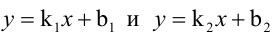 определяется формулой
определяется формулой 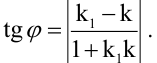 Так как угловой коэффициент
Так как угловой коэффициент 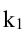 исходной прямой
исходной прямой 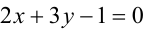 равен
равен 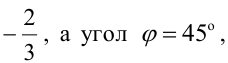 то имеем уравнение для определения
то имеем уравнение для определения 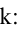
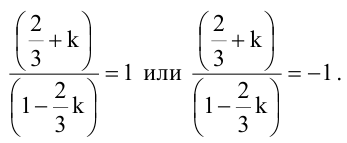
Имеем два значения 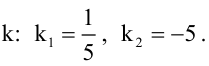 Находя соответствующие значения b по формуле
Находя соответствующие значения b по формуле 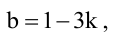 получим две искомые прямые, уравнения которых:
получим две искомые прямые, уравнения которых: 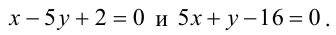
Пример:
При каком значении параметра t прямые, уравнения которых 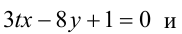
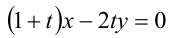 параллельны ?
параллельны ?
Решение:
Прямые, заданные общими уравнениями, параллельны, если коэффициенты при x и y пропорциональны, т.е. 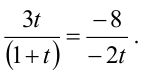 Решая полученное уравнение, находим t:
Решая полученное уравнение, находим t:
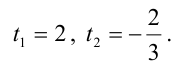
Пример:
Найти уравнение общей хорды двух окружностей: 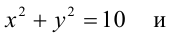 и
и 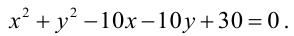
Решение:
Найдем точки пересечения окружностей, для этого решим систему уравнений: 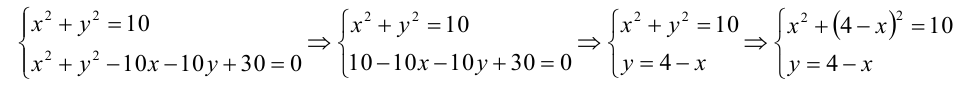 Решая первое уравнение, находим значения
Решая первое уравнение, находим значения 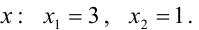 Из второго уравнения -соответствующие значения
Из второго уравнения -соответствующие значения 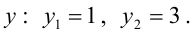 Теперь получим уравнение общей хорды, зная две точки А(3,1) и В(1,3), принадлежащие этой прямой:
Теперь получим уравнение общей хорды, зная две точки А(3,1) и В(1,3), принадлежащие этой прямой: 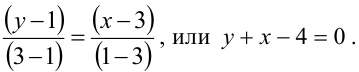
Пример:
Как расположены на плоскости точки, координаты которых удовлетворяют условиям 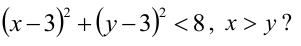
Решение:
Первое неравенство системы определяет внутренность круга, не включая границу, т.е. окружность с центром в точке (3,3) и радиуса 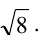 Второе неравенство задает полуплоскость, определяемую прямой, уравнение которой х = у, причем, так как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие обоим неравенствам, то искомая область - внутренность полукруга.
Второе неравенство задает полуплоскость, определяемую прямой, уравнение которой х = у, причем, так как неравенство строгое, точки самой прямой не принадлежат полуплоскости, а все точки ниже этой прямой принадлежат полуплоскости. Поскольку мы ищем точки, удовлетворяющие обоим неравенствам, то искомая область - внутренность полукруга.
Пример:
Вычислить длину стороны квадрата, вписанного в эллипс, уравнение которого 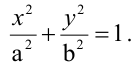
Решение:
Пусть 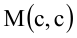 - вершина квадрата, лежащая в первой четверти. Тогда сторона квадрата будет равна 2с. Т.к. точка М принадлежит эллипсу, ее координаты удовлетворяют уравнению эллипса
- вершина квадрата, лежащая в первой четверти. Тогда сторона квадрата будет равна 2с. Т.к. точка М принадлежит эллипсу, ее координаты удовлетворяют уравнению эллипса 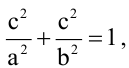 откуда
откуда 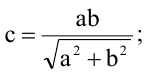 значит, сторона квадрата —
значит, сторона квадрата — 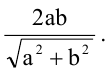
Пример:
Зная уравнение асимптот гиперболы 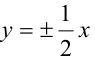 и одну из ее точек
и одну из ее точек 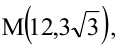 составить уравнение гиперболы.
составить уравнение гиперболы.
Решение:
Запишем каноническое уравнение гиперболы: 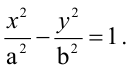 Асимптоты гиперболы задаются уравнениями
Асимптоты гиперболы задаются уравнениями 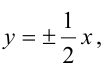 значит,
значит, 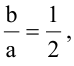 откуда
откуда 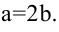 Поскольку М - точка гиперболы, то ее координаты удовлетворяют уравнению гиперболы, т.е.
Поскольку М - точка гиперболы, то ее координаты удовлетворяют уравнению гиперболы, т.е. 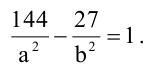 Учитывая, что а=2b , найдем b:
Учитывая, что а=2b , найдем b: 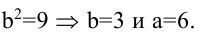 Тогда уравнение гиперболы
Тогда уравнение гиперболы 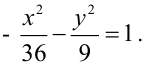
Пример:
Вычислить длину стороны правильного треугольника АВС, вписанного в параболу с параметром р, предполагая, что точка А совпадает с вершиной параболы.
Решение:
Каноническое уравнение параболы с параметром р имеет вид 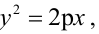 вершина ее совпадает с началом координат, и парабола симметрична относительно оси абсцисс. Так как прямая АВ образует с осью Оx угол в 30°, то уравнение прямой имеет вид:
вершина ее совпадает с началом координат, и парабола симметрична относительно оси абсцисс. Так как прямая АВ образует с осью Оx угол в 30°, то уравнение прямой имеет вид: 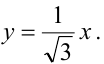 Следовательно, мы можем найти координаты точки В, решая систему уравнений
Следовательно, мы можем найти координаты точки В, решая систему уравнений 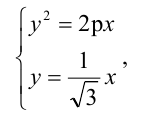 откуда
откуда 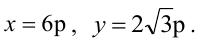 Значит, расстояние между точками
Значит, расстояние между точками 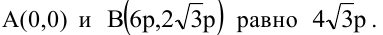
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |