
Уравнения и неравенства - определение и вычисление с примерами решения
Содержание:
Уравнения и неравенства
О появлении посторонних корней и потере решений уравнений
Вы знаете, что далеко не каждое преобразование уравнения сохраняет неизменным множество его корней. В одном случае это множество может сузиться, то есть корни будут потеряны, в другом — расшириться, то есть появятся посторонние корни.
Приведем несколько примеров.
При переходе от уравнения 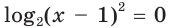
Возведение обеих частей уравнения 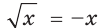 в квадрат приводит к появлению постороннего корня
в квадрат приводит к появлению постороннего корня 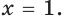
Заменяя уравнение 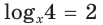 уравнением
уравнением 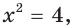 получаем посторонний корень
получаем посторонний корень 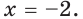
Метод решения уравнения, при котором данное уравнение заменяют на уравнение-следствие, а затем полученные корни подвергают проверке, называют методом следствий. Его применяют тогда, когда выполнить проверку несложно.
Однако так бывает не всегда. Например, число 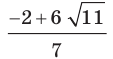 является корнем уравнения
является корнем уравнения 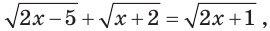 но чтобы в этом убедиться, надо провести довольно большую вычислительную работу.
но чтобы в этом убедиться, надо провести довольно большую вычислительную работу.
Для подобных ситуаций возможен другой путь решения — метод равносильных преобразований. С этим методом вы ознакомились в 10 классе.
Подчеркнем, что, применяя как метод следствий, так и метод равносильных преобразований, важно знать причины потери корней и появления посторонних корней. Рассмотрим некоторые из этих причин.
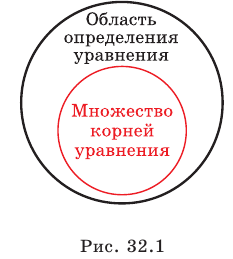
Изменение области определения уравнения
Вне области определения уравнения корней нет (рис. 32.1). Поэтому преобразование уравнения, при котором расширяется область его определения, может привести к появлению посторонних корней.
Например, областью определения уравнения 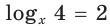 является множество
является множество 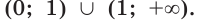 Пользуясь определением логарифма, получаем уравнение
Пользуясь определением логарифма, получаем уравнение 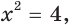 , областью определения которого является множество
, областью определения которого является множество 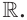 Расширение области определения исходного уравнения привело к появлению постороннего корня
Расширение области определения исходного уравнения привело к появлению постороннего корня 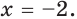
Пример:
Решите уравнение
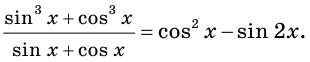
Решение:
Если дробь в левой части данного уравнения сократить на 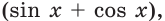 то получим уравнение
то получим уравнение 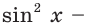
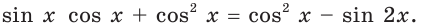 При таком преобразовании область определения исходного уравнения расширяется на множество чисел, которые являются корнями уравнения
При таком преобразовании область определения исходного уравнения расширяется на множество чисел, которые являются корнями уравнения 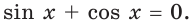 Поэтому на самом деле данное в условии уравнение равносильно системе
Поэтому на самом деле данное в условии уравнение равносильно системе
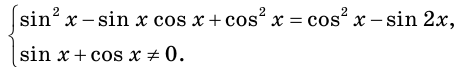
Найдем корни уравнения системы. Имеем:
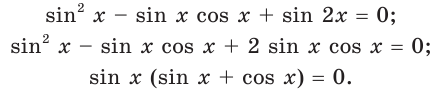
Поскольку 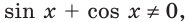 то получаем
то получаем 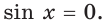 Отсюда
Отсюда 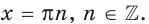 Осталось заметить, что при
Осталось заметить, что при 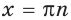 значение выражения
значение выражения 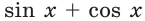 отлично от нуля.
отлично от нуля.
Ответ: 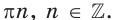
Если расширение области определения уравнения может привести к появлению посторонних корней, то ее сужение — возможная причина потери корней.
Например, областью определения уравнения 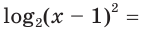
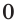 является множество
является множество  а областью определения уравнения
а областью определения уравнения 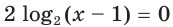 является множество
является множество 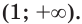 Множество
Множество 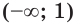 содержит корень
содержит корень 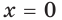 первого уравнения. Поэтому при переходе от уравнения
первого уравнения. Поэтому при переходе от уравнения  к уравнению
к уравнению 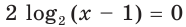 этот корень потерян.
этот корень потерян.
Часто причиной изменения множества корней уравнения является применение равенств, правая и левая части которых имеют разные области определения.
Приведем примеры таких равенств:
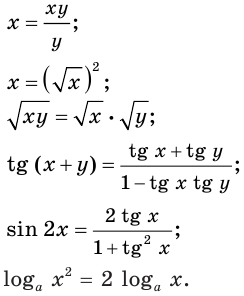
В каждом из этих равенств область определения выражения, стоящего в правой части, является подмножеством области определения выражения, стоящего в левой части. Поэтому применение этих равенств слева направо может привести к потере корней, а справа налево — к появлению посторонних корней.
Пример:
Решите уравнение 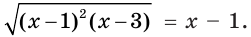
Решение:
Областью определения данного уравнения является множество 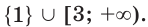 Очевидно, число 1 является корнем данного уравнения.
Очевидно, число 1 является корнем данного уравнения.
Однако применение формулы 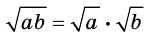 приводит к уравнению
приводит к уравнению
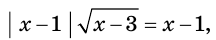
область определения которого — множество 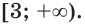 Поэтому число 1 не является корнем полученного уравнения, то есть такой переход ведет к потере этого корня.
Поэтому число 1 не является корнем полученного уравнения, то есть такой переход ведет к потере этого корня.
Решим данное уравнение методом равносильных переходов.
Данное в условии уравнение равносильно системе
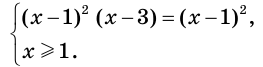
Отсюда 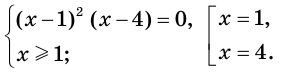
Ответ: 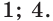
Умножение обеих частей уравнения на выражение, содержащее переменную
Иногда бывает целесообразным умножить обе части уравнения на некоторое выражение. Рассмотрим последствия такого преобразования. Перейдем от уравнения
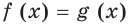
к уравнению
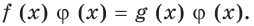
При таком переходе множество корней уравнения может измениться под влиянием двух факторов: области определения функции и множества корней уравнения 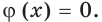 Например, если обе части уравнения
Например, если обе части уравнения 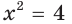 умножить
умножить
на выражение 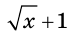 и перейти к уравнению
и перейти к уравнению 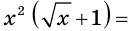
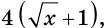 то тем самым теряем корень
то тем самым теряем корень 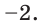 Если же обе части этого уравнения умножить на
Если же обе части этого уравнения умножить на 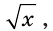 то теряем корень
то теряем корень 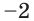 и одновременно получаем посторонний корень
и одновременно получаем посторонний корень 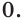
Следовательно, если при решении уравнения возникла потребность умножить обе его части на выражение 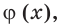 то надо учитывать как область определения этого выражения, так и множество корней уравнения
то надо учитывать как область определения этого выражения, так и множество корней уравнения 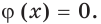
Пример:
Решите уравнение 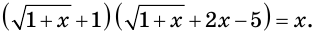
Решение:
Умножим обе части данного уравнения на выражение 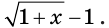 Поскольку
Поскольку 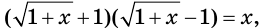 то получим:
то получим:
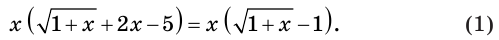
Это преобразование не изменяет области определения исходного уравнения. Появление же посторонних корней возможно за счет корней уравнения 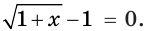 Следовательно, полученное уравнение
Следовательно, полученное уравнение 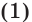 — следствие уравнения, данного в условии.
— следствие уравнения, данного в условии.
Уравнение 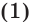 равносильно совокупности
равносильно совокупности
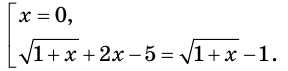
Решим второе уравнение совокупности. Его следствием будет уравнение 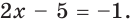 Отсюда
Отсюда 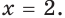
Осталось выполнить проверку. Легко убедиться, что число 2 является корнем данного в условии уравнения, а число 0 — нет.
Ответ: 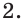
Переход от уравнения f (x) = g (x) к уравнению φ (f (x)) = φ (g (x))
Переход от уравнения 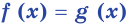 к уравнению
к уравнению 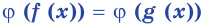
Почему уравнения
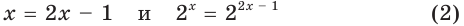
равносильны, а уравнения
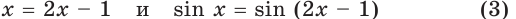
не являются равносильными?
Дело в том, что свойства функции 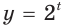 отличаются от свойств функции
отличаются от свойств функции 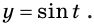
Если определенная на 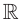 функция
функция 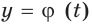 обратима, то равенство
обратима, то равенство 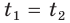 выполняется тогда и только тогда, когда
выполняется тогда и только тогда, когда 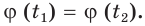 Поэтому в этом случае уравнения
Поэтому в этом случае уравнения 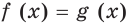 и
и 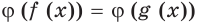 равносильны.
равносильны.
Если же определенная на 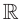 функция
функция 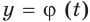 не является обратимой, то из равенства
не является обратимой, то из равенства 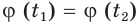 не обязательно следует, что
не обязательно следует, что 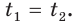 Поэтому уравнение
Поэтому уравнение 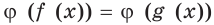 является следствием уравнения
является следствием уравнения 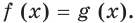
Так, уравнения 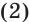 равносильны, потому что функция
равносильны, потому что функция 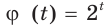 обратима. Поскольку функция
обратима. Поскольку функция 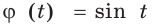 не является обратимой, то уравнения
не является обратимой, то уравнения 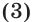 не являются равносильными.
не являются равносильными.
Вы знаете, что возведение обеих частей уравнения в четную степень приводит к уравнению-следствию, а возведение в нечетную степень — к равносильному уравнению.
Это связано с тем, что функция 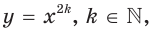 не является обратимой, а функция
не является обратимой, а функция 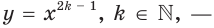 обратимая.
обратимая.
Функция 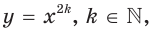 обратима на множестве
обратима на множестве 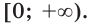
В 10 классе вы пользовались этим фактом в виде такой теоремы.
Теорема 32.1. Если для любого 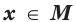 выполняются неравенства
выполняются неравенства 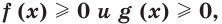 то уравнения
то уравнения 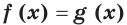
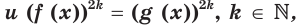 равносильны на множестве
равносильны на множестве 
Эту теорему вы использовали при решении иррациональных уравнений.
Рассмотрим пример, в котором появление постороннего корня связано с необратимостью функции 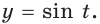
Пример:
Решите уравнение
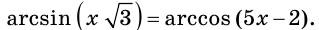
Решение:
Поскольку определенная на 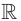 функция
функция 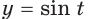 не является обратимой, то уравнение
не является обратимой, то уравнение 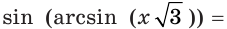
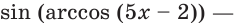 следствие данного. Поэтому решение уравнения должно завершиться проверкой корней. Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
следствие данного. Поэтому решение уравнения должно завершиться проверкой корней. Следовательно, можно не бояться далее переходить к новым уравнениям-следствиям.
Напомним, что имеют место равенства 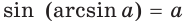
и 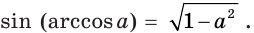 Поэтому можно записать:
Поэтому можно записать:
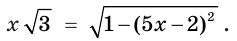
Ответ: 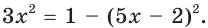
Далее имеем: 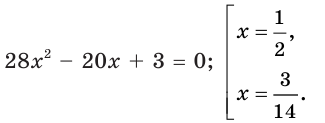
Проверим полученные корни.
При 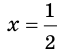 имеем:
имеем: 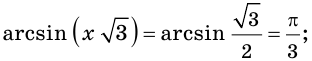
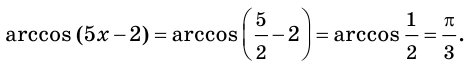
Следовательно, число 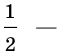 корень исходного уравнения.
корень исходного уравнения.
При 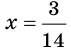 имеем:
имеем: 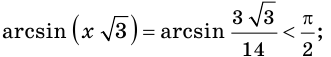
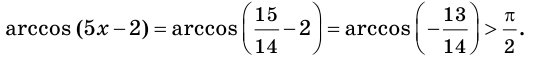
Следовательно, число 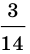 не является корнем исходного уравнения.
не является корнем исходного уравнения.
Ответ: 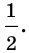
Основные методы решения уравнений
В таблице приведены схемы решения некоторых типовых уравнений.

Часто решение уравнений сводится к решению типовых уравнений, приведенных в таблице. Это иллюстрируют упражнения №№ 33.1, 33.2. К тем уравнениям, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод разложения на множители
Хорошо, если удается левую часть уравнения 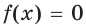 представить в виде произведения нескольких выражений. Как правило, этот шаг полезен, поскольку позволяет вместо данного уравнения решить совокупность более простых уравнений.
представить в виде произведения нескольких выражений. Как правило, этот шаг полезен, поскольку позволяет вместо данного уравнения решить совокупность более простых уравнений.
Рассмотрим примеры.
Пример:
Решите уравнение 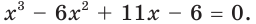
Решение:
Очевидно, что число 1 является корнем данного уравнения. Тогда левую часть уравнения можно представить в виде произведения 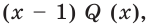 где
где 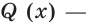 квадратный трехчлен. Для нахождения
квадратный трехчлен. Для нахождения 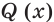 разделим «уголком» многочлен
разделим «уголком» многочлен 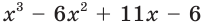 на двучлен
на двучлен 
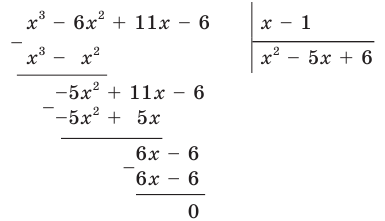
Получили, что 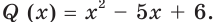
Имеем: 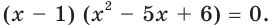
Это уравнение равносильно совокупности 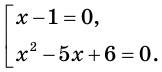
Отсюда 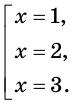
Ответ: 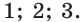
Пример:
Решите уравнение 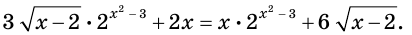
Решение:
Имеем: 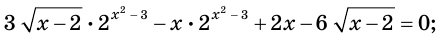
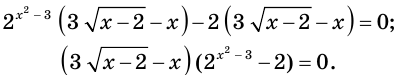
Ошибочным было бы считать, что это уравнение равносильно совокупности
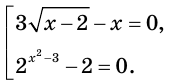
Действительно, корень 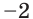 второго уравнения совокупности не входит в область определения исходного уравнения. На самом деле исходное уравнение равносильно системе
второго уравнения совокупности не входит в область определения исходного уравнения. На самом деле исходное уравнение равносильно системе
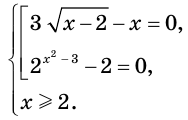
Отсюда 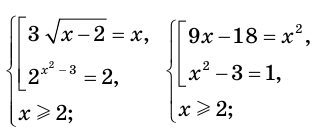
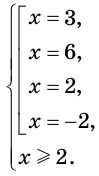
Ответ: 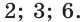
Метод замены переменной
Пример:
Решите уравнение 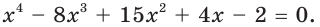
Решение:
Преобразуем данное уравнение так:
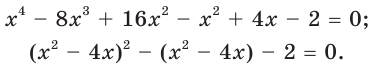
Сделав замену 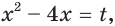 получаем уравнение
получаем уравнение 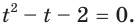
Отсюда 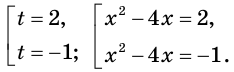
Ответ: 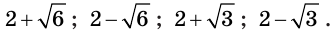
Пример:
Решите уравнение 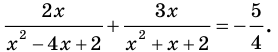
Решение:
Поскольку число 0 не является корнем данного уравнения, то, разделив числитель и знаменатель каждой из дробей левой части уравнения на 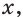 получаем уравнение, равносильное данному:
получаем уравнение, равносильное данному:
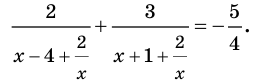
Сделаем замену 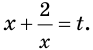 Тогда
Тогда
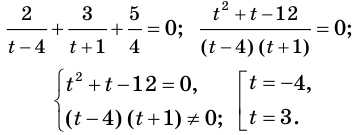
Имеем: 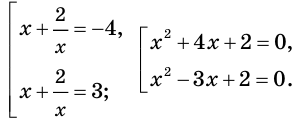
Ответ: 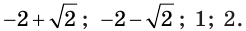
Пример:
Решите уравнение 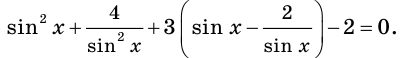
Решение:
Пусть 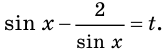 Тогда
Тогда 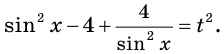
Отсюда 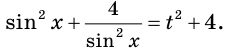
Исходное уравнение принимает вид 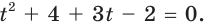
Отсюда 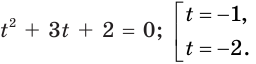
Получаем, что исходное уравнение равносильно совокупности
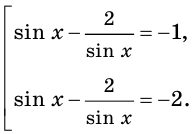
Отсюда 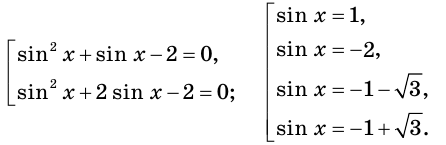
Поскольку 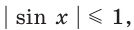 то получаем
то получаем 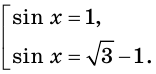
Отсюда 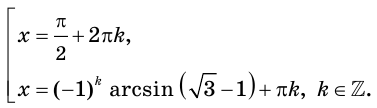
Пример:
Решите уравнение 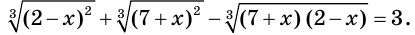
Решение:
Пусть 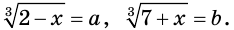 Тогда
Тогда
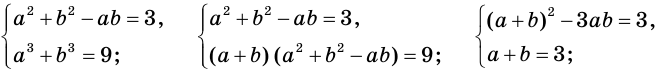
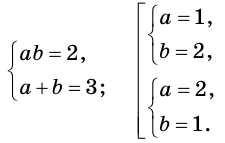
Теперь можно записать: 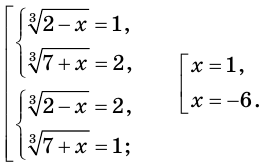
Ответ: 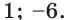
Применение свойств функций
Поиск области определения функции 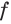 может быть ключом к решению уравнения
может быть ключом к решению уравнения 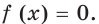
Пример:
Решите уравнение 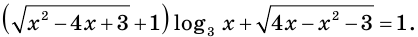
Решение:
Применение любых приемов, связанных с преобразованием левой части данного уравнения, вряд ли приведет к успеху. Вместе с тем нахождение области определения уравнения — путь вполне естественный.
Имеем: 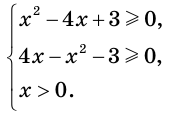
Решив эту систему, получим, что областью определения рассматриваемого уравнения является двухэлементное множество 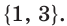 Проверка показывает, что число 1 не подходит, а число 3 является корнем исходного уравнения.
Проверка показывает, что число 1 не подходит, а число 3 является корнем исходного уравнения.
Ответ: 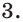
Пусть функции 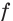 и
и 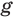 таковы, что для любого
таковы, что для любого 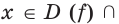
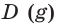 выполняются неравенства
выполняются неравенства 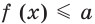 и
и 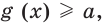 где
где  некоторое число. Тогда уравнение
некоторое число. Тогда уравнение 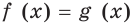 равносильно системе
равносильно системе
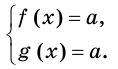
С помощью этих очевидных соображений можно решить целый ряд уравнений.
Пример:
Решите уравнение 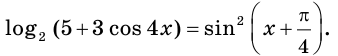
Решение:
Поскольку 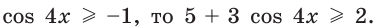
Отсюда 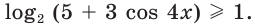 В то же время
В то же время 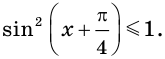
Поэтому исходное уравнение равносильно системе
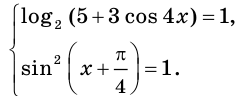
Отсюда 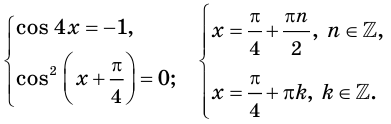
Ответ: 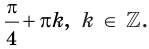
Вы знаете, что если функция 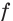 является возрастающей (убывающей), то уравнение
является возрастающей (убывающей), то уравнение 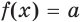 имеет не более одного корня. Если удается корень угадать, то решение такого уравнения завершено.
имеет не более одного корня. Если удается корень угадать, то решение такого уравнения завершено.
Пример:
Решите уравнение 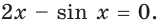
Решение:
Рассмотрим функцию 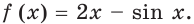
Имеем: 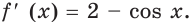 Поскольку для любого
Поскольку для любого 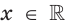 выполняется неравенство
выполняется неравенство 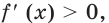 то функция
то функция 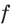 возрастает на
возрастает на 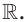 Следовательно, уравнение
Следовательно, уравнение 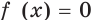 имеет не более одного корня. Очевидно, что число 0 является корнем данного уравнения.
имеет не более одного корня. Очевидно, что число 0 является корнем данного уравнения.
Ответ: 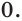
Пример:
Решите уравнение 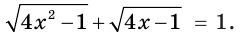
Решение:
Рассмотрим функцию 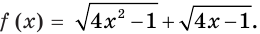
Легко определить, что 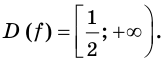
Каждая из функций 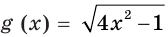 и
и 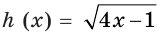 является возрастающей на
является возрастающей на 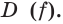 Следовательно, функция
Следовательно, функция 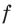 также возрастает на
также возрастает на 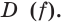
Очевидно, что число 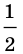 является корнем исходного уравнения. Этот корень единственный.
является корнем исходного уравнения. Этот корень единственный.
Ответ: 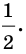
Основные методы решения неравенств
В таблице приведены схемы решения некоторых типовых неравенств.
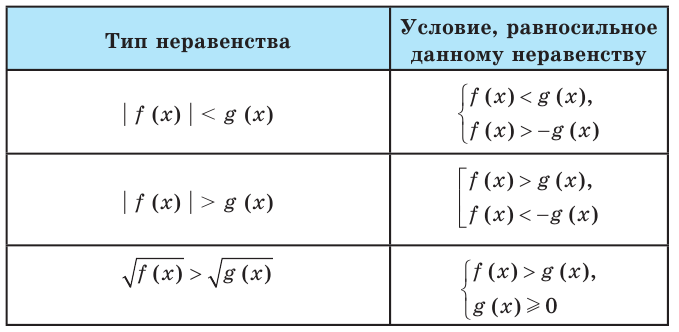

Часто решение неравенств сводится к решению типовых неравенств, приведенных в таблице. Это иллюстрируют упражнения №№ 34.1-34.10. К тем неравенствам, которые не сводятся к типовым, применяют специальные методы и приемы. Рассмотрим некоторые из них.
Метод равносильных преобразований
Пример:
Решите неравенство 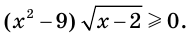
Решение:
Заметим, что ошибочными являются следующие соображения: «Поскольку при 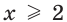 выполняется неравенство
выполняется неравенство 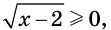 то исходное неравенство равносильно системе
то исходное неравенство равносильно системе 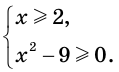 Отсюда
Отсюда 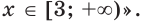 Несложно увидеть, что при таком «решении» теряется решение
Несложно увидеть, что при таком «решении» теряется решение 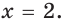
Правильным решением данного неравенства является, например, переход к совокупности:
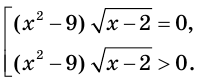
Решением уравнения совокупности являются числа 2 и 3, множеством решений неравенства — промежуток 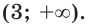
Ответ: 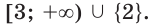
Пример:
Решите неравенство 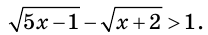
Решение:
Сразу возводить обе части неравенства в квадрат не является рациональным шагом, поскольку этот переход требует учитывать такое дополнительное условие: 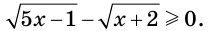
Данное в условии неравенство целесообразно записать так:
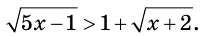
Поскольку обе части последнего неравенства могут принимать только неотрицательные значения, то можно перейти к равносильному неравенству: 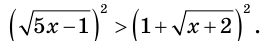
Далее получаем:
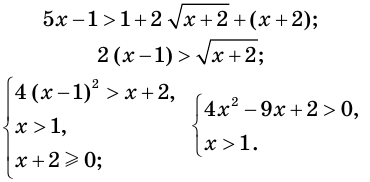
Отсюда 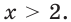
Ответ: 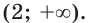
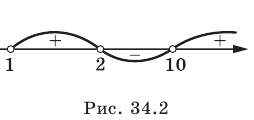
Метод интервалов
Пусть нули функции и ее точки разрыва разбивают область определения функции на некоторые промежутки (рис. 34.1). Тогда из следствия из теоремы Больцано-Коши (см. пункт 5) следует, что эти промежутки являются промежутками знакопостоянства функции. Определить знак функции на каждом из таких промежутков можно с помощью «пробных точек».
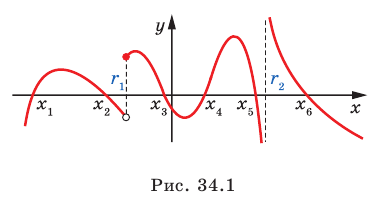
Эти соображения являются основой для решения широкого класса неравенств.
Пример:
Решите неравенство 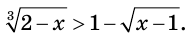
Решение:
Рассмотрим функцию 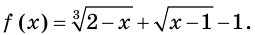
Имеем: 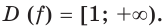 Найдем нули функции
Найдем нули функции 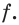 Для этого решим уравнение
Для этого решим уравнение 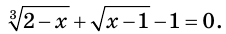
Сделаем замену: 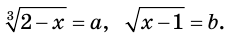 Имеем:
Имеем: 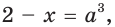
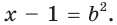
Отсюда 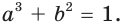 Получаем систему:
Получаем систему: 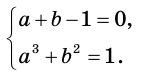
Отсюда 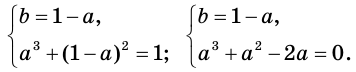
Эта система имеет три решения: 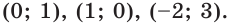
Теперь можно записать: 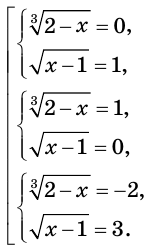 Отсюда
Отсюда 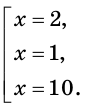
Поскольку функция 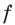 непрерывна, то ее нули, то есть числа 1, 2, 10, разбивают ее область определения
непрерывна, то ее нули, то есть числа 1, 2, 10, разбивают ее область определения  на промежутки знакопостоянства:
на промежутки знакопостоянства: 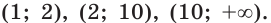
Имеем:
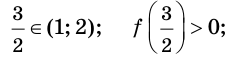
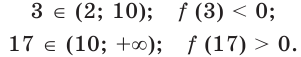
Знаки функции на промежутках знакопостоянства показаны на рисунке 34.2. Ответ: 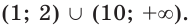
Применение свойств функций
При решении примера 3 было использовано такое свойство функции, как непрерывность. Нередко ключом к решению могут быть и другие свойства функций: периодичность, четность (нечетность), возрастание (убывание), наибольшее и наименьшее значения функции и т. д.
Например, если 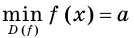 и
и 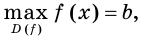 то множеством решений каждого из неравенств
то множеством решений каждого из неравенств 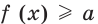 и
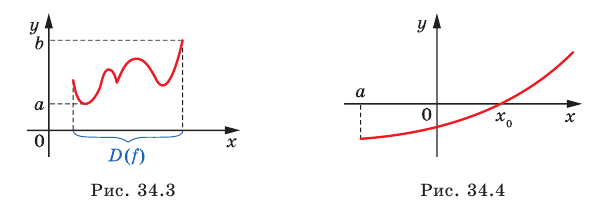
и 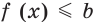 является множество
является множество  (рис. 34.3).
(рис. 34.3).
Еще один пример: если функция 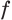 возрастает на промежутке
возрастает на промежутке 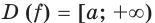 и
и 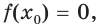 то множеством решений неравенства
то множеством решений неравенства 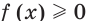 является промежуток
является промежуток 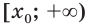 (рис. 34.4). Рассмотрим примеры, иллюстрирующие вышесказанное.
(рис. 34.4). Рассмотрим примеры, иллюстрирующие вышесказанное.
Пример:
Решите неравенство 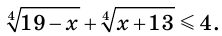
Решение:
Рассмотрим функцию 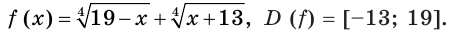
Имеем: 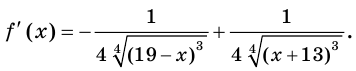
Решив уравнение 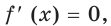 получим
получим 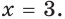
Сравнивая числа 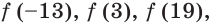 приходим к выводу, что
приходим к выводу, что 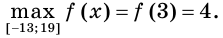
Тогда неравенство 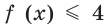 выполняется для всех
выполняется для всех 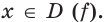
Ответ: 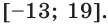
Пример:
Решите неравенство 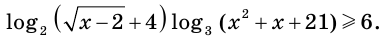
Решение:
Областью определения данного неравенства является промежуток 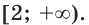
Поскольку 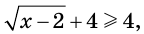 то
то 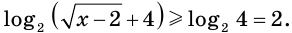
При 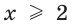 получаем, что
получаем, что 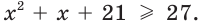 Тогда
Тогда 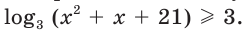
Имеем: 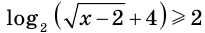 и
и 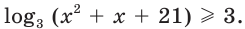 Отсюда для всех
Отсюда для всех 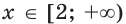 выполняется неравенство
выполняется неравенство
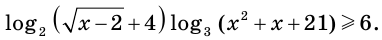
Ответ: 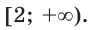
Пример:
Решите неравенство
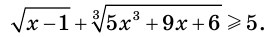
Решение:
Рассмотрим функцию
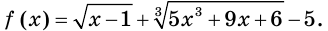
Легко показать, что эта функция возрастает на 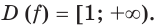 Очевидно, что
Очевидно, что 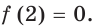 Тогда множеством решений неравенства
Тогда множеством решений неравенства 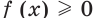 является промежуток
является промежуток 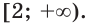
Ответ: 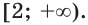
---10клас
Графики уравнений и неравенств с двумя переменными
Построение графиков функции вида 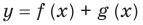
Если нам известны графики функций 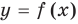 и
и 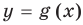 , то эскиз графика функции
, то эскиз графика функции 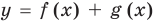 можно построить так: изобразить водной системе координат графики функций
можно построить так: изобразить водной системе координат графики функций 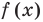 и
и 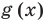 , а потом построить искомый график по точкам, выполняя для каждого значения
, а потом построить искомый график по точкам, выполняя для каждого значения 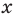 (из области определения функции
(из области определения функции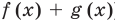 ) необходимые операции с отрезками, изображающими соответствующие ординаты
) необходимые операции с отрезками, изображающими соответствующие ординаты 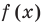 и
и 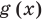 .
.
Аналогично можно построить и схематические графики функций
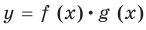 и
и 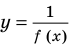
Пример:
Постройте график функции 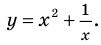
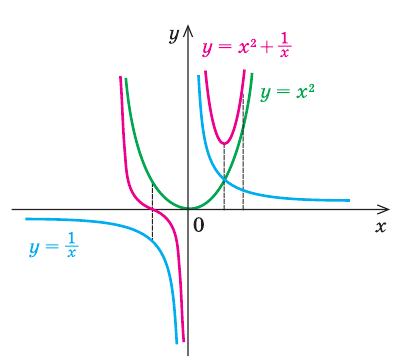
Комментарий:
Построим в одной системе координат графики функций-слагаемых: 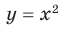 и
и 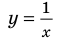 (на рисунке они показаны соответственно зеленой и синими линиями). Для каждого значения
(на рисунке они показаны соответственно зеленой и синими линиями). Для каждого значения 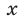 (кроме
(кроме 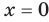 , которое не принадлежит области определения заданной функции) справа от оси
, которое не принадлежит области определения заданной функции) справа от оси 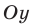 прибавляем соответствующие отрезки — значения функций
прибавляем соответствующие отрезки — значения функций 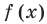 и
и 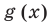 (обе функции имеют одинаковые знаки), слева от оси
(обе функции имеют одинаковые знаки), слева от оси  — вычитаем (функции имеют противоположные знаки). На рисунке розовой линией изображен график функции
— вычитаем (функции имеют противоположные знаки). На рисунке розовой линией изображен график функции 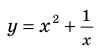
2. Графики уравнений и неравенств с двумя переменными
Определение: Графиком уравнения (неравенства) с двумя переменными 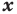 и
и 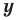 называется множество всех точек координатной плоскости с координатами
называется множество всех точек координатной плоскости с координатами 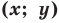 , где пара чисел
, где пара чисел 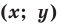 является решением соответствующего уравнения.
является решением соответствующего уравнения.
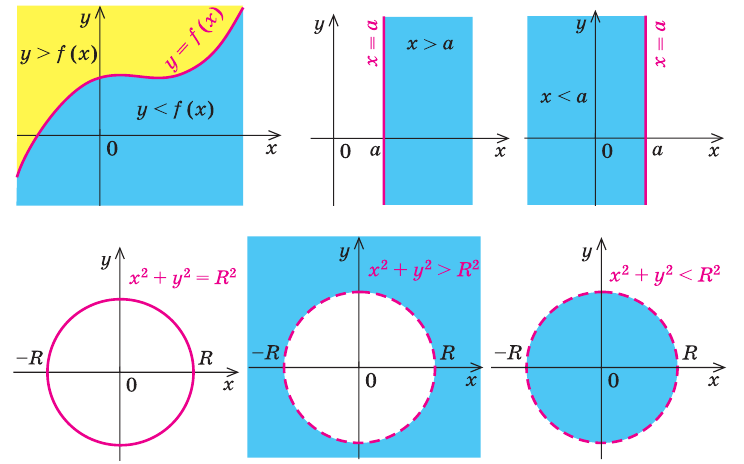
Графики некоторых уравнений и неравенств
3. Геометрические преобразования графика уравнения 
Преобразование
Параллельный перенос графика уравнения  на вектор
на вектор 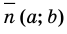
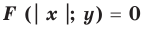
Часть графика уравнения 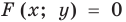 справа от оси
справа от оси  (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси
(и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси  .
.
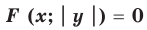
Часть графика уравнения 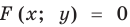 выше оси
выше оси  (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси
(и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси  .
.
Объяснение и обоснование:
Построение графиков функции вида y=f(x)+g(x)
Построение графиков функций вида 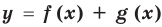 .
.
Если известны графики функций 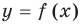 и
и 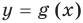 , то можно построить ориентировочный вид графика функции
, то можно построить ориентировочный вид графика функции 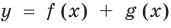 , или
, или 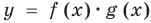 , или
, или 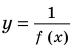 . Для этого достаточно изобразить в одной системе координат f М
. Для этого достаточно изобразить в одной системе координат f М
графики функций 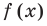 и
и 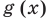 , а потом построить искомый график по точкам, выполняя для каждого значения
, а потом построить искомый график по точкам, выполняя для каждого значения 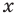 (из области определения заданной функции) необходимые операции над отрезками (или над длинами этих отрезков), которые изображают соответствующие ординаты функций
(из области определения заданной функции) необходимые операции над отрезками (или над длинами этих отрезков), которые изображают соответствующие ординаты функций 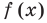 и
и 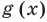 .
.
Пример построения графика функции вида 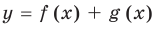 приведен
приведен
в таблице 13, а графика функции вида 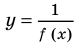 далее в задаче 1 (в последнем случае удобно строить графики функций
далее в задаче 1 (в последнем случае удобно строить графики функций 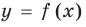 и
и 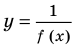 не в одной системе координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
не в одной системе координат, а в разных, расположенных так, чтобы их оси ординат находились на одной прямой).
Заметим, что такой способ построения графика функции не всегда дает возможность определить все характерные особенности поведения графика (часто это можно сделать только в результате специального исследования функции, которое будет рассмотрено в учебнике для 11 класса), но во многих случаях приведенный способ позволяет получить определенное представление о виде графика заданной функции.
Графики уравнений и неравенств с двумя переменными
С понятием графика уравнения с двумя переменными вы ознакомились в курсе алгебры. Аналогично вводится и понятие графика неравенства с двумя переменными. Поэтому можно дать общее определение этих графиков:
Графиком уравнения (неравенства) с двумя переменными  и
и  называется множество всех точек координатной плоскости с координатами
называется множество всех точек координатной плоскости с координатами  , где пара чисел
, где пара чисел  является решением соответствующего уравнения (неравенства).
является решением соответствующего уравнения (неравенства).
Для построения графика неравенства 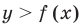 (или
(или 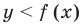 ) достаточно иметь график функции
) достаточно иметь график функции 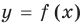 . Действительно, по определению график функции
. Действительно, по определению график функции 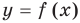 состоит из всех точек
состоит из всех точек  координатной плоскости с координатами
координатной плоскости с координатами 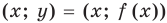 . Тогда для каждого значения
. Тогда для каждого значения 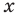 точки, координаты которых удовлетворяют неравенству
точки, координаты которых удовлетворяют неравенству 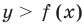 , будут находиться выше точки
, будут находиться выше точки 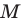 (рис. 55, а), а точки, координаты которых удовлетворяют неравенству
(рис. 55, а), а точки, координаты которых удовлетворяют неравенству 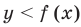 , будут находиться ниже точки
, будут находиться ниже точки 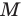 (рис. 55, б). Таким образом,
(рис. 55, б). Таким образом,
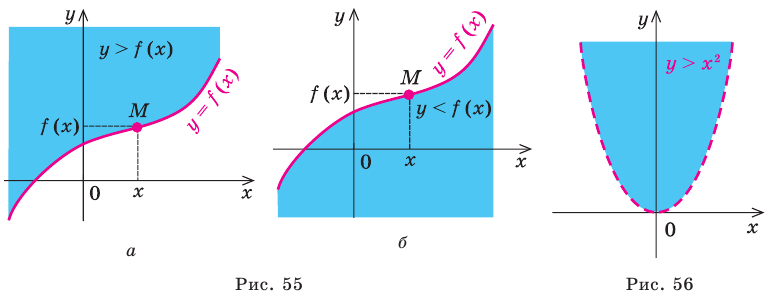
график неравенства 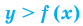 состоит из всех точек координатной плоскости, находящихся выше графика функции
состоит из всех точек координатной плоскости, находящихся выше графика функции 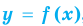 , а график неравенства
, а график неравенства 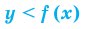 состоит из всех точек координатной плоскости, находящихся ниже графика функции
состоит из всех точек координатной плоскости, находящихся ниже графика функции 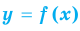 .
.
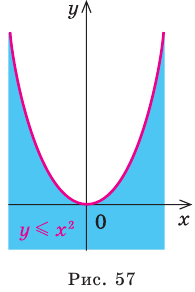
Например, на рисунке 56 изображен график неравенства 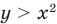 , а на рисунке 57 — график неравенства
, а на рисунке 57 — график неравенства 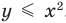 . Поскольку точки графика
. Поскольку точки графика 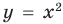 не принадлежат графику неравенства
не принадлежат графику неравенства 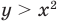 , то на первом графике парабола
, то на первом графике парабола 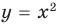 изображена штриховой линией; а так как точки графика
изображена штриховой линией; а так как точки графика 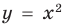 принадлежат графику неравенства
принадлежат графику неравенства 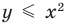 , то на втором графике парабола
, то на втором графике парабола 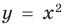 изображена сплошной линией.
изображена сплошной линией.
Аналогично, если на координатной плоскости есть прямая 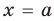 , то графиком неравенства
, то графиком неравенства  будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства
будут все точки координатной плоскости, находящиеся справа от этой прямой, а графиком неравенства  будут все точки координатной плоскости, находящиеся слева от этой прямой.
будут все точки координатной плоскости, находящиеся слева от этой прямой.
Например, на рисунке 58 изображен график неравенства 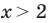 , а на рисунке 59 — график неравенства
, а на рисунке 59 — график неравенства 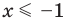 .
.

Отметим, что в том случае, когда на координатной плоскости есть изображение окружности 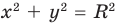 , то
, то
графиком неравенства 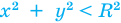 будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства
будут все точки координатной плоскости, находящиеся внутри окружности, а графиком неравенства 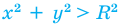 будут все точки координатной плоскости, находящиеся вне окружности.
будут все точки координатной плоскости, находящиеся вне окружности.
Действительно, если на координатной плоскости рассмотреть точку 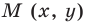 , то
, то 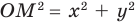 (
( — начало координат). Если
— начало координат). Если 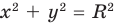 (где
(где 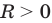 ), то
), то 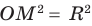 , таким образом,
, таким образом, 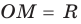 — точка
— точка 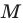 лежит на окружности радиуса
лежит на окружности радиуса 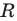 с центром в начале координат (рис. 60, а). Если
с центром в начале координат (рис. 60, а). Если 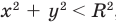 , то
, то 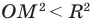 , таким образом,
, таким образом, 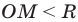 . То есть неравенству
. То есть неравенству 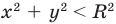 удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса
удовлетворяют координаты всех точек (и только этих точек), которые находятся внутри круга, ограниченного окружностью радиуса 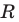 с центром в начале координат (рис. 60, б).
с центром в начале координат (рис. 60, б).
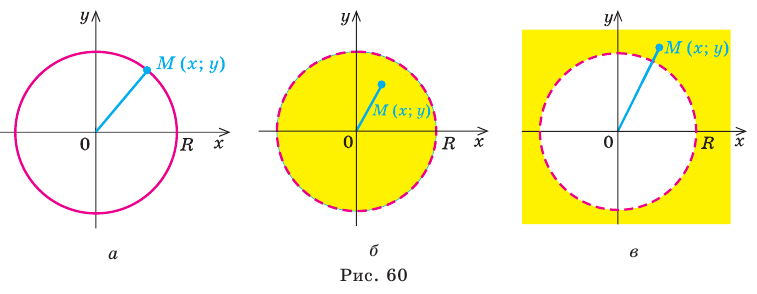
Если 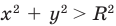 , то
, то 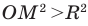 , таким образом,
, таким образом, 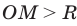 . То есть неравенству
. То есть неравенству 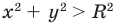 удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса
удовлетворяют координаты всех точек (и только этих точек), которые находятся вне круга, ограниченного окружностью радиуса 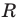 с центром в начале координат (рис. 60, в). Аналогично, если на плоскости есть изображение окружности
с центром в начале координат (рис. 60, в). Аналогично, если на плоскости есть изображение окружности 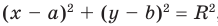 , то графиком неравенства
, то графиком неравенства 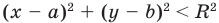 будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства
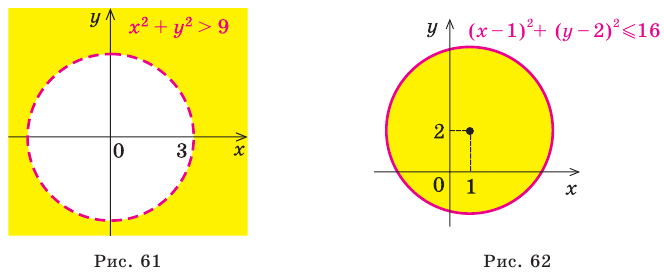
будут все точки координатной плоскости, находящиеся внутри этой окружности, а графиком неравенства 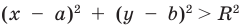 будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства
будут все точки координатной плоскости, находящиеся вне окружности. Например, на рисунке 61 изображен график неравенства 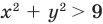 , а на рисунке 62 — график неравенства
, а на рисунке 62 — график неравенства 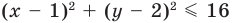 .
.
Геометрические преобразования графика уравнения F (x: y) =0
Геометрические преобразования графика уравнения 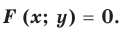
По определению график уравнения
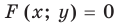 (1)
(1)
состоит из всех точек 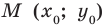 координатной плоскости, координаты
координатной плоскости, координаты 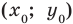 которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел
которых являются решениями этого уравнения. Это означает, что при подстановке пары чисел 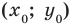 в данное уравнение оно обращается в верное числовое равенство, таким образом,
в данное уравнение оно обращается в верное числовое равенство, таким образом, 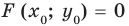 — верное равенство.
— верное равенство.
Рассмотрим точку 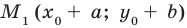 . Если координаты этой точки подставить в уравнение
. Если координаты этой точки подставить в уравнение
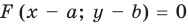 , (2)
, (2)
то получим верное равенство 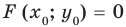 . Поэтому координаты точки
. Поэтому координаты точки 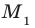 являются решениями уравнения (2), значит, точка
являются решениями уравнения (2), значит, точка 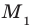 принадлежит графику уравнения
принадлежит графику уравнения 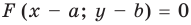 .
.
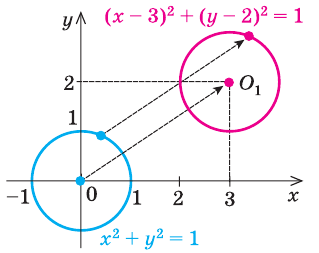
Точку 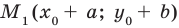 можно получить из точки
можно получить из точки 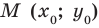 параллельным переносом ее на вектор
параллельным переносом ее на вектор 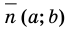 . Поскольку каждая точка
. Поскольку каждая точка 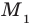 графика уравнения
графика уравнения 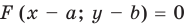 получается из точки
получается из точки 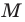 графика уравнения
графика уравнения 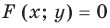 параллельным переносом ее на вектор
параллельным переносом ее на вектор 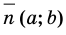 (рис. 63), то и весь
(рис. 63), то и весь
график уравнения 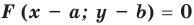 можно получить из графика уравнения
можно получить из графика уравнения 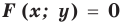 параллельным переносом его на вектор
параллельным переносом его на вектор 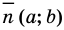 .
.
Для обоснования связи между графиками 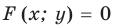 и
и 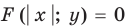 достаточно заметить, что при
достаточно заметить, что при  уравнение
уравнение 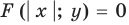 совпадает с уравнением
совпадает с уравнением 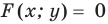 , таким образом, совпадают и их графики справа от оси
, таким образом, совпадают и их графики справа от оси  и на самой оси. Пусть точка
и на самой оси. Пусть точка 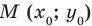 (где
(где 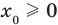 ) — одна из общих точек этих графиков. Тогда
) — одна из общих точек этих графиков. Тогда 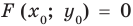 — верное равенство.
— верное равенство.
Рассмотрим точку 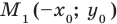 . Если координаты этой точки подставить в уравнение
. Если координаты этой точки подставить в уравнение 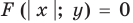 и учесть, что
и учесть, что 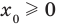 , то получим верное равенство
, то получим верное равенство 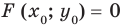 . Поэтому координаты точки
. Поэтому координаты точки 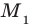 являются решениями уравнения
являются решениями уравнения 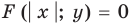 , значит, точка
, значит, точка 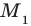 принадлежит графику этого уравнения. Учитывая, что точки
принадлежит графику этого уравнения. Учитывая, что точки 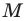 и
и 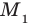 симметричны относительно оси
симметричны относительно оси 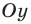 (рис. 64):
(рис. 64):
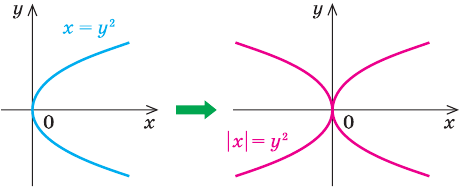
график уравнения 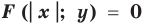 можно получить из графика уравнения
можно получить из графика уравнения 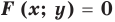 следующим образом: часть графика уравнения
следующим образом: часть графика уравнения 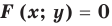 справа от оси
справа от оси 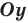 (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси
(и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси 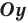 .
.
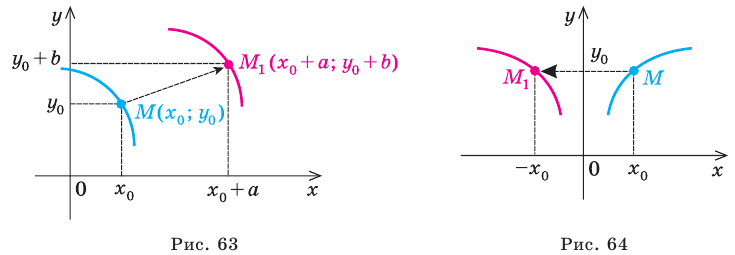
Аналогично обосновывается, что
для построения графика уравнения 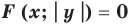 часть графика уравнения
часть графика уравнения 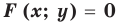 выше оси
выше оси  (и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси
(и на самой оси) остается без изменений, и эта же часть графика отображается симметрично относительно оси  .
.
В таблице 13 приведены простейшие примеры использования геометрических преобразований графиков уравнений. Указанные соотношения приходится применять в заданиях типа: построить график уравнения или неравенства или изобразить на координатной плоскости множество точек, координаты которых удовлетворяют заданному уравнению (неравенству).
Примеры решения задач:
Пример №426
Постройте график функции 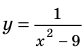
Решение:
► 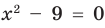 при
при 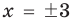 . Поэтому область определения заданной функции:
. Поэтому область определения заданной функции:
 то есть
то есть 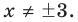
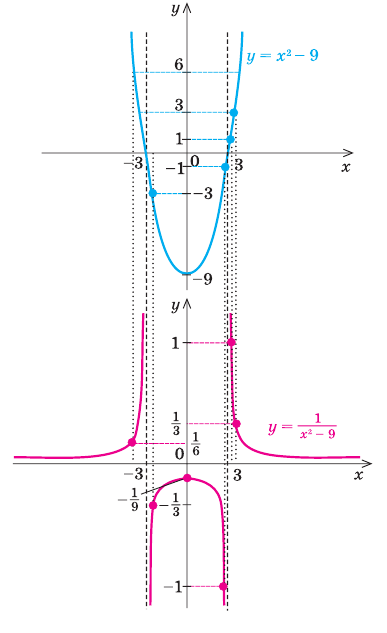
Комментарий:
Построим две системы координат так, чтобы оси ординат были у них на одной прямой. В тех точках, где функция 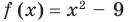 равна нулю
равна нулю 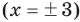 , не существует графика функции
, не существует графика функции 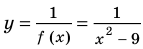 . Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции
. Поэтому проведем через эти точки вертикальные прямые, которые не пересекают график функции 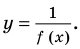
Затем для каждого значения 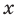 разделим 1 на соответствующее значение ординаты
разделим 1 на соответствующее значение ординаты 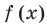 (используя то, что ординаты
(используя то, что ординаты 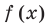 отмечены на верхнем графике). На рисунке розовой линией изображен результат — график функции
отмечены на верхнем графике). На рисунке розовой линией изображен результат — график функции 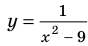 . (Для построения этого графика масштаб по осям
. (Для построения этого графика масштаб по осям  и
и  выбран разный.)
выбран разный.)
Пример №427
Покажите штриховкой на координатной плоскости множество точек, координаты которых удовлетворяют системе
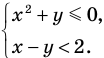
Решение:
► Заданная система равносильна системе 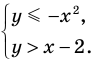
Изобразим штриховкой графики неравенств системы (первого — вертикальной штриховкой, второго — горизонтальной):
Тогда множество точек, координаты которых удовлетворяют системе, будет таким:
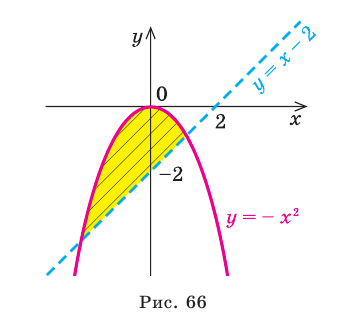
Комментарий:
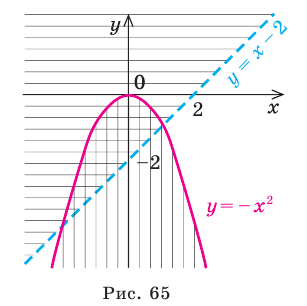
Перепишем заданную систему так, чтобы было удобно изображать графики данных неравенств (то есть запишем неравенства в виде 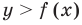 или
или 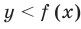 ). Множество точек, координаты которых удовлетворяют неравенству
). Множество точек, координаты которых удовлетворяют неравенству 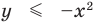 , является объединением точек параболы
, является объединением точек параболы 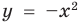 и точек координатной плоскости, находящихся ниже параболы (на рис. 65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству
и точек координатной плоскости, находящихся ниже параболы (на рис. 65 это множество обозначено вертикальной штриховкой). Множество точек, координаты которых удовлетворяют неравенству 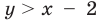 , состоит из точек координатной плоскости, находящихся выше прямой
, состоит из точек координатной плоскости, находящихся выше прямой 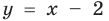 (на рисунке это множество обозначено горизонтальной штриховкой).
(на рисунке это множество обозначено горизонтальной штриховкой).
Системе неравенств удовлетворяют координаты тех и только тех точек, которые принадлежат пересечению множеств точек, заданных каждым из неравенств данной системы (на рисунке пересечению множеств соответствует та область, где штриховки наложились одна на другую).
Заметим, что в подобных заданиях можно не выполнять промежуточных рисунков, а сразу штриховать искомое множество точек координатной плоскости (выше прямой 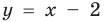 и ниже параболы
и ниже параболы 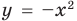 вместе с той частью параболы, которая лежит выше прямой; рис. 66).
вместе с той частью параболы, которая лежит выше прямой; рис. 66).
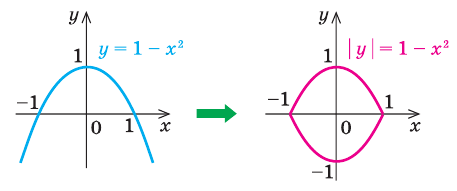
Пример №428
Постройте график уравнения 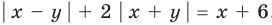 .
.
Ориентир
Для упрощения выражения с несколькими модулями с двумя переменными можно найти нули подмодульных выражений (то есть приравнять их к нулю) и разбить область определения рассматриваемого выражения на несколько частей, в каждой из которых знаки всех модулей раскрываются однозначно.
Используя этот ориентир, получаем план решения примера. Приравняем к нулю подмодульные выражения 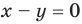 (отсюда
(отсюда 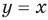 ) и
) и 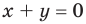 (отсюда
(отсюда 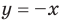 ). Прямые
). Прямые 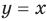 и
и 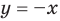 разбивают координатную плоскость на четыре области. В каждой из этих областей знак каждого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
разбивают координатную плоскость на четыре области. В каждой из этих областей знак каждого модуля раскрывается однозначно, после преобразования полученного равенства строим соответствующую часть графика заданного уравнения.
Решение:
► 1. Область определения: 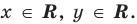
2. 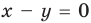 при
при 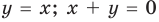 при
при 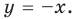
3. Прямые 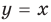 и
и 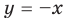 разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго подмодульных выражений (рис. 67, а). (Будем считать, что каждая область берется вместе с лучами, которые ее ограничивают.) Действительно, если точки находятся в области I или на ее границе, то их координаты удовлетворяют системе неравенств
разбивают координатную плоскость на четыре части, в каждой из которых обозначены знаки первого и второго подмодульных выражений (рис. 67, а). (Будем считать, что каждая область берется вместе с лучами, которые ее ограничивают.) Действительно, если точки находятся в области I или на ее границе, то их координаты удовлетворяют системе неравенств 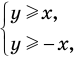 которую можно записать так:
которую можно записать так: 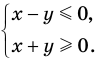
Тогда в области I первое подмодульное выражение отрицательно, а второе — положительно, поэтому данное уравнение имеет вид 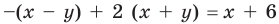 . Отсюда
. Отсюда 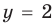 . Строим ту часть графика этой функции, которая находится в области I (рис. 67, б).
. Строим ту часть графика этой функции, которая находится в области I (рис. 67, б).
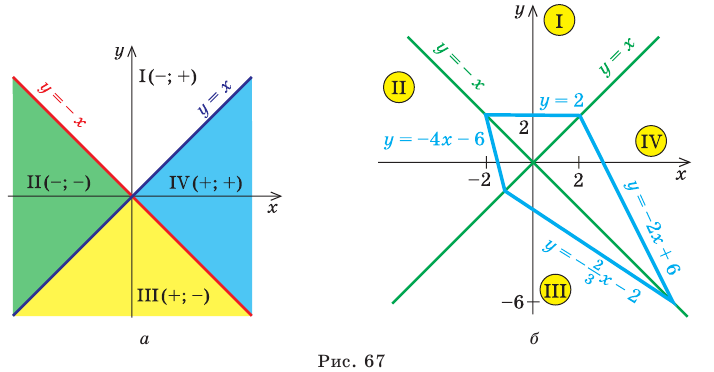
Аналогично для точек области II: 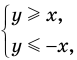 то есть
то есть 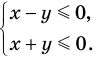
Таким образом, в области II данное уравнение имеет вид 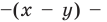
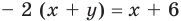 . Отсюда
. Отсюда 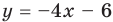 . Строим ту часть графика этой
. Строим ту часть графика этой
функции, которая находится в области II.
Если точки находятся в области III, то 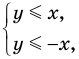 то есть
то есть 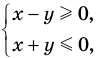 из данного уравнения получаем
из данного уравнения получаем 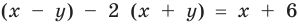 . Отсюда
. Отсюда 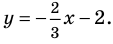
Если точки находятся в области IV, то 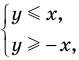 то есть
то есть 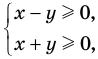 из
из
данного уравнения имеем 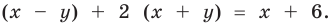 Отсюда
Отсюда 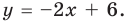
Окончательный вид графика уравнения приведен на рисунке 67, б.
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |