
Уравнение линии - определение с примерами решения
Содержание:
Множества:
Под множеством X = {х, х\ х", ...} понимается собрание (совокупность) некоторых элементов х, х\ х'\ ... . Если х есть элемент множества X, то пишут х € X (читается: х принадлежит X); если у не является элементом множества X, то пишут у t X (читается: у не принадлежит множеству X).
Пример:
X — множество всех студентов в данной аудитории.
Пример:
Х = {1,2, 3, ...} — множество натуральных чисел.
Удобно ввести понятие пустого множества 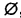
Пример:
Множество трехголовых людей пусто.
Множества X и X' считаются равными, т. е. X = X', если они состоят из одних и тех же элементов.
Определение: Множество У, состоящее из части элементов множества X или совпадающее с ним, называется подмножеством множества X; в этом случае пишут

Условились считать, что пустое множество есть подмножество любого множества.
Если множества изображать «логическими фигурами», то соотношению (1) соответствует рис. 10.
Если под символом V понимать «для любого», то соотношение (1) эквивалентно следующему:
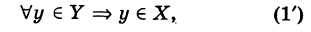
где стрелка 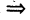 заменяет слово «следует».
заменяет слово «следует».
Пример:
Пусть X — множество всех студентов первого курса, У — множество студенток первого курса. Очевидно, 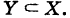
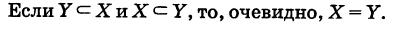
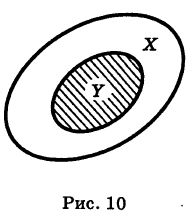
Определение: Под объединением (суммой) двух множеств X и Y понимается множество X U У (U — знак объединения), состоящее из всех элементов, принадлежащих хотя бы одному из данных множеств, т. е. входящих или в X, или в У, или в X и в У одновременно (рис. 11).
Аналогично определяется объединение большего числа множеств. Так, под объединением X U У U Z трех множеств понимается множество всех элементов, принадлежащих хотя бы одному из множеств X, У, Z. Логически знак объединения множеств соответствует союзу «или» (соединительному).
Например: {1, 2, 3} U {2, 3, 4} - {1, 2, 3, 4}.
Определение: Под пересечением (произведением) двух множеств X и У понимается множество 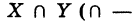 знак пересечения), состоящее из всех элементов, принадлежащих как одному у так и другому множествам, т. е. входящих ив множество X, и в множество У (общая часть множеств) (рис. 11).
знак пересечения), состоящее из всех элементов, принадлежащих как одному у так и другому множествам, т. е. входящих ив множество X, и в множество У (общая часть множеств) (рис. 11).
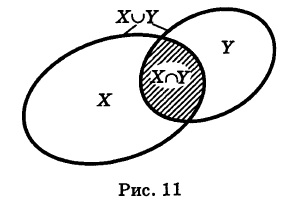
Таким образом, знак пересечения множеств логически соответствует союзу «и». Если множества X и У не имеют общих элементов, то их пересечение пусто:
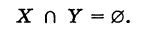
Аналогично определяется пересечение большего числа множеств. Так, под пересечением 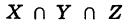 трех множеств понимается множество всех элементов, принадлежащих одновременно множествам X, Y и Z.
трех множеств понимается множество всех элементов, принадлежащих одновременно множествам X, Y и Z.
Например: {1, 2, 3} 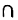 {2, 3, 4} = = {2, 3}.
{2, 3, 4} = = {2, 3}.
Определение: Для множеств X и У под их разностью Х\У понимается множество, содержащее все элементы множества X, не входящие в множество У (рис. 12).
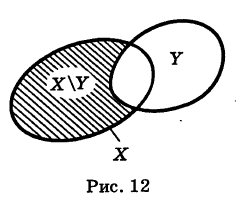
Если У X, то множество Ус = Х\У называется дополнением множества У до множества X (рис. 13).
Очевидно, 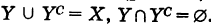 .
.
Например: {1, 2, 3}\{2, 3, 4} = {1}. 
Метод координат на плоскости
Раздел математики, занимающийся изучением свойств геометрических фигур с помощью алгебры, носит название аналитической геометрии, а использование для этой цели координат называется методом координат.
Выше мы применили метод координат для решения ряда важных, но частных задач. Теперь мы приступим к систематическому изложению того, как в аналитической геометрии решается общая задача, состоящая в исследовании методами математического анализа формы, расположения и свойств данной линии.
Пусть мы имеем некоторую линию на плоскости (рис. 14). Координаты х и у точки М, лежащей на этой линии, не могут быть вполне произвольными; они должны быть подчинены известным ограничениям, обусловленным геометрическими свойствами данной линии. Тот факт, что числа х и у являются координатами точки, лежащей на данной линии, аналитически записывается в виде некоторого уравнения. Это уравнение называется уравнением линии на плоскости.
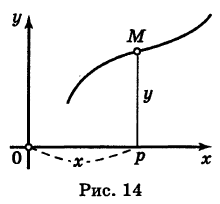
Сущность метода координат на плоскости заключается в том, что всякой плоской линии сопоставляется ее уравнение1*, а затем свойства этой линии изучаются путем аналитического исследования соответствующего уравнения.
Линия как множество точек
Линия на плоскости обычно задается как множество точек, обладающих некоторыми геометрическими свойствами, исключительно им присущими.
Пример:
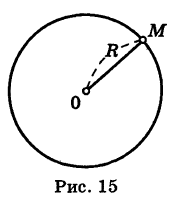
Окружность радиуса R (рис. 15) есть множество всех точек плоскости, удаленных на расстояние R от некоторой ее точки О (центр окружности).
Иными словами, на окружности расположены те и только те точки, расстояние которых от центра окружности равно ее радиусу.
Пример:
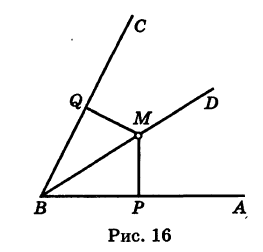
Биссектриса угла ABC (рис. 16) есть множество всех точек, лежащих внутри угла и равноудаленных от его сторон. Этим утверждается, что: 1) для каждой точки М, лежащей на биссектрисе BZ), длины перпендикуляров MP и MQ, опущенных соответственно на стороны ВА и ВС угла, равны между собой: MP = MQ, и 2) всякая точка, находящаяся внутри угла ABC и не лежащая на его биссектрисе, будет ближе к одной стороне угла, чем к другой.
Уравнение линии на плоскости
Сформулируем теперь точнее определение уравнения линии1* на плоскости.
Определение: Уравнением линии (уравнением кривой) на плоскости Оху называется уравнение, которому удовлетворяют координаты х и у каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
Таким образом, для того чтобы установить, что данное уравнение является уравнением некоторой линии К, необходимо и достаточно: 1) доказать, что координаты .любой точки, лежащей на линии К у удовлетворяют этому уравнению, и 2) доказать, обратно, что если координаты некоторой точки удовлетворяют этому уравнению, то точка обязательно лежит на линии К.
Отсюда уже автоматически будет следовать, что: 1') если координаты какой-нибудь точки не удовлетворяют данному уравнению, то точка эта не лежит на линии К, и 2') если точка не лежит на линии К, то ее координаты не удовлетворяют данному уравнению.
Если точка М (*, у) передвигается по линии К, то ее координаты х и у, изменяясь, все время удовлетворяют уравнению этой кривой. Поэтому координаты точки М (х, у) называются текущими координатами точки линии К.
На плоскости Оху текущие координаты точки М данной кривой К обычно обозначаются через х и у, причем первая из них есть абсцисса точки М, а вторая — ее ордината. Однако, если это целесообразно, текущие координаты точки М можно обозначать.
Линию мы часто будем называть кривой независимо от того, прямолинейна она или не прямолинейна любыми буквами, например М (X, У) или М 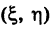 и т. п. Так, например, уравнения
и т. п. Так, например, уравнения
у = 2х и У = 2Х,
где точки N (х, у) и N (X, У) расположены на плоскости Оху, представляют собой уравнение одной и той же прямой на этой плоскости.
Основное понятие аналитической геометрии — уравнение линии — поясним на ряде примеров.
Пример:
Составить уравнение окружности данного радиуса R с центром в начале координат.
Решение:
Возьмем на окружности (рис. 17) произвольную точку М (х, у) и соединим ее с центром О. По определению окружности имеем ОМ = R,
т. е. 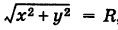 , откуда
, откуда
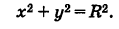
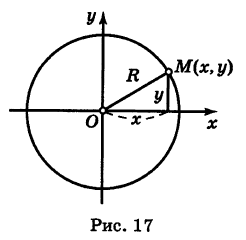
Уравнение (1) связывает между собой координаты х и у каждой точки данной окружности. Обратно, если координаты точки М (х, у) удовлетворяют уравнению (1), то, очевидно, ОМ = R и, следовательно, эта точка лежит на нашей окружности. Таким образом, уравнение (1) представляет собой уравнение окружности радиуса R с центром в начале координат.
Пример:
Составить уравнения биссектрис координатных углов.
Решение:
Рассмотрим сначала биссектрису I и III координатных углов (рис. 18, а). Возьмем на ней произвольную точку М (х, у). Если точка М лежит в I квадранте, то абсцисса и ордината ее обе положительны и равны между собой (по свойству биссектрисы). Если же точка М (jc, у) лежит в III квадранте, то абсцисса и ордината будут обе отрицательны, а модули их равны, поэтому будут равны и координаты хм у этой точки. Следовательно, в обоих случаях имеем

Обратно, если координаты х и у какой-нибудь точки М (х, у) удовлетворяют уравнению (2), то эта точка, очевидно, лежит на биссектрисе 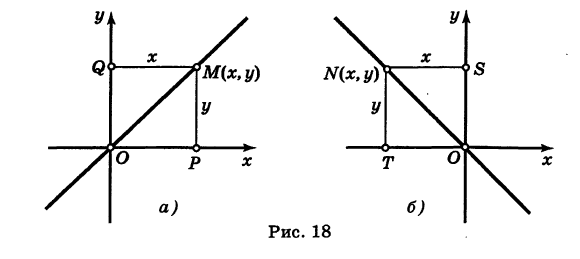
I и III координатных углов. Поэтому уравнение (2) представляет собой уравнение биссектрисы I и III координатных углов.
Рассмотрим теперь биссектрису II и IV координатных углов (рис. 18, б). Возьмем на ней произвольную точку N (х, у). В каком бы квадранте — II или IV — ни была расположена эта точка, координаты ее х и у равны по модулю и отличаются знаками.
Следовательно, в обоих случаях имеем

Обратно, если для какой-нибудь точки N (,х, у) выполнено уравнение (3), то эта точка, очевидно, лежит на биссектрисе II и IV координатных углов. Таким образом, уравнение (3) есть уравнение биссектрисы II и IV координатных углов.
Пример:
Составить уравнение прямой, параллельной оси ординат.
Решение:
Пусть прямая АВ || О у и пусть отрезок OA = а (рис. 19, а). Тогда для любой точки М (х, у) прямой АВ ее абсцисса х равна а:
х = а. (4)
Обратно, если абсцисса некоторой точки М (х, у) равна а, то эта точка лежит на прямой АВ.
Таким образом, уравнение (4) представляет собой уравнение прямой, параллельной оси Оу и отстоящей от нее на расстоянии, равном числовому значению а; при этом если прямая расположена справа от оси Оу, то а положительно; если же прямая расположена слева от оси Оу, то а отрицательно.
В частности, при а = 0 получаем уравнение оси ординат: х = 0.
Пример:
Составить уравнение прямой, параллельной оси абсцисс.
Решение:
Совершенно аналогично, если прямая CD || Ох и ОС = Ь (рис. 19, б), то ее уравнение будет
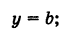
при этом если прямая CD расположена выше оси Оху то Ъ положительно, если же прямая CD расположена ниже оси Ох, то b отрицательно.
В частности, при b = 0 получаем уравнение оси абсцисс: у = 0. 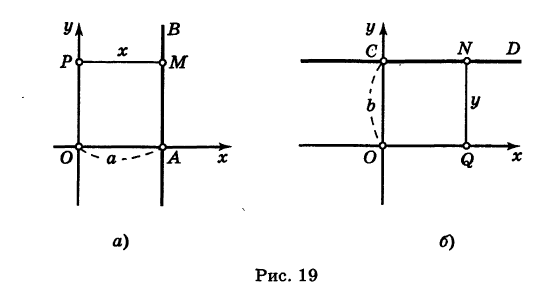
Пример:
Найти линию, расстояние точек которой от точки В (12, 16) в два раза больше, чем от точки А (3, 4).
Решение:
Если М (х, у) — произвольная точка искомой линии, то согласно условию задачи имеем

Чтобы составить уравнение этой линии, надо выразить AM и ВМ через координаты х и у точки М. На основании формулы расстояния между двумя точками имеем
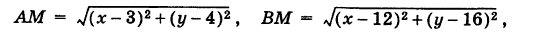
откуда, согласно соотношению (5),
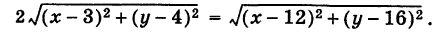
Это и есть уравнение искомой линии.
Но в таком виде трудно судить, какую линию представляет это уравнение, поэтому упростим его. Возведя обе части в квадрат и раскрыв скобки, получим
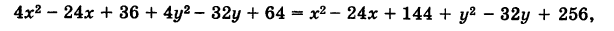
или после несложных преобразований имеем равносильное уравнение
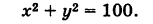
Сравнивая полученное уравнение с уравнением (1), мы видим, что искомая линия является окружностью радиуса 10 с центром в начале координат.
Построение линии по ее уравнению
Если переменные х и у связаны некоторым уравнением, то множество точек М (х, у), координаты которых удовлетворяют этому уравнению, представляет собой, вообще говоря, некоторую линию на плоскости (геометрический образ уравнения).
В частных случаях эта линия может вырождаться в одну или несколько точек. Возможны также случаи, когда уравнению не соответствует никакое множество точек.
Например, уравнению
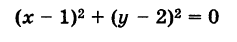
соответствует единственная точка (1, 2), так как этому уравнению удовлетворяет единственная пара значений: х = 1 и у = 2.
Уравнению
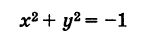
не соответствует никакое множество точек, так как этому уравнению нельзя удовлетворить никакими действительными значениями x и у.
Зная уравнение линии, можно по точкам построить эту линию.
Пример:
Построить линию, выражаемую уравнением

(обычно говорят короче: построить линию у = х2).
Решение:
Давая абсциссе х в уравнении (1) числовые значения и вычисляя соответствующие значения ординаты у, получим следующую таблицу:
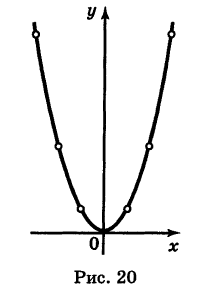
Нанося соответствующие точки на плоскость, мы видим, что конфигурация этих точек определяет начертание некоторой линии; при этом чем гуще построена сеть точек, тем отчетливее выступает ее контур. Соединяя построенные точки линией, характер которой учитывает положение промежуточных точек1*, мы и получаем линию, определяемую данным уравнением (1) (рис. 20). Эта линия называется параболой.
Некоторые элементарные задачи с решением
Если известно уравнение линии, то легко могут быть решены простейшие задачи, связанные с расположением этой линии на плоскости.
Задача 1. Заданы уравнение линии К и координаты точки М (а, Ь). Определить, лежит точка М на линии К или нет.
Иными словами, требуется узнать, проходит линия К через точку М или не проходит.
На основании понятия уравнения линии получаем правило:
чтобы определить, лежит ли точка М на данной линии К, нужно в уравнение этой линии подставить координаты нашей точки. Если при этом уравнение удовлетворится (т. е. в результате подстановки получится тождество), то точка лежит на линии; в противном случае, если координаты точки не удовлетворяют уравнению линии, данная точка не лежит на линии.
Для того чтобы иметь возможность судить о положении промежуточных точек линии, мы должны предварительно изучить общие свойства уравнения этой линии (подробнее см. в гл. XI).
В частном случае линия проходит через начало координат тогда и только тогда, когда уравнение линии удовлетворяется при х = 0 и у — 0.
Пример:
Дана окружность

Определить, лежат ли на ней точки М (-3, 4) и N (4, -2).
Решение:
Подставляя координаты точки М в уравнение (1), получаем тождество
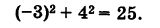
Следовательно, точка М лежит на данной окружности.
Аналогично, подставляя координаты точки N в уравнение (1), будем иметь
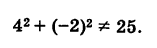
Следовательно, точка N не лежит на данной окружности.
Задача 2. Найти точку пересечения двух линий, заданных своими уравнениями.
Точка пересечения одновременно находится как на первой линии, так и на второй. Следовательно, координаты этой точки удовлетворяют уравнениям обеих линий. Отсюда получаем правило:
чтобы найти координаты точки пересечения двух линий, достаточно совместно решить систему их уравнений.
Если эта система не имеет действительных решений, то линии не пересекаются.
Пример:
Найти точки пересечения параболы у = х2 и прямой у - 4.
Решение:
Решая систему
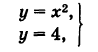
получаем две точки пересечения: А (-2, 4) и В (2, 4).
Задача 3. Найти точки пересечения данной линии с осями координат.
Эта задача является частным случаем задачи 2. Учитывая, что уравнение оси Ох есть у = 0, получаем правило: '
чтобы найти абсциссы точек пересечения данной линии с осью Ох, в уравнении этой линии нужно положить у = 0 и решить полученное уравнение относительно х.
Аналогично, так как уравнение оси Оу есть х — 0, то получаем правило:
чтобы найти ординаты точек пересечения данной линии с осью Оу, нужно в уравнении этой линии положить д: = 0 и решить полученное уравнение относительно у.
Пример:
Найти точки пересечения окружности 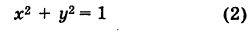 с осями координат.
с осями координат.
Решение:
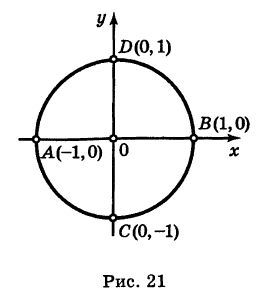
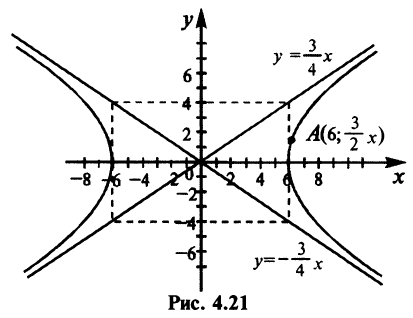
Полагая у = 0 в уравнении (2), получаем х2= 1, т. е. х1 = -1 и х2 = 1. Отсюда находим две точки пересечения данной окружности с осью Ох (рис. 21): А (-1, 0) и В (1, 0).
Аналогично, полагая х = 0 в уравнении (2), получаем у2 = 1, т. е. ух = -1 и у2 = 1. Следовательно, имеются две точки пересечения данной окружности с осью Оу (рис. 21): С (0, -1) и D (0, 1).
Две основные задачи аналитической геометрии на плоскости
Резюмируя содержание этой главы, можно сказать, что всякой линии на плоскости соответствует некоторое уравнение между текущими координатами (х, у) точки этой линии. Наоборот, всякому уравнению между х и г/, где х и у — координаты точки на плоскости, соответствует, вообще говоря, некоторая линия, свойства которой вполне определяются данным уравнением.
Отсюда, естественно, возникают две основные задачи аналитической геометрии на плоскости.
Задача 1 .Дана линия, рассматриваемая как множество точек. Составить уравнение этой линии.
Задача 2. Дано уравнение некоторой линии. Изучить по этому уравнению ее геометрические свойства (форму и расположение).
Алгебраические линии
Определение: Линия называется линией (или кривой) n-го порядка(п = 1, 2,...), если она определяется уравнением п-й степени относительно текущих прямоугольных координат.
Такие линии называются алгебраическими. Например, линии
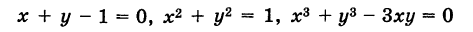
являются кривыми соответственно первого, второго и третьего порядков.
Общий вид кривых первого порядка есть
Ах + By + С = О,
где коэффициенты А и Б не равны нулю одновременно, т. е. 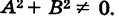 Как будет доказано ниже (см. гл. III), все кривые первого порядка — прямые линии.
Как будет доказано ниже (см. гл. III), все кривые первого порядка — прямые линии.
Общий вид кривых второго порядка следующий:
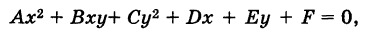
где коэффициенты А, Б и С не равны нулю одновременно, т. е. 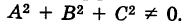
Заметим, что не всякому уравнению второго порядка соответствует действительная кривая. Например, уравнению 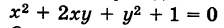 не отвечает никакая кривая на плоскости Оху, так как, очевидно, нет действительных чисел х и z/, удовлетворяющих этому уравнению.
не отвечает никакая кривая на плоскости Оху, так как, очевидно, нет действительных чисел х и z/, удовлетворяющих этому уравнению.
В следующих главах мы подробно изучим кривую первого порядка (прямую линию) и рассмотрим важнейшие представители кривых второго порядка (окружность, эллипс, гипербола, парабола).
Уравнение кривой n-го порядка может быть записано в следующем виде:
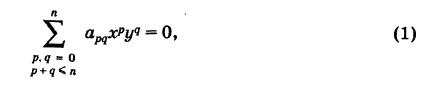
где хотя бы один из старших коэффициентов apqt т. е. таких, что p + q = п, отличен от нуля (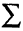 — знак суммирования).
— знак суммирования).
Отметим важное свойство: порядок кривой (1) не зависит от выбора прямоугольной системы координат.
Действительно, выбирая другую систему прямоугольных координат О'х'уна основании формул перехода имеем
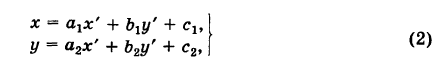
где 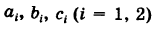 — некоторые постоянные коэффициенты.
— некоторые постоянные коэффициенты.
Отсюда уравнение кривой (1) в новых координатах О'х'у' будет иметь вид
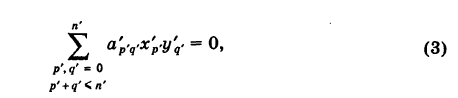
где п' — порядок преобразованной кривой. Очевидно, что п' < п. Аналогично, исходя из уравнения (3) и совершая обратный переход от координат х', у' к координатам х, у, получим уравнение (1), в котором п < п, следовательно, 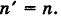
Определение уравнения линии на плоскости
Уравнение линии является важнейшим понятием аналитической геометрии.
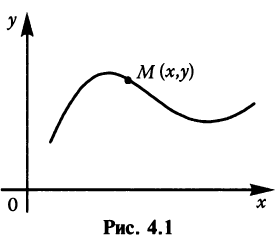
Пусть мы имеем на плоскости некоторую линию (кривую) (рис. 4.1). Координаты 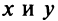 точки, лежащей на этой линии, не могут быть произвольными, они должны быть определенным образом связаны. Такая связь аналитически записывается в виде некоторого уравнения.
точки, лежащей на этой линии, не могут быть произвольными, они должны быть определенным образом связаны. Такая связь аналитически записывается в виде некоторого уравнения.
Определение. Уравнением линии (кривой) на плоскости 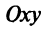 называется уравнение, которому удовлетворяют координаты
называется уравнение, которому удовлетворяют координаты 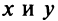 каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
каждой точки данной линии и не удовлетворяют координаты любой точки, не лежащей на этой линии.
В общем случае уравнение линии может быть записано в виде 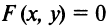 или (если это возможно)
или (если это возможно) 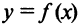 , где
, где 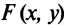 и
и 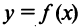 — некоторые функции (функции будут рассмотрены в гл. 5).
— некоторые функции (функции будут рассмотрены в гл. 5).
Если точка 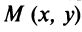 передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии! Поэтому координаты
передвигается по линии, то ее координаты, изменяясь, удовлетворяют уравнению этой линии! Поэтому координаты 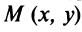 называются текущими координатами (от слова «текут», меняются).
называются текущими координатами (от слова «текут», меняются).
Пример:
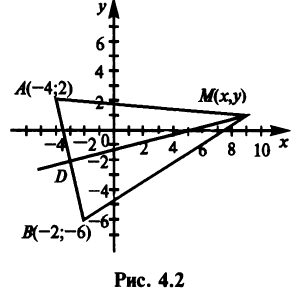
Найти уравнение множества точек, равноудаленных от точек 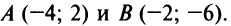
Решение:
Расстояние между двумя точками 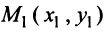 и
и 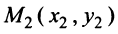 определяется по формуле (3.5):
определяется по формуле (3.5):
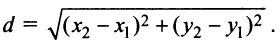
Если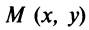 — произвольная точка искомой линии, то согласно условию имеем
— произвольная точка искомой линии, то согласно условию имеем 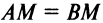 (рис. 4.2) или, учитывая (3.5),
(рис. 4.2) или, учитывая (3.5),
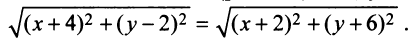
Возведя обе части уравнения в квадрат, получим после преобразований уравнение 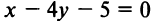 или
или 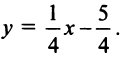
Очевидно, это уравнение прямой 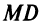 — перпендикуляра, восставленного из середины отрезка
— перпендикуляра, восставленного из середины отрезка 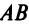 (см. рис. 4.2). ►
(см. рис. 4.2). ►
Любую линию в принципе можно выразить соответствующим уравнением (хотя на практике это не всегда просто сделать). Однако не всякое уравнение определяет на плоскости некоторую линию.
Например, уравнение 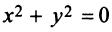 определяет только одну точку
определяет только одну точку 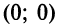 , а уравнение
, а уравнение 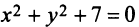 не определяет никакого множества точек, ибо левая часть уравнения не может равняться нулю.
не определяет никакого множества точек, ибо левая часть уравнения не может равняться нулю.
Чтобы убедиться, лежит ли точка 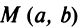 на данной линии
на данной линии 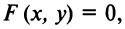 надо проверить, удовлетворяют ли координаты этой точки уравнению
надо проверить, удовлетворяют ли координаты этой точки уравнению 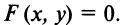
Уравнение прямой
Пусть прямая пересекает ось 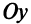 в точке
в точке 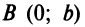 и образует с осью
и образует с осью 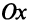 угол
угол 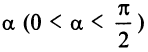 (см. рис. 4.3).
(см. рис. 4.3).
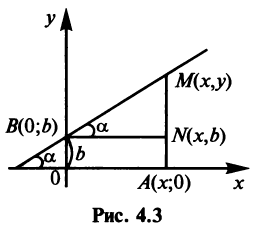
Возьмем на прямой произвольную точку 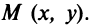 Тогда тангенс угла а наклона прямой найдем из прямоугольного треугольника
Тогда тангенс угла а наклона прямой найдем из прямоугольного треугольника 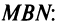
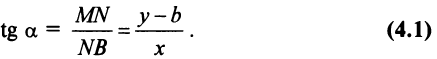
Введем угловой коэффициент прямой 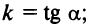 получим
получим
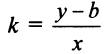 и
и

Можно показать, что формула (4.2) остается справедливой и для случая 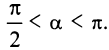
Итак, мы доказали, что координаты каждой точки прямой удовлетворяют уравнению (4.2). Нетрудно показать, что координаты любой точки, не лежащей на прямой, не удовлетворяют уравнению (4.2).
Уравнение (4.2) называется уравнением прямой с угловым коэффициентом.
Рассмотрим частные случаи уравнения (4.2). 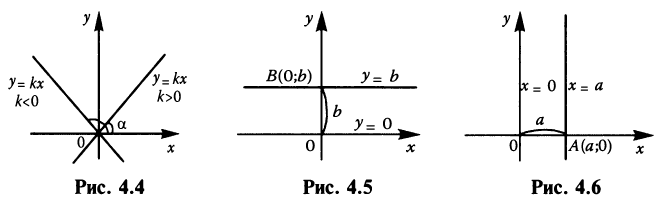
- Если
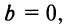 то получаем
то получаем 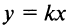 — уравнение прямой, проходящей через начало координат и образующей при
— уравнение прямой, проходящей через начало координат и образующей при 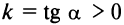 острый угол
острый угол 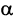 с осью
с осью 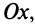 а при
а при 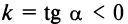 — тупой угол (см. рис. 4.4). В частности, уравнение биссектрисы I и III координатных углов имеет вид
— тупой угол (см. рис. 4.4). В частности, уравнение биссектрисы I и III координатных углов имеет вид 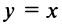 (так как
(так как 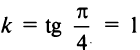 ), а уравнение биссектрисы II и IV координатных углов
), а уравнение биссектрисы II и IV координатных углов 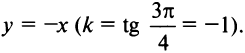
- Если
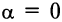 , то
, то 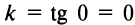 , и уравнение прямой, параллельной оси
, и уравнение прямой, параллельной оси 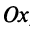 , имеет вид
, имеет вид 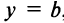 , а самой оси
, а самой оси 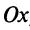 - вид
- вид 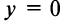 (см. рис. 4.5).
(см. рис. 4.5). - Если
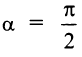 , то прямая перпендикулярна оси
, то прямая перпендикулярна оси 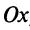 (см.рис. 4.6) и
(см.рис. 4.6) и 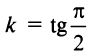 — не существует, т.е. вертикальная прямая не имеет углового коэффициента. Предположим, что эта прямая отсекает на оси
— не существует, т.е. вертикальная прямая не имеет углового коэффициента. Предположим, что эта прямая отсекает на оси 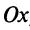 отрезок, равный
отрезок, равный 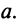 Очевидно, что уравнение такой прямой
Очевидно, что уравнение такой прямой 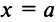 (так как абсцисса любой точки прямой равна а), а уравнение оси
(так как абсцисса любой точки прямой равна а), а уравнение оси 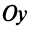 есть
есть 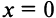 .
.
Уравнение прямой, проходящей через данную точку в данном направлении
Пусть прямая проходит через точку 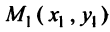 и образует с осью
и образует с осью 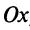 угол
угол 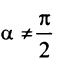 (Рис- 4.7).
(Рис- 4.7). 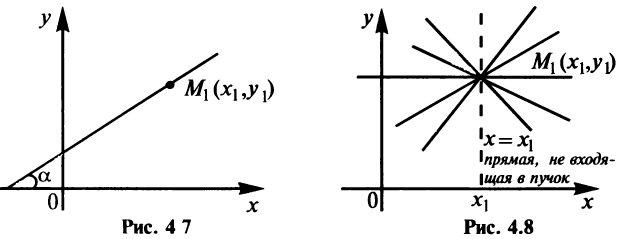
Так как точка 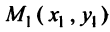 лежит на прямой, то ее координаты удовлетворяют уравнению (4 2), т.е.
лежит на прямой, то ее координаты удовлетворяют уравнению (4 2), т.е.

Вычитая равенство (4.3) из равенства (4.2), получим уравнение искомой прямой

Уравнение пучка прямых. Если в уравнении (4.4) 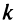 — произвольное число, то это уравнение определяет пучок прямых, проводящих через точку
— произвольное число, то это уравнение определяет пучок прямых, проводящих через точку 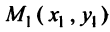 , кроме прямой, параллельной оси
, кроме прямой, параллельной оси 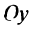 и не имеющей углового коэффициента (рис. 4.8).
и не имеющей углового коэффициента (рис. 4.8).
Пример:
Составить уравнение прямой проходящей через точку А (3;-2): а) под углом 135° к оси 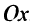 б) параллельно оси
б) параллельно оси 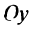 2. Найти уравнение пучка прямых.
2. Найти уравнение пучка прямых.
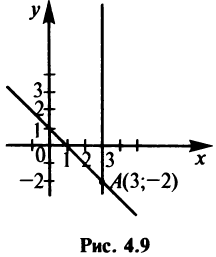
Решение:
1. а) угловой коэффициент прямой 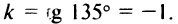
Уравнение прямой, проходящей через точку А (3; -2) (см. рис. 4.9), по формуле (4.4) имеет вид у + 2 = -1 (х —3) или у = -х + 1
б) Уравнение прямой, параллельной оси 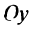 , х = 3.
, х = 3.
2. Уравнение пучка прямых, проходящих через точку А (3;-2), имеет вид
у + 2 = к (х -3).
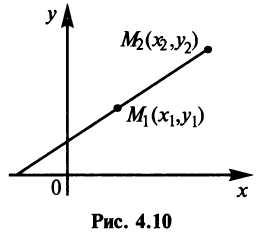
Уравнение прямой, проходящей через две данные точки
Пусть даны две точки 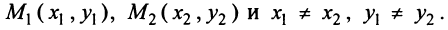
Для составления уравнения прямой 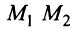 (рис. 4.10) запишем уравнение пучка прямых, проходящих через точку
(рис. 4.10) запишем уравнение пучка прямых, проходящих через точку 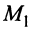 :
: 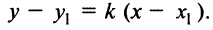
Так как точка 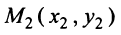 лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки
лежит на данной прямой, то чтобы выделить ее из пучка, подставим координаты точки 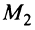 в уравнение пучка
в уравнение пучка 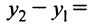
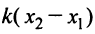
и найдем угловой коэффициент прямой

Теперь уравнение искомой прямой примет вид
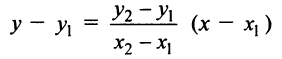 или
или

Пример:
Составить уравнение прямой, проходящей через точки 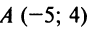 и
и 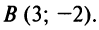
Решение:
По уравнению (4.6): 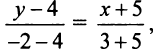 откуда после преобразований
откуда после преобразований 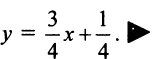
Уравнение прямой в отрезках
Найдем уравнение прямой по заданным отрезкам 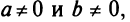 отсекаемым на осях координат. Используя (4.6), уравнение прямой, проходящей через точки
отсекаемым на осях координат. Используя (4.6), уравнение прямой, проходящей через точки 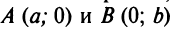 (рис. 4.11), примет вид
(рис. 4.11), примет вид 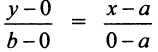 или после преобразований
или после преобразований 
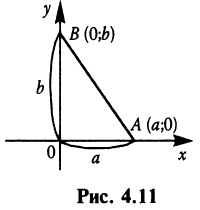
Уравнение (4.7) называется уравнением прямой в отрезках.
Пример:
Составить уравнение прямой, проходящей через точку А (2; —1), если эта прямая отсекает от положительной полуоси 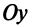 отрезок, вдвое больший, чем на положительной полуоси
отрезок, вдвое больший, чем на положительной полуоси 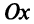 (рис. 4.12).
(рис. 4.12).
Решение:
По условию 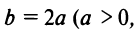
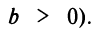 Подставляя это выражение в уравнение (4.7), получим
Подставляя это выражение в уравнение (4.7), получим 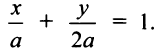
Так как точка А (2; —1) лежит на прямой, то ее координаты удовлетворяют этому уравнению, т.е. 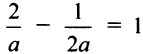 , откуда
, откуда 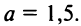
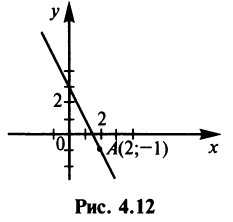
Итак, уравнение искомой прямой имеет вид 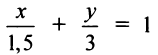 или
или 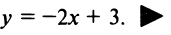
Общее уравнение прямой и его исследование
Рассмотрим уравнение первой степени с двумя переменными в общем виде

в котором коэффициенты 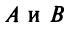 не равны одновременно нулю, т.е.
не равны одновременно нулю, т.е. 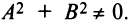
1. Пусть 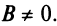 Тогда уравнение (4.8) можно записать в виде
Тогда уравнение (4.8) можно записать в виде 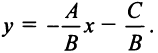
Обозначим 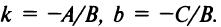 Если
Если 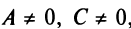 , то получим
, то получим 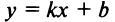 (уравнение прямой с угловым коэффициентом); если
(уравнение прямой с угловым коэффициентом); если 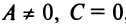 , то
, то 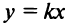 (уравнение прямой, проходящей через начало координат); если
(уравнение прямой, проходящей через начало координат); если 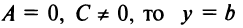 (уравнение прямой, параллельной оси
(уравнение прямой, параллельной оси 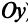 ) если
) если 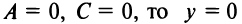 (уравнение оси
(уравнение оси 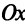 ).
).
2.Пусть 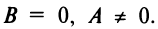 Тогда уравнение (4.8) примет вид
Тогда уравнение (4.8) примет вид 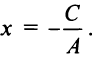 Обозначим
Обозначим 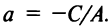 Если
Если 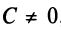 , то получим
, то получим 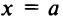 (уравнение прямой, параллельной оси
(уравнение прямой, параллельной оси 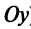 ); если
); если 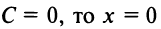 (уравнение оси
(уравнение оси 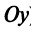 ).
).
Таким образом, при любых значениях коэффициентов 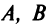 (не равных одновременно нулю) и
(не равных одновременно нулю) и 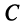 уравнение (4.8) есть уравнение некоторой прямой линии на плоскости
уравнение (4.8) есть уравнение некоторой прямой линии на плоскости 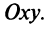
Уравнение (4.8) называется общим уравнением прямой. Заметим, что в отличие от уравнения пучка прямых (4.4) общее уравнение (4.8) включает и уравнение любой вертикальной прямой, параллельной оси 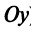 .
.
Угол между двумя прямыми
Пусть заданы две прямые
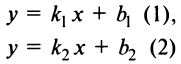
и требуется определить угол 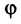 между ними.
между ними.
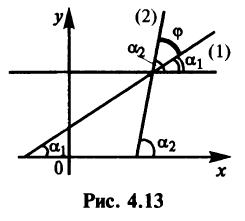
Из рис. 4.13 видно, что 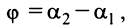 причем
причем 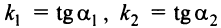 ,
, 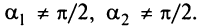 Тогда
Тогда
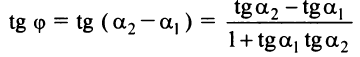 или
или
где стрелка означает, что угол 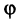 получается поворотом прямой (1) к прямой (2) против часовой стрелки.
получается поворотом прямой (1) к прямой (2) против часовой стрелки.
Условия параллельности и перпендикулярности прямых
Если прямые 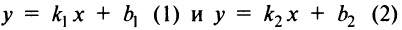 параллельны, то угол
параллельны, то угол 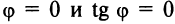 , откуда из формулы (4.9)
, откуда из формулы (4.9) 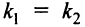 . И наоборот, если
. И наоборот, если 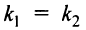 , то по формуле (4.9)
, то по формуле (4.9) 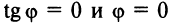 . Таким образом, равенство угловых коэффициентов является необходимым и достаточным условием параллельности двух прямых.
. Таким образом, равенство угловых коэффициентов является необходимым и достаточным условием параллельности двух прямых.
Если прямые перпендикулярны, то 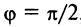 , при этом
, при этом 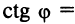
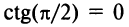
или 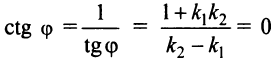 откуда
откуда 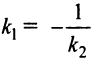
или 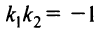 . Справедливо также и обратное утверждение. Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
. Справедливо также и обратное утверждение. Таким образом, для перпендикулярности прямых необходимо и достаточно, чтобы их угловые коэффициенты были обратны по величине и противоположны по знаку.
Если прямые заданы общими уравнениями 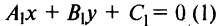 и
и 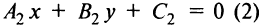 , то учитывая, что их угловые коэффициенты
, то учитывая, что их угловые коэффициенты 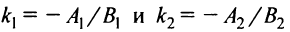 , условие параллельности прямых
, условие параллельности прямых  примет вид
примет вид 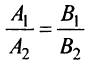 . Следовательно, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных.
. Следовательно, условием параллельности прямых, заданных общими уравнениями, является пропорциональность коэффициентов при переменных.
Условие перпендикулярности прямых 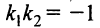 в этом случае примет вид
в этом случае примет вид 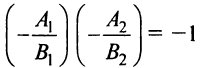 или
или 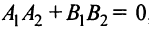 , т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных
, т.е. условием перпендикулярности двух прямых, заданных общими уравнениями, является равенство нулю суммы произведений коэффициентов при переменных 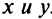
Пример:
Составить уравнения двух прямых, проходящих через точку 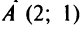 , одна из которых параллельна прямой
, одна из которых параллельна прямой 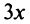
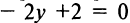 , а другая перпендикулярна той же прямой.
, а другая перпендикулярна той же прямой.
Решение:
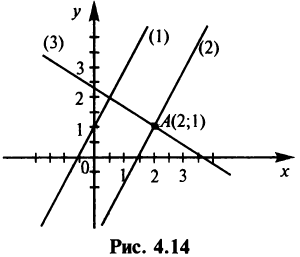
Уравнение пучка прямых, проходящих через точку 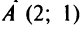 , имеет вид
, имеет вид 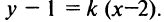 Из этого пучка надо выделить две прямые (2) и (3) — параллельную и перпендикулярную данной (рис. 4.14). Угловой коэффициент прямой (1)
Из этого пучка надо выделить две прямые (2) и (3) — параллельную и перпендикулярную данной (рис. 4.14). Угловой коэффициент прямой (1) 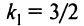 (так как уравнение прямой (1) можно представить
(так как уравнение прямой (1) можно представить
в виде 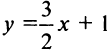 ). По условию параллельности угловой коэффициент прямой (2)
). По условию параллельности угловой коэффициент прямой (2) 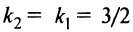 и ее уравнение имеет вид
и ее уравнение имеет вид 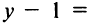
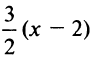 или
или 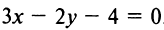 . По условию перпендикулярности угловой коэффициент прямой (3)
. По условию перпендикулярности угловой коэффициент прямой (3) 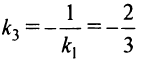 и уравнение этой прямой
и уравнение этой прямой 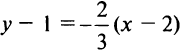 или
или 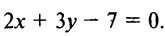
Задачу можно решить и другим способом. Прямая 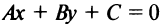 будет параллельна прямой
будет параллельна прямой 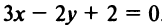 , если ее коэффициенты при
, если ее коэффициенты при 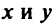 пропорциональны, т.е.
пропорциональны, т.е. 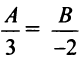 . Взяв
. Взяв 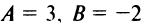 (при коэффициенте пропорциональности, равном 1), получим уравнение
(при коэффициенте пропорциональности, равном 1), получим уравнение 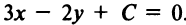 . Коэффициент
. Коэффициент 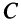 найдем с учетом того, что координаты точки
найдем с учетом того, что координаты точки 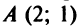 , лежащей на прямой, должны удовлетворять ее уравнению, т.е.
, лежащей на прямой, должны удовлетворять ее уравнению, т.е. 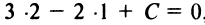 , откуда
, откуда 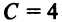 и уравнение прямой (2)
и уравнение прямой (2) 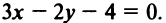
Уравнение прямой, перпендикулярной данной 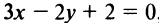 , будет иметь вид:
, будет иметь вид: 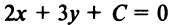 (ибо в этом случае сумма произведений коэффициентов при переменных х и у равна нулю, т.е.
(ибо в этом случае сумма произведений коэффициентов при переменных х и у равна нулю, т.е. 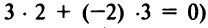 . Теперь подставляя координаты точки
. Теперь подставляя координаты точки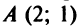 в уравнение прямой, получим
в уравнение прямой, получим 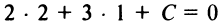 , откуда
, откуда 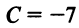 и уравнение прямой (3)
и уравнение прямой (3) 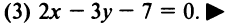
Точка пересечения прямых
Пусть даны две прямые 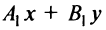
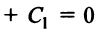 ,
, 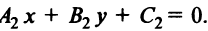 Очевидно, координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы
Очевидно, координаты их точки пересечения должны удовлетворять уравнению каждой прямой, т.е. они могут быть найдены из системы
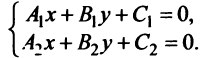
Если прямые не параллельны, т.е.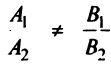 , то решение системы дает единственную точку пересечения прямых.
, то решение системы дает единственную точку пересечения прямых.
Расстояние от точки до прямой
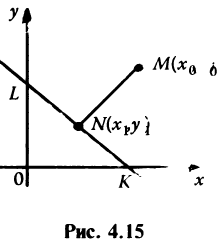
Пусть даны точка 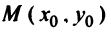 и прямая
и прямая 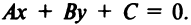 Под расстоянием от точки
Под расстоянием от точки 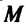 до прямой
до прямой 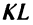 понимается длина перпендикуляра
понимается длина перпендикуляра 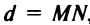 , опушенного из точки
, опушенного из точки 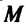 на прямую
на прямую 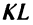 (рис. 4.15). Для определения расстояния
(рис. 4.15). Для определения расстояния 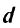 необходимо: а) составить уравнение прямой
необходимо: а) составить уравнение прямой 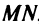 перпендикулярной данной и проходящей через точку
перпендикулярной данной и проходящей через точку 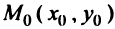 ; б) найти точку
; б) найти точку 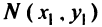 пересечения прямых, решив систему уравнений этих прямых, в) по формуле (3.5) определить расстояние между двумя точками, т.е. найти
пересечения прямых, решив систему уравнений этих прямых, в) по формуле (3.5) определить расстояние между двумя точками, т.е. найти 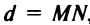 В результате преобразований получим
В результате преобразований получим
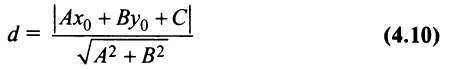
(доказательстю формулы (4.10) опускаем).
Пример:
Найти расстояние между параллельными прямыми 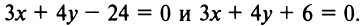
Решение:
Возьмем на одной из прямых, например прямой 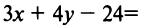
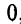 , произвольную точку
, произвольную точку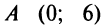 ( Рис. 4.16)
( Рис. 4.16)
Тогда искомое расстояние равно расстоянию от точки 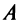 до прямой
до прямой 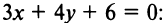
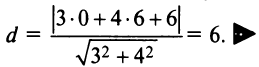
Окружность, эллипс и линия
Изучение кривых второго порядка, описываемых уравнениями второй степени с двумя переменными, начнем с окружности.
Пусть дана окружность радиуса 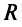 с центром
с центром 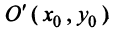 (рис. 4.17). Найдем ее уравнение. Для произвольной — точки
(рис. 4.17). Найдем ее уравнение. Для произвольной — точки 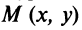 окружности выполняется равенство
окружности выполняется равенство 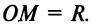 Используя формулу (3.5) расстояния между двумя точками, получим
Используя формулу (3.5) расстояния между двумя точками, получим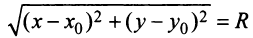 или после возведения в квадрат (двух положительных частей уравнения) получим равносильное уравнение
или после возведения в квадрат (двух положительных частей уравнения) получим равносильное уравнение
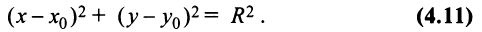
Итак, координаты каждой точки окружности 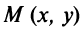 удовлетворяют уравнению (4.11). Нетрудно показать, что координаты любой точки, не лежащей на окружности, этому уравнению не удовлетворяют.
удовлетворяют уравнению (4.11). Нетрудно показать, что координаты любой точки, не лежащей на окружности, этому уравнению не удовлетворяют.
Уравнение (4.11) называется нормальным уравнением окружности. В частности, уравнение окружности с центром в начале координат 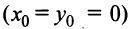 имеет вид
имеет вид

Рассмотрим уравнение второй степени с двумя переменными в общем виде
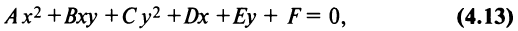
в котором 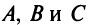 не равны нулю одновременно, т.е.
не равны нулю одновременно, т.е. 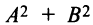
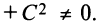 . Выясним, при каких условиях это уравнение является уравнением окружности. С этой целью представим уравнение (4.11) в виде
. Выясним, при каких условиях это уравнение является уравнением окружности. С этой целью представим уравнение (4.11) в виде
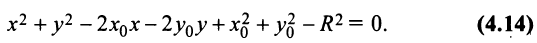
Чтобы уравнения (4.13) и (4.14) представляли одну и ту же линию, коэффициент 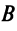 должен равняться нулю, т.е.
должен равняться нулю, т.е. 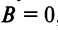 , а все остальные коэффициенты — пропорциональны, в частности
, а все остальные коэффициенты — пропорциональны, в частности 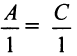 , откуда
, откуда
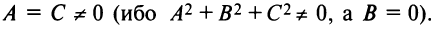 Тогда получим уравнение
Тогда получим уравнение
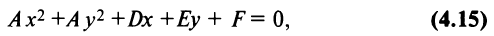
называемое общим уравнением окружности.
Поделив обе части уравнения на 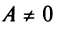 и дополнив члены, содержащие
и дополнив члены, содержащие 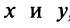 , до полного квадрата, получим
, до полного квадрата, получим 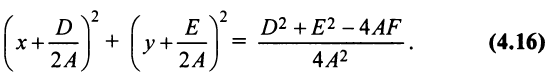 Сравнивая уравнение (4.16) с уравнением окружности (4.11), можно сделать вывод, что уравнение (4.13) есть уравнение действительной окружности, если
Сравнивая уравнение (4.16) с уравнением окружности (4.11), можно сделать вывод, что уравнение (4.13) есть уравнение действительной окружности, если
1)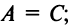 2)
2)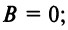 3)
3)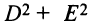
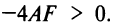 При выполнении этих условий центр окружности (4.13) расположен в точке
При выполнении этих условий центр окружности (4.13) расположен в точке 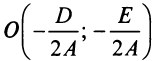 , а ее радиус
, а ее радиус
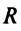
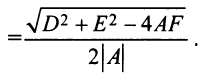
Пример:
Найти координаты центра и радиус окружности
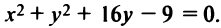
Решение:
Дополнив члены, содержащие 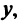 до полного квадрата, получим
до полного квадрата, получим
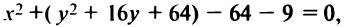 или
или 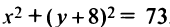 , т.е. центр окружности в точке
, т.е. центр окружности в точке 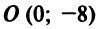 , а ее радиус
, а ее радиус 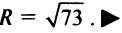
Рассмотрим уравнение кривой второго порядка (4.13), в котором по-прежнему будем полагать 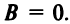 Перепишем уравнение в виде
Перепишем уравнение в виде
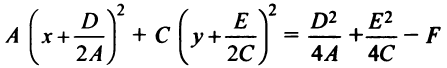
или
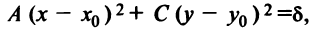 где
где
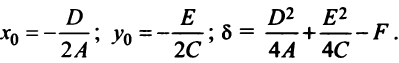
Будем предполагать для простоты исследования, что центр кривой находится в начале координат, т.е. 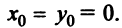 Тогда уравнение кривой примет вид
Тогда уравнение кривой примет вид

Кривая второго порядка (4.17) называется эллипсом (точнее кривой эллиптического типа), если коэффициенты 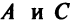 имеют одинаковые знаки.
имеют одинаковые знаки.
Для определенности будем полагать, что 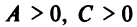 (в противном случае обе части уравнения можно умножить на (—1).
(в противном случае обе части уравнения можно умножить на (—1).
Возможны три случая: 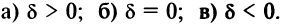
Очевидно, что в третьем случае (при 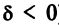 ) кривая (4.17) не имеет действительных точек, а во втором случае (при
) кривая (4.17) не имеет действительных точек, а во втором случае (при 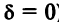 ) кривая (4.17) представляет собой одну точку
) кривая (4.17) представляет собой одну точку 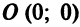 . Поэтому остановимся на первом случае
. Поэтому остановимся на первом случае 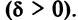 Получаемое при этом уравнение
Получаемое при этом уравнение

называется каноническим уравнением эллипса с полуосями 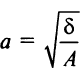 и
и 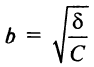 (рис. 4.18). При
(рис. 4.18). При 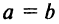 уравнение (4.18) представляет частный случай — уравнение окружности
уравнение (4.18) представляет частный случай — уравнение окружности 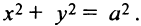 Точки
Точки 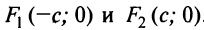 , где
, где

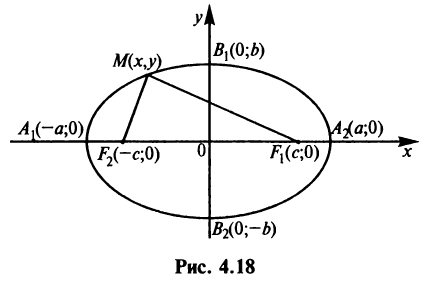 называются фокусами эллипса, а отношение
называются фокусами эллипса, а отношение

его эксцентриситетом. Эксцентриситет характеризует форму эллипса. Очевидно, что 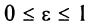 , причем для окружности
, причем для окружности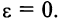 Точки
Точки 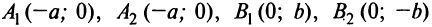 называются вершинами эллипса.
называются вершинами эллипса.
Найдем сумму расстояний от любой точки эллипса 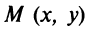 до ее фокусов, используя формулу (3.5):
до ее фокусов, используя формулу (3.5):
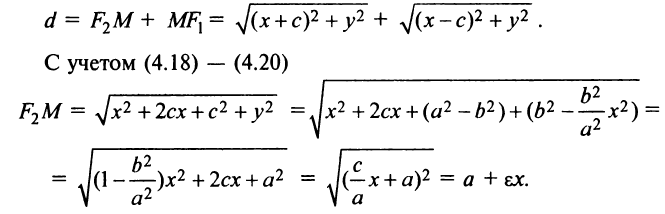
Аналогично можно получить, что 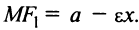 В результате
В результате 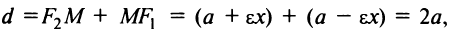 т.е. для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянная, равная
т.е. для любой точки эллипса сумма расстояний этой точки до фокусов есть величина постоянная, равная 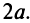 Это характеристическое свойство эллипса часто принимается за определение эллипса.
Это характеристическое свойство эллипса часто принимается за определение эллипса.
Пример:
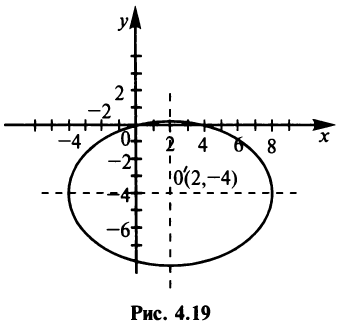
Определить вид и расположение кривой
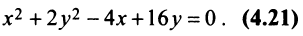
Решение:
Так как 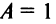 и
и 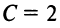 — числа одного знака, то данное уравнение кривой — эллиптического типа. Дополняя члены, содержащие
— числа одного знака, то данное уравнение кривой — эллиптического типа. Дополняя члены, содержащие 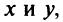 до полного квадрата, получим
до полного квадрата, получим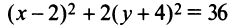 или
или
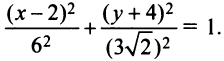
Следовательно, кривая (4.21) представляет эллипс с полуосями 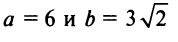 , центр которого находится в точке
, центр которого находится в точке 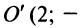
Гипербола и парабола
Кривая второго порядка (4.17) называется гиперболой (точнее кривой гиперболического типа), если коэффициенты 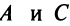 имеют противоположные знаки, т.е.
имеют противоположные знаки, т.е. 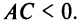
Пусть для определенности 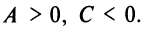 Возможны три случая:
Возможны три случая:
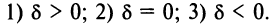
В первом случае (при 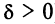 ) имеем гиперболу, каноническое уравнение которой
) имеем гиперболу, каноническое уравнение которой

где 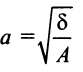 — действительная полуось;
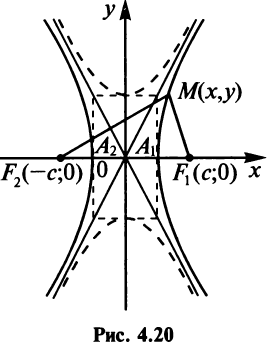
— действительная полуось; 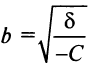 -мнимая полуось (рис. 4.20).
-мнимая полуось (рис. 4.20).
Фокусы гиперболы — точки 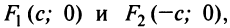 где
где 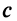
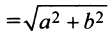 , а ее эксцентриситет
, а ее эксцентриситет 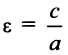 принимает любые значения, большие 1. Вершины гиперболы — точки
принимает любые значения, большие 1. Вершины гиперболы — точки 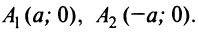
Можно показать (аналогично тому, как мы поступали при исследовании эллипса), что для любой точки гиперболы абсолютная величина разности ее расстояний до фокусов есть величина постоянная, равная 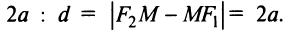 Это характеристическое свойство гиперболы часто принимается за определение гиперболы.
Это характеристическое свойство гиперболы часто принимается за определение гиперболы.
Перепишем уравнение гиперболы (4.21) в виде

При достаточно больших 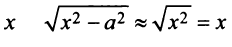 и уравнение (4.23) примет вид
и уравнение (4.23) примет вид 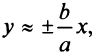 т.е. при
т.е. при  ветви гиперболы как угодно близко подходят к прямым
ветви гиперболы как угодно близко подходят к прямым 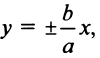 называемым асимптотами гиперболы.
называемым асимптотами гиперболы.
Для равносторонней гиперболы 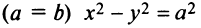 асимптоты
асимптоты 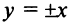 взаимно перпендикулярны и представляют биссектрисы координатных углов.
взаимно перпендикулярны и представляют биссектрисы координатных углов.
Во втором случае (при 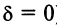 ) уравнение кривой (4.17) примет вид
) уравнение кривой (4.17) примет вид 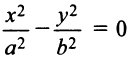 , т.е. получаем пару пересекающихся прямых
, т.е. получаем пару пересекающихся прямых
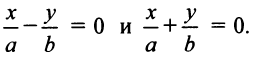
В третьем случае (при 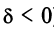 ) получим гиперболу
) получим гиперболу 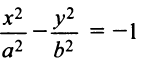
с полуосями 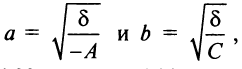 называемую сопряженной с гиперболой (4.22) (на рис. 4.20 она изображена пунктиром).
называемую сопряженной с гиперболой (4.22) (на рис. 4.20 она изображена пунктиром).
Пример:
Написать уравнение гиперболы с асимптотами 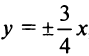 , проходящими через точку (6; 3/2). Найти расстояние между ее вершинами.
, проходящими через точку (6; 3/2). Найти расстояние между ее вершинами.
Решение:
Так как точка (6; 3/2) лежит на гиперболе, то ее координаты должны удовлетворять уравнению (4.22) 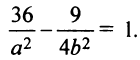 Кроме того,
Кроме того, 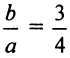 , так как
, так как
асимптоты гиперболы 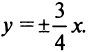 Решая полученную систему двух уравнений, найдем
Решая полученную систему двух уравнений, найдем 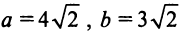 т.е. уравнение гиперболы
т.е. уравнение гиперболы 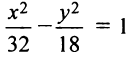 (рис. 4.21). Расстояние между вершинами гиперболы равно
(рис. 4.21). Расстояние между вершинами гиперболы равно 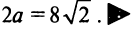
Рассмотрим обратную пропорциональную зависимость, задаваемую уравнением 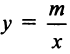 или
или 
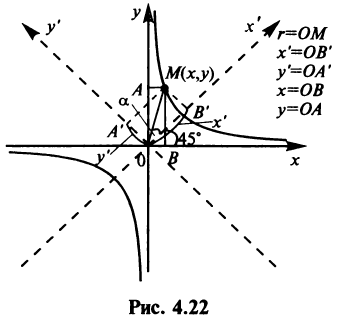
Выбрав в качестве новых осей 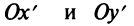 биссектрисы координатных углов (рис. 4.22), представим уравнение (4.24) через новые координаты
биссектрисы координатных углов (рис. 4.22), представим уравнение (4.24) через новые координаты 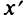 и
и 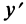 . Пусть
. Пусть 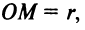 тогда
тогда
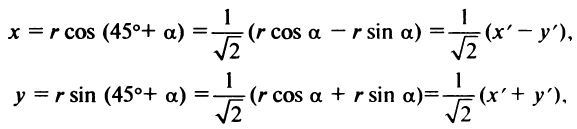
так как из 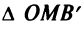
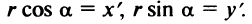
Теперь уравнение (4.24) в новой системе координат 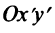 примет вид
примет вид 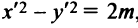 , т.е. график обратной пропорциональной зависимости есть равносторонняя гипербола с асимптотами — осями координат.
, т.е. график обратной пропорциональной зависимости есть равносторонняя гипербола с асимптотами — осями координат.
При 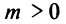 ветви гиперболы расположены в I и I I квадрантах, при
ветви гиперболы расположены в I и I I квадрантах, при 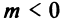 — во II и IV квадрантах. Нетрудно установить, что координаты любой вершины гиперболы равны (по абсолютной величине), т.е.
— во II и IV квадрантах. Нетрудно установить, что координаты любой вершины гиперболы равны (по абсолютной величине), т.е. 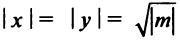 , а их знаки определяются в зависимости от квадранта, в котором расположена каждая вершина.
, а их знаки определяются в зависимости от квадранта, в котором расположена каждая вершина.
Рассмотрим график дробно-линейной функции

где 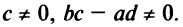
Преобразуя (4.25), получим
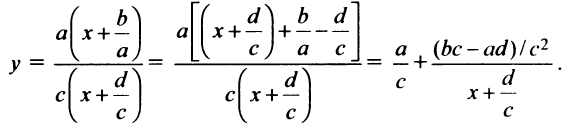
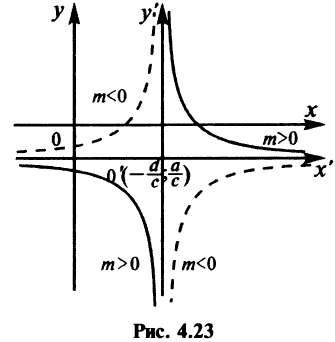
Введем новые координаты
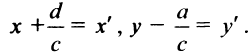
Обозначим 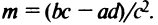 Тогда в новой системе координат
Тогда в новой системе координат 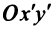 , полученной параллельным переносом осей координат, с новым центром в точке
, полученной параллельным переносом осей координат, с новым центром в точке 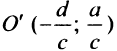 (см. рис. 4.23) уравнение примет вид
(см. рис. 4.23) уравнение примет вид 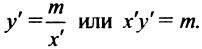
Итак, график дробно-линейной функции (4.25) есть равносторонняя гипербола с асимптотами 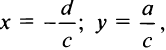 параллельными осям координат.
параллельными осям координат.
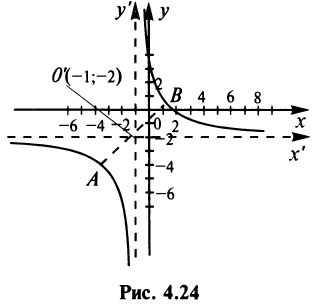
Пример:
Найти координаты центра, вершин и уравнения асимптот гиперболы 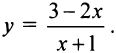
Решение:
Преобразуем уравнение, выделив целую часть дробно-линейной функции:
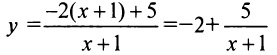
или 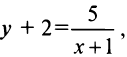 откуда
откуда
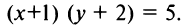
Полагая 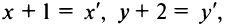 получим
получим 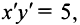 т.е. заданное уравнение есть уравнение равносторонней гиперболы с центром
т.е. заданное уравнение есть уравнение равносторонней гиперболы с центром 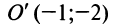 и асимптотами
и асимптотами 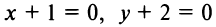 (рис. 4.24). Так как
(рис. 4.24). Так как 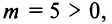 то гипербола располагается в I и III квадрантах, а новые координаты ее вершин
то гипербола располагается в I и III квадрантах, а новые координаты ее вершин 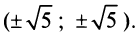 Переходя к старым координатам по формулам
Переходя к старым координатам по формулам 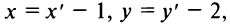 найдем старые координаты вершин гиперболы
найдем старые координаты вершин гиперболы 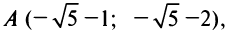
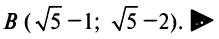
Пусть в уравнении кривой второго порядка (4.13)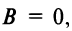 а также один из коэффициентов
а также один из коэффициентов  равен нулю; для определенности
равен нулю; для определенности 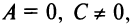 т.е.
т.е.
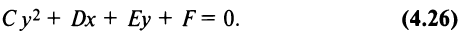
Пусть также 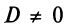 (в противном случае мы имели бы пару параллельных горизонтальных прямых
(в противном случае мы имели бы пару параллельных горизонтальных прямых 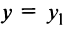 и
и 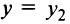 , где
, где 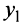 и
и 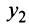 — корни уравнения
— корни уравнения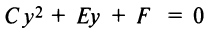 или отсутствие каких-либо линий и точек вообще). Дополним члены, содержащие
или отсутствие каких-либо линий и точек вообще). Дополним члены, содержащие 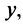 до полного квадрата
до полного квадрата
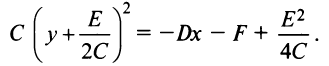
Полагая 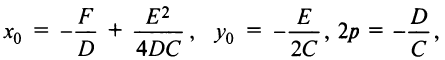 получим
получим
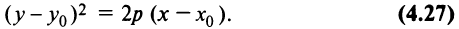
Кривая (4.27) называется параболой, а точка 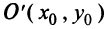 — вершиной параболы,
— вершиной параболы, 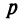 — параметром параболы. При
— параметром параболы. При 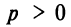 ветви параболы направлены вправо, при
ветви параболы направлены вправо, при 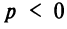 — влево (рис. 4.25). Прямая
— влево (рис. 4.25). Прямая 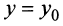 является осью симметрии параболы.
является осью симметрии параболы.
Если вершина параболы находится в начале координат, то уравнение (4.27) принимает вид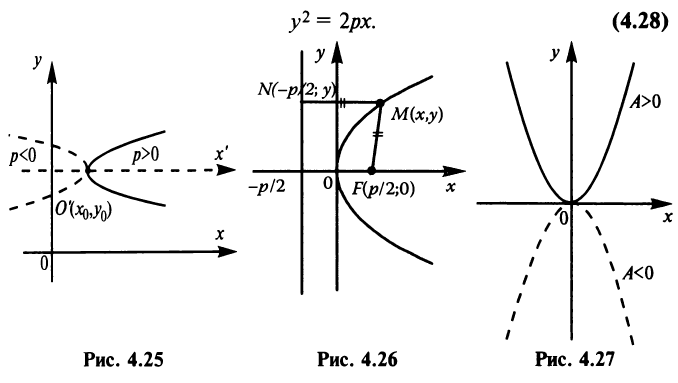
Точка 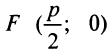 называется фокусом параболы, а прямая
называется фокусом параболы, а прямая 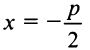 — ее директрисой.
— ее директрисой.
Для произвольной точки 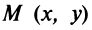 параболы расстояние до фокуса по формуле (3.5) равно
параболы расстояние до фокуса по формуле (3.5) равно
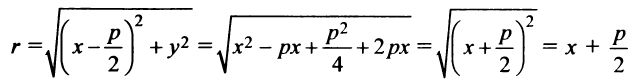
(так как 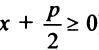 ). С другой стороны, расстояние до директрисы
). С другой стороны, расстояние до директрисы 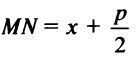 (рис. 4.26).
(рис. 4.26).
Таким образом, парабола представляет множество всех точек плоскости, равноотстоящих от данной тонки (фокуса) 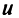 от данной прямой (директрисы). Это характеристическое свойство параболы часто принимается за определение параболы.
от данной прямой (директрисы). Это характеристическое свойство параболы часто принимается за определение параболы.
Если в уравнении (4.28) поменять местами 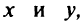 то получим
то получим 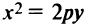 — уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат. Это уравнение
— уравнение параболы с вершиной в начале координат, симметричной относительно оси ординат. Это уравнение
обычно записывают в виде 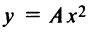 , где
, где 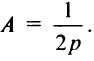 При
При 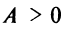 ветви параболы направлены вверх, при
ветви параболы направлены вверх, при 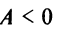 — вниз (рис. 4.27). Рассмотрим квадратный трехчлен
— вниз (рис. 4.27). Рассмотрим квадратный трехчлен 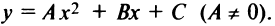
Отсюда 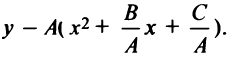 выражение, стоящее А А
выражение, стоящее А А
в скобках, до полного квадрата, получим
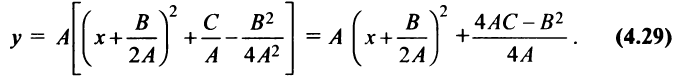
Обозначив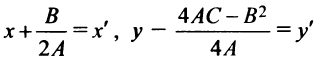 в новой системе координат
в новой системе координат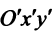 с центром
с центром 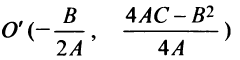 уравнение (4.29) примет вид
уравнение (4.29) примет вид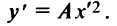
Таким образом, график квадратного трехчлена 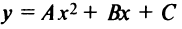 есть парабола с вершинои в точке
есть парабола с вершинои в точке 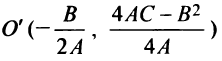 и осью симметрии
и осью симметрии 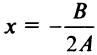 , параллельной оси
, параллельной оси 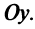
Пример:
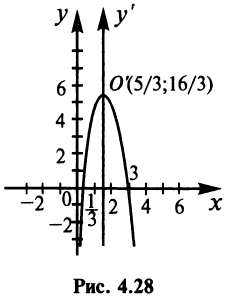
Построить кривую 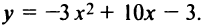
Решение:
Вынося коэффициент при 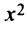 и дополняя правую часть уравнения до полного квадрата, получим
и дополняя правую часть уравнения до полного квадрата, получим
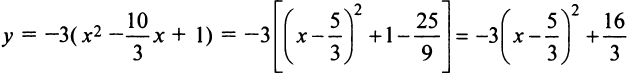 или
или
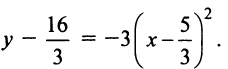 Полагая
Полагая 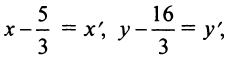 получим
получим 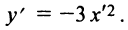
Таким образом, заданная кривая есть парабола с вершиной в точке 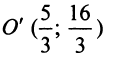 и осью симметрии
и осью симметрии 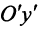 , параллельной оси
, параллельной оси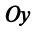 (рис. 4.28). ►
(рис. 4.28). ►
Пример:
Даны уравнения сторон треугольника
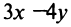
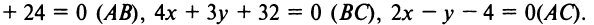
Составить уравнение высоты, медианы и биссектрисы, проведенных из вершины 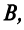 и найти их длины.
и найти их длины.
Решение:
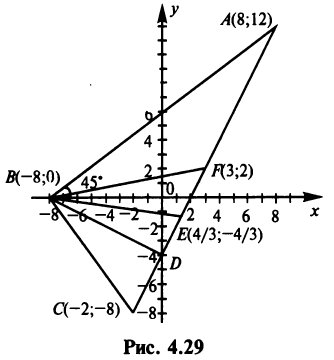
1. Найдем координаты вершин треугольника, решив соответствующие системы уравнений сторон. Так, координаты вершины 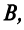 определим из системы уравнений прямых
определим из системы уравнений прямых 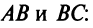
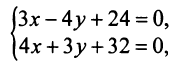
откуда 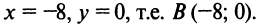
Аналогично находим координаты вершин 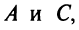 решив системы уравнений прямых
решив системы уравнений прямых 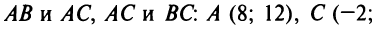
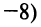 (рис. 4.29).
(рис. 4.29).
2. Пучок прямых, проходящих через точку 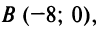 по формуле (4.4) имеет вид:
по формуле (4.4) имеет вид:

Из уравнения прямой 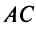 следует, что ее угловой коэффициент
следует, что ее угловой коэффициент 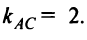 На основании условия перпендикулярности двух прямых
На основании условия перпендикулярности двух прямых 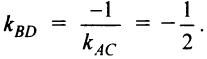 Уравнение высоты
Уравнение высоты 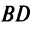 примет вид
примет вид
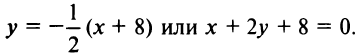
3. Из школьного курса математики известно, что координаты середины отрезка равны полусуммам соответствующих координат его концов, т.е.
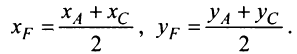
Поэтому 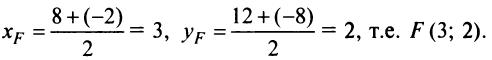
По формуле (4.5) угловой коэффициент
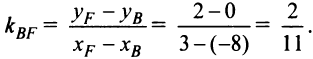
Подставляя 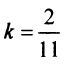 в формулу (4.30), получим уравнение медианы
в формулу (4.30), получим уравнение медианы 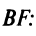
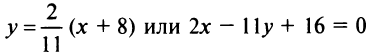
(уравнение 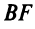 можно было получить и по формуле (4.6) как уравнение прямой, проходящей через две точки:
можно было получить и по формуле (4.6) как уравнение прямой, проходящей через две точки: 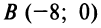 и
и 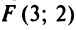 ).
).
4. Из уравнений прямых 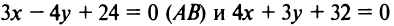
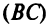 следует, что они перпендикулярны, так как их угловые коэффициент
следует, что они перпендикулярны, так как их угловые коэффициент 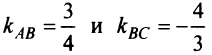 — обратны по величине и противоположны по знаку. Поэтому биссектриса
— обратны по величине и противоположны по знаку. Поэтому биссектриса 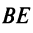 образует с каждой из этих сторон угол 45°. По формуле (4.9).
образует с каждой из этих сторон угол 45°. По формуле (4.9).
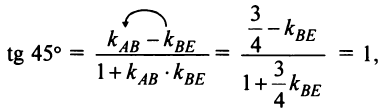
откуда 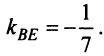 Теперь по формуле (4.30) получим уравнение биссектрисы
Теперь по формуле (4.30) получим уравнение биссектрисы 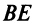
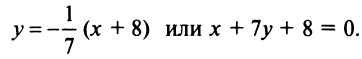
(Если «не заметить», что 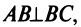 то угловой коэффициент биссектрисы
то угловой коэффициент биссектрисы 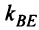 можно найти из равенства
можно найти из равенства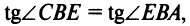 т.е.
т.е. 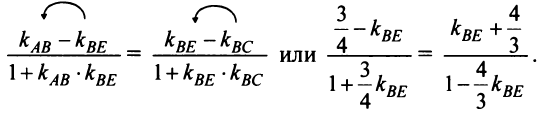 Решая уравнение, найдем два корня
Решая уравнение, найдем два корня 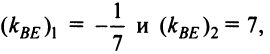 из которых чертежу задачи удовлетворяет первый корень.) 5. Длину медианы
из которых чертежу задачи удовлетворяет первый корень.) 5. Длину медианы 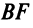 найдем по формуле (3.5) расстояния между двумя точками
найдем по формуле (3.5) расстояния между двумя точками 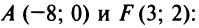
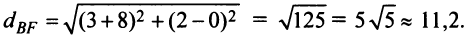 6. Для нахождения длины биссектрисы
6. Для нахождения длины биссектрисы 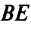 найдем вначале координаты ее точки пересечения
найдем вначале координаты ее точки пересечения 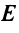 со стороной
со стороной 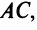 решив систему уравнений
решив систему уравнений
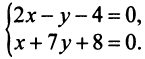 Откуда
Откуда 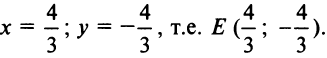
Теперь по формуле (3.5)
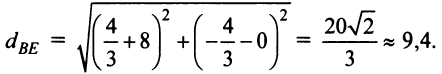 7. Длину высоты
7. Длину высоты 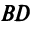 можно было найти аналогично тому, как находили длину биссектрисы. Но проще это сделать по формуле (4.10) расстояния от точки
можно было найти аналогично тому, как находили длину биссектрисы. Но проще это сделать по формуле (4.10) расстояния от точки 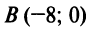 до прямой
до прямой 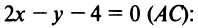
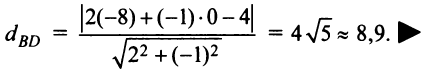
Пример:
Найти расстояние от начала координат до прямой, проходящей через центр гиперболы 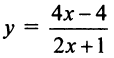 вершину параболы
вершину параболы 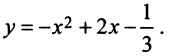 Составить уравнение окружности, касающейся гиперболы в ее вершинах.
Составить уравнение окружности, касающейся гиперболы в ее вершинах.
Решение:
1. В уравнении гиперболы выделим целую часть; получим
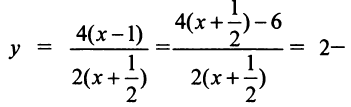
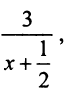 откуда
откуда 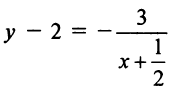 или
или 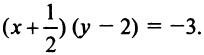
Полагая 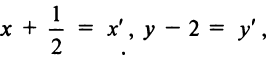 получим в новой системе координат
получим в новой системе координат 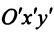 с центром
с центром 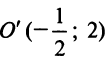 гиперболу
гиперболу 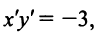 ветви которой расположены во II и IV квадрантах (рис. 4.30).
ветви которой расположены во II и IV квадрантах (рис. 4.30).
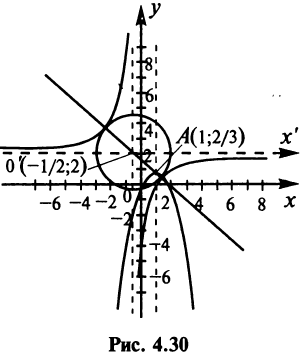
2. Выделив полный квадрат, представим уравнение параболы в виде
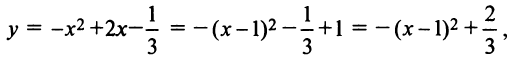 откуда следует, что вершина параболы находится в точке
откуда следует, что вершина параболы находится в точке 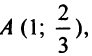 а ветви ее направлены вниз.
а ветви ее направлены вниз.
3. Составляем уравнение прямой 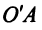 по формуле (4.5)
по формуле (4.5)
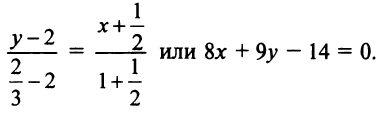
4. Находим расстояние от точки 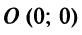 до прямой
до прямой 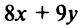
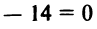 по формуле (4.10)
по формуле (4.10)
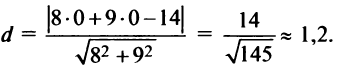
5. Очевидно, что центр искомой окружности должен совпасть с центром гиперболы 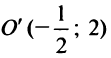 и иметь радиус
и иметь радиус 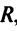 , равный расстоянию от точки
, равный расстоянию от точки 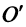 до любой из вершин гиперболы. Для гиперболы
до любой из вершин гиперболы. Для гиперболы 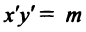 координаты любой вершины (по абсолютной величине)
координаты любой вершины (по абсолютной величине) 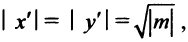 поэтому расстояние ее от нового начала координат
поэтому расстояние ее от нового начала координат 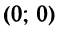 по формуле (3.5) равно
по формуле (3.5) равно 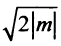 . Следовательно,
. Следовательно, 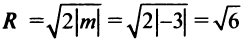 . Итак, уравнение искомой окружности по формуле (4.11) есть
. Итак, уравнение искомой окружности по формуле (4.11) есть 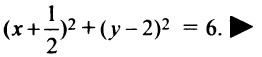
Понятие об уравнении плоскости и прямой в пространстве
Общее уравнение плоскости. Пусть плоскость 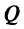 проходит через точку
проходит через точку 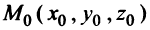 перпендикулярно вектору
перпендикулярно вектору 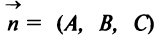 (рис. 4.31).
(рис. 4.31).
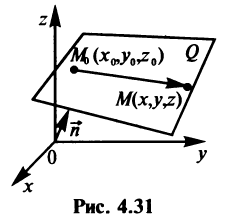
Этими условиями определяется единственная плоскость в пространстве 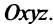 /Вектор
/Вектор 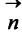 называется нормальным вектором плоскости
называется нормальным вектором плоскости 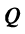 . Возьмем в плоскости
. Возьмем в плоскости 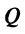 произвольную точку
произвольную точку 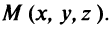 Тогда вектор
Тогда вектор 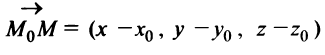 будет перпендикулярен вектору
будет перпендикулярен вектору 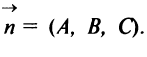 Следовательно, скалярное произведение этих векторов равно нулю, т.е.
Следовательно, скалярное произведение этих векторов равно нулю, т.е. 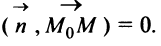 Полученное уравнение представим в координатной форме:
Полученное уравнение представим в координатной форме:
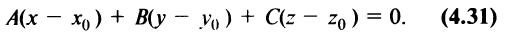
Уравнение (4.31) представляет уравнение плоскости, перпендикулярной данному вектору 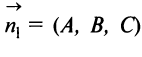 и проходящей через данную точку
и проходящей через данную точку 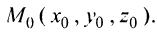
Уравнение плоскости, записанное в виде
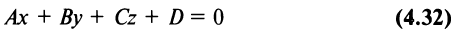
(где 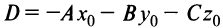 ), называется общим уравнением плоскости.
), называется общим уравнением плоскости.
Можно доказать, что всякое уравнение первой степени с тремя переменными есть уравнение плоскости.
Если 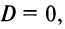 то уравнение
то уравнение 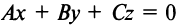 определяет плоскость, проходящую через начало координат. Другие частные случаи определяются расположением нормального вектора
определяет плоскость, проходящую через начало координат. Другие частные случаи определяются расположением нормального вектора 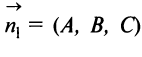 . Так, например, если
. Так, например, если 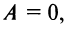 то уравнение
то уравнение 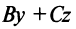
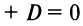 определяет плоскость, параллельную оси
определяет плоскость, параллельную оси 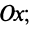 если
если 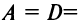
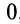 , то уравнение
, то уравнение 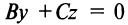 определяет плоскость, проходящую через ось
определяет плоскость, проходящую через ось 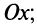 если
если 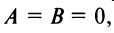 то уравнение
то уравнение 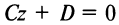 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 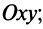 если
если 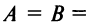
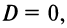 то уравнение
то уравнение 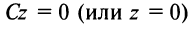 определяет координатную плоскость
определяет координатную плоскость 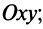
Условия параллельности и перпендикулярности плоскостей определяются условиями коллинеарности и перпендикулярности нормальных векторов 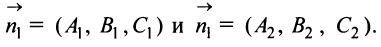
Условием параллельности двух плоскостей является пропорциональность коэффициентов при одноименных переменных
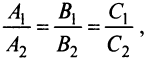 а условием их перпендикулярности
а условием их перпендикулярности
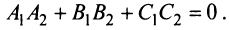
Прямая в пространстве может быть задана как линия пересечения двух плоскостей, т.е. как множество точек, удовлетворяющих системе
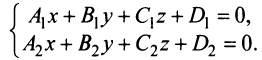
Если прямая параллельна вектору
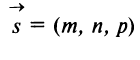 (называемому направляющим вектором) и проходит через точку
(называемому направляющим вектором) и проходит через точку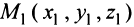 (рис. 4.32), то ее уравнения могут быть получены из условия коллинеарности векторов
(рис. 4.32), то ее уравнения могут быть получены из условия коллинеарности векторов 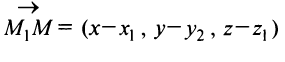 (где
(где 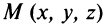 — произвольная точка прямой) и
— произвольная точка прямой) и 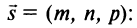
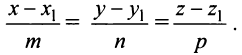

Эти уравнения называются каноническими уравнениями прямой линии в пространстве.
Уравнения прямой линии в пространстве
Прямая в пространстве однозначно определяется точкой 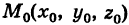 и направлением (т. е. некоторым вектором).
и направлением (т. е. некоторым вектором).
Пусть 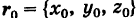 — радиус-вектор точки
— радиус-вектор точки 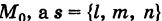 — ненулевой направляющий вектор прямой (длина его произвольна). Обозначая через
— ненулевой направляющий вектор прямой (длина его произвольна). Обозначая через 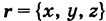 радиус-вектор произвольной точки М прямой (текущий радиус-вектор), из векторного треугольника
радиус-вектор произвольной точки М прямой (текущий радиус-вектор), из векторного треугольника 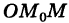 (рис. 201) имеем
(рис. 201) имеем

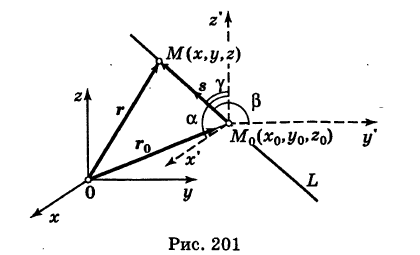
Так как векторы 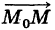 и s коллинеарны, то
и s коллинеарны, то

где 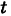 — некоторый скаляр
— некоторый скаляр 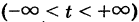 . Подставляя это выражение в уравнение (1), получим векторное уравнение прямой линии в пространстве
. Подставляя это выражение в уравнение (1), получим векторное уравнение прямой линии в пространстве

(t — параметр).
Проецируя равенство (3) на координатные оси, будем иметь параметрические уравнения прямой линии в пространстве

Если из уравнений (4) исключить параметр то получим так называемые канонические уравнения прямой линии в пространстве
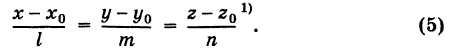
Система (5) содержит два уравнения, например при 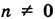 можно положить
можно положить
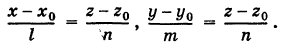
Эти уравнения представляют собой уравнения двух плоскостей, пересечением которых является данная прямая. Заметим, что первое уравнение не содержит координаты у, а второе — координаты х. Следовательно, первая плоскость параллельна оси Оу, а вторая параллельна оси Ох, т.е. эти плоскости являются плоскостями, проецирующими нашу прямую на координатную плоскость Oxz и соответственно на координатную плоскость Oyz.
Числа 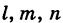 называются направляющими коэффициентами прямой линии. Обозначая через
называются направляющими коэффициентами прямой линии. Обозначая через 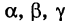 углы, образованные прямой с координатными осями (рис. 201), и учитывая, что cos а,
углы, образованные прямой с координатными осями (рис. 201), и учитывая, что cos а, 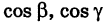 являются направляющими косинусами вектора s, будем иметь
являются направляющими косинусами вектора s, будем иметь
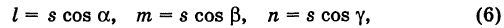
где
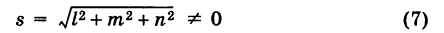
— длина вектора s. Отсюда получаем
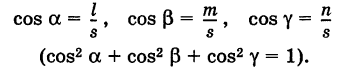
Таким образом, направляющие коэффициенты прямой пропорциональны соответствующим направляющим косинусам этой прямой.
Уравнения прямой (5) можно записать в стандартном виде
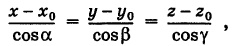
где  — направляющие косинусы прямой.
— направляющие косинусы прямой.
Пример:
Уравнения движения ракеты  , где время t дано в секундах, а координаты (х, у, z) движущейся точки — в километрах.
, где время t дано в секундах, а координаты (х, у, z) движущейся точки — в километрах.
Какова траектория ракеты? На каком расстоянии будет находиться ракета М от точки старта О (0, 0, 0) через 10 с?
Решение:
Исключая из данных уравнений время получим уравнения траектории 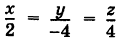 или
или
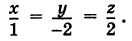
Таким образом, траектория представляет собой прямую линию, проходящую через начало координат.
При f = 10 с имеем х = 20, у = -40, z = 40 и
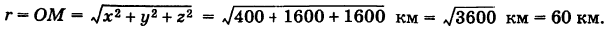
Пример:
Написать уравнения прямой, проходящей через две несовпадающие точки 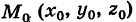 и
и 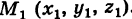 . За направляющий вектор прямой можно принять
. За направляющий вектор прямой можно принять
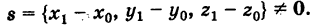
Следовательно, на основании (5) имеем
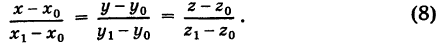
Пример:
Написать уравнения прямой, проходящей через точку 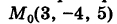 и параллельной оси Oz.
и параллельной оси Oz.
Решение:
Очевидно, имеем 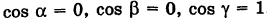 . Таким образом, в силу (5') получаем уравнения искомой прямой
. Таким образом, в силу (5') получаем уравнения искомой прямой 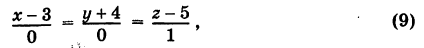 эквивалентные паре уравнений
эквивалентные паре уравнений
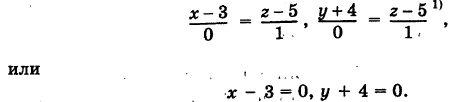
Направляющий вектор прямой (9) есть {0, 0, 1}, т.е. эта прямая перпендикулярна осям Ох и Оу.
Прямую L в пространстве можно задать также как линию пересечения двух плоскостей Р и Р' (рис. 202):
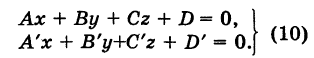
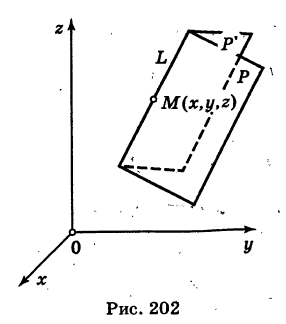
Предполагается, что плоскости не параллельны и не сливаются. Векторы 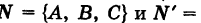
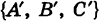 являются нормальными векторами этих плоскостей. Направляющий вектор s прямой, очевидно, удовлетворяет условиям
являются нормальными векторами этих плоскостей. Направляющий вектор s прямой, очевидно, удовлетворяет условиям 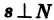 и
и 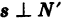 . Можно положить
. Можно положить
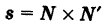
(х — знак векторного произведения.
Пример:
Определить направляющие косинусы прямой
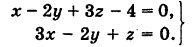
Решение:
Имеем 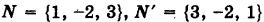 . Отсюда
. Отсюда
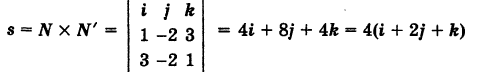 За направляющий вектор прямой можно принять
За направляющий вектор прямой можно принять 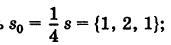 длина его
длина его 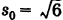 . Отсюда
. Отсюда
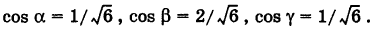
| Рекомендую подробно изучить предметы: |
| Ещё лекции с примерами решения и объяснением: |