Уравнение Бернулли - основные понятия, формулы и определения с примерами

Уравнение Бернулли:

При изучении статики жидкости мы выяснили, как распределяется давление в неподвижной жидкости. А как распределяется давление в движущейся жидкости? Выясним это экспериментально. Возьмем трубку переменного сечения с небольшими отверстиями в стенке, в которые вставлены открытые сверху манометрические трубочки (рис. 190). Отверстия в стенке практически  не влияют на распределение давления в жидкости. При стационарном течении жидкость в манометрических трубочках поднимется на определенную высоту. Высота столба жидкости от некоторого уровня показывает разность между давлением жидкости в трубке в месте расположения отверстий и атмосферным давлением. Опыт показывает, что в широких местах трубки давление больше, чем в узких. Но по уравнению неразрывности, чем больше сечение трубки, тем меньше скорость течения жидкости. Следовательно, можно сделать вывод:
при стационарном течении жидкости давление больше в тех местах, где меньше скорость течения, и, наоборот, меньше в тех местах, где скорость течения больше.

Эта зависимость была установлена швейцарским физиком Д. Бернулли и называется законом Бернулли.

Качественное объяснение этого закона основано на уравнении неразрывности и втором законе Ньютона.

Выделим небольшой объем жидкости, который движется вдоль трубки. При переходе из широкой части трубки в узкую его скорость увеличивается от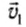

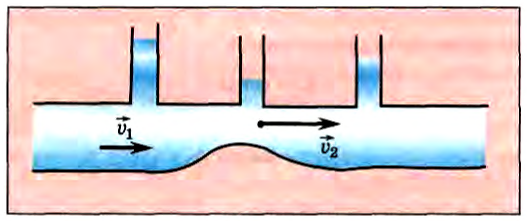
Рис. 190

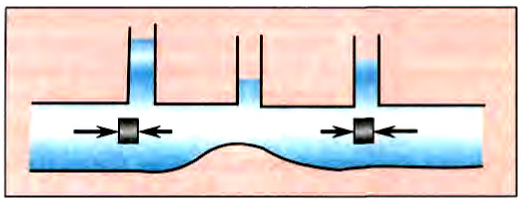
Рис. 191

Д. Бернулли также установил зависимость давления идеальной жидкости от скорости ее стационарного течения и перепада высоты.

Выделим в потоке идеальной жидкости тонкую трубку тока, а в ней некоторый объем между сечениями AB и CD (рис. 192).

Рис. 192

Пусть площадь поперечного сечения, давление и модуль скорости потока в сечении AB соответственно равны S₁, p_l, υ₁, а в сечении CD — S₂, p₂, υ₂. Под действием сил давления 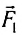и и 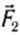силы тяжести выделенный объем жидкости за малый промежуток времени Δt сместится вправо и займет положение между сечениями A₁B₁ и C_lD_l. Силы давления 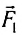и 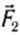совершат работу:
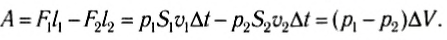    (1)

Существенно, что при стационарном течении жидкости энергия объема жидкости, заключенного между сечениями A₁B₁ и CD (см. рис. 192), остается неизменной. Все происходит так, как если бы жидкость, занимавшая объем ABB₁A₁, переместилась и заняла объем CDC₁D₁. Поэтому достаточно учесть лишь изменение энергии жидкости, переходящей из области ABA₁B₁ в область CDD₂C₂. При этом изменяются кинетическая энергия К и потенциальная энергия П. Изменение полной энергии W выделенного объема жидкости равно:

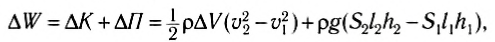
где h₁ и h₂ — высоты расположения соответствующих объемов (см. рис. 192).

Поскольку мы рассматриваем идеальную жидкость, в которой нет сил трения, то в данном случае можно использовать закон сохранения энергии в форме ∆W = А. C учетом этого получаем:

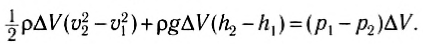
После сокращения на ΔV соберем величины с одинаковыми индексами в одной части равенства.
В результате получим:

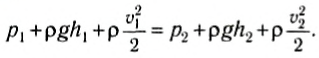
Мы произвольно выбирали поперечные сечения трубки тока. Поэтому выражение

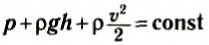 является постоянным в любом сечении трубки тока. Это и есть уравнение Бернулли.

Выясним физический смысл входящих в формулу (3) величин. Величину
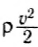 можно записать:

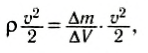
где ∆m — масса выделенного малого объема жидкости, ΔV— его объем. Следовательно, 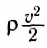есть кинетическая энергия единичного объема и называется плотностью кинетической энергии. Аналогично можно показать, что pgh — плотность потенциальной энергии.

Итак, сумма давления и плотностей кинетической и потенциальной энергий (трехчлен Бернулли) при стационарном течении идеальной жидкости остается постоянной для любого сечения трубки тока.

В уравнении (3) площадь поперечного сечения отсутствует. Следовательно, можно выбрать очень тонкую трубку тока, которая фактически представляет собой линию тока. Поэтому уравнение Бернулли часто формулируют так:
при стационарном течении идеальной жидкости трехчлен Бернулли 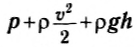 постоянен вдоль любой линии тока.

Используя уравнение Бернулли, можно объяснить ряд интересных явлений и решить многие задачи.

Так, при горизонтальном течении жидкости плотность потенциальной энергии постоянна и уравнение Бернулли примет вид:

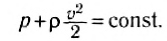
Отсюда следует, что в тех точках пространства, где скорость больше, давление меньше. Это подтверждается опытом, описанным в начале этого параграфа. C помощью уравнения Бернулли можно найти скорость истечения жидкости из отверстия, расположенного в сосуде на глубине h относительно поверхности жидкости (рис. 193). Выделим в сосуде линию тока 1—2, как показано на рисунке. Пусть атмосферное давление p₀. Записав уравнение Бернулли для точек 1 и 2, получим:
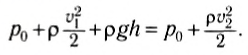    (4)

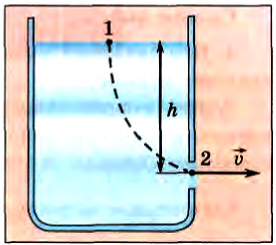
Рис. 193

Считая площадь отверстия малой по сравнению с площадью поперечного сечения сосуда, можно пренебречь скоростью опускания уровня жидкости в сосуде, положив υ₁ = 0. Тогда из формулы (4) следует формула Торричелли:

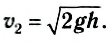
Истечение происходит с той же скоростью, какую имело бы тело при свободном падении с высоты h.

Зависимость давления в жидкости и газе от их скорости лежит в основе принципа действия многих устройств и приборов. На рисунке 194 изображена схема устройства водоструйного насоса. Струя воды подается в трубку А, имеющую на одном конце сужение. По сужению вода течет с большей скоростью. Из-за этого давление в струе в этом месте оказывается меньше атмосферного, воздух из сосуда всасывается в струю через трубку В и удаляется вместе с водой.

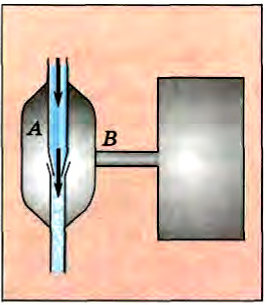
Рис. 194

На рисунке 195 изображен простейший пульверизатор, состоящий из двух трубок, расположенных перпендикулярно. Через горизонтальную трубку продувается воздух. В узкой части струи при выходе из трубки давление меньше атмосферного. Жидкость поднимается по вертикальной трубке из-за разности давлений и распыляется струей воздуха. Точно так же работают различные краскораспылители.

Рис. 195

Главные выводы:

1. При движении жидкости в тех местах, где скорость течения больше, давление меньше.
2. При стационарном течении идеальной жидкости сумма давления и плотности кинетической и потенциальной энергий жидкости постоянна вдоль линии тока.