Цепи с распределенными параметрами

Содержание:

Цепи с распределенными параметрами:

Как было показано в гл. I, электрическое и магнитное поле, а также превращение электромагнитной энергии в тепло, имеют место в каждом элементарном участке любых электрических устройств — индуктивных катушках, обмотках электрических машин и трансформаторов, линиях передачи электрической энергии и т. п. Следовательно, все устройства являются цепями с распределенными индуктивностью, емкостью и сопротивлением.

Однако, когда эти устройства рассматриваются в целом, они обычно заменяются эквивалентными двухполюсниками или четырехполюсниками с сосредоточенными параметрами г, L и С. Если устройство работает при одной частоте, эквивалентные схемы приводятся к простейшим — последовательному или параллельному соединению активного и реактивного сопротивлений для двухполюсника и к Т-образной или П-образной схеме с теми же элементами для четырехполюсника.

Если необходимо провести анализ для некоторого диапазона частот, эквивалентная схема становится тем сложней, чем шире этот диапазон. В общем случае приходится рассматривать цепь такой, какая она есть в действительности, т. е. как цепь с распределенными параметрами.

Необходимость рассмотрения устройств как цепей с распределенными параметрами возникает также в тех случаях, когда анализ должен выявить соотношения внутри устройства, например требуется определить напряжение и ток в разных точках линии передачи.

Далее методы расчета цепей с распределенными параметрами изучаются на примере однородных линий передач, широко применяемых в электроэнергетике и технике электрической связи.

Уравнения однородной линии

В двухпроводных однородных линиях индуктивность и сопротивление линии, а также емкость и проводимость через несовершенную изоляцию между проводами можно считать распределенными равномерно. Эти параметры на единицу длины двухпроводной линии, подсчитанные для линий различной конфигурации, в дальнейшем обозначены, соответственно, L, г, с, g.

Бесконечно малый элемент двухпроводной линии длиной dx может быть заменен эквивалентной схемой с параметрами Ldx, rdx, Cdx и rdx. На рис. 20.1 эта схема изображена жирными линиями и выбраны управления напряжений и токов. При этом индуктивность и сопротивление являются продольными параметрами линии, а емкость и проводимость — ее поперечными параметрами.

В каждом элементе dx линии происходит падение напряжения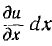

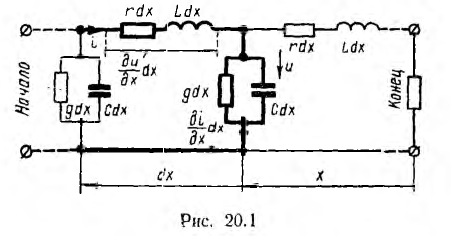
В общем случае переменных напряжений и токов для элемента, расположенного на расстоянии х от конца линии и отмеченного на рис. 20.1 жирными линиями,

.

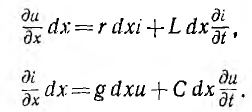После сокращения на dx получается система уравнений в частных производных для мгновенных значений напряжений и токов:

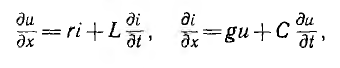
решение которой при заданных начальных и граничных условиях определит u и i в функции х и t.

При анализе процессов в трехфазной линии каждая ее фаза может рассматриваться, как однофазная двухпроводная линия. Не приводя вывода, можно, например, указать, что для симметричной трехфазной воздушной линии, провода которой расположены в вершинах равностороннего треугольника и удалены от земли, эквивалентная каждой фазе двухпроводная линия имеет индуктивность I, вдвое меньшую, а емкость С, вдвое большую, чем двухпроводная линия с таким же расстоянием между проводами, как и трехфазная линия. Сопротивление г эквивалентной двухпроводной линии равно сопротивлению провода одной фазы, а проводимость g — проводимости одной фазы по отношению к земле.

Решение уравнений однородной линии для установившихся режимов

Режим постоянного напряжения:

Если к началу линии приложено постоянное напряжение U₀₁, npи установившемся режиме напряжения и токи в линии будут также постоянными. При подстановке в уравнения линии вместо переменных мгновенных значений u и i постоянных во времени U₀ и I₀ в каждой точке линии производные по t будут равны нулю и уравнения станут обыкновенными дифференциальными уравнениями, в которых независимой переменной является x — расстояние от конца линии:

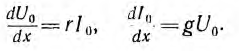
Для получения из приведенной выше системы одного уравнения с одним неизвестным U₀ надо взять производную по х от первого уравнения:

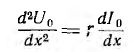
и подставить сюда значение 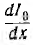из второго:

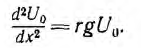
Если положить, что 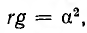, то

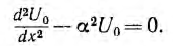
Характеристическое уравнение и его корни имеют вид:

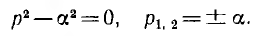
Общее решение для напряжения на расстоянии х от конца линии получает вид:

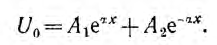
Следовательно, ток в этой точке

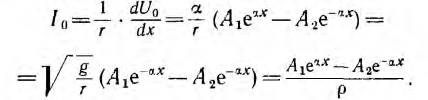
Отсюда видно, что однородную линию характеризуют две величины: 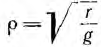— волновое сопротивление и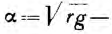коэффициент распространения.

Постоянные интегрирования определяются из граничных условий, которыми могут быть две из четырех величин, например напряжение U₀₁ ток I₀₁ в начале линии или U₀₂, I₀₂ в конце линии. Пусть заданы напряжение U₀₂ и сопротивление r₂ нагрузки и тем самым ток 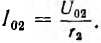Тогда для конца линии, т. е. при х = О,

Откуда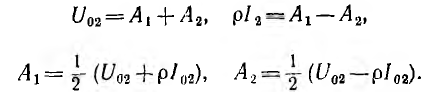

Следовательно, напряжение и ток на расстоянии х от конца линии будут:

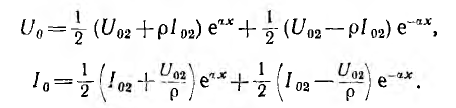
Таким образом, напряжение и ток в любой точке линии определяются алгебраическими суммами ординат двух экспоненциальных кривых. Ординаты кривой с 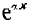уменьшаются от начала к концу линии, а ординаты кривой 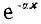— от конца к началу. На рис.. 20.2 показаны составляющие и суммарные кривые U₀ и I₀ для случая r₂ > р. Если включенное в конце линии сопротивление равно волновому, т. е. r₂ = р, вторые члены выражений для U₀ и I₀ пропадают, и распределение U₀ и I₀ = 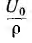вдоль линии представляется одной зкспонентой.

Следовательно, в однородной линии постоянного тока происходит затухание напряжения и тока вдоль линии, определяемое коэффициентом распространения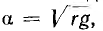 который в данном случае является также коэффициентом затухания.

Режим синусоидального напряжения

Если к началу линии приложено синусоидальное напряжение постоянной угловой частоты ω, при установившемся режиме напряжение и ток в каждой точке линии будут также синусоидальными функциями времени той же частоты. Так как синусоидальные напряжение и ток являются частным случаем переменных и и i, в расчетах надо учесть все параметры линии рис. 20.1, т. е. r, L, g и С.

Применяя символический метод, можно использовать результаты расчета для линии постоянного тока (п. 1), заменив продольное сопротивление r комплексным сопротивлением 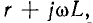а поперечную про водимость g комплексной проводимостью 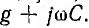. Тогда характеристиками линии будут волновое сопротивление Z коэффициент распространения y:

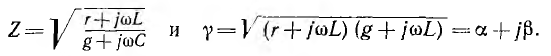
Вещественная часть а коэффициента распространения является коэффициентом затухания, а мнимая 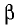называется коэффициентом фазы.

При указанном переходе от постоянного тока к синусоидальному комплексные напряжения и ток на расстоянии х от конца линии получают вид:

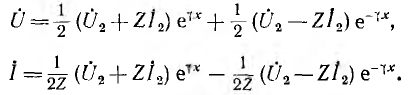
Если ввести гиперболические функции

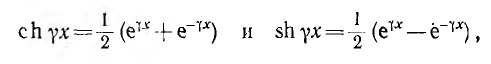
выражения для 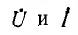будут:

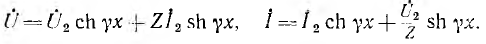
Эти уравнения аналогичны уравнениям для однородных симметричных цепных схем, что и следовало ожидать, так как однородная линия рассматривалась как однородная цепная схема с бесконечно большим числом элементарных звеньев.

Однородная линия в целом является симметричным пассивным четырехполюсником. Его уравнения получают из последних выражений при х =1, где 1 — длина линии:

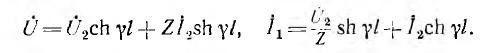
Параметры этого четырехполюсника

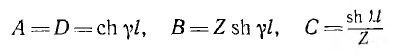
подчиняются условию

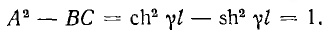
Из уравнений линии видно, что напряжение и ток в любой точке линии являются также функцией частоты ω, так как от нее зависят волновое сопротивление Z, коэффициент распространения у и его составляющие 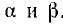. Это значит, что в случае сложной формы кривых напряжения и тока, имеющей место в линиях связи, отдельные гармоники будут передаваться с разным коэффициентом затухания а, что вызывает нежелательные искажения. Чтобы их избежать, строят линии, у которых 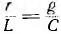юТогда коэффициент распространения

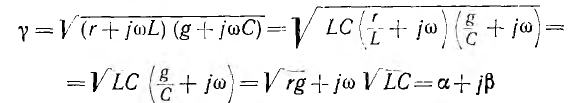
и, следовательно, коэффициент затухания а = 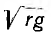не зависит от частоты. Волновое сопротивление такой линии

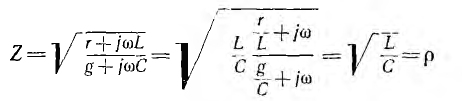
является вещественным числом, т. е. активным сопротивлением, также независящим от частоты. В результате передача будет осуществляться без искажения. Такая линия называемся неискажающей.

Бегущие и стоячие волны

Уравнения линии для режима синусоидального напряжения могут быть преобразованы. После введения значения 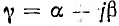и обозначений

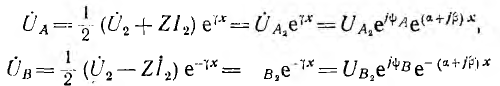
комплекс напряжения в линии получает вид:

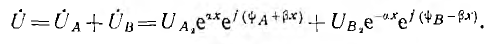
Переходя к мгновенному значению напряжения

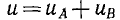
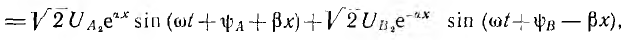
его можно рассматривать как сумму двух составляющих 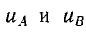, зависящих от х и t.

В любой фиксированный момент времени первая составляющая иА распределена вдоль линии по закону синуса с амплитудой, которая и соответствии с множителем е" возрастает от конца линии к ее началу, т. е. затухает от начала линии к ее концу. Если в данный момент времени I' в точке х'

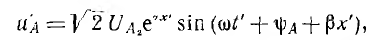
то в точке х" <.х в момент времени 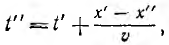где v имеет размерность скорости,

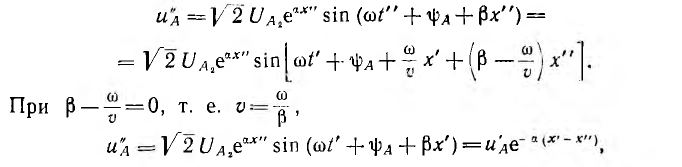
т. е. значение напряжения u_А перемещается вдоль линии со скоростью 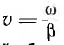одновременно затухая. Иными словами, является прямой волной, бегущей от начала линии к ее концу (рис. 20.3). Длина X волны, т. е. расстояние, на котором фаза волны изменяется на 2π, определяется соотношением (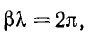, откуда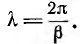

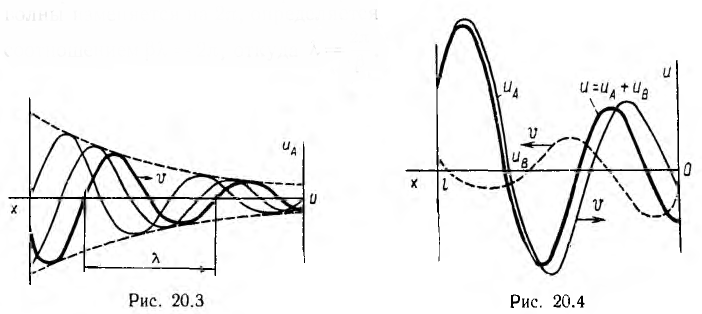
Скорость 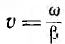называется фазовой скоростью, так как с такой скоростью движется точка, для которой фаза остается неизменной. Например, для неискажающей линии, для которой 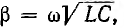, фазовая скорость

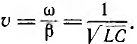
Аналогично, вторая составляющая u_B является волной такой же длины 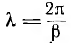, но бегущей вдоль линии со скоростью 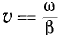от конца к началу. Амплитуда этой обратной волны в соответствии с множителем 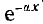затухает по мере продвижения волны от конца линии к ее началу. На рис. 20.4 изображены прямая и обратная волны напряжения и их сумма и для одного и того же момента времени.

Так как выражение комплексного тока I имеет такой же вид, как и комплексного напряжения U, ток i также можно рассматривать как наложение двух затухающих синусоидальных волн 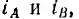бегущих навстречу друг другу с той же скоростью 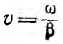(рис. 20.5).

Подставив в выражение фазовой скорости для неискажающей воздушной линии значения ее емкости С и индуктивности l на единицу длины:

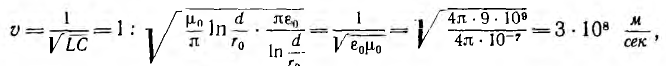
т. е. фазовая скорость равна скорости света в пустоте. Длина волны при частоте f = 50 гц

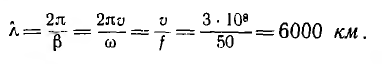
Следовательно, длина современных воздушных линий, служащих для передачи электрической энергии, меньше четверти длины волны. В телефонных линиях связи при частоте f = 1000 гц длина волны составляет 300 км, т. е. в телефонной линии может уложиться несколько длин волн. Линии, применяемые в радиоаппаратуре, работающей при высоких частотах, имеют длину, во много раз большую, чем длина волны.

В кабельных линиях фазовая скорость, а следовательно, и длины волн при тех же частотах будут примерно вдвое меньше, так как диэлектрическая проницаемость изоляции кабеля, которую надо подставить в формулу для v, близка к .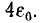

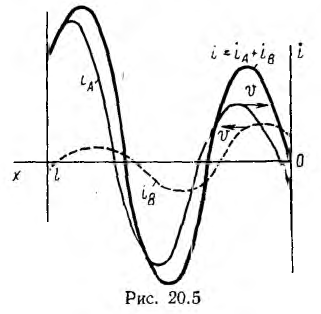
Комплексные полные сопротивления для прямых и обратных волн равны отношению комплексных действующих значений напряжений и токов одноименных волн:

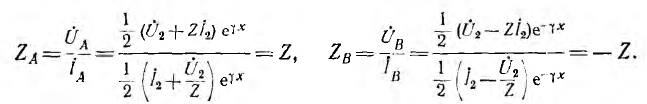
Следовательно, эти сопротивления равны волновому сопротивлению Z линии со знаком плюс или минус и не зависят от сопротивления приемника 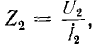, хотя амплитуды напряжения и тока от него зависят.

Обратные волны можно рассматривать как результат отражения прямых волн от конца линии. Тогда обратные волны называют отраженными, а прямые падающими. Коэффициенты отражения волны напряжения q_u и волны тока 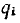равны отношению соответствующих комплексных амплитуд отраженной и надающей волн в конце линии. Тогда из выражений для 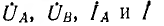при х = 0 и из соотношения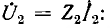

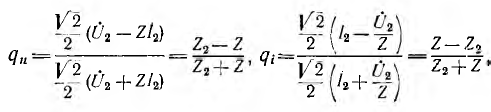т.е.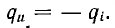

При разомкнутой линии 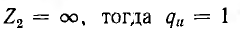и q_i=—1, т. е. волна напряжения отражается без перемены знака, а волна тока — с переменой знака. Для линии, замкнутой на конце накоротко, Z₂ = 0; тогда q_n = 1 и q_i = 1, т. е. волна напряжения отражается с переменой знака, а волна тока — без перемены знака. В этих двух случаях отражение происходит без изменения величины падающего напряжения и тока.

Если замкнуть линию на сопротивление, равное волновому (Z₂ = Z), отраженных волн не будет. Такое согласование параметров линии и нагрузки часто применяют в устройствах связи, так как условие отсутствия отраженных волн близко к условию, при котором приемник получает максимальную мощность.

Интересен идеальный случай линии без потерь, когда r = 0 и g = 0. Тогда 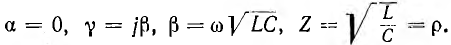При холостом ходе 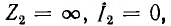и уравнения линии получают вид:

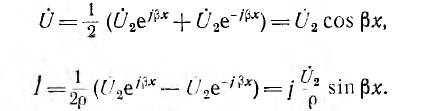
В этом случае распределения напряжения и тока вдоль линии представляют собой стоячие волны (рис. 20.6). В точках линии, где 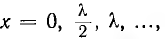имеют место пучности напряжения, так как cos βх обращается в±1, и узлы тока, так как sin βx = 0. В точках линии, где .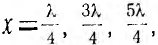, имеют место узлы напряжения и пучности тока (здесь).

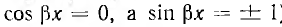Стоячие волны будут также при коротком замыкании линии без потерь, и при нагрузке индуктивным или емкостным сопротивлением, т. е. тогда, когда средняя мощность равна нулю. Во всех этих случаях не происходит передачи энергии вдоль всей линии, так как узлах, где u = 0 или i = 0, мгновенная мощность равна нулю и чергия через эти узлы не передается. Если энергия расходуется в приемнике, в линии или в линии и приемнике, должны существовать бегуне волны напряжения и тока, обеспечивающие процесс передачи энергии вдоль всей линии.

Распределение напряжения и тока вдоль линии

Разложение напряжения и тока на прямую и обратную волны при установившемся синусоидальном режиме облегчает анализ явлений. В действительности же в каждой точке в каждый момент времени существуют одно напряжение и один ток, являющиеся алгебраической суммой ординат падающей и отраженной волн для этого момента времени. Из рис. 20.4 и 20.5 видно, что распределение действительных мгновенных значений напряжения и тока носит волнообразный характер, и их значения вдоль линии могут отличаться не только по величине, но и по знаку.

Для практики основной интерес представляет распределение действующих значений напряжения U и тока I вдоль линии. Выражения для 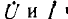через гиперболические функции, если положить 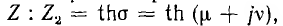, можно привести к виду:

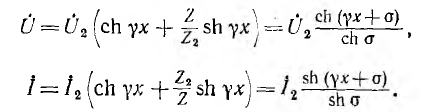
Квадраты модулей комплексов 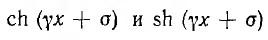равны:

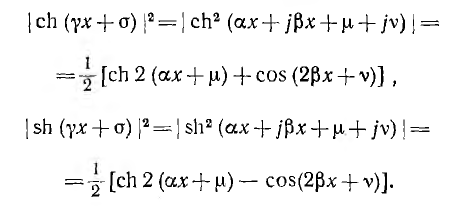
Следовательно, квадраты действующих значений

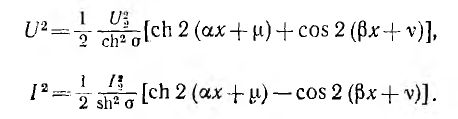
Кривые 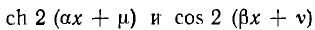для некоторого частного значения Z : Z₂, от которого зависят 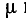и v, а также сумма этих кривых, характеризующая распределение U₂, и их разность, характере зующая распределение I², прив< дены на рис. 20.7.

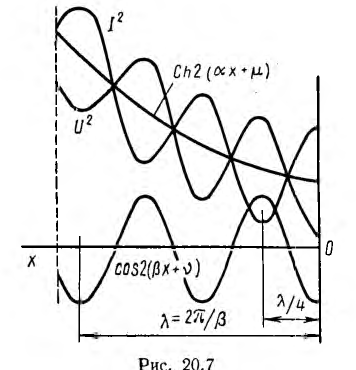
Из этих кривы видно, что максимумы и минимумы как U, так и I, чередуются почти через четверть длины волны, при чем максимумы U сдвинуты относительно максимумов I также почти на четверть длины волны. В линиях, длина которых не превышает четверти длины волны, при принятом соотношении Z : Z₂ действующее значение тока возрастает, а действующее значение напряжения убывает в направлении от начала линии к ее концу.

Переходные процессы в однородных линиях

Общее решение уравнений переходного процесса:

При включении и выключении линий и изменениях нагрузки, а также под влиянием атмосферных разрядов в линиях возникают переходные процессы. Уравнения, связывающие напряжение u и ток i в любой точке линии, были выведены:

Если продифференцировать первое уравнение по х, а второе по I:

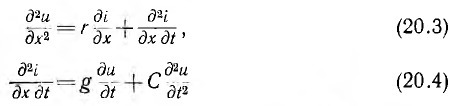
и подставить в выражение (20.3) значения 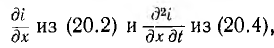получается дифференциальное уравнение в частных производных относительно напряжения:

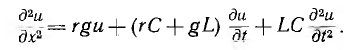
В общем виде решение этого дифференциального уравнения в частных производных весьма сложно. Сравнительно простое решение получается для неискажающей линии, у которой

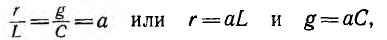
где а — постоянная. После подстановки значений r и g уравнение получит вид:

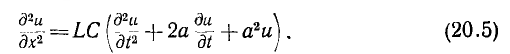
Решение уравнения для напряжения можно искать в виде

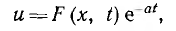
где F (х, t) — функция координаты и времени. После подстановки в (20.5) значения u и его производных

-

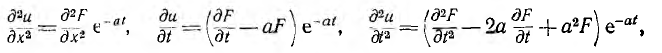получается уравнение

или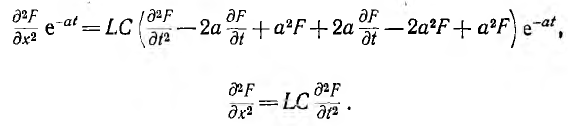

Оно совпадает с уравнением колебаний струны, имеющим решение

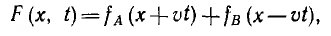
где скорость 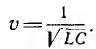Правильность этого решения может быть проверена подстановкой.

Таким образом, для неискажающей линии напряжение вдоль линии изменяется в зависимости от места и времени следующим образом:

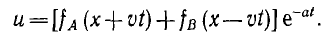
Уравнение для тока можно получить из выражения (20.2), если подставить 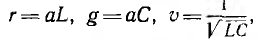значения 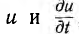и учесть, что
тогда 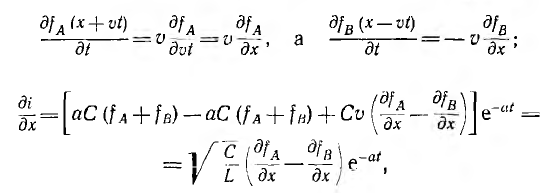и окончательно после интегрирования

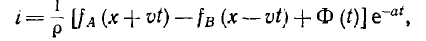
где р =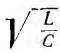 — волновое сопротивление неискажающей линии Ф (t)—некоторая функция второй переменной—времени.

Подстановка последнего выражения в уравнение (20.1) после упрoщений приводит к равенству:

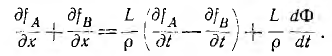
Перейдя к новым переменным 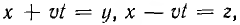, можно написать последнее уравнение в виде:

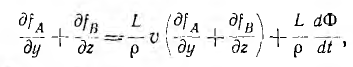
так как - 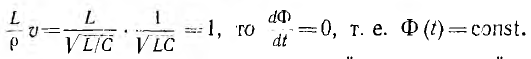Можно показать, что ток не содержит постоянной составляющей, следовательно, Ф (t) = 0 и окончательно

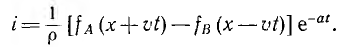
Здесь получен только общий вид функциональных зависимостей напряжения и тока от x и t. Конкретный вид функций f_A (х + vt) и 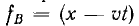будет определяться условиями задачи.

Переходные процессы в однородных линиях можно рассчитать также операторным методом. Так как напряжение и ток являются функциями двух переменных t и х, их операторные изображения будут функциями и оператора р и х. Тогда уравнения для однородной линии в операторной форме при нулевых начальных условиях имеют вид:

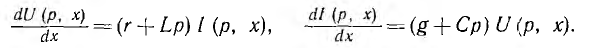
Таким образом, переход от мгновенных значений u (t) и i (t) к их операторным изображениям U (р, х) и I (р, х) превратил дифференциальные уравнения в частных производных в обыкновенные дифференциальные уравнения. После решения этих уравнений для перехода к оригиналу можно применить обратное преобразование Лапласа.

Бегущие волны

Можно показать, что выведенные в п. 1 выражения для u и i представляют напряжения и ток линии в виде наложения прямой и обратной волн, бегущих со скоростью v.

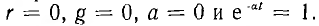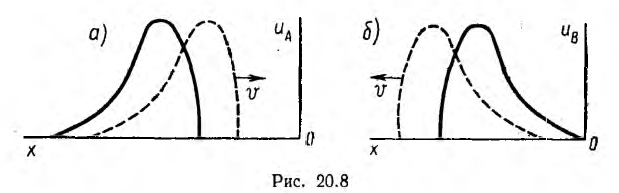
В линии без потерь . Пусть в некоторый момент времени t = t₁, составляющая напряжения u_А = 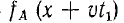имеет распределение, показанное на рис. 20.8, а. Для всех точек, для которых х+ vt = const или 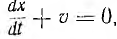, напряжение этой слагающей имеет одно и то же значение, а это значит, что кривая pаспределения напряжения u_А перемещается со скоростью 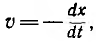т.е. в направлении конца линии, от которого ведется отсчет расстояний. Слагающая 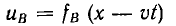представляет также волну, но гремещающуюся в обратную сторону (рис. 20.8, б). Действительное определение напряжения равно сумме прямой и обратной волн.

Как видно из выражения для тока, обе его составляющие получаются с помощью делении составляющих напряжения на волновое сопротивление р, соответственно со знаком плюс и минус и поэтому удут подобны последним, но действительное распределение тока авно арифметической разности прямой и обратной волн.

При наличии потерь в линии прямая и обратная волны также существуют, но множитель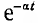 указывает на затухание волн по мере их движения. Алгебраические суммы напряжений и токов падающей и отраженной волн у конца линии должны равняться напряжению u₂ и току приемника:

откуда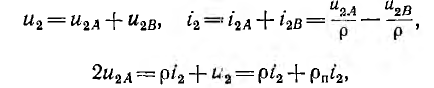

т. е. ток i2 в конце линии равен току эквивалентной схемы, состоящей из последовательного соединения сопротивления р и переходного сопротивления приемника 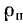включенной на напряжение 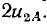. После определения тока i2 отраженные волны напряжения и тока могут быть определены из соотношений:

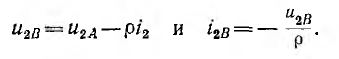
Например, если линия замкнута на активное сопротивление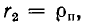

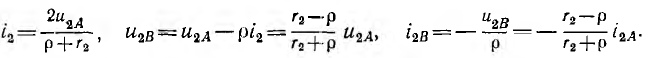
Мощность р₂ в конце линии, т. е. мощность приемника

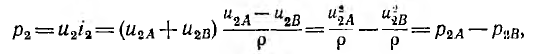
равна разности мощностей падающих р_2A и отраженных р_2В волн, при сопротивлении r₂ приемника, равном волновому сопротивлению р линии, 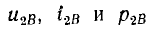становятся равными нулю, т. е. отраженние волны не возникают, в линии наступает установившийся режим, вся мощность падающих волн потребляется приемником.

Для разомкнутой линии 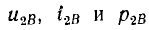для короткозамкнутой линии r₂ = 0, откуда 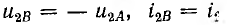т. е. в этих случаях отраженные волны имеют ту же величину, что падающие, причем с переменой знака в разомкнутой линии отражает, волна тока, а в короткозамкнутой — волна напряжения

Энергии магнитного и электрического полей прямых волн u_А и на участке dx линии

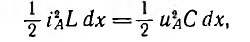
так как 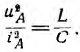Таким образом, энергии магнитного и электрического полей прямой волны на участке линии, а следовательно, и во всей линии равны друг другу. Такое же соотношение имеет место и для обратной волны. Для результирующих электрического и магнитного полей равенства энергий нет.

Процесс включения линии

Когда длина линии I мала по сравнению с длиной волны 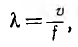, время пробега волны вдоль всей линии

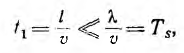
т. е. много меньше периода Т_$ синусоидального напряжения, на которое включается линия. Поэтому можно пренебречь изменением этого напряжения за время начальной стадии переходного процесса включения и ограничиться рассмотрением включения линии на постоянное напряжение U₀, равное в момент включения мгновенному значению напряжения u₁(0). Таким образом, волновые процессы при включении линии на синусоидальное и на постоянное напряжение при 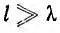будут аналогичными.

В качестве примера рассматривается включение на постоянное напряжение U₀ линии без потерь на основе соотношений, полученных в п. 2 этого параграфа. При этом предполагается, что источник напряжения имеет относительно большую мощность, т. е. его внутренним сопротивлением можно пренебречь. Тогда волны напряжения и тока будут отражаться от начала линии так, как будто оно замкнуто накоротко.

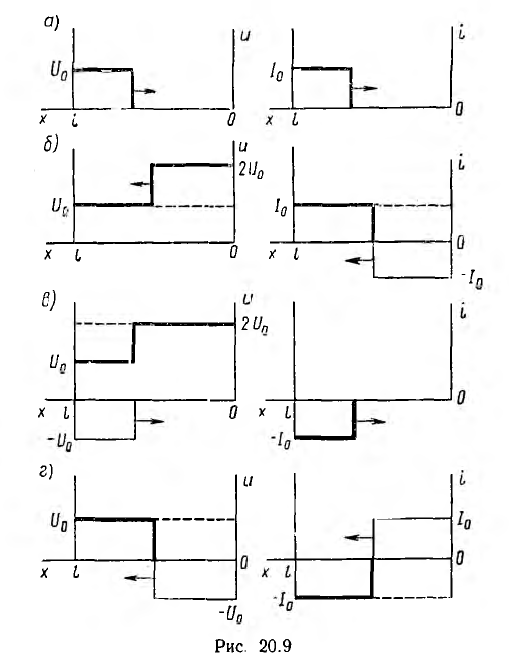
После включения разомкнутой на конце линии, т. е. при режиме холостого хода, вдоль нее пойдут волны напряжения и тока, пока занные на рис. 20.9, а со стрелкой в направлении их движение

Через время, равное 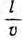волны дойдут до конца линии и тогда в любой ее точке напряжение будет равно U₀, а ток 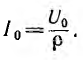Затем произойдет отражение волны напряжения без перемены знака, а тока. — с перечной знака. Отраженные волны пойдут к началу линии, увеличивая напряжение до 2U₀ и уменьшая ток до нуля (рис. 20.9, б). В начале линии также произойдет отражение, но теперь волна напряжения U₀ отразится с переменой знака, а тока — I₀ без перемены. Отраженные волны пойдут опять вдоль линии, на которой напряжение станет равным U₀, а ток — I₀ (рис. 20.9, в).

В результате третьего отражения к началу пойдет отрицательная волна напряжения и положительная волна тока, уменьшающие напряжение и ток в линии до нуля (рис. 20.9, г). В момент прихода этих волн к началу линии вся линия будет без напряжения и тока, как и в начальный момент, после чего процессы начнут повторяться. Время полного цикла

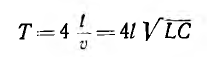
называется периодом собственных колебаний линий

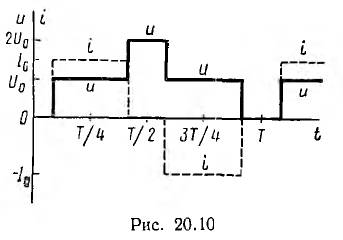
Используя рис. 20.9, построен график изменения во времени напряжения и тока в точке, расположенной на расстоянии 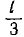от начала линии (рис. 20.10); напряжение колеблется от нуля до 2U₀, а ток изменяется от I₀ до — I₀ При включении той же линии, но к концу которой подключено активное сопротивление r₂, волны напряжения U₀ и тока I₀ при 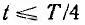будут такими же, как в предыдущем случае (см. рис. 20.9, а). Пусть r₂ > р, тогда коэффициент отражения n от конца линии равен отношению отраженной волны к падающей, вычисленному в п. 2:

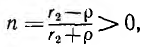
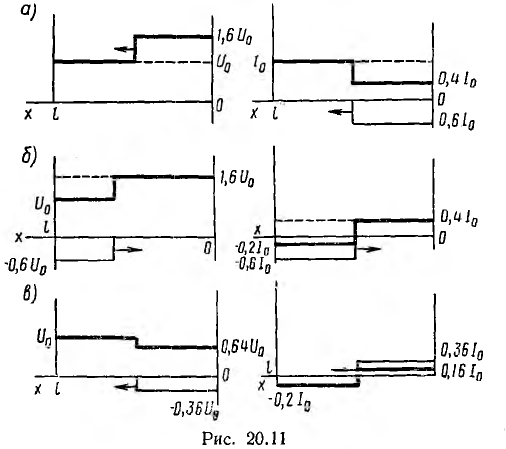
и. волна напряжения U₀ отразится от конца линии без перемены знака, а волна тока I₀ с переменой знака. На рис. 20.11, а показан напряжение и ток линии после отражения для г₂ = 4р, т.е. для = 0,6. Отраженные волны 0,6 U₀ и — 0,6 I₀ увеличивают напряжение до 1,6 U₀ и уменьшают ток до 0,4 I₀. После отражения от начала инии волна — 0,6 U₀ снизит напряжение линии до U₀, а волна — 6 I₀ снизит ток до — 0,2 I₀ (рис. 20.11, б). В результате второго отра-ения от конца линии напряжение на ней будет 0,64 U₀, а ток 0,16 I₀ же. 20.11, в) и т. д.

При включении короткозамкнутой линии ее конец, как. и начало, удут отражать волну напряжения с переменой знака, а волну тока — без перемены. При включении такой линии волны напряжения U₀ I тока I₀ при t < Т/4 будут такими же, как и в двух предыдущих :лучаях (см. рис. 20.9, а). Затем отраженная от конца линии волна — U₀ понизит напряжение линии до нуля (рис. 20.12, а), но после отражения от начала волна U₀ восстановит его значение (рис. 20.12, б) и т. д. Волна тока I₀ после отражения от конца линии увеличит ток линии до 2I₀ (см. рис. 20.12, а), после отражения от начала — до 3 I₀ (см. рис. 20.12, б) и т. д.

В линии с потерями волны напряжения и тока постепенно затухают, а напряжение и ток приближаются к тем значениям, которые они должны иметь при установившемся режиме.

Цепи с распределенными параметрами. Первичные параметры однородной линии

До сих пор рассматривались электрические цепи с сосредоточенными параметрами, т. е. предполагалось, что электрическая цепь представляет собой совокупность некоторых самостоятельно существующих элементов r, L и С, сосредоточенных в различных точках ее. Напряжение и ток этих элементов связываются соотношениями

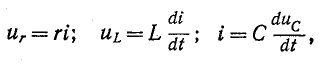
основанными на предположении, что ток, входящий в каждый из этих элементов цепи, равен току, выходящему из него. Решение этих уравнений дает закон изменения исследуемой электрической величины в зависимости от времени, но не от координаты длины, которая в эти уравнения не входит.

Однако представление электротехнических устройств в виде цепей с сосредоточенными параметрами не всегда возможно. Например, рассматривая электромагнитные процессы, происходящие в электрических линиях, при помощи которых электрическая энергия или сигналы передаются на расстояние, необходимо иметь в виду, что магнитное и электрическое поля распределены по всей длине линии и превращение электромагнитной энергии в тепло также происходит по всей длине линии. Таким образом, линия является цепью с распределенными параметрами.

Если мысленно выделить какой-либо конечный участок этой линии, то токи на концах этого участка окажутся неодинаковыми вследствие наличия токов смещения, обусловленных емкостью между токоведущими проводниками, и токов утечки через изоляцию. Только при бесконечном уменьшении участков линии токи на концах их можно считать равными друг другу.

Следовательно, приведенные выше уравнения непосредственно не применимы ко всей линии в целом или конечным участкам ее; строго говоря, они могут быть применимы только к участкам бесконечно малой длины.

Магнитный поток, который сцепляется с контуром тока, образуемым токоведущими проводниками, определяет индуктивность цепи.

Емкость между проводами, а также емкости этих проводов по отношению к земле (или соответственно к корпусу машины, самолета, корабля и т. д.) и другим соседним проводам определяют емкость цепи.

Тепловые потери в проводах с учетом поверхностного эффекта и эффекта близости обусловливают продольное активное сопротивление цепи.

Наконец, несовершенство изоляции (проводимость изоляции и диэлектрические потери, возникающие в ней) определяет поперечную активную проводимость цепи.

В качестве цепи с распределенными параметрами ниже рассматривается однородная двухпроводная л и н и я, т. е. такая линия, индуктивность, емкость, активное сопротивление и проводимость которой равномерно распределены вдоль всей длины линии. Эти электрические параметры, отнесенные к единице длины линии,

называются первичными параметрами линии; они обозначаются через L, С, r и g*.

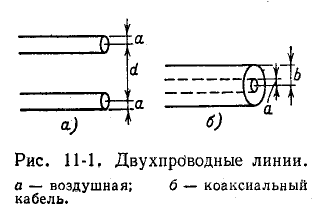
Однородная двухпроводная линия является распространенным типом линии; она используется в электропроводной связи и радиотехнике и выполняется в виде параллельных проводников (рис. 11-1, а) или коаксиального кабеля (рис. 11-1, б).

Уравнения для напряжений и токов такой линии в принципе применимы и к другим типам линий — трехфазным и многопроводным.

Первичные параметры линии зависят от ее конструкции и частоты. Вычисление первичных параметров относится к задачам теории электромагнитного поля, составляющей содержание третьей части курса «Теоретические основы электротехники».

В области радиочастот первичные параметры однородной двухпроводной линии с медными проводами вычисляются по следующим формулам (размеры в метрах).

Воздушная линия (параллельные провода) (рис, 11-1, а):

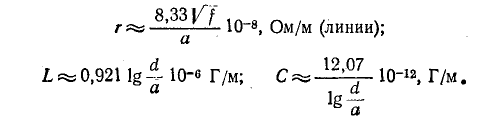
* Следует обратить внимание на то, что здесь 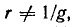так как параметры линии г и g не связаны друг с другом: параметр r — продольный (активное сопротивление проводов), параметр g — поперечный (активная проводимость изоляции).

Коаксиальный кабель (рис. 11-1, б):

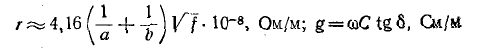
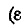— угол диэлектрических потерь);

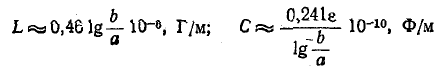
(е — относительная диэлектрическая проницаемость изоляции).

С повышением частоты угол потерь 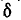уменьшается. Изоляция, применяемая для коаксиальных кабелей, обычно имеет 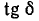порядка

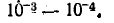
Активная проводимость g между параллельными проводами, зависящая от метеорологических условий, состояния изоляторов, к которым подвешены провода, и других факторов, определяется экспериментально.

Практически во многих случаях можно считать, что

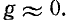
На высоких частотах ввиду значительного преобладания индуктйвного сопротивления токоведущего проводника над его активным сопротивлением последним можно во многих случаях пренебречь.

Следует заметить, что на низких частотах и при малой длине линии, когда емкостная и активная проводимости незначительны, токи в начале и конце линии практически одинаковы; в этом случае линия с достаточной точностью может рассматриваться как цепь с сосредоточенными параметрами. Разграничение понятий «короткая» и «длинная» линии связано с частотой, на которой работает рассматриваемая линия.

Дифференциальные уравнения однородной линии

Напряжение и ток в линии являются функциями двух независимых переменных: пространственной координаты х, определяющей место наблюдения, и времени t, определяющего момент наблюдения. Здесь предполагается, что направление координатной оси х совпадает с направлением оси линии.

Нашей ближайшей задачей является нахождение пространственно-временного распределения-тока в линии 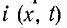и напряжения между проводами 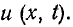При этом в общем

случае может рассматриваться передача электромагнитной энергии по линии, когда источник и приемник имеются на обоих концах линии.

Выберем положительное направление тока в линии слева направо (рис. 11-2) и условимся называть «началом» линии левый конец, а «концом» линии — правый конец. Расстояние до произвольной точки линии от начала обозначим через х, а от конца — через х'. Таким образом, вся длина линии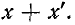

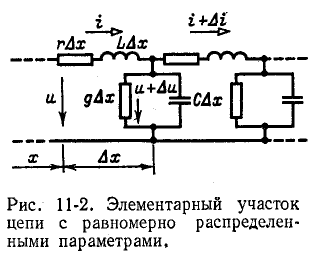
Выделим элементарный участок линии длиной Да:, находящийся на расстоянии х от начала. Пользуясь первичными параметрами r, g, L и С, отнесенными к единице длины линии, приближенно представим рассматриваемый элементарный участок линии в виде последовательно включенных сопротивления 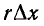и индуктивности 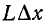и параллельно включенных активной проводимости 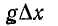и емкости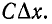

Обозначим:

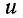— напряжение между верхним и нижним проводами в точке х

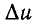— приращение напряжения на участке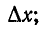

i — ток в точке х

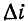— приращение тока на участке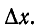

Уравнения для приращений напряжений и тока на элементе длины 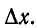запишутся следующим образом:

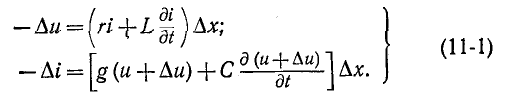
Ввиду наличия двух независимых переменных (х н t) уравнения записываются в частных производных.

По мере стремления 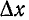к нулю степень точности этих уравнений повышается, причем величина второго порядка параметрами.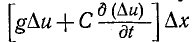в правой части нижнего уравнения(11-1) может быть опущена.

Итак, линия рассматривается как цепная схема с бесконечно большим числом звеньев, электрические параметры которых бесконечно малы.

Разделив обе части уравнений (11-1) на 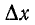и перейдя к пределу 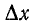= 0, получаем дифференциальные уравнения линии:

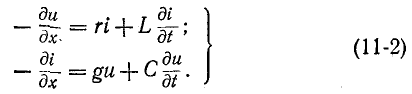
Эти уравнения известны в литературе под названием телеграфных уравнений.

Если за начало отсчета принять конец линии, т. е. ввести координату 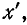то уравнения примут вид:

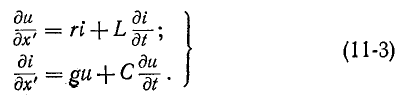
Уравнения (11-2) или (11-3) могут быть решены однозначно при использовании начальных и граничных условий. Начальными условиями будут значения напряжения и тока в начале или конце линии в момент времени, принятый за нуль. Граничные условия определяются связями между напряжением и током в начале или конце линии, зависящими от заданного режима работы линии.

Решение указанных выше уравнений дает функциональные зависимости напряжения и тока в линии от переменных х (или х') и t.
 

Синусоидальный режим в однородной линии

При периодическом режиме под воздействием приложенного к линии синусоидального напряжения в любой точке линии напряжение и ток изменяются синусоидально с частотой источника 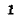. Обозначим комплексные действующие значения напряжения и тока на расстоянии х от начала линии через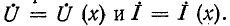

¹ Обоснованием высказанного положения является линейность уравнений (11-2) и (11-3), так как только в таких уравнениях сохраняется синусоидальность всех функций.

Применяя комплексную форму записи, перепишем уравнения в комплексном виде:

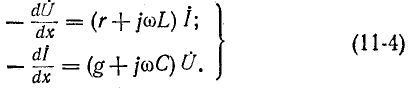
Ввиду того что комплексные значения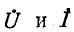не зависят от t и являются только функциями х, при переходе от уравнений (11-2) к (11-4) частные производные по х заменены обыкновенными.

Исключая из системы (11-4) ток 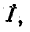получаем уравнение относительно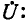

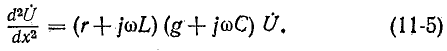
Аналогично, исключая из (11-4) напряжение 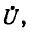получаем уравнение относительно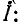

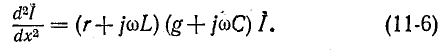
Обозначим квадратный корень из комплексного множителя пр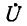и или 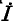через

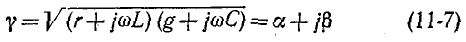
и назовем эту величину коэффициентом распространения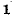. Смысл такого названия выяснится позже. Итак, уравнения (11-5) и (11-6) записываются в виде

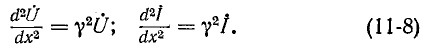
Получились одинаковые однородные линейные дифференциальные уравнения второго порядка. Решение первого из них имеет вид:

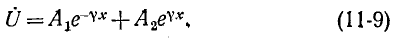
Ток 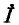после этого получается подстановкой (11-9) в первое уравнение (11-4):

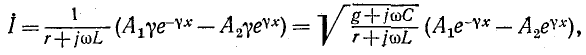
или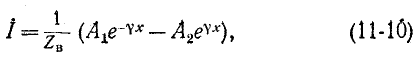

где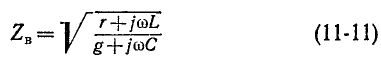

называется    волновым сопротивлением линии

Смысл такого названия объяснен дальше. Подставив (11-7) в (11-9), получим: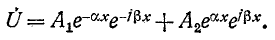

Мгновенное значение напряжения в точке х равно мнимой части выражения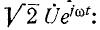

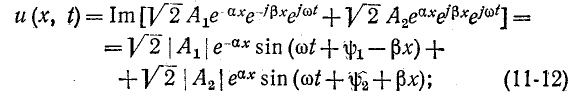
здесь 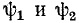— аргументы комплексных величин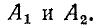

Таким образом, мгновенное значение напряжения в любой точке линии слагается из двух функций.

Рассмотрим вначале первую из этих слагающих функций.

Если считать точку х фиксированной и рассматривать изменение напряжения в данной точке в зависимости от времени, то первая слагающая выражения (11-12) представит собой синусоидальную функцию с постоянной амплитудой.

Если же считать момент времени t фиксированным и рассматривать изменение мгновенного напряжения вдоль линии (т. е. в зависимости от х), то получим затухающую синусоидальную волну напряжения, амплитуда которой 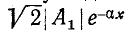убывает с ростом х, т. е. по мере удаления-от начала линии к концу.

Величина а, характеризующая изменение амплитуды волны на единицу длины линии, называется коэффициентом ослабления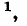а величина  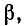равная изменению фазы на единицу длины линии, называется к о-эффициентом фазы.

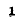Ранее применялся термин коэффициент затухания.

Убывание амплитуды волны вдоль линии обусловливается потерями в линии, а изменение фазы — конечной скоростью распространения электромагнитных колебаний.

Оба эти коэффициента а и 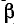 входят в комплексный параметр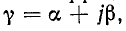который, следовательно, характеризует распространение волны напряжения и тока по линии.

На рис. 11-3, а буквой 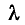обозначена длина волны напряжения, равная расстоянию между двумя точками линии, в которых фазы рассматриваемой слагающей напряжения различаются на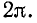

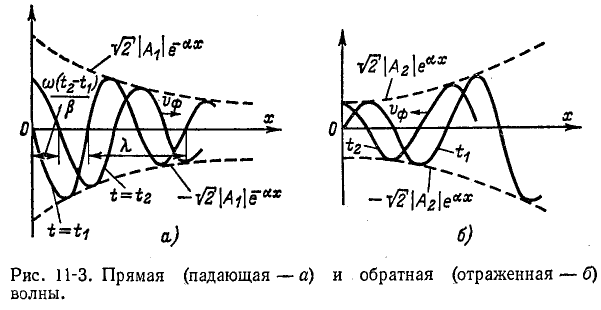
Следовательно,

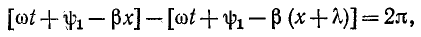
откуда

Полученная формула выражает зависимость, существующую между длиной волны и коэффициентом фазы линии.

На рис. 11-3, а изображены волны напряжения, соответствующие двум следующим друг за другом моментам времени: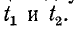 

С течением времени волна перемещается от начала линии к ее концу; она носит название прямой, или п а-дающей, волны.

Скорость перемещения падающей волны вдоль линии, называемая фазовой скоростью волны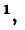 определяется как скорость перемещения точки, фаза колебания в которой остается постоянной.

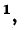Скорость распространения группы смежных по частоте волн характеризуется понятием групповой скорости].

Эго условие записывается для прямой волны в виде

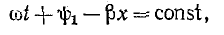
откуда

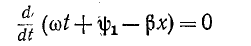
и, следовательно,

Аналогичное исследование второго слагаемого выражения (11-12) показывает, что для произвольного момента времени оно представляет синусоидальную волну, амплитуда которой 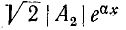еах возрастает с увеличением х, т. е. по мере удаления от начала линии к ее концу. С течением времени волна перемещается от конца линии к ее началу (рис. 11-3,6); она называется обратной, или отраженной, волной.

Фазовая скорость обратной волны получается равной

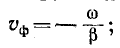 знак минус указывает, что обратная волна

движется в направлении, противоположном направлению прямой волны.

Итак, мгновенное напряжение можно рассматривать как сумму двух волн, движущихся в противоположных направлениях, причем каждая из этих волн затухает в направлении движения.

На основании (11-13) и (11-14)

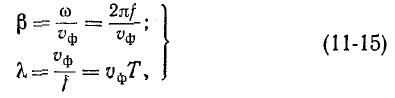
т. е. за время, равное одному периоду, как падающая, так и отраженная волны перемещаются на расстояние, равное длине волны.

Линии, физическая длина которых соизмерима с длиной волны, считаются длинными линиями. При достаточно высоких частотах практически любая протяженная электрическая цепь становится «длинной» по отношению к длине волны.

Как будет показано ниже, фазовая скорость в воздушной линии близка к скорости света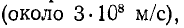

и поэтому частоте 50 Гц будет соответствовать длина волны 6000 км, а частоте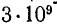 Гц — длина волны 10 см. Следовательно, в первом случае длинной линией будет линия, измеряемая многими сотнями или тысячами километров, а во втором случае — цепь протяженностью в несколько сантиметров.

Возвращаясь к уравнениям (11-9) и (11-10) и записывая прямую и обратную волны в комплексной форме, имеем: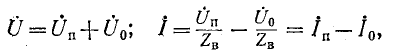

где

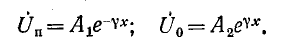
Напряжение и ток прямой и соответственно обратной волн связаны законом Ома:

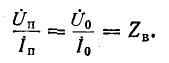
Это соотношение объясняет смысл названия 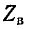— волновое сопротивление.

Постоянные интегрирования 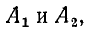входящие в (11-9) и (11-10), находятся в зависимости от напряжения и тока в начале линии (граничные условия), если они заданы. При х = 0

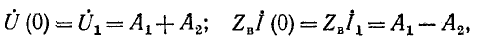
откуда

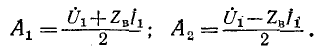
Введем понятие коэффициента отражения волны в начале линии:

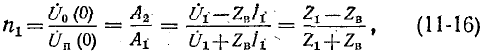
где 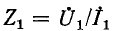— входное сопротивление линии.

Подстановка выражений для 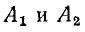в (11-9) и (11-10) с учетом (11-16) дает:

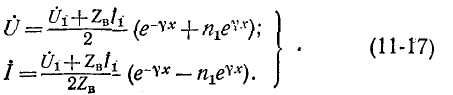
Если заданы граничные условия на конце линии, то удобнее отсчитывать расстояние от конца, приняв координату х'.

Заменяя в уравнениях (11-9) и (11-10) х на (l — х') и используя заданные граничные условия 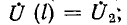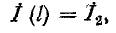получаем для 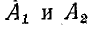следующие выражения:

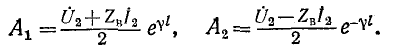
Подставив их в (11-9) и (11-10), получим окончательные выражения для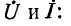

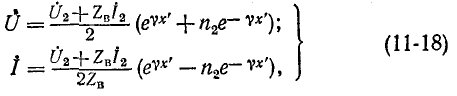
где аналогично предыдущему 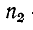— коэффициент отражения в конце линии:

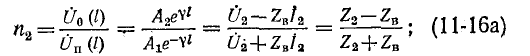
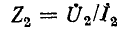— выходное сопротивление на конце линии или в случае приемника входное сопротивление его.

Если сопротивление приемника равно волновому сопротивлению линии 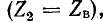то коэффициент отражения равен нулю 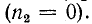При этом в линии имеется только одна прямая волна; обратная волна отсутствует.

Это важное свойство реализуется в линиях связи, отражения в которых нежелательны по ряду причин.

Во-первых, если затухание в линии невелико, то отраженная волна создает эффект эха в начале линии.

Во-вторых, отражения связаны с потерей энергии. Часть энергии, достигшая приемного конца, не поступает в приемник, а возвращается по линии в виде энергии отраженной волны. При этом возникают дополнительные потери энергии в сопротивлении r и проводимости g линии. Если сопротивление источника, питающего линию, не равно волновому сопротивлению линии, то отраженная волна, достигнув начала линии, претерпевает повторное отражение и т. д. Происходящая вследствие этого потеря энергии в линии понижает общий к. п. д. передачи.

В-третьих, в случае отражений может иметь место нежелательное увеличение напряжения или тока в линии.

Вследствие указанных причин на практике стремятся согласовать сопротивление приемника с волновым сопротивлением линии. При согласовании нагрузки с линией выражения (11-18) упрощаются: с учетом того, что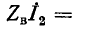 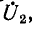находим:

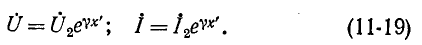
Эти выражения показывают, что при перемещении точки наблюдения вдоль линии, нагруженной согласованно-на конце, в направлении от конца к началу линии, модуль напряжения возрастает в 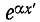раз, а фаза — на 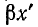рад.

Уравнения (11-19) аналогичны уравнениям симметричного четырехполюсника при согласованной нагрузке. Поэтому показатель распространения на всю длину линии 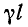эквивалентен мере передачи четырехполюсника g, а волновое сопротивление линии 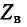аналогично характеристическому сопротивлению четырехполюсника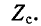

Выражения (11-19) показывают, что при согласованной нагрузке 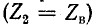геометрическим местом конца вектора напряжения 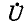является логарифмическая спираль. На рис. 11-4, иллюстрирующем сказанное, принято 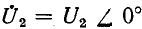(вектор 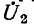направлен по действительной оси).

Большой   интерес   представляет также рассмотрение двух   частных   случаев   нагрузки линии, а именно случаев, когда   линия   на   конце   разомкнута (режим холостого хода)

или замкнута (режим короткого замыкания). В первом случае 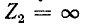и соответственно коэффициент отражения во втором случае

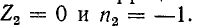
К рассмотрению этих двух случаев мы вернемся несколько позже.

Система уравнений (11-18) может быть переписана в следующем виде: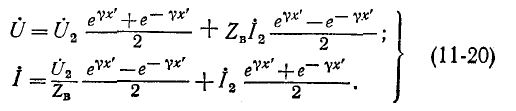

Уравнения (11-18) и (11-20) представляют собой уравнения линии в показательной (или волновой) форме при отсчете расстояния от конца линии. Они преобразуются с помощью гиперболических функций:

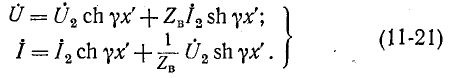
Положив в этих уравнениях х' = l, получим уравнения линии в гиперболической форме, выражающие напряжение и ток в начале через напряжение и ток в конце линии:

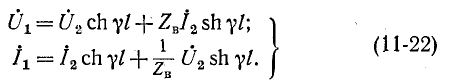
Обращает на себя внимание сходство полученных уравнений с уравнениями симметричного четырехполюсника. Эти уравнения показывают, что однородная линия представляет собой симметричный четырехполюсник с характеристическими параметрам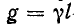и и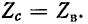 

Применяя параметры 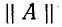четырехполюсника, получим связь между коэффициентами его и параметрами линии:

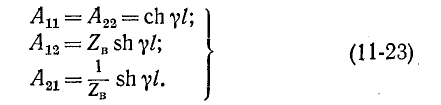
Показательная и гиперболическая формы записи уравнений линии (11-18) и (11-21) дополняют друг друга и применяются в зависимости от условий задачи.

Преимущество показательной формы записи уравнений заключается в большей наглядности рассмотрения физических процессов в линии с помощью прямых и обратных волн и удобстве построения геометрических мест на комплексной плоскости. Поэтому уравнения (11-18) широко использованы в последующих параграфах данной главы.

Гиперболическая форма записи уравнений также представляет в ряде случаев известные удобства с точки зрения исследования и расчета электрических величин в линии и их фазовых соотношений.

Рассмотрение линии как четырехполюсника базируется обычно на гиперболической форме записи уравнений.

Вторичные параметры однородной линии

Вторичными, или характеристическими, параметрами линии являются коэффициент ослабления, коэффициент фазы 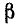и волновое сопротивление 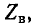которые в свою очередь выражаются через первичные параметры линии и частоту.

Из выражения

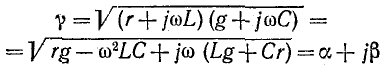следует, что

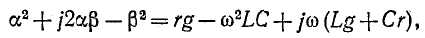
откуда

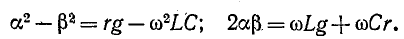
Совместное решение этих уравнений дает:

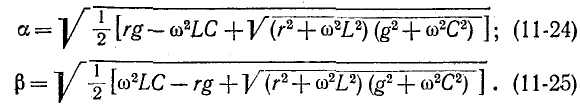
Из полученных выражений следует, что 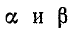в общем случае зависят от частоты. Однако, как показывает исследование, в отличие от коэффициента ослабления, который изменяется в сравнительно ограниченных пределах, коэффициент фазы неограниченно растет с частотой.

Формула (11-25) позволяет выразить фазовую скорость распространения электромагнитной волны через первичные параметры линии и частоту по формуле (11-14).

Выражения (11-24) и (11-25) неудобны для практического использования ввиду их громоздкости. Существует ряд приближенных расчетных формул для вычисления вторичных параметров линии, учитывающих, что в области высоких частот (порядка 1 МГц и выше) сопротивление r весьма мало по сравнению 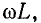а проводимость g ничтожно мала по сравнению с 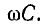Первое допущение 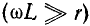обусловлено тем, что индуктивное сопротивление прямо пропорционально частоте, между тем как сопротивление проводов r пропорционально квадратному корню из частоты вследствие поверхностного эффекта. Второе допущение справедливо для высокочастотных фидеров, которые, будучи «длинными» по сравнению с длиной волны, имеют весьма малую физическую длину и поэтому могут иметь надежную изоляцию между проводами. Особенно ничтожно мала проводимость g кабельных линий.

Используя для выражения

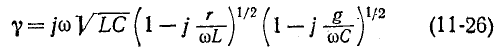
бином Ньютона, ограничиваясь первыми двумя членами разложения

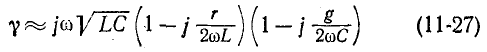
и пренебрегая ввиду малости слагаемым — 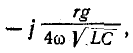получим окончательно:

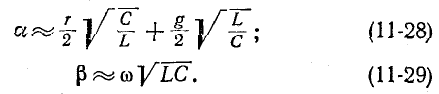
Эти формулы представляют собой пределы, к которым стремятся коэффициент ослабления и коэффициент фазы с ростом частоты.

Выражение (11-28) не следует понимать в том смысле, что а не зависит от частоты; входящие в него параметры r и g сами являются функциями частоты.

Первое слагаемое в правой части выражения (11-28) определяет ту долю ослабления, которая обусловливается продольным активным сопротивлением линии. Второе слагаемое определяет долю ослабления, которая вносится в передачу вследствие наличия поперечной активной проводимости линии.

Для уменьшения потерь при передаче электромагнитной энергии по линии стремятся к тому, чтобы сопротивление линии r и проводимость изоляции g были по возможности малы.

Фазовая скорость согласно (11-14) и (11-29) равна:

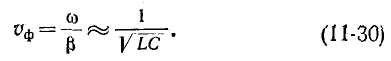
Это предельная фазовая скорость распространения волны вдоль линии при бесконечно большой частоте. При постоянном токе 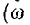= 0) понятия коэффициент фазы и фазовая скорость теряют физический смысл; на основании выведенной ранее формулы для 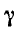(11-7) при 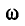= О

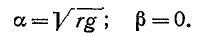
На рис. 11-5 показан характер изменений а и 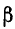в зависимости от частоты; коэффициент р с ростом частоты асимптотически приближается к прямой, образующей с осью 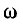угол

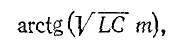
где m — масштабный коэффициент.

Для кабельных линий характерна резко выраженная емкостная проводимость 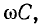по сравнению с которой проводимость изоляции g ничтожно мала. Кроме того, если частота не очень велика, то индуктивное сопротивление 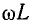мало по сравнению с активным сопротивлением r из-за малого расстояния между жилами. Поэтому в случае кабельной линии, пренебрегая параметрами g и L по сравнению с r и С, получаем упрощенные расчетные формулы

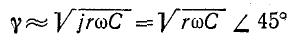
или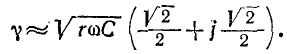

Следовательно,

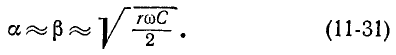
Соответственно фазовая скорость распространения волны в кабельной линии равна

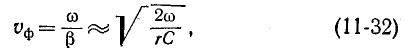
т. е. прямо пропорциональна корню квадратному из частоты.

В теории электромагнитного поля доказывается, что произведение удельных значений индуктивности и емкости в линии

где с — скорость света в пустоте (около 3* 108 м/с); 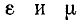— диэлектрическая и магнитная проницаемости среды, окружающей токоведущие проводники.

Предел, к которому с ростом частоты стремится фазовая скорость волны, равен на основании (11-30) и (11-33):

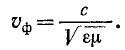
В случае воздушной линии 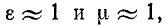и потому фазовая скорость в пределе стремится к скорости света в пустоте.

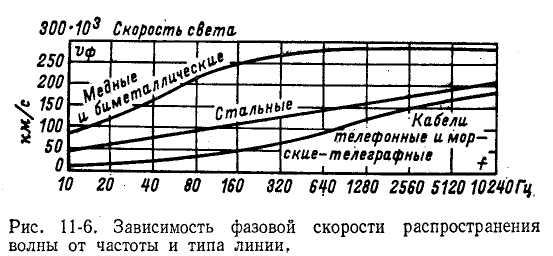
В случае кабельной линии 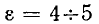и поэтому предельная фазовая скорость примерно вдвое меньше скорости света в пустоте.

Рисунок 11-6 иллюстрирует зависимость фазовой скорости волны от частоты и типа линии.
Волновое сопротивление линии

при постоянном токе 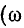= 0) и бесконечной частоте 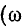= оо) имеет действительные значения

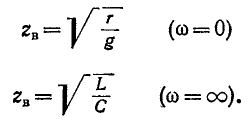
В остальной части диапазона частот волновое сопротивление линии имеет емкостный характер, так как обычно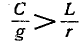[аргумент знаменателя в

правой части (11-34) больше аргумента числителя].

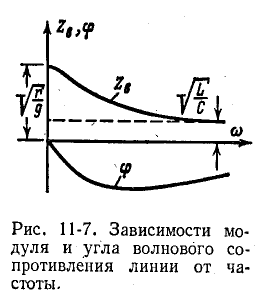
На рис. 11-7 показаны кривые изменения модуля 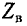и угла 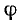волнового сопротивления линии в зависимости от частоты.

Подставив выражения для L и С  в формулу 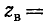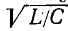, получим приближенные расчетные формулы для высоких частот в зависимости от размеров:

Средние значения 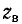для воздушных линий 400—500 Ом, для кабелей 50—70 Ом.

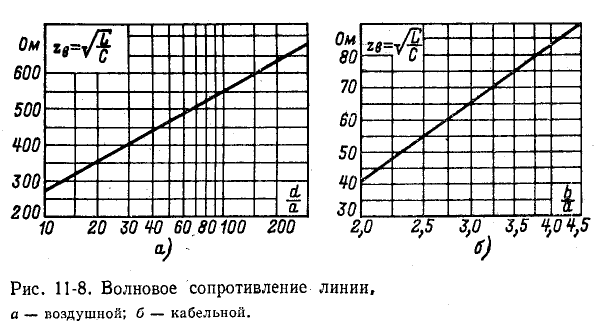
Рисунок 11-8 иллюстрирует графические зависимости 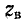от d/a и 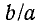для воздушных и кабельных линий, построенные по формулам (11-35).

Линия без искажений

Сигналы, передаваемые по линии связи, представляют собой совокупность множества различных частот: дискретных — в случае периодических несинусоидальных сигналов и образующих непрерывный спектр — в случае непериодических сигналов.

Неискаженной передачей сигнала называется такая передача, при которой форма сигнала в начале и конце линии одинакова, т. е. все ординаты кривой напряжения или тока в конце линии прямо пропорциональны соответствующим ординатам кривой в начале линии. Такое явление имеет место в том случае, когда коэффициент ослабления линии, а также фазовая скорость на всех частотах одинаковы.

Неодинаковое затухание на разных частотах создает так называемые амплитудные искажения, а неодинаковая скорость волн на разных частотах — фазовые искажения.

Согласно (П-31) и (11-32) коэффициент ослабления и фазовая скорость в случае кабельных линий пропорциональны квадратному корню из частоты. В случае воздушных линий также существует зависимость а и 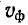от частоты. В результате этого получаются амплитудные и фазовые искажения.

Итак, для неискаженной передачи требуется, чтобы коэффициент ослабления а не зависел от частоты, а коэффициент фазы 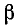был прямо'пропорционален частоте; в последнем случае фазовая скорость 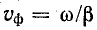получается не зависящей от частоты.

Такое положение имеет место при условии, что

В этом случае коэффициент распространения равен:

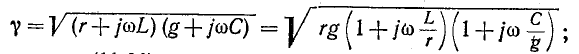
с учетом (11-36)

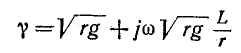
или

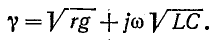
Если считать, что первичные параметры линии не зависят от частоты, то коэффициент ослабления в данном случае будет постоянен:

а коэффициент фазы — прямо пропорционален частоте:

Линия, параметры которой удовлетворяют условию (11-36), называется линией без искажений, поскольку любые сигналы распространяются по ней с сохранением их формы. Линия без искажений является одновременно и линией с минимальным затуханием, которое только и возможно при заданных параметрах r и g.

Волновое сопротивление линии без искажений — действительное число, что равносильно активному сопротивлению, не зависящему от частоты; в соответствии с (11-34) оно выражается простой формулой

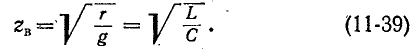
Фазовая скорость в линии без искажений постоянна и совпадает с полученным ранее выражением (11-30) для предельной скорости распространения волны вдоль линии при бесконечно большой частоте:

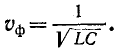
Для устранения искажений, вызываемых несогласованностью сопротивления приемника с сопротивлением линии, т. е. во избежание возникновения отражений на приемном конце, сопротивление приемника должно быть равно 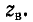Коэффициент полезного действия линии имеет в этом случае наибольшее возможное значение, равное 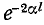как в линии при согласованной нагрузке.

Ввиду того что волновое сопротивление линии без искажений является активным, при согласованной нагрузке напряжение и ток в любой точке линии совпадают по фазе. Отношение мгновенных значений напряжения и тока в любой точке такой линии равно:

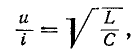
откуда

Следовательно, на любом отрезке линии без искажений, нагруженной согласованно, энергия магнитного поля в каждый момент времени равна энергии электрического поля.

Следует заметить, что на практике условие (11-36), как правило, не выполняется; отношение 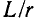обычно значительно меньше отношения C/g. Вследствие этого затухание линии всегда превышает минимальное. Наименее соответствуют условию (11-36) кабельные линии.

Чтобы линия наиболее соответствовала условию (11-36), следовало бы изменить какой-либо первичный параметр, например уменьшить r или С либо увеличить g или L.

Уменьшение активного сопротивления r возможно за счет применения проводов большего диаметра, что, однако, значительно удорожало бы линию. Увеличение проводимости изоляции g невыгодно, так как при этом возросло бы затухание линии.

Наилучшим средством для приближения первичных электрических параметров к оптимальному соотношению (11-36) является искусственное увеличение индуктивности включением в линию через определенное расстояние индуктивных катушек или применением кабеля, проводящие жилы которого обмотаны тонкой лентой из материала с высокой магнитной проницаемостью.

Линия без потерь

Независимо от того, соблюдается ли оптимальное соотношение первичных параметров (11-36) или не соблюдается, во всех случаях желательно, чтобы активное сопротивление r и проводимость изоляции g были по возможности малы (для уменьшения потерь энергии).

В воздушных линиях обычно индуктивное сопротивление линии 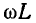превышает активное сопротивление r, а емкостная проводимость 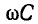превышает активную проводимость g. С ростом частоты разница между указанными величинами становится еще более значительной.

В ряде случаев оказывается полезным в первом приближении рассматривать линию, не имеющую потерь, т. е. пренебрегать активными сопротивлением и проводимостью по сравнению с соответствующими реактивными составляющими. Такая идеализация допускается для приближенной качественной и количественной оценки исследуемых явлений. При этом весьма упрощаются расчетные выражения и гиперболические уравнения линии переходят в тригонометрические.

Итак, основным исходным предложением, которое делают при рассмотрении линии без потерь, .является приближенное условие, что 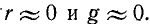В этом случае вторичные параметры линии принимают весьма простой вид, а именно:

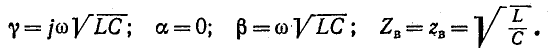
Саедовательно, в линии без потерь ослабление отсутствует. Ввиду постоянства фазовой скорости

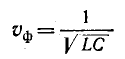
отсутствуют также фазовые искажения.

Выражения для коэффициента фазы, фазовой скорости и волнового сопротивления линии без потерь совпадают с выражениями, полученными для линии без искажений. Следовательно, все сказанное о линии без искажений полностью относится и к линии без потерь.

Ввиду того, что гиперболические функции с мнимым аргументом преобразуются в тригонометрические функции, гиперболические уравнения линии (11-21) принимают тригонометрическую форму:

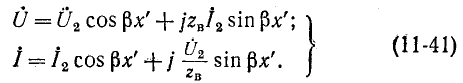
Эти уравнения используются ниже при рассмотрении стоячих волн в линии без потерь.

Энергия, передаваемая по линии, складывается из энергии электрического и магнитного полей.

В том случае, когда к концу линии без потерь присоединено сопротивление, равное волновому, на любом отрезке линии соблюдается условие (11-40), полученное для линии без искажении. При этом вся энергия, доставляемая падающей волной, поглощается в сопротивлении нагрузки.

Если сопротивление нагрузки отлично от волнового, то в месте присоединения нагрузки энергия перераспределяется между полями, в результате чего возникают отражения.

В предельном случае, когда линия на конце разомкнута, падающая волна встречает бесконечно большое сопротивление; ток в конце линии обращается в нуль, и соответственно энергия магнитного поля переходит в энергию электрического поля. Напряжение на разомкнутом конце линии удваивается, и возникает отраженная волна того же знака, что и падающая 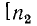= 1; см. (11-16а)].

В другом предельном случае, когда линия на конце замкнута накоротко,, падающая волна встречает сопротивление, равное нулю, напряжение в конце линии обращается в нуль и соответственно энергия электрического поля переходит в энергию магнитного поля. Ток на короткозамкнутом конце линии удваивается, и возникает отраженная волна, знак которой противоположен знаку падающей волны 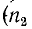=—1).

При активной нагрузке 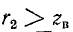коэффициент отражения 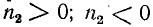при 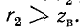Поэтому в первом случае возрастает напряжение и убывает ток, а во втором случае, наоборот, убывает напряжение и возрастает ток по сравнению с режимом согласованной нагрузки 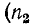= 0).

Режимы работы линии без потерь. Стоячие волны

Исследуем закон распределения действующих напряжения и тока вдоль линии без потерь. С этой целью воспользуемся уравнениями линии (11-18) и (11-41) в комплексной и гиперболической формах.

Приняв в (11-18) мнимый коэффициент распространения 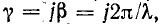получим для любой точки линии на расстоянии х' от конца:

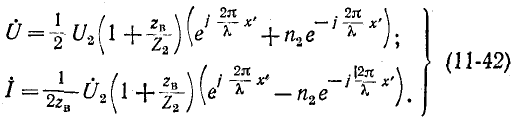
Входящий в эти уравнения коэффициент отражения

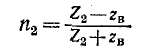
представляет собой в общем случае комплексную величину.

Выражения (11-42) наглядно свидетельствуют о том, что комплексное напряжение в любой точке х' слагается

из падающей и отраженной волн напряжения, амплитуды которых находятся в соотношении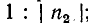 в свою очередь комплексный ток равен разности падающей и отраженной волн тока с тем же соотношением амплитуд.

Точкам 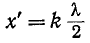(k — целое число), удовлетворяющим условию

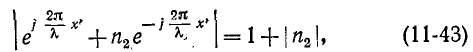
соответствует максимальное действующее значение U, так как при этом фазы падающей и отраженной волн напряжения совпадают. На расстоянии 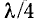от этих точек падающая и отраженная волны оказываются в противофазе и действующее напряжение имеет минимум. При этом удовлетворяется условие

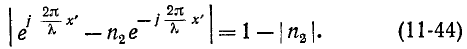
Координаты максимумов и минимумов U, являющиеся многозначными функциями 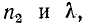не зависят от времени, т. е. с течением времени они остаются на одном и том же месте; минимум U располагается посредине между двумя соседними' максимумами U, причем расстояние между ближайшими максимумами (или минимумами) составляет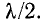

Таким образом, кривая действующих значений напряжения вдоль линии без потерь представляет собой волнообразную кривую, максимумы и минимумы которой чередуются (см. дальше рис. 11-10, б и г).

Аналогичные рассуждения приводят к выводу, что и кривая действующих значений тока вдоль линии без потерь представляет собой волнообразную кривую, смещенную относительно кривой действующих значений напряжения на четверть длины волны. Места максимумов напряжения совпадают с местами минимумов тока и, наоборот, минимумы U совпадают с максимумами I.

При отсутствии отраженной волны 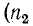= 0) действующие значения U и I вдоль линии без потерь не изменяются.

Чем больше приближается коэффициент отражения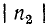 к единице, тем больше разнятся максимумы и минимумы U (или I).

При 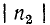= 1, т. е. при равенстве амплитуд прямой и обратной волн, в линии устанавливаются стоячие волны напряжения и тока. Кривые действующих значений U и I вдоль линии представляют собой в этом случае «выпрямленные» синусоиды; на линии образуются у з л ы, т. е. точки, в которых U или I равны нулю, и п у ч н о с т и, т. е. точки, в которых U или I максимальны.

Из сказанного выше следует, что узлы напряжения совпадают с пучностями тока и, наоборот, узлы тока сов-

падают с пучностями напряжения. Соответственно узлы (или пучности) напряжения и тока сдвинуты на четверть длины волны друг относительно друга.

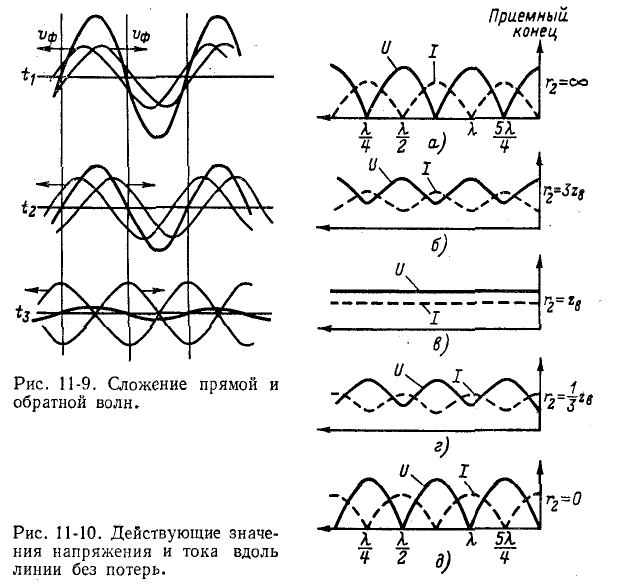
На рис. 11-9 в виде примера показано сложение прямой и обратной волн напряжения, имеющих одинаковые амплитуды, для трех моментов времени: 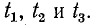Сумма бегущих в противоположные стороны волн образует стоячую волну, показанную на рис. 11-9 в виде мгновенных значений для моментов времени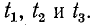

Из этого рисунка видно, что на протяжении всего участка между двумя соседними узлами стоячей волны синусоидальное изменение напряжения во времени происходит с одинаковой начальной фазой: при прохождении узла начальная фаза синусоидальных колебаний изменяется скачкообразно на величину 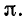Сказанное в равной мере относится и к стоячей волне тока.

На основании приведенного выше выражения для коэффициента отражения 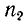можно заключить, что условие 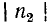= 1 выполнимо в трех случаях: при 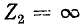(холостой ход), 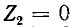(короткое зашивание) и 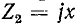(реактивная нагрузка). Этим условиям соответствуют стоячие волны, возникающие в линии без потерь.

Распределение действующих значений напряжения и тока вдоль линии для холостого хода и короткого замыкания иллюстрируется на рис. 11-10, а и д.

Для сравнения на рис. 11-10 показано распределение напряжения и тока для других режимов работы линии.

При активной нагрузке 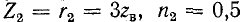(случай б) максимумы и минимумы U и I совпадают по своему местоположению с аналогичными значениями для режима холостого хода; при активной нагрузке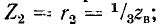 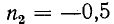(случай з) максимумы и минимумы расположены так же, как при коротком замыкании; при согласованной нагрузке 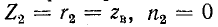(случай в) кривые U и I изображаются прямыми, параллельными оси абсцисс.

Стоячие волны легко исследуются с помощью уравнений (11-41).линии без потерь.

При холостом ходе 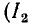= 0)

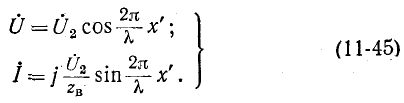
Узлы напряжения находятся в точках, для которых

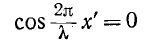
или

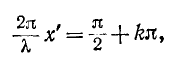
откуда

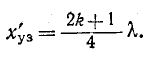
Пучности напряжения находятся в точках, для которых

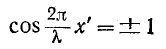
или

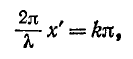
откуда

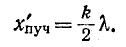
Разомкнутый конец линии совпадает с узлом тока и пучностью напряжения (рис. 11-10, а).

Как видно из (11-45), ток опережает по фазе напряжение на 90°, когда 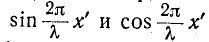имеют одинаковый знак  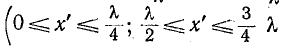и т.д.) и отстает на 90° от напряжения, когда знаки 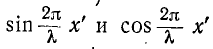различны

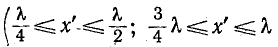и т. д.).

При коротком замыкании, положив в (11-41) 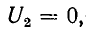получим

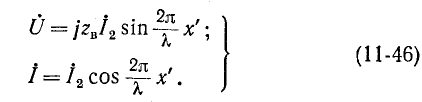
На замкнутом конце линии х' = 0 и в точках, удаленных от него на целое число полуволн х' 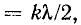находятся узлы напряжения и пучности тока, а в точках, удаленных от конца на нечетное число четвертей волн

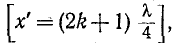находятся пучности напряжения и узлы тока (рис. 11-10,5).

Как видно из (11-46), ток отстает по фазе от напряжения на 90°, когда 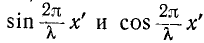имеют одинаковые знаки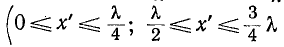и т. д.). и опережает на 90° напряжение, когда знаки 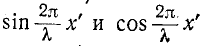различны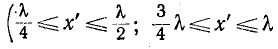и т. д.).

Следует заметить, что наличие хотя бы самых малых потерь в реальных линиях приводит к тому, что действующие значения U и I не снижаются до нуля, а достигают некоторых минимальных значений в точках, соответствующих узлам.

В случае стоячих волн мощность в узлах напряжения и тока равна нулю. В остальных точках линии имеет место только реактивная мощность, так как напряжение и ток сдвинуты по фазе на 90°. В этом случае энергия не передается вдоль линии, а происходит лишь обмен энергией между электрическим и магнитным нолями на участках линии, ограниченных узлами напряжения и тока.

Если в линии имеются потери или приемник потребляет активную мощность, то узлы исчезают; амплитуда падающей волны превышает амплитуду отраженной волны, н за счет разности амплитуд происходит процесс передачи энергии вдоль линии.

Для количественной оценки степени согласования линии с нагрузкой в радиотехнике используется коэффициент бегущей волны, под которым понимается отношение минимума кривой распределения U или I к максимуму той же величины:

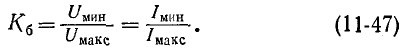
С учетом (11-43) и (11-44) имеем:

откуда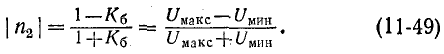

В случае активной нагрузки выражение (Н-48) упрощается. При 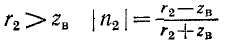и согласно (11 -48)

при 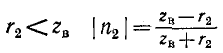и, следовательно,

В реальных условиях коэффициент бегущей волны обычно не ниже 0,5—0,6.

Кривую распределения действующих значений напря* жения вдоль линии используют на практике для измерения длины волны или частоты. Длина волны определяется удвоенным расстоянием между соседними максимумами или минимумами кривой распределения, а частота вычисляется по длине волны на основании (11-15).

Входное сопротивление линии

Входное сопротивление линии, измеренное в произвольной точке на _ расстоянии х' от конца, определяется отношением 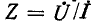и может быть представлено в комплексной или гиперболической форме. Ради общности рассмотрения вопроса будем считать, что линия нагружена на конце некоторым сопротивлением 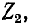которое в зависимости от условий может быть любым.

Комплексная форма выражения для входного сопротивления линии получается на основании (11-18):

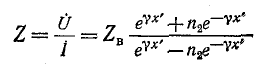
или

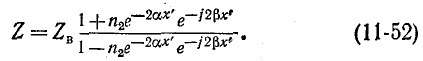
Данное выражение показывает, что с изменением координаты х' модуль входного сопротивления линии колеблется между некоторыми максимумами и минимумами (которые в общем случае отличаются друг от друга).

Допустим, что модуль Z достигает некоторого максимума в точке 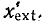Тогда максимумы будут также в точках, соответствующих изменению аргумента 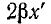на величину 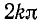, что даст:

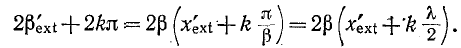
Следовательно, максимумы чередуются через каждые полволны. Посредине между максимумами будут минимумы, которые также чередуются через каждые полволны.

Если вместо координаты 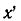варьировать коэффициентом фазы меняя частоту источника, то получится аналогичная волнообразная кривая, причем максимумы и соответственно минимумы будут отстоять друг от друга на 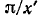(здесь х' = const). Исследуя изменение входного Сопротивления линии при плавном изменении частоты источника, можно зафиксировать два следующих друг за другом максимума (или минимума) z, соответствующих частотам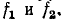

В этом случае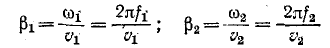
и, следовательно,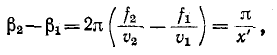
откуда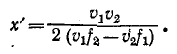
При малом расхождении частот 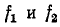фазовые скорости 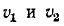почти одинаковы: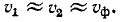

При этом

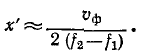
Данная формула позволяет определить расстояние от точки наблюдения до ближайшей точки линии, в которой имеет место отражение (например, при коротком замыкании на линии), производя измерение только в одной точке.
Волнообразный характер кривой z подчиняется в общем случае закону изменения модуля гиперболического тангенса с комплексным аргументом, что видно из следующего вывода.

Непосредственно из (11-21) следует:

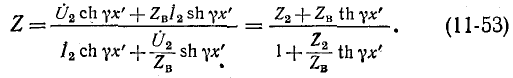
Обозначив 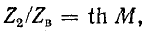 имеем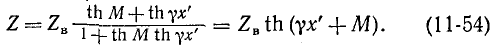
При холостом ходе  входное сопротивление линии согласно (11-53) равно:

а при коротком замыкании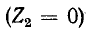

С учетом (11-55) и (11-56) входное сопротивление Z легко выразить через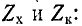

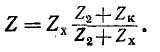
Этой формулой пользуются в том случае, когда из опытов холостого хода и короткого замыкания известны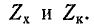

Данные опытов холостого хода и короткого замыкания используются также для вычисления характеристических параметров линии.

На основании (11-55) и (11-56)

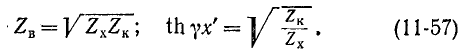
Эти формулы совпадают с (9-35). Ввиду того что коэффициент фазы р определяется по (11-57) неоднозначно, при вычислении производится проверка на основании (11-14), причем первоначально фазовая скорость 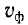выбирается ориентировочно.

Вычисление характеристических параметров по формулам (11-57) иллюстрировано ниже примером 11-1.

На рис. 11-11 показаны кривые изменения модулей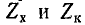 в зависимости от координаты х'. В пределе, т. е. при х' 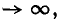максимумы и минимумы кривой стремятся к значению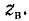

Входные сопротивления линии без потерь при холостом ходе и коротком замыкании могут быть получены из (11-55) и (11-56) заменой

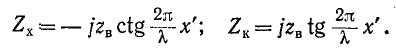
Эти реактивные входные сопротивления с учетом их знака изображаются котангенсоидами и тангенсоидами (рис. 11-12). Аргументом может служить также величина 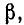если изменять частоту при постоянной длине х’.

Сопоставляя эти графики с частотными характеристиками сопротивлений реактивных двухполюсников, легко убедиться в их сходстве: резонансы напряжений и токов чередуются, однако в отличие от двухполюсников, имеющих ограниченное число резонансов, линия без потерь имеет бесконечное число резонансных точек, что соответствует представлению линии как цепочки из бесконечного числа индуктивностей и емкостей.

Входное сопротивление линии без потерь при 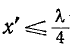индуктивно в случае короткого замыкания и емкостно в случае холостого хода. При 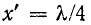в первом случае наступает резонанс токов (z = 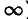), во втором случае — резонанс напряжений (z= 0).

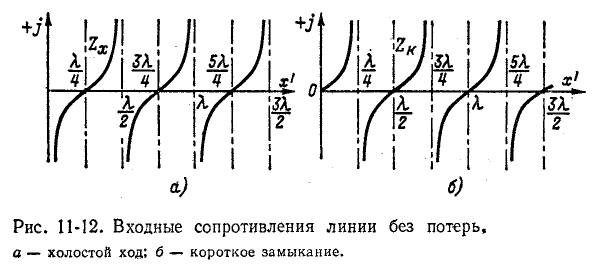
Следует отметить, что в реальных условиях вследствие наличия потерь входное сопротивление линии никогда не снижается до нуля и никогда не достигает бесконечного значения.

При этом короткозамкнутая линия при 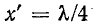имеет большее входное сопротивление, чем разомкнутая линия при 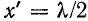, а разомкнутая линия при 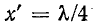имеет меньшее входное сопротивление, чем короткозамкнутая при .

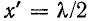Пример 11-1.

Даны результаты измерения входных сопротивлений линии длиной 160 км на частоте 1000 Гц при холостом ходе и коротком замыкании: 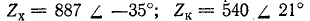Ом. Требуется вычислить первичные и вторичные параметры линии.

Расчет начинается с вычисления волнового сопротивления и коэффициента распространения:

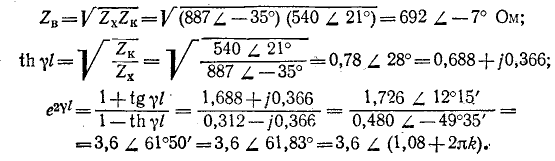
Целое число к находится на основании ориентировочного расчета величины 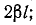если исходить из приближенного значения фазовой скорости 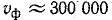км/с (если линия воздушная), то

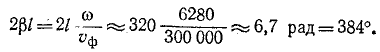
Следовательно, надо принять

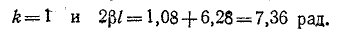
Итак,

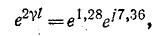
откуда

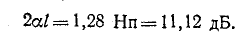
Коэффициент ослабления

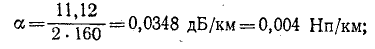
коэффициент фазы

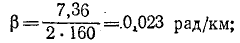
коэффициент распространения

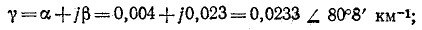
фазовая скорость

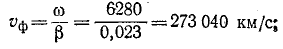
длина волны

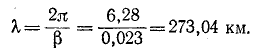
Первичные параметры линии находятся на основании выражений:

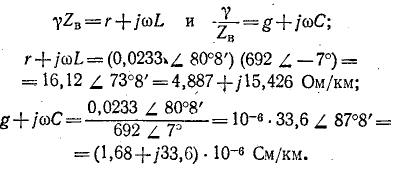
Таким образом,

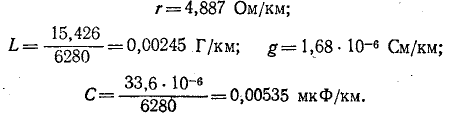
Линия как элемент резонансной цепи

Четвертьволновая линия с малыми потерями, разомкнутая на конце, обладает свойствами резонансной цепи, состоящей из последовательно соединенных r, L и С. При частоте, при которой на линии укладывается четверть волны (такую частоту условимся называть резонансной), входное сопротивление линии будет активным и притом минимальным.

При малом отклонении частоты от резонансной модуль входного сопротивления линии резко возрастает: входное сопротивление приобретает емкостный характер при понижении частоты и индуктивный характер — при повышении.

Входное сопротивление линии с малыми потерями, разомкнутой на конце, можно получить из (11-21), разлагая 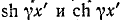по формулам тригонометрии и приняв ввиду малости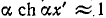

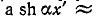
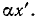
Выражение примет вид:

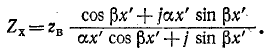
Вблизи резонансной частоты 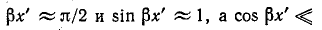1. Поэтому

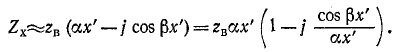
Если через 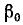обозначить коэффициент фазы при резонансной частоте, т. е. принять 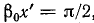и учесть соотношение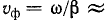 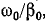то 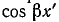можно преобразовать следующим образом:

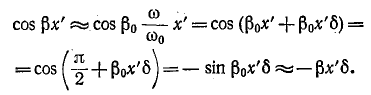
Здесь, так же как и 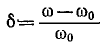 расстройка частоты по отношению к резонансной. Следовательно,

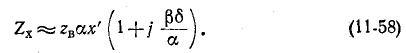
Было показано, что при частоте, близкой к резонансной, когда 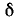значительно, меньше единицы, комплексное сопротивление резонансной цепи равно:

Рассматривая четвертьволновую линию как резонансную цепь, можно в силу одинаковой структуры выражений (11-58) и (11-59) считать, что добротность линии равна:

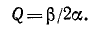
При этом резонансные характеристики, приведенные, применимы и к рассматриваемой линии.

Соответственно полоса пропускания, представляющая собой величину, обратную добротности, равна:

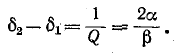
Здесь под полосой пропускания, подразумевается отнесенная к резонансной частоте ширина резонансной кривой между точками, соответствующими половине максимальной мощности (когда).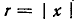

При малых значениях коэффициента а добротность получается высокой, достигая примерно 1000—4000, что намного превышает добротность контуров r, L и С, В связи с этим возрастает и острота настройки.
 

Искусственные линии

Искусственной линией называется цепь с сосредоточенными параметрами, приближающаяся по своим частотным характеристикам (в заданном диапазоне частот) к цепи с распределенными параметрами.

Искусственные линии находят широкое применение в лабораторных условиях и в особенности в современной импульсной радиотехнике для получения требуемого запаздывания сигналов.

Отмечалось, что всякая однородная линия представляет собой симметричный четырехполюсник с. мерой передачи, равной

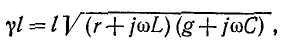
и характеристическим сопротивлением, равным волновому:

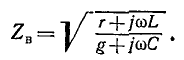
Заменяя линию эквивалентным Т-образным четырехполюсником, согласно рис. 9-17, а получаем на основании формул (11-23) расчетные выражения:

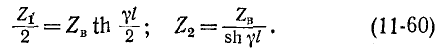
Для какой-либо фиксированной частоты такой Т-образный четырехполюсник может быть осуществлен. Однако при передаче сигналов в некоторой заданной полосе частот величины 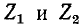представляют сложные функции от частоты, не реализуемые в виде простейших элементов. В этом случае искусственная линия создается в виде цепной схемы, каждое звено которой с достаточной степенью точности заменяет весьма малый участок однородной линии.