Цепи периодического несинусоидального тока

Содержание:

Цепи периодического несинусоидального тока:

До сих пор изучались линейные электрические цепи однофазного и трехфазного токов, в которых все э. д. с., токи и напряжения изменялись синусоидально с одинаковой частотой.

При разборе принципа генерирования синусоидальной э. д. с. отмечалось, что для получения синусоидальной э. д. с. в обмотке как явнополюсного, так и неявнополюсного генератора стремятся получить синусоидальную форму распределения магнитной индукции в воздушном зазоре между статором и ротором. В действительности, однако, распределение магнитной индукции может отступать от синусоиды, вследствие чего э. д. с., наводимая генератором, может быть не точно синусоидальной. Электронные генераторы, применяемые в технике высоких частот, генерируют токи, которые в зависимости от режима работы электровакуумных и полупроводниковых приборов также могут в большей или меньшей степени отличаться от синусоидальных. По этим причинам, а также если источники синусоидальных э. д. с., присоединенные к цепи, имеют разные частоты, напряжения и токи в цепи оказываются несинусоидальными.

Во многих электротехнических и радиотехнических устройствах несинусоидальный режим работы цепи является нормальным режимом. Особенно характерен такой режим для нелинейных цепей. Даже при синусоидальной э. д. с. форма кривой тока может резко отличаться от синусоиды при наличии в цепи нелинейного элемента1 (электрической дуги, индуктивной катушки с насыщенным магнитопроводом, полупроводникового прибора и т. п.).

Настоящая глава посвящена исследованию периодических процессов в линейных электрических цепях, находящихся под воздействием несинусоидальных э. д. с. Электрические и магнитные величины в таких цепях представляют собой периодические несинусоидальные функции.

Явления, происходящие в линейной электрической цепи с периодической несинусоидальной э. д. с., проще всего поддаются исследованию, если эту э. д. с. разложить на сумму постоянной и синусоидальных слагающих (называемых гармониками), затем на основе уже изученных методов расчета линейных электрических цепей определить токи и напряжения, вызванные каждой слагающей э. д. с. в отдельности, и, наконец, просуммировать соответствующие величины. Полученные таким образом токи и напряжения будут представлять собой периодические несинусоидальные функции времени, причем их период будет равен периоду заданной несинусоидальной э. д. с.

Кроме вычисления токов и напряжений в электрической цепи по заданной несинусоидальной э. д. с. источника (или заданному току источника тока), на практике может возникнуть необходимость выявления гармонического состава или степени отклонения от синусоиды той или иной периодической функции времени, полученной, например, экспериментально в результате осциллографирования.

На рис. 13-1 в виде примера показана периодическая несинусоидальная функция времени с периодом Т:

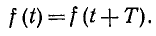
Вид разложения такой функции зависит от выбора начала отсчета.

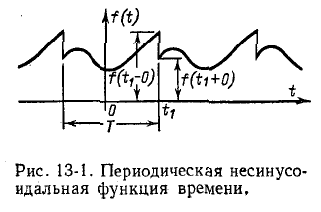
В пределах интервала времени Т функция f (t) может быть либо непрерывной, либо иметь точки разрыва непрерывности. Будем считать, что все эти точки разрыва непрерывности обладают следующим свойством: если функция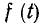претерпевает разрыв непрерывности в точке 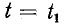(рис. 13-1), то существуют конечные пределы функции f (t) при приближении к точке разрыва как справа (т. е. от значений так и слева (т. е. 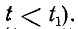от значений -Эти пределы условно обозначаются 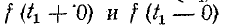или, что то же, 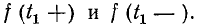Как известно, такие точки разрыва непрерывности называются точками разрыва первого рода.

Будем также считать, что в пределах интервала времени Г число разрывов первого рода, а также число максимумов и минимумов функции f (t) конечны.

Таким образом, будем рассматривать функции, удовлетворяющие условиям Дирихле; следует заметить, что э. д. с., токи и напряжения в реальных электрических цепях удовлетворяют этим условиям.

Известно, что периодическая несинусоидальная функция, удовлетворяющая условиям Дирихле, может быть представлена в виде бесконечно гармонического ряда — ряда Фурье. Сумма этого ряда совпадает со значениями
 

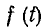для всех точек непрерывности этой функции, а в точках разрыва дает среднее арифметическое левого и правого предельных значений 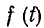, т. е.

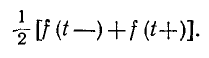
Обозначим 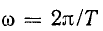и будем называть со основной угловой частотой. Синусоидальная и косинусоидальная слагающие с угловой частотой о образуют основную гармонику. Слагающие с более высокими угловыми частотами представляют собой высшие гармоники.

Гармонический ряд в тригонометрической форме имеет вид:

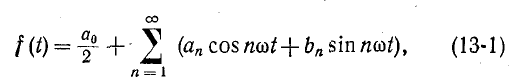
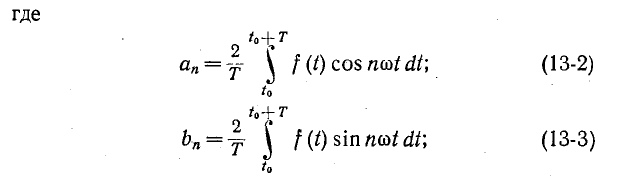
здесь 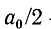— постоянная слагающая; 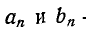— амплитуды косинусоидальных и синусоидальных членов ряда.
     

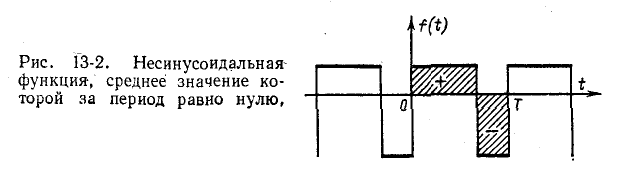
Постоянная слагающая 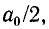определяемая на основании (13-2) при n — О, представляет собой среднее значение функции f (t) за период. Она равна нулю, когда площади положительных и отрицательных значений f (t) одинаковы (рис. 13-2).

Коэффициенты ряда Фурье 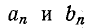не зависят от 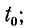поэтому значение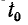может быть выбрано произвольно. В этом легко убедиться, если учесть, что подынтегральные функции в (13-2) и (13-3) имеют период Т. Обозначив подынтегральную функцию через g (t), получим:

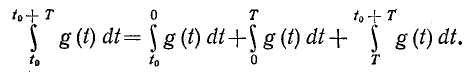
Так как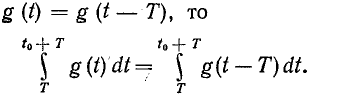
Заменой переменной x — t — T находим:

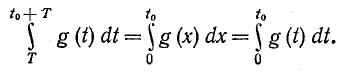
Следовательно,

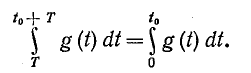
Полученный результат можно еще объяснить так: площади, выражаемые интегралами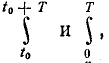 равны, так как в силу периодичности подынтегральной функции любое изменение 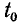не меняет площади, ограниченной данной функцией и осью абсцисс за период.

Положив 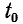= 0 и введя новую переменную а = 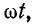найдем (с учетом того, что,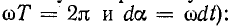

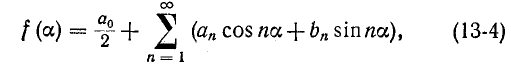
где

Если принять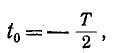то пределы интегрирования

будут равны соответственно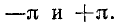

Сумма косинусоид и синусоид, выражаемая формулой (13-1) или (13-4), может быть представлена в виде суммы только одних синусоид с соответствующими начальными фазами.

Так, если принять

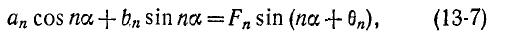
где

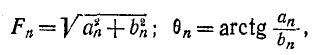
то ряд получит вид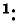

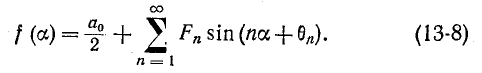
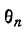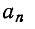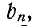Напомним, что угол находится с учетом знаков и определяющих знаки синуса и косинуса.

Форма (13-8) удобна в том случае, когда требуется знать процентное содержание каждой гармоники; она обычно применяется для расчета несинусоидальных токов и напряжений в электрических цепях.

Хотя теоретически ряд Фурье содержит бесконечное число слагаемых, однако он обычно быстро сходится. Сходящийся ряд может выражать заданную функцию с любой требуемой степенью точности; если он сходится быстро, то практически достаточно взять небольшое число гармоник для получения требуемой степени точности.

Встречающиеся на практике периодические несинусоидальные функции могут быть разбиты на две группы. Первая группа включает в себя кривые геометрически правильной формы. Вторая группа включает в себя кривые более сложной формы; разложение их в ряд Фурье производится графоаналитически.

Иногда периодическую функцию представляют в виде следующего ряда:

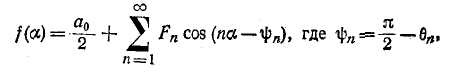
что следует из равенства

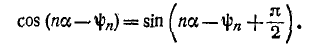
Графоаналитический метод разложения в ряд Фурье представляет приближенный метод численного интегрирования, при котором вычисление определенного интеграла заменяется нахождением суммы конечного числа слагаемых. С этой целью период функции f (а) , равный 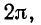разбивается на m равных интервалов 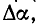так что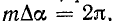

Расстояние от начала координат до середины k-го интервала составляет угол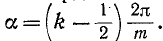

Пусть 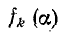есть значение периодической несинусоидальной функции в середине k-го интервала.

Интегралы, входящие в (13-5) и (13-6), заменяются суммами:

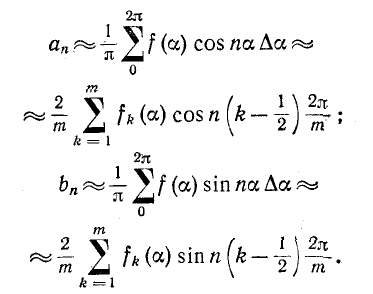
Если в пределах периода имеются точки разрыва, то при указанном графическом методе разложения целесообразно делать разбивку на интервалы так, чтобы точки разрыва не были в серединах интервалов.

В описанной выше технике выполнения графоаналитического разложения в ряд Фурье брались значения функции в середине интервалов; если вместо этого брать значения в конце или начале интервалов, то в случае четной функции наряду с косинусоидами в разложении появятся и синусоиды, которых четная функция не содержит.

Случаи симметрии

Периодические несинусоидальные функции, изображающие электрические и магнитные величины, обладают обычно каким-либо видом симметрии и это облегчает разложение их в ряд Фурье.

Рассмотрим следующие случаи симметрии:

1.    Функция f (а) симметрична относительно оси ординат (рис. 13-3), т. е.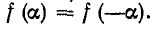 Такие функции называются четными. Поскольку синусоиды любых частот являются нечетными функциями, они не входят в состав ряда.

Поэтому при данном виде симметрии

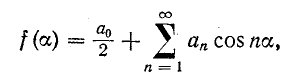
т. е. четная функция может содержать только косинусоиды и постоянную составляющую.

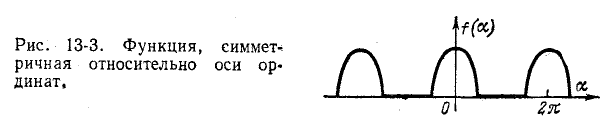
Важным свойством четных функций является также то, что для определения коэффициентов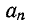 достаточно пользоваться кривой f (а) за половину периода, т.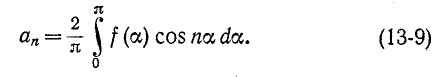

Это следует из равенства

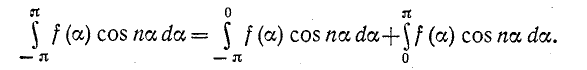
Замена в первом интеграле а на —а приводит к (13-9).

2.    Функция f (а) симметрична относительно начала координат (рис. 13-4), т. е. f(а) = —f (—а). Та'кие функции называются нечетными. Поскольку постоянная слагающая и косинусоиды этому условию не удовлетворяют, при данном виде симметрии ряд примет вид:

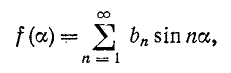
т. е. нечетная функция может содержать только синусоиды.

В этом случае, так же как и в предыдущем, для определения коэффициентов Ьп достаточно пользоваться кривой f (а) за половину периода, т. е.

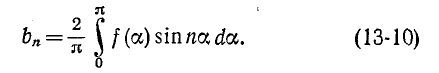
3.    Функция f (а) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени (рис. 13-5), т. е.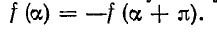

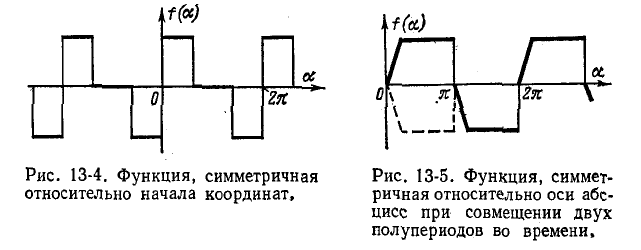
Заменяя f.(а) в соответствии с (13-4), получаем:

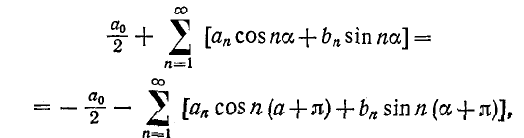
откуда для четных n

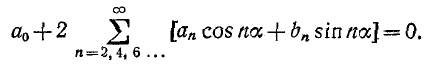
Это условие удовлетворяется при произвольных значениях а только в том случае, если 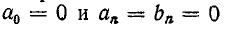при четных n.

Поэтому при данном виде симметрии

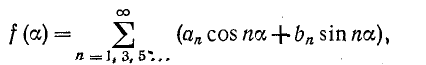
т. е. функция, симметричная относительно оси абсцисс при совмещении двух полупериодов во времени, содержит только нечетные гармоники.

Коэффициенты 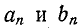могут вычисляться в этом случае по формулам (13-9) и (13-10).

Раскладывая периодическую несинусоидальную функцию в ряд Фурье, следует предварительно выяснить, не обладает ли заданная функция каким-либо видом симметрии. Наличие симметрии позволяет заранее предсказать, каких гармоник следует ожидать в разложении.

Если одновременно выполняются условия симметрии по пп. 1 и 3, то в разложении содержатся только нечетные косинусоиды, если по пп. 2 и 3, то содержатся только нечетные синусоиды.

Допустим, что функция, содержащая только нечетные косинусоиды, удовлетворяет, кроме того, условию f (а) = —f 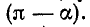Так как при нечетных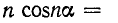 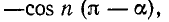то в этом случае для определения коэффициентов 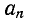достаточно пользоваться кривой f (а) за четверть периода:

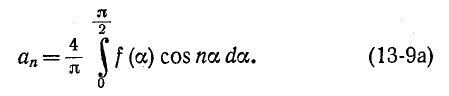
В свою очередь если функция, содержащая только нечетные синусоиды, удовлетворяет условию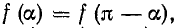то ввиду того что при нечетных n sin na = sin 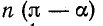и в этом случае для определения коэффициентов 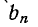достаточно пользоваться кривой f (а) за четверть периода:

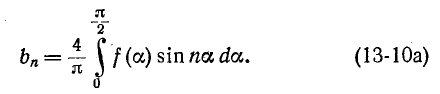
Виды симметрии зависят от выбора начала отсчета. Если начало отсчета может быть выбрано произвольно, то целесообразно выбрать его так, чтобы получить наибольшую симметрию.

Данные о коэффициентах ряда Фурье, относящиеся к разобранным выше случаям симметрии, сведены в табл. 13-1.

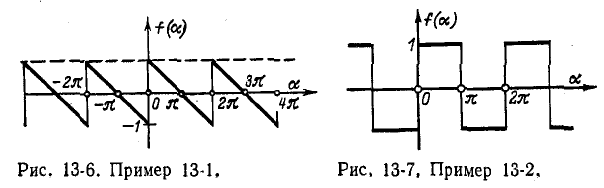
Пример 13-1. Требуется разложить в ряд Фурье пилообразную функцию, показанную на рис. 13-6. Эта функция удовлетворяет условию

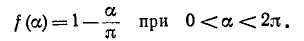
Заданная функция является нечетной, поэтому в разложении в ряд отсутствуют постоянная составляющая и косинусоиды; на основа-
 

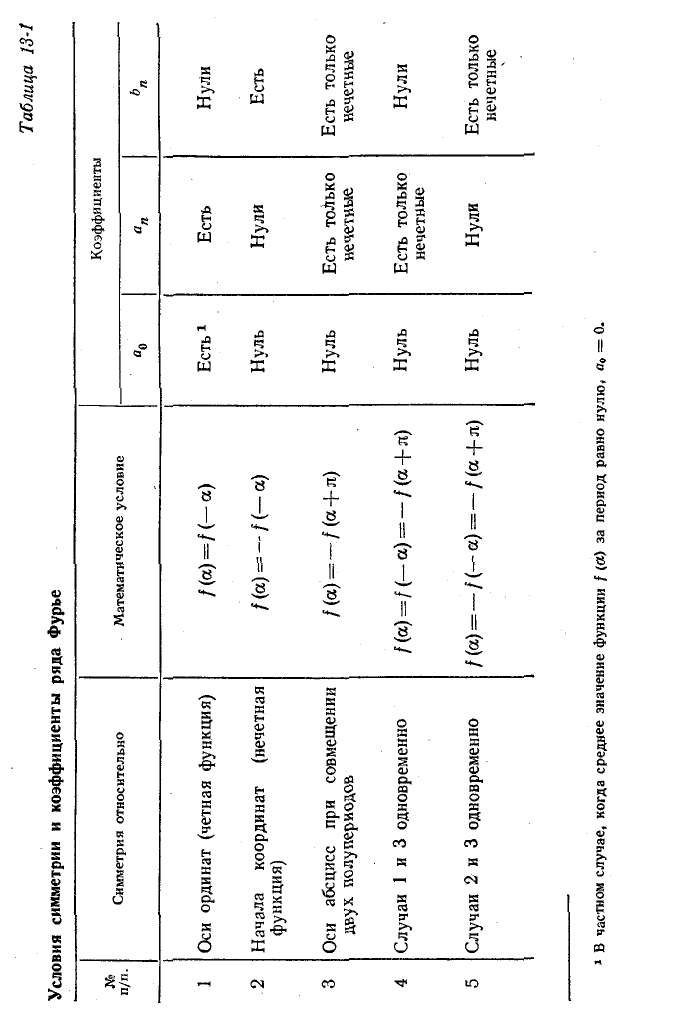
нии (13-10)

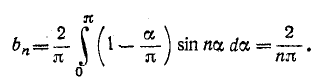
Следовательно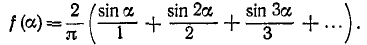

В точках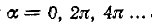 сумма ряда равна нулю, т. е. среднему арифметическому левого и правого предельных значений функции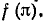

 

Пример 13-2.

Требуется разложить в ряд Фурье знакопеременную прямоугольную функцию, показанную на рис. 13-7. Эта функция удовлетворяет условиям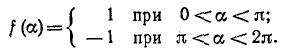
Заданная функция нечетна и, кроме того, симметрична относительно оси абсцисс при совмещении полу периодов. Поэтому в разложении в ряд отсутствуют постоянная составляющая, все косинусоиды и четные синусоиды. Кроме того, выполняется условие 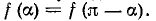Поэтому для определения коэффициентов 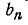воспользуемся формулой (13- 10а):

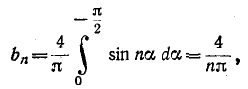
где л — нечетно, отсюда

 

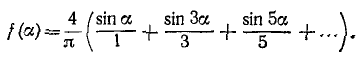
Перенос начала отсчета

Положим, что для некоторой периодической несинусоидальной функции f (а) коэффициенты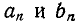 являются заданными, т. е. известно разложение данной функции в ряд Фурье:

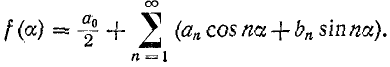
Если сместить начало отсчета на некоторый отрезок р вправо или влево относительно исходного начала координат, то разложение в ряд Фурье относительно новой координатной системы будет получено заменой 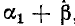, где 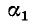— абсцисса в новой системе координат; положительное значение 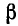соответствует смещению нового начала отсчета вправо, а отрицательное — влево. Итак,

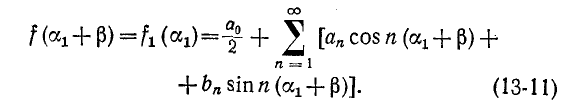
Эта формула позволяет быстро находить разложение в ряд Фурье функции, если известны коэффициенту ряда

Фурье для другой функции, получаемой в результате смещения первой по оси абсцисс на постоянное значение.

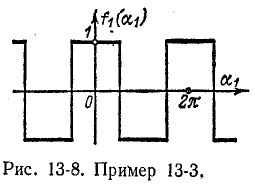
Пример 13-3.

Требуется найти разложение в ряд Фурье функции, изображенной на рис. 13-8, использовав результаты примера 13-2.

Функция на рис. 13-8 получается при переносе начала координат на рис. 13-7 (точка 0) вправо на отрезок 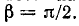Следовательно, в соответствии с (13-11)

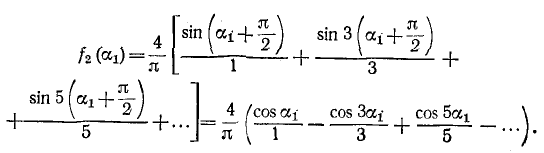
Комплексная форма ряда Фурье

Тригонометрическая форма ряда Фурье может быть преобразована в комплексную следующим образом. Исходя из того, что

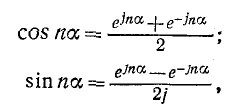
выражение, заключенное в скобки в формуле (13-4), приводится к виду

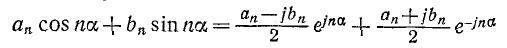
и ряд (13-4) записывается следующим образом:

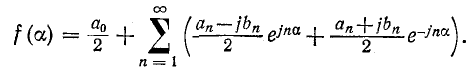
На основании (13-5) и (13-6) 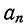четная, а 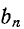нечетная функция относительно n, т. е. 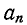сохраняет свой знак при отрицательных значениях n, а 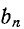меняет его:

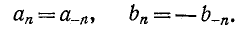
Поэтому с учетом того, что

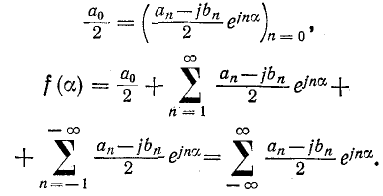
Таким образом, ряд Фурье в комплексной форме имеет
вид:

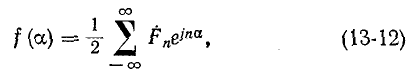
где комплексный коэффициент (комплексная амплитуда)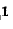согласно (13-5) и (13-6)

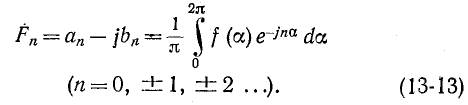
^1. Применявшаяся ранее для представления синусоидальной функции комплексная амплитуда, например 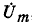, связана с введенным здесь одноименным понятием соотношением

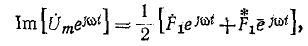
откуда следует: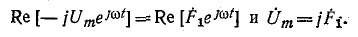

Как указывалось выше, следовательно, ряд (13-12) содержит два бесконечных ряда сопряженных относительно действительной оси векторов, вращающихся в противоположные стороны с угловыми скоростями 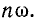Геометрическая сумма каждой пары сопряженных векторов дает только действительное значение (рис. 13-9). В результате суммирования двух бесконечных рядов сопряженных векторов получается действительная функция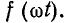

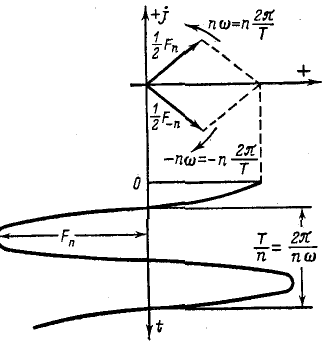
Рис. 13-9. Синусоидальная функция как сумма двух сопряженных векторов, вращающихся в противоположных направлениях.

Применение ряда Фурье к расчету периодического несинусоидального процесса

Пусть требуется найти ток в электрической цепи под воздействием периодической несинусоидальной э. д. с.

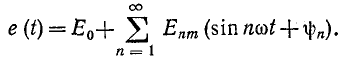
Здесь индексом т обозначены амплитуды гармоник. Если цепь линейна, т. е. параметры г, L, М и С неизменны, то ток в цепи находится методом наложения, путем суммирования токов, создаваемых каждой из слагающих э. д. с. в отдельности:

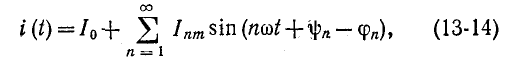
где

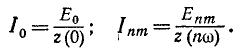
Под z (0) подразумевается сопротивление цепи при частоте, равной нулю, т. е. сопротивление постоянному току; 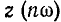— полное сопротивление при частоте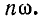

Угол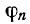 определяется как арктангенс отношения реактивного сопротивления цепи к ее активному сопротивлению при частоте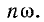

В случае, когда цепь состоит из последовательно соединенных элементов r, L и С,

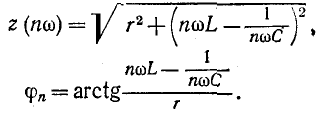
При этом 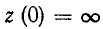, так как цепь для постоянного тока разомкнута.

По мере повышения номера гармоники, т. е. с увеличением частоты то, индуктивное сопротивление 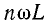растет по закону прямой линии, а емкостное сопротивление 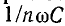убывает по закону гиперболы. Поэтому в цепи, состоящей из последовательно соединенных r и L, гармоники тока выражены слабее, чем в э. д. с. источника. В отличие от этого высшие гармоники тока в цепи, состоящей из r и С могут достигать больших значений.

В смешанной индуктивно-емкостной цепи при 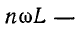 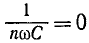наступает явление резонанса для n-й гармоники.

В общем случае цепи, состоящей из элементов r, L и С, как реактивное, так и активное сопротивления являются функциями частоты.

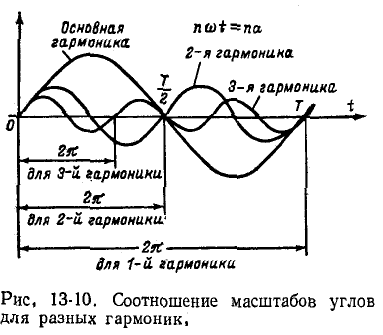
Периоды различных гармоник обратно пропорциональны номеру гармоники. Поэтому если по оси абсцисс откладывается не время t, а угол 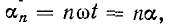то углу а основной гармоники соответствует на той же абсциссе угол на для n-й гармоники (рис. 13-10).

Расчет периодических несинусоидальных токов и напряжений в разветвленных электрических цепях ведется, как правило, в комплексной форме.

Если периодическая несинусоидальная э. д. с. задана в тригонометрической форме ряда Фурье вида (13-8), то э. д. с. и ток могут быть представлены так:

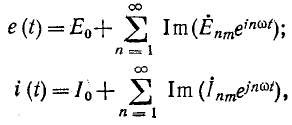
где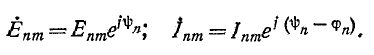

Следовательно, комплексная форма расчета периодического несинусоидального тока заключается в нахождении комплексных амплитуд токов 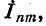соответствующих

заданным комплексным амплитудам э. д. с. 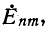для разных значений т. При этом, ввиду того что отдельные слагающие имеют неодинаковые частоты, не складываются непосредственно комплексные амплитуды, а суммируются проекции векторов, вращающихся с разными угловыми

скоростями 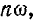т. е. суммируются мгновенные значения отдельных гармоник.

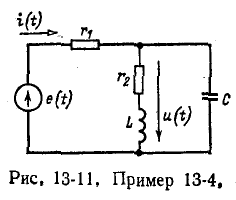
Пример 13-4.

Вычислить суммарный ток в схеме на рис. 13-11. Задано:

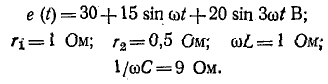
Искомый ток находится методом наложения, т. е, поочередным вычислением постоянной слагающей и гармоник тока с последующим суммированием их.

Сопротивление постоянному току 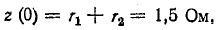Постоянная слагающая тока

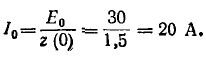
Комплексное Сопротивление цепи для основной частоты 

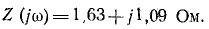
Комплексная амплитуда тока основной частоты 

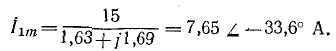
Комплексное сопротивление цепи для утроенной частоты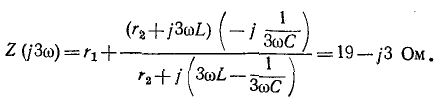

Комплексная амплитуда тока третьей гармоники 

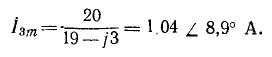
Мгновенное значение суммарного тока

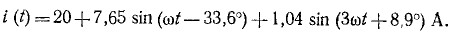
В заключение следует отметить, что в простых случаях установившийся периодический ток может быть получен не только в виде суммы гармоник, но и в более удобной форме аналитического выражения, справедливого для определенного интервала времени (например, полу-периода). Для этого интервала записывается дифференциальное уравнение для тока, которое решается так называемым классическим методом или с помощью преобразования Лапласа . Полученное решение включает в себя неизвестное начальное значение тока, которое затем находят из условия периодичности.

Рассмотрим простой пример. Пусть в цепи последовательно соединенных г и L действует периодическая знакопеременная э. д. с. такого вида, как изображено на рис. 13-7. Тогда для первого полупериода справедливо уравнение 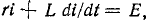решение которого имеет вид

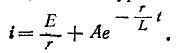При 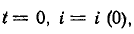следовательно,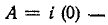

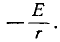 Кривая тока, так же как и кривая э. д. с., будет симметрична

относительно оси времени и не будет иметь скачков благодаря индуктивному характеру цепи. Поэтому 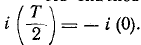то дает:

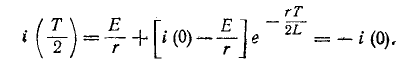
Отсюда находится i (0)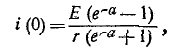

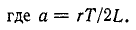
Подставив это в выражение для тока, получим окончательно для первого полупериода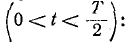

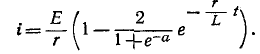
Во втором полупериоде кривая тока будет иметь тот же вид, но противоположный знак.

Итак, периодическая несинусоидальная функция представляется не только в виде ряда Фурье, но и в замкнутой форме, т. е. в виде аналитического выражения с конечным числом слагаемых, справедливого для выбранного интервала времени.

Действующее и среднее значения периодической несинусоидальной функции

Действующее значение периодической несинусоидальной функции / (0 определяется по формуле 

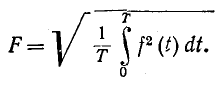
Если функция задана в виде (13-8), то после возведения ее в квадрат интеграл под знаком корня разложится на ряд интегралов, дающих в результате сумму квадрата постоянной слагающей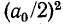, и средних значений квадратов отдельных гармоник (которые согласно равны 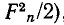, средние же значения удвоенных произведений гармоник разных порядков или произведений постоянной слагающей на отдельные гармоники будут равны нулю.

Следовательно, действующее значение периодической несинусоидальной функции выражается формулой

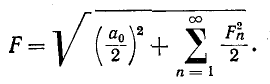
Поскольку 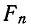— амплитуда n-й гармоники, 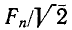— действующее значение гармоники. Таким образом, полученное выражение показывает, что действующее значение периодической несинусоидальной функции равно корню квадратному из суммы квадратов действующих значений гармоник и квадрата постоянной слагающей.

Отсюда следует, что действующее значение функции, представляющее собой сумму гармоник разных частот, не зависит от начальных фаз этих гармоник, а всецело определяется их действующими значениями.

Например, если несинусоидальный ток выражается формулой (13-14), то действующее значение тока равно:

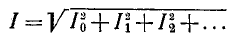
Действующее значение периодической несинусоидальной функции может быть измерено, так же как и при синусоидальных токах, с помощью электроизмерительного прибора электромагнитной, электродинамической, тепло-вой или других систем.

Наряду с понятием действующего значения периодической несинусоидальной функции в электротехнике и радиотехнике пользуются понятием среднего значения функции, взятого по абсолютному значению; последнее в соответствии  выражается интегралом вида

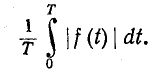
Этот интеграл равен среднему значению функции 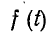за положительный полупериод, если 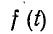имеет одинаковые положительную и отрицательную полуволны:

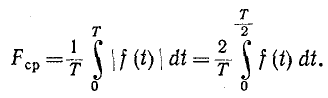
Среднее значение функции за полупериод измеряется с помощью магнитоэлектрического прибора с выпрямителем (магнитоэлектрический прибор без выпрямителя измеряет постоянную слагающую).

Мощность в цепи периодического несинусоидального тока

В соответствии с (2-26) активная мощность равна среднему значению мощности:

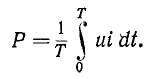
Если вместо и и i подставить их выражения через тригонометрический ряд вида (13-8), то интеграл разложится на ряд интегралов, дающих в результате сумму произведения постоянных слагающих напряжения и тока и средних значений произведений гармоник напряжения и тока одного и того же порядка. Остальные интегралы будут равны нулю, так как они представляют собой средние значения произведений гармоник разных порядков или произведений постоянной слагающей на отдельные гармоники.

Итак,

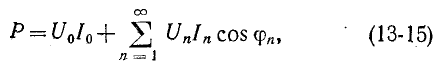
т. е. активная мощность периодического несинусоидального тока равна сумме активных мощностей отдельных гармоник плюс мощность постоянных слагающих.

Иначе говоря, активная мощность от взаимодействия разноименных гармоник напряжений и токов или взаимодействия гармоник с постоянными слагающими равна нулю.

По аналогии с понятием реактивной мощности для синусоидальных функций может быть введено понятие реактивной мощности в цепи с периодическими несинусоидальными величинами. Она определяется как сумма реактивных мощностей отдельных гармоник.

Содержание в одной из кривых (напряжения или тока) гармоник, отсутствующих в другой кривой, не отражается на величинах активной и реактивной мощностей, но повышает действующее значение той функции, которая содержит эти гармоники. Поэтому, если полную мощное ть в рассматриваемой цепи определять как произведение действующих напряжения и тока 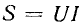, то на основании сказанного можно заключить, что в отличие от синусоидального режима сумма квадратов активной и реактивной мощностей в цепи с периодическими несинусоидальными величинами не равна квадрату полной мощности:

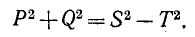
Величина Т носит название мощности искажения; она характеризует степень различия в формах кривых напряжения u и тока i. Если сопротивление цепи активное, то кривые напряжения и тока подобны; при этом Q = 0 и Т = 0.

Пример 13-5.

Вычислить активную мощность, поступающую в цепь в примере 13-4.

е (/) = 30    15 sin <£>l + 20 sin 3to/;

i    (/) = 20 + 7,65 sin (со/ - 33,6°) + 1,04 sin (3co/ + 8,9°).

На основании (13-15)

 

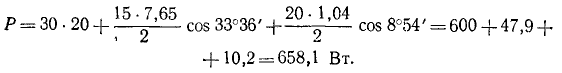
Коэффициенты, характеризующие периодические несинусоидальные функции

По аналогии с синусоидальными функциями отношение активной мощности при несинусоидальных токах к полной мощности называется коэффициентом мощности и обозначается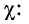

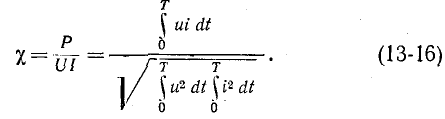
Отношение в правой части (13-16) обращается в единицу только при наличии прямой пропорциональности между u и i.

Положим, что напряжение синусоидально, а ток несинусоидален. В этом случае активная мощность в соответствии с (13-15) определяется мощностью первой гармоники:

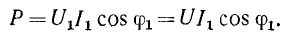
При этом действующее значение тока

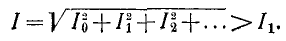
Следовательно, коэффициент мощности

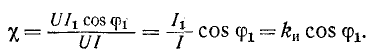
Множитель 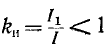называется коэффициентом искажения.

В радиотехнике и электротехнике пользуются также коэффициентами формы кривой 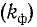и амплитуды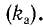

Коэффициент формы кривой определяется как отношение действующего значения функции к среднему,взятому по абсолютному значению,

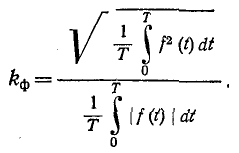
Для синусоиды

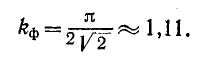
Коэффициент амплитуды определяется как отношение максимального значения функции к действующему значению ее:

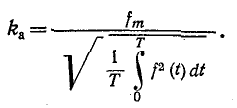
Для синусоиды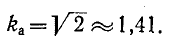
Несинусоидальные кривые напряжения и тока заменяются в ряде случаев эквивалентными синусоидами. Замена производится таким образом, что действующие значения синусоидальных функций принимаются равными действующим значениям несинусоидальных функций, а угол сдвига фаз между эквивалентными синусоидами принимается равным углу 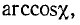где 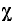определяется из (13-16).

Высшие гармоники в трехфазных электрических цепях

При установившемся режиме в симметричных трехфазных электрических цепях кривые напряжения и тока во второй и третьей фазах аналогичны кривой напряжения и тока первой фазы со сдвигом на треть периода. Так, например, если напряжение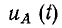 в фазе А выражается функцией

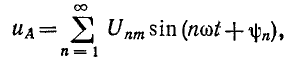
то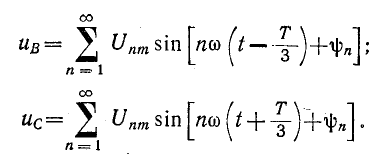

Гармоники порядка, кратного 3 (n = 3, 6, 9, ...), во всех фазах тождественны, так как

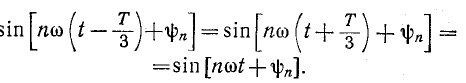
Поэтому они образуют систему напряжений нулевой последовательности.

Гармоники порядка 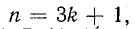где k — любое целое число, т. е. при n = 1, 4, 7, 10, 13 и т. д., образуют симметричную систему напряжений прямой последовательности, так как при этом:

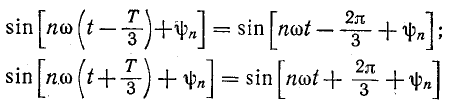
и, следовательно, n-я гармоника в фазе В отстает от n-й гармоники в фазе А на 120°, а в фазе С опережает ее на 120°.

Наконец, гармоники при n = 3k—1, где k — любое целое число, т. е. при n= 2, 5, 8, 11, 14 и т. д., образуют симметричную систему напряжений обратной последовательности, так как при этом:

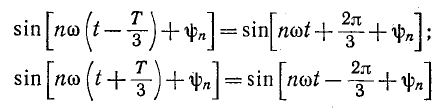
и, следовательно, n-я гармоника в фазе В опережает n-ю гармонику в фазе А на 120°, а в фазе С отстает от нее на 120°. Все эти случаи весьма наглядно представляются на векторных диаграммах, построенных для каждой частоты в отдельности.

В практически встречающихся случаях постоянная составляющая и четные гармоники обычно отсутствуют, и поэтому в дальнейшем можно ограничиться рассмотрением только нечетных гармоник.

При соединении источника электроэнергии и нагрузки звездой с нейтральным проводом в последнем в соответствии с изложенным выше протекает ток, равный сумме всех гармоник с порядковым номером, кратным 3:

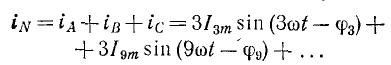
Действующее значение этого тока определится:

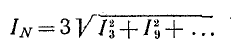
При отсутствии нейтрального провода токи в фазах не содержат гармоник порядка, кратного 3.

В линейных напряжениях, равных разностям фазных напряжений, будут отсутствовать гармоники с порядковым номером, кратным 3.

Ввиду отсутствия в линейных напряжениях гармоник порядка, кратного 3, отношение действующего линейного напряжения к действующему фазному напряжению при несинусоидальных напряжениях получается меньше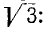

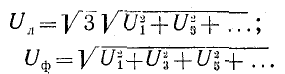
Если фазы генератора соединены треугольником, то во внешней цепи гармоники порядка, кратного 3, отсутствуют; в обмотках же генераторов, соединенных треугольником, действует э. д. с., равная утроенной сумме высших гармоник, кратным 3. Однако она полностью уравновешивается падением напряжения в контуре треугольника от токов этих гармоник. Поэтому гармоники, порядок которых кратен 3, отсутствуют не только в линейных токах и напряжениях, но и в фазных напряжениях.

Разность потенциалов на выводах вторичной обмотки трансформатора напряжения, соединенной разомкнутым треугольником (см. рис. 12-28, в), в случае несинусоидальных фазных напряжений равна:

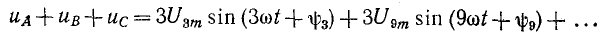
Действующее значение этого напряжения

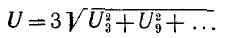
Поэтому даже при симметричной трехфазной электрической цепи возможно появление составляющих токов и напряжений нулевой последовательности, обусловливаемых несинусоидальностью фазных э. д. с. генераторов.